Lý thuyết Ăng-ten - Véc tơ Poynting
Anten bức xạ năng lượng điện từ để truyền hoặc nhận thông tin. Do đó, các điều khoảnEnergy và Powercó liên quan đến các sóng điện từ này và chúng ta phải thảo luận về chúng. Một sóng điện từ có cả điện trường và từ trường.
Xem xét sóng tại bất kỳ thời điểm nào, có thể được xem theo cả hai vectơ. Hình dưới đây cho thấy sự biểu diễn của các thành phần điện trường và từ trường trong sóng điện từ.
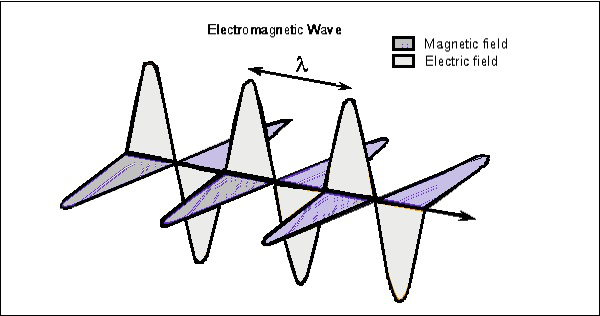
Sóng điện có phương thẳng đứng đối với phương truyền của sóng EM, trong khi sóng từ hướng theo phương ngang. Cả hai trường đều vuông góc với nhau.
Véc tơ Poynting
Véc tơ Poynting mô tả năng lượng của Sóng EM trên một đơn vị thời gian trên một đơn vị diện tích tại bất kỳ thời điểm nhất định nào. John Henry Poynting lần đầu tiên xuất phát vector này vào năm 1884 và do đó nó được đặt theo tên của ông.
Definition - "Véc tơ Poynting cho tốc độ truyền năng lượng trên một đơn vị diện tích"
hoặc là
“Năng lượng mà sóng mang theo trong một đơn vị thời gian trên một đơn vị diện tích được cho bởi vectơ Poynting.”
Véc tơ Poynting được đại diện bởi Ŝ.
Các đơn vị
Đơn vị SI của vectơ Poynting là W/m2.
Biểu thức toán học
Đại lượng dùng để mô tả công suất liên kết với sóng điện từ là công suất tức thời Poynting vector, được định nghĩa là
$$ \ hat {S} = \ hat {E} \ times \ hat {H} $$Ở đâu
$ \ hat {S} $ là vectơ Poynting tức thời (W/m2).
$ \ hat {E} $ là cường độ điện trường tức thời (V/m).
$ \ hat {H} $ là cường độ từ trường tức thời (A/m).
Điểm quan trọng cần lưu ý ở đây là độ lớn của E lớn hơn H trong sóng EM. Tuy nhiên, cả hai đều đóng góp một lượng năng lượng như nhau. Ŝ là vectơ, có cả hướng và độ lớn. Hướng của Ŝ giống với vận tốc của sóng. Độ lớn của nó phụ thuộc vào E và H.
Nguồn gốc của véc tơ Poynting
Để có một ý tưởng rõ ràng về vectơ Poynting, chúng ta hãy xem xét dẫn xuất của vectơ Poynting này, theo quy trình từng bước.
Chúng ta hãy tưởng tượng rằng một sóng EM, đi qua một khu vực (A) vuông góc với trục X mà sóng truyền đi. Trong khi đi qua A, theo thời gian vô cực (dt), sóng truyền được một quãng đường (dx).
$$ dx = C \ dt $$Ở đâu
$$ C = vận tốc \ of \ light = 3 \ times 10 ^ {8} m / s $$ $$ volume, dv = Adx = AC \ dt $$ $$ d \ mu = \ mu \ dv = (\ epsilon_ {0} E ^ {2}) (AC \ dt) $$ $$ = \ epsilon_ {0} AC \ E ^ {2} \ dt $$Do đó, Năng lượng truyền theo thời gian (dt) trên mỗi diện tích (A) là -
$$ S = \ frac {Energy} {Time \ times Area} = \ frac {dW} {dt \ A} = \ frac {\ epsilon_ {0} ACE ^ {2} \ dt} {dt \ A} = \ epsilon_ {0} C \: E ^ {2} $$Từ
$$ \ frac {E} {H} = \ sqrt {\ frac {\ mu_ {0}} {\ epsilon_ {0}}} \ then \ S = \ frac {CB ^ {2}} {\ mu_ {0 }} $$Từ
$$ C = \ frac {E} {H} \ then \ S = \ frac {EB} {\ mu_ {0}} $$ $$ = \ hat {S} = \ frac {1} {\ mu_ {0 }} (\ hat {E} \ hat {H}) $$Ŝ biểu thị vector Poynting.
Phương trình trên cho chúng ta năng lượng trên một đơn vị thời gian, trên một đơn vị diện tích tại bất kỳ khoảng thời gian nhất định nào, được gọi là Poynting vector.