Đồng bộ hóa chủ đề
Đồng bộ hóa luồng có thể được định nghĩa là một phương pháp với sự trợ giúp của chúng ta có thể yên tâm rằng hai hoặc nhiều luồng đồng thời không truy cập đồng thời vào phân đoạn chương trình được gọi là phần quan trọng. Mặt khác, như chúng ta biết rằng phần quan trọng là phần của chương trình nơi tài nguyên được chia sẻ được truy cập. Do đó, chúng ta có thể nói rằng đồng bộ hóa là quá trình đảm bảo rằng hai hoặc nhiều luồng không giao tiếp với nhau bằng cách truy cập các tài nguyên cùng một lúc. Sơ đồ dưới đây cho thấy bốn luồng đang cố gắng truy cập vào phần quan trọng của một chương trình cùng một lúc.
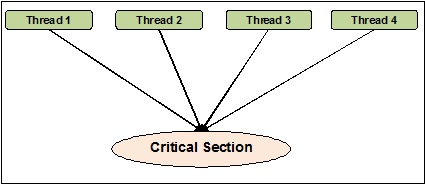
Để làm cho nó rõ ràng hơn, giả sử hai hoặc nhiều chủ đề cố gắng thêm đối tượng trong danh sách cùng một lúc. Hành động này không thể dẫn đến kết thúc thành công vì nó sẽ làm rơi một hoặc tất cả các đối tượng hoặc nó sẽ làm hỏng hoàn toàn trạng thái của danh sách. Ở đây, vai trò của đồng bộ hóa là chỉ một luồng tại một thời điểm có thể truy cập danh sách.
Sự cố trong đồng bộ hóa chuỗi
Chúng tôi có thể gặp sự cố khi triển khai lập trình đồng thời hoặc áp dụng đồng bộ hóa nguyên thủy. Trong phần này, chúng ta sẽ thảo luận về hai vấn đề lớn. Các vấn đề là -
- Deadlock
- Điều kiện của cuộc đua
Điều kiện của cuộc đua
Đây là một trong những vấn đề lớn trong lập trình đồng thời. Truy cập đồng thời vào các tài nguyên được chia sẻ có thể dẫn đến tình trạng chủng tộc. Điều kiện chủng tộc có thể được định nghĩa là sự xuất hiện của một điều kiện khi hai hoặc nhiều luồng có thể truy cập dữ liệu được chia sẻ và sau đó cố gắng thay đổi giá trị của nó cùng một lúc. Do đó, giá trị của các biến có thể không thể đoán trước và thay đổi tùy thuộc vào thời gian chuyển đổi ngữ cảnh của các quy trình.
Thí dụ
Hãy xem xét ví dụ này để hiểu khái niệm về tình trạng chủng tộc -
Step 1 - Trong bước này, chúng ta cần nhập mô-đun luồng -
import threadingStep 2 - Bây giờ, hãy xác định một biến toàn cục, chẳng hạn như x, cùng với giá trị của nó là 0 -
x = 0Step 3 - Bây giờ, chúng ta cần xác định increment_global() hàm, sẽ tăng 1 trong hàm tổng thể x -
def increment_global():
global x
x += 1Step 4 - Trong bước này, chúng tôi sẽ xác định taskofThread()hàm, sẽ gọi hàm increment_global () trong một số lần cụ thể; ví dụ của chúng tôi là 50000 lần -
def taskofThread():
for _ in range(50000):
increment_global()Step 5- Bây giờ, xác định hàm main () trong đó các luồng t1 và t2 được tạo. Cả hai sẽ được bắt đầu với sự trợ giúp của hàm start () và đợi cho đến khi chúng hoàn thành công việc của mình với sự trợ giúp của hàm join ().
def main():
global x
x = 0
t1 = threading.Thread(target= taskofThread)
t2 = threading.Thread(target= taskofThread)
t1.start()
t2.start()
t1.join()
t2.join()Step 6- Bây giờ, chúng ta cần cung cấp phạm vi cho bao nhiêu lần lặp chúng ta muốn gọi hàm main (). Ở đây, chúng tôi đang gọi nó trong 5 lần.
if __name__ == "__main__":
for i in range(5):
main()
print("x = {1} after Iteration {0}".format(i,x))Trong kết quả hiển thị bên dưới, chúng ta có thể thấy ảnh hưởng của điều kiện chủng tộc vì giá trị của x sau mỗi lần lặp được mong đợi là 100000. Tuy nhiên, có rất nhiều sự thay đổi trong giá trị. Điều này là do sự truy cập đồng thời của các luồng vào biến chung x.
Đầu ra
x = 100000 after Iteration 0
x = 54034 after Iteration 1
x = 80230 after Iteration 2
x = 93602 after Iteration 3
x = 93289 after Iteration 4Đối phó với tình trạng cuộc đua bằng cách sử dụng khóa
Như chúng ta đã thấy ảnh hưởng của điều kiện chủng tộc trong chương trình trên, chúng ta cần một công cụ đồng bộ hóa, có thể xử lý tình trạng chủng tộc giữa nhiều luồng. Trong Python,<threading>mô-đun cung cấp lớp Khóa để đối phó với tình trạng chủng tộc. Hơn nữa,Locklớp cung cấp các phương thức khác nhau với sự trợ giúp mà chúng ta có thể xử lý tình trạng chủng tộc giữa nhiều luồng. Các phương pháp được mô tả dưới đây:
phương thức get ()
Phương pháp này được sử dụng để lấy, tức là chặn một khóa. Khóa có thể chặn hoặc không chặn tùy thuộc vào giá trị đúng hoặc sai sau:
With value set to True - Nếu phương thức get () được gọi với True, là đối số mặc định, thì việc thực thi luồng sẽ bị chặn cho đến khi khóa được mở khóa.
With value set to False - Nếu phương thức get () được gọi với False, không phải là đối số mặc định, thì việc thực thi luồng sẽ không bị chặn cho đến khi nó được đặt thành true, tức là cho đến khi nó bị khóa.
phương thức release ()
Phương pháp này được sử dụng để phát hành một khóa. Sau đây là một số nhiệm vụ quan trọng liên quan đến phương pháp này:
Nếu khóa bị khóa, thì release()phương pháp sẽ mở khóa nó. Công việc của nó là cho phép chính xác một luồng tiến hành nếu nhiều luồng bị chặn và chờ khóa được mở khóa.
Nó sẽ nâng cao một ThreadError nếu khóa đã được mở khóa.
Bây giờ, chúng ta có thể viết lại chương trình trên với lớp khóa và các phương thức của nó để tránh điều kiện đua. Chúng ta cần xác định phương thức taskofThread () với đối số lock và sau đó cần sử dụng các phương thức get () và release () để chặn và không chặn các khóa để tránh tình trạng chạy đua.
Thí dụ
Sau đây là ví dụ về chương trình python để hiểu khái niệm khóa để xử lý điều kiện chủng tộc -
import threading
x = 0
def increment_global():
global x
x += 1
def taskofThread(lock):
for _ in range(50000):
lock.acquire()
increment_global()
lock.release()
def main():
global x
x = 0
lock = threading.Lock()
t1 = threading.Thread(target = taskofThread, args = (lock,))
t2 = threading.Thread(target = taskofThread, args = (lock,))
t1.start()
t2.start()
t1.join()
t2.join()
if __name__ == "__main__":
for i in range(5):
main()
print("x = {1} after Iteration {0}".format(i,x))Kết quả sau đây cho thấy ảnh hưởng của tình trạng chủng tộc bị bỏ qua; vì giá trị của x, sau mỗi & mỗi lần lặp, bây giờ là 100000, đúng như kỳ vọng của chương trình này.
Đầu ra
x = 100000 after Iteration 0
x = 100000 after Iteration 1
x = 100000 after Iteration 2
x = 100000 after Iteration 3
x = 100000 after Iteration 4Bế tắc - Vấn đề của các triết gia ăn uống
Bế tắc là một vấn đề rắc rối mà người ta có thể gặp phải khi thiết kế các hệ thống đồng thời. Chúng ta có thể minh họa vấn đề này với sự trợ giúp của vấn đề triết học ăn uống như sau:
Edsger Dijkstra ban đầu đã giới thiệu vấn đề triết học ăn uống, một trong những minh họa nổi tiếng về một trong những vấn đề lớn nhất của hệ thống đồng thời được gọi là bế tắc.
Trong bài toán này, có năm nhà triết học nổi tiếng đang ngồi ở một bàn tròn ăn một số thức ăn từ bát của họ. Năm triết gia có thể dùng nĩa để ăn thức ăn của họ. Tuy nhiên, các triết gia quyết định sử dụng hai nĩa cùng một lúc để ăn thức ăn của họ.
Bây giờ, có hai điều kiện chính cho các triết gia. Thứ nhất, mỗi nhà triết học có thể đang ăn hoặc đang trong trạng thái suy nghĩ và thứ hai, trước tiên họ phải có được cả hai cái nĩa, tức là trái và phải. Vấn đề nảy sinh khi mỗi người trong số năm nhà triết học chọn ngã rẽ trái cùng một lúc. Bây giờ tất cả họ đang chờ đợi một chiếc nĩa phù hợp được miễn phí nhưng họ sẽ không bao giờ từ bỏ chiếc nĩa của mình cho đến khi họ ăn hết thức ăn của mình và chiếc nĩa phù hợp sẽ không bao giờ có sẵn. Do đó, sẽ có một trạng thái bế tắc tại bàn ăn.
Bế tắc trong hệ thống đồng thời
Bây giờ nếu chúng ta thấy, vấn đề tương tự cũng có thể phát sinh trong các hệ thống đồng thời của chúng ta. Các nhánh trong ví dụ trên sẽ là tài nguyên của hệ thống và mỗi nhà triết học có thể đại diện cho quá trình đang cạnh tranh để có được tài nguyên.
Giải pháp với chương trình Python
Giải pháp của vấn đề này có thể được tìm thấy bằng cách chia các triết gia thành hai loại - greedy philosophers và generous philosophers. Chủ yếu là một triết gia tham lam sẽ cố gắng nhặt cái ngã ba bên trái và đợi cho đến khi nó ở đó. Sau đó, anh ta sẽ đợi đến đúng cái nĩa ở đó, nhặt nó lên, ăn và sau đó đặt nó xuống. Mặt khác, một nhà triết học hào phóng sẽ cố gắng nhặt ngã ba bên trái và nếu nó không ở đó, anh ta sẽ đợi và thử lại sau một thời gian. Nếu họ nhận được ngã ba bên trái thì họ sẽ cố gắng đến bên phải. Nếu chúng cũng lấy đúng nĩa thì chúng sẽ ăn và nhả cả hai nĩa. Tuy nhiên, nếu họ không nhận được ngã ba bên phải thì họ sẽ thả ngã ba bên trái.
Thí dụ
Chương trình Python sau đây sẽ giúp chúng ta tìm ra giải pháp cho vấn đề triết gia ăn uống -
import threading
import random
import time
class DiningPhilosopher(threading.Thread):
running = True
def __init__(self, xname, Leftfork, Rightfork):
threading.Thread.__init__(self)
self.name = xname
self.Leftfork = Leftfork
self.Rightfork = Rightfork
def run(self):
while(self.running):
time.sleep( random.uniform(3,13))
print ('%s is hungry.' % self.name)
self.dine()
def dine(self):
fork1, fork2 = self.Leftfork, self.Rightfork
while self.running:
fork1.acquire(True)
locked = fork2.acquire(False)
if locked: break
fork1.release()
print ('%s swaps forks' % self.name)
fork1, fork2 = fork2, fork1
else:
return
self.dining()
fork2.release()
fork1.release()
def dining(self):
print ('%s starts eating '% self.name)
time.sleep(random.uniform(1,10))
print ('%s finishes eating and now thinking.' % self.name)
def Dining_Philosophers():
forks = [threading.Lock() for n in range(5)]
philosopherNames = ('1st','2nd','3rd','4th', '5th')
philosophers= [DiningPhilosopher(philosopherNames[i], forks[i%5], forks[(i+1)%5]) \
for i in range(5)]
random.seed()
DiningPhilosopher.running = True
for p in philosophers: p.start()
time.sleep(30)
DiningPhilosopher.running = False
print (" It is finishing.")
Dining_Philosophers()Chương trình trên sử dụng khái niệm triết gia tham lam và hào phóng. Chương trình cũng đã sử dụngacquire() và release() phương pháp của Lock lớp của <threading>mô-đun. Chúng ta có thể thấy giải pháp trong đầu ra sau:
Đầu ra
4th is hungry.
4th starts eating
1st is hungry.
1st starts eating
2nd is hungry.
5th is hungry.
3rd is hungry.
1st finishes eating and now thinking.3rd swaps forks
2nd starts eating
4th finishes eating and now thinking.
3rd swaps forks5th starts eating
5th finishes eating and now thinking.
4th is hungry.
4th starts eating
2nd finishes eating and now thinking.
3rd swaps forks
1st is hungry.
1st starts eating
4th finishes eating and now thinking.
3rd starts eating
5th is hungry.
5th swaps forks
1st finishes eating and now thinking.
5th starts eating
2nd is hungry.
2nd swaps forks
4th is hungry.
5th finishes eating and now thinking.
3rd finishes eating and now thinking.
2nd starts eating 4th starts eating
It is finishing.