Mã hóa khóa công khai

Mật mã khóa công khai

Không giống như mật mã khóa đối xứng, chúng tôi không tìm thấy lịch sử sử dụng mật mã khóa công khai. Nó là một khái niệm tương đối mới.

Mật mã đối xứng rất phù hợp cho các tổ chức như chính phủ, quân đội và các tập đoàn tài chính lớn có liên quan đến thông tin liên lạc được phân loại.

Với sự lan rộng của các mạng máy tính không an toàn hơn trong vài thập kỷ gần đây, nhu cầu thực sự là sử dụng mật mã ở quy mô lớn hơn. Khóa đối xứng được cho là không thực tế do những thách thức mà nó phải đối mặt đối với việc quản lý khóa. Điều này đã tạo ra các hệ thống mật mã khóa công khai.

Quá trình mã hóa và giải mã được mô tả trong hình minh họa sau:

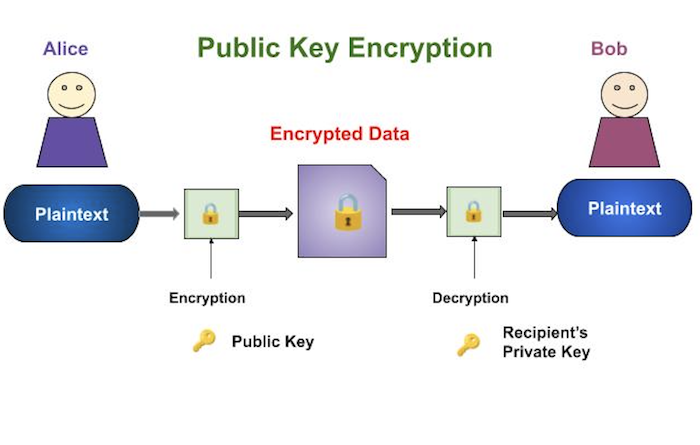
Các thuộc tính quan trọng nhất của lược đồ mã hóa khóa công khai là:

Các khóa khác nhau được sử dụng để mã hóa và giải mã. Đây là một thuộc tính đặt lược đồ này khác với lược đồ mã hóa đối xứng.
Mỗi người nhận sở hữu một khóa giải mã duy nhất, thường được gọi là khóa riêng của mình.
Người nhận cần xuất bản khóa mã hóa, được gọi là khóa công khai của mình.
Một số đảm bảo về tính xác thực của khóa công khai là cần thiết trong chương trình này để tránh bị kẻ thù là người nhận giả mạo. Nói chung, loại hệ thống mật mã này liên quan đến bên thứ ba đáng tin cậy xác nhận rằng một khóa công khai cụ thể chỉ thuộc về một cá nhân hoặc tổ chức cụ thể.
Thuật toán mã hóa đủ phức tạp để ngăn kẻ tấn công suy diễn bản rõ từ bản mã và khóa mã hóa (công khai).
Mặc dù các khóa riêng tư và khóa công khai có liên quan với nhau về mặt toán học, nhưng không khả thi khi tính khóa riêng tư từ khóa công khai. Trên thực tế, phần thông minh của bất kỳ hệ thống mật mã khóa công khai nào là thiết kế mối quan hệ giữa hai khóa.

Có ba loại lược đồ Mã hóa khóa công khai. Chúng ta thảo luận về chúng trong các phần sau -

Hệ thống mật mã RSA

Hệ thống mật mã này là một trong những hệ thống ban đầu. Nó vẫn còn được sử dụng nhiều nhất cho đến ngày nay. Hệ thống được phát minh bởi ba học giảRon Rivest, Adi Shamir, và Len Adleman và do đó, nó được gọi là hệ thống mật mã RSA.

Chúng ta sẽ thấy hai khía cạnh của hệ thống mật mã RSA, thứ nhất là tạo cặp khóa và thứ hai là các thuật toán mã hóa-giải mã.

Tạo cặp khóa RSA

Mỗi người hoặc một bên muốn tham gia giao tiếp bằng cách sử dụng mã hóa cần tạo một cặp khóa, đó là khóa công khai và khóa cá nhân. Quá trình tiếp theo trong quá trình tạo khóa được mô tả dưới đây:

Generate the RSA modulus (n)
- Chọn hai số nguyên tố lớn là p và q.
- Tính n = p * q. Đối với mã hóa mạnh không thể phá vỡ, hãy gọi n là một số lớn, thường tối thiểu là 512 bit.
Find Derived Number (e)
- Con số e phải lớn hơn 1 và nhỏ hơn (p - 1) (q - 1).
- Không được có thừa số chung cho e và (p - 1) (q - 1) trừ 1. Nói cách khác hai số e và (p - 1) (q - 1) là nguyên tố.
Form the public key
- Cặp số (n, e) tạo thành khóa công khai RSA và được công khai.
- Điều thú vị là, mặc dù n là một phần của khóa công khai, khó khăn trong việc phân tích một số nguyên tố lớn đảm bảo rằng kẻ tấn công không thể tìm thấy trong thời gian hữu hạn hai số nguyên tố (p & q) được sử dụng để lấy n. Đây là điểm mạnh của RSA.
Generate the private key
- Khóa riêng d được tính từ p, q và e. Với n và e cho trước, có số duy nhất d.
- Số d là nghịch đảo của e modulo (p - 1) (q - 1). Điều này có nghĩa rằng d là số nhỏ hơn (p - 1) (q - 1) sao cho khi nhân với e, nó có giá trị bằng 1 modulo (p - 1) (q - 1).
- Mối quan hệ này được viết bằng toán học như sau:

ed = 1 mod (p − 1)(q − 1)

Thuật toán Euclid mở rộng lấy p, q và e làm đầu vào và cho d làm đầu ra.

Thí dụ

Dưới đây là một ví dụ về việc tạo cặp Khóa RSA. (Để dễ hiểu, các số nguyên tố p & q lấy ở đây là các giá trị nhỏ. Thực tế, các giá trị này rất cao).

Cho hai số nguyên tố là p = 7 và q = 13. Như vậy, môđun n = pq = 7 x 13 = 91.
Chọn e = 5, là lựa chọn hợp lệ vì không có số nào là nhân tử chung của 5 và (p - 1) (q - 1) = 6 × 12 = 72, trừ 1.
Cặp số (n, e) = (91, 5) tạo thành khóa công khai và có thể được cung cấp cho bất kỳ ai mà chúng tôi muốn có thể gửi cho chúng tôi tin nhắn được mã hóa.
Nhập p = 7, q = 13 và e = 5 vào Thuật toán Euclid mở rộng. Đầu ra sẽ là d = 29.
Kiểm tra xem d được tính là đúng bằng máy tính -

de = 29 × 5 = 145 = 1 mod 72

Do đó, khóa công khai là (91, 5) và khóa riêng là (91, 29).

Mã hóa và Giải mã

Khi cặp khóa đã được tạo, quá trình mã hóa và giải mã tương đối đơn giản và dễ dàng về mặt tính toán.

Điều thú vị là RSA không trực tiếp hoạt động trên các chuỗi bit như trong trường hợp mã hóa khóa đối xứng. Nó hoạt động trên số modulo n. Do đó, cần phải biểu diễn bản rõ là một dãy số nhỏ hơn n.

Mã hóa RSA

Giả sử người gửi muốn gửi một số tin nhắn văn bản cho ai đó có khóa công khai là (n, e).
Sau đó, người gửi biểu diễn bản rõ là một chuỗi các số nhỏ hơn n.
Để mã hóa bản rõ đầu tiên P, là một số modulo n. Quá trình mã hóa là bước toán học đơn giản như:

C = P^e mod n

Nói cách khác, bản mã C bằng bản rõ P nhân với chính nó e lần và sau đó rút gọn modulo n. Điều này có nghĩa là C cũng là một số nhỏ hơn n.
Quay lại ví dụ Tạo khóa của chúng tôi với bản rõ P = 10, chúng tôi nhận được bản mã C -

C = 10⁵ mod 91

Giải mã RSA

Quá trình giải mã RSA cũng rất đơn giản. Giả sử rằng bộ nhận cặp khóa công khai (n, e) đã nhận được một bản mã C.
Người nhận nâng C lên thành sức mạnh của khóa riêng của mình d. Kết quả modulo n sẽ là P bản rõ.

Plaintext = C^d mod n

Quay trở lại ví dụ số của chúng ta, bản mã C = 82 sẽ được giải mã thành số 10 bằng cách sử dụng khóa riêng 29 -

Plaintext = 82²⁹ mod 91 = 10

Phân tích RSA

Tính bảo mật của RSA phụ thuộc vào điểm mạnh của hai chức năng riêng biệt. Hệ thống mật mã RSA là hệ thống mật mã khóa công khai phổ biến nhất dựa trên độ khó thực tế của việc tính toán các số rất lớn.

Encryption Function - Nó được coi là hàm một chiều chuyển bản rõ thành bản mã và nó có thể được đảo ngược chỉ với kiến thức về khóa riêng d.
Key Generation- Khó khăn trong việc xác định khóa cá nhân từ khóa công khai RSA tương đương với việc tính toán mô đun n. Do đó, kẻ tấn công không thể sử dụng kiến thức về khóa công khai RSA để xác định khóa riêng RSA trừ khi anh ta có thể nhân tố n. Nó cũng là một hàm một chiều, đi từ giá trị p & q đến môđun n thì dễ dàng nhưng ngược lại thì không.

Nếu một trong hai chức năng này được chứng minh là không theo một chiều, thì RSA sẽ bị hỏng. Trên thực tế, nếu một kỹ thuật bao thanh toán hiệu quả được phát triển thì RSA sẽ không còn an toàn nữa.

Sức mạnh của mã hóa RSA giảm mạnh so với các cuộc tấn công nếu số p và q không phải là số nguyên tố lớn và / hoặc khóa công khai e được chọn là số nhỏ.

Hệ thống mật mã ElGamal

Cùng với RSA, có các hệ thống mật mã khóa công khai khác được đề xuất. Nhiều người trong số họ dựa trên các phiên bản khác nhau của Bài toán Logarit rời rạc.

Hệ mật mã ElGamal, được gọi là Biến thể đường cong Elliptic, dựa trên Bài toán Logarit rời rạc. Nó suy ra sức mạnh từ giả định rằng không thể tìm thấy logarit rời rạc trong khung thời gian thực tế cho một số nhất định, trong khi phép toán nghịch đảo của lũy thừa có thể được tính toán một cách hiệu quả.

Chúng ta hãy xem qua một phiên bản đơn giản của ElGamal hoạt động với số modulo p. Trong trường hợp các biến thể của đường cong elliptic, nó dựa trên các hệ thống số khá khác nhau.

Thế hệ cặp chìa khóa ElGamal

Mỗi người dùng hệ thống mật mã ElGamal tạo ra cặp khóa thông qua như sau:

Choosing a large prime p. Nói chung, một số nguyên tố có độ dài từ 1024 đến 2048 bit được chọn.
Choosing a generator element g.
- Số này phải từ 1 đến p - 1, nhưng không được là bất kỳ số nào.
- Nó là một bộ sinh của nhóm nhân số nguyên modulo p. Điều này có nghĩa là với mọi số nguyên m đồng nguyên tố với p, có một số nguyên k sao cho g ^k = a mod n.
  
  Ví dụ: 3 là máy phát của nhóm 5 (Z ₅ = {1, 2, 3, 4}).

N	3 ⁿ	3 ⁿ mod 5
1	3	3
2	9	4
3	27	2
4	81	1

Choosing the private key. Khóa riêng x là bất kỳ số nào lớn hơn 1 và nhỏ hơn p − 1.
Computing part of the public key. Giá trị y được tính từ các tham số p, g và khóa riêng x như sau:

y = g^x mod p

Obtaining Public key. Khóa công khai ElGamal bao gồm ba tham số (p, g, y).

Ví dụ, giả sử rằng p = 17 và g = 6 (Có thể khẳng định rằng 6 là máy phát của nhóm Z ₁₇ ). Khóa riêng x có thể là bất kỳ số nào lớn hơn 1 và nhỏ hơn 71, vì vậy chúng tôi chọn x = 5. Giá trị y sau đó được tính như sau:

y = 6⁵ mod 17 = 7

Như vậy khóa riêng là 62 và khóa công khai là (17, 6, 7).

Mã hóa và Giải mã

Việc tạo cặp khóa ElGamal tương đối đơn giản hơn so với quy trình tương đương cho RSA. Nhưng mã hóa và giải mã phức tạp hơn RSA một chút.

Mã hóa ElGamal

Giả sử người gửi muốn gửi một bản rõ cho ai đó có khóa công khai ElGamal là (p, g, y), thì -

Người gửi biểu diễn bản rõ dưới dạng một chuỗi số modulo p.
Để mã hóa bản rõ đầu tiên P, được biểu diễn dưới dạng một modulo số p. Quá trình mã hóa để có được bản mã C như sau:
- Tạo ngẫu nhiên một số k;
- Tính hai giá trị C1 và C2, trong đó -

C1 = g^k mod p
C2 = (P^*y^k) mod p

Gửi bản mã C, bao gồm hai giá trị riêng biệt (C1, C2), được gửi cùng nhau.
Đề cập đến ví dụ tạo khóa ElGamal của chúng tôi ở trên, văn bản rõ P = 13 được mã hóa như sau:
- Tạo ngẫu nhiên một số, giả sử k = 10
- Tính hai giá trị C1 và C2, trong đó -

C1 = 6¹⁰ mod 17
C2 = (13^*7¹⁰) mod 17 = 9

Gửi bản mã C = (C1, C2) = (15, 9).

Giải mã ElGamal

Để giải mã bản mã (C1, C2) bằng khóa riêng x, hai bước sau được thực hiện:
- Tính toán nghịch đảo mô đun của (C1) ^x modulo p, là (C1) ^-x , thường được gọi là hệ số giải mã.
- Lấy bản rõ bằng cách sử dụng công thức sau:

C2 × (C1)^-x mod p = Plaintext

Trong ví dụ của chúng tôi, để giải mã bản mã C = (C1, C2) = (15, 9) sử dụng khóa riêng x = 5, hệ số giải mã là

15^-5 mod 17 = 9

Trích xuất bản rõ P = (9 × 9) mod 17 = 13.

Phân tích ElGamal

Trong hệ thống ElGamal, mỗi người dùng có một khóa riêng x. và cóthree components của khóa công khai - prime modulus p, generator g, and public Y = g^x mod p. Điểm mạnh của ElGamal dựa trên độ khó của bài toán logarit rời rạc.

Kích thước khóa an toàn thường> 1024 bit. Ngày nay, ngay cả khóa dài 2048 bit cũng được sử dụng. Về mặt tốc độ xử lý, Elgamal khá chậm, nó được sử dụng chủ yếu cho các giao thức xác thực chính. Do hiệu quả xử lý cao hơn, các biến thể Đường cong Elliptic của ElGamal ngày càng trở nên phổ biến.

Mật mã đường cong Elliptic (ECC)

Mật mã đường cong Elliptic (ECC) là một thuật ngữ được sử dụng để mô tả một bộ công cụ và giao thức mật mã có tính bảo mật dựa trên các phiên bản đặc biệt của bài toán logarit rời rạc. Nó không sử dụng số modulo p.

ECC dựa trên các tập hợp số được liên kết với các đối tượng toán học được gọi là đường cong elliptic. Có các quy tắc để cộng và tính toán bội số của những số này, cũng giống như các số modulo p.

ECC bao gồm các biến thể của nhiều lược đồ mật mã ban đầu được thiết kế cho các số mô-đun như mã hóa ElGamal và Thuật toán chữ ký số.

Người ta tin rằng bài toán logarit rời rạc khó hơn nhiều khi áp dụng cho các điểm trên đường cong elliptic. Điều này sẽ nhắc chuyển từ số modulo p sang các điểm trên đường cong elliptic. Cũng có thể đạt được mức bảo mật tương đương với các khóa ngắn hơn nếu chúng ta sử dụng các biến thể dựa trên đường cong elliptic.

Các khóa ngắn hơn dẫn đến hai lợi ích:

Dễ dàng quản lý khóa
Tính toán hiệu quả

Những lợi ích này làm cho các biến thể dựa trên đường cong elliptic của lược đồ mã hóa rất hấp dẫn đối với ứng dụng khi tài nguyên máy tính bị hạn chế.

Lược đồ RSA và ElGamal - So sánh

Hãy để chúng tôi so sánh ngắn gọn các lược đồ RSA và ElGamal trên các khía cạnh khác nhau.

RSA	ElGamal
Nó hiệu quả hơn cho việc mã hóa.	Nó hiệu quả hơn để giải mã.
Nó kém hiệu quả hơn cho việc giải mã.	Nó hiệu quả hơn để giải mã.
Đối với một mức bảo mật cụ thể, cần có các khóa dài trong RSA.	Để có cùng mức độ bảo mật, cần có các khóa rất ngắn.
Nó được chấp nhận và sử dụng rộng rãi.	Nó là mới và không phải là rất phổ biến trên thị trường.