Các phương pháp phân loại khác
Ở đây chúng ta sẽ thảo luận về các phương pháp phân loại khác như Giải thuật di truyền, Phương pháp tiếp cận tập hợp thô và Phương pháp tiếp cận tập hợp mờ.
Thuật toán di truyền
Ý tưởng về thuật toán di truyền có nguồn gốc từ quá trình tiến hóa tự nhiên. Trong thuật toán di truyền, trước hết, quần thể ban đầu được tạo ra. Quần thể ban đầu này bao gồm các quy tắc được tạo ngẫu nhiên. Chúng ta có thể biểu diễn mỗi quy tắc bằng một chuỗi bit.
Ví dụ, trong một tập huấn luyện nhất định, các mẫu được mô tả bởi hai thuộc tính Boolean như A1 và A2. Và tập huấn luyện đã cho này chứa hai lớp như C1 và C2.
Chúng tôi có thể mã hóa quy tắc IF A1 AND NOT A2 THEN C2 thành một chuỗi bit 100. Trong biểu diễn bit này, hai bit ngoài cùng bên trái đại diện cho thuộc tính A1 và A2 tương ứng.
Tương tự như vậy, quy tắc IF NOT A1 AND NOT A2 THEN C1 có thể được mã hóa thành 001.
Note- Nếu thuộc tính có K giá trị mà K> 2 thì ta có thể sử dụng K bit để mã hóa các giá trị thuộc tính. Các lớp cũng được mã hóa theo cách tương tự.
Những điểm cần nhớ -
Dựa trên khái niệm về sự sống sót của những người khỏe mạnh nhất, một quần thể mới được hình thành bao gồm các quy tắc phù hợp nhất trong quần thể hiện tại và các giá trị con cái của các quy tắc này.
Tính phù hợp của một quy tắc được đánh giá bằng độ chính xác phân loại của nó trên một tập hợp các mẫu đào tạo.
Các toán tử di truyền như trao đổi chéo và đột biến được áp dụng để tạo ra con cái.
Trong phép lai chéo, chuỗi con từ cặp quy tắc được đổi chỗ để tạo thành một cặp quy tắc mới.
Trong đột biến, các bit được chọn ngẫu nhiên trong chuỗi quy tắc được đảo ngược.
Phương pháp tiếp cận tập hợp thô
Chúng ta có thể sử dụng cách tiếp cận tập hợp thô để khám phá mối quan hệ cấu trúc trong dữ liệu không chính xác và nhiễu.
Note- Cách tiếp cận này chỉ có thể được áp dụng trên các thuộc tính có giá trị rời rạc. Do đó, các thuộc tính có giá trị liên tục phải được loại bỏ trước khi sử dụng.
Lý thuyết tập hợp thô dựa trên việc thiết lập các lớp tương đương trong dữ liệu đào tạo đã cho. Các bộ giá trị tạo thành lớp tương đương là không thể nhận thấy. Nó có nghĩa là các mẫu giống hệt nhau về các thuộc tính mô tả dữ liệu.
Có một số lớp trong dữ liệu thế giới thực đã cho, không thể phân biệt được về các thuộc tính có sẵn. Chúng ta có thể sử dụng các bộ thô đểroughly định nghĩa các lớp như vậy.
Đối với một lớp C nhất định, định nghĩa tập hợp thô được xấp xỉ bởi hai tập hợp như sau:
Lower Approximation of C - Giá trị xấp xỉ dưới của C bao gồm tất cả các bộ dữ liệu mà dựa trên kiến thức về thuộc tính, chắc chắn thuộc về lớp C.
Upper Approximation of C - Giá trị xấp xỉ trên của C bao gồm tất cả các bộ giá trị mà dựa trên kiến thức về các thuộc tính, không thể được mô tả là không thuộc C.
Biểu đồ sau đây cho thấy xấp xỉ trên và xấp xỉ dưới của lớp C -

Phương pháp tiếp cận tập hợp mờ
Lý thuyết tập hợp mờ còn được gọi là Lý thuyết khả năng. Lý thuyết này được Lotfi Zadeh đề xuất vào năm 1965 như một giải pháp thay thếtwo-value logic và probability theory. Lý thuyết này cho phép chúng ta làm việc ở mức độ trừu tượng cao. Nó cũng cung cấp cho chúng tôi phương tiện để xử lý việc đo lường dữ liệu không chính xác.
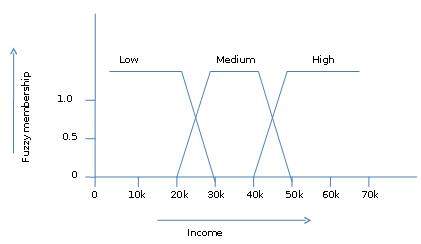
Lý thuyết tập mờ cũng cho phép chúng ta giải quyết các sự kiện mơ hồ hoặc không chính xác. Ví dụ, chính xác là trở thành thành viên của một nhóm có thu nhập cao (ví dụ: nếu 50.000 đô la cao thì khoảng 49.000 đô la và 48.000 đô la). Không giống như tập CRISP truyền thống trong đó phần tử thuộc S hoặc phần bù của nó nhưng trong lý thuyết tập mờ, phần tử có thể thuộc nhiều hơn một tập mờ.
Ví dụ: giá trị thu nhập $ 49,000 thuộc cả tập mờ trung bình và cao nhưng ở các mức độ khác nhau. Ký hiệu tập hợp mờ cho giá trị thu nhập này như sau:
mmedium_income($49k)=0.15 and mhigh_income($49k)=0.96trong đó 'm' là hàm thành viên hoạt động trên các tập mờ tương ứng của medium_income và high_income. Ký hiệu này có thể được hiển thị theo sơ đồ như sau: