Mạch điện tử - Bộ chỉnh lưu
Bất cứ khi nào có nhu cầu chuyển đổi nguồn AC sang DC, một mạch chỉnh lưu sẽ xuất hiện để giải cứu. Một diode tiếp giáp PN đơn giản hoạt động như một bộ chỉnh lưu. Các điều kiện phân cực thuận và phân cực ngược của diode thực hiện chỉnh lưu.
Chỉnh lưu
Dòng điện xoay chiều có tính chất thay đổi trạng thái liên tục. Điều này được hiểu bằng cách quan sát sóng hình sin mà dòng điện xoay chiều được chỉ ra. Nó tăng theo hướng tích cực lên đến giá trị cực đại dương, giảm từ đó xuống bình thường và một lần nữa chuyển sang phần âm và đạt đến đỉnh âm và một lần nữa trở lại bình thường và tiếp tục.
Trong quá trình hình thành sóng của nó, chúng ta có thể quan sát thấy sóng đi theo hướng dương và âm. Trên thực tế, nó thay đổi hoàn toàn và do đó có tên là dòng điện xoay chiều.
Nhưng trong quá trình chỉnh lưu, dòng điện xoay chiều này được biến đổi thành dòng điện một chiều. Sóng chảy theo cả chiều dương và âm cho đến lúc đó, sẽ bị giới hạn hướng của nó chỉ theo hướng dương, khi được chuyển đổi thành DC. Do đó dòng điện chỉ được phép chạy theo chiều dương và chống lại theo chiều âm, giống như trong hình dưới đây.

Mạch chỉnh lưu được gọi là Rectifier circuit. Một diode được sử dụng như một bộ chỉnh lưu, để cấu tạo một mạch chỉnh lưu.
Các loại mạch chỉnh lưu
Có hai loại mạch chỉnh lưu chính, tùy thuộc vào đầu ra của chúng. họ đang
- Bộ chỉnh lưu nửa sóng
- Bộ chỉnh lưu toàn sóng
Mạch chỉnh lưu nửa sóng chỉ chỉnh lưu nửa chu kỳ dương của nguồn cung cấp đầu vào trong khi mạch chỉnh lưu toàn sóng chỉnh lưu cả nửa chu kỳ dương và âm của nguồn cung cấp đầu vào.
Bộ chỉnh lưu nửa sóng
Bản thân tên bộ chỉnh lưu nửa sóng nói rằng rectification được thực hiện chỉ cho halfcủa chu kỳ. Tín hiệu AC được đưa ra thông qua một biến áp đầu vào có bước lên hoặc xuống tùy theo cách sử dụng. Chủ yếu là một biến áp bước xuống được sử dụng trong các mạch chỉnh lưu, để giảm điện áp đầu vào.
Tín hiệu đầu vào được cấp cho máy biến áp được đưa qua một diode tiếp giáp PN đóng vai trò như một bộ chỉnh lưu. Diode này chuyển đổi điện áp xoay chiều thành xung một chiều chỉ trong nửa chu kỳ dương của đầu vào. Cuối đoạn mạch mắc một điện trở tải. Hình dưới đây cho thấy mạch của một bộ chỉnh lưu nửa sóng.
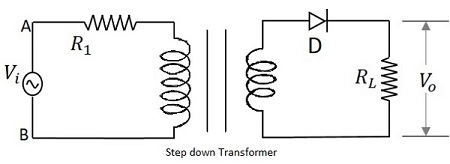
Làm việc của một HWR
Tín hiệu đầu vào được cấp cho máy biến áp để giảm mức điện áp. Đầu ra từ máy biến áp được đưa đến điốt hoạt động như một bộ chỉnh lưu. Diode này được BẬT (dẫn) trong nửa chu kỳ tích cực của tín hiệu đầu vào. Do đó có dòng điện chạy trong mạch và sẽ có sự sụt giảm điện áp trên điện trở tải. Diode bị TẮT (không dẫn điện) trong nửa chu kỳ âm và do đó đầu ra cho nửa chu kỳ âm sẽ là, $ i_ {D} = 0 $ và $ V_ {o} = 0 $.
Do đó đầu ra chỉ hiện diện cho nửa chu kỳ dương của điện áp đầu vào (bỏ qua dòng rò ngược). Đầu ra này sẽ tạo xung được đưa qua điện trở tải.
Các dạng sóng của HWR
Các dạng sóng đầu vào và đầu ra như trong hình sau.
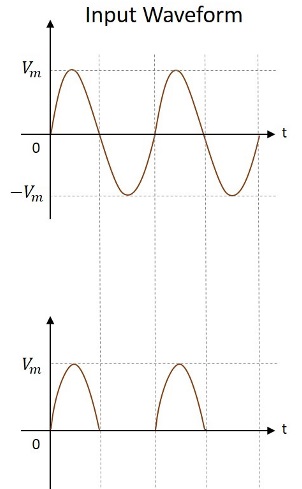
Do đó đầu ra của bộ chỉnh lưu nửa sóng là một xung dc. Chúng ta hãy thử phân tích mạch trên bằng cách hiểu một vài giá trị nhận được từ đầu ra của bộ chỉnh lưu nửa sóng.
Phân tích bộ chỉnh lưu nửa sóng
Để phân tích mạch chỉnh lưu nửa sóng, chúng ta hãy xem xét phương trình của điện áp đầu vào.
$$ v_ {i} = V_ {m} \ sin \ omega t $$
$ V_ {m} $ là giá trị lớn nhất của điện áp cung cấp.
Hãy giả sử rằng diode là lý tưởng.
- Điện trở theo chiều thuận, tức là ở trạng thái BẬT là $ R_f $.
- Điện trở theo hướng ngược lại, tức là, ở trạng thái TẮT là $ R_r $.
Hiện tại i trong diode hoặc điện trở tải $ R_L $ được cung cấp bởi
$ i = I_m \ sin \ omega t \ quad cho \ quad 0 \ leq \ omega t \ leq 2 \ pi $
$ i = 0 \ quad \ quad \ quad \ quad cho \ quad \ pi \ leq \ omega t \ leq 2 \ pi $
Ở đâu
$$ I_m = \ frac {V_m} {R_f + R_L} $$
Dòng điện đầu ra DC
Hiện tại trung bình $ I_ {dc} $ được cung cấp bởi
$$ I_ {dc} = \ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} i \: d \ left (\ omega t \ right) $$
$$ = \ frac {1} {2 \ pi} \ left [\ int_ {0} ^ {\ pi} I_m \ sin \ omega t \: d \ left (\ omega t \ right) + \ int_ {0} ^ {2 \ pi} 0 \: d \ left (\ omega t \ right) \ right] $$
$$ = \ frac {1} {2 \ pi} \ left [I_m \ left \ {- \ cos \ omega t \ right \} _ {0} ^ {\ pi} \ right] $$
$$ = \ frac {1} {2 \ pi} \ left [I_m \ left \ {+ 1- \ left (-1 \ right) \ right \} \ right] = \ frac {I_m} {\ pi} = 0,318 I_m $$
Thay thế giá trị của $ I_m $, chúng ta nhận được
$$ I_ {dc} = \ frac {V_m} {\ pi \ left (R_f + R_L \ right)} $$
Nếu $ R_L >> R_f $, thì
$$ I_ {dc} = \ frac {V_m} {\ pi R_L} = 0,318 \ frac {V_m} {R_L} $$
Điện áp đầu ra DC
Điện áp đầu ra DC được cung cấp bởi
$$ V_ {dc} = I_ {dc} \ times R_L = \ frac {I_m} {\ pi} \ times R_L $$
$$ = \ frac {V_m \ times R_L} {\ pi \ left (R_f + R_L \ right)} = \ frac {V_m} {\ pi \ left \ {1+ \ left (R_f / R_L \ right) \ right \}} $$
Nếu $ R_L >> R_f $, thì
$$ V_ {dc} = \ frac {V_m} {\ pi} = 0,318 V_m $$
RMS hiện tại và điện áp
Giá trị của dòng điện RMS được đưa ra bởi
$$ I_ {rms} = \ left [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} i ^ {2} d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$
$$ I_ {rms} = \ left [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} I_ {m} ^ {2} \ sin ^ {2} \ omega t \: d \ left (\ omega t \ right) + \ frac {1} {2 \ pi} \ int _ {\ pi} ^ {2 \ pi} 0 \: d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$
$$ = \ left [\ frac {I_ {m} ^ {2}} {2 \ pi} \ int_ {0} ^ {\ pi} \ left (\ frac {1- \ cos 2 \ omega t} {2 } \ right) d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$
$$ = \ left [\ frac {I_ {m} ^ {2}} {4 \ pi} \ left \ {\ left (\ omega t \ right) - \ frac {\ sin 2 \ omega t} {2} \ right \} _ {0} ^ {\ pi} \ right] ^ {\ frac {1} {2}} $$
$$ = \ left [\ frac {I_ {m} ^ {2}} {4 \ pi} \ left \ {\ pi - 0 - \ frac {\ sin 2 \ pi} {2} + \ sin 0 \ right \} \ right] ^ {\ frac {1} {2}} $$
$$ = \ left [\ frac {I_ {m} ^ {2}} {4 \ pi} \ right] ^ {\ frac {1} {2}} = \ frac {I_m} {2} $$
$$ = \ frac {V_m} {2 \ left (R_f + R_L \ right)} $$
Điện áp RMS trên tải là
$$ V_ {rms} = I_ {rms} \ times R_L = \ frac {V_m \ times R_L} {2 \ left (R_f + R_L \ right)} $$
$$ = \ frac {V_m} {2 \ left \ {1+ \ left (R_f / R_L \ right) \ right \}} $$
Nếu $ R_L >> R_f $, thì
$$ V_ {rms} = \ frac {V_m} {2} $$
Hiệu quả chỉnh lưu
Bất kỳ mạch nào cũng cần phải hoạt động hiệu quả để có đầu ra tốt hơn. Để tính toán hiệu suất của bộ chỉnh lưu nửa sóng, tỷ số giữa công suất đầu ra và công suất đầu vào phải được xem xét.
Hiệu suất chỉnh lưu được định nghĩa là
$$ \ eta = \ frac {dcpower \: \: đã giao \: \: tới \: \: \: \: tải} {acinput \: \: power \: \: từ \: \: biến áp \: \ : Secondary} = \ frac {P_ {ac}} {P_ {dc}} $$
Hiện nay
$$ P_ {dc} = \ left ({I_ {dc}} \ right) ^ 2 \ times R_L = \ frac {I_m R_L} {\ pi ^ 2} $$
Thêm nữa
$$ P_ {ac} = P_a + P_r $$
Ở đâu
$ P_a = power \: tiêu tan \: tại \: điểm giao nhau \: của \: diode $
$$ = I_ {rms} ^ {2} \ times R_f = \ frac {I_ {m} ^ {2}} {4} \ times R_f $$
Và
$$ P_r = power \: tiêu tan \: trong \: \: tải \: kháng $$
$$ = I_ {rms} ^ {2} \ times R_L = \ frac {I_ {m} ^ {2}} {4} \ times R_L $$
$$ P_ {ac} = \ frac {I_ {m} ^ {2}} {4} \ times R_f + \ frac {I_ {m} ^ {2}} {4} \ times R_L = \ frac {I_ {m } ^ {2}} {4} \ left (R_f + R_L \ right) $$
Từ cả hai biểu thức của $ P_ {ac} $ và $ P_ {dc} $, chúng ta có thể viết
$$ \ eta = \ frac {I_ {m} ^ {2} R_L / \ pi ^ 2} {I_ {m} ^ {2} \ left (R_f + R_L \ right) / 4} = \ frac {4} {\ pi ^ 2} \ frac {R_L} {\ left (R_f + R_L \ right)} $$
$$ = \ frac {4} {\ pi ^ 2} \ frac {1} {\ left \ {1+ \ left (R_f / R_L \ right) \ right \}} = \ frac {0.406} {\ left \ {1+ \ left (R_f / R_L \ right) \ right \}} $$
Phần trăm hiệu suất chỉnh lưu
$$ \ eta = \ frac {40.6} {\ lbrace1 + \ lgroup \: R_ {f} / R_ {L} \ rgroup \ rbrace} $$
Về mặt lý thuyết, giá trị lớn nhất của hiệu suất bộ chỉnh lưu của bộ chỉnh lưu nửa sóng là 40,6% khi $ R_ {f} / R_ {L} = 0 $
Hơn nữa, hiệu quả có thể được tính theo cách sau
$$ \ eta = \ frac {P_ {dc}} {P_ {ac}} = \ frac {\ left (I_ {dc} \ right) ^ 2R_L} {\ left (I_ {rms} \ right) ^ 2R_L} = \ frac {\ left (V_ {dc} / R_L \ right) ^ 2R_L} {\ left (V_ {rms} / R_L \ right) ^ 2R_L} = \ frac {\ left (V_ {dc} \ right) ^ 2} {\ left (V_ {rms} \ right) ^ 2} $$
$$ = \ frac {\ left (V_m / \ pi \ right) ^ 2} {\ left (V_m / 2 \ right) ^ 2} = \ frac {4} {\ pi ^ 2} = 0,406 $$
$$ = 40,6 \% $$
Yếu tố Ripple
Đầu ra được chỉnh lưu chứa một số lượng thành phần AC có trong nó, ở dạng gợn sóng. Điều này được hiểu bằng cách quan sát dạng sóng đầu ra của bộ chỉnh lưu nửa sóng. Để có được một dc tinh khiết, chúng ta cần phải có một ý tưởng về thành phần này.
Hệ số gợn sóng cho biết mức độ nghiêm trọng của đầu ra được điều chỉnh. Nó được ký hiệu lày. Điều này có thể được định nghĩa là tỷ số giữa giá trị hiệu dụng của thành phần xoay chiều của điện áp hoặc dòng điện với giá trị trực tiếp hoặc giá trị trung bình.
$$ \ gamma = \ frac {ripple \ :tage} {dc \: áp} = \ frac {rms \: value \: of \: compleonent} {dcvalue \: of \: wave} = \ frac {\ left ( V_r \ right) _ {rms}} {v_ {dc}} $$
Đây,
$$ \ left (V_r \ right) _ {rms} = \ sqrt {V_ {rms} ^ {2} -V_ {dc} ^ {2}} $$
Vì thế,
$$ \ gamma = \ frac {\ sqrt {V_ {rms} ^ {2} -V_ {dc} ^ {2}}} {V_ {dc}} = \ sqrt {\ left (\ frac {V_ {rms} } {V_ {dc}} \ right) ^ 2-1} $$
Hiện nay,
$$ V_ {rms} = \ left [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} V_ {m} ^ {2} \ sin ^ 2 \ omega t \: d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$
$$ = V_m \ left [\ frac {1} {4 \ pi} \ int_ {0} ^ {\ pi} \ left (1- \ cos2 \: \ omega t \ right) d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} = \ frac {V_m} {2} $$
$$ V_ {dc} = V_ {av} = \ frac {1} {2 \ pi} \ left [\ int_ {0} ^ {\ pi} V_m \ sin \ omega t \: d \ left (\ omega t \ right) + \ int_ {0} ^ {2 \ pi} 0.d \ left (\ omega t \ right) \ right] $$
$$ = \ frac {V_m} {2 \ pi} \ left [- \ cos \ omega t \ right] _ {0} ^ {\ pi} = \ frac {V_m} {\ pi} $$
$$ \ gamma = \ sqrt {\ left [\ left \ {\ frac {\ left (V_m / 2 \ right)} {\ left (V_m / \ pi \ right)} \ right \} ^ 2-1 \ right ]} = \ sqrt {\ left \ {\ left (\ frac {\ pi} {2} \ right) ^ 2-1 \ right \}} = 1,21 $$
Yếu tố gợn sóng cũng được định nghĩa là
$$ \ gamma = \ frac {\ left (I_r \ right) _ {rms}} {I_ {dc}} $$
Vì giá trị của hệ số gợn sóng hiện diện trong bộ chỉnh lưu nửa sóng là 1,21, điều đó có nghĩa là lượng điện xoay chiều hiện diện trong đầu ra là $ 121 \% $ của điện áp một chiều
Quy định
Dòng điện qua tải có thể thay đổi tùy thuộc vào điện trở tải. Nhưng ngay cả ở điều kiện như vậy, chúng tôi hy vọng điện áp đầu ra của chúng tôi được đưa qua điện trở tải đó, là không đổi. Vì vậy, điện áp của chúng ta cần được điều chỉnh ngay cả trong các điều kiện tải khác nhau.
Sự thay đổi của điện áp đầu ra DC với sự thay đổi của dòng tải DC được định nghĩa là Regulation. Quy định phần trăm được tính như sau.
$$ Percentage \: quy định = \ frac {V_ {no \: load} -V_ {full \: load}} {V_ {full \: load}} \ times 100 \% $$
Quy định phần trăm càng thấp thì nguồn cung cấp điện càng tốt. Một nguồn cung cấp điện lý tưởng sẽ có quy định phần trăm bằng không.
Hệ số sử dụng máy biến áp
Nguồn một chiều được cung cấp cho tải, trong mạch chỉnh lưu quyết định định mức của máy biến áp được sử dụng trong mạch.
Vì vậy, hệ số sử dụng máy biến áp được định nghĩa là
$$ TUF = \ frac {dcpower \: to \: be \: delivery \: to \: the \: load} {acrating \: of \: the \: MBA \: Secondary} $$
$$ = \ frac {P_ {dc}} {P_ {ac \ left (đã xếp hạng \ phải)}} $$
Theo lý thuyết về máy biến áp, điện áp định mức của cuộn thứ cấp sẽ là
$$ V_m / \ sqrt {2} $$
Điện áp RMS thực tế chạy qua nó sẽ là
$$ I_m / 2 $$
vì thế
$$ TUF = \ frac {\ left (I_m / \ pi \ right) ^ 2 \ times R_L} {\ left (V_m / \ sqrt {2} \ right) \ times \ left (I_m / 2 \ right)} $ $
Nhưng
$$ V_m = I_m \ left (R_f + R_L \ right) $$
vì thế
$$ TUF = \ frac {\ left (I_m / \ pi \ right) ^ 2 \ times R_L} {\ left \ {I_m \ left (R_f + R_L \ right) / \ sqrt {2} \ right \} \ lần \ left (I_m / 2 \ right)} $$
$$ = \ frac {2 \ sqrt {2}} {\ pi ^ 2} \ times \ frac {R_L} {\ left (R_f + R_L \ right)} $$
$$ = \ frac {2 \ sqrt {2}} {\ pi ^ 2} = 0,287 $$
Điện áp nghịch đảo đỉnh
Một diode khi được kết nối theo phân cực ngược, phải được làm việc ở mức điện áp được kiểm soát. Nếu điện áp an toàn vượt quá, diode sẽ bị hỏng. Do đó, điều rất quan trọng là phải biết về điện áp tối đa đó.
Điện áp nghịch đảo tối đa mà điốt có thể chịu được mà không bị phá hủy được gọi là Peak Inverse Voltage. Nói ngắn gọn,PIV.
Ở đây PIV không là gì khác ngoài Vm
Yếu tố hình thức
Đây có thể hiểu là giá trị trung bình toán học của các giá trị tuyệt đối của tất cả các điểm trên dạng sóng. Cácform factorđược định nghĩa là tỷ lệ giữa giá trị RMS với giá trị trung bình. Nó được ký hiệu làF.
$$ F = \ frac {rms \: value} {average \: value} = \ frac {I_m / 2} {I_m / \ pi} = \ frac {0.5I_m} {0.318I_m} = 1.57 $$
Hệ số đỉnh
Giá trị của đỉnh trong gợn sóng phải được xem xét để biết hiệu quả của việc điều chỉnh. Giá trị của hệ số đỉnh cũng là một yếu tố quan trọng cần xem xét.Peak factor được định nghĩa là tỷ số giữa giá trị đỉnh và giá trị RMS.
vì thế
$$ Hệ số đỉnh = \ frac {Đỉnh \: value} {rms \: value} = \ frac {V_m} {V_m / 2} = 2 $$
Tất cả những điều này là các thông số quan trọng cần được xem xét khi nghiên cứu về một bộ chỉnh lưu.