Thuật toán di truyền - Hướng dẫn nhanh

Thuật toán di truyền (GA) là một kỹ thuật tối ưu hóa dựa trên tìm kiếm dựa trên các nguyên tắc của Genetics and Natural Selection. Nó thường được sử dụng để tìm các giải pháp tối ưu hoặc gần tối ưu cho các vấn đề khó mà nếu không sẽ mất cả đời để giải quyết. Nó thường được sử dụng để giải quyết các vấn đề tối ưu hóa, trong nghiên cứu và học máy.

Giới thiệu về Tối ưu hóa

Tối ưu hóa là quá trình making something better. Trong bất kỳ quá trình nào, chúng ta có một tập hợp các đầu vào và một tập hợp các đầu ra như trong hình sau.

Tối ưu hóa đề cập đến việc tìm kiếm các giá trị của đầu vào theo cách mà chúng tôi nhận được giá trị đầu ra "tốt nhất". Định nghĩa "tốt nhất" thay đổi theo từng vấn đề, nhưng trong thuật ngữ toán học, nó đề cập đến việc tối đa hóa hoặc tối thiểu hóa một hoặc nhiều hàm mục tiêu, bằng cách thay đổi các tham số đầu vào.

Tập hợp tất cả các giải pháp hoặc giá trị có thể có mà đầu vào có thể chiếm không gian tìm kiếm. Trong không gian tìm kiếm này, nằm một điểm hoặc một tập hợp các điểm đưa ra giải pháp tối ưu. Mục đích của tối ưu hóa là tìm điểm đó hoặc tập hợp các điểm trong không gian tìm kiếm.

Thuật toán di truyền là gì?

Thiên nhiên luôn là nguồn cảm hứng dồi dào cho cả nhân loại. Thuật toán di truyền (GA) là thuật toán tìm kiếm dựa trên các khái niệm về chọn lọc tự nhiên và di truyền. GA là một tập con của một nhánh tính toán lớn hơn nhiều, được gọi làEvolutionary Computation.

GA được phát triển bởi John Holland và các sinh viên và đồng nghiệp của ông tại Đại học Michigan, nổi bật nhất là David E. Goldberg và kể từ đó đã được thử nghiệm trên các vấn đề tối ưu hóa khác nhau với mức độ thành công cao.

Trong GAs, chúng tôi có pool or a population of possible solutionscho vấn đề đã cho. Các giải pháp này sau đó trải qua quá trình tái tổ hợp và đột biến (giống như trong di truyền tự nhiên), tạo ra những đứa trẻ mới và quá trình này được lặp lại qua nhiều thế hệ khác nhau. Mỗi cá thể (hoặc giải pháp ứng cử viên) được chỉ định một giá trị phù hợp (dựa trên giá trị hàm mục tiêu của nó) và các cá thể phù hợp có cơ hội giao phối cao hơn và mang lại nhiều cá thể "hợp lứa" hơn. Điều này phù hợp với Lý thuyết của Darwin về “Sự sống sót của những người khỏe mạnh nhất”.

Bằng cách này, chúng tôi tiếp tục “phát triển” các cá nhân hoặc giải pháp tốt hơn qua nhiều thế hệ, cho đến khi chúng tôi đạt được tiêu chí dừng.

Các thuật toán di truyền về bản chất là đủ ngẫu nhiên, nhưng chúng hoạt động tốt hơn nhiều so với tìm kiếm cục bộ ngẫu nhiên (trong đó chúng tôi chỉ thử các giải pháp ngẫu nhiên khác nhau, theo dõi các giải pháp tốt nhất cho đến nay), vì chúng cũng khai thác thông tin lịch sử.

Ưu điểm của GAs

GA có nhiều lợi thế khác nhau đã làm cho chúng trở nên vô cùng phổ biến. Chúng bao gồm -

Không yêu cầu bất kỳ thông tin phái sinh nào (có thể không có sẵn cho nhiều vấn đề trong thế giới thực).
Nhanh hơn và hiệu quả hơn so với các phương pháp truyền thống.
Có khả năng song song rất tốt.
Tối ưu hóa cả các chức năng liên tục và rời rạc và cả các bài toán đa mục tiêu.
Cung cấp danh sách các giải pháp “tốt” chứ không chỉ là một giải pháp duy nhất.
Luôn nhận được câu trả lời cho vấn đề, vấn đề này sẽ tốt hơn theo thời gian.
Hữu ích khi không gian tìm kiếm rất lớn và có một số lượng lớn các tham số liên quan.

Hạn chế của GAs

Giống như bất kỳ kỹ thuật nào, GAs cũng gặp phải một số hạn chế. Chúng bao gồm -

GAs không phù hợp cho tất cả các vấn đề, đặc biệt là các vấn đề đơn giản và có sẵn thông tin phái sinh.
Giá trị thể chất được tính toán nhiều lần có thể tốn kém về mặt tính toán đối với một số vấn đề.
Là ngẫu nhiên, không có gì đảm bảo về tính tối ưu hoặc chất lượng của giải pháp.
Nếu không được triển khai đúng cách, GA có thể không hội tụ thành giải pháp tối ưu.

GA - Động lực

Thuật toán di truyền có khả năng cung cấp một giải pháp “đủ tốt” “đủ nhanh”. Điều này làm cho các thuật toán di truyền trở nên hấp dẫn để sử dụng trong việc giải các bài toán tối ưu hóa. Các lý do tại sao GAs là cần thiết như sau:

Giải quyết các vấn đề khó khăn

Trong khoa học máy tính, có một loạt các vấn đề, đó là NP-Hard. Điều này về cơ bản có nghĩa là, ngay cả những hệ thống máy tính mạnh nhất cũng phải mất một thời gian rất dài (thậm chí hàng năm!) Để giải quyết vấn đề đó. Trong trường hợp như vậy, GAs chứng tỏ là một công cụ hiệu quả để cung cấpusable near-optimal solutions trong một khoảng thời gian ngắn.

Thất bại của các phương pháp dựa trên Gradient

Các phương pháp dựa trên giải tích truyền thống hoạt động bằng cách bắt đầu tại một điểm ngẫu nhiên và bằng cách di chuyển theo hướng của gradient, cho đến khi chúng ta lên đến đỉnh đồi. Kỹ thuật này hiệu quả và hoạt động rất tốt cho các hàm mục tiêu một đỉnh như hàm chi phí trong hồi quy tuyến tính. Tuy nhiên, trong hầu hết các tình huống thực tế, chúng ta gặp phải một vấn đề rất phức tạp được gọi là cảnh quan, được tạo bởi nhiều đỉnh và nhiều thung lũng, khiến các phương pháp như vậy không thành công, vì chúng có xu hướng cố hữu là bị mắc kẹt ở hệ tối ưu cục bộ. như trong hình sau.

Nhận giải pháp tốt nhanh chóng

Một số bài toán khó như Bài toán Nhân viên Bán hàng Đi du lịch (TSP), có các ứng dụng trong thế giới thực như tìm đường và Thiết kế VLSI. Bây giờ, hãy tưởng tượng rằng bạn đang sử dụng hệ thống Định vị GPS của mình và mất vài phút (hoặc thậm chí vài giờ) để tính toán đường đi “tối ưu” từ nguồn đến đích. Sự chậm trễ trong các ứng dụng trong thế giới thực như vậy là không thể chấp nhận được và do đó giải pháp “đủ tốt”, được cung cấp “nhanh chóng” là điều cần thiết.

Phần này giới thiệu các thuật ngữ cơ bản cần thiết để hiểu GAs. Ngoài ra, cấu trúc chung của GA được trình bày trong cả haipseudo-code and graphical forms. Người đọc nên hiểu đúng tất cả các khái niệm được giới thiệu trong phần này và ghi nhớ chúng khi đọc các phần khác của hướng dẫn này.

Thuật ngữ cơ bản

Trước khi bắt đầu thảo luận về Thuật toán di truyền, điều cần thiết là phải làm quen với một số thuật ngữ cơ bản sẽ được sử dụng trong suốt hướng dẫn này.

Population- Nó là một tập hợp con của tất cả các giải pháp có thể (được mã hóa) cho vấn đề đã cho. Dân số cho một GA tương tự với dân số cho con người ngoại trừ việc thay vì con người, chúng tôi có các Giải pháp Ứng viên đại diện cho con người.
Chromosomes - Một nhiễm sắc thể là một trong những giải pháp như vậy cho vấn đề đã cho.
Gene - Một gen là một vị trí thành phần của nhiễm sắc thể.
Allele - Đó là giá trị mà một gen nhận được cho một nhiễm sắc thể cụ thể.

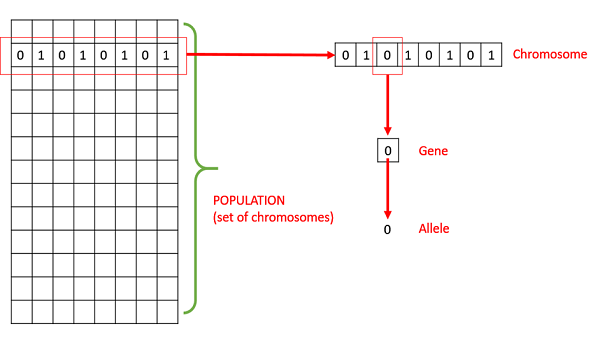
Genotype- Kiểu gen là quần thể trong không gian tính toán. Trong không gian tính toán, các giải pháp được trình bày theo cách có thể dễ dàng hiểu và thao tác bằng hệ thống máy tính.
Phenotype - Kiểu hình là quần thể trong không gian giải pháp thế giới thực trong đó các giải pháp được biểu diễn theo cách chúng được biểu diễn trong các tình huống thế giới thực.
Decoding and Encoding - Đối với các vấn đề đơn giản, phenotype and genotypekhông gian giống nhau. Tuy nhiên, trong hầu hết các trường hợp, không gian kiểu hình và kiểu gen là khác nhau. Giải mã là một quá trình biến đổi một giải pháp từ kiểu gen sang không gian kiểu hình, trong khi mã hóa là một quá trình chuyển từ kiểu hình sang không gian kiểu gen. Việc giải mã phải nhanh chóng vì nó được thực hiện nhiều lần trong GA trong quá trình tính toán giá trị phù hợp.

Ví dụ, hãy xem xét vấn đề Knapsack 0/1. Không gian Kiểu hình bao gồm các giải pháp chỉ chứa số mục của các mục được chọn.

Tuy nhiên, trong không gian kiểu gen, nó có thể được biểu diễn dưới dạng một chuỗi nhị phân có độ dài n (với n là số mục). A0 at position x đại diện cho điều đó x^thmục được chọn trong khi số 1 đại diện cho điều ngược lại. Đây là một trường hợp mà không gian kiểu gen và kiểu hình khác nhau.

Fitness Function- Một hàm phù hợp được định nghĩa đơn giản là một hàm lấy giải pháp làm đầu vào và tạo ra tính phù hợp của giải pháp làm đầu ra. Trong một số trường hợp, chức năng thể dục và chức năng mục tiêu có thể giống nhau, trong khi ở những trường hợp khác, nó có thể khác tùy theo vấn đề.
Genetic Operators- Những điều này làm thay đổi thành phần di truyền của thế hệ con. Chúng bao gồm trao đổi chéo, đột biến, chọn lọc, v.v.

Cấu trúc cơ bản

Cấu trúc cơ bản của GA như sau:

Chúng tôi bắt đầu với một quần thể ban đầu (có thể được tạo ra một cách ngẫu nhiên hoặc được gieo mầm bởi các nhà nghiên cứu khác), chọn các cặp bố mẹ từ quần thể này để giao phối. Áp dụng các toán tử giao thoa và đột biến trên bố mẹ để tạo ra các lò xo mới. Và cuối cùng những con suối tắt này thay thế các cá thể hiện có trong quần thể và quá trình này lặp lại. Bằng cách này, các thuật toán di truyền thực sự cố gắng bắt chước sự tiến hóa của con người ở một mức độ nào đó.

Mỗi bước sau đây được đề cập thành một chương riêng biệt ở phần sau của hướng dẫn này.

Mã giả tổng quát cho GA được giải thích trong chương trình sau:

GA()
   initialize population
   find fitness of population
   
   while (termination criteria is reached) do
      parent selection
      crossover with probability pc
      mutation with probability pm
      decode and fitness calculation
      survivor selection
      find best
   return best

Một trong những quyết định quan trọng nhất cần thực hiện trong khi triển khai thuật toán di truyền là quyết định cách biểu diễn mà chúng tôi sẽ sử dụng để đại diện cho các giải pháp của mình. Người ta đã quan sát thấy rằng đại diện không đúng có thể dẫn đến hiệu suất kém của GA.

Vì vậy, việc lựa chọn một đại diện thích hợp, xác định đúng các ánh xạ giữa không gian kiểu hình và kiểu gen là điều cần thiết cho sự thành công của một GA.

Trong phần này, chúng tôi trình bày một số biểu diễn thường được sử dụng nhất cho các thuật toán di truyền. Tuy nhiên, cách biểu diễn rất cụ thể về vấn đề và người đọc có thể thấy rằng một cách biểu diễn khác hoặc kết hợp các cách biểu diễn được đề cập ở đây có thể phù hợp với vấn đề của mình hơn.

Biểu diễn nhị phân

Đây là một trong những cách biểu diễn đơn giản nhất và được sử dụng rộng rãi nhất trong GAs. Trong kiểu biểu diễn này, kiểu gen bao gồm các chuỗi bit.

Đối với một số vấn đề khi không gian giải pháp bao gồm các biến quyết định Boolean - có hoặc không, biểu diễn nhị phân là đương nhiên. Lấy ví dụ vấn đề Knapsack 0/1. Nếu có n mục, chúng ta có thể biểu diễn một nghiệm bằng một chuỗi nhị phân gồm n phần tử, trong đó phần tử ^thứ x cho biết mục x có được chọn (1) hay không (0).

Đối với các bài toán khác, cụ thể là những bài toán liên quan đến số, chúng ta có thể biểu diễn các số bằng biểu diễn nhị phân của chúng. Vấn đề với kiểu mã hóa này là các bit khác nhau có ý nghĩa khác nhau và do đó các toán tử đột biến và giao nhau có thể gây ra những hậu quả không mong muốn. Điều này có thể được giải quyết ở một mức độ nào đó bằng cách sử dụngGray Coding, vì sự thay đổi trong một bit không có ảnh hưởng lớn đến giải pháp.

Đại diện có giá trị thực

Đối với các vấn đề mà chúng ta muốn xác định các gen bằng cách sử dụng các biến liên tục thay vì rời rạc, biểu diễn có giá trị thực là tự nhiên nhất. Tuy nhiên, độ chính xác của các số có giá trị thực hoặc dấu phẩy động này bị giới hạn trong máy tính.

Biểu diễn số nguyên

Đối với các gen có giá trị rời rạc, chúng ta không phải lúc nào cũng giới hạn không gian nghiệm thành nhị phân 'có' hoặc 'không'. Ví dụ: nếu chúng ta muốn mã hóa bốn khoảng cách - Bắc, Nam, Đông và Tây, chúng ta có thể mã hóa chúng thành{0,1,2,3}. Trong những trường hợp như vậy, biểu diễn số nguyên là mong muốn.

Biểu diễn hoán vị

Trong nhiều bài toán, lời giải được biểu diễn bằng thứ tự các phần tử. Trong những trường hợp như vậy, biểu diễn hoán vị là phù hợp nhất.

Một ví dụ kinh điển của cách biểu diễn này là vấn đề nhân viên bán hàng lưu động (TSP). Trong điều này, nhân viên bán hàng phải đi một vòng quanh tất cả các thành phố, thăm chính xác mỗi thành phố một lần và quay trở lại thành phố xuất phát. Tổng khoảng cách của chuyến tham quan phải được giảm thiểu. Giải pháp cho TSP này tự nhiên là một thứ tự hoặc hoán vị của tất cả các thành phố và do đó sử dụng một biểu diễn hoán vị có ý nghĩa cho vấn đề này.

Dân số là một tập hợp con của các giải pháp trong thế hệ hiện tại. Nó cũng có thể được định nghĩa là một bộ nhiễm sắc thể. Có một số điều cần lưu ý khi xử lý tập hợp GA -

Sự đa dạng của quần thể cần được duy trì nếu không có thể dẫn đến sự hội tụ sớm.
Không nên để kích thước quần thể quá lớn vì nó có thể khiến GA chậm lại, trong khi một quần thể nhỏ hơn có thể không đủ cho một đàn giao phối tốt. Do đó, một quy mô dân số tối ưu cần phải được quyết định bằng thử và sai.

Tổng thể thường được định nghĩa là một mảng hai chiều của - size population, size x, chromosome size.

Khởi tạo dân số

Có hai phương pháp chính để khởi tạo một tập hợp trong GA. Họ là -

Random Initialization - Làm dân số ban đầu bằng các nghiệm hoàn toàn ngẫu nhiên.
Heuristic initialization - Điền dân số ban đầu bằng cách sử dụng phương pháp heuristic đã biết cho vấn đề.

Người ta quan sát thấy rằng toàn bộ quần thể không nên được khởi tạo bằng cách sử dụng phương pháp heuristic, vì nó có thể dẫn đến việc quần thể có các giải pháp tương tự và rất ít đa dạng. Thực nghiệm đã quan sát thấy rằng các giải pháp ngẫu nhiên là những giải pháp thúc đẩy dân số đến mức tối ưu. Do đó, với việc khởi tạo heuristic, chúng tôi chỉ gieo vào dân số một vài giải pháp tốt, lấp đầy phần còn lại bằng các giải pháp ngẫu nhiên thay vì lấp đầy toàn bộ dân số bằng các giải pháp dựa trên heuristic.

Người ta cũng quan sát thấy rằng khởi tạo heuristic trong một số trường hợp, chỉ ảnh hưởng đến sự phù hợp ban đầu của dân số, nhưng cuối cùng, chính sự đa dạng của các giải pháp dẫn đến tính tối ưu.

Mô hình dân số

Có hai mô hình dân số được sử dụng rộng rãi -

Trạng thái ổn định

Ở trạng thái ổn định GA, chúng tôi tạo ra một hoặc hai lò xo tắt trong mỗi lần lặp lại và chúng thay thế một hoặc hai cá thể từ quần thể. GA trạng thái ổn định còn được gọi làIncremental GA.

Thế hệ

Trong một mô hình thế hệ, chúng tôi tạo ra 'n' off-spring, trong đó n là kích thước dân số và toàn bộ tổng thể được thay thế bằng tổng thể mới vào cuối lần lặp.

Hàm thể dục được định nghĩa đơn giản là một hàm có candidate solution to the problem as input and produces as output giải pháp “phù hợp” như thế nào đối với vấn đề đang được xem xét.

Việc tính toán giá trị thể chất được thực hiện lặp đi lặp lại trong GA và do đó nó phải đủ nhanh. Việc tính toán chậm giá trị thể chất có thể ảnh hưởng xấu đến GA và khiến nó trở nên chậm đặc biệt.

Trong hầu hết các trường hợp, hàm phù hợp và hàm mục tiêu giống như mục tiêu là tối đa hóa hoặc tối thiểu hóa hàm mục tiêu đã cho. Tuy nhiên, đối với các vấn đề phức tạp hơn với nhiều mục tiêu và ràng buộc,Algorithm Designer có thể chọn có một chức năng thể dục khác.

Một chức năng thể dục phải có các đặc điểm sau:

Chức năng thể dục phải đủ nhanh để tính toán.
Nó phải đo lường định lượng mức độ phù hợp của một giải pháp nhất định hoặc mức độ phù hợp của các cá nhân có thể được tạo ra từ giải pháp đã cho.

Trong một số trường hợp, việc tính toán hàm thể dục trực tiếp có thể không thực hiện được do sự phức tạp vốn có của vấn đề. Trong những trường hợp như vậy, chúng tôi thực hiện ước lượng sức khỏe phù hợp với nhu cầu của mình.

Hình ảnh sau đây cho thấy tính toán phù hợp cho một giải pháp của Knapsack 0/1. Đây là một chức năng thể dục đơn giản chỉ tính tổng giá trị lợi nhuận của các vật phẩm được chọn (có 1), quét các phần tử từ trái sang phải cho đến khi túi đầy.

Lựa chọn bố mẹ là quá trình lựa chọn các cặp bố mẹ giao phối và tái tổ hợp để tạo ra các con lai cho thế hệ tiếp theo. Lựa chọn của cha mẹ là rất quan trọng đối với tỷ lệ hội tụ của GA vì cha mẹ tốt hướng các cá nhân đến một giải pháp tốt hơn và phù hợp hơn.

Tuy nhiên, cần cẩn thận để ngăn chặn một giải pháp cực kỳ phù hợp tiếp quản toàn bộ dân số trong một vài thế hệ, vì điều này dẫn đến việc các giải pháp gần nhau trong không gian giải pháp, do đó làm mất tính đa dạng. Maintaining good diversitytrong quần thể là cực kỳ quan trọng cho sự thành công của GA. Điều này chiếm toàn bộ dân số bằng một giải pháp cực kỳ phù hợp được gọi làpremature convergence và là một điều kiện không mong muốn trong GA.

Lựa chọn cân đối về thể chất

Lựa chọn cân đối về thể chất là một trong những cách lựa chọn phổ biến nhất của phụ huynh. Trong điều này, mọi cá nhân đều có thể trở thành cha mẹ với một xác suất tỷ lệ thuận với sức khỏe của nó. Do đó, các cá thể fitter có cơ hội giao phối và truyền bá các tính năng của chúng cho thế hệ tiếp theo cao hơn. Do đó, một chiến lược chọn lọc như vậy áp dụng một áp lực chọn lọc đối với những cá thể phù hợp hơn trong quần thể, tiến hóa những cá thể tốt hơn theo thời gian.

Hãy xem xét một bánh xe tròn. Bánh xe được chia thànhn pies, với n là số lượng cá thể trong quần thể. Mỗi cá nhân nhận được một phần của vòng tròn tỷ lệ với giá trị thể chất của nó.

Có thể triển khai hai lựa chọn tương ứng về thể lực -

Lựa chọn bánh xe Roulette

Trong lựa chọn bánh xe roulette, bánh xe tròn được chia như mô tả trước đây. Người ta chọn một điểm cố định trên chu vi bánh xe như hình vẽ và cho bánh xe quay. Vùng của bánh xe phía trước điểm cố định được chọn làm vùng chính. Đối với cha mẹ thứ hai, quá trình tương tự được lặp lại.

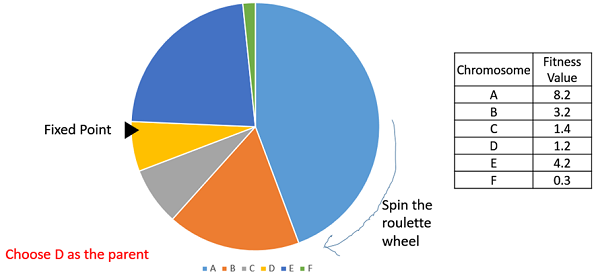
Rõ ràng là một cá nhân lắp bánh xe có bánh lái lớn hơn và do đó cơ hội hạ cánh trước điểm cố định cao hơn khi bánh xe quay. Do đó, xác suất chọn một cá thể phụ thuộc trực tiếp vào thể lực của nó.

Triển khai khôn ngoan, chúng tôi sử dụng các bước sau:

Tính S = tổng của một tinh.
Tạo một số ngẫu nhiên giữa 0 và S.
Bắt đầu từ phần trên cùng của dân số, tiếp tục cộng các số tinh vào tổng một phần P, cho đến khi P <S.
Cá nhân mà P vượt quá S là cá nhân được chọn.

Lấy mẫu chung ngẫu nhiên (SUS)

Stochastic Universal Sampling khá giống với lựa chọn bánh xe Roulette, tuy nhiên thay vì chỉ có một điểm cố định, chúng ta có nhiều điểm cố định như trong hình sau. Vì vậy, tất cả các phụ huynh được chọn chỉ trong một vòng quay của bánh xe. Ngoài ra, cách thiết lập như vậy khuyến khích những cá nhân phù hợp cao được chọn ít nhất một lần.

Cần lưu ý rằng các phương pháp lựa chọn tương ứng với thể lực không hoạt động đối với những trường hợp thể dục có thể có giá trị âm.

Lựa chọn giải đấu

Trong lựa chọn giải đấu K-Way, chúng tôi chọn ngẫu nhiên K cá thể từ quần thể và chọn người tốt nhất trong số này để trở thành bố mẹ. Quy trình tương tự được lặp lại để chọn cha mẹ tiếp theo. Lựa chọn giải đấu cũng rất phổ biến trong văn học vì nó thậm chí có thể hoạt động với các giá trị thể dục tiêu cực.

Lựa chọn xếp hạng

Lựa chọn Xếp hạng cũng hoạt động với các giá trị thể lực âm và chủ yếu được sử dụng khi các cá thể trong quần thể có giá trị thể lực rất gần nhau (điều này thường xảy ra vào cuối cuộc chạy). Điều này dẫn đến việc mỗi cá nhân có một phần gần như bằng nhau của chiếc bánh (như trong trường hợp lựa chọn tương xứng về thể lực) như được hiển thị trong hình ảnh sau đây và do đó mỗi cá nhân bất kể phù hợp với nhau như thế nào đều có xác suất được chọn là cha mẹ. Điều này dẫn đến việc giảm áp lực lựa chọn đối với các cá thể phù hợp, khiến GA đưa ra lựa chọn bố mẹ kém trong những tình huống như vậy.

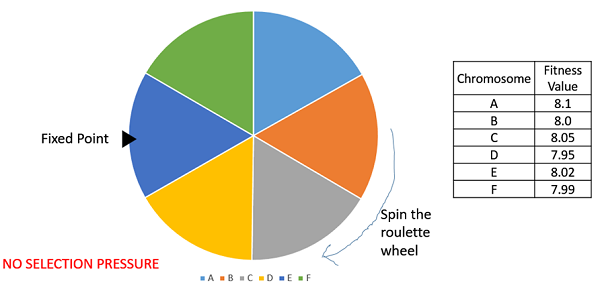
Trong điều này, chúng tôi loại bỏ khái niệm về giá trị thể chất khi chọn cấp độ gốc. Tuy nhiên, mọi cá nhân trong dân số đều được xếp hạng theo thể lực của họ. Việc lựa chọn của cha mẹ phụ thuộc vào cấp bậc của từng cá nhân chứ không phải thể lực. Những cá nhân được xếp hạng cao hơn được ưu tiên hơn những người được xếp hạng thấp hơn.

Nhiễm sắc thể	Giá trị thể chất	Cấp
A	8.1	1
B	8.0	4
C	8.05	2
D	7.95	6
E	8.02	3
F	7.99	5

Lựa chọn ngẫu nhiên

Trong chiến lược này, chúng tôi chọn ngẫu nhiên các cặp bố mẹ từ dân số hiện có. Không có áp lực lựa chọn đối với các cá nhân phù hợp và do đó chiến lược này thường được tránh.

Trong chương này, chúng ta sẽ thảo luận về Crossover Operator cùng với các mô-đun khác của nó, cách sử dụng và lợi ích của chúng.

Giới thiệu về Crossover

Toán tử giao nhau tương tự như tái tạo và giao nhau sinh học. Trong trường hợp này, nhiều hơn một cá thể bố mẹ được chọn và một hoặc nhiều con non được tạo ra bằng cách sử dụng vật liệu di truyền của bố mẹ. Kết hợp chéo thường được áp dụng trong GA với xác suất cao -p_c .

Các nhà khai thác chéo

Trong phần này, chúng ta sẽ thảo luận về một số toán tử chéo được sử dụng phổ biến nhất. Cần lưu ý rằng các toán tử giao nhau này rất chung chung và Nhà thiết kế GA cũng có thể chọn triển khai toán tử giao nhau cụ thể cho từng vấn đề.

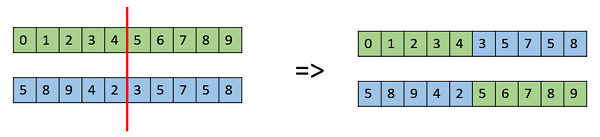
Giao nhau một điểm

Trong sự giao nhau một điểm này, một điểm giao nhau ngẫu nhiên được chọn và các đuôi của hai cha mẹ của nó được hoán đổi để có được các lò xo mới.

Chéo đa điểm

Sự giao nhau đa điểm là sự tổng quát của sự giao nhau một điểm trong đó các đoạn xen kẽ được hoán đổi để tạo ra các lò xo mới.

Đồng phục chéo

Trong một sự trao đổi chéo đồng đều, chúng ta không chia nhiễm sắc thể thành các đoạn, thay vào đó chúng ta xử lý từng gen riêng biệt. Trong điều này, về cơ bản, chúng tôi lật một đồng xu cho mỗi nhiễm sắc thể để quyết định xem nó có được đưa vào giai đoạn ngoài xuân hay không. Chúng ta cũng có thể thiên vị đồng xu cho một người cha hoặc mẹ để có nhiều vật chất di truyền hơn ở đứa trẻ từ người cha mẹ đó.

Tổng hợp lại toàn bộ số học

Điều này thường được sử dụng cho các biểu diễn số nguyên và hoạt động bằng cách lấy trung bình có trọng số của hai bậc cha mẹ bằng cách sử dụng các công thức sau:

Con1 = α.x + (1-α) .y
Con2 = α.x + (1-α) .y

Rõ ràng, nếu α = 0,5, thì cả hai con sẽ giống hệt nhau như trong hình sau.

Davis 'Order Crossover (OX1)

OX1 được sử dụng để hoán vị chéo dựa trên mục đích truyền thông tin về thứ tự tương đối đến các lò xo. Nó hoạt động như sau:

Tạo hai điểm giao nhau ngẫu nhiên ở bố mẹ và sao chép đoạn giữa chúng từ bố mẹ đầu tiên sang thế hệ con đầu tiên.
Bây giờ, bắt đầu từ điểm giao nhau thứ hai trong mã mẹ thứ hai, hãy sao chép các số chưa sử dụng còn lại từ mã mẹ thứ hai sang con đầu tiên, bao quanh danh sách.
Lặp lại cho trẻ thứ hai với vai trò của phụ huynh được đảo ngược.

Có rất nhiều crossover khác như Crossover được ánh xạ một phần (PMX), Order based crossover (OX2), Shuffle Crossover, Ring Crossover, v.v.

Giới thiệu về đột biến

Nói một cách dễ hiểu, đột biến có thể được định nghĩa là một sự thay đổi ngẫu nhiên nhỏ trong nhiễm sắc thể, để có được một giải pháp mới. Nó được sử dụng để duy trì và giới thiệu sự đa dạng trong quần thể di truyền và thường được áp dụng với xác suất thấp -p_m. Nếu xác suất rất cao, GA sẽ được giảm xuống thành một tìm kiếm ngẫu nhiên.

Đột biến là một phần của GA có liên quan đến việc "khám phá" không gian tìm kiếm. Người ta đã quan sát thấy rằng đột biến là yếu tố cần thiết cho sự hội tụ của GA trong khi sự trao đổi chéo thì không.

Toán tử đột biến

Trong phần này, chúng tôi mô tả một số toán tử đột biến được sử dụng phổ biến nhất. Giống như các toán tử chéo, đây không phải là một danh sách đầy đủ và nhà thiết kế GA có thể tìm thấy sự kết hợp của các phương pháp này hoặc toán tử đột biến cụ thể cho vấn đề hữu ích hơn.

Đột biến lật bit

Trong đột biến lật bit này, chúng tôi chọn một hoặc nhiều bit ngẫu nhiên và lật chúng. Điều này được sử dụng cho các GA được mã hóa nhị phân.

Đặt lại ngẫu nhiên

Đặt lại ngẫu nhiên là một phần mở rộng của phép lật bit cho biểu diễn số nguyên. Trong trường hợp này, một giá trị ngẫu nhiên từ tập hợp các giá trị cho phép được gán cho một gen được chọn ngẫu nhiên.

Hoán đổi đột biến

Trong đột biến hoán đổi, chúng ta chọn ngẫu nhiên hai vị trí trên nhiễm sắc thể và hoán đổi các giá trị. Điều này là phổ biến trong mã hóa dựa trên hoán vị.

Đột biến tranh giành

Đột biến xáo trộn cũng phổ biến với các biểu diễn hoán vị. Trong trường hợp này, từ toàn bộ nhiễm sắc thể, một tập hợp con của các gen được chọn và giá trị của chúng được xáo trộn hoặc xáo trộn một cách ngẫu nhiên.

Đột biến đảo ngược

Trong đột biến đảo ngược, chúng tôi chọn một tập hợp con của các gen giống như trong đột biến xáo trộn, nhưng thay vì xáo trộn tập hợp con, chúng tôi chỉ đảo ngược toàn bộ chuỗi trong tập hợp con.

Chính sách Tuyển chọn Người sống sót xác định những cá nhân nào sẽ bị loại bỏ và những cá nhân nào sẽ được giữ lại trong thế hệ tiếp theo. Điều quan trọng là nó phải đảm bảo rằng các cá thể thuần chủng không bị đuổi ra khỏi quần thể, đồng thời phải duy trì sự đa dạng trong quần thể.

Một số GA sử dụng Elitism. Nói một cách dễ hiểu, nó có nghĩa là thành viên khỏe mạnh nhất hiện tại của quần thể luôn được truyền sang thế hệ tiếp theo. Do đó, trong bất kỳ trường hợp nào cũng không thể thay thế thành viên khỏe mạnh nhất trong quần thể hiện tại.

Chính sách đơn giản nhất là loại bỏ các thành viên ngẫu nhiên ra khỏi quần thể, nhưng cách tiếp cận như vậy thường có các vấn đề về hội tụ, do đó các chiến lược sau đây được sử dụng rộng rãi.

Lựa chọn dựa trên độ tuổi

Trong Lựa chọn dựa trên độ tuổi, chúng tôi không có khái niệm về thể lực. Nó dựa trên tiền đề rằng mỗi cá thể được phép ở trong quần thể trong một thế hệ hữu hạn nơi nó được phép sinh sản, sau đó, nó bị đuổi ra khỏi quần thể cho dù thể lực của nó có tốt đến đâu.

Ví dụ, trong ví dụ sau, tuổi là số thế hệ mà cá thể đó đã có trong quần thể. Các thành viên lớn tuổi nhất của dân số, tức là P4 và P7 bị đuổi ra khỏi dân số và tuổi của các thành viên còn lại được tăng thêm một.

Lựa chọn dựa trên thể chất

Trong sự lựa chọn dựa trên thể lực này, con cái có xu hướng thay thế những cá thể kém khỏe nhất trong quần thể. Việc lựa chọn những cá nhân kém phù hợp nhất có thể được thực hiện bằng cách sử dụng một biến thể của bất kỳ chính sách tuyển chọn nào được mô tả trước đây - lựa chọn giải đấu, lựa chọn cân đối thể lực, v.v.

Ví dụ, trong hình ảnh sau, con cái thay thế các cá thể P1 và P10 kém phù hợp nhất của quần thể. Cần lưu ý rằng vì P1 và P9 có cùng giá trị sức khỏe nên quyết định loại bỏ cá thể nào khỏi quần thể là tùy ý.

Điều kiện kết thúc của Thuật toán di truyền rất quan trọng trong việc xác định thời điểm chạy GA sẽ kết thúc. Người ta quan sát thấy rằng ban đầu, GA tiến triển rất nhanh với các giải pháp tốt hơn sau mỗi vài lần lặp lại, nhưng điều này có xu hướng bão hòa trong các giai đoạn sau khi các cải tiến là rất nhỏ. Chúng tôi thường muốn một điều kiện kết thúc sao cho giải pháp của chúng tôi gần với mức tối ưu, vào cuối quá trình chạy.

Thông thường, chúng tôi giữ một trong các điều kiện chấm dứt sau:

Khi không có sự cải thiện về dân số cho X lần lặp.
Khi chúng ta đạt đến số thế hệ tuyệt đối.
Khi giá trị hàm mục tiêu đã đạt đến một giá trị xác định trước nhất định.

Ví dụ, trong một thuật toán di truyền, chúng tôi giữ một bộ đếm theo dõi các thế hệ mà dân số không có sự cải thiện. Ban đầu, chúng tôi đặt bộ đếm này bằng không. Mỗi khi chúng tôi không tạo ra những con non tốt hơn những cá thể trong quần thể, chúng tôi sẽ tăng số đếm.

Tuy nhiên, nếu sức khỏe của bất kỳ lò xo nào tốt hơn, thì chúng tôi đặt lại bộ đếm về không. Thuật toán kết thúc khi bộ đếm đạt đến giá trị xác định trước.

Giống như các tham số khác của GA, điều kiện kết thúc cũng rất cụ thể về vấn đề và nhà thiết kế GA nên thử các tùy chọn khác nhau để xem điều gì phù hợp nhất với vấn đề cụ thể của mình.

Cho đến bây giờ trong hướng dẫn này, bất cứ điều gì chúng ta đã thảo luận đều tương ứng với mô hình tiến hóa của Darwin - chọn lọc tự nhiên và biến đổi di truyền thông qua tái tổ hợp và đột biến. Trong tự nhiên, chỉ những thông tin có trong kiểu gen của cá thể mới có thể được truyền cho thế hệ sau. Đây là cách tiếp cận mà chúng tôi đã làm theo trong hướng dẫn cho đến nay.

Tuy nhiên, các mô hình thích ứng trọn đời khác - Lamarckian Model và Baldwinian Modelcũng tồn tại. Cần lưu ý rằng mô hình nào là tốt nhất vẫn còn mở để tranh luận và các kết quả mà các nhà nghiên cứu thu được cho thấy rằng sự lựa chọn thích ứng trọn đời là một vấn đề rất cụ thể.

Thông thường, chúng tôi kết hợp GA với tìm kiếm cục bộ - như trong Thuật toán Memetic. Trong những trường hợp như vậy, người ta có thể chọn làm với Mô hình Lamarckian hoặc Baldwinian để quyết định phải làm gì với các cá nhân được tạo ra sau khi tìm kiếm cục bộ.

Mô hình Lamarckian

Mô hình Lamarckian về cơ bản nói rằng những đặc điểm mà một cá nhân có được trong cuộc đời của họ có thể được truyền lại cho thế hệ con cháu của họ. Nó được đặt theo tên của nhà sinh vật học người Pháp Jean-Baptiste Lamarck.

Mặc dù vậy, sinh học tự nhiên đã hoàn toàn coi thường bệnh Lamarckism vì chúng ta đều biết rằng chỉ có thông tin trong kiểu gen mới được truyền đi. Tuy nhiên, từ quan điểm tính toán, người ta đã chỉ ra rằng việc áp dụng mô hình Lamarckian cho kết quả tốt đối với một số vấn đề.

Trong mô hình Lamarckian, một toán tử tìm kiếm cục bộ kiểm tra vùng lân cận (thu nhận các đặc điểm mới) và nếu tìm thấy nhiễm sắc thể tốt hơn, nó sẽ trở thành con.

Mô hình Baldwinian

Mô hình Baldwinian là một ý tưởng trung gian được đặt theo tên của James Mark Baldwin (1896). Trong mô hình Baldwin, các nhiễm sắc thể có thể mã hóa xu hướng học các hành vi có lợi. Điều này có nghĩa là, không giống như mô hình Lamarckian, chúng tôi không truyền những đặc điểm có được cho thế hệ tiếp theo, và chúng tôi cũng không hoàn toàn bỏ qua những đặc điểm có được như trong Mô hình Darwin.

Mô hình Baldwin nằm ở giữa hai thái cực này, trong đó xu hướng của một cá nhân đạt được các đặc điểm nhất định được mã hóa hơn là bản thân các đặc điểm.

Trong Mô hình Baldwinian này, một toán tử tìm kiếm cục bộ kiểm tra vùng lân cận (thu nhận các đặc điểm mới) và nếu tìm thấy nhiễm sắc thể tốt hơn, nó chỉ chỉ định mức độ phù hợp đã được cải thiện cho nhiễm sắc thể và không sửa đổi bản thân nhiễm sắc thể đó. Sự thay đổi về thể chất biểu thị khả năng nhiễm sắc thể để “có được đặc điểm”, mặc dù nó không được truyền trực tiếp cho các thế hệ tương lai.

GA về bản chất rất chung chung và chỉ áp dụng chúng cho bất kỳ vấn đề tối ưu hóa nào sẽ không cho kết quả tốt. Trong phần này, chúng tôi mô tả một số điểm sẽ giúp ích và hỗ trợ người thiết kế GA hoặc người triển khai GA trong công việc của họ.

Giới thiệu kiến thức miền cụ thể của vấn đề

Người ta nhận thấy rằng chúng tôi kết hợp càng nhiều kiến thức miền cụ thể về vấn đề vào GA; các giá trị khách quan tốt hơn mà chúng tôi nhận được. Việc thêm thông tin cụ thể về vấn đề có thể được thực hiện bằng cách sử dụng toán tử chéo hoặc đột biến cụ thể của vấn đề, biểu diễn tùy chỉnh, v.v.

Hình ảnh sau đây cho thấy góc nhìn của Michalewicz (1990) về EA -

Giảm đông đúc

Sự đông đúc xảy ra khi một nhiễm sắc thể phù hợp cao sẽ sinh sản nhiều và trong một vài thế hệ, toàn bộ quần thể chứa đầy các giải pháp tương tự có thể trạng tương tự. Điều này làm giảm tính đa dạng, một yếu tố rất quan trọng để đảm bảo sự thành công của GA. Có nhiều cách để hạn chế sự đông đúc. Một số trong số họ là -

Mutation để giới thiệu sự đa dạng.
Chuyển sang rank selection và tournament selection có nhiều áp lực tuyển chọn hơn là lựa chọn tương xứng về thể lực cho những cá nhân có thể lực tương tự.
Fitness Sharing - Trong trường hợp này sức khỏe của một cá thể bị giảm sút nếu quần thể đã có những cá thể tương tự.

Ngẫu nhiên hóa giúp!

Thực nghiệm đã quan sát thấy rằng các giải pháp tốt nhất được thúc đẩy bởi các nhiễm sắc thể ngẫu nhiên khi chúng truyền sự đa dạng cho quần thể. Người triển khai GA nên cẩn thận để giữ đủ số lượng ngẫu nhiên và đa dạng trong quần thể để có kết quả tốt nhất.

Kết hợp GA với Tìm kiếm cục bộ

Tìm kiếm cục bộ đề cập đến việc kiểm tra các giải pháp trong vùng lân cận của một giải pháp nhất định để tìm kiếm các giá trị khách quan tốt hơn.

Đôi khi có thể hữu ích khi kết hợp GA với tìm kiếm cục bộ. Hình ảnh sau đây cho thấy các địa điểm khác nhau mà tìm kiếm cục bộ có thể được giới thiệu trong GA.

Sự thay đổi của các tham số và kỹ thuật

Trong thuật toán di truyền, không có “một kích thước phù hợp với tất cả” hay một công thức kỳ diệu nào phù hợp với mọi vấn đề. Ngay cả sau khi GA ban đầu đã sẵn sàng, cần rất nhiều thời gian và nỗ lực để tìm hiểu các tham số như kích thước quần thể, đột biến và xác suất chéo, v.v. để tìm ra những tham số phù hợp với vấn đề cụ thể.

Trong phần này, chúng tôi giới thiệu một số chủ đề nâng cao trong Giải thuật di truyền. Một người đọc chỉ tìm kiếm phần giới thiệu về GAs có thể chọn bỏ qua phần này.

Các vấn đề về tối ưu hóa hạn chế

Các vấn đề tối ưu hóa bị ràng buộc là những vấn đề tối ưu hóa trong đó chúng ta phải tối đa hóa hoặc tối thiểu hóa một giá trị hàm mục tiêu nhất định chịu những ràng buộc nhất định. Do đó, không phải tất cả các kết quả trong không gian giải pháp đều khả thi, và không gian giải pháp chứa các vùng khả thi như thể hiện trong hình sau.

Trong trường hợp như vậy, các toán tử giao nhau và đột biến có thể cung cấp cho chúng ta các giải pháp không khả thi. Do đó, các cơ chế bổ sung phải được sử dụng trong GA khi giải quyết các Vấn đề về tối ưu hóa bị hạn chế.

Một số phương pháp phổ biến nhất là -

Sử dụng penalty functions điều này làm giảm tính phù hợp của các giải pháp không khả thi, tốt nhất là để tính phù hợp bị giảm tương ứng với số lượng các ràng buộc bị vi phạm hoặc khoảng cách so với vùng khả thi.
Sử dụng repair functions đưa ra một giải pháp không khả thi và sửa đổi nó để các ràng buộc bị vi phạm được thỏa mãn.
Not allowing infeasible solutions để nhập vào dân số ở tất cả.
Sử dụng một special representation or decoder functions đảm bảo tính khả thi của các giải pháp.

Cơ sở lý thuyết cơ bản

Trong phần này, chúng ta sẽ thảo luận về giản đồ và định lý NFL cùng với giả thuyết khối xây dựng.

Định lý giản đồ

Các nhà nghiên cứu đã cố gắng tìm ra toán học đằng sau hoạt động của các thuật toán di truyền, và Định lý Lược đồ Holland là một bước đi theo hướng đó. Trong nhiều năm, nhiều cải tiến và đề xuất đã được thực hiện đối với Định lý Lược đồ để làm cho nó trở nên tổng quát hơn.

Trong phần này, chúng tôi không đi sâu vào toán học của Định lý Lược đồ, thay vào đó chúng tôi cố gắng phát triển sự hiểu biết cơ bản về Định lý Lược đồ là gì. Các thuật ngữ cơ bản cần biết như sau:

A Schemalà một "mẫu". Về mặt hình thức, nó là một chuỗi trên bảng chữ cái = {0,1, *},

trong đó * không được quan tâm và có thể nhận bất kỳ giá trị nào.

Do đó, * 10 * 1 có thể có nghĩa là 01001, 01011, 11001 hoặc 11011

Về mặt hình học, một lược đồ là một siêu phẳng trong không gian tìm kiếm lời giải.
Order của một giản đồ là số vị trí cố định xác định trong một gen.

Defining length là khoảng cách giữa hai kí hiệu xa nhất cố định trong gen.

Định lý lược đồ cho biết rằng lược đồ này với mức độ phù hợp trên trung bình, độ dài xác định ngắn và bậc thấp hơn có nhiều khả năng tồn tại sự giao nhau và đột biến hơn.

Giả thuyết về khối xây dựng

Các Khối xây dựng là các khối có thứ tự thấp, schemata có độ dài xác định thấp với thể lực trung bình đã cho ở trên. Giả thuyết về khối xây dựng nói rằng các khối xây dựng như vậy đóng vai trò là nền tảng cho sự thành công và thích ứng của GAs trong GAs khi nó tiến triển bằng cách liên tục xác định và kết hợp lại các “khối xây dựng” như vậy.

Định lý Không có Bữa trưa Miễn phí (NFL)

Wolpert và Macready vào năm 1997 đã xuất bản một bài báo có tiêu đề "Không có định lý bữa trưa miễn phí để tối ưu hóa." Về cơ bản, nó nói rằng nếu chúng ta tính trung bình trên không gian của tất cả các vấn đề có thể xảy ra, thì tất cả các thuật toán hộp đen không truy cập lại sẽ thể hiện cùng một hiệu suất.

Có nghĩa là chúng ta càng hiểu nhiều vấn đề, GA của chúng ta càng trở nên cụ thể hơn về vấn đề và mang lại hiệu suất tốt hơn, nhưng nó bù đắp lại điều đó bằng cách hoạt động kém hơn đối với các vấn đề khác.

Học máy dựa trên GA

Thuật toán di truyền cũng tìm thấy ứng dụng trong Học máy. Classifier systems là một dạng của genetics-based machine learning(GBML) hệ thống thường được sử dụng trong lĩnh vực máy học. Các phương pháp GBML là một cách tiếp cận thích hợp cho học máy.

Có hai loại hệ thống GBML -

The Pittsburg Approach - Trong cách tiếp cận này, một nhiễm sắc thể mã hóa một giải pháp, và do đó tính phù hợp được chỉ định cho các giải pháp.
The Michigan Approach - một giải pháp thường được đại diện bởi nhiều nhiễm sắc thể và do đó sự phù hợp được chỉ định cho các giải pháp từng phần.

Cần lưu ý rằng vấn đề tiêu chuẩn như giao nhau, đột biến, Lamarckian hoặc Darwin, v.v. cũng có trong hệ thống GBML.

Thuật toán di truyền chủ yếu được sử dụng trong các bài toán tối ưu hóa các loại, nhưng chúng cũng thường được sử dụng trong các lĩnh vực ứng dụng khác.

Trong phần này, chúng tôi liệt kê một số lĩnh vực mà Thuật toán di truyền thường được sử dụng. Đây là -

Optimization- Thuật toán di truyền được sử dụng phổ biến nhất trong các bài toán tối ưu hóa, trong đó chúng ta phải tối đa hóa hoặc tối thiểu hóa một giá trị hàm mục tiêu nhất định dưới một tập hợp các ràng buộc nhất định. Cách tiếp cận để giải quyết vấn đề Tối ưu hóa đã được nêu bật trong suốt hướng dẫn.
Economics - GA cũng được sử dụng để mô tả các mô hình kinh tế khác nhau như mô hình mạng nhện, độ phân giải cân bằng lý thuyết trò chơi, định giá tài sản, v.v.
Neural Networks - GA cũng được sử dụng để huấn luyện mạng nơ-ron, đặc biệt là mạng nơ-ron tuần hoàn.
Parallelization - GAs cũng có khả năng song song rất tốt, và được chứng minh là phương tiện rất hiệu quả trong việc giải quyết một số vấn đề nhất định, và cũng cung cấp một lĩnh vực tốt để nghiên cứu.
Image Processing - GA được sử dụng cho các tác vụ xử lý hình ảnh kỹ thuật số (DIP) khác nhau cũng như đối sánh pixel dày đặc.
Vehicle routing problems - Với nhiều cửa sổ thời gian mềm, nhiều kho và một đội xe không đồng nhất.
Scheduling applications - GA cũng được sử dụng để giải quyết các vấn đề lập lịch trình khác nhau, đặc biệt là vấn đề tính toán thời gian.
Machine Learning - như đã thảo luận, học máy dựa trên di truyền học (GBML) là một lĩnh vực thích hợp trong học máy.
Robot Trajectory Generation - GAs đã được sử dụng để lập kế hoạch đường đi mà một cánh tay robot sẽ di chuyển từ điểm này sang điểm khác.
Parametric Design of Aircraft - GA đã được sử dụng để thiết kế máy bay bằng cách thay đổi các thông số và phát triển các giải pháp tốt hơn.
DNA Analysis - GAs đã được sử dụng để xác định cấu trúc của DNA bằng cách sử dụng dữ liệu đo phổ về mẫu.
Multimodal Optimization - GA rõ ràng là cách tiếp cận rất tốt để tối ưu hóa đa phương thức, trong đó chúng ta phải tìm ra nhiều giải pháp tối ưu.
Traveling salesman problem and its applications - GAs đã được sử dụng để giải quyết TSP, đây là một bài toán tổ hợp nổi tiếng bằng cách sử dụng các chiến lược đóng gói và chéo mới.

Có thể tham khảo những cuốn sách sau để nâng cao hơn nữa kiến thức của người đọc về Thuật toán di truyền và Tính toán tiến hóa nói chung -

Thuật toán di truyền trong Tìm kiếm, Tối ưu hóa và Máy học bằng David E. Goldberg.
Thuật toán di truyền + Cấu trúc dữ liệu = Các chương trình tiến hóa bởi Zbigniew Michalewicz.
Các thuật toán di truyền thực tế của Randy L. Haupt và Sue Ellen Haupt.
Tối ưu hóa Đa mục tiêu bằng cách sử dụng Thuật toán tiến hóa bằng Kalyanmoy Deb.