Điện tử công suất - Thông số hiệu suất
Điều quan trọng là phải xác định các tham số hiệu suất cho các bộ chuyển đổi khác nhau có cấu trúc liên kết có thể là một pha hoặc nhiều pha.
Giả định
- Các thiết bị được sử dụng là lý tưởng, tức là chúng không có bất kỳ tổn thất nào
- Các thiết bị có tải điện trở
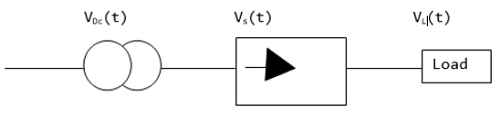
Điện áp DC khi tải
$$ V_ {DC} = \ frac {1} {T} \ int_ {0} ^ {T} V_ {L} \ left (t \ right) dt $$Điện áp RMS khi tải
$$ V_ {L} = \ sqrt {\ frac {1} {T}} \ int_ {0} ^ {T} V_ {L} ^ {2} \ left (t \ right) dt $$Yếu tố hình thức
$$ FF = \ frac {V_ {L}} {V_ {DC}} $$Yếu tố Ripple
$$ RF = \ frac {\ sqrt {V_ {L} ^ {2} -V_ {DC} ^ {2}}} {V_ {DC}} = \ sqrt {FF ^ {2} -1} $$Hiệu quả (Hệ số chỉnh lưu)
$$ \ eta = \ frac {P_ {DC}} {P_ {L} + P_ {D}} $$Trong đó những điều trên được định nghĩa là -
$ P_ {DC} = V_ {DC} \ times I_ {DC} $
$ P_ {L} = V_ {L} \ lần I_ {L} $
$ P_ {D} = R_ {D} \ times I_ {L} ^ {2} $ ($ P_ {D} $ là tổn thất của bộ chỉnh lưu và $ R_ {D} $ là điện trở)
$$ \ eta = \ frac {V_ {DC} I_ {DC}} {\ left (V_ {L} I_ {L} \ right) + \ left (R_ {D} I_ {L} ^ {2} \ right )} = \ frac {V_ {DC} ^ {2}} {V_ {L} ^ {2}} \ times \ frac {1} {1+ \ frac {R_ {D}} {R_ {L}}} $$Nhưng $ R_ {D} = 0 $
Vì thế,
$$ \ eta = \ left (\ frac {V_ {DC}} {V_ {L}} \ right) ^ {2} = \ left (\ frac {1} {FF} \ right) ^ {2} $$Hệ số sử dụng máy biến áp
$$ TUF = \ frac {P_ {DC}} {VA \: Xếp hạng \: of \: the \: Transformer} = \ frac {P_ {DC}} {\ frac {VA_ {p} + VA_ {s}} {2}} $$VA p và VA s là định mức công suất sơ cấp và thứ cấp của máy biến áp.