Python - Chia rẽ và chinh phục
Trong cách tiếp cận phân chia và chinh phục, bài toán trong tay được chia thành các bài toán con nhỏ hơn và sau đó mỗi bài toán được giải quyết độc lập. Khi chúng ta tiếp tục chia các bài toán con thành các bài toán con nhỏ hơn, cuối cùng chúng ta có thể đạt đến một giai đoạn mà không thể phân chia được nữa. Những vấn đề con nhỏ nhất có thể có "nguyên tử" (phân số) được giải quyết. Lời giải của tất cả các bài toán con cuối cùng được hợp nhất để có được lời giải của một bài toán ban đầu.
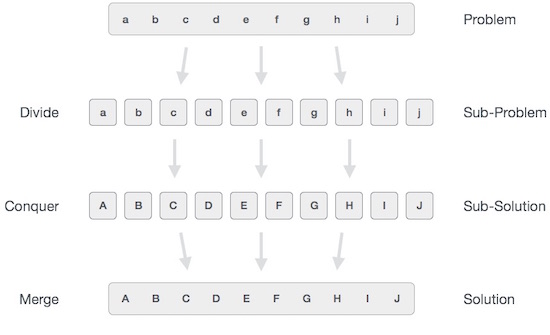
Nói chung, chúng ta có thể hiểu divide-and-conquer cách tiếp cận theo quy trình ba bước.
Chia / ngắt
Bước này liên quan đến việc chia nhỏ vấn đề thành các vấn đề phụ nhỏ hơn. Các vấn đề phụ nên đại diện cho một phần của vấn đề ban đầu. Bước này thường sử dụng một cách tiếp cận đệ quy để chia bài toán cho đến khi không có bài toán con nào có thể chia được nữa. Ở giai đoạn này, các vấn đề phụ trở thành nguyên tử về bản chất nhưng vẫn thể hiện một phần nào đó của vấn đề thực tế.
Chinh phục / Giải quyết
Bước này nhận được rất nhiều vấn đề nhỏ hơn cần giải quyết. Nói chung, ở cấp độ này, các vấn đề được coi là 'tự giải quyết'.
Hợp nhất / Kết hợp
Khi các bài toán con nhỏ hơn được giải quyết, giai đoạn này kết hợp chúng một cách đệ quy cho đến khi chúng tạo thành một giải pháp của bài toán ban đầu. Cách tiếp cận thuật toán này hoạt động đệ quy và các bước chinh phục & hợp nhất hoạt động gần nhau đến mức chúng xuất hiện như một.
Ví dụ
Chương trình sau đây là một ví dụ về divide-and-conquer cách tiếp cận lập trình trong đó tìm kiếm nhị phân được thực hiện bằng python.
Triển khai tìm kiếm nhị phân
Trong tìm kiếm nhị phân, chúng tôi lấy một danh sách các phần tử đã được sắp xếp và bắt đầu tìm kiếm một phần tử ở giữa danh sách. Nếu giá trị tìm kiếm khớp với giá trị giữa trong danh sách, chúng tôi hoàn thành việc tìm kiếm. Nếu không, chúng tôi chọn một nửa danh sách các phần tử bằng cách chọn tăng lên với nửa bên phải hoặc bên trái của danh sách tùy thuộc vào giá trị của mục được tìm kiếm. Điều này có thể thực hiện được vì danh sách được sắp xếp và nhanh hơn nhiều so với tìm kiếm tuyến tính. Ở đây chúng tôi chia danh sách đã cho và chinh phục bằng cách chọn một nửa thích hợp của danh sách. Chúng tôi lặp lại điều này cho đến khi chúng tôi tìm thấy yếu tố hoặc kết luận về sự vắng mặt của nó trong danh sách.
def bsearch(list, val):
list_size = len(list) - 1
idx0 = 0
idxn = list_size
# Find the middle most value
while idx0 <= idxn:
midval = (idx0 + idxn)// 2
if list[midval] == val:
return midval
# Compare the value the middle most value
if val > list[midval]:
idx0 = midval + 1
else:
idxn = midval - 1
if idx0 > idxn:
return None
# Initialize the sorted list
list = [2,7,19,34,53,72]
# Print the search result
print(bsearch(list,72))
print(bsearch(list,11))Khi đoạn mã trên được thực thi, nó tạo ra kết quả sau:
5
None