SciPy - CSGraph
CSGraph là viết tắt của Compressed Sparse Graph, trong đó tập trung vào các thuật toán đồ thị nhanh dựa trên biểu diễn ma trận thưa thớt.
Biểu diễn đồ thị
Để bắt đầu, chúng ta hãy hiểu biểu đồ thưa thớt là gì và nó giúp ích như thế nào trong việc biểu diễn đồ thị.
Chính xác thì đồ thị thưa thớt là gì?
Đồ thị chỉ là một tập hợp các nút, có các liên kết giữa chúng. Đồ thị có thể đại diện cho hầu hết mọi thứ - kết nối mạng xã hội, trong đó mỗi nút là một người và được kết nối với những người quen; hình ảnh, trong đó mỗi nút là một pixel và được kết nối với các pixel lân cận; các điểm trong phân bố chiều cao, nơi mỗi nút được kết nối với các nút lân cận gần nhất của nó; và thực tế là bất cứ điều gì khác mà bạn có thể tưởng tượng.
Một cách rất hiệu quả để biểu diễn dữ liệu đồ thị là trong một ma trận thưa thớt: chúng ta hãy gọi nó là G. Ma trận G có kích thước N x N và G [i, j] cung cấp giá trị của kết nối giữa nút 'i' và nút 'j'. Một biểu đồ thưa thớt chứa hầu hết các số không - tức là hầu hết các nút chỉ có một vài kết nối. Tính chất này hóa ra đúng trong hầu hết các trường hợp quan tâm.
Việc tạo ra mô-đun con đồ thị thưa thớt được thúc đẩy bởi một số thuật toán được sử dụng trong scikit-learning bao gồm những điều sau:
Isomap - Một thuật toán học đa tạp, yêu cầu tìm các đường đi ngắn nhất trong đồ thị.
Hierarchical clustering - Một thuật toán phân cụm dựa trên cây khung tối thiểu.
Spectral Decomposition - Một thuật toán chiếu dựa trên laplacian đồ thị thưa thớt.
Như một ví dụ cụ thể, hãy tưởng tượng rằng chúng tôi muốn biểu diễn đồ thị vô hướng sau:
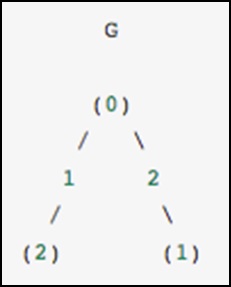
Đồ thị này có ba nút, trong đó nút 0 và 1 được nối với nhau bởi một cạnh trọng số 2, và các nút 0 và 2 được nối với nhau bởi một cạnh trọng số 1. Chúng ta có thể xây dựng các biểu diễn dày đặc, che khuất và thưa thớt như được hiển thị trong ví dụ sau , hãy nhớ rằng đồ thị vô hướng được biểu diễn bằng ma trận đối xứng.
G_dense = np.array([ [0, 2, 1],
[2, 0, 0],
[1, 0, 0] ])
G_masked = np.ma.masked_values(G_dense, 0)
from scipy.sparse import csr_matrix
G_sparse = csr_matrix(G_dense)
print G_sparse.dataChương trình trên sẽ tạo ra kết quả sau.
array([2, 1, 2, 1])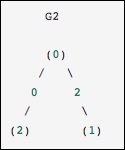
Điều này giống với đồ thị trước đó, ngoại trừ các nút 0 và 2 được nối với nhau bằng một cạnh có trọng số bằng không. Trong trường hợp này, biểu diễn dày đặc ở trên dẫn đến sự không rõ ràng - làm thế nào có thể biểu diễn các cạnh không, nếu số 0 là một giá trị có nghĩa. Trong trường hợp này, phải sử dụng biểu diễn có mặt nạ hoặc biểu diễn thưa thớt để loại bỏ sự mơ hồ.
Chúng ta hãy xem xét ví dụ sau.
from scipy.sparse.csgraph import csgraph_from_dense
G2_data = np.array
([
[np.inf, 2, 0 ],
[2, np.inf, np.inf],
[0, np.inf, np.inf]
])
G2_sparse = csgraph_from_dense(G2_data, null_value=np.inf)
print G2_sparse.dataChương trình trên sẽ tạo ra kết quả sau.
array([ 2., 0., 2., 0.])Thang từ sử dụng đồ thị thưa thớt
Thang chữ là một trò chơi do Lewis Carroll phát minh, trong đó các từ được liên kết với nhau bằng cách thay đổi một chữ cái ở mỗi bước. Ví dụ -
APE → APT → AIT → BIT → BIG → BAG → MAG → MAN
Ở đây, chúng ta đã chuyển từ "APE" sang "MAN" trong bảy bước, thay đổi một ký tự mỗi lần. Câu hỏi đặt ra là - Chúng ta có thể tìm ra đường đi ngắn hơn giữa những từ này bằng cách sử dụng cùng một quy tắc không? Bài toán này được thể hiện một cách tự nhiên như một bài toán đồ thị thưa thớt. Các nút sẽ tương ứng với các từ riêng lẻ và chúng tôi sẽ tạo các kết nối giữa các từ chỉ khác nhau nhiều nhất - một chữ cái.
Lấy một danh sách các từ
Đầu tiên, tất nhiên, chúng ta phải có được một danh sách các từ hợp lệ. Tôi đang chạy Mac và Mac có một từ điển từ ở vị trí được cung cấp trong khối mã sau. Nếu bạn đang sử dụng một kiến trúc khác, bạn có thể phải tìm kiếm một chút để tìm từ điển hệ thống của mình.
wordlist = open('/usr/share/dict/words').read().split()
print len(wordlist)Chương trình trên sẽ tạo ra kết quả sau.
235886Bây giờ chúng ta muốn xem xét các từ có độ dài 3, vì vậy chúng ta hãy chỉ chọn những từ có độ dài chính xác. Chúng tôi cũng sẽ loại bỏ các từ bắt đầu bằng chữ hoa (danh từ riêng) hoặc chứa các ký tự không phải chữ và số như dấu nháy đơn và dấu gạch nối. Cuối cùng, chúng tôi sẽ đảm bảo mọi thứ ở dạng chữ thường để so sánh sau này.
word_list = [word for word in word_list if len(word) == 3]
word_list = [word for word in word_list if word[0].islower()]
word_list = [word for word in word_list if word.isalpha()]
word_list = map(str.lower, word_list)
print len(word_list)Chương trình trên sẽ tạo ra kết quả sau.
1135Bây giờ, chúng tôi có một danh sách gồm 1135 từ gồm ba chữ cái hợp lệ (con số chính xác có thể thay đổi tùy thuộc vào danh sách cụ thể được sử dụng). Mỗi từ này sẽ trở thành một nút trong biểu đồ của chúng tôi và chúng tôi sẽ tạo các cạnh nối các nút được liên kết với mỗi cặp từ, chúng chỉ khác nhau một chữ cái.
import numpy as np
word_list = np.asarray(word_list)
word_list.dtype
word_list.sort()
word_bytes = np.ndarray((word_list.size, word_list.itemsize),
dtype = 'int8',
buffer = word_list.data)
print word_bytes.shapeChương trình trên sẽ tạo ra kết quả sau.
(1135, 3)Chúng tôi sẽ sử dụng khoảng cách Hamming giữa mỗi điểm để xác định cặp từ nào được kết nối với nhau. Khoảng cách Hamming đo tỷ lệ mục nhập giữa hai vectơ, khác nhau: hai từ bất kỳ có khoảng cách hamming bằng 1 / N1 / N, trong đó NN là số chữ cái, được nối với nhau trong thang từ.
from scipy.spatial.distance import pdist, squareform
from scipy.sparse import csr_matrix
hamming_dist = pdist(word_bytes, metric = 'hamming')
graph = csr_matrix(squareform(hamming_dist < 1.5 / word_list.itemsize))Khi so sánh các khoảng cách, chúng tôi không sử dụng bình đẳng vì điều này có thể không ổn định đối với các giá trị dấu phẩy động. Bất đẳng thức tạo ra kết quả mong muốn miễn là không có hai mục nào trong danh sách từ giống nhau. Bây giờ, đồ thị của chúng ta đã được thiết lập, chúng ta sẽ sử dụng tìm kiếm đường đi ngắn nhất để tìm đường đi giữa hai từ bất kỳ trong đồ thị.
i1 = word_list.searchsorted('ape')
i2 = word_list.searchsorted('man')
print word_list[i1],word_list[i2]Chương trình trên sẽ tạo ra kết quả sau.
ape, manChúng ta cần kiểm tra xem các từ này có khớp nhau không, vì nếu các từ không có trong danh sách sẽ có lỗi trong đầu ra. Bây giờ, tất cả những gì chúng ta cần là tìm đường đi ngắn nhất giữa hai chỉ số này trong biểu đồ. Chúng tôi sẽ sử dụngdijkstra’s vì nó cho phép chúng ta tìm đường dẫn cho chỉ một nút.
from scipy.sparse.csgraph import dijkstra
distances, predecessors = dijkstra(graph, indices = i1, return_predecessors = True)
print distances[i2]Chương trình trên sẽ tạo ra kết quả sau.
5.0Do đó, chúng ta thấy rằng con đường ngắn nhất giữa 'vượn' và 'người' chỉ có năm bước. Chúng ta có thể sử dụng các giá trị tiền nhiệm do thuật toán trả về để tạo lại đường dẫn này.
path = []
i = i2
while i != i1:
path.append(word_list[i])
i = predecessors[i]
path.append(word_list[i1])
print path[::-1]i2]Chương trình trên sẽ tạo ra kết quả sau.
['ape', 'ope', 'opt', 'oat', 'mat', 'man']