Kontextfreie Grammatik Einführung
Definition - Eine kontextfreie Grammatik (CFG), die aus einem endlichen Satz von Grammatikregeln besteht, ist ein Vierfacher (N, T, P, S) wo
N ist eine Reihe von nicht-terminalen Symbolen.
T ist eine Reihe von Terminals, wo N ∩ T = NULL.
P ist ein Regelwerk, P: N → (N ∪ T)*dh die linke Seite der Produktionsregel P hat einen rechten oder linken Kontext.
S ist das Startsymbol.
Example
- Die Grammatik ({A}, {a, b, c}, P, A), P: A → aA, A → abc.
- Die Grammatik ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε
- Die Grammatik ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε
Generierung des Ableitungsbaums
Ein Ableitungsbaum oder Analysebaum ist ein geordneter Wurzelbaum, der die semantische Information einer Zeichenfolge grafisch darstellt, die aus einer kontextfreien Grammatik abgeleitet wurde.
Darstellungstechnik
Root vertex - Muss mit dem Startsymbol gekennzeichnet sein.
Vertex - Mit einem nicht terminalen Symbol gekennzeichnet.
Leaves - Beschriftet mit einem Terminalsymbol oder ε.
Wenn S → x 1 x 2 …… x n eine Produktionsregel in einem CFG ist, lautet der Analysebaum / Ableitungsbaum wie folgt:

Es gibt zwei verschiedene Ansätze, um einen Ableitungsbaum zu zeichnen:
Top-down Approach −
Beginnt mit dem Startsymbol S
Geht mit Produktionen zu Baumblättern hinunter
Bottom-up Approach −
Startet von Baumblättern
Geht nach oben zur Wurzel, die das Startsymbol ist S
Ableitung oder Ertrag eines Baumes
Die Ableitung oder der Ertrag eines Analysebaums ist die endgültige Zeichenfolge, die durch Verketten der Beschriftungen der Blätter des Baums von links nach rechts unter Ignorieren der Nullen erhalten wird. Wenn jedoch alle Blätter Null sind, ist die Ableitung Null.
Example
Sei ein CFG {N, T, P, S}
N = {S}, T = {a, b}, Startsymbol = S, P = S → SS | aSb | ε
Eine Ableitung von der obigen CFG ist "abaabb"
S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

Sentential Form und Partial Derivation Tree
Ein partieller Ableitungsbaum ist ein Unterbaum eines Ableitungsbaums / Analysebaums, sodass sich entweder alle untergeordneten Elemente im Unterbaum oder keines im Unterbaum befinden.
Example
Wenn in irgendeiner CFG die Produktionen sind -
S → AB, A → aaA | ε, B → Bb | ε
Der partielle Ableitungsbaum kann folgender sein:
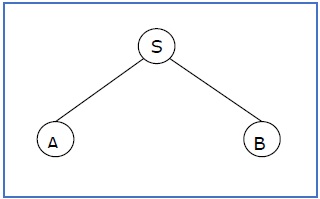
Wenn ein partieller Ableitungsbaum die Wurzel S enthält, heißt er a sentential form. Der obige Unterbaum ist ebenfalls in sententialer Form.
Ableitung eines Strings ganz links und ganz rechts
Leftmost derivation - Eine Ableitung ganz links wird erhalten, indem in jedem Schritt die Produktion auf die Variable ganz links angewendet wird.
Rightmost derivation - Eine Ableitung ganz rechts wird erhalten, indem in jedem Schritt die Produktion auf die Variable ganz rechts angewendet wird.
Example
Lassen Sie einen beliebigen Satz von Produktionsregeln in einer CFG sein
X → X + X | X * X | X | ein
über ein Alphabet {a}.
Die Ableitung ganz links für die Zeichenfolge "a+a*a" kann sein -
X → X + X → a + X → a + X * X → a + a * X → a + a * a
Die schrittweise Ableitung der obigen Zeichenfolge ist wie folgt dargestellt:

Die Ableitung ganz rechts für die obige Zeichenfolge "a+a*a" kann sein -
X → X * X → X * a → X + X * a → X + a * a → a + a * a
Die schrittweise Ableitung der obigen Zeichenfolge ist wie folgt dargestellt:

Rekursive Grammatik links und rechts
In einer kontextfreien Grammatik G, wenn es eine Produktion in der Form gibt X → Xa wo X ist ein nicht-terminales und ‘a’ ist eine Folge von Terminals, es heißt a left recursive production. Die Grammatik mit einer linksrekursiven Produktion heißt aleft recursive grammar.
Und wenn in einer kontextfreien Grammatik G, wenn es eine Produktion gibt, ist in der Form X → aX wo X ist ein nicht-terminales und ‘a’ ist eine Folge von Terminals, es heißt a right recursive production. Die Grammatik mit einer richtigen rekursiven Produktion heißt aright recursive grammar.