CNTK - Recurrent Neural Network
Lassen Sie uns nun verstehen, wie ein wiederkehrendes neuronales Netzwerk (RNN) in CNTK aufgebaut wird.
Einführung
Wir haben gelernt, wie man Bilder mit einem neuronalen Netzwerk klassifiziert, und dies ist eine der wichtigsten Aufgaben beim Deep Learning. Ein weiterer Bereich, in dem sich neuronale Netze auszeichnen und in dem viel Forschung betrieben wird, sind Recurrent Neural Networks (RNN). Hier werden wir wissen, was RNN ist und wie es in Szenarien verwendet werden kann, in denen wir mit Zeitreihendaten umgehen müssen.
Was ist ein wiederkehrendes neuronales Netzwerk?
Wiederkehrende neuronale Netze (RNNs) können als die spezielle Rasse von NNs definiert werden, die im Laufe der Zeit argumentieren können. RNNs werden hauptsächlich in Szenarien verwendet, in denen wir uns mit Werten befassen müssen, die sich im Laufe der Zeit ändern, dh Zeitreihendaten. Um es besser zu verstehen, lassen Sie uns einen kleinen Vergleich zwischen regulären neuronalen Netzen und wiederkehrenden neuronalen Netzen anstellen -
Da wir wissen, dass wir in einem regulären neuronalen Netzwerk nur eine Eingabe bereitstellen können. Dies beschränkt sich darauf, nur eine Vorhersage zu ergeben. Um Ihnen ein Beispiel zu geben, können wir Textaufträge mithilfe regulärer neuronaler Netze übersetzen.
Andererseits können wir in wiederkehrenden neuronalen Netzen eine Folge von Stichproben bereitstellen, die zu einer einzigen Vorhersage führen. Mit anderen Worten, unter Verwendung von RNNs können wir eine Ausgabesequenz basierend auf einer Eingabesequenz vorhersagen. Zum Beispiel gab es einige erfolgreiche Experimente mit RNN bei Übersetzungsaufgaben.
Verwendung von wiederkehrenden neuronalen Netzen
RNNs können auf verschiedene Arten verwendet werden. Einige von ihnen sind wie folgt -
Vorhersage einer einzelnen Ausgabe
Bevor wir uns eingehend mit den Schritten befassen, wie RNN eine einzelne Ausgabe basierend auf einer Sequenz vorhersagen kann, wollen wir uns ansehen, wie ein grundlegendes RNN aussieht

Wie wir im obigen Diagramm sehen können, enthält RNN eine Loopback-Verbindung zum Eingang und verarbeitet jedes Mal, wenn wir eine Folge von Werten eingeben, jedes Element in der Folge als Zeitschritte.
Darüber hinaus kann RNN aufgrund der Loopback-Verbindung die generierte Ausgabe mit der Eingabe für das nächste Element in der Sequenz kombinieren. Auf diese Weise baut RNN über die gesamte Sequenz einen Speicher auf, der zur Vorhersage verwendet werden kann.
Um mit RNN eine Vorhersage zu treffen, können wir die folgenden Schritte ausführen:
Um einen anfänglichen verborgenen Zustand zu erzeugen, müssen wir zuerst das erste Element der Eingabesequenz füttern.
Um danach einen aktualisierten verborgenen Zustand zu erzeugen, müssen wir den anfänglichen verborgenen Zustand nehmen und ihn mit dem zweiten Element in der Eingabesequenz kombinieren.
Um den endgültigen verborgenen Zustand zu erzeugen und die Ausgabe für das RNN vorherzusagen, müssen wir schließlich das letzte Element in der Eingabesequenz nehmen.
Auf diese Weise können wir mithilfe dieser Loopback-Verbindung einem RNN beibringen, Muster zu erkennen, die im Laufe der Zeit auftreten.
Vorhersage einer Sequenz
Das oben diskutierte Grundmodell von RNN kann auch auf andere Anwendungsfälle erweitert werden. Zum Beispiel können wir damit eine Folge von Werten basierend auf einer einzelnen Eingabe vorhersagen. In diesem Szenario können wir die folgenden Schritte ausführen, um eine Vorhersage mit RNN zu treffen:
Um einen anfänglichen verborgenen Zustand zu erzeugen und das erste Element in der Ausgabesequenz vorherzusagen, müssen wir zuerst eine Eingangsabtastung in das neuronale Netzwerk einspeisen.
Danach müssen wir den anfänglichen verborgenen Zustand mit demselben Beispiel kombinieren, um einen aktualisierten verborgenen Zustand und das zweite Element in der Ausgabesequenz zu erzeugen.
Um den verborgenen Zustand noch einmal zu aktualisieren und das endgültige Element in der Ausgabesequenz vorherzusagen, füttern wir die Probe ein weiteres Mal.
Vorhersagen von Sequenzen
Wie wir gesehen haben, wie man einen einzelnen Wert basierend auf einer Sequenz vorhersagt und wie man eine Sequenz basierend auf einem einzelnen Wert vorhersagt. Nun wollen wir sehen, wie wir Sequenzen für Sequenzen vorhersagen können. In diesem Szenario können wir die folgenden Schritte ausführen, um eine Vorhersage mit RNN zu treffen:
Um einen anfänglichen verborgenen Zustand zu erzeugen und das erste Element in der Ausgabesequenz vorherzusagen, müssen wir zuerst das erste Element in der Eingabesequenz nehmen.
Danach müssen wir den anfänglichen verborgenen Zustand annehmen, um den verborgenen Zustand zu aktualisieren und das zweite Element in der Ausgabesequenz vorherzusagen.
Um das letzte Element in der Ausgabesequenz vorherzusagen, müssen wir den aktualisierten verborgenen Zustand und das letzte Element in der Eingabesequenz übernehmen.
Arbeiten von RNN
Um die Funktionsweise wiederkehrender neuronaler Netze (RNNs) zu verstehen, müssen wir zunächst verstehen, wie wiederkehrende Schichten im Netzwerk funktionieren. Lassen Sie uns zunächst diskutieren, wie e die Ausgabe mit einer wiederkehrenden Standardschicht vorhersagen kann.
Vorhersage der Ausgabe mit Standard-RNN-Schicht
Wie bereits erwähnt, unterscheidet sich eine Basisschicht in RNN erheblich von einer regulären Schicht in einem neuronalen Netzwerk. Im vorherigen Abschnitt haben wir im Diagramm auch die grundlegende Architektur von RNN demonstriert. Um den verborgenen Status für die erste Einstiegssequenz zu aktualisieren, können wir die folgende Formel verwenden:

In der obigen Gleichung berechnen wir den neuen verborgenen Zustand, indem wir das Punktprodukt zwischen dem anfänglichen verborgenen Zustand und einer Reihe von Gewichten berechnen.
Für den nächsten Schritt wird nun der verborgene Zustand für den aktuellen Zeitschritt als anfänglicher verborgener Zustand für den nächsten Zeitschritt in der Sequenz verwendet. Um den verborgenen Status für den zweiten Zeitschritt zu aktualisieren, können wir die im ersten Schritt durchgeführten Berechnungen wie folgt wiederholen:
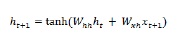
Als nächstes können wir den Vorgang des Aktualisierens des verborgenen Zustands für den dritten und letzten Schritt in der Sequenz wie folgt wiederholen:

Und wenn wir alle oben genannten Schritte in der Sequenz verarbeitet haben, können wir die Ausgabe wie folgt berechnen:

Für die obige Formel haben wir einen dritten Satz von Gewichten und den verborgenen Zustand aus dem letzten Zeitschritt verwendet.
Erweiterte wiederkehrende Einheiten
Das Hauptproblem bei der wiederkehrenden Grundschicht ist das Verschwinden des Gradientenproblems, und aufgrund dessen ist es nicht sehr gut, Langzeitkorrelationen zu lernen. Mit einfachen Worten, die wiederkehrende Grundebene verarbeitet lange Sequenzen nicht sehr gut. Aus diesem Grund sind einige andere wiederkehrende Ebenentypen, die für die Arbeit mit längeren Sequenzen viel besser geeignet sind, wie folgt:
Langzeit-Kurzzeitgedächtnis (LSTM)

Langzeit-Kurzzeitgedächtnis-Netzwerke (LSTMs) wurden von Hochreiter & Schmidhuber eingeführt. Es löste das Problem, eine grundlegende wiederkehrende Ebene zu erhalten, um sich lange an Dinge zu erinnern. Die Architektur von LSTM ist oben im Diagramm angegeben. Wie wir sehen können, hat es Eingangsneuronen, Speicherzellen und Ausgangsneuronen. Um das Problem des verschwindenden Gradienten zu bekämpfen, verwenden Langzeit-Kurzzeitgedächtnisnetzwerke eine explizite Speicherzelle (speichert die vorherigen Werte) und die folgenden Gatter:
Forget gate- Wie der Name schon sagt, weist es die Speicherzelle an, die vorherigen Werte zu vergessen. Die Speicherzelle speichert die Werte, bis das Gate, dh 'Gate vergessen', es auffordert, sie zu vergessen.
Input gate- Wie der Name schon sagt, werden der Zelle neue Inhalte hinzugefügt.
Output gate- Wie der Name schon sagt, entscheidet das Ausgangsgatter, wann die Vektoren von der Zelle zum nächsten verborgenen Zustand weitergeleitet werden sollen.
Gated Recurrent Units (GRUs)

Gradient recurrent units(GRUs) ist eine geringfügige Variation des LSTM-Netzwerks. Es hat ein Gate weniger und ist etwas anders verdrahtet als LSTMs. Die Architektur ist im obigen Diagramm dargestellt. Es hat Eingangsneuronen, gesteuerte Speicherzellen und Ausgangsneuronen. Gated Recurrent Units Netzwerk hat die folgenden zwei Gates -
Update gate- Es bestimmt die folgenden zwei Dinge -
Welche Menge an Informationen sollte vom letzten Zustand ferngehalten werden?
Welche Menge an Informationen sollte aus der vorherigen Ebene eingelassen werden?
Reset gate- Die Funktionalität des Reset-Gatters ähnelt der des Vergessens-Gatters des LSTM-Netzwerks. Der einzige Unterschied ist, dass es etwas anders liegt.
Im Gegensatz zum Langzeit-Kurzzeitspeicher-Netzwerk sind Gated Recurrent Unit-Netzwerke etwas schneller und einfacher auszuführen.
RNN-Struktur erstellen
Bevor wir beginnen können, Vorhersagen über die Ausgabe einer unserer Datenquellen zu treffen, müssen wir zuerst RNN konstruieren, und die Konstruktion von RNN ist ziemlich dieselbe, wie wir im vorherigen Abschnitt ein reguläres neuronales Netzwerk aufgebaut hatten. Es folgt der Code zum Erstellen von one−
from cntk.losses import squared_error
from cntk.io import CTFDeserializer, MinibatchSource, INFINITELY_REPEAT, StreamDefs, StreamDef
from cntk.learners import adam
from cntk.logging import ProgressPrinter
from cntk.train import TestConfig
BATCH_SIZE = 14 * 10
EPOCH_SIZE = 12434
EPOCHS = 10Mehrere Schichten stecken
Wir können auch mehrere wiederkehrende Schichten in CNTK stapeln. Zum Beispiel können wir die folgende Kombination von Schichten verwenden
from cntk import sequence, default_options, input_variable
from cntk.layers import Recurrence, LSTM, Dropout, Dense, Sequential, Fold
features = sequence.input_variable(1)
with default_options(initial_state = 0.1):
model = Sequential([
Fold(LSTM(15)),
Dense(1)
])(features)
target = input_variable(1, dynamic_axes=model.dynamic_axes)Wie wir im obigen Code sehen können, haben wir die folgenden zwei Möglichkeiten, wie wir RNN in CNTK modellieren können:
Erstens, wenn wir nur die endgültige Ausgabe einer wiederkehrenden Ebene wollen, können wir die verwenden Fold Schicht in Kombination mit einer wiederkehrenden Schicht wie GRU, LSTM oder sogar RNNStep.
Zweitens können wir alternativ auch das verwenden Recurrence Block.
Training RNN mit Zeitreihendaten
Sobald wir das Modell erstellt haben, wollen wir sehen, wie wir RNN in CNTK trainieren können -
from cntk import Function
@Function
def criterion_factory(z, t):
loss = squared_error(z, t)
metric = squared_error(z, t)
return loss, metric
loss = criterion_factory(model, target)
learner = adam(model.parameters, lr=0.005, momentum=0.9)Um die Daten in den Trainingsprozess zu laden, müssen Sequenzen aus einer Reihe von CTF-Dateien deserialisiert werden. Der folgende Code hat diecreate_datasource Funktion, eine nützliche Dienstprogrammfunktion zum Erstellen der Trainings- und Testdatenquelle.
target_stream = StreamDef(field='target', shape=1, is_sparse=False)
features_stream = StreamDef(field='features', shape=1, is_sparse=False)
deserializer = CTFDeserializer(filename, StreamDefs(features=features_stream, target=target_stream))
datasource = MinibatchSource(deserializer, randomize=True, max_sweeps=sweeps)
return datasource
train_datasource = create_datasource('Training data filename.ctf')#we need to provide the location of training file we created from our dataset.
test_datasource = create_datasource('Test filename.ctf', sweeps=1) #we need to provide the location of testing file we created from our dataset.Nachdem wir die Datenquellen, das Modell und die Verlustfunktion eingerichtet haben, können wir den Trainingsprozess starten. Es ist ziemlich ähnlich wie in den vorherigen Abschnitten mit grundlegenden neuronalen Netzen.
progress_writer = ProgressPrinter(0)
test_config = TestConfig(test_datasource)
input_map = {
features: train_datasource.streams.features,
target: train_datasource.streams.target
}
history = loss.train(
train_datasource,
epoch_size=EPOCH_SIZE,
parameter_learners=[learner],
model_inputs_to_streams=input_map,
callbacks=[progress_writer, test_config],
minibatch_size=BATCH_SIZE,
max_epochs=EPOCHS
)Wir werden die Ausgabe wie folgt erhalten -
Ausgabe−
average since average since examples
loss last metric last
------------------------------------------------------
Learning rate per minibatch: 0.005
0.4 0.4 0.4 0.4 19
0.4 0.4 0.4 0.4 59
0.452 0.495 0.452 0.495 129
[…]Validierung des Modells
Das tatsächliche Rediktieren mit einem RNN ähnelt dem Vorhersagen mit jedem anderen CNK-Modell. Der einzige Unterschied besteht darin, dass wir Sequenzen anstelle einzelner Stichproben bereitstellen müssen.
Jetzt, da unser RNN endlich mit dem Training fertig ist, können wir das Modell validieren, indem wir es anhand einiger Beispielsequenzen wie folgt testen:
import pickle
with open('test_samples.pkl', 'rb') as test_file:
test_samples = pickle.load(test_file)
model(test_samples) * NORMALIZEAusgabe−
array([[ 8081.7905],
[16597.693 ],
[13335.17 ],
...,
[11275.804 ],
[15621.697 ],
[16875.555 ]], dtype=float32)