Physik - Sphärische Linsen
Einführung
Ein transparentes Material (normalerweise Glas), das durch zwei Oberflächen gebunden ist, von denen eine oder beide Oberflächen kugelförmig sind, wird als "sphärische Linse" bezeichnet.

Konvexe Linse
Eine Linse kann zwei sphärische Oberflächen haben, die sich nach außen wölben (wie in dem unten angegebenen Bild gezeigt) und als konvexe Linse oder doppelte konvexe Linse bekannt sind.
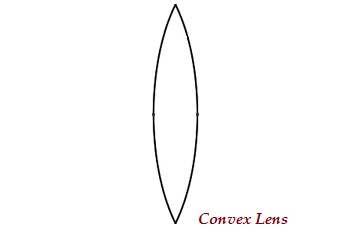
Der mittlere Teil dieser Linse ist gewölbt (dicker) und an beiden Enden schmal.
Konvexlinse konvergiert die Lichtstrahlen; daher ist es auch bekannt alsconverging lens.
Konkave Linse
Eine Linse kann zwei nach innen gekrümmte sphärische Oberflächen haben (wie in dem unten angegebenen Bild gezeigt), die als Konkavlinse oder Doppelkonkavlinse bekannt ist.
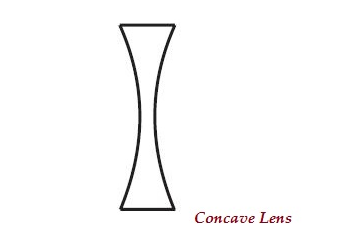
Der mittlere Teil dieser Linse ist schmal (nach innen gebogen) und beide Kanten sind dicker.
Konkavlinse divergiert die Lichtstrahlen; daher ist es auch bekannt alsdiverging lens.
Eine Linse, entweder eine konkave oder eine konvexe, hat zwei sphärische Oberflächen und jede dieser Oberflächen bildet einen Teil der Kugel. Die Zentren dieser Kugeln sind bekannt alscenters of curvature, vertreten durch den englischen Buchstaben 'C. '
Da es zwei Krümmungszentren gibt, werden sie als "C 1 " und "C 2" dargestellt .
Eine imaginäre gerade Linie, die durch beide Krümmungszentren einer Linse verläuft, ist bekannt als principal axis.
Das optische Zentrum ist der Mittelpunkt einer Linse. Es wird vertreten durch 'O. '
Eine Apertur ist der tatsächliche Durchmesser des kreisförmigen Umrisses einer sphärischen Linse.
Der Hauptfokus der Linse wird dargestellt durch 'F. '
Eine Linse hat normalerweise zwei Brennpunkte, die als F 1 und F 2 dargestellt sind .
Focal lengthist der Abstand zwischen dem Hauptfokus und dem optischen Zentrum einer Linse. Es wird vertreten durch 'f. '
Die folgende Tabelle zeigt die Art und Position von Bildern, die von einer konvexen Linse erzeugt werden.
| Position des Objekts | Position des Bildes | Größe des Bildes | Natur des Bildes | Bild |
|---|---|---|---|---|
| Im Unendlichen | Im Fokus F 2 | Stark verkleinert, spitz | Real und invertiert |
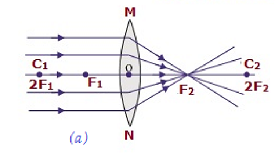
|
| Jenseits von 2F 1 | S / w F 2 und 2F 2 | Vermindert | Real und invertiert |
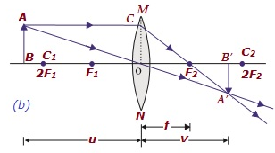
|
| Bei 2F 1 | Bei 2F 2 | Gleiche Größe | Real und invertiert |
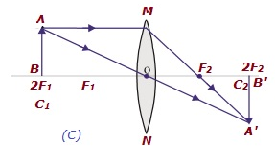
|
| S / w F 1 & 2F 1 | Jenseits von 2F 2 | Vergrößert | Real und invertiert |

|
| Im Fokus F 1 | Im Unendlichen | Unendlich groß oder stark vergrößert | Real & inverte d |
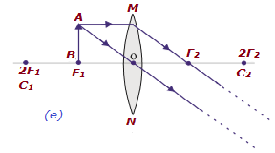
|
| S / W-Fokus F 1 & optisches Zentrum O. | Auf der gleichen Seite der Linse wie das Objekt | Vergrößert | Virtuell und aufrecht |
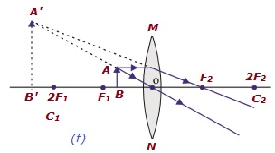
|
Die folgende Tabelle zeigt die Art und Position der von einer Konkavlinse erzeugten Bilder -
| Position des Objekts | Position des Bildes | Relative Bildgröße | Natur des Bildes | Bild |
|---|---|---|---|---|
| Im Unendlichen | Im Fokus F 1 | Stark verkleinert d, punktförmig | Virtuell und aufrecht |
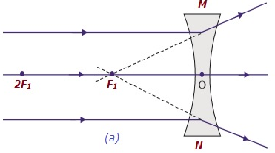
|
| S / w unendlich & optisches Zentrum O der Linse | S / w F 1 & optisches Zentrum O. | Diminishe d | Virtuell und aufrecht |
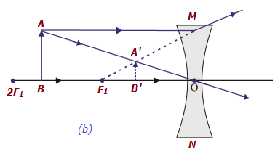
|
Linsenformel
Die Formel wird ausgedrückt als -
Die Linsenformel drückt die Beziehungen zwischen der Objektentfernung aus (dh u), Bildabstand (dh v) und Brennweite (dh f) einer Linse.
$$ \ frac {1} {v} - \ frac {1} {u} = \ frac {1} {f} $$