Zeitbasisgeneratoren - Übersicht
Nachdem wir die Grundlagen von Impulsschaltungen besprochen haben, wollen wir nun verschiedene Schaltungen durchgehen, die erzeugen und damit umgehen Saw tooth waves. Eine Sägezahnwelle nimmt linear mit der Zeit zu und nimmt plötzlich ab. Dies wird auch als bezeichnetTime base signal. Tatsächlich ist dies die ideale Ausgabe eines Zeitbasisgenerators.
Was ist ein Zeitbasisgenerator?
Ein elektronischer Generator, der die erzeugt high frequency saw tooth waves kann als bezeichnet werden Time Base Generator. Es kann auch als eine elektronische Schaltung verstanden werden, die eine Ausgangsspannungs- oder Stromwellenform erzeugt, von der ein Teil davon istvaries linearly with time. Die Horizontalgeschwindigkeit eines Zeitbasisgenerators muss konstant sein.
Um die zeitlichen Schwankungen eines Signals auf einem Oszilloskop anzuzeigen, muss an die Ablenkplatten eine Spannung angelegt werden, die sich linear mit der Zeit ändert. Dies bewirkt, dass das Signal den Strahl horizontal über den Bildschirm streicht. Daher wird die Spannung als bezeichnetSweep Voltage. Die Zeitbasisgeneratoren heißen alsSweep Circuits.
Merkmale eines Zeitbasissignals
Um eine Zeitbasiswellenform in einem CRO oder einer Bildröhre zu erzeugen, steigt die Ablenkspannung linear mit der Zeit an. Im Allgemeinen wird ein Zeitbasisgenerator verwendet, bei dem der Strahl linear über den Bildschirm abgelenkt wird und zu seinem Startpunkt zurückkehrt. Dies geschieht während des Prozesses vonScanning. Eine Kathodenstrahlröhre und auch eine Bildröhre arbeiten nach dem gleichen Prinzip. Der Strahl wird über den Bildschirm von einer Seite zur anderen abgelenkt (im Allgemeinen von links nach rechts) und kehrt zum selben Punkt zurück.
Dieses Phänomen wird als bezeichnet Trace und Retrace. Die Ablenkung des Strahls über den Bildschirm von links nach rechts wird als bezeichnetTrace, während die Rückkehr des Strahls von rechts nach links als bezeichnet wird Retrace oder Fly back. Normalerweise ist dieser Rücklauf nicht sichtbar. Dieser Vorgang erfolgt mit Hilfe eines Sägezahnwellengenerators, der mit Hilfe der verwendeten RC-Komponenten den Zeitraum der Auslenkung einstellt.
Versuchen wir, die Teile einer Sägezahnwelle zu verstehen.

In dem obigen Signal wird die Zeit, während der der Ausgang linear ansteigt, als bezeichnet Sweep Time (TS) und die Zeit, die das Signal benötigt, um zu seinem Anfangswert zurückzukehren, wird als bezeichnet Restoration Time oder Fly back Time oder Retrace Time (Tr). Beide Zeiträume bilden zusammen den Zeitraum eines Zyklus des Zeitbasissignals.
Tatsächlich ist diese Sweep-Spannungswellenform, die wir erhalten, die praktische Ausgabe einer Sweep-Schaltung, während die ideale Ausgabe die in der obigen Abbildung gezeigte Sägezahn-Wellenform sein muss.
Arten von Zeitbasisgeneratoren
Es gibt zwei Arten von Zeitbasisgeneratoren. Sie sind -
Voltage Time Base Generators - Ein Zeitbasisgenerator, der eine Ausgangsspannungswellenform liefert, die sich linear mit der Zeit ändert, wird als Spannungszeitbasisgenerator bezeichnet.
Current Time Base Generator - Ein Zeitbasisgenerator, der eine Ausgangsstromwellenform liefert, die sich linear mit der Zeit ändert, wird als Stromzeitbasisgenerator bezeichnet.
Anwendungen
Zeitbasisgeneratoren werden in CROs, Fernsehgeräten, RADAR-Displays, präzisen Zeitmesssystemen und Zeitmodulation verwendet.
Fehler von Sweep-Signalen
Nach dem Erzeugen der Wobbelsignale ist es Zeit, diese zu übertragen. Das übertragene Signal kann einer Abweichung von der Linearität ausgesetzt sein. Um die aufgetretenen Fehler zu verstehen und zu korrigieren, müssen wir einige Kenntnisse über die häufig auftretenden Fehler haben.
Die Abweichung von der Linearität wird auf drei verschiedene Arten ausgedrückt. Sie sind -
- Der Slope- oder Sweep-Geschwindigkeitsfehler
- Der Verschiebungsfehler
- Der Übertragungsfehler
Lassen Sie uns diese im Detail diskutieren.
Der Slope- oder Sweep-Geschwindigkeitsfehler (e s )
Eine Sweep-Spannung muss linear mit der Zeit ansteigen. Die Änderungsrate der Wobbelspannung mit der Zeit muss konstant sein. Diese Abweichung von der Linearität ist definiert alsSlope Speed Error oder Sweep Speed Error.
Slope oder Sweep Geschwindigkeit eror e s = $ \ frac {Differenz \: in \: Steigung \: at \: die \: Anfang \: und \: end \: von \: Sweep} {Anfangs \: value \: of \ : Steigung} $
$$ = \ frac {\ left (\ frac {\ mathrm {d} V_0} {\ mathrm {d} t} \ right) _ {t = 0} - \ left (\ frac {\ mathrm {d} V_0} {\ mathrm {d} t} \ right) _ {t = T_s}} {\ left (\ frac {\ mathrm {d} V_0} {\ mathrm {d} t} \ right) _ {t = 0}} $$
Der Verschiebungsfehler (e d )
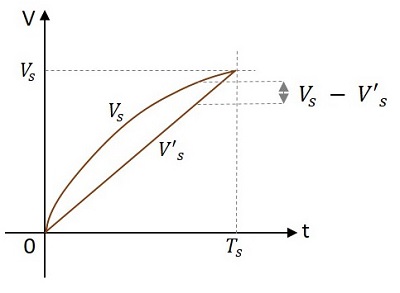
Ein wichtiges Kriterium für die Linearität ist die maximale Differenz zwischen der tatsächlichen Durchlaufspannung und dem linearen Durchlauf, der durch den Anfangs- und Endpunkt des tatsächlichen Durchlaufs verläuft.
Dies ist aus der folgenden Abbildung ersichtlich.
Der Verschiebungsfehler ed ist definiert als
e d = $ \ frac {(tatsächliche \: Geschwindigkeit) \ thicksim (linear \ \ Sweep \: das \: passiert \: Anfang \: und \: Ende \: von \: tatsächlich \: Sweep)} {Amplitude \: von \: sweep \: at \: the \: end \: von \: sweep \: time} $
$$ = \: \ frac {(V_s - V′_s) _ {max}} {V_s} $$
Wobei V s der tatsächliche Sweep und V ' s der lineare Sweep ist.
Der Übertragungsfehler (e t )
Wenn ein Wobbelsignal eine Hochpassschaltung durchläuft, weicht der Ausgang wie unten gezeigt vom Eingang ab.
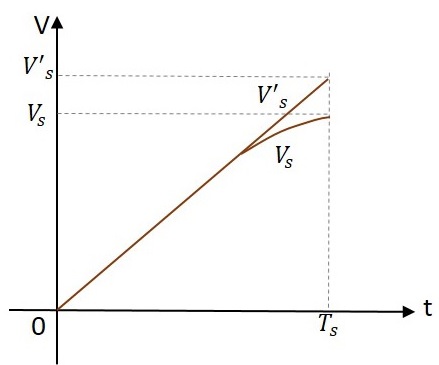
Diese Abweichung wird als Übertragungsfehler ausgedrückt.
Übertragungsfehler = $ \ frac {(Eingabe) \: \ thicksim \ :( Ausgabe)} {Eingabe \: at \: the \: end \: of \: the \: sweep} $
$$ e_t = \ frac {V′_s - V} {V′_s} $$
Wobei V ' s der Eingang und V s der Ausgang am Ende des Sweeps ist, dh bei t = T s .
Wenn die Abweichung von der Linearität sehr klein ist und die Wobbelspannung durch die Summe der linearen und quadratischen Terme in t angenähert werden kann, dann hängen die obigen drei Fehler als zusammen
$$ e_d = \ frac {e_s} {8} = \ frac {e_t} {4} $$
$$ e_s = 2e_t = 8e_d $$
Der Wobbelgeschwindigkeitsfehler ist dominanter als der Verschiebungsfehler.