Python Deep Learning - Implementierungen

Bei dieser Implementierung von Deep Learning ist es unser Ziel, den Kundenabrieb oder die Abwanderung von Daten für eine bestimmte Bank vorherzusagen - welche Kunden diesen Bankdienst wahrscheinlich verlassen werden. Der verwendete Datensatz ist relativ klein und enthält 10000 Zeilen mit 14 Spalten. Wir verwenden die Anaconda-Distribution und Frameworks wie Theano, TensorFlow und Keras. Keras basiert auf Tensorflow und Theano, die als Backends fungieren.

# Artificial Neural Network
# Installing Theano
pip install --upgrade theano

# Installing Tensorflow
pip install –upgrade tensorflow

# Installing Keras
pip install --upgrade keras

Schritt 1: Datenvorverarbeitung

In[]:

# Importing the libraries
   import numpy as np
   import matplotlib.pyplot as plt
   import pandas as pd
 
# Importing the database
   dataset = pd.read_csv('Churn_Modelling.csv')

Schritt 2

Wir erstellen Matrizen der Merkmale des Datensatzes und der Zielvariablen in Spalte 14, die als "Beendet" gekennzeichnet ist.

Das anfängliche Aussehen der Daten ist wie folgt:

In[]:
X = dataset.iloc[:, 3:13].values
Y = dataset.iloc[:, 13].values
X

Ausgabe

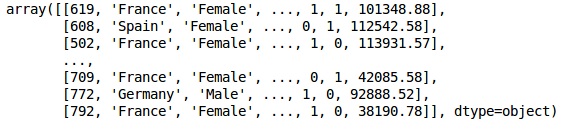
Schritt 3

Ausgabe

array([1, 0, 1, ..., 1, 1, 0], dtype = int64)

Schritt 4

Wir vereinfachen die Analyse, indem wir Zeichenfolgenvariablen codieren. Wir verwenden die ScikitLearn-Funktion 'LabelEncoder', um die verschiedenen Beschriftungen in den Spalten mit Werten zwischen 0 und n_classes-1 automatisch zu codieren.

from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder_X_1 = LabelEncoder() 
X[:,1] = labelencoder_X_1.fit_transform(X[:,1]) 
labelencoder_X_2 = LabelEncoder() 
X[:, 2] = labelencoder_X_2.fit_transform(X[:, 2])
X

Ausgabe

In der obigen Ausgabe werden Ländernamen durch 0, 1 und 2 ersetzt. während männlich und weiblich durch 0 und 1 ersetzt werden.

Schritt 5

Labelling Encoded Data

Wir benutzen das gleiche ScikitLearn Bibliothek und eine andere Funktion namens OneHotEncoder um einfach die Spaltennummer zu übergeben und eine Dummy-Variable zu erstellen.

onehotencoder = OneHotEncoder(categorical features = [1])
X = onehotencoder.fit_transform(X).toarray()
X = X[:, 1:]
X

Jetzt repräsentieren die ersten beiden Spalten das Land und die vierte Spalte das Geschlecht.

Ausgabe

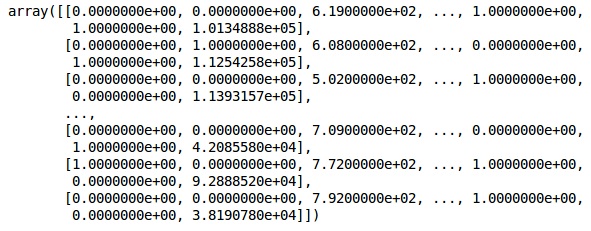
Wir teilen unsere Daten immer in Schulungs- und Testteile auf. Wir trainieren unser Modell anhand von Trainingsdaten und überprüfen dann die Genauigkeit eines Modells anhand von Testdaten, um die Effizienz des Modells zu bewerten.

Schritt 6

Wir verwenden ScikitLearns train_test_splitFunktion zum Aufteilen unserer Daten in Trainingssatz und Testsatz. Wir behalten das Split-Verhältnis von Zug zu Test bei 80:20.

#Splitting the dataset into the Training set and the Test Set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)

Einige Variablen haben Werte in Tausend, während andere Werte in Zehnern oder Einsen haben. Wir skalieren die Daten so, dass sie repräsentativer sind.

Schritt 7

In diesem Code passen wir die Trainingsdaten mit dem an und transformieren sie StandardScalerFunktion. Wir standardisieren unsere Skalierung so, dass wir die gleiche angepasste Methode zum Transformieren / Skalieren von Testdaten verwenden.

# Feature Scaling

fromsklearn.preprocessing import StandardScaler 
sc = StandardScaler() 
X_train = sc.fit_transform(X_train) 
X_test = sc.transform(X_test)

Ausgabe

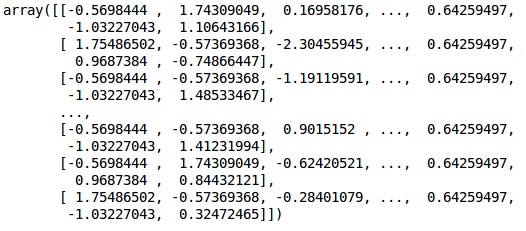
Die Daten sind jetzt richtig skaliert. Schließlich sind wir mit unserer Datenvorverarbeitung fertig. Jetzt beginnen wir mit unserem Modell.

Schritt 8

Wir importieren hier die benötigten Module. Wir benötigen das sequentielle Modul zum Initialisieren des neuronalen Netzwerks und das dichte Modul zum Hinzufügen der verborgenen Schichten.

# Importing the Keras libraries and packages 
import keras 
from keras.models import Sequential 
from keras.layers import Dense

Schritt 9

Wir werden das Modell als Klassifikator bezeichnen, da unser Ziel darin besteht, die Kundenabwanderung zu klassifizieren. Dann verwenden wir das sequentielle Modul zur Initialisierung.

#Initializing Neural Network 
classifier = Sequential()

Schritt 10

Wir fügen die verborgenen Ebenen einzeln mit der Funktion "Dicht" hinzu. Im folgenden Code sehen wir viele Argumente.

Unser erster Parameter ist output_dim. Dies ist die Anzahl der Knoten, die wir dieser Ebene hinzufügen.initist die Initialisierung des Stochastic Gradient Decent. In einem neuronalen Netzwerk weisen wir jedem Knoten Gewichte zu. Bei der Initialisierung sollten die Gewichte nahe Null sein, und wir initialisieren die Gewichte zufällig mit der einheitlichen Funktion. Dasinput_dimDer Parameter wird nur für die erste Ebene benötigt, da das Modell die Anzahl unserer Eingabevariablen nicht kennt. Hier beträgt die Gesamtzahl der Eingabevariablen 11. In der zweiten Ebene kennt das Modell automatisch die Anzahl der Eingabevariablen aus der ersten verborgenen Ebene.

Führen Sie die folgende Codezeile aus, um die Eingabeebene und die erste verborgene Ebene hinzuzufügen:

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu', input_dim = 11))

Führen Sie die folgende Codezeile aus, um die zweite verborgene Ebene hinzuzufügen:

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu'))

Führen Sie die folgende Codezeile aus, um die Ausgabeebene hinzuzufügen:

classifier.add(Dense(units = 1, kernel_initializer = 'uniform', 
activation = 'sigmoid'))

Schritt 11

Compiling the ANN

Wir haben unserem Klassifikator bisher mehrere Ebenen hinzugefügt. Wir werden sie jetzt mit dem kompilierencompileMethode. Argumente, die in der endgültigen Kompilierungssteuerung hinzugefügt wurden, vervollständigen das neuronale Netzwerk. Daher müssen wir in diesem Schritt vorsichtig sein.

Hier ist eine kurze Erklärung der Argumente.

Das erste Argument ist OptimizerDies ist ein Algorithmus, der verwendet wird, um den optimalen Satz von Gewichten zu finden. Dieser Algorithmus heißtStochastic Gradient Descent (SGD). Hier verwenden wir einen von mehreren Typen, den "Adam-Optimierer". Der SGD hängt vom Verlust ab, daher ist unser zweiter Parameter der Verlust. Wenn unsere abhängige Variable binär ist, verwenden wir die aufgerufene logarithmische Verlustfunktion‘binary_crossentropy’und wenn unsere abhängige Variable mehr als zwei Kategorien in der Ausgabe hat, verwenden wir ‘categorical_crossentropy’. Wir möchten die Leistung unseres neuronalen Netzwerks basierend auf verbessernaccuracy, so fügen wir hinzu metrics als Genauigkeit.

# Compiling Neural Network 
classifier.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])

Schritt 12

In diesem Schritt muss eine Reihe von Codes ausgeführt werden.

Anpassen des ANN an das Trainingsset

Wir trainieren jetzt unser Modell anhand der Trainingsdaten. Wir nehmen dasfitMethode für unser Modell. Wir optimieren auch die Gewichte, um die Modelleffizienz zu verbessern. Dazu müssen wir die Gewichte aktualisieren.Batch size ist die Anzahl der Beobachtungen, nach denen wir die Gewichte aktualisieren. Epochist die Gesamtzahl der Iterationen. Die Werte für Chargengröße und Epoche werden nach der Trial-and-Error-Methode ausgewählt.

classifier.fit(X_train, y_train, batch_size = 10, epochs = 50)

Vorhersagen treffen und das Modell bewerten

# Predicting the Test set results
y_pred = classifier.predict(X_test)
y_pred = (y_pred > 0.5)

Vorhersage einer einzelnen neuen Beobachtung

# Predicting a single new observation
"""Our goal is to predict if the customer with the following data will leave the bank:
Geography: Spain
Credit Score: 500
Gender: Female
Age: 40
Tenure: 3
Balance: 50000
Number of Products: 2
Has Credit Card: Yes
Is Active Member: Yes

Schritt 13

Predicting the test set result

Das Vorhersageergebnis gibt Ihnen die Wahrscheinlichkeit, dass der Kunde das Unternehmen verlässt. Wir werden diese Wahrscheinlichkeit in binäre 0 und 1 umwandeln.

# Predicting the Test set results 
y_pred = classifier.predict(X_test) 
y_pred = (y_pred > 0.5)

new_prediction = classifier.predict(sc.transform
(np.array([[0.0, 0, 500, 1, 40, 3, 50000, 2, 1, 1, 40000]])))
new_prediction = (new_prediction > 0.5)

Schritt 14

Dies ist der letzte Schritt, in dem wir unsere Modellleistung bewerten. Wir haben bereits Originalergebnisse und können daher eine Verwirrungsmatrix erstellen, um die Genauigkeit unseres Modells zu überprüfen.

Making the Confusion Matrix

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
print (cm)

Ausgabe

loss: 0.3384 acc: 0.8605
[ [1541 54]
[230 175] ]

Aus der Verwirrungsmatrix kann die Genauigkeit unseres Modells berechnet werden als -

Accuracy = 1541+175/2000=0.858

We achieved 85.8% accuracy, was gut ist.

Der Vorwärtsausbreitungsalgorithmus

In diesem Abschnitt erfahren Sie, wie Sie Code schreiben, um die Vorwärtsausbreitung (Vorhersage) für ein einfaches neuronales Netzwerk durchzuführen.

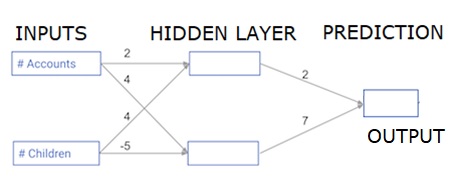
Jeder Datenpunkt ist ein Kunde. Die erste Eingabe gibt an, wie viele Konten sie haben, und die zweite Eingabe gibt an, wie viele Kinder sie haben. Das Modell wird vorhersagen, wie viele Transaktionen der Benutzer im nächsten Jahr tätigt.

Die Eingabedaten sind als Eingabedaten vorinstalliert, und die Gewichte befinden sich in einem Wörterbuch, das als Gewichte bezeichnet wird. Das Array von Gewichten für den ersten Knoten in der verborgenen Schicht ist in Gewichten ['node_0'] und für den zweiten Knoten in der verborgenen Schicht in Gewichten ['node_1'] angegeben.

Die in den Ausgabeknoten eingespeisten Gewichte sind in Gewichten verfügbar.

Die gleichgerichtete lineare Aktivierungsfunktion

Eine "Aktivierungsfunktion" ist eine Funktion, die an jedem Knoten funktioniert. Es wandelt die Eingabe des Knotens in eine Ausgabe um.

Die gleichgerichtete lineare Aktivierungsfunktion ( ReLU genannt ) ist in sehr leistungsstarken Netzwerken weit verbreitet. Diese Funktion verwendet eine einzelne Zahl als Eingabe und gibt 0 zurück, wenn der Eingang negativ ist, und den Eingang als Ausgang, wenn der Eingang positiv ist.

Hier einige Beispiele -

relu (4) = 4
relu (-2) = 0

Wir füllen die Definition der Funktion relu () aus

Wir verwenden die Funktion max (), um den Wert für die Ausgabe von relu () zu berechnen.
Wir wenden die Funktion relu () auf node_0_input an, um node_0_output zu berechnen.
Wir wenden die Funktion relu () auf node_1_input an, um node_1_output zu berechnen.

import numpy as np
input_data = np.array([-1, 2])
weights = {
   'node_0': np.array([3, 3]),
   'node_1': np.array([1, 5]),
   'output': np.array([2, -1])
}
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = np.tanh(node_0_input)
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = np.tanh(node_1_input)
hidden_layer_output = np.array(node_0_output, node_1_output)
output =(hidden_layer_output * weights['output']).sum()
print(output)

def relu(input):
   '''Define your relu activation function here'''
   # Calculate the value for the output of the relu function: output
   output = max(input,0)
      # Return the value just calculated
   return(output)
# Calculate node 0 value: node_0_output
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = relu(node_0_input)

# Calculate node 1 value: node_1_output
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = relu(node_1_input)

# Put node values into array: hidden_layer_outputs
hidden_layer_outputs = np.array([node_0_output, node_1_output])

# Calculate model output (do not apply relu)
odel_output = (hidden_layer_outputs * weights['output']).sum()
print(model_output)# Print model output

Ausgabe

0.9950547536867305
-3

Anwenden des Netzwerks auf viele Beobachtungen / Datenzeilen

In diesem Abschnitt erfahren Sie, wie Sie eine Funktion namens Predict_with_network () definieren. Diese Funktion generiert Vorhersagen für mehrere Datenbeobachtungen, die aus dem oben genannten Netzwerk als Eingabedaten stammen. Die im obigen Netzwerk angegebenen Gewichte werden verwendet. Die Funktionsdefinition relu () wird ebenfalls verwendet.

Definieren wir eine Funktion namens Predict_with_network (), die zwei Argumente akzeptiert - input_data_row und weight - und eine Vorhersage aus dem Netzwerk als Ausgabe zurückgibt.

Wir berechnen die Eingabe- und Ausgabewerte für jeden Knoten und speichern sie als: node_0_input, node_0_output, node_1_input und node_1_output.

Um den Eingabewert eines Knotens zu berechnen, multiplizieren wir die relevanten Arrays miteinander und berechnen ihre Summe.

Um den Ausgabewert eines Knotens zu berechnen, wenden wir die Funktion relu () auf den Eingabewert des Knotens an. Wir verwenden eine 'for-Schleife', um über input_data zu iterieren -

Wir verwenden auch unser Predict_with_network (), um Vorhersagen für jede Zeile der input_data - input_data_row zu generieren. Wir hängen auch jede Vorhersage an die Ergebnisse an.

# Define predict_with_network()
def predict_with_network(input_data_row, weights):
   # Calculate node 0 value
   node_0_input = (input_data_row * weights['node_0']).sum()
   node_0_output = relu(node_0_input)
   
   # Calculate node 1 value
   node_1_input = (input_data_row * weights['node_1']).sum()
   node_1_output = relu(node_1_input)
   
   # Put node values into array: hidden_layer_outputs
   hidden_layer_outputs = np.array([node_0_output, node_1_output])
   
   # Calculate model output
   input_to_final_layer = (hidden_layer_outputs*weights['output']).sum()
   model_output = relu(input_to_final_layer)
# Return model output
   return(model_output)

# Create empty list to store prediction results
results = []
for input_data_row in input_data:
   # Append prediction to results
   results.append(predict_with_network(input_data_row, weights))
print(results)# Print results

Ausgabe

[0, 12]

Hier haben wir die Relu-Funktion verwendet, wobei Relu (26) = 26 und Relu (-13) = 0 und so weiter.

Tiefe mehrschichtige neuronale Netze

Hier schreiben wir Code für die Vorwärtsausbreitung eines neuronalen Netzwerks mit zwei verborgenen Schichten. Jede verborgene Schicht hat zwei Knoten. Die Eingabedaten wurden als vorinstalliertinput_data. Die Knoten in der ersten verborgenen Schicht heißen node_0_0 und node_0_1.

Ihre Gewichte sind als Gewichte ['node_0_0'] bzw. Gewichte ['node_0_1'] vorinstalliert.

Die Knoten in der zweiten verborgenen Schicht werden aufgerufen node_1_0 and node_1_1. Ihre Gewichte sind als vorinstalliertweights['node_1_0'] und weights['node_1_1'] beziehungsweise.

Anschließend erstellen wir eine Modellausgabe aus den ausgeblendeten Knoten mit den vorinstallierten Gewichten als weights['output'].

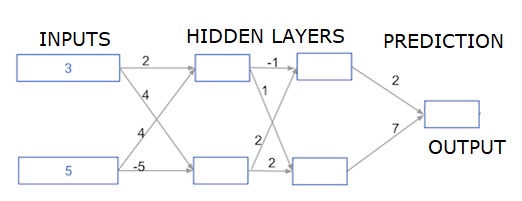
Wir berechnen node_0_0_input anhand seiner Gewichtungsgewichte ['node_0_0'] und der angegebenen input_data. Wenden Sie dann die Funktion relu () an, um node_0_0_output zu erhalten.

Wir machen dasselbe wie oben für node_0_1_input, um node_0_1_output zu erhalten.

Wir berechnen node_1_0_input anhand seiner Gewichtungsgewichte ['node_1_0'] und der Ausgaben der ersten verborgenen Ebene - hidden_0_outputs. Wir wenden dann die Funktion relu () an, um node_1_0_output zu erhalten.

Wir machen dasselbe wie oben für node_1_1_input, um node_1_1_output zu erhalten.

Wir berechnen model_output mit den Gewichten ['output'] und den Ausgaben des Arrays hidden_1_outputs der zweiten verborgenen Schicht. Wir wenden die Funktion relu () nicht auf diese Ausgabe an.

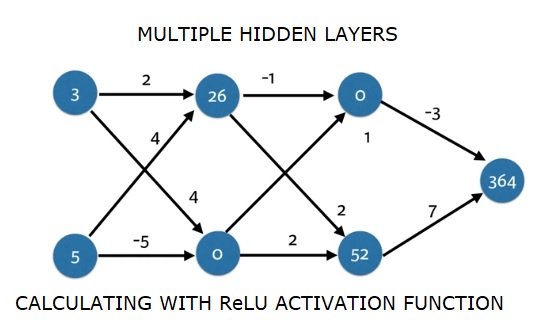
import numpy as np
input_data = np.array([3, 5])
weights = {
   'node_0_0': np.array([2, 4]),
   'node_0_1': np.array([4, -5]),
   'node_1_0': np.array([-1, 1]),
   'node_1_1': np.array([2, 2]),
   'output': np.array([2, 7])
}
def predict_with_network(input_data):
   # Calculate node 0 in the first hidden layer
   node_0_0_input = (input_data * weights['node_0_0']).sum()
   node_0_0_output = relu(node_0_0_input)
   
   # Calculate node 1 in the first hidden layer
   node_0_1_input = (input_data*weights['node_0_1']).sum()
   node_0_1_output = relu(node_0_1_input)
   
   # Put node values into array: hidden_0_outputs
   hidden_0_outputs = np.array([node_0_0_output, node_0_1_output])
   
   # Calculate node 0 in the second hidden layer
   node_1_0_input = (hidden_0_outputs*weights['node_1_0']).sum()
   node_1_0_output = relu(node_1_0_input)
   
   # Calculate node 1 in the second hidden layer
   node_1_1_input = (hidden_0_outputs*weights['node_1_1']).sum()
   node_1_1_output = relu(node_1_1_input)
   
   # Put node values into array: hidden_1_outputs
   hidden_1_outputs = np.array([node_1_0_output, node_1_1_output])
   
   # Calculate model output: model_output
   model_output = (hidden_1_outputs*weights['output']).sum()
      # Return model_output
   return(model_output)
output = predict_with_network(input_data)
print(output)

Ausgabe