Python-Entwurfsmuster - Sätze
Eine Menge kann als ungeordnete Sammlung definiert werden, die iterierbar und veränderbar ist und keine doppelten Elemente enthält. In Python ist die Mengenklasse eine Notation der mathematischen Menge. Der Hauptvorteil der Verwendung eines Satzes besteht darin, dass er eine hochoptimierte Methode zur Überprüfung eines bestimmten Elements enthält.
Python enthält eine separate Kategorie namens Frozen Sets. Diese Mengen sind unveränderliche Objekte, die nur Methoden und Operatoren unterstützen, die ein erforderliches Ergebnis liefern.
Wie implementiere ich Sets?
Das folgende Programm hilft bei der Implementierung von Sets -
# Set in Python
# Creating two sets
set1 = set()
set2 = set()
# Adding elements to set1
for i in range(1, 6):
set1.add(i)
# Adding elements to set2
for i in range(3, 8):
set2.add(i)
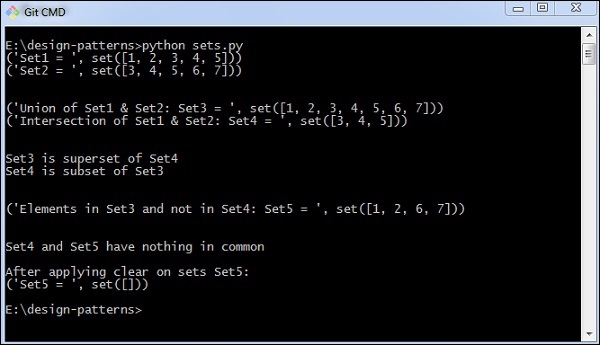
print("Set1 = ", set1)
print("Set2 = ", set2)
print("\n")
# Union of set1 and set2
set3 = set1 | set2# set1.union(set2)
print("Union of Set1 & Set2: Set3 = ", set3)
# Intersection of set1 and set2
set4 = set1 & set2# set1.intersection(set2)
print("Intersection of Set1 & Set2: Set4 = ", set4)
print("\n")
# Checking relation between set3 and set4
if set3 > set4: # set3.issuperset(set4)
print("Set3 is superset of Set4")
elif set3 < set4: # set3.issubset(set4)
print("Set3 is subset of Set4")
else : # set3 == set4
print("Set3 is same as Set4")
# displaying relation between set4 and set3
if set4 < set3: # set4.issubset(set3)
print("Set4 is subset of Set3")
print("\n")
# difference between set3 and set4
set5 = set3 - set4
print("Elements in Set3 and not in Set4: Set5 = ", set5)
print("\n")
# checkv if set4 and set5 are disjoint sets
if set4.isdisjoint(set5):
print("Set4 and Set5 have nothing in common\n")
# Removing all the values of set5
set5.clear()
print("After applying clear on sets Set5: ")
print("Set5 = ", set5)Ausgabe
Das obige Programm erzeugt die folgende Ausgabe -
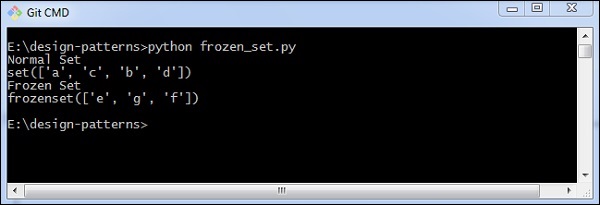
Das eingefrorene Set kann mit dem folgenden Programm demonstriert werden:
normal_set = set(["a", "b","c"])
# Adding an element to normal set is fine
normal_set.add("d")
print("Normal Set")
print(normal_set)
# A frozen set
frozen_set = frozenset(["e", "f", "g"])
print("Frozen Set")
print(frozen_set)Ausgabe
Das obige Programm erzeugt die folgende Ausgabe -