PyTorch - Kurzanleitung

PyTorch ist als Open Source-Bibliothek für maschinelles Lernen für Python definiert. Es wird für Anwendungen wie die Verarbeitung natürlicher Sprache verwendet. Es wurde ursprünglich von der Facebook-Forschungsgruppe für künstliche Intelligenz und der darauf aufbauenden Pyro-Software von Uber für probabilistische Programmierung entwickelt.

Ursprünglich wurde PyTorch von Hugh Perkins als Python-Wrapper für das LusJIT basierend auf dem Torch-Framework entwickelt. Es gibt zwei PyTorch-Varianten.

PyTorch entwirft und implementiert Torch in Python, während dieselben Kern-C-Bibliotheken für den Backend-Code verwendet werden. PyTorch-Entwickler haben diesen Back-End-Code so optimiert, dass Python effizient ausgeführt wird. Sie behielten auch die GPU-basierte Hardwarebeschleunigung sowie die Erweiterungsfunktionen bei, die Lua-basierte Torch ausmachten.

Eigenschaften

Die Hauptfunktionen von PyTorch sind unten aufgeführt -

Easy Interface- PyTorch bietet eine benutzerfreundliche API. Daher wird es als sehr einfach zu bedienen angesehen und läuft auf Python. Die Codeausführung in diesem Framework ist recht einfach.

Python usage- Diese Bibliothek wird als Pythonic betrachtet, die sich nahtlos in den Python Data Science-Stack integrieren lässt. Auf diese Weise können alle von der Python-Umgebung angebotenen Dienste und Funktionen genutzt werden.

Computational graphs- PyTorch bietet eine hervorragende Plattform, die dynamische Berechnungsgraphen bietet. Somit kann ein Benutzer sie zur Laufzeit ändern. Dies ist sehr nützlich, wenn ein Entwickler keine Ahnung hat, wie viel Speicher zum Erstellen eines neuronalen Netzwerkmodells erforderlich ist.

PyTorch ist dafür bekannt, drei Abstraktionsebenen zu haben, wie unten angegeben -

Tensor - Imperatives n-dimensionales Array, das auf einer GPU ausgeführt wird.
Variable - Knoten im Rechengraphen. Hier werden Daten und Farbverläufe gespeichert.
Modul - Neuronale Netzwerkschicht, in der Zustands- oder lernbare Gewichte gespeichert werden.

Vorteile von PyTorch

Das Folgende sind die Vorteile von PyTorch -

Es ist einfach, den Code zu debuggen und zu verstehen.
Es enthält viele Schichten als Fackel.
Es enthält viele Verlustfunktionen.
Es kann als NumPy-Erweiterung für GPUs betrachtet werden.
Es ermöglicht den Aufbau von Netzwerken, deren Struktur von der Berechnung selbst abhängt.

TensorFlow gegen PyTorch

Wir werden die Hauptunterschiede zwischen TensorFlow und PyTorch im Folgenden untersuchen -

PyTorch	TensorFlow
PyTorch ist eng mit dem lua-basierten Torch-Framework verwandt, das in Facebook aktiv verwendet wird.	TensorFlow wird von Google Brain entwickelt und bei Google aktiv eingesetzt.
PyTorch ist im Vergleich zu anderen Wettbewerbstechnologien relativ neu.	TensorFlow ist nicht neu und wird von vielen Forschern und Fachleuten als To-Go-Tool angesehen.
PyTorch enthält alles auf zwingende und dynamische Weise.	TensorFlow enthält statische und dynamische Diagramme als Kombination.
Das Berechnungsdiagramm in PyTorch wird zur Laufzeit definiert.	TensorFlow enthält keine Laufzeitoption.
PyTorch enthält die Bereitstellung für mobile und eingebettete Frameworks.	TensorFlow funktioniert besser für eingebettete Frameworks.

PyTorch ist ein beliebtes Deep-Learning-Framework. In diesem Tutorial betrachten wir "Windows 10" als unser Betriebssystem. Die Schritte für eine erfolgreiche Einrichtung der Umgebung sind wie folgt:

Schritt 1

Der folgende Link enthält eine Liste von Paketen, die geeignete Pakete für PyTorch enthalten.

https://drive.google.com/drive/folders/0B-X0-FlSGfCYdTNldW02UGl4MXM

Sie müssen lediglich die entsprechenden Pakete herunterladen und wie in den folgenden Screenshots gezeigt installieren.

Schritt 2

Dabei wird die Installation des PyTorch-Frameworks mithilfe des Anaconda-Frameworks überprüft.

Der folgende Befehl wird verwendet, um dasselbe zu überprüfen:

conda list

"Conda-Liste" zeigt die Liste der installierten Frameworks.

Der hervorgehobene Teil zeigt, dass PyTorch erfolgreich in unserem System installiert wurde.

Mathematik ist in jedem Algorithmus für maschinelles Lernen von entscheidender Bedeutung und umfasst verschiedene Kernkonzepte der Mathematik, um den richtigen Algorithmus auf eine bestimmte Art und Weise zu entwickeln.

Die Bedeutung von Mathematikthemen für maschinelles Lernen und Datenwissenschaft wird nachstehend erwähnt -

Konzentrieren wir uns nun auf die wichtigsten mathematischen Konzepte des maschinellen Lernens, die aus Sicht der Verarbeitung natürlicher Sprache wichtig sind:

Vektoren

Der Vektor wird als Array von Zahlen betrachtet, das entweder stetig oder diskret ist, und der Raum, der aus Vektoren besteht, wird als Vektorraum bezeichnet. Die Raumdimensionen von Vektoren können entweder endlich oder unendlich sein, es wurde jedoch beobachtet, dass sich maschinelles Lernen und datenwissenschaftliche Probleme mit Vektoren fester Länge befassen.

Die Vektordarstellung wird wie folgt angezeigt -

temp = torch.FloatTensor([23,24,24.5,26,27.2,23.0])
temp.size()
Output - torch.Size([6])

Beim maschinellen Lernen beschäftigen wir uns mit mehrdimensionalen Daten. Vektoren werden daher sehr wichtig und werden als Eingabemerkmale für jede Vorhersageproblemaussage betrachtet.

Skalare

Skalare haben Nulldimensionen, die nur einen Wert enthalten. Wenn es um PyTorch geht, enthält es keinen speziellen Tensor mit Nulldimensionen. daher wird die Erklärung wie folgt abgegeben:

x = torch.rand(10)
x.size()
Output - torch.Size([10])

Matrizen

Die meisten strukturierten Daten werden normalerweise in Form von Tabellen oder einer bestimmten Matrix dargestellt. Wir werden einen Datensatz namens Boston House Prices verwenden, der in der Python Scikit-Learn-Bibliothek für maschinelles Lernen verfügbar ist.

boston_tensor = torch.from_numpy(boston.data)
boston_tensor.size()
Output: torch.Size([506, 13])
boston_tensor[:2]
Output:
Columns 0 to 7
0.0063 18.0000 2.3100 0.0000 0.5380 6.5750 65.2000 4.0900
0.0273 0.0000 7.0700 0.0000 0.4690 6.4210 78.9000 4.9671
Columns 8 to 12
1.0000 296.0000 15.3000 396.9000 4.9800
2.0000 242.0000 17.8000 396.9000 9.1400

Das Hauptprinzip des neuronalen Netzwerks umfasst eine Sammlung von Grundelementen, dh künstliches Neuron oder Perzeptron. Es enthält mehrere grundlegende Eingänge wie x1, x2… .. xn, die einen Binärausgang erzeugen, wenn die Summe größer als das Aktivierungspotential ist.

Die schematische Darstellung des Probenneurons wird unten erwähnt -

Die erzeugte Ausgabe kann als gewichtete Summe mit Aktivierungspotential oder Vorspannung betrachtet werden.

$$ Output = \ sum_jw_jx_j + Bias $$

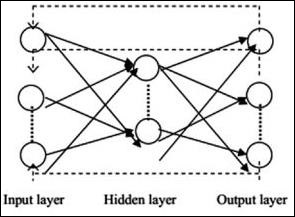
Die typische neuronale Netzwerkarchitektur wird unten beschrieben -

Die Schichten zwischen Eingabe und Ausgabe werden als verborgene Schichten bezeichnet, und die Dichte und Art der Verbindungen zwischen Schichten ist die Konfiguration. Beispielsweise sind bei einer vollständig verbundenen Konfiguration alle Neuronen der Schicht L mit denen von L + 1 verbunden. Für eine ausgeprägtere Lokalisierung können wir nur eine lokale Nachbarschaft, beispielsweise neun Neuronen, mit der nächsten Schicht verbinden. Abbildung 1-9 zeigt zwei verborgene Schichten mit dichten Verbindungen.

Die verschiedenen Arten von neuronalen Netzen sind wie folgt:

Feedforward Neuronale Netze

Feedforward-Neuronale Netze umfassen Grundeinheiten der Familie der Neuronalen Netze. Die Bewegung von Daten in diesem Typ eines neuronalen Netzwerks erfolgt von der Eingangsschicht zur Ausgangsschicht über gegenwärtige verborgene Schichten. Die Ausgabe einer Schicht dient als Eingabeschicht mit Einschränkungen für jede Art von Schleifen in der Netzwerkarchitektur.

Wiederkehrende neuronale Netze

Wiederkehrende neuronale Netze treten auf, wenn sich das Datenmuster über einen Zeitraum hinweg ändert. In RNN wird dieselbe Schicht angewendet, um die Eingabeparameter zu akzeptieren und Ausgabeparameter in einem bestimmten neuronalen Netzwerk anzuzeigen.

Neuronale Netze können mit dem Paket torch.nn aufgebaut werden.

Es ist ein einfaches Feed-Forward-Netzwerk. Es nimmt die Eingabe auf, führt sie nacheinander durch mehrere Ebenen und gibt schließlich die Ausgabe aus.

Mit Hilfe von PyTorch können wir die folgenden Schritte für ein typisches Trainingsverfahren für ein neuronales Netzwerk ausführen:

Definieren Sie das neuronale Netzwerk mit einigen lernbaren Parametern (oder Gewichten).
Iterieren Sie über einen Datensatz von Eingaben.
Eingaben über das Netzwerk verarbeiten.
Berechnen Sie den Verlust (wie weit ist die Ausgabe von der Richtigkeit entfernt).
Übertragen Sie Gradienten zurück in die Netzwerkparameter.
Aktualisieren Sie die Gewichte des Netzwerks, normalerweise mithilfe eines einfachen Updates, wie unten angegeben

rule: weight = weight -learning_rate * gradient

Künstliche Intelligenz ist heutzutage in größerem Maße im Trend. Maschinelles Lernen und tiefes Lernen bilden künstliche Intelligenz. Das unten erwähnte Venn-Diagramm erklärt die Beziehung zwischen maschinellem Lernen und tiefem Lernen.

Maschinelles Lernen

Maschinelles Lernen ist die Kunst der Wissenschaft, die es Computern ermöglicht, gemäß den entworfenen und programmierten Algorithmen zu handeln. Viele Forscher glauben, dass maschinelles Lernen der beste Weg ist, um Fortschritte in Richtung KI auf menschlicher Ebene zu erzielen. Es enthält verschiedene Arten von Mustern wie -

Überwachtes Lernmuster
Unüberwachtes Lernmuster

Tiefes Lernen

Deep Learning ist ein Teilgebiet des maschinellen Lernens, in dem betroffene Algorithmen von der Struktur und Funktion des Gehirns inspiriert sind, die als künstliche neuronale Netze bezeichnet werden.

Deep Learning hat durch überwachtes Lernen oder Lernen aus gekennzeichneten Daten und Algorithmen an Bedeutung gewonnen. Jeder Algorithmus im Deep Learning durchläuft denselben Prozess. Es enthält eine Hierarchie der nichtlinearen Transformation von Eingaben und wird zum Erstellen eines statistischen Modells als Ausgabe verwendet.

Der maschinelle Lernprozess wird anhand der folgenden Schritte definiert:

Identifiziert relevante Datensätze und bereitet sie für die Analyse vor.
Wählt den zu verwendenden Algorithmus aus.
Erstellt ein analytisches Modell basierend auf dem verwendeten Algorithmus.
Trainiert das Modell anhand von Testdatensätzen und überarbeitet es nach Bedarf.
Führt das Modell aus, um Testergebnisse zu generieren.

In diesem Kapitel werden wir den Hauptunterschied zwischen maschinellen und Deep-Learning-Konzepten diskutieren.

Datenmenge

Maschinelles Lernen arbeitet mit unterschiedlichen Datenmengen und wird hauptsächlich für kleine Datenmengen verwendet. Deep Learning hingegen funktioniert effizient, wenn die Datenmenge schnell zunimmt. Das folgende Diagramm zeigt die Funktionsweise von maschinellem Lernen und Tiefenlernen in Bezug auf die Datenmenge -

Hardware-Abhängigkeiten

Deep-Learning-Algorithmen sind so konzipiert, dass sie im Gegensatz zu herkömmlichen Algorithmen für maschinelles Lernen stark von High-End-Maschinen abhängen. Deep-Learning-Algorithmen führen eine große Anzahl von Matrixmultiplikationsoperationen aus, die eine enorme Hardwareunterstützung erfordern.

Feature Engineering

Feature Engineering ist der Prozess, bei dem Domänenwissen in bestimmte Features integriert wird, um die Komplexität von Daten zu verringern und Muster zu erstellen, die für Lernalgorithmen sichtbar sind.

Beispielsweise konzentrieren sich traditionelle maschinelle Lernmuster auf Pixel und andere Attribute, die für den Feature-Engineering-Prozess benötigt werden. Deep-Learning-Algorithmen konzentrieren sich auf Funktionen auf hoher Ebene aus Daten. Es reduziert die Aufgabe, für jedes neue Problem einen neuen Feature-Extraktor zu entwickeln.

PyTorch enthält eine spezielle Funktion zum Erstellen und Implementieren neuronaler Netze. In diesem Kapitel erstellen wir ein einfaches neuronales Netzwerk mit einer verborgenen Schicht, die eine einzelne Ausgabeeinheit entwickelt.

Wir werden die folgenden Schritte ausführen, um das erste neuronale Netzwerk mit PyTorch zu implementieren:

Schritt 1

Zuerst müssen wir die PyTorch-Bibliothek mit dem folgenden Befehl importieren:

import torch 
import torch.nn as nn

Schritt 2

Definieren Sie alle Ebenen und die Stapelgröße, um die Ausführung des neuronalen Netzwerks wie unten gezeigt zu starten.

# Defining input size, hidden layer size, output size and batch size respectively
n_in, n_h, n_out, batch_size = 10, 5, 1, 10

Schritt 3

Da das neuronale Netzwerk eine Kombination von Eingabedaten enthält, um die jeweiligen Ausgabedaten zu erhalten, werden wir das gleiche Verfahren wie unten angegeben befolgen -

# Create dummy input and target tensors (data)
x = torch.randn(batch_size, n_in)
y = torch.tensor([[1.0], [0.0], [0.0], 
[1.0], [1.0], [1.0], [0.0], [0.0], [1.0], [1.0]])

Schritt 4

Erstellen Sie mithilfe der integrierten Funktionen ein sequentielles Modell. Erstellen Sie mit den folgenden Codezeilen ein sequentielles Modell -

# Create a model
model = nn.Sequential(nn.Linear(n_in, n_h),
   nn.ReLU(),
   nn.Linear(n_h, n_out),
   nn.Sigmoid())

Schritt 5

Konstruieren Sie die Verlustfunktion mit Hilfe des Gradient Descent-Optimierers wie unten gezeigt -

Construct the loss function
criterion = torch.nn.MSELoss()
# Construct the optimizer (Stochastic Gradient Descent in this case)
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)

Schritt 6

Implementieren Sie das Gradientenabstiegsmodell mit der iterierenden Schleife mit den angegebenen Codezeilen -

# Gradient Descent
for epoch in range(50):
   # Forward pass: Compute predicted y by passing x to the model
   y_pred = model(x)

   # Compute and print loss
   loss = criterion(y_pred, y)
   print('epoch: ', epoch,' loss: ', loss.item())

   # Zero gradients, perform a backward pass, and update the weights.
   optimizer.zero_grad()

   # perform a backward pass (backpropagation)
   loss.backward()

   # Update the parameters
   optimizer.step()

Schritt 7

Die erzeugte Ausgabe ist wie folgt:

epoch: 0 loss: 0.2545787990093231
epoch: 1 loss: 0.2545052170753479
epoch: 2 loss: 0.254431813955307
epoch: 3 loss: 0.25435858964920044
epoch: 4 loss: 0.2542854845523834
epoch: 5 loss: 0.25421255826950073
epoch: 6 loss: 0.25413978099823
epoch: 7 loss: 0.25406715273857117
epoch: 8 loss: 0.2539947032928467
epoch: 9 loss: 0.25392240285873413
epoch: 10 loss: 0.25385022163391113
epoch: 11 loss: 0.25377824902534485
epoch: 12 loss: 0.2537063956260681
epoch: 13 loss: 0.2536346912384033
epoch: 14 loss: 0.25356316566467285
epoch: 15 loss: 0.25349172949790955
epoch: 16 loss: 0.25342053174972534
epoch: 17 loss: 0.2533493936061859
epoch: 18 loss: 0.2532784342765808
epoch: 19 loss: 0.25320762395858765
epoch: 20 loss: 0.2531369626522064
epoch: 21 loss: 0.25306645035743713
epoch: 22 loss: 0.252996027469635
epoch: 23 loss: 0.2529257833957672
epoch: 24 loss: 0.25285571813583374
epoch: 25 loss: 0.25278574228286743
epoch: 26 loss: 0.25271597504615784
epoch: 27 loss: 0.25264623761177063
epoch: 28 loss: 0.25257670879364014
epoch: 29 loss: 0.2525072991847992
epoch: 30 loss: 0.2524380087852478
epoch: 31 loss: 0.2523689270019531
epoch: 32 loss: 0.25229987502098083
epoch: 33 loss: 0.25223103165626526
epoch: 34 loss: 0.25216227769851685
epoch: 35 loss: 0.252093642950058
epoch: 36 loss: 0.25202515721321106
epoch: 37 loss: 0.2519568204879761
epoch: 38 loss: 0.251888632774353
epoch: 39 loss: 0.25182053446769714
epoch: 40 loss: 0.2517525553703308
epoch: 41 loss: 0.2516847252845764
epoch: 42 loss: 0.2516169846057892
epoch: 43 loss: 0.2515493929386139
epoch: 44 loss: 0.25148195028305054
epoch: 45 loss: 0.25141456723213196
epoch: 46 loss: 0.2513473629951477
epoch: 47 loss: 0.2512802183628082
epoch: 48 loss: 0.2512132525444031
epoch: 49 loss: 0.2511464059352875

Das Training eines Deep-Learning-Algorithmus umfasst die folgenden Schritte:

Erstellen einer Datenpipeline
Aufbau einer Netzwerkarchitektur
Auswertung der Architektur mit einer Verlustfunktion
Optimieren der Netzwerkarchitekturgewichte mithilfe eines Optimierungsalgorithmus

Das Trainieren eines bestimmten Deep-Learning-Algorithmus ist die genaue Voraussetzung für die Konvertierung eines neuronalen Netzwerks in Funktionsblöcke, wie unten gezeigt -

In Bezug auf das obige Diagramm beinhaltet jeder Deep-Learning-Algorithmus das Abrufen der Eingabedaten und das Erstellen der jeweiligen Architektur, die eine Reihe von darin eingebetteten Schichten enthält.

Wenn Sie das obige Diagramm betrachten, wird die Genauigkeit unter Verwendung einer Verlustfunktion in Bezug auf die Optimierung der Gewichte des neuronalen Netzwerks bewertet.

In diesem Kapitel werden einige der am häufigsten verwendeten Begriffe in PyTorch erläutert.

PyTorch NumPy

Ein PyTorch-Tensor ist identisch mit einem NumPy-Array. Ein Tensor ist ein n-dimensionales Array und bietet in Bezug auf PyTorch viele Funktionen, um mit diesen Tensoren zu arbeiten.

PyTorch-Tensoren verwenden normalerweise GPUs, um ihre numerischen Berechnungen zu beschleunigen. Diese in PyTorch erstellten Tensoren können verwendet werden, um ein zweischichtiges Netzwerk an zufällige Daten anzupassen. Der Benutzer kann die Vorwärts- und Rückwärtsdurchläufe durch das Netzwerk manuell implementieren.

Variablen und Autograd

Bei Verwendung von Autograd definiert der Vorwärtsdurchlauf Ihres Netzwerks a computational graph - Knoten im Diagramm sind Tensoren, und Kanten sind Funktionen, die Ausgangstensoren aus Eingangstensoren erzeugen.

PyTorch-Tensoren können als variable Objekte erstellt werden, bei denen eine Variable einen Knoten im Rechengraphen darstellt.

Dynamische Diagramme

Statische Diagramme sind nett, weil der Benutzer das Diagramm im Voraus optimieren kann. Wenn Programmierer denselben Graphen immer wieder verwenden, kann diese möglicherweise kostspielige Voraboptimierung beibehalten werden, da derselbe Graph immer wieder wiederholt wird.

Der Hauptunterschied zwischen ihnen besteht darin, dass die Rechengraphen von Tensor Flow statisch sind und PyTorch dynamische Rechengraphen verwendet.

Optim-Paket

Das Optimierungspaket in PyTorch abstrahiert die Idee eines Optimierungsalgorithmus, der auf viele Arten implementiert ist und häufig verwendete Optimierungsalgorithmen veranschaulicht. Dies kann innerhalb der import-Anweisung aufgerufen werden.

Mehrfachverarbeitung

Multiprocessing unterstützt dieselben Operationen, sodass alle Tensoren auf mehreren Prozessoren arbeiten. Die Daten der Warteschlange werden in den gemeinsam genutzten Speicher verschoben und senden nur ein Handle an einen anderen Prozess.

PyTorch enthält ein Paket namens torchvision, mit dem der Datensatz geladen und vorbereitet wird. Es enthält zwei Grundfunktionen, nämlich Dataset und DataLoader, die beim Transformieren und Laden des Datasets helfen.

Datensatz

Der Datensatz wird zum Lesen und Transformieren eines Datenpunkts aus dem angegebenen Datensatz verwendet. Die zu implementierende grundlegende Syntax wird unten erwähnt -

trainset = torchvision.datasets.CIFAR10(root = './data', train = True,
   download = True, transform = transform)

DataLoader wird zum Mischen und Stapeln von Daten verwendet. Es kann verwendet werden, um die Daten parallel zu Multiprozessor-Workern zu laden.

trainloader = torch.utils.data.DataLoader(trainset, batch_size = 4,
   shuffle = True, num_workers = 2)

Beispiel: Laden einer CSV-Datei

Wir verwenden das Python-Paket Panda, um die CSV-Datei zu laden. Die Originaldatei hat das folgende Format: (Bildname, 68 Orientierungspunkte - jeder Orientierungspunkt hat Axt- und Y-Koordinaten).

landmarks_frame = pd.read_csv('faces/face_landmarks.csv')

n = 65
img_name = landmarks_frame.iloc[n, 0]
landmarks = landmarks_frame.iloc[n, 1:].as_matrix()
landmarks = landmarks.astype('float').reshape(-1, 2)

In diesem Kapitel konzentrieren wir uns auf ein grundlegendes Beispiel für die Implementierung einer linearen Regression mit TensorFlow. Die logistische oder lineare Regression ist ein überwachter Ansatz des maschinellen Lernens zur Klassifizierung diskreter Kategorien. Unser Ziel in diesem Kapitel ist es, ein Modell zu erstellen, mit dem ein Benutzer die Beziehung zwischen Prädiktorvariablen und einer oder mehreren unabhängigen Variablen vorhersagen kann.

Die Beziehung zwischen diesen beiden Variablen wird als linear betrachtet, dh wenn y die abhängige Variable und x als unabhängige Variable betrachtet wird, sieht die lineare Regressionsbeziehung zweier Variablen wie die unten erwähnte Gleichung aus -

Y = Ax+b

Als nächstes werden wir einen Algorithmus für die lineare Regression entwerfen, der es uns ermöglicht, zwei wichtige Konzepte zu verstehen, die unten angegeben sind -

Kostenfunktion
Gradientenabstiegsalgorithmen

Die schematische Darstellung der linearen Regression wird unten erwähnt

Das Ergebnis interpretieren

$$ Y = ax + b $$

Der Wert von a ist die Steigung.
Der Wert von b ist der y − intercept.
r ist der correlation coefficient.
r² ist der correlation coefficient.

Die grafische Ansicht der Gleichung der linearen Regression wird unten erwähnt -

Die folgenden Schritte werden zum Implementieren der linearen Regression mit PyTorch verwendet:

Schritt 1

Importieren Sie die erforderlichen Pakete zum Erstellen einer linearen Regression in PyTorch mit dem folgenden Code:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import seaborn as sns
import pandas as pd
%matplotlib inline

sns.set_style(style = 'whitegrid')
plt.rcParams["patch.force_edgecolor"] = True

Schritt 2

Erstellen Sie einen einzelnen Trainingssatz mit dem verfügbaren Datensatz wie unten gezeigt -

m = 2 # slope
c = 3 # interceptm = 2 # slope
c = 3 # intercept
x = np.random.rand(256)

noise = np.random.randn(256) / 4

y = x * m + c + noise

df = pd.DataFrame()
df['x'] = x
df['y'] = y

sns.lmplot(x ='x', y ='y', data = df)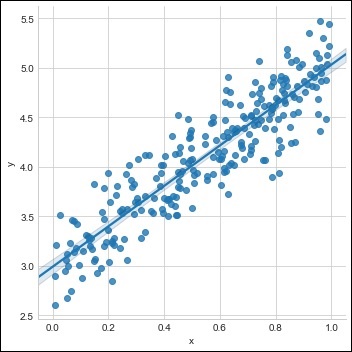

Schritt 3

Implementieren Sie die lineare Regression mit PyTorch-Bibliotheken wie unten erwähnt -

import torch
import torch.nn as nn
from torch.autograd import Variable
x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')

class LinearRegressionModel(nn.Module):
   def __init__(self, input_dim, output_dim):
      super(LinearRegressionModel, self).__init__()
      self.linear = nn.Linear(input_dim, output_dim)

   def forward(self, x):
      out = self.linear(x)
      return out
input_dim = x_train.shape[1]
output_dim = y_train.shape[1]
input_dim, output_dim(1, 1)
model = LinearRegressionModel(input_dim, output_dim)
criterion = nn.MSELoss()
[w, b] = model.parameters()

def get_param_values():
   return w.data[0][0], b.data[0]

def plot_current_fit(title = ""):
plt.figure(figsize = (12,4))
plt.title(title)
plt.scatter(x, y, s = 8)
w1 = w.data[0][0]
b1 = b.data[0]
x1 = np.array([0., 1.])
y1 = x1 * w1 + b1
plt.plot(x1, y1, 'r', label = 'Current Fit ({:.3f}, {:.3f})'.format(w1, b1))
plt.xlabel('x (input)')
plt.ylabel('y (target)')
plt.legend()
plt.show()
plot_current_fit('Before training')

Der erzeugte Plot ist wie folgt:

Deep Learning ist eine Abteilung des maschinellen Lernens und wird von Forschern in den letzten Jahrzehnten als ein entscheidender Schritt angesehen. Die Beispiele für die Implementierung von Deep Learning umfassen Anwendungen wie Bilderkennung und Spracherkennung.

Die zwei wichtigen Arten von tiefen neuronalen Netzen sind unten angegeben -

Faltungsneurale Netze
Wiederkehrende neuronale Netze.

In diesem Kapitel konzentrieren wir uns auf den ersten Typ, dh Convolutional Neural Networks (CNN).

Faltungsneurale Netze

Faltungs-Neuronale Netze dienen zur Verarbeitung von Daten über mehrere Arrays. Diese Art von neuronalen Netzen wird in Anwendungen wie der Bilderkennung oder der Gesichtserkennung verwendet.

Der Hauptunterschied zwischen CNN und jedem anderen gewöhnlichen neuronalen Netzwerk besteht darin, dass CNN die Eingabe als zweidimensionales Array verwendet und direkt auf die Bilder einwirkt, anstatt sich auf die Merkmalsextraktion zu konzentrieren, auf die sich andere neuronale Netzwerke konzentrieren.

Der vorherrschende Ansatz von CNN beinhaltet die Lösung von Erkennungsproblemen. Top-Unternehmen wie Google und Facebook haben in Forschungs- und Entwicklungsprojekte von Anerkennungsprojekten investiert, um Aktivitäten schneller durchzuführen.

Jedes Faltungs-Neuronale Netzwerk enthält drei Grundideen:

Lokale entsprechende Felder
Convolution
Pooling

Lassen Sie uns jede dieser Terminologien im Detail verstehen.

Lokale jeweilige Felder

CNN verwendet räumliche Korrelationen, die in den Eingabedaten vorhanden sind. Jedes in den gleichzeitigen Schichten neuronaler Netze verbindet einige Eingangsneuronen. Diese spezifische Region wird als lokales Empfangsfeld bezeichnet. Es konzentriert sich nur auf versteckte Neuronen. Das versteckte Neuron verarbeitet die Eingabedaten innerhalb des genannten Feldes, ohne die Änderungen außerhalb der spezifischen Grenze zu realisieren.

Die Diagrammdarstellung der Erzeugung lokaler entsprechender Felder wird unten erwähnt -

Faltung

In der obigen Abbildung beobachten wir, dass jede Verbindung ein Gewicht eines versteckten Neurons mit einer damit verbundenen Verbindung mit der Bewegung von einer Schicht zur anderen lernt. Hier führen einzelne Neuronen von Zeit zu Zeit eine Verschiebung durch. Dieser Vorgang wird als "Faltung" bezeichnet.

Die Zuordnung von Verbindungen von der Eingabeebene zur verborgenen Feature-Map wird als "gemeinsame Gewichtung" definiert, und die enthaltene Verzerrung wird als "gemeinsame Verzerrung" bezeichnet.

Pooling

Faltungs-Neuronale Netze verwenden Pooling-Schichten, die unmittelbar nach der CNN-Deklaration positioniert werden. Die Eingabe des Benutzers wird als Feature-Map verwendet, die aus Faltungsnetzwerken hervorgeht und eine komprimierte Feature-Map erstellt. Das Zusammenlegen von Ebenen hilft beim Erstellen von Ebenen mit Neuronen früherer Ebenen.

Implementierung von PyTorch

Die folgenden Schritte werden verwendet, um mit PyTorch ein Faltungs-Neuronales Netzwerk zu erstellen.

Schritt 1

Importieren Sie die erforderlichen Pakete zum Erstellen eines einfachen neuronalen Netzwerks.

from torch.autograd import Variable
import torch.nn.functional as F

Schritt 2

Erstellen Sie eine Klasse mit Batch-Darstellung des Faltungsnetzwerks. Unsere Stapelform für Eingabe x hat die Dimension (3, 32, 32).

class SimpleCNN(torch.nn.Module):
   def __init__(self):
      super(SimpleCNN, self).__init__()
      #Input channels = 3, output channels = 18
      self.conv1 = torch.nn.Conv2d(3, 18, kernel_size = 3, stride = 1, padding = 1)
      self.pool = torch.nn.MaxPool2d(kernel_size = 2, stride = 2, padding = 0)
      #4608 input features, 64 output features (see sizing flow below)
      self.fc1 = torch.nn.Linear(18 * 16 * 16, 64)
      #64 input features, 10 output features for our 10 defined classes
      self.fc2 = torch.nn.Linear(64, 10)

Schritt 3

Berechnen Sie die Aktivierung der ersten Faltungsgrößenänderungen von (3, 32, 32) zu (18, 32, 32).

Die Größe der Bemaßung ändert sich von (18, 32, 32) zu (18, 16, 16). Umformen der Datendimension der Eingangsschicht des neuronalen Netzes, aufgrund derer sich die Größe von (18, 16, 16) auf (1, 4608) ändert.

Denken Sie daran, dass -1 diese Dimension von der anderen angegebenen Dimension ableitet.

def forward(self, x):
   x = F.relu(self.conv1(x))
   x = self.pool(x)
   x = x.view(-1, 18 * 16 *16)
   x = F.relu(self.fc1(x))
   #Computes the second fully connected layer (activation applied later)
   #Size changes from (1, 64) to (1, 10)
   x = self.fc2(x)
   return(x)

Wiederkehrende neuronale Netze sind eine Art von Deep-Learning-orientiertem Algorithmus, der einem sequentiellen Ansatz folgt. In neuronalen Netzen gehen wir immer davon aus, dass jeder Ein- und Ausgang unabhängig von allen anderen Schichten ist. Diese Art von neuronalen Netzen wird als wiederkehrend bezeichnet, da sie nacheinander mathematische Berechnungen durchführen und eine Aufgabe nach der anderen ausführen.

Das folgende Diagramm zeigt den vollständigen Ansatz und die Funktionsweise wiederkehrender neuronaler Netze.

In der obigen Figur werden c1, c2, c3 und x1 als Eingaben betrachtet, die einige versteckte Eingabewerte enthalten, nämlich h1, h2 und h3, die die jeweilige Ausgabe von o1 liefern. Wir werden uns nun auf die Implementierung von PyTorch konzentrieren, um mithilfe wiederkehrender neuronaler Netze eine Sinuswelle zu erzeugen.

Während des Trainings verfolgen wir einen Trainingsansatz für unser Modell mit jeweils einem Datenpunkt. Die Eingabesequenz x besteht aus 20 Datenpunkten, und die Zielsequenz wird als dieselbe wie die Eingabesequenz angesehen.

Schritt 1

Importieren Sie die erforderlichen Pakete zum Implementieren wiederkehrender neuronaler Netze mit dem folgenden Code:

import torch
from torch.autograd import Variable
import numpy as np
import pylab as pl
import torch.nn.init as init

Schritt 2

Wir werden die Modell-Hyperparameter mit der Größe der Eingabeebene auf 7 setzen. Es werden 6 Kontextneuronen und 1 Eingangsneuron zum Erstellen der Zielsequenz vorhanden sein.

dtype = torch.FloatTensor
input_size, hidden_size, output_size = 7, 6, 1
epochs = 300
seq_length = 20
lr = 0.1
data_time_steps = np.linspace(2, 10, seq_length + 1)
data = np.sin(data_time_steps)
data.resize((seq_length + 1, 1))

x = Variable(torch.Tensor(data[:-1]).type(dtype), requires_grad=False)
y = Variable(torch.Tensor(data[1:]).type(dtype), requires_grad=False)

Wir werden Trainingsdaten generieren, wobei x die Eingabedatensequenz und y die erforderliche Zielsequenz ist.

Schritt 3

Die Gewichte werden im wiederkehrenden neuronalen Netzwerk unter Verwendung der Normalverteilung mit dem Mittelwert Null initialisiert. W1 repräsentiert die Akzeptanz von Eingangsvariablen und w2 repräsentiert die Ausgabe, die wie unten gezeigt erzeugt wird -

w1 = torch.FloatTensor(input_size, 
hidden_size).type(dtype)
init.normal(w1, 0.0, 0.4)
w1 = Variable(w1, requires_grad = True)
w2 = torch.FloatTensor(hidden_size, output_size).type(dtype)
init.normal(w2, 0.0, 0.3)
w2 = Variable(w2, requires_grad = True)

Schritt 4

Jetzt ist es wichtig, eine Funktion für die Vorwärtskopplung zu erstellen, die das neuronale Netzwerk eindeutig definiert.

def forward(input, context_state, w1, w2):
   xh = torch.cat((input, context_state), 1)
   context_state = torch.tanh(xh.mm(w1))
   out = context_state.mm(w2)
   return (out, context_state)

Schritt 5

Der nächste Schritt besteht darin, mit dem Trainingsverfahren für die Sinuswellenimplementierung eines wiederkehrenden neuronalen Netzwerks zu beginnen. Die äußere Schleife durchläuft jede Schleife und die innere Schleife durchläuft das Sequenzelement. Hier berechnen wir auch den Mean Square Error (MSE), der bei der Vorhersage kontinuierlicher Variablen hilft.

for i in range(epochs):
   total_loss = 0
   context_state = Variable(torch.zeros((1, hidden_size)).type(dtype), requires_grad = True)
   for j in range(x.size(0)):
      input = x[j:(j+1)]
      target = y[j:(j+1)]
      (pred, context_state) = forward(input, context_state, w1, w2)
      loss = (pred - target).pow(2).sum()/2
      total_loss += loss
      loss.backward()
      w1.data -= lr * w1.grad.data
      w2.data -= lr * w2.grad.data
      w1.grad.data.zero_()
      w2.grad.data.zero_()
      context_state = Variable(context_state.data)
   if i % 10 == 0:
      print("Epoch: {} loss {}".format(i, total_loss.data[0]))

context_state = Variable(torch.zeros((1, hidden_size)).type(dtype), requires_grad = False)
predictions = []

for i in range(x.size(0)):
   input = x[i:i+1]
   (pred, context_state) = forward(input, context_state, w1, w2)
   context_state = context_state
   predictions.append(pred.data.numpy().ravel()[0])

Schritt 6

Jetzt ist es an der Zeit, die Sinuswelle so zu zeichnen, wie sie benötigt wird.

pl.scatter(data_time_steps[:-1], x.data.numpy(), s = 90, label = "Actual")
pl.scatter(data_time_steps[1:], predictions, label = "Predicted")
pl.legend()
pl.show()

Ausgabe

Die Ausgabe für den obigen Prozess ist wie folgt:

In diesem Kapitel werden wir uns mehr darauf konzentrieren torchvision.datasetsund seine verschiedenen Arten. PyTorch enthält folgende Datensatzlader:

MNIST
COCO (Captioning and Detection)

Der Datensatz enthält die meisten der unten angegebenen zwei Arten von Funktionen:

Transform- Eine Funktion, die ein Bild aufnimmt und eine modifizierte Version von Standardmaterial zurückgibt. Diese können zusammen mit Transformationen zusammengesetzt werden.
Target_transform- eine Funktion, die das Ziel nimmt und es transformiert. Nimmt beispielsweise die Beschriftungszeichenfolge auf und gibt einen Tensor von Weltindizes zurück.

MNIST

Das Folgende ist der Beispielcode für den MNIST-Datensatz -

dset.MNIST(root, train = TRUE, transform = NONE, 
target_transform = None, download = FALSE)

Die Parameter sind wie folgt:

root - Stammverzeichnis des Datensatzes, in dem verarbeitete Daten vorhanden sind.
train - Richtig = Trainingssatz, Falsch = Testsatz
download - True = lädt den Datensatz aus dem Internet herunter und legt ihn im Stammverzeichnis ab.

COCO

Dazu muss die COCO-API installiert sein. Das folgende Beispiel wird verwendet, um die COCO-Implementierung eines Datensatzes mit PyTorch zu demonstrieren.

import torchvision.dataset as dset
import torchvision.transforms as transforms
cap = dset.CocoCaptions(root = ‘ dir where images are’, 
annFile = ’json annotation file’,
transform = transforms.ToTensor())
print(‘Number of samples: ‘, len(cap))
print(target)

Die erzielte Ausgabe ist wie folgt:

Number of samples: 82783
Image Size: (3L, 427L, 640L)

Bei Convents dreht sich alles darum, das CNN-Modell von Grund auf neu zu erstellen. Die Netzwerkarchitektur enthält eine Kombination der folgenden Schritte:

Conv2d
MaxPool2d
Gleichgerichtete Lineareinheit
View
Lineare Schicht

Das Modell trainieren

Das Training des Modells ist der gleiche Prozess wie bei Problemen mit der Bildklassifizierung. Das folgende Codefragment vervollständigt den Vorgang eines Trainingsmodells für den bereitgestellten Datensatz:

def fit(epoch,model,data_loader,phase 
= 'training',volatile = False):
   if phase == 'training':
      model.train()
   if phase == 'training':
      model.train()
   if phase == 'validation':
      model.eval()
   volatile=True
   running_loss = 0.0
   running_correct = 0
   for batch_idx , (data,target) in enumerate(data_loader):
      if is_cuda:
         data,target = data.cuda(),target.cuda()
         data , target = Variable(data,volatile),Variable(target)
      if phase == 'training':
         optimizer.zero_grad()
         output = model(data)
         loss = F.nll_loss(output,target)
         running_loss + = 
         F.nll_loss(output,target,size_average = 
         False).data[0]
         preds = output.data.max(dim = 1,keepdim = True)[1]
         running_correct + = 
         preds.eq(target.data.view_as(preds)).cpu().sum()
         if phase == 'training':
            loss.backward()
            optimizer.step()
   loss = running_loss/len(data_loader.dataset)
   accuracy = 100. * running_correct/len(data_loader.dataset)
   print(f'{phase} loss is {loss:{5}.{2}} and {phase} accuracy is {running_correct}/{len(data_loader.dataset)}{accuracy:{return loss,accuracy}})

Die Methode enthält unterschiedliche Logik für Training und Validierung. Es gibt zwei Hauptgründe für die Verwendung unterschiedlicher Modi:

Im Zugmodus entfernt Dropout einen Prozentsatz der Werte, die in der Validierungs- oder Testphase nicht auftreten sollten.
Für den Trainingsmodus berechnen wir Gradienten und ändern den Parameterwert des Modells. Während der Test- oder Validierungsphase ist jedoch keine Rückausbreitung erforderlich.

In diesem Kapitel konzentrieren wir uns darauf, ein Kloster von Grund auf neu zu erstellen. Dies führt zur Erstellung des jeweiligen Klosters oder Beispiels eines neuronalen Netzwerks mit einer Taschenlampe.

Schritt 1

Erstellen Sie eine notwendige Klasse mit entsprechenden Parametern. Die Parameter umfassen Gewichte mit zufälligem Wert.

class Neural_Network(nn.Module):
   def __init__(self, ):
      super(Neural_Network, self).__init__()
      self.inputSize = 2
      self.outputSize = 1
      self.hiddenSize = 3
      # weights
      self.W1 = torch.randn(self.inputSize, 
      self.hiddenSize) # 3 X 2 tensor
      self.W2 = torch.randn(self.hiddenSize, self.outputSize) # 3 X 1 tensor

Schritt 2

Erstellen Sie ein Feed-Forward-Funktionsmuster mit Sigmoid-Funktionen.

def forward(self, X):
   self.z = torch.matmul(X, self.W1) # 3 X 3 ".dot" 
   does not broadcast in PyTorch
   self.z2 = self.sigmoid(self.z) # activation function
   self.z3 = torch.matmul(self.z2, self.W2)
   o = self.sigmoid(self.z3) # final activation 
   function
   return o
   def sigmoid(self, s):
      return 1 / (1 + torch.exp(-s))
   def sigmoidPrime(self, s):
      # derivative of sigmoid
      return s * (1 - s)
   def backward(self, X, y, o):
      self.o_error = y - o # error in output
      self.o_delta = self.o_error * self.sigmoidPrime(o) # derivative of sig to error
      self.z2_error = torch.matmul(self.o_delta, torch.t(self.W2))
      self.z2_delta = self.z2_error * self.sigmoidPrime(self.z2)
      self.W1 + = torch.matmul(torch.t(X), self.z2_delta)
      self.W2 + = torch.matmul(torch.t(self.z2), self.o_delta)

Schritt 3

Erstellen Sie ein Trainings- und Vorhersagemodell wie unten erwähnt -

def train(self, X, y):
   # forward + backward pass for training
   o = self.forward(X)
   self.backward(X, y, o)
def saveWeights(self, model):
   # Implement PyTorch internal storage functions
   torch.save(model, "NN")
   # you can reload model with all the weights and so forth with:
   # torch.load("NN")
def predict(self):
   print ("Predicted data based on trained weights: ")
   print ("Input (scaled): \n" + str(xPredicted))
   print ("Output: \n" + str(self.forward(xPredicted)))

Faltungs-Neuronale Netze umfassen ein Hauptmerkmal: extraction. Die folgenden Schritte werden verwendet, um die Merkmalsextraktion eines Faltungs-Neuronalen Netzwerks zu implementieren.

Schritt 1

Importieren Sie die entsprechenden Modelle, um das Feature-Extraktionsmodell mit „PyTorch“ zu erstellen.

import torch
import torch.nn as nn
from torchvision import models

Schritt 2

Erstellen Sie eine Klasse von Feature-Extraktoren, die bei Bedarf aufgerufen werden können.

class Feature_extractor(nn.module):
   def forward(self, input):
      self.feature = input.clone()
      return input
new_net = nn.Sequential().cuda() # the new network
target_layers = [conv_1, conv_2, conv_4] # layers you want to extract`
i = 1
for layer in list(cnn):
   if isinstance(layer,nn.Conv2d):
      name = "conv_"+str(i)
      art_net.add_module(name,layer)
      if name in target_layers:
         new_net.add_module("extractor_"+str(i),Feature_extractor())
      i+=1
   if isinstance(layer,nn.ReLU):
      name = "relu_"+str(i)
      new_net.add_module(name,layer)
   if isinstance(layer,nn.MaxPool2d):
      name = "pool_"+str(i)
      new_net.add_module(name,layer)
new_net.forward(your_image)
print (new_net.extractor_3.feature)

In diesem Kapitel konzentrieren wir uns mit Hilfe von Klöstern auf das Datenvisualisierungsmodell. Die folgenden Schritte sind erforderlich, um ein perfektes Bild der Visualisierung mit einem herkömmlichen neuronalen Netzwerk zu erhalten.

Schritt 1

Importieren Sie die erforderlichen Module, die für die Visualisierung herkömmlicher neuronaler Netze wichtig sind.

import os
import numpy as np
import pandas as pd
from scipy.misc import imread
from sklearn.metrics import accuracy_score

import keras
from keras.models import Sequential, Model
from keras.layers import Dense, Dropout, Flatten, Activation, Input
from keras.layers import Conv2D, MaxPooling2D
import torch

Schritt 2

Um mögliche Zufälligkeiten mit Trainings- und Testdaten zu stoppen, rufen Sie den entsprechenden Datensatz auf, wie im folgenden Code angegeben -

seed = 128
rng = np.random.RandomState(seed)
data_dir = "../../datasets/MNIST"
train = pd.read_csv('../../datasets/MNIST/train.csv')
test = pd.read_csv('../../datasets/MNIST/Test_fCbTej3.csv')
img_name = rng.choice(train.filename)
filepath = os.path.join(data_dir, 'train', img_name)
img = imread(filepath, flatten=True)

Schritt 3

Zeichnen Sie die erforderlichen Bilder, um die Trainings- und Testdaten mit dem folgenden Code perfekt zu definieren.

pylab.imshow(img, cmap ='gray')
pylab.axis('off')
pylab.show()

Die Ausgabe wird wie folgt angezeigt:

In diesem Kapitel schlagen wir einen alternativen Ansatz vor, der stattdessen auf einem einzigen neuronalen 2D-Faltungsnetzwerk über beide Sequenzen beruht. Jede Schicht unseres Netzwerks codiert Quell-Token auf der Grundlage der bisher erzeugten Ausgabesequenz neu. Aufmerksamkeitsähnliche Eigenschaften sind daher im gesamten Netzwerk allgegenwärtig.

Hier konzentrieren wir uns creating the sequential network with specific pooling from the values included in dataset. Dieser Prozess wird auch am besten im „Bilderkennungsmodul“ angewendet.

Die folgenden Schritte werden verwendet, um mit PyTorch ein Sequenzverarbeitungsmodell mit Klöstern zu erstellen:

Schritt 1

Importieren Sie die erforderlichen Module für die Durchführung der Sequenzverarbeitung mithilfe von Konventen.

import keras 
from keras.datasets import mnist 
from keras.models import Sequential 
from keras.layers import Dense, Dropout, Flatten 
from keras.layers import Conv2D, MaxPooling2D 
import numpy as np

Schritt 2

Führen Sie die erforderlichen Vorgänge aus, um ein Muster in der entsprechenden Reihenfolge mit dem folgenden Code zu erstellen:

batch_size = 128 
num_classes = 10 
epochs = 12
# input image dimensions 
img_rows, img_cols = 28, 28
# the data, split between train and test sets 
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000,28,28,1) 
x_test = x_test.reshape(10000,28,28,1)
print('x_train shape:', x_train.shape) 
print(x_train.shape[0], 'train samples') 
print(x_test.shape[0], 'test samples')
y_train = keras.utils.to_categorical(y_train, num_classes) 
y_test = keras.utils.to_categorical(y_test, num_classes)

Schritt 3

Kompilieren Sie das Modell und passen Sie das Muster wie unten gezeigt in das erwähnte konventionelle neuronale Netzwerkmodell ein.

model.compile(loss = 
keras.losses.categorical_crossentropy, 
optimizer = keras.optimizers.Adadelta(), metrics = 
['accuracy'])
model.fit(x_train, y_train, 
batch_size = batch_size, epochs = epochs, 
verbose = 1, validation_data = (x_test, y_test)) 
score = model.evaluate(x_test, y_test, verbose = 0) 
print('Test loss:', score[0]) 
print('Test accuracy:', score[1])

Die erzeugte Ausgabe ist wie folgt:

In diesem Kapitel werden wir das berühmte Worteinbettungsmodell - word2vec - verstehen. Das Word2vec-Modell wird verwendet, um mithilfe einer Gruppe verwandter Modelle eine Worteinbettung zu erstellen. Das Word2vec-Modell wird mit reinem C-Code implementiert und der Gradient wird manuell berechnet.

Die Implementierung des word2vec-Modells in PyTorch wird in den folgenden Schritten erläutert:

Schritt 1

Implementieren Sie die Bibliotheken in der Worteinbettung wie unten erwähnt -

import torch
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F

Schritt 2

Implementieren Sie das Skip-Gram-Modell der Worteinbettung mit der Klasse word2vec. Es enthältemb_size, emb_dimension, u_embedding, v_embedding Art der Attribute.

class SkipGramModel(nn.Module):
   def __init__(self, emb_size, emb_dimension):
      super(SkipGramModel, self).__init__()
      self.emb_size = emb_size
      self.emb_dimension = emb_dimension
      self.u_embeddings = nn.Embedding(emb_size, emb_dimension, sparse=True)
      self.v_embeddings = nn.Embedding(emb_size, emb_dimension, sparse = True)
      self.init_emb()
   def init_emb(self):
      initrange = 0.5 / self.emb_dimension
      self.u_embeddings.weight.data.uniform_(-initrange, initrange)
      self.v_embeddings.weight.data.uniform_(-0, 0)
   def forward(self, pos_u, pos_v, neg_v):
      emb_u = self.u_embeddings(pos_u)
      emb_v = self.v_embeddings(pos_v)
      score = torch.mul(emb_u, emb_v).squeeze()
      score = torch.sum(score, dim = 1)
      score = F.logsigmoid(score)
      neg_emb_v = self.v_embeddings(neg_v)
      neg_score = torch.bmm(neg_emb_v, emb_u.unsqueeze(2)).squeeze()
      neg_score = F.logsigmoid(-1 * neg_score)
      return -1 * (torch.sum(score)+torch.sum(neg_score))
   def save_embedding(self, id2word, file_name, use_cuda):
      if use_cuda:
         embedding = self.u_embeddings.weight.cpu().data.numpy()
      else:
         embedding = self.u_embeddings.weight.data.numpy()
      fout = open(file_name, 'w')
      fout.write('%d %d\n' % (len(id2word), self.emb_dimension))
      for wid, w in id2word.items():
         e = embedding[wid]
         e = ' '.join(map(lambda x: str(x), e))
         fout.write('%s %s\n' % (w, e))
def test():
   model = SkipGramModel(100, 100)
   id2word = dict()
   for i in range(100):
      id2word[i] = str(i)
   model.save_embedding(id2word)

Schritt 3

Implementieren Sie die Hauptmethode, um das Worteinbettungsmodell ordnungsgemäß anzuzeigen.

if __name__  ==  '__main__':
   test()

Tiefe neuronale Netze verfügen über eine exklusive Funktion, um Durchbrüche beim maschinellen Lernen zu ermöglichen und den Prozess der natürlichen Sprache zu verstehen. Es wird beobachtet, dass die meisten dieser Modelle Sprache als eine flache Folge von Wörtern oder Zeichen behandeln und eine Art Modell verwenden, das als wiederkehrendes neuronales Netzwerk oder RNN bezeichnet wird.

Viele Forscher kommen zu dem Schluss, dass Sprache am besten in Bezug auf den hierarchischen Phrasenbaum verstanden wird. Dieser Typ ist in rekursiven neuronalen Netzen enthalten, die eine bestimmte Struktur berücksichtigen.

PyTorch verfügt über eine spezielle Funktion, die diese komplexen Verarbeitungsmodelle für natürliche Sprachen erheblich vereinfacht. Es ist ein voll funktionsfähiges Framework für alle Arten von Deep Learning mit starker Unterstützung für Computer Vision.

Merkmale des rekursiven neuronalen Netzes

Ein rekursives neuronales Netzwerk wird so erstellt, dass es denselben Satz von Gewichten mit unterschiedlichen graphähnlichen Strukturen anwendet.
Die Knoten werden in topologischer Reihenfolge durchlaufen.
Diese Art von Netzwerk wird durch den umgekehrten Modus der automatischen Differenzierung trainiert.
Die Verarbeitung natürlicher Sprache umfasst einen Sonderfall rekursiver neuronaler Netze.
Dieses rekursive neuronale Tensornetzwerk enthält verschiedene Zusammensetzungsfunktionsknoten im Baum.

Das Beispiel eines rekursiven neuronalen Netzwerks wird unten gezeigt -