Satellitenkommunikation - Keplers Gesetze
Wir wissen, dass sich der Satellit um die Erde dreht, ähnlich wie sich die Erde um die Sonne dreht. Die Prinzipien, die auf die Erde und ihre Bewegung um die Sonne angewendet werden, gelten also auch für den Satelliten und seine Bewegung um die Erde.
Viele Wissenschaftler haben von Anfang an verschiedene Arten von Theorien aufgestellt. Aber nurJohannes Kepler (1571-1630) war einer der anerkanntesten Wissenschaftler bei der Beschreibung des Prinzips eines Satelliten, der sich um die Erde bewegt.
Kepler formulierte drei Gesetze, die die gesamte Theorie und Beobachtung der Satellitenkommunikation veränderten. Diese sind im Volksmund bekannt alsKepler’s laws. Diese sind hilfreich, um die Bewegung durch den Raum zu visualisieren.
Keplers erstes Gesetz
Keplers erstes Gesetz besagt, dass der Pfad, dem ein Satellit um seine Primärseite (die Erde) folgt, ein Pfad sein wird ellipse. Diese Ellipse hat zwei Brennpunkte (Brennpunkte) F1 und F2, wie in der folgenden Abbildung gezeigt. Der Massenschwerpunkt der Erde wird immer an einem der beiden Brennpunkte der Ellipse liegen.
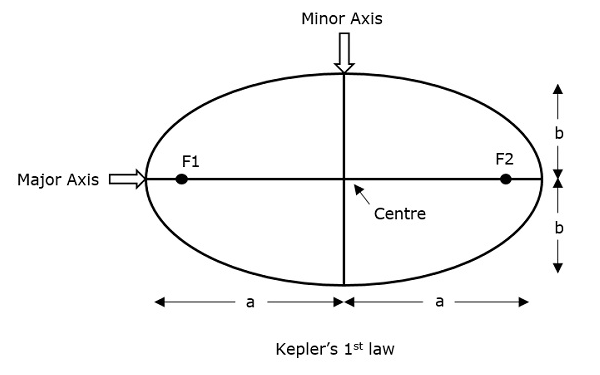
Wenn der Abstand vom Mittelpunkt des Objekts zu einem Punkt auf seinem elliptischen Pfad berücksichtigt wird, wird der am weitesten vom Zentrum entfernte Punkt einer Ellipse als bezeichnet apogee und der kürzeste Punkt einer Ellipse vom Zentrum wird als bezeichnet perigee.
Eccentricity "e" dieses Systems kann geschrieben werden als -
$$ e = \ frac {\ sqrt {a ^ 2 - b ^ 2}} {a} $$
Wo, a & b sind die Längen der Semi-Major-Achse und der Semi-Minor-Achse der Ellipse.
Für ein elliptical pathliegt der Wert der Exzentrizität (e) immer zwischen 0 und 1, dh $ 0 $ < $ e $ < $ 1 $ , da a größer als b ist. Angenommen, wenn der Wert der Exzentrizität (e) Null ist, hat der Pfad keine elliptische Form mehr, sondern wird in eine Kreisform umgewandelt.
Keplers zweites Gesetz
Keplers zweites Gesetz besagt, dass für gleiche Zeitintervalle die areaDie vom Satelliten abgedeckte Fläche ist in Bezug auf den Massenschwerpunkt der Erde gleich. Dies kann anhand der folgenden Abbildung verstanden werden.
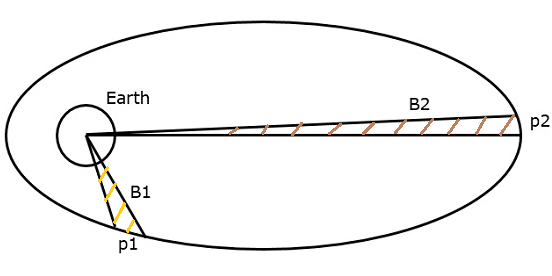
Angenommen, der Satellit legt im gleichen Zeitintervall die Entfernungen p1 und p2 zurück. Dann sind die vom Satelliten in diesen beiden Fällen abgedeckten Bereiche B1 und B2 gleich.
Keplers drittes Gesetz
Keplers drittes Gesetz besagt, dass das Quadrat der periodischen Zeit einer elliptischen Umlaufbahn proportional zum Würfel seiner Halbhauptachsenlänge ist. Mathematicallykann es wie folgt geschrieben werden -
$$ T ^ 2 \: \ alpha \: a ^ 3 $$
$$ => T ^ 2 = \ left (\ frac {4 \ pi ^ 2} {\ mu} \ right) a ^ 3 $$
Dabei ist $ \ frac {4 \ pi ^ 2} {\ mu} $ die Proportionalitätskonstante.
$ \ mu $ ist die Kepler-Konstante und ihr Wert ist gleich 3,986005 x 10 14 m 3 / s 2
$$ 1 = \ left (\ frac {2 \ pi} {T} \ right) ^ 2 \ left (\ frac {a ^ 2} {\ mu} \ right) $$
$$ 1 = n ^ 2 \ left (\ frac {a ^ 3} {\ mu} \ right) $$
$$ => a ^ 3 = \ frac {\ mu} {n ^ 2} $$
Wo, ‘n’ ist die mittlere Bewegung des Satelliten im Bogenmaß pro Sekunde.
Note- Ein Satellit erfährt, wenn er sich um die Erde dreht, eine Zugkraft von der Erde, die Gravitationskraft. In ähnlicher Weise erfährt es eine weitere Zugkraft von Sonne und Mond. Daher muss ein Satellit diese beiden Kräfte ausgleichen, um sich in seiner Umlaufbahn zu halten.