Zeitreihen - Kurzanleitung

Eine Zeitreihe ist eine Folge von Beobachtungen über einen bestimmten Zeitraum. Eine univariate Zeitreihe besteht aus den Werten, die eine einzelne Variable in periodischen Zeitinstanzen über einen Zeitraum hinweg erfasst, und eine multivariate Zeitreihe besteht aus den Werten, die mehrere Variablen in denselben periodischen Zeitinstanzen über einen Zeitraum hinweg erfassen. Das einfachste Beispiel für eine Zeitreihe, auf die wir alle täglich stoßen, ist die Temperaturänderung im Laufe des Tages, der Woche, des Monats oder des Jahres.

Die Analyse von Zeitdaten kann uns nützliche Einblicke geben, wie sich eine Variable im Laufe der Zeit ändert oder wie sie von der Änderung der Werte anderer Variablen abhängt. Diese Beziehung einer Variablen zu ihren vorherigen Werten und / oder anderen Variablen kann für die Vorhersage von Zeitreihen analysiert werden und hat zahlreiche Anwendungen in der künstlichen Intelligenz.

Ein grundlegendes Verständnis jeder Programmiersprache ist für einen Benutzer wichtig, um mit Problemen des maschinellen Lernens arbeiten oder diese entwickeln zu können. Eine Liste der bevorzugten Programmiersprachen für alle, die am maschinellen Lernen arbeiten möchten, finden Sie unten -

Python

Es ist eine hochinterpretierte Programmiersprache, die schnell und einfach zu codieren ist. Python kann entweder prozeduralen oder objektorientierten Programmierparadigmen folgen. Das Vorhandensein einer Vielzahl von Bibliotheken vereinfacht die Implementierung komplizierter Prozeduren. In diesem Tutorial werden wir in Python codieren und die entsprechenden Bibliotheken, die für die Zeitreihenmodellierung nützlich sind, werden in den kommenden Kapiteln erläutert.

R.

Ähnlich wie Python ist R eine interpretierte Multi-Paradigmen-Sprache, die statistische Berechnungen und Grafiken unterstützt. Die Vielzahl der Pakete erleichtert die Implementierung der Modellierung des maschinellen Lernens in R.

Java

Es handelt sich um eine interpretierte objektorientierte Programmiersprache, die für eine Vielzahl von Paketverfügbarkeiten und ausgefeilten Datenvisualisierungstechniken bekannt ist.

C / C ++

Dies sind kompilierte Sprachen und zwei der ältesten Programmiersprachen. Diese Sprachen werden häufig bevorzugt, um ML-Funktionen in die bereits vorhandenen Anwendungen zu integrieren, da Sie damit die Implementierung von ML-Algorithmen einfach anpassen können.

MATLAB

MATrix LABoratory ist eine Multi-Paradigmen-Sprache, die das Arbeiten mit Matrizen ermöglicht. Es ermöglicht mathematische Operationen für komplexe Probleme. Es wird hauptsächlich für numerische Operationen verwendet, aber einige Pakete ermöglichen auch die grafische Mehrdomänensimulation und das modellbasierte Design.

Andere bevorzugte Programmiersprachen für Probleme beim maschinellen Lernen sind JavaScript, LISP, Prolog, SQL, Scala, Julia, SAS usw.

Python erfreut sich aufgrund seiner einfach zu schreibenden und leicht verständlichen Codestruktur sowie einer Vielzahl von Open-Source-Bibliotheken einer etablierten Beliebtheit bei Personen, die maschinelles Lernen durchführen. Einige dieser Open-Source-Bibliotheken, die wir in den kommenden Kapiteln verwenden werden, wurden im Folgenden vorgestellt.

NumPy

Numerical Python ist eine Bibliothek für wissenschaftliches Rechnen. Es arbeitet mit einem N-dimensionalen Array-Objekt und bietet grundlegende mathematische Funktionen wie Größe, Form, Mittelwert, Standardabweichung, Minimum, Maximum sowie einige komplexere Funktionen wie lineare algebraische Funktionen und Fourier-Transformation. In diesem Tutorial erfahren Sie mehr darüber.

Pandas

Diese Bibliothek bietet hocheffiziente und benutzerfreundliche Datenstrukturen wie Serien, Datenrahmen und Panels. Es hat die Funktionalität von Python von der reinen Datenerfassung und -aufbereitung bis zur Datenanalyse verbessert. Die beiden Bibliotheken Pandas und NumPy machen jede Operation mit kleinen bis sehr großen Datenmengen sehr einfach. Um mehr über diese Funktionen zu erfahren, folgen Sie diesem Tutorial.

SciPy

Science Python ist eine Bibliothek für wissenschaftliches und technisches Rechnen. Es bietet Funktionen für Optimierung, Signal- und Bildverarbeitung, Integration, Interpolation und lineare Algebra. Diese Bibliothek ist praktisch, wenn Sie maschinelles Lernen durchführen. Wir werden diese Funktionen in diesem Tutorial diskutieren.

Scikit Learn

Diese Bibliothek ist ein SciPy-Toolkit, das häufig für statistische Modellierung, maschinelles Lernen und Deep Learning verwendet wird, da es verschiedene anpassbare Regressions-, Klassifizierungs- und Clustering-Modelle enthält. Es funktioniert gut mit Numpy, Pandas und anderen Bibliotheken, was die Verwendung erleichtert.

Statistikmodelle

Wie Scikit Learn wird diese Bibliothek zur statistischen Datenexploration und statistischen Modellierung verwendet. Es funktioniert auch gut mit anderen Python-Bibliotheken.

Matplotlib

Diese Bibliothek wird zur Datenvisualisierung in verschiedenen Formaten wie Liniendiagramm, Balkendiagramm, Wärmekarten, Streudiagrammen, Histogramm usw. verwendet. Sie enthält alle grafikbezogenen Funktionen, die vom Zeichnen bis zur Beschriftung erforderlich sind. Wir werden diese Funktionen in diesem Tutorial diskutieren.

Diese Bibliotheken sind sehr wichtig, um mit dem maschinellen Lernen mit jeder Art von Daten zu beginnen.

Neben den oben diskutierten ist eine weitere Bibliothek, die für die Behandlung von Zeitreihen von besonderer Bedeutung ist, -

Terminzeit

Diese Bibliothek mit ihren beiden Modulen - Datum / Uhrzeit und Kalender - bietet alle erforderlichen Datums- / Uhrzeitfunktionen zum Lesen, Formatieren und Bearbeiten der Zeit.

Wir werden diese Bibliotheken in den kommenden Kapiteln verwenden.

Zeitreihen sind eine Folge von Beobachtungen, die in gleichmäßigen Zeitintervallen indiziert sind. Daher sollten die Reihenfolge und Kontinuität in jeder Zeitreihe beibehalten werden.

Der Datensatz, den wir verwenden werden, ist eine multivariate Zeitreihe mit stündlichen Daten für ungefähr ein Jahr für die Luftqualität in einer stark verschmutzten italienischen Stadt. Der Datensatz kann über den unten angegebenen Link heruntergeladen werden -https://archive.ics.uci.edu/ml/datasets/air+quality.

Es muss sichergestellt werden, dass -

Die Zeitreihen sind gleichmäßig verteilt und
Es gibt keine redundanten Werte oder Lücken.

Falls die Zeitreihe nicht kontinuierlich ist, können wir sie hoch- oder runterabtasten.

Zeige df.head ()

In [122]:

import pandas

In [123]:

df = pandas.read_csv("AirQualityUCI.csv", sep = ";", decimal = ",")
df = df.iloc[ : , 0:14]

In [124]:

len(df)

Out [124]:

In [125]:

df.head()

Out [125]:

Für die Vorverarbeitung der Zeitreihen stellen wir sicher, dass der Datensatz keine NaN-Werte (NULL) enthält. Wenn dies der Fall ist, können wir sie entweder durch 0 oder Durchschnittswerte oder durch vorhergehende oder nachfolgende Werte ersetzen. Das Ersetzen ist eine bevorzugte Wahl gegenüber dem Löschen, damit die Kontinuität der Zeitreihen erhalten bleibt. In unserem Datensatz scheinen die letzten Werte jedoch NULL zu sein, und daher hat das Löschen keinen Einfluss auf die Kontinuität.

NaN fallen lassen (keine Zahl)

In [126]:

df.isna().sum()
Out[126]:
Date             114
Time             114
CO(GT)           114
PT08.S1(CO)      114
NMHC(GT)         114
C6H6(GT)         114
PT08.S2(NMHC)    114
NOx(GT)          114
PT08.S3(NOx)     114
NO2(GT)          114
PT08.S4(NO2)     114
PT08.S5(O3)      114
T                114
RH               114
dtype: int64

In [127]:

df = df[df['Date'].notnull()]

In [128]:

df.isna().sum()

Out [128]:

Date             0
Time             0
CO(GT)           0
PT08.S1(CO)      0
NMHC(GT)         0
C6H6(GT)         0
PT08.S2(NMHC)    0
NOx(GT)          0
PT08.S3(NOx)     0
NO2(GT)          0
PT08.S4(NO2)     0
PT08.S5(O3)      0
T                0
RH               0
dtype: int64

Zeitreihen werden normalerweise als Liniendiagramme gegen die Zeit dargestellt. Dazu kombinieren wir nun die Spalte Datum und Uhrzeit und konvertieren sie aus Zeichenfolgen in ein Datum / Uhrzeit-Objekt. Dies kann mithilfe der datetime-Bibliothek erreicht werden.

Konvertieren in ein Datum / Uhrzeit-Objekt

In [129]:

df['DateTime'] = (df.Date) + ' ' + (df.Time)
print (type(df.DateTime[0]))

<class 'str'>

In [130]:

import datetime

df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))
print (type(df.DateTime[0]))

Lassen Sie uns sehen, wie sich einige Variablen wie die Temperatur mit der Zeit ändern.

Diagramme anzeigen

In [131]:

df.index = df.DateTime

In [132]:

import matplotlib.pyplot as plt
plt.plot(df['T'])

Out [132]:

[<matplotlib.lines.Line2D at 0x1eaad67f780>]

In [208]:

plt.plot(df['C6H6(GT)'])

Out [208]:

[<matplotlib.lines.Line2D at 0x1eaaeedff28>]

Box-Plots sind eine weitere nützliche Art von Diagrammen, mit denen Sie viele Informationen zu einem Datensatz in einem einzigen Diagramm zusammenfassen können. Es zeigt den Mittelwert, 25% und 75% Quartil und Ausreißer einer oder mehrerer Variablen. Wenn die Anzahl der Ausreißer gering ist und sehr weit vom Mittelwert entfernt ist, können wir die Ausreißer eliminieren, indem wir sie auf den Mittelwert oder den Quartilwert von 75% setzen.

Boxplots anzeigen

In [134]:

plt.boxplot(df[['T','C6H6(GT)']].values)

Out [134]:

{'whiskers': [<matplotlib.lines.Line2D at 0x1eaac16de80>,
   <matplotlib.lines.Line2D at 0x1eaac16d908>,
   <matplotlib.lines.Line2D at 0x1eaac177a58>,
   <matplotlib.lines.Line2D at 0x1eaac177cf8>],
   'caps': [<matplotlib.lines.Line2D at 0x1eaac16d2b0>,
   <matplotlib.lines.Line2D at 0x1eaac16d588>,
   <matplotlib.lines.Line2D at 0x1eaac1a69e8>,
   <matplotlib.lines.Line2D at 0x1eaac1a64a8>],
   'boxes': [<matplotlib.lines.Line2D at 0x1eaac16dc50>,
   <matplotlib.lines.Line2D at 0x1eaac1779b0>],
   'medians': [<matplotlib.lines.Line2D at 0x1eaac16d4a8>,
   <matplotlib.lines.Line2D at 0x1eaac1a6c50>],
   'fliers': [<matplotlib.lines.Line2D at 0x1eaac177dd8>,
   <matplotlib.lines.Line2D at 0x1eaac1a6c18>],'means': []
}

Einführung

Eine Zeitreihe besteht aus 4 Komponenten wie unten angegeben -

Level - Es ist der Mittelwert, um den sich die Reihe ändert.
Trend - Es ist das zunehmende oder abnehmende Verhalten einer Variablen mit der Zeit.
Seasonality - Es ist das zyklische Verhalten von Zeitreihen.
Noise - Es ist der Fehler in den Beobachtungen, der aufgrund von Umweltfaktoren hinzugefügt wurde.

Zeitreihenmodellierungstechniken

Um diese Komponenten zu erfassen, gibt es eine Reihe gängiger Zeitreihenmodellierungstechniken. Dieser Abschnitt enthält eine kurze Einführung in jede Technik. Wir werden sie jedoch in den kommenden Kapiteln ausführlich erörtern.

Naive Methoden

Dies sind einfache Schätztechniken, beispielsweise wird dem vorhergesagten Wert der Wert gegeben, der dem Mittelwert der vorhergehenden Werte der zeitabhängigen Variablen oder dem vorherigen tatsächlichen Wert entspricht. Diese werden zum Vergleich mit ausgefeilten Modellierungstechniken verwendet.

Automatische Regression

Die automatische Regression sagt die Werte zukünftiger Zeiträume als Funktion der Werte früherer Zeiträume voraus. Vorhersagen der automatischen Regression passen möglicherweise besser zu den Daten als die naiven Methoden, können jedoch die Saisonalität möglicherweise nicht berücksichtigen.

ARIMA-Modell

Ein automatisch regressiver integrierter gleitender Durchschnitt modelliert den Wert einer Variablen als lineare Funktion vorheriger Werte und Restfehler bei früheren Zeitschritten einer stationären Zeitreihe. Die Daten der realen Welt können jedoch instationär sein und Saisonalität aufweisen. Daher wurden Seasonal-ARIMA und Fractional-ARIMA entwickelt. ARIMA arbeitet an univariaten Zeitreihen, um mehrere Variablen zu verarbeiten. VARIMA wurde eingeführt.

Exponentielle Glättung

Es modelliert den Wert einer Variablen als exponentiell gewichtete lineare Funktion vorheriger Werte. Dieses statistische Modell kann auch Trend und Saisonalität verarbeiten.

LSTM

Das Long Short-Term Memory-Modell (LSTM) ist ein wiederkehrendes neuronales Netzwerk, das für Zeitreihen verwendet wird, um Langzeitabhängigkeiten zu berücksichtigen. Es kann mit einer großen Datenmenge trainiert werden, um die Trends in verschiedenen Zeitreihen zu erfassen.

Die genannten Modellierungstechniken werden für die Zeitreihenregression verwendet. Lassen Sie uns in den kommenden Kapiteln nun alle diese nacheinander untersuchen.

Einführung

Jedes statistische oder maschinelle Lernmodell weist einige Parameter auf, die einen großen Einfluss darauf haben, wie die Daten modelliert werden. Zum Beispiel hat ARIMA p-, d- und q-Werte. Diese Parameter sind so zu entscheiden, dass der Fehler zwischen Istwerten und Modellwerten minimal ist. Die Parameterkalibrierung gilt als die wichtigste und zeitaufwändigste Aufgabe der Modellanpassung. Daher ist es für uns sehr wichtig, optimale Parameter zu wählen.

Methoden zur Kalibrierung von Parametern

Es gibt verschiedene Möglichkeiten, Parameter zu kalibrieren. In diesem Abschnitt werden einige davon ausführlich beschrieben.

Hit-and-Try

Eine gängige Methode zum Kalibrieren von Modellen ist die Handkalibrierung, bei der Sie zunächst die Zeitreihen visualisieren und einige Parameterwerte intuitiv ausprobieren und immer wieder ändern, bis Sie eine ausreichend gute Anpassung erzielen. Es erfordert ein gutes Verständnis des Modells, das wir versuchen. Für das ARIMA-Modell erfolgt die Handkalibrierung mithilfe des Autokorrelationsdiagramms für den Parameter 'p', des partiellen Autokorrelationsdiagramms für den Parameter 'q' und des ADF-Tests, um die Stationarität der Zeitreihen zu bestätigen und den Parameter 'd' einzustellen . Wir werden all dies in den kommenden Kapiteln ausführlich besprechen.

Rastersuche

Eine andere Möglichkeit, Modelle zu kalibrieren, ist die Rastersuche. Dies bedeutet im Wesentlichen, dass Sie versuchen, ein Modell für alle möglichen Kombinationen von Parametern zu erstellen und das Modell mit dem minimalen Fehler auszuwählen. Dies ist zeitaufwändig und daher nützlich, wenn die Anzahl der zu kalibrierenden Parameter und der Wertebereich geringer sind, da dies mehrere verschachtelte for-Schleifen umfasst.

Genetischen Algorithmus

Der genetische Algorithmus basiert auf dem biologischen Prinzip, dass sich eine gute Lösung schließlich zur optimalsten Lösung entwickelt. Es nutzt biologische Operationen wie Mutation, Crossover und Selektion, um schließlich zu einer optimalen Lösung zu gelangen.

Weitere Informationen finden Sie in anderen Techniken zur Parameteroptimierung wie der Bayes'schen Optimierung und der Schwarmoptimierung.

Einführung

Naive Methoden wie die Annahme, dass der vorhergesagte Wert zum Zeitpunkt 't' der tatsächliche Wert der Variablen zum Zeitpunkt 't-1' oder der rollierende Mittelwert der Reihen ist, werden verwendet, um abzuwägen, wie gut die statistischen Modelle und Modelle für maschinelles Lernen funktionieren können und betonen ihre Notwendigkeit.

Lassen Sie uns in diesem Kapitel diese Modelle anhand einer der Funktionen unserer Zeitreihendaten testen.

Zuerst sehen wir den Mittelwert des Temperaturmerkmals unserer Daten und die Abweichung um diese herum. Es ist auch nützlich, maximale und minimale Temperaturwerte anzuzeigen. Wir können hier die Funktionen der Numpy-Bibliothek verwenden.

Statistiken anzeigen

In [135]:

import numpy
print (
   'Mean: ',numpy.mean(df['T']), '; 
   Standard Deviation: ',numpy.std(df['T']),'; 
   \nMaximum Temperature: ',max(df['T']),'; 
   Minimum Temperature: ',min(df['T'])
)

Wir haben die Statistiken für alle 9357 Beobachtungen über einen zeitlichen Abstand, die für das Verständnis der Daten hilfreich sind.

Jetzt werden wir die erste naive Methode ausprobieren, indem wir den vorhergesagten Wert zum gegenwärtigen Zeitpunkt gleich dem tatsächlichen Wert zum vorherigen Zeitpunkt setzen und den quadratischen Mittelwertfehler (RMSE) berechnen, um die Leistung dieser Methode zu quantifizieren.

Es werden 1 ^st naive Verfahren

In [136]:

df['T']
df['T_t-1'] = df['T'].shift(1)

In [137]:

df_naive = df[['T','T_t-1']][1:]

In [138]:

from sklearn import metrics
from math import sqrt

true = df_naive['T']
prediction = df_naive['T_t-1']
error = sqrt(metrics.mean_squared_error(true,prediction))
print ('RMSE for Naive Method 1: ', error)

RMSE für naive Methode 1: 12.901140576492974

Lassen Sie uns die nächste naive Methode sehen, bei der der vorhergesagte Wert zum gegenwärtigen Zeitpunkt dem Mittelwert der vorhergehenden Zeiträume gleichgesetzt wird. Wir werden den RMSE auch für diese Methode berechnen.

Es wird 2 ^nd naive Methode

In [139]:

df['T_rm'] = df['T'].rolling(3).mean().shift(1)
df_naive = df[['T','T_rm']].dropna()

In [140]:

true = df_naive['T']
prediction = df_naive['T_rm']
error = sqrt(metrics.mean_squared_error(true,prediction))
print ('RMSE for Naive Method 2: ', error)

RMSE for Naive Method 2: 14.957633272839242

Hier können Sie mit verschiedenen Anzahl früherer Zeiträume experimentieren, die auch als "Verzögerungen" bezeichnet werden und die hier berücksichtigt werden sollen. Diese werden hier als 3 beibehalten. In diesen Daten ist zu sehen, dass mit zunehmender Anzahl von Verzögerungen und Fehlern der Fehler zunimmt. Wenn die Verzögerung 1 beibehalten wird, entspricht sie der zuvor verwendeten naiven Methode.

Points to Note

Sie können eine sehr einfache Funktion zur Berechnung des quadratischen Mittelwertfehlers schreiben. Hier haben wir die mittlere quadratische Fehlerfunktion aus dem Paket 'sklearn' verwendet und dann ihre Quadratwurzel gezogen.
In Pandas kann df ['Spaltenname'] auch als df.Spaltenname geschrieben werden. Für diesen Datensatz funktioniert df.T jedoch nicht wie df ['T'], da df.T die Funktion zum Transponieren eines Datenrahmens ist. Verwenden Sie also nur df ['T'] oder benennen Sie diese Spalte um, bevor Sie die andere Syntax verwenden.

Für eine stationäre Zeitreihe sieht ein Auto-Regressionsmodell den Wert einer Variablen zum Zeitpunkt 't' als lineare Funktion der vorangegangenen Zeitschritte 'p'. Mathematisch kann es geschrieben werden als -

$$y_{t} = \:C+\:\phi_{1}y_{t-1}\:+\:\phi_{2}Y_{t-2}+...+\phi_{p}y_{t-p}+\epsilon_{t}$$

Wobei 'p' der automatisch regressive Trendparameter ist

$\epsilon_{t}$ ist weißes Rauschen und

$y_{t-1}, y_{t-2}\:\: ...y_{t-p}$ bezeichnen den Wert der Variablen in früheren Zeiträumen.

Der Wert von p kann mit verschiedenen Methoden kalibriert werden. Eine Möglichkeit, den passenden Wert von 'p' zu ermitteln, besteht darin, das Autokorrelationsdiagramm zu zeichnen.

Note- Wir sollten die Daten in Zug und Test im Verhältnis 8: 2 der verfügbaren Gesamtdaten aufteilen, bevor wir eine Analyse der Daten durchführen, da die Testdaten nur dazu dienen, die Genauigkeit unseres Modells herauszufinden, und davon ausgehen, dass sie uns nicht zur Verfügung stehen bis nachdem Vorhersagen gemacht wurden. Bei Zeitreihen ist die Reihenfolge der Datenpunkte sehr wichtig, daher sollte beachtet werden, dass die Reihenfolge beim Aufteilen der Daten nicht verloren geht.

Ein Autokorrelationsdiagramm oder ein Korrelogramm zeigt die Beziehung einer Variablen zu sich selbst in früheren Zeitschritten. Es verwendet die Pearson-Korrelation und zeigt die Korrelationen innerhalb des 95% -Konfidenzintervalls. Mal sehen, wie es für die 'Temperatur'-Variable unserer Daten aussieht.

ACP anzeigen

In [141]:

split = len(df) - int(0.2*len(df))
train, test = df['T'][0:split], df['T'][split:]

In [142]:

from statsmodels.graphics.tsaplots import plot_acf

plot_acf(train, lags = 100)
plt.show()

Es wird angenommen, dass alle Verzögerungswerte, die außerhalb des schattierten blauen Bereichs liegen, eine Korrelation aufweisen.

Für eine stationäre Zeitreihe sieht ein Modell mit gleitendem Durchschnitt den Wert einer Variablen zum Zeitpunkt 't' als eine lineare Funktion von Restfehlern aus 'q'-Zeitschritten davor. Der Restfehler wird berechnet, indem der Wert zum Zeitpunkt 't' mit dem gleitenden Durchschnitt der vorhergehenden Werte verglichen wird.

Mathematisch kann es geschrieben werden als -

$$y_{t} = c\:+\:\epsilon_{t}\:+\:\theta_{1}\:\epsilon_{t-1}\:+\:\theta_{2}\:\epsilon_{t-2}\:+\:...+:\theta_{q}\:\epsilon_{t-q}\:$$

Dabei ist 'q' der Trendparameter für den gleitenden Durchschnitt

$\epsilon_{t}$ ist weißes Rauschen und

$\epsilon_{t-1}, \epsilon_{t-2}...\epsilon_{t-q}$ sind die Fehlerbedingungen in früheren Zeiträumen.

Der Wert von 'q' kann mit verschiedenen Methoden kalibriert werden. Eine Möglichkeit, den passenden Wert von 'q' zu finden, besteht darin, das partielle Autokorrelationsdiagramm zu zeichnen.

Ein partielles Autokorrelationsdiagramm zeigt die Beziehung einer Variablen zu sich selbst in früheren Zeitschritten, wobei indirekte Korrelationen entfernt wurden. Im Gegensatz zum Autokorrelationsdiagramm, das sowohl direkte als auch indirekte Korrelationen zeigt, wollen wir sehen, wie es für die 'Temperatur'-Variable von uns aussieht Daten.

PACP anzeigen

In [143]:

from statsmodels.graphics.tsaplots import plot_pacf

plot_pacf(train, lags = 100)
plt.show()

Eine partielle Autokorrelation wird wie ein Korrelogramm gelesen.

Wir haben bereits verstanden, dass für eine stationäre Zeitreihe eine Variable zum Zeitpunkt 't' eine lineare Funktion früherer Beobachtungen oder Restfehler ist. Daher ist es Zeit für uns, beide zu kombinieren und ein ARMA-Modell (Auto-Regressive Moving Average) zu haben.

Manchmal ist die Zeitreihe jedoch nicht stationär, dh die statistischen Eigenschaften einer Reihe wie der Mittelwert ändern sich mit der Zeit. Und die statistischen Modelle, die wir bisher untersucht haben, gehen davon aus, dass die Zeitreihen stationär sind. Daher können wir einen Vorverarbeitungsschritt zum Differenzieren der Zeitreihen einschließen, um sie stationär zu machen. Jetzt ist es wichtig für uns herauszufinden, ob die Zeitreihen, mit denen wir uns befassen, stationär sind oder nicht.

Verschiedene Methoden, um die Stationarität einer Zeitreihe zu ermitteln, suchen nach Saisonalität oder Trend in der Darstellung von Zeitreihen und überprüfen den Mittelwert- und Varianzunterschied für verschiedene Zeiträume, den Augmented Dickey-Fuller (ADF) -Test, den KPSS-Test, den Hurst-Exponenten usw. .

Lassen Sie uns mithilfe des ADF-Tests sehen, ob die Temperaturvariable unseres Datensatzes eine stationäre Zeitreihe ist oder nicht.

In [74]:

from statsmodels.tsa.stattools import adfuller

result = adfuller(train)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value In result[4].items()
   print('\t%s: %.3f' % (key, value))

ADF-Statistik: -10.406056

p-Wert: 0,000000

Kritische Werte:

1%: -3,431

5%: -2,862

10%: -2,567

Nachdem wir den ADF-Test durchgeführt haben, interpretieren wir das Ergebnis. Zuerst werden wir die ADF-Statistik mit den kritischen Werten vergleichen. Ein niedrigerer kritischer Wert sagt uns, dass die Reihe höchstwahrscheinlich nicht stationär ist. Als nächstes sehen wir den p-Wert. Ein p-Wert größer als 0,05 deutet auch darauf hin, dass die Zeitreihe nicht stationär ist.

Alternativ deuten ein p-Wert kleiner oder gleich 0,05 oder eine ADF-Statistik kleiner als kritische Werte darauf hin, dass die Zeitreihe stationär ist.

Daher ist die Zeitreihe, mit der wir uns befassen, bereits stationär. Bei stationären Zeitreihen setzen wir den Parameter 'd' auf 0.

Wir können die Stationarität von Zeitreihen auch mit dem Hurst-Exponenten bestätigen.

In [75]:

import hurst

H, c,data = hurst.compute_Hc(train)
print("H = {:.4f}, c = {:.4f}".format(H,c))

H = 0,1660, c = 5,0740

Der Wert von H <0,5 zeigt ein anti-persistentes Verhalten und H> 0,5 zeigt ein persistentes Verhalten oder eine Trendreihe. H = 0,5 zeigt zufälliges Gehen / Brownsche Bewegung. Der Wert von H <0,5 bestätigt, dass unsere Serie stationär ist.

Für instationäre Zeitreihen setzen wir den Parameter 'd' auf 1. Außerdem wird der Wert des automatisch regressiven Trendparameters 'p' und des Trendparameters 'q' für den gleitenden Durchschnitt für die stationäre Zeitreihe berechnet, dh durch Zeichnen ACP und PACP nach Differenzierung der Zeitreihen.

Das ARIMA-Modell, das durch 3 Parameter (p, d, q) gekennzeichnet ist, ist uns jetzt klar. Lassen Sie uns also unsere Zeitreihen modellieren und die zukünftigen Temperaturwerte vorhersagen.

In [156]:

from statsmodels.tsa.arima_model import ARIMA

model = ARIMA(train.values, order=(5, 0, 2))
model_fit = model.fit(disp=False)

In [157]:

predictions = model_fit.predict(len(test))
test_ = pandas.DataFrame(test)
test_['predictions'] = predictions[0:1871]

In [158]:

plt.plot(df['T'])
plt.plot(test_.predictions)
plt.show()

In [167]:

error = sqrt(metrics.mean_squared_error(test.values,predictions[0:1871]))
print ('Test RMSE for ARIMA: ', error)

Testen Sie RMSE für ARIMA: 43.21252940234892

Im vorherigen Kapitel haben wir nun gesehen, wie das ARIMA-Modell funktioniert und welche Einschränkungen es hat, dass es keine saisonalen Daten oder multivariaten Zeitreihen verarbeiten kann. Daher wurden neue Modelle eingeführt, die diese Funktionen enthalten.

Ein Blick auf diese neuen Modelle wird hier gegeben -

Vector Auto-Regression (VAR)

Es ist eine verallgemeinerte Version des automatischen Regressionsmodells für multivariate stationäre Zeitreihen. Es ist durch den Parameter 'p' gekennzeichnet.

Vector Moving Average (VMA)

Es ist eine verallgemeinerte Version des gleitenden Durchschnittsmodells für multivariate stationäre Zeitreihen. Es ist durch den Parameter 'q' gekennzeichnet.

Vector Auto Regression Moving Average (VARMA)

Es ist die Kombination von VAR und VMA und einer verallgemeinerten Version des ARMA-Modells für multivariate stationäre Zeitreihen. Es ist durch die Parameter 'p' und 'q' gekennzeichnet. Ähnlich wie ARMA sich wie ein AR-Modell verhalten kann, indem der Parameter 'q' auf 0 gesetzt wird, und wie ein MA-Modell, indem der Parameter 'p' auf 0 gesetzt wird, kann sich VARMA auch wie ein VAR-Modell verhalten, indem der Parameter 'q' eingestellt wird als 0 und als VMA-Modell durch Setzen des Parameters 'p' auf 0.

In [209]:

df_multi = df[['T', 'C6H6(GT)']]
split = len(df) - int(0.2*len(df))
train_multi, test_multi = df_multi[0:split], df_multi[split:]

In [211]:

from statsmodels.tsa.statespace.varmax import VARMAX

model = VARMAX(train_multi, order = (2,1))
model_fit = model.fit()
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\statespace\varmax.py:152: 
   EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, 
   due especially to identification issues. 
   EstimationWarning)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\base\tsa_model.py:171: 
   ValueWarning: No frequency information was provided, so inferred frequency H will be used. 
  % freq, ValueWarning)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\base\model.py:508: 
   ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals 
  "Check mle_retvals", ConvergenceWarning)

In [213]:

predictions_multi = model_fit.forecast( steps=len(test_multi))
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\base\tsa_model.py:320: 
   FutureWarning: Creating a DatetimeIndex by passing range endpoints is deprecated.  Use `pandas.date_range` instead.
   freq = base_index.freq)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\statespace\varmax.py:152: 
   EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, due especially to identification issues.
   EstimationWarning)

In [231]:

plt.plot(train_multi['T'])
plt.plot(test_multi['T'])
plt.plot(predictions_multi.iloc[:,0:1], '--')
plt.show()

plt.plot(train_multi['C6H6(GT)'])
plt.plot(test_multi['C6H6(GT)'])
plt.plot(predictions_multi.iloc[:,1:2], '--')
plt.show()

Der obige Code zeigt, wie das VARMA-Modell zur Modellierung multivariater Zeitreihen verwendet werden kann, obwohl dieses Modell für unsere Daten möglicherweise nicht am besten geeignet ist.

VARMA mit exogenen Variablen (VARMAX)

Es ist eine Erweiterung des VARMA-Modells, bei der zusätzliche Variablen, sogenannte Kovariaten, verwendet werden, um die primäre Variable zu modellieren, an der wir interessiert sind.

Saisonaler automatischer regressiver integrierter gleitender Durchschnitt (SARIMA)

Dies ist die Erweiterung des ARIMA-Modells für den Umgang mit saisonalen Daten. Es unterteilt die Daten in saisonale und nicht saisonale Komponenten und modelliert sie auf ähnliche Weise. Es ist durch 7 Parameter gekennzeichnet, für nicht saisonale Teilparameter (p, d, q) wie für das ARIMA-Modell und für saisonale Teilparameter (P, D, Q, m), wobei 'm' die Anzahl der saisonalen Perioden und ist P, D, Q ähneln den Parametern des ARIMA-Modells. Diese Parameter können mithilfe der Rastersuche oder eines genetischen Algorithmus kalibriert werden.

SARIMA mit exogenen Variablen (SARIMAX)

Dies ist die Erweiterung des SARIMA-Modells um exogene Variablen, die uns helfen, die Variable zu modellieren, an der wir interessiert sind.

Es kann nützlich sein, eine Ko-Beziehungsanalyse für Variablen durchzuführen, bevor diese als exogene Variablen verwendet werden.

In [251]:

from scipy.stats.stats import pearsonr
x = train_multi['T'].values
y = train_multi['C6H6(GT)'].values

corr , p = pearsonr(x,y)
print ('Corelation Coefficient =', corr,'\nP-Value =',p)
Corelation Coefficient = 0.9701173437269858
P-Value = 0.0

Die Pearson-Korrelation zeigt eine lineare Beziehung zwischen zwei Variablen. Um die Ergebnisse zu interpretieren, betrachten wir zunächst den p-Wert. Wenn er kleiner als 0,05 ist, ist der Wert des Koeffizienten signifikant, andernfalls ist der Wert des Koeffizienten nicht signifikant. Für einen signifikanten p-Wert zeigt ein positiver Wert des Korrelationskoeffizienten eine positive Korrelation an, und ein negativer Wert zeigt eine negative Korrelation an.

Daher scheinen für unsere Daten 'Temperatur' und 'C6H6' eine sehr positive Korrelation zu haben. Deshalb werden wir

In [297]:

from statsmodels.tsa.statespace.sarimax import SARIMAX

model = SARIMAX(x, exog = y, order = (2, 0, 2), seasonal_order = (2, 0, 1, 1), enforce_stationarity=False, enforce_invertibility = False)
model_fit = model.fit(disp = False)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\base\model.py:508: 
   ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
   "Check mle_retvals", ConvergenceWarning)

In [298]:

y_ = test_multi['C6H6(GT)'].values
predicted = model_fit.predict(exog=y_)
test_multi_ = pandas.DataFrame(test)
test_multi_['predictions'] = predicted[0:1871]

In [299]:

plt.plot(train_multi['T'])
plt.plot(test_multi_['T'])
plt.plot(test_multi_.predictions, '--')

Out [299]:

[<matplotlib.lines.Line2D at 0x1eab0191c18>]

Die Vorhersagen hier scheinen jetzt größere Variationen zu haben als die univariate ARIMA-Modellierung.

Selbstverständlich kann SARIMAX als ARX-, MAX-, ARMAX- oder ARIMAX-Modell verwendet werden, indem nur die entsprechenden Parameter auf Werte ungleich Null gesetzt werden.

Fractional Auto Regressive Integrated Moving Average (FARIMA)

Manchmal kann es vorkommen, dass unsere Serie nicht stationär ist, aber eine Differenzierung mit dem Parameter 'd', der den Wert 1 annimmt, kann ihn überdifferenzieren. Wir müssen also die Zeitreihen anhand eines Bruchwerts differenzieren.

In der Welt der Datenwissenschaft gibt es kein überlegenes Modell. Das Modell, das mit Ihren Daten arbeitet, hängt stark von Ihrem Datensatz ab. Die Kenntnis verschiedener Modelle ermöglicht es uns, eines auszuwählen, das an unseren Daten arbeitet, und mit diesem Modell zu experimentieren, um die besten Ergebnisse zu erzielen. Die Ergebnisse sollten sowohl als Plot- als auch als Fehlermetrik betrachtet werden. Manchmal kann auch ein kleiner Fehler schlecht sein. Daher ist das Zeichnen und Visualisieren der Ergebnisse unerlässlich.

Im nächsten Kapitel werden wir uns ein anderes statistisches Modell ansehen, die exponentielle Glättung.

In diesem Kapitel werden wir über die Techniken sprechen, die bei der exponentiellen Glättung von Zeitreihen eine Rolle spielen.

Einfache exponentielle Glättung

Die exponentielle Glättung ist eine Technik zum Glätten univariater Zeitreihen durch Zuweisen exponentiell abnehmender Gewichte zu Daten über einen bestimmten Zeitraum.

Mathematisch ist der Wert der Variablen zum Zeitpunkt 't + 1', der zum Zeitpunkt t, y_ (t + 1 | t) gegeben ist, definiert als -

$$y_{t+1|t}\:=\:\alpha y_{t}\:+\:\alpha\lgroup1 -\alpha\rgroup y_{t-1}\:+\alpha\lgroup1-\alpha\rgroup^{2}\:y_{t-2}\:+\:...+y_{1}$$

wo,$0\leq\alpha \leq1$ ist der Glättungsparameter und

$y_{1},....,y_{t}$ sind vorherige Werte des Netzwerkverkehrs zu den Zeitpunkten 1, 2, 3,…, t.

Dies ist eine einfache Methode, um eine Zeitreihe ohne klaren Trend oder Saisonalität zu modellieren. Die exponentielle Glättung kann aber auch für Zeitreihen mit Trend und Saisonalität verwendet werden.

Dreifache exponentielle Glättung

Bei der dreifachen exponentiellen Glättung (TES) oder der Holtschen Wintermethode wird die exponentielle Glättung dreimal angewendet - ebene Glättung $l_{t}$, Trendglättung $b_{t}$und saisonale Glättung $S_{t}$mit $\alpha$, $\beta^{*}$ und $\gamma$ als Glättungsparameter mit 'm' als Häufigkeit der Saisonalität, dh der Anzahl der Jahreszeiten pro Jahr.

Je nach Art der saisonalen Komponente hat TES zwei Kategorien:

Holt-Winter's Additive Method - Wenn die Saisonalität von Natur aus additiv ist.
Holt-Winter’s Multiplicative Method - Wenn die Saisonalität multiplikativer Natur ist.

Für nicht saisonale Zeitreihen haben wir nur Trendglättung und Pegelglättung, die als Holts lineare Trendmethode bezeichnet wird.

Versuchen wir, unsere Daten dreifach exponentiell zu glätten.

In [316]:

from statsmodels.tsa.holtwinters import ExponentialSmoothing

model = ExponentialSmoothing(train.values, trend= )
model_fit = model.fit()

In [322]:

predictions_ = model_fit.predict(len(test))

In [325]:

plt.plot(test.values)
plt.plot(predictions_[1:1871])

Out [325]:

[<matplotlib.lines.Line2D at 0x1eab00f1cf8>]

Hier haben wir das Modell einmal mit einem Trainingssatz trainiert und machen dann weiterhin Vorhersagen. Ein realistischerer Ansatz besteht darin, das Modell nach einem oder mehreren Zeitschritten neu zu trainieren. Wenn wir die Vorhersage für die Zeit 't + 1' aus den Trainingsdaten 'bis zur Zeit' t 'erhalten, kann die nächste Vorhersage für die Zeit' t + 2 'unter Verwendung der Trainingsdaten' bis zur Zeit 't + 1' als die tatsächliche gemacht werden Der Wert bei 't + 1' ist dann bekannt. Diese Methode, Vorhersagen für einen oder mehrere zukünftige Schritte zu treffen und das Modell anschließend neu zu trainieren, wird als fortlaufende Vorhersage oder Vorwärtsvalidierung bezeichnet.

Bei der Zeitreihenmodellierung werden die Vorhersagen im Zeitverlauf immer ungenauer. Daher ist es realistischer, das Modell mit tatsächlichen Daten neu zu trainieren, sobald es für weitere Vorhersagen verfügbar ist. Da das Training statistischer Modelle nicht zeitaufwändig ist, ist die Walk-Forward-Validierung die am meisten bevorzugte Lösung, um genaueste Ergebnisse zu erzielen.

Lassen Sie uns unsere Daten in einem Schritt vorwärts validieren und mit den Ergebnissen vergleichen, die wir zuvor erhalten haben.

In [333]:

prediction = []
data = train.values
for t In test.values:
   model = (ExponentialSmoothing(data).fit())
   y = model.predict()
   prediction.append(y[0])
   data = numpy.append(data, t)

In [335]:

test_ = pandas.DataFrame(test)
test_['predictionswf'] = prediction

In [341]:

plt.plot(test_['T'])
plt.plot(test_.predictionswf, '--')
plt.show()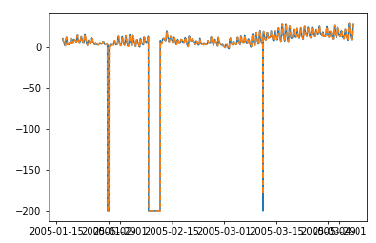

In [340]:

error = sqrt(metrics.mean_squared_error(test.values,prediction))
print ('Test RMSE for Triple Exponential Smoothing with Walk-Forward Validation: ', error)
Test RMSE for Triple Exponential Smoothing with Walk-Forward Validation:  11.787532205759442

Wir können sehen, dass unser Modell jetzt deutlich besser abschneidet. Tatsächlich wird der Trend so genau verfolgt, dass sich die Vorhersagen auf dem Plot mit den tatsächlichen Werten überschneiden. Sie können auch versuchen, die Walk-Forward-Validierung auf ARIMA-Modelle anzuwenden.

Im Jahr 2017 hat Facebook Open-Source das Prophetenmodell entwickelt, mit dem die Zeitreihen mit starken Mehrfachsaisonalitäten auf Tages-, Wochen-, Jahres- usw. und Trendniveau modelliert werden konnten. Es verfügt über intuitive Parameter, die ein weniger erfahrener Datenwissenschaftler für bessere Prognosen einstellen kann. Im Kern handelt es sich um ein additives regressives Modell, das Änderungspunkte zur Modellierung der Zeitreihen erkennen kann.

Der Prophet zerlegt die Zeitreihen in Trendkomponenten $g_{t}$Saisonalität $S_{t}$ und Feiertage $h_{t}$.

$$y_{t}=g_{t}+s_{t}+h_{t}+\epsilon_{t}$$

Wo, $\epsilon_{t}$ ist der Fehlerbegriff.

Ähnliche Pakete für die Vorhersage von Zeitreihen wie kausale Auswirkungen und Erkennung von Anomalien wurden in R von Google bzw. Twitter eingeführt.

Jetzt sind wir mit der statistischen Modellierung von Zeitreihen vertraut, aber maschinelles Lernen ist derzeit der letzte Schrei. Daher ist es wichtig, auch mit einigen Modellen des maschinellen Lernens vertraut zu sein. Wir beginnen mit dem beliebtesten Modell im Zeitreihenbereich - dem Langzeit-Kurzzeitgedächtnismodell.

LSTM ist eine Klasse von wiederkehrenden neuronalen Netzen. Bevor wir zu LSTM springen können, ist es wichtig, neuronale Netze und wiederkehrende neuronale Netze zu verstehen.

Neuronale Netze

Ein künstliches neuronales Netzwerk ist eine Schichtstruktur verbundener Neuronen, die von biologischen neuronalen Netzwerken inspiriert ist. Es ist nicht ein Algorithmus, sondern eine Kombination verschiedener Algorithmen, die es uns ermöglicht, komplexe Operationen an Daten durchzuführen.

Wiederkehrende neuronale Netze

Es ist eine Klasse neuronaler Netze, die auf zeitliche Daten zugeschnitten sind. Die Neuronen von RNN haben einen Zellzustand / Speicher, und die Eingabe wird gemäß diesem internen Zustand verarbeitet, der mit Hilfe von Schleifen im neuronalen Netzwerk erreicht wird. Es gibt wiederkehrende Module von 'tanh'-Schichten in RNNs, mit denen sie Informationen speichern können. Allerdings nicht lange, weshalb wir LSTM-Modelle brauchen.

LSTM

Es ist eine spezielle Art von wiederkehrendem neuronalen Netzwerk, das in der Lage ist, langfristige Abhängigkeiten in Daten zu lernen. Dies wird erreicht, weil das wiederkehrende Modul des Modells eine Kombination von vier Schichten aufweist, die miteinander interagieren.

Das obige Bild zeigt vier neuronale Netzwerkschichten in gelben Kästchen, punktweise Operatoren in grünen Kreisen, Eingaben in gelben Kreisen und Zellzustände in blauen Kreisen. Ein LSTM-Modul hat einen Zellenzustand und drei Gatter, die es ihnen ermöglichen, Informationen von jeder der Einheiten selektiv zu lernen, zu verlernen oder zu speichern. Der Zellzustand in LSTM hilft, dass die Informationen durch die Einheiten fließen, ohne verändert zu werden, indem nur wenige lineare Wechselwirkungen zugelassen werden. Jede Einheit verfügt über einen Eingang, einen Ausgang und ein Vergessensgatter, mit dem die Informationen zum Zellenzustand hinzugefügt oder daraus entfernt werden können. Das Vergessensgatter entscheidet, welche Informationen aus dem vorherigen Zellenzustand vergessen werden sollen, für die es eine Sigmoidfunktion verwendet. Das Eingangsgatter steuert den Informationsfluss zum aktuellen Zellenzustand unter Verwendung einer punktweisen Multiplikationsoperation von 'sigmoid' bzw. 'tanh'. Schließlich entscheidet das Ausgangsgatter, welche Informationen an den nächsten verborgenen Zustand weitergegeben werden sollen

Nachdem wir die interne Funktionsweise des LSTM-Modells verstanden haben, lassen Sie es uns implementieren. Um die Implementierung von LSTM zu verstehen, beginnen wir mit einem einfachen Beispiel - einer geraden Linie. Lassen Sie uns sehen, ob LSTM die Beziehung einer geraden Linie lernen und vorhersagen kann.

Lassen Sie uns zunächst den Datensatz erstellen, der eine gerade Linie darstellt.

In [402]:

x = numpy.arange (1,500,1)
y = 0.4 * x + 30
plt.plot(x,y)

Out [402]:

[<matplotlib.lines.Line2D at 0x1eab9d3ee10>]

In [403]:

trainx, testx = x[0:int(0.8*(len(x)))], x[int(0.8*(len(x))):]
trainy, testy = y[0:int(0.8*(len(y)))], y[int(0.8*(len(y))):]
train = numpy.array(list(zip(trainx,trainy)))
test = numpy.array(list(zip(trainx,trainy)))

Nachdem die Daten erstellt und in Zug und Test aufgeteilt wurden. Lassen Sie uns die Zeitreihendaten in Form von überwachten Lerndaten gemäß dem Wert der Rückblickperiode umwandeln, der im Wesentlichen der Anzahl der Verzögerungen entspricht, die den Wert zum Zeitpunkt 't' vorhersagen.

Also eine Zeitreihe wie diese -

time variable_x
t1  x1
t2  x2
 :   :
 :   :
T   xT

Wenn der Rückblickzeitraum 1 ist, wird in - konvertiert

x1   x2
x2   x3
 :    :
 :    :
xT-1 xT

In [404]:

def create_dataset(n_X, look_back):
   dataX, dataY = [], []
   for i in range(len(n_X)-look_back):
      a = n_X[i:(i+look_back), ]
      dataX.append(a)
      dataY.append(n_X[i + look_back, ])
   return numpy.array(dataX), numpy.array(dataY)

In [405]:

look_back = 1
trainx,trainy = create_dataset(train, look_back)
testx,testy = create_dataset(test, look_back)

trainx = numpy.reshape(trainx, (trainx.shape[0], 1, 2))
testx = numpy.reshape(testx, (testx.shape[0], 1, 2))

Jetzt werden wir unser Modell trainieren.

Kleine Stapel von Trainingsdaten werden dem Netzwerk angezeigt. Ein Durchlauf, bei dem dem Modell die gesamten Trainingsdaten in Stapeln angezeigt werden und der Fehler berechnet wird, wird als Epoche bezeichnet. Die Epochen sollen bis zu dem Zeitpunkt ausgeführt werden, an dem sich der Fehler verringert.

Im [ ]:

from keras.models import Sequential
from keras.layers import LSTM, Dense

model = Sequential()
model.add(LSTM(256, return_sequences = True, input_shape = (trainx.shape[1], 2)))
model.add(LSTM(128,input_shape = (trainx.shape[1], 2)))
model.add(Dense(2))
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
model.fit(trainx, trainy, epochs = 2000, batch_size = 10, verbose = 2, shuffle = False)
model.save_weights('LSTMBasic1.h5')

In [407]:

model.load_weights('LSTMBasic1.h5')
predict = model.predict(testx)

Nun wollen wir sehen, wie unsere Vorhersagen aussehen.

In [408]:

plt.plot(testx.reshape(398,2)[:,0:1], testx.reshape(398,2)[:,1:2])
plt.plot(predict[:,0:1], predict[:,1:2])

Out [408]:

[<matplotlib.lines.Line2D at 0x1eac792f048>]

Nun sollten wir versuchen, eine Sinus- oder Cosinuswelle auf ähnliche Weise zu modellieren. Sie können den unten angegebenen Code ausführen und mit den Modellparametern spielen, um zu sehen, wie sich die Ergebnisse ändern.

In [409]:

x = numpy.arange (1,500,1)
y = numpy.sin(x)
plt.plot(x,y)

Out [409]:

[<matplotlib.lines.Line2D at 0x1eac7a0b3c8>]

In [410]:

trainx, testx = x[0:int(0.8*(len(x)))], x[int(0.8*(len(x))):]
trainy, testy = y[0:int(0.8*(len(y)))], y[int(0.8*(len(y))):]
train = numpy.array(list(zip(trainx,trainy)))
test = numpy.array(list(zip(trainx,trainy)))

In [411]:

look_back = 1
trainx,trainy = create_dataset(train, look_back)
testx,testy = create_dataset(test, look_back)
trainx = numpy.reshape(trainx, (trainx.shape[0], 1, 2))
testx = numpy.reshape(testx, (testx.shape[0], 1, 2))

Im [ ]:

model = Sequential()
model.add(LSTM(512, return_sequences = True, input_shape = (trainx.shape[1], 2)))
model.add(LSTM(256,input_shape = (trainx.shape[1], 2)))
model.add(Dense(2))
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
model.fit(trainx, trainy, epochs = 2000, batch_size = 10, verbose = 2, shuffle = False)
model.save_weights('LSTMBasic2.h5')

In [413]:

model.load_weights('LSTMBasic2.h5')
predict = model.predict(testx)

In [415]:

plt.plot(trainx.reshape(398,2)[:,0:1], trainx.reshape(398,2)[:,1:2])
plt.plot(predict[:,0:1], predict[:,1:2])

Out [415]:

[<matplotlib.lines.Line2D at 0x1eac7a1f550>]

Jetzt können Sie mit jedem Datensatz fortfahren.

Für uns ist es wichtig, die Leistung eines Modells zu quantifizieren, um es als Feedback und Vergleich zu verwenden. In diesem Tutorial haben wir einen der beliebtesten Fehlermetrik-Root-Mean-Squared-Fehler verwendet. Es stehen verschiedene andere Fehlermetriken zur Verfügung. In diesem Kapitel werden sie kurz erläutert.

Mittlerer quadratischer Fehler

Es ist der Durchschnitt des Differenzquadrats zwischen den vorhergesagten und den wahren Werten. Sklearn bietet es als Funktion. Es hat die gleichen Einheiten wie die wahren und vorhergesagten Werte im Quadrat und ist immer positiv.

$$MSE = \frac{1}{n} \displaystyle\sum\limits_{t=1}^n \lgroup y'_{t}\:-y_{t}\rgroup^{2}$$

Wo $y'_{t}$ ist der vorhergesagte Wert,

$y_{t}$ ist der tatsächliche Wert und

n ist die Gesamtzahl der Werte im Testsatz.

Aus der Gleichung geht hervor, dass MSE größere Fehler oder Ausreißer stärker bestraft.

Root Mean Square Error

Es ist die Quadratwurzel des mittleren Quadratfehlers. Es ist auch immer positiv und liegt im Bereich der Daten.

$$RMSE = \sqrt{\frac{1}{n} \displaystyle\sum\limits_{t=1}^n \lgroup y'_{t}-y_{t}\rgroup ^2}$$

Wo, $y'_{t}$ ist der vorhergesagte Wert

$y_{t}$ ist der tatsächliche Wert und

n ist die Gesamtzahl der Werte im Testsatz.

Es liegt in der Kraft der Einheit und ist daher im Vergleich zu MSE besser interpretierbar. RMSE bestraft auch größere Fehler. In unserem Tutorial haben wir die RMSE-Metrik verwendet.

Mittlerer absoluter Fehler

Dies ist der Durchschnitt der absoluten Differenz zwischen vorhergesagten und wahren Werten. Es hat die gleichen Einheiten wie der vorhergesagte und wahre Wert und ist immer positiv.

$$MAE = \frac{1}{n}\displaystyle\sum\limits_{t=1}^{t=n} | y'{t}-y_{t}\lvert$$

Wo, $y'_{t}$ ist vorhergesagter Wert,

$y_{t}$ ist der tatsächliche Wert und

n ist die Gesamtzahl der Werte im Testsatz.

Mittlerer prozentualer Fehler

Dies ist der Prozentsatz des Durchschnitts der absoluten Differenz zwischen vorhergesagten und wahren Werten, geteilt durch den wahren Wert.

$$MAPE = \frac{1}{n}\displaystyle\sum\limits_{t=1}^n\frac{y'_{t}-y_{t}}{y_{t}}*100\: \%$$

Wo, $y'_{t}$ ist vorhergesagter Wert,

$y_{t}$ ist der tatsächliche Wert und n ist die Gesamtzahl der Werte im Testsatz.

Der Nachteil der Verwendung dieses Fehlers besteht jedoch darin, dass sich der positive Fehler und der negative Fehler gegenseitig ausgleichen können. Daher wird der mittlere absolute prozentuale Fehler verwendet.

Mittlerer absoluter prozentualer Fehler

Dies ist der Prozentsatz des Durchschnitts der absoluten Differenz zwischen vorhergesagten und wahren Werten, geteilt durch den wahren Wert.

$$MAPE = \frac{1}{n}\displaystyle\sum\limits_{t=1}^n\frac{|y'_{t}-y_{t}\lvert}{y_{t}}*100\: \%$$

Wo $y'_{t}$ ist der vorhergesagte Wert

$y_{t}$ ist der tatsächliche Wert und

n ist die Gesamtzahl der Werte im Testsatz.

In diesem Lernprogramm haben wir die Zeitreihenanalyse erörtert. Dadurch haben wir verstanden, dass Zeitreihenmodelle zuerst den Trend und die Saisonalität aus den vorhandenen Beobachtungen erkennen und dann einen Wert prognostizieren, der auf diesem Trend und dieser Saisonalität basiert. Eine solche Analyse ist in verschiedenen Bereichen nützlich, wie z.

Financial Analysis - Es umfasst Umsatzprognosen, Bestandsanalysen, Börsenanalysen und Preisschätzungen.
Weather Analysis - Es umfasst Temperaturschätzung, Klimawandel, saisonale Schichterkennung und Wettervorhersage.
Network Data Analysis - Es umfasst die Vorhersage der Netzwerknutzung, die Erkennung von Anomalien oder Eindringlingen sowie die vorausschauende Wartung.
Healthcare Analysis - Es umfasst die Vorhersage der Volkszählung, die Vorhersage der Versicherungsleistungen und die Überwachung der Patienten.

Maschinelles Lernen befasst sich mit verschiedenen Arten von Problemen. Tatsächlich können fast alle Bereiche mithilfe des maschinellen Lernens automatisiert oder verbessert werden. Einige dieser Probleme, an denen viel gearbeitet wird, sind nachstehend aufgeführt.

Zeitreihendaten

Dies sind die Daten, die sich mit der Zeit ändern, und daher spielt die Zeit eine entscheidende Rolle, die wir in diesem Tutorial ausführlich besprochen haben.

Nicht-Zeitreihendaten

Es handelt sich um zeitunabhängige Daten, und ein Großteil der ML-Probleme betrifft Nicht-Zeitreihendaten. Der Einfachheit halber werden wir es weiter kategorisieren als -

Numerical Data - Computer verstehen im Gegensatz zu Menschen nur Zahlen, sodass alle Arten von Daten letztendlich für maschinelles Lernen in numerische Daten konvertiert werden. Beispielsweise werden Bilddaten in (r, b, g) -Werte konvertiert, Zeichen in ASCII-Codes oder Wörter konvertiert werden in Zahlen indiziert, Sprachdaten werden in mfcc-Dateien konvertiert, die numerische Daten enthalten.
Image Data - Computer Vision hat die Welt der Computer revolutioniert, es hat verschiedene Anwendungen in den Bereichen Medizin, Satellitenbildgebung usw.
Text Data- Natural Language Processing (NLP) wird zur Klassifizierung von Texten, zur Erkennung von Paraphrasen und zur Zusammenfassung von Sprachen verwendet. Das macht Google und Facebook schlau.
Speech Data- Sprachverarbeitung beinhaltet Spracherkennung und Stimmungsverständnis. Es spielt eine entscheidende Rolle, wenn es darum geht, Computern menschenähnliche Eigenschaften zu verleihen.