Aprendizaje sin supervisión

Como sugiere el nombre, este tipo de aprendizaje se realiza sin la supervisión de un profesor. Este proceso de aprendizaje es independiente. Durante el entrenamiento de ANN bajo aprendizaje no supervisado, los vectores de entrada de tipo similar se combinan para formar grupos. Cuando se aplica un nuevo patrón de entrada, la red neuronal da una respuesta de salida que indica la clase a la que pertenece el patrón de entrada. En esto, no habría retroalimentación del entorno sobre cuál debería ser el resultado deseado y si es correcto o incorrecto. Por lo tanto, en este tipo de aprendizaje, la propia red debe descubrir los patrones, las características de los datos de entrada y la relación entre los datos de entrada y los de salida.

Redes en las que el ganador se lo lleva todo

Este tipo de redes se basan en la regla de aprendizaje competitivo y utilizarán la estrategia en la que elija la neurona con las mayores entradas totales como ganadora. Las conexiones entre las neuronas de salida muestran la competencia entre ellas y una de ellas estaría 'ENCENDIDA', lo que significa que sería la ganadora y otras estarían 'APAGADAS'.

A continuación, se muestran algunas de las redes basadas en este concepto simple que utilizan el aprendizaje no supervisado.

Red Hamming

En la mayoría de las redes neuronales que utilizan el aprendizaje no supervisado, es fundamental calcular la distancia y realizar comparaciones. Este tipo de red es la red Hamming, donde por cada vector de entrada dado, se agruparía en diferentes grupos. A continuación se presentan algunas características importantes de Hamming Networks:

Lippmann comenzó a trabajar en las redes Hamming en 1987.
Es una red de una sola capa.
Las entradas pueden ser binarias {0, 1} o bipolares {-1, 1}.
Los pesos de la red se calculan mediante los vectores ejemplares.
Es una red de peso fijo, lo que significa que los pesos seguirían siendo los mismos incluso durante el entrenamiento.

Max neto

Esta es también una red de peso fijo, que sirve como subred para seleccionar el nodo que tiene la entrada más alta. Todos los nodos están completamente interconectados y existen pesos simétricos en todas estas interconexiones ponderadas.

Arquitectura

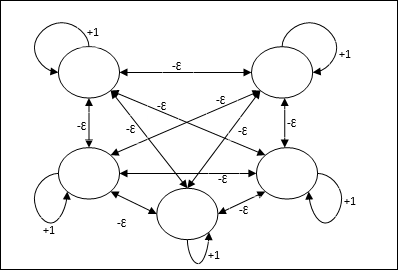
Utiliza el mecanismo que es un proceso iterativo y cada nodo recibe entradas inhibitorias de todos los demás nodos a través de conexiones. El único nodo cuyo valor es máximo sería activo o ganador y las activaciones de todos los demás nodos estarían inactivas. Max Net usa la función de activación de identidad con $$ f (x) \: = \: \ begin {cases} x & if \: x> 0 \\ 0 & if \: x \ leq 0 \ end {cases} $$

La tarea de esta red se logra mediante el peso de autoexcitación de +1 y la magnitud de inhibición mutua, que se establece como [0 <ɛ <$ \ frac {1} {m} $] donde “m” es el número total de nodos.

Aprendizaje competitivo en ANN

Se ocupa del entrenamiento no supervisado en el que los nodos de salida intentan competir entre sí para representar el patrón de entrada. Para comprender esta regla de aprendizaje tendremos que comprender la red competitiva que se explica a continuación:

Concepto básico de red competitiva

Esta red es como una red de alimentación directa de una sola capa que tiene una conexión de retroalimentación entre las salidas. Las conexiones entre las salidas son de tipo inhibitorio, lo que se muestra con líneas de puntos, lo que significa que los competidores nunca se apoyan a sí mismos.

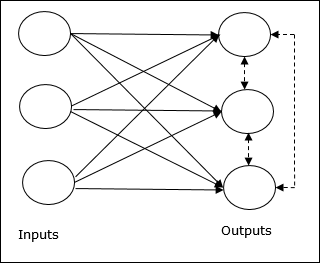
Concepto básico de regla de aprendizaje competitivo

Como se dijo anteriormente, habría competencia entre los nodos de salida, por lo que el concepto principal es: durante el entrenamiento, la unidad de salida que tenga la activación más alta para un patrón de entrada dado, será declarada ganadora. Esta regla también se llama El ganador se lo lleva todo porque solo se actualiza la neurona ganadora y el resto de las neuronas no se modifican.

Formulación matemática

A continuación se presentan los tres factores importantes para la formulación matemática de esta regla de aprendizaje:

Condición para ser un ganador

Supongamos que una neurona y_k quiere ser el ganador, entonces habría la siguiente condición

$$ y_ {k} \: = \: \ begin {cases} 1 & if \: v_ {k}> v_ {j} \: para \: todos \: \: j, \: j \: \ neq \ : k \\ 0 y de lo contrario \ end {cases} $$

Significa que si alguna neurona, digamos, y_k quiere ganar, entonces su campo local inducido (la salida de la unidad de suma), digamos v_k, debe ser la más grande entre todas las demás neuronas de la red.
Condición de la suma total de peso

Otra restricción sobre la regla de aprendizaje competitivo es que la suma total de pesos de una neurona de salida en particular será 1. Por ejemplo, si consideramos neurona k luego

$$ \ Displaystyle \ sum \ limits_ {k} w_ {kj} \: = \: 1 \: \: \: \: para \: todos \: \: k $$
Cambio de peso para el ganador

Si una neurona no responde al patrón de entrada, entonces no tiene lugar ningún aprendizaje en esa neurona. Sin embargo, si una neurona en particular gana, entonces los pesos correspondientes se ajustan de la siguiente manera:

$$ \ Delta w_ {kj} \: = \: \ begin {cases} - \ alpha (x_ {j} \: - \: w_ {kj}), y si \: neuron \: k \: gana \\ 0 y si \: neurona \: k \: pérdidas \ end {casos} $$

Aquí $ \ alpha $ es la tasa de aprendizaje.

Esto muestra claramente que estamos favoreciendo a la neurona ganadora ajustando su peso y si se pierde una neurona, entonces no necesitamos molestarnos en reajustar su peso.

Algoritmo de agrupación de K-means

K-means es uno de los algoritmos de agrupamiento en clúster más populares en el que usamos el concepto de procedimiento de partición. Comenzamos con una partición inicial y movemos patrones repetidamente de un clúster a otro, hasta que obtenemos un resultado satisfactorio.

Algoritmo

Step 1 - Seleccionar kpuntos como centroides iniciales. Inicializark prototipos (w₁,…,w_k), por ejemplo, podemos identificarlos con vectores de entrada elegidos al azar -

$$ W_ {j} \: = \: i_ {p}, \: \: \: donde \: j \: \ in \ lbrace1, ...., k \ rbrace \: y \: p \: \ en \ lbrace1, ...., n \ rbrace $$

Cada grupo C_j está asociado con el prototipo w_j.

Step 2 - Repita el paso 3-5 hasta que E ya no disminuya o la membresía del clúster ya no cambie.

Step 3 - Para cada vector de entrada i_p dónde p ∈ {1,…,n}, poner i_p en el cluster C_j* con el prototipo más cercano w_j* teniendo la siguiente relación

$$ | i_ {p} \: - \: w_ {j *} | \: \ leq \: | i_ {p} \: - \: w_ {j} |, \: j \: \ in \ lbrace1, ...., k \ rbrace $$

Step 4 - Para cada grupo C_j, dónde j ∈ { 1,…,k}, actualiza el prototipo w_j para ser el centroide de todas las muestras actualmente en C_j , así que eso

$$ w_ {j} \: = \: \ sum_ {i_ {p} \ in C_ {j}} \ frac {i_ {p}} {| C_ {j} |} $$

Step 5 - Calcule el error de cuantificación total de la siguiente manera -

$$ E \: = \: \ sum_ {j = 1} ^ k \ sum_ {i_ {p} \ in w_ {j}} | i_ {p} \: - \: w_ {j} | ^ 2 $$

Neocognitron

Es una red feedforward multicapa, que fue desarrollada por Fukushima en la década de 1980. Este modelo se basa en el aprendizaje supervisado y se utiliza para el reconocimiento visual de patrones, principalmente caracteres escritos a mano. Es básicamente una extensión de la red Cognitron, que también fue desarrollada por Fukushima en 1975.

Arquitectura

Es una red jerárquica, que comprende muchas capas y existe un patrón de conectividad local en esas capas.

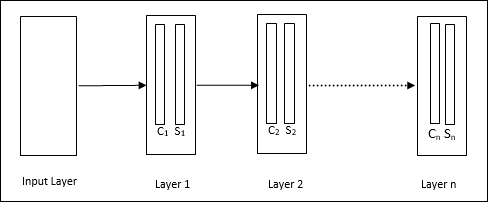
Como hemos visto en el diagrama anterior, el neocognitrón se divide en diferentes capas conectadas y cada capa tiene dos celdas. La explicación de estas celdas es la siguiente:

S-Cell - Se llama celda simple, que está entrenada para responder a un patrón particular o un grupo de patrones.

C-Cell- Se llama celda compleja, que combina la salida de la celda S y simultáneamente reduce el número de unidades en cada matriz. En otro sentido, la célula C desplaza el resultado de la célula S.

Algoritmo de entrenamiento

Se encuentra que el entrenamiento del neocognitrón progresa capa por capa. Los pesos de la capa de entrada a la primera capa se entrenan y congelan. Luego, se entrenan los pesos de la primera capa a la segunda capa, y así sucesivamente. Los cálculos internos entre la celda S y la celda C dependen de los pesos provenientes de las capas anteriores. Por lo tanto, podemos decir que el algoritmo de entrenamiento depende de los cálculos en la celda S y la celda C.