Circuitos digitales - Guía rápida
Si la base o la raíz de un sistema numérico es 'r', entonces los números presentes en ese sistema numérico van de cero a r-1. Los números totales presentes en ese sistema numérico es 'r'. Entonces, obtendremos varios sistemas numéricos, eligiendo los valores de la base como mayor o igual a dos.
En este capítulo, analicemos la popular number systemsy cómo representar un número en el sistema numérico respectivo. Los siguientes sistemas numéricos son los más utilizados.
- Sistema de números decimales
- Sistema de números binarios
- Sistema de número octal
- Sistema numérico hexadecimal
Sistema de números decimales
los base o la base del sistema numérico decimal es 10. Entonces, los números que van del 0 al 9 se usan en este sistema numérico. La parte del número que se encuentra a la izquierda deldecimal pointse conoce como parte entera. De manera similar, la parte del número que se encuentra a la derecha del punto decimal se conoce como parte fraccionaria.
En este sistema numérico, las posiciones sucesivas a la izquierda del punto decimal tienen pesos de 10 0 , 10 1 , 10 2 , 10 3 y así sucesivamente. Del mismo modo, las posiciones sucesivas a la derecha del punto decimal tienen pesos de 10 -1 , 10 -2 , 10-3 y así sucesivamente. Eso significa que cada puesto tiene un peso específico, que espower of base 10
Ejemplo
Considera el decimal number 1358.246. La parte entera de este número es 1358 y la parte fraccionaria de este número es 0,246. Los dígitos 8, 5, 3 y 1 tienen pesos de 100, 101, 10 2 y 10 3 respectivamente. De manera similar, los dígitos 2, 4 y 6 tienen pesos de 10 -1 , 10 -2 y 10-3 respectivamente.
Mathematically, podemos escribirlo como
1358.246 = (1 × 10 3 ) + (3 × 10 2 ) + (5 × 10 1 ) + (8 × 10 0 ) + (2 × 10 -1 ) +
(4 × 10 -2 ) + (6 × 10-3 )
Después de simplificar los términos del lado derecho, obtendremos el número decimal, que está en el lado izquierdo.
Sistema de números binarios
Todos los circuitos y sistemas digitales utilizan este sistema de números binarios. losbase o la base de este sistema numérico es 2. Entonces, los números 0 y 1 se usan en este sistema numérico.
La parte del número, que se encuentra a la izquierda del binary pointse conoce como parte entera. De manera similar, la parte del número que se encuentra a la derecha del punto binario se conoce como parte fraccionaria.
En este sistema numérico, las posiciones sucesivas a la izquierda del punto binario tienen pesos de 2 0 , 2 1 , 2 2 , 2 3 y así sucesivamente. De manera similar, las posiciones sucesivas a la derecha del punto binario tienen pesos de 2 -1 , 2 -2 , 2 -3 y así sucesivamente. Eso significa que cada puesto tiene un peso específico, que espower of base 2.
Ejemplo
Considera el binary number 1101.011. La parte entera de este número es 1101 y la parte fraccionaria de este número es 0.011. Los dígitos 1, 0, 1 y 1 de la parte entera tienen pesos de 2 0 , 2 1 , 2 2 , 2 3 respectivamente. De manera similar, los dígitos 0, 1 y 1 de la parte fraccionaria tienen pesos de 2 -1 , 2 -2 , 2-3 respectivamente.
Mathematically, podemos escribirlo como
1101.011 = (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 ) + (0 × 2 -1 ) +
(1 × 2 -2 ) + (1 × 2-3 )
Después de simplificar los términos del lado derecho, obtendremos un número decimal, que es equivalente al número binario del lado izquierdo.
Sistema de números octales
los base o la raíz del sistema de números octales es 8. Entonces, los números que van del 0 al 7 se usan en este sistema numérico. La parte del número que se encuentra a la izquierda deloctal pointse conoce como parte entera. De manera similar, la parte del número que se encuentra a la derecha del punto octal se conoce como parte fraccionaria.
En este sistema numérico, las posiciones sucesivas a la izquierda del punto octal tienen pesos de 8 0 , 8 1 , 8 2 , 8 3 y así sucesivamente. De manera similar, las posiciones sucesivas a la derecha del punto octal tienen pesos de 8 -1 , 8 -2 , 8-3 y así sucesivamente. Eso significa que cada puesto tiene un peso específico, que espower of base 8.
Ejemplo
Considera el octal number 1457.236. La parte entera de este número es 1457 y la parte fraccionaria de este número es 0,236. Los dígitos 7, 5, 4 y 1 tienen pesos de 8 0 , 8 1 , 8 2 y 8 3 respectivamente. De manera similar, los dígitos 2, 3 y 6 tienen pesos de 8 -1 , 8 -2 , 8-3 respectivamente.
Mathematically, podemos escribirlo como
1457.236 = (1 × 8 3 ) + (4 × 8 2 ) + (5 × 8 1 ) + (7 × 8 0 ) + (2 × 8 -1 ) +
(3 × 8 -2 ) + (6 × 8-3 )
Después de simplificar los términos del lado derecho, obtendremos un número decimal, que es equivalente al número octal del lado izquierdo.
Sistema numérico hexadecimal
los base o la base del sistema numérico hexa-decimal es 16. Entonces, los números que van del 0 al 9 y las letras de la A a la F se usan en este sistema numérico. El equivalente decimal de los dígitos hexadecimales de la A a la F es de 10 a 15.
La parte del número, que se encuentra a la izquierda del hexadecimal pointse conoce como parte entera. De manera similar, la parte del número que se encuentra a la derecha del punto hexadecimal se conoce como parte fraccionaria.
En este sistema numérico, las posiciones sucesivas a la izquierda del punto hexadecimal tienen pesos de 16 0 , 16 1 , 16 2 , 16 3 y así sucesivamente. Del mismo modo, las posiciones sucesivas a la derecha de la coma decimal hexadecimal tienen pesos de 16 -1 , 16 -2 , 16-3 y así sucesivamente. Eso significa que cada puesto tiene un peso específico, que espower of base 16.
Ejemplo
Considera el Hexa-decimal number 1A05.2C4. La parte entera de este número es 1A05 y la parte fraccionaria de este número es 0.2C4. Los dígitos 5, 0, A y 1 tienen pesos de 16 0 , 16 1 , 16 2 y 16 3 respectivamente. De manera similar, los dígitos 2, C y 4 tienen pesos de 16 -1 , 16 -2 y 16-3 respectivamente.
Mathematically, podemos escribirlo como
1A05.2C4 = (1 × 16 3 ) + (10 × 16 2 ) + (0 × 16 1 ) + (5 × 16 0 ) + (2 × 16 -1 ) +
(12 × 16 -2 ) + (4 × 16-3 )
Después de simplificar los términos del lado derecho, obtendremos un número decimal, que es equivalente al número hexadecimal del lado izquierdo.
En el capítulo anterior, hemos visto los cuatro sistemas numéricos destacados. En este capítulo, convertiremos los números de un sistema numérico a otro para encontrar el valor equivalente.
Conversión de número decimal a otras bases
Si el número decimal contiene tanto una parte entera como una parte fraccionaria, convierta ambas partes del número decimal en otra base individualmente. Siga estos pasos para convertir el número decimal en su número equivalente de cualquier base 'r'.
Hacer division de parte entera del número decimal y successive quotientscon base 'r' y anote el resto hasta que el cociente sea cero. Considere los restos en orden inverso para obtener la parte entera del número equivalente de base 'r'. Eso significa que el primer y último residuo denotan el dígito menos significativo y el dígito más significativo respectivamente.
Hacer multiplication de parte fraccionaria del número decimal y successive fractionscon la base 'r' y anote el acarreo hasta que el resultado sea cero o se obtenga el número deseado de dígitos equivalentes. Considere la secuencia normal de acarreo para obtener la parte fraccionaria del número equivalente de base 'r'.
Conversión de decimal a binario
Se llevan a cabo los siguientes dos tipos de operaciones, mientras se convierte un número decimal en su número binario equivalente.
- División de parte entera y cocientes sucesivos con base 2.
- Multiplicación de parte fraccionaria y fracciones sucesivas con base 2.
Example
Considera el decimal number 58.25. Aquí, la parte entera es 58 y la parte fraccionaria es 0.25.
Step 1 - División de 58 y cocientes sucesivos con base 2.
| Operación | Cociente | Recordatorio |
|---|---|---|
| 58/2 | 29 | 0 (LSB) |
| 29/2 | 14 | 1 |
| 14/2 | 7 | 0 |
| 7/2 | 3 | 1 |
| 3/2 | 1 | 1 |
| 1/2 | 0 | 1(MSB) |
⇒ (58) 10 = (111010) 2
Por lo tanto, los integer part de número binario equivalente es 111010.
Step 2 - Multiplicación de 0,25 y fracciones sucesivas con base 2.
| Operación | Resultado | Llevar |
|---|---|---|
| 0,25 x 2 | 0,5 | 0 |
| 0,5 x 2 | 1.0 | 1 |
| - | 0.0 | - |
⇒ (.25) 10 = (.01) 2
Por lo tanto, los fractional part de número binario equivalente es .01
⇒ (58,25) 10 = (111010,01) 2
Por lo tanto, los binary equivalent del número decimal 58.25 es 111010.01.
Conversión de decimal a octal
Se llevan a cabo los siguientes dos tipos de operaciones, mientras se convierte un número decimal en su número octal equivalente.
División de parte entera y cocientes sucesivos con base 8.
Multiplicación de parte fraccionaria y fracciones sucesivas con base 8.
Example
Considera el decimal number 58.25. Aquí, la parte entera es 58 y la parte fraccionaria es 0.25.
Step 1 - División de 58 y cocientes sucesivos con base 8.
| Operación | Cociente | Recordatorio |
|---|---|---|
| 58/8 | 7 | 2 |
| 7/8 | 0 | 7 |
⇒ (58) 10 = (72) 8
Por lo tanto, los integer part del número octal equivalente es 72.
Step 2 - Multiplicación de 0,25 y fracciones sucesivas con base 8.
| Operación | Resultado | Llevar |
|---|---|---|
| 0,25 x 8 | 2,00 | 2 |
| - | 0,00 | - |
⇒ (.25) 10 = (.2) 8
Por lo tanto, los fractional part del número octal equivalente es .2
⇒ (58,25) 10 = (72,2) 8
Por lo tanto, los octal equivalent del número decimal 58.25 es 72.2.
Conversión de decimal a hexadecimal
Los siguientes dos tipos de operaciones tienen lugar, mientras se convierte un número decimal en su número hexa-decimal equivalente.
- División de parte entera y cocientes sucesivos con base 16.
- Multiplicación de parte fraccionaria y fracciones sucesivas con base 16.
Example
Considera el decimal number 58.25. Aquí, la parte entera es 58 y la parte decimal es 0.25.
Step 1 - División de 58 y cocientes sucesivos con base 16.
| Operación | Cociente | Recordatorio |
|---|---|---|
| 58/16 | 3 | 10 = A |
| 3/16 | 0 | 3 |
⇒ (58) 10 = (3A) 16
Por lo tanto, los integer part del número hexadecimal equivalente es 3A.
Step 2 - Multiplicación de 0,25 y fracciones sucesivas de base 16.
| Operación | Resultado | Llevar |
|---|---|---|
| 0,25 x 16 | 4,00 | 4 |
| - | 0,00 | - |
⇒ (.25) 10 = (.4) 16
Por lo tanto, los fractional part del número hexadecimal equivalente es .4.
⇒(58.25)10 = (3A.4)16
Por lo tanto, los Hexa-decimal equivalent del número decimal 58.25 es 3A.4.
Conversión de números binarios a otras bases
El proceso de convertir un número de binario a decimal es diferente al proceso de convertir un número binario a otras bases. Ahora, analicemos la conversión de un número binario a sistemas numéricos decimales, octales y hexadecimales, uno por uno.
Conversión de binario a decimal
Para convertir un número binario en su número decimal equivalente, primero multiplique los bits del número binario con los respectivos pesos posicionales y luego agregue todos esos productos.
Example
Considera el binary number 1101.11.
Mathematically, podemos escribirlo como
(1101.11) 2 = (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 ) + (1 × 2 -1 ) +
(1 × 2 -2 )
⇒ (1101.11) 2 = 8 + 4 + 0 + 1 + 0.5 + 0.25 = 13.75
⇒ (1101,11) 2 = (13,75) 10
Por lo tanto, los decimal equivalent del número binario 1101.11 es 13.75.
Conversión de binario a octal
Sabemos que las bases de los sistemas numéricos binarios y octales son 2 y 8 respectivamente. Tres bits de número binario equivalen a un dígito octal, ya que 2 3 = 8.
Siga estos dos pasos para convertir un número binario en su número octal equivalente.
Comience desde el punto binario y haga grupos de 3 bits en ambos lados del punto binario. Si uno o dos bits son menores al formar el grupo de 3 bits, incluya el número requerido de ceros en los lados extremos.
Escribe los dígitos octales correspondientes a cada grupo de 3 bits.
Example
Considera el binary number 101110.01101.
Step 1 - Hacer los grupos de 3 bits a ambos lados del punto binario.
101110.011 01
Aquí, en el lado derecho del punto binario, el último grupo tiene solo 2 bits. Por lo tanto, incluya un cero en el extremo para convertirlo en un grupo de 3 bits.
⇒ 101110,011 010
Step 2 - Escribe los dígitos octales correspondientes a cada grupo de 3 bits.
⇒ (101110,011010) 2 = (56,32) 8
Por lo tanto, los octal equivalent del número binario 101110.01101 es 56.32.
Conversión binaria a hexadecimal
Sabemos que las bases de los sistemas numéricos binarios y hexadecimales son 2 y 16 respectivamente. Cuatro bits de número binario equivalen a un dígito hexadecimal, ya que 2 4 = 16.
Siga estos dos pasos para convertir un número binario en su número hexadecimal equivalente.
Comience desde el punto binario y haga grupos de 4 bits en ambos lados del punto binario. Si algunos bits son menores al formar el grupo de 4 bits, incluya el número requerido de ceros en los lados extremos.
Escriba los dígitos hexadecimales correspondientes a cada grupo de 4 bits.
Example
Considera el binary number 101110.01101
Step 1 - Hacer los grupos de 4 bits a ambos lados del punto binario.
10 1110.0110 1
Aquí, el primer grupo tiene solo 2 bits. Por lo tanto, incluya dos ceros en el lado extremo para formar un grupo de 4 bits. De manera similar, incluya tres ceros en el lado extremo para hacer que el último grupo también sea un grupo de 4 bits.
⇒ 0010 1110,0110 1000
Step 2 - Escribir los dígitos hexadecimales correspondientes a cada grupo de 4 bits.
⇒ (0010 1110.0110 1000) 2 = (2E.68) 16
Por lo tanto, los Hexa-decimal equivalent del número binario 101110.01101 es (2E.68).
Conversión de número octal a otras bases
El proceso de convertir un número de octal a decimal es diferente al proceso de convertir un número octal a otras bases. Ahora, hablemos sobre la conversión de un número octal a sistemas numéricos decimales, binarios y hexadecimales uno por uno.
Conversión de octal a decimal
Para convertir un número octal en su número decimal equivalente, primero multiplique los dígitos del número octal con los respectivos pesos posicionales y luego agregue todos esos productos.
Example
Considera el octal number 145.23.
Mathematically, podemos escribirlo como
(145,23) 8 = (1 × 8 2 ) + (4 × 8 1 ) + (5 × 8 0 ) + (2 × 8 -1 ) + (3 × 8 -2 )
⇒ (145,23) 8 = 64 + 32 + 5 + 0,25 + 0,05 = 101,3
⇒ (145,23) 8 = (101,3) 10
Por lo tanto, los decimal equivalent del número octal 145.23 es 101.3.
Conversión de octal a binario
El proceso de convertir un número octal en un número binario equivalente es exactamente opuesto al de la conversión de binario a octal. Al representar cada dígito octal con 3 bits, obtendremos el número binario equivalente.
Example
Considera el octal number 145.23.
Represente cada dígito octal con 3 bits.
(145.23) 8 = (001100101.010 011) 2
El valor no cambia al eliminar los ceros, que están en el extremo.
⇒ (145,23) 8 = (1100101,010011) 2
Por lo tanto, los binary equivalent del número octal 145.23 es 1100101.010011.
Conversión de octal a hexadecimal
Siga estos dos pasos para convertir un número octal en su número hexadecimal equivalente.
- Convierta el número octal en su número binario equivalente.
- Convierta el número binario anterior en su número hexadecimal equivalente.
Example
Considera el octal number 145.23
En el ejemplo anterior, obtuvimos el equivalente binario del número octal 145.23 como 1100101.010011.
Siguiendo el procedimiento de conversión de binario a hexadecimal, obtendremos
(1100101.010011) 2 = (65,4C) 16
⇒ (145,23) 8 = (65,4C) 16
Por lo tanto, los Hexa-decimal equivalentde número octal 145.23 es 65,4 C .
Conversión de número hexadecimal a otras bases
El proceso de convertir un número hexadecimal en decimal es diferente al proceso de convertir un número hexadecimal en otras bases. Ahora, hablemos sobre la conversión de números hexadecimales a sistemas numéricos decimales, binarios y octales uno por uno.
Conversión de hexadecimal a decimal
Para convertir un número hexadecimal en su número decimal equivalente, primero multiplique los dígitos del número hexadecimal con los respectivos pesos posicionales y luego agregue todos esos productos.
Example
Considera el Hexa-decimal number 1A5.2
Mathematically, podemos escribirlo como
(1A5.2) 16 = (1 × 16 2 ) + (10 × 16 1 ) + (5 × 16 0 ) + (2 × 16 -1 )
⇒ (1A5.2) 16 = 256 + 160 + 5 + 0.125 = 421.125
⇒ (1A5.2) 16 = (421.125) 10
Por lo tanto, los decimal equivalent del número hexadecimal 1A5.2 es 421.125.
Conversión hexadecimal a binaria
El proceso de convertir un número hexadecimal en su número binario equivalente es exactamente opuesto al de la conversión de binario a hexadecimal. Al representar cada dígito hexadecimal con 4 bits, obtendremos el número binario equivalente.
Example
Considera el Hexa-decimal number 65.4C
Represente cada dígito hexadecimal con 4 bits.
(65,4C) 6 = (0110 0101,0100 1100) 2
El valor no cambia al eliminar los ceros, que se encuentran en dos lados extremos.
⇒ (65,4C) 16 = (1100101,010011) 2
Por lo tanto, los binary equivalent del número hexadecimal 65.4C es 1100101.010011.
Conversión de hexadecimal a octal
Siga estos dos pasos para convertir un número hexadecimal en su número octal equivalente.
- Convierta un número hexadecimal en su número binario equivalente.
- Convierta el número binario anterior en su número octal equivalente.
Example
Considera el Hexa-decimal number 65.4C
En el ejemplo anterior, obtuvimos el equivalente binario del número hexadecimal 65.4C como 1100101.010011.
Siguiendo el procedimiento de conversión de binario a octal, obtendremos
(1100101.010011) 2 = (145.23) 8
⇒ (65,4C) 16 = (145,23)
Por lo tanto, los octal equivalentdel número hexadecimal 65,4 C es 145,23.
Podemos convertir los números binarios en los siguientes dos grupos: Unsigned numbers y Signed numbers.
Números sin firmar
Los números sin signo contienen solo la magnitud del número. No tienen ninguna señal. Eso significa que todos los números binarios sin signo son positivos. Como en el sistema numérico decimal, colocar un signo positivo delante del número es opcional para representar números positivos. Por lo tanto, todos los números positivos, incluido el cero, pueden tratarse como números sin signo si no se asigna un signo positivo delante del número.
Números firmados
Los números con signo contienen tanto el signo como la magnitud del número. Generalmente, el letrero se coloca delante del número. Entonces, tenemos que considerar el signo positivo para números positivos y el signo negativo para números negativos. Por lo tanto, todos los números pueden tratarse como números con signo si se asigna el signo correspondiente delante del número.
Si el bit de signo es cero, indica que el número binario es positivo. De manera similar, si el bit de signo es uno, lo que indica que el número binario es negativo.
Representación de números binarios sin firmar
Los bits presentes en el número binario sin signo contienen el magnitudede un número. Eso significa, si el número binario sin firmar contiene‘N’ bits, luego todos N los bits representan la magnitud del número, ya que no tiene ningún bit de signo.
Example
Considera el decimal number 108. El equivalente binario de este número es1101100. Esta es la representación de un número binario sin signo.
(108) 10 = (1101100) 2
Tiene 7 bits. Estos 7 bits representan la magnitud del número 108.
Representación de números binarios firmados
El bit más significativo (MSB) de los números binarios con signo se utiliza para indicar el signo de los números. Por lo tanto, también se llamasign bit. El signo positivo se representa colocando '0' en el bit de signo. De manera similar, el signo negativo se representa colocando '1' en el bit de signo.
Si el número binario con signo contiene 'N' bits, entonces (N-1) bits solo representan la magnitud del número ya que un bit (MSB) está reservado para representar el signo del número.
Hay tres types of representations para números binarios con signo
- Formulario de magnitud de signo
- Forma de complemento a 1
- Forma de complemento a 2
La representación de un número positivo en todas estas 3 formas es la misma. Pero, solo la representación del número negativo diferirá en cada forma.
Example
Considera el positive decimal number +108. El equivalente binario de la magnitud de este número es 1101100. Estos 7 bits representan la magnitud del número 108. Dado que es un número positivo, considere el bit de signo como cero, que se coloca en el lado izquierdo de la magnitud.
(+108) 10 = (01101100) 2
Por lo tanto, los signed binary representationdel número decimal positivo +108 es. Entonces, la misma representación es válida en forma de signo-magnitud, forma de complemento a 1 y forma de complemento a 2 para el número decimal positivo +108.
Formulario de magnitud de signo
En forma de signo de magnitud, el MSB se utiliza para representar sign del número y los bits restantes representan el magnitudedel número. Por lo tanto, solo incluya el bit de signo en el extremo izquierdo del número binario sin signo. Esta representación es similar a la representación de números decimales con signo.
Example
Considera el negative decimal number -108. La magnitud de este número es 108. Sabemos que la representación binaria sin signo de 108 es 1101100. Tiene 7 bits. Todos estos bits representan la magnitud.
Dado que el número dado es negativo, considere el bit de signo como uno, que se coloca en el lado izquierdo de la magnitud.
(−108) 10 = (11101100) 2
Por lo tanto, la representación de magnitud de signo de -108 es 11101100.
Forma de complemento a 1
El complemento a 1 de un número se obtiene mediante complementing all the bitsde número binario con signo. Entonces, el complemento de 1 del número positivo da un número negativo. De manera similar, el complemento a 1 del número negativo da un número positivo.
Eso significa que si realiza el complemento de dos veces 1 de un número binario que incluye el bit de signo, obtendrá el número binario con signo original.
Example
Considera el negative decimal number -108. La magnitud de este número es 108. Sabemos que la representación binaria con signo de 108 es 01101100.
Tiene 8 bits. El MSB de este número es cero, lo que indica un número positivo. El complemento de cero es uno y viceversa. Entonces, reemplace los ceros por unos y los unos por ceros para obtener el número negativo.
(−108) 10 = (10010011) 2
Por lo tanto, los 1’s complement of (108)10 es (10010011)2.
Forma de complemento a 2
El complemento a 2 de un número binario se obtiene mediante adding one to the 1’s complementde número binario con signo. Entonces, el complemento a 2 del número positivo da un número negativo. De manera similar, el complemento a 2 del número negativo da un número positivo.
Eso significa que si realiza dos veces el complemento a 2 de un número binario que incluye el bit de signo, obtendrá el número binario con signo original.
Example
Considera el negative decimal number -108.
Conocemos el complemento a 1 de (108)10 es (10010011)2
Complemento de 2 de (108) 10 = Complemento de 1 de (108) 10 + 1.
= 10010011 + 1
= 10010100
Por lo tanto, los 2’s complement of (108)10 es (10010100)2.
En este capítulo, analicemos las operaciones aritméticas básicas, que se pueden realizar en dos números binarios con signo cualesquiera utilizando el método del complemento a 2. losbasic arithmetic operations son sumas y restas.
Suma de dos números binarios firmados
Considere los dos números binarios con signo A y B, que se representan en forma de complemento a 2. Podemos realizar eladditionde estos dos números, que es similar a la suma de dos números binarios sin signo. Pero, si la suma resultante contiene llevar a cabo desde el bit de signo, deséchelo (ignórelo) para obtener el valor correcto.
Si la suma resultante es positiva, puede encontrar su magnitud directamente. Pero, si la suma resultante es negativa, entonces tome el complemento de 2 para obtener la magnitud.
Ejemplo 1
Realicemos el addition de dos números decimales +7 and +4 usando el método del complemento a 2.
los 2’s complement Las representaciones de +7 y +4 con 5 bits cada una se muestran a continuación.
(+7) 10 = (00111) 2
(+4) 10 = (00100) 2
La suma de estos dos números es
(+7) 10 + (+ 4) 10 = (00111) 2 + (00100) 2
⇒ (+7) 10 + (+ 4) 10 = (01011) 2 .
La suma resultante contiene 5 bits. Por lo tanto, no hay ejecución desde el bit de signo. El bit de signo '0' indica que la suma resultante espositive. Entonces, la magnitud de la suma es 11 en el sistema numérico decimal. Por lo tanto, la suma de dos números positivos dará otro número positivo.
Ejemplo 2
Realicemos el addition de dos números decimales -7 y -4 usando el método del complemento a 2.
los 2’s complement La representación de -7 y -4 con 5 bits cada uno se muestra a continuación.
(−7) 10 = (11001) 2
(−4) 10 = (11100) 2
La suma de estos dos números es
(−7) 10 + (−4) 10 = (11001) 2 + (11100) 2
⇒ (−7) 10 + (−4) 10 = (110101) 2 .
La suma resultante contiene 6 bits. En este caso, el acarreo se obtiene a partir del bit de signo. Entonces, podemos eliminarlo
La suma resultante después de eliminar el acarreo es (−7) 10 + (−4) 10 =(10101)2.
El bit de signo '1' indica que la suma resultante es negative. Entonces, tomando el complemento a 2, obtendremos la magnitud de la suma resultante como 11 en el sistema numérico decimal. Por lo tanto, la suma de dos números negativos dará otro número negativo.
Resta de dos números binarios con signo
Considere los dos números binarios con signo A y B, que se representan en forma de complemento a 2. Sabemos que el complemento a 2 del número positivo da un número negativo. Entonces, siempre que tengamos que restar un número B del número A, luego tome el complemento a 2 de B y sume a A. Entonces,mathematically podemos escribirlo como
A - B = A + (2's complement of B)
De manera similar, si tenemos que restar el número A del número B, entonces toma el complemento a 2 de A y súmalo a B. Entonces, mathematically podemos escribirlo como
B - A = B + (2's complement of A)
Entonces, la resta de dos números binarios con signo es similar a la suma de dos números binarios con signo. Pero tenemos que tomar el complemento a 2 del número, que se supone que se resta. Este es eladvantagede la técnica del complemento a 2. Siga las mismas reglas de suma de dos números binarios con signo.
Ejemplo 3
Realicemos el subtraction de dos números decimales +7 and +4 usando el método del complemento a 2.
La resta de estos dos números es
(+7) 10 - (+4) 10 = (+7) 10 + (−4) 10 .
los 2’s complement La representación de +7 y -4 con 5 bits cada uno se muestra a continuación.
(+7) 10 = (00111) 2
(+4) 10 = (11100) 2
⇒ (+7) 10 + (+4) 10 = (00111) 2 + (11100) 2 = (00011) 2
Aquí, el acarreo obtenido del bit de signo. Entonces, podemos eliminarlo. La suma resultante después de eliminar el acarreo es
(+7) 10 + (+4) 10 =(00011)2
El bit de signo '0' indica que la suma resultante es positive. Entonces, su magnitud es 3 en el sistema numérico decimal. Por lo tanto, la resta de dos números decimales +7 y +4 es +3.
Ejemplo 4
Realicemos el subtraction of dos números decimales +4 y +7 usando el método del complemento a 2.
La resta de estos dos números es
(+4) 10 - (+7) 10 = (+4) 10 + (−7) 10 .
los 2’s complement La representación de +4 y -7 con 5 bits cada uno se muestra a continuación.
(+4) 10 = (00100) 2
(-7) 10 = (11001) 2
⇒ (+4) 10 + (-7) 10 = (00100) 2 + (11001) 2 = (11101) 2
Aquí, el acarreo no se obtiene del bit de signo. El bit de signo '1' indica que la suma resultante esnegative. Entonces, al tomar el complemento a 2, obtendremos la magnitud de la suma resultante como 3 en el sistema numérico decimal. Por lo tanto, la resta de dos números decimales +4 y +7 es -3.
En la codificación, cuando los números o letras están representados por un grupo específico de símbolos, se dice que ese número o letra se codifica. El grupo de símbolos se denominacode. Los datos digitales se representan, almacenan y transmiten como un grupo de bits. Este grupo de bits también se denominabinary code.
Los códigos binarios se pueden clasificar en dos tipos.
- Códigos ponderados
- Códigos no ponderados
Si el código tiene pesos posicionales, entonces se dice que es weighted code. De lo contrario, es un código no ponderado. Los códigos ponderados se pueden clasificar además como códigos ponderados positivamente y códigos ponderados negativamente.
Códigos binarios para dígitos decimales
La siguiente tabla muestra los distintos códigos binarios para los dígitos decimales del 0 al 9.
| Dígito decimal | 8421 Código | 2421 Código | 84-2-1 Código | Exceso de 3 código |
|---|---|---|---|---|
| 0 | 0000 | 0000 | 0000 | 0011 |
| 1 | 0001 | 0001 | 0111 | 0100 |
| 2 | 0010 | 0010 | 0110 | 0101 |
| 3 | 0011 | 0011 | 0101 | 0110 |
| 4 | 0100 | 0100 | 0100 | 0111 |
| 5 | 0101 | 1011 | 1011 | 1000 |
| 6 | 0110 | 1100 | 1010 | 1001 |
| 7 | 0111 | 1101 | 1001 | 1010 |
| 8 | 1000 | 1110 | 1000 | 1011 |
| 9 | 1001 | 1111 | 1111 | 1100 |
Tenemos 10 dígitos en el sistema numérico decimal. Para representar estos 10 dígitos en binario, necesitamos un mínimo de 4 bits. Pero, con 4 bits habrá 16 combinaciones únicas de ceros y unos. Dado que solo tenemos 10 dígitos decimales, las otras 6 combinaciones de ceros y unos no son necesarias.
8 4 2 1 código
Los pesos de este código son 8, 4, 2 y 1.
Este código tiene todos los pesos positivos. Entonces, es unpositively weighted code.
Este código también se denomina natural BCD (Decimal codificado en binario) code.
Example
Encontremos el equivalente en BCD del número decimal 786. Este número tiene 3 dígitos decimales 7, 8 y 6. De la tabla, podemos escribir los códigos BCD (8421) de 7, 8 y 6 son 0111, 1000 y 0110 respectivamente. .
∴ (786)10 = (011110000110)BCD
Hay 12 bits en representación BCD, ya que cada código BCD de dígito decimal tiene 4 bits.
2 4 2 1 código
Los pesos de este código son 2, 4, 2 y 1.
Este código tiene todos los pesos positivos. Entonces, es unpositively weighted code.
Es un unnatural BCDcódigo. La suma de los pesos de los códigos BCD no naturales es igual a 9.
Es un self-complementingcódigo. Los códigos autocomplementados proporcionan el complemento de 9 de un número decimal, simplemente intercambiando 1 y 0 en su representación equivalente 2421.
Example
Encontremos el 2421 equivalente al número decimal 786. Este número tiene 3 dígitos decimales 7, 8 y 6. De la tabla, podemos escribir los 2421 códigos de 7, 8 y 6 son 1101, 1110 y 1100 respectivamente.
Por lo tanto, el equivalente 2421 del número decimal 786 es 110111101100.
8 4-2 -1 código
Los pesos de este código son 8, 4, -2 y -1.
Este código tiene pesos negativos junto con pesos positivos. Entonces, es unnegatively weighted code.
Es un unnatural BCD código.
Es un self-complementing código.
Example
Encontremos el 8 4-2-1 equivalente al número decimal 786. Este número tiene 3 dígitos decimales 7, 8 y 6. De la tabla, podemos escribir los códigos 8 4-2 -1 de 7, 8 y 6 son 1001, 1000 y 1010 respectivamente.
Por lo tanto, el equivalente 8 4-2 -1 del número decimal 786 es 100110001010.
Exceso de 3 código
Este código no tiene pesos. Entonces, es unun-weighted code.
Obtendremos el código de Exceso 3 de un número decimal sumando tres (0011) al equivalente binario de ese número decimal. Por lo tanto, se denomina código Exceso 3.
Es un self-complementing código.
Example
Encontremos el Exceso 3 equivalente al número decimal 786. Este número tiene 3 dígitos decimales 7, 8 y 6. De la tabla, podemos escribir los Exceso 3 códigos de 7, 8 y 6 son 1010, 1011 y 1001 respectivamente.
Por lo tanto, el Exceso 3 equivalente al número decimal 786 es 101010111001
Código gris
La siguiente tabla muestra los códigos Gray de 4 bits correspondientes a cada código binario de 4 bits.
| Número decimal | Código binario | Código gris |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
Este código no tiene pesos. Entonces, es unun-weighted code.
En la tabla anterior, los códigos Gray sucesivos se diferencian en la posición de un solo bit. Por lo tanto, este código se llamaunit distance código.
Conversión de código binario a código Gray
Siga estos pasos para convertir un código binario en su código Gray equivalente.
Considere el código binario dado y coloque un cero a la izquierda de MSB.
Compare los dos bits sucesivos comenzando desde cero. Si los 2 bits son iguales, entonces la salida es cero. De lo contrario, la salida es uno.
Repita el paso anterior hasta obtener el código LSB de Gray.
Example
De la tabla, sabemos que el código Gray correspondiente al código binario 1000 es 1100. Ahora, verifiquémoslo usando el procedimiento anterior.
Dado, el código binario es 1000.
Step 1 - Colocando cero a la izquierda de MSB, el código binario será 01000.
Step 2 - Al comparar dos bits sucesivos de nuevo código binario, obtendremos el código gris como 1100.
Sabemos que los bits 0 y 1 corresponden a dos rangos diferentes de voltajes analógicos. Por lo tanto, durante la transmisión de datos binarios de un sistema a otro, también se puede agregar ruido. Debido a esto, puede haber errores en los datos recibidos en otro sistema.
Eso significa que un bit 0 puede cambiar a 1 o un bit 1 puede cambiar a 0. No podemos evitar la interferencia del ruido. Pero, primero podemos recuperar los datos originales detectando si hay algún error y luego corrigiéndolos. Para ello, podemos utilizar los siguientes códigos.
- Códigos de detección de errores
- Códigos de corrección de errores
Error detection codes- se utilizan para detectar los errores presentes en los datos recibidos (flujo de bits). Estos códigos contienen algunos bits, que se incluyen (se añaden) al flujo de bits original. Estos códigos detectan el error, si se produce durante la transmisión de los datos originales (flujo de bits).Example - Código de paridad, código de Hamming.
Error correction codes − are used to correct the error(s) present in the received data (bit stream) so that, we will get the original data. Error correction codes also use the similar strategy of error detection codes.Example − Hamming code.
Therefore, to detect and correct the errors, additional bit(s) are appended to the data bits at the time of transmission.
Parity Code
It is easy to include (append) one parity bit either to the left of MSB or to the right of LSB of original bit stream. There are two types of parity codes, namely even parity code and odd parity code based on the type of parity being chosen.
Even Parity Code
The value of even parity bit should be zero, if even number of ones present in the binary code. Otherwise, it should be one. So that, even number of ones present in even parity code. Even parity code contains the data bits and even parity bit.
The following table shows the even parity codes corresponding to each 3-bit binary code. Here, the even parity bit is included to the right of LSB of binary code.
| Binary Code | Even Parity bit | Even Parity Code |
|---|---|---|
| 000 | 0 | 0000 |
| 001 | 1 | 0011 |
| 010 | 1 | 0101 |
| 011 | 0 | 0110 |
| 100 | 1 | 1001 |
| 101 | 0 | 1010 |
| 110 | 0 | 1100 |
| 111 | 1 | 1111 |
Here, the number of bits present in the even parity codes is 4. So, the possible even number of ones in these even parity codes are 0, 2 & 4.
If the other system receives one of these even parity codes, then there is no error in the received data. The bits other than even parity bit are same as that of binary code.
If the other system receives other than even parity codes, then there will be an error(s) in the received data. In this case, we can’t predict the original binary code because we don’t know the bit position(s) of error.
Therefore, even parity bit is useful only for detection of error in the received parity code. But, it is not sufficient to correct the error.
Odd Parity Code
The value of odd parity bit should be zero, if odd number of ones present in the binary code. Otherwise, it should be one. So that, odd number of ones present in odd parity code. Odd parity code contains the data bits and odd parity bit.
The following table shows the odd parity codes corresponding to each 3-bit binary code. Here, the odd parity bit is included to the right of LSB of binary code.
| Binary Code | Odd Parity bit | Odd Parity Code |
|---|---|---|
| 000 | 1 | 0001 |
| 001 | 0 | 0010 |
| 010 | 0 | 0100 |
| 011 | 1 | 0111 |
| 100 | 0 | 1000 |
| 101 | 1 | 1011 |
| 110 | 1 | 1101 |
| 111 | 0 | 1110 |
Here, the number of bits present in the odd parity codes is 4. So, the possible odd number of ones in these odd parity codes are 1 & 3.
If the other system receives one of these odd parity codes, then there is no error in the received data. The bits other than odd parity bit are same as that of binary code.
If the other system receives other than odd parity codes, then there is an error(s) in the received data. In this case, we can’t predict the original binary code because we don’t know the bit position(s) of error.
Therefore, odd parity bit is useful only for detection of error in the received parity code. But, it is not sufficient to correct the error.
Hamming Code
Hamming code is useful for both detection and correction of error present in the received data. This code uses multiple parity bits and we have to place these parity bits in the positions of powers of 2.
The minimum value of 'k' for which the following relation is correct (valid) is nothing but the required number of parity bits.
$$2^k\geq n+k+1$$
Where,
‘n’ is the number of bits in the binary code (information)
‘k’ is the number of parity bits
Therefore, the number of bits in the Hamming code is equal to n + k.
Let the Hamming code is $b_{n+k}b_{n+k-1}.....b_{3}b_{2}b_{1}$ & parity bits $p_{k}, p_{k-1}, ....p_{1}$. We can place the ‘k’ parity bits in powers of 2 positions only. In remaining bit positions, we can place the ‘n’ bits of binary code.
Based on requirement, we can use either even parity or odd parity while forming a Hamming code. But, the same parity technique should be used in order to find whether any error present in the received data.
Follow this procedure for finding parity bits.
Find the value of p1, based on the number of ones present in bit positions b3, b5, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 20.
Find the value of p2, based on the number of ones present in bit positions b3, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 21.
Find the value of p3, based on the number of ones present in bit positions b5, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 22.
Similarly, find other values of parity bits.
Follow this procedure for finding check bits.
Find the value of c1, based on the number of ones present in bit positions b1, b3, b5, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 20.
Find the value of c2, based on the number of ones present in bit positions b2, b3, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 21.
Find the value of c3, based on the number of ones present in bit positions b4, b5, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 22.
Similarly, find other values of check bits.
The decimal equivalent of the check bits in the received data gives the value of bit position, where the error is present. Just complement the value present in that bit position. Therefore, we will get the original binary code after removing parity bits.
Example 1
Let us find the Hamming code for binary code, d4d3d2d1 = 1000. Consider even parity bits.
The number of bits in the given binary code is n=4.
We can find the required number of parity bits by using the following mathematical relation.
$$2^k\geq n+k+1$$
Substitute, n=4 in the above mathematical relation.
$$\Rightarrow 2^k\geq 4+k+1$$
$$\Rightarrow 2^k\geq 5+k$$
The minimum value of k that satisfied the above relation is 3. Hence, we require 3 parity bits p1, p2, and p3. Therefore, the number of bits in Hamming code will be 7, since there are 4 bits in binary code and 3 parity bits. We have to place the parity bits and bits of binary code in the Hamming code as shown below.
The 7-bit Hamming code is $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}=d_{4}d_{3}d_{2}p_{3}d_{1}p_{2}bp_{1}$
By substituting the bits of binary code, the Hamming code will be $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1} = 100p_{3}Op_{2}p_{1}$. Now, let us find the parity bits.
$$p_{1}=b_{7}\oplus b_{5}\oplus b_{3}=1 \oplus 0 \oplus 0=1$$
$$p_{2}=b_{7}\oplus b_{6}\oplus b_{3}=1 \oplus 0 \oplus 0=1$$
$$p_{3}=b_{7}\oplus b_{6}\oplus b_{5}=1 \oplus 0 \oplus 0=1$$
By substituting these parity bits, the Hamming code will be $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001011$.
Example 2
In the above example, we got the Hamming code as $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001011$. Now, let us find the error position when the code received is $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001111$.
Now, let us find the check bits.
$$c_{1}=b_{7}\oplus b_{5}\oplus b_{3}\oplus b_{1}=1 \oplus 0 \oplus 1 \oplus1 =1$$
$$c_{2}=b_{7}\oplus b_{6}\oplus b_{3}\oplus b_{2}=1 \oplus 0 \oplus 1 \oplus1 =1$$
$$c_{3}=b_{7}\oplus b_{6}\oplus b_{5}\oplus b_{4}=1 \oplus 0 \oplus 0 \oplus1 =0$$
The decimal value of check bits gives the position of error in received Hamming code.
$$c_{3}c_{2}c_{1} = \left ( 011 \right )_{2}=\left ( 3 \right )_{10}$$
Therefore, the error present in third bit (b3) of Hamming code. Just complement the value present in that bit and remove parity bits in order to get the original binary code.
Boolean Algebra is an algebra, which deals with binary numbers & binary variables. Hence, it is also called as Binary Algebra or logical Algebra. A mathematician, named George Boole had developed this algebra in 1854. The variables used in this algebra are also called as Boolean variables.
The range of voltages corresponding to Logic ‘High’ is represented with ‘1’ and the range of voltages corresponding to logic ‘Low’ is represented with ‘0’.
Postulates and Basic Laws of Boolean Algebra
In this section, let us discuss about the Boolean postulates and basic laws that are used in Boolean algebra. These are useful in minimizing Boolean functions.
Boolean Postulates
Consider the binary numbers 0 and 1, Boolean variable (x) and its complement (x’). Either the Boolean variable or complement of it is known as literal. The four possible logical OR operations among these literals and binary numbers are shown below.
x + 0 = x
x + 1 = 1
x + x = x
x + x '= 1
Del mismo modo, los cuatro posibles logical AND las operaciones entre esos literales y números binarios se muestran a continuación.
x.1 = x
x.0 = 0
xx = x
x.x '= 0
Estos son los postulados booleanos simples. Podemos verificar estos postulados fácilmente, sustituyendo la variable booleana con '0' o '1'.
Note- El complemento de complemento de cualquier variable booleana es igual a la propia variable. es decir, (x ')' = x.
Leyes básicas del álgebra de Boole
A continuación se presentan las tres leyes básicas del álgebra booleana.
- Ley conmutativa
- Ley asociativa
- Ley distributiva
Ley conmutativa
Si cualquier operación lógica de dos variables booleanas da el mismo resultado independientemente del orden de esas dos variables, entonces se dice que la operación lógica es Commutative. Las operaciones lógicas OR y lógicas AND de dos variables booleanas x e y se muestran a continuación
x + y = y + x
xy = yx
El símbolo '+' indica una operación lógica OR. Del mismo modo, el símbolo '.' indica operación lógica AND y es opcional representar. La ley conmutativa obedece a operaciones lógicas OR y lógicas AND.
Ley asociativa
Si una operación lógica de dos variables booleanas se realiza primero y luego se realiza la misma operación con la variable restante da el mismo resultado, entonces se dice que la operación lógica es Associative. Las operaciones lógicas OR y lógicas Y de tres variables booleanas x, y & z se muestran a continuación.
x + (y + z) = (x + y) + z
x. (yz) = (xy) .z
La ley asociativa obedece a operaciones lógicas OR y lógicas AND.
Ley distributiva
Si cualquier operación lógica se puede distribuir a todos los términos presentes en la función booleana, entonces se dice que esa operación lógica es Distributive. La distribución de operaciones lógicas OR y lógicas AND de tres variables booleanas x, y & z se muestra a continuación.
x. (y + z) = xy + xz
x + (yz) = (x + y). (x + z)
La ley distributiva obedece a operaciones lógicas OR y lógicas AND.
Estas son las leyes básicas del álgebra de Boole. Podemos verificar estas leyes fácilmente, sustituyendo las variables booleanas con '0' o '1'.
Teoremas del álgebra booleana
Los dos teoremas siguientes se utilizan en álgebra de Boole.
- Teorema de dualidad
- Teorema de DeMorgan
Teorema de dualidad
Este teorema establece que el dualde la función booleana se obtiene intercambiando el operador lógico AND con el operador lógico OR y los ceros con unos. Para cada función booleana, habrá una función Dual correspondiente.
Hagamos las ecuaciones (relaciones) booleanas que discutimos en la sección de postulados booleanos y leyes básicas en dos grupos. La siguiente tabla muestra estos dos grupos.
| Grupo 1 | Grupo 2 |
|---|---|
| x + 0 = x | x.1 = x |
| x + 1 = 1 | x.0 = 0 |
| x + x = x | xx = x |
| x + x '= 1 | x.x '= 0 |
| x + y = y + x | xy = yx |
| x + (y + z) = (x + y) + z | x. (yz) = (xy) .z |
| x. (y + z) = xy + xz | x + (yz) = (x + y). (x + z) |
En cada fila, hay dos ecuaciones booleanas y son duales entre sí. Podemos verificar todas estas ecuaciones booleanas de Group1 y Group2 usando el teorema de dualidad.
Teorema de DeMorgan
Este teorema es útil para encontrar el complement of Boolean function. Establece que el complemento del O lógico de al menos dos variables booleanas es igual al Y lógico de cada variable complementada.
El teorema de DeMorgan con 2 variables booleanas xey se puede representar como
(x + y) '= x'.y'
El dual de la función booleana anterior es
(xy) '= x' + y '
Por lo tanto, el complemento del Y lógico de dos variables booleanas es igual al O lógico de cada variable complementada. De manera similar, también podemos aplicar el teorema de DeMorgan para más de 2 variables booleanas.
Simplificación de funciones booleanas
Hasta ahora, discutimos los postulados, leyes básicas y teoremas del álgebra de Boole. Ahora, simplifiquemos algunas funciones booleanas.
Ejemplo 1
Nos deja simplify la función booleana, f = p'qr + pq'r + pqr '+ pqr
Podemos simplificar esta función en dos métodos.
Method 1
Dada la función booleana, f = p'qr + pq'r + pqr '+ pqr.
Step 1- En primer y segundo términos r es común y en tercer y cuarto términos pq es común. Entonces, tome los términos comunes usandoDistributive law.
⇒ f = (p'q + pq ') r + pq (r' + r)
Step 2- Los términos presentes en el primer paréntesis se pueden simplificar a operación Ex-OR. Los términos presentes en el segundo paréntesis se pueden simplificar a '1' usandoBoolean postulate
⇒ f = (p ⊕q) r + pq (1)
Step 3- El primer término no se puede simplificar más. Pero, el segundo término se puede simplificar a pq usandoBoolean postulate.
⇒ f = (p ⊕q) r + pq
Por lo tanto, la función booleana simplificada es f = (p⊕q)r + pq
Method 2
Dada la función booleana, f = p'qr + pq'r + pqr '+ pqr.
Step 1 - Utilice el Boolean postulate, x + x = x. Eso significa que la operación O lógica con cualquier variable booleana 'n' veces será igual a la misma variable. Entonces, podemos escribir el último término pqr dos veces más.
⇒ f = p'qr + pq'r + pqr '+ pqr + pqr + pqr
Step 2 - utilizar Distributive lawpara 1 st y 4 th términos, 2 nd y 5 th términos, 3 rd y 6 th términos.
⇒ f = qr (p '+ p) + pr (q' + q) + pq (r '+ r)
Step 3 - utilizar Boolean postulate, x + x '= 1 para simplificar los términos presentes en cada paréntesis.
⇒ f = qr (1) + pr (1) + pq (1)
Step 4 - utilizar Boolean postulate, x.1 = x para simplificar los tres términos anteriores.
⇒ f = qr + pr + pq
⇒ f = pq + qr + pr
Por lo tanto, la función booleana simplificada es f = pq + qr + pr.
Entonces, obtuvimos dos funciones booleanas diferentes después de simplificar la función booleana dada en cada método. Funcionalmente, esas dos funciones booleanas son las mismas. Entonces, según el requisito, podemos elegir una de esas dos funciones booleanas.
Ejemplo 2
Encontremos el complement de la función booleana, f = p'q + pq '.
El complemento de la función booleana es f '= (p'q + pq') '.
Step 1 - Utilice el teorema de DeMorgan, (x + y) '= x'.y'.
⇒ f '= (p'q)'. (Pq ')'
Step 2 - Utilice el teorema de DeMorgan, (xy) '= x' + y '
⇒ f '= {(p') '+ q'}. {P '+ (q') '}
Step3 - Utilice el postulado booleano, (x ')' = x.
⇒ f '= {p + q'}. {P '+ q}
⇒ f '= pp' + pq + p'q '+ qq'
Step 4 - Utilice el postulado booleano, xx '= 0.
⇒ f = 0 + pq + p'q '+ 0
⇒ f = pq + p'q '
Por lo tanto, los complement de la función booleana, p'q + pq 'es pq + p’q’.
Obtendremos cuatro términos de producto booleanos combinando dos variables xey con la operación lógica AND. Estos términos de productos booleanos se denominanmin terms o standard product terms. Los términos mínimos son x'y ', x'y, xy' y xy.
De manera similar, obtendremos cuatro términos de suma booleana combinando dos variables xey con la operación lógica OR. Estos términos de suma booleana se denominanMax terms o standard sum terms. Los términos Max son x + y, x + y ', x' + y y x '+ y'.
La siguiente tabla muestra la representación de términos mínimos y términos MAX para 2 variables.
| X | y | Términos mínimos | Términos máximos |
|---|---|---|---|
| 0 | 0 | m 0 = x'y ' | M 0 = x + y |
| 0 | 1 | m 1 = x'y | M 1 = x + y ' |
| 1 | 0 | m 2 = xy ' | M 2 = x '+ y |
| 1 | 1 | m 3 = xy | M 3 = x '+ y' |
Si la variable binaria es '0', entonces se representa como complemento de la variable en el término mínimo y como la propia variable en el término máximo. De manera similar, si la variable binaria es '1', entonces se representa como complemento de la variable en el término máximo y como la propia variable en el término mínimo.
En la tabla anterior, podemos notar fácilmente que los términos mínimos y los términos máximos se complementan entre sí. Si hay 'n' variables booleanas, entonces habrá 2 n términos mínimos y 2 n términos máximos.
Formularios canónicos SoP y PoS
Una tabla de verdad consta de un conjunto de entradas y salidas. Si hay 'n' variables de entrada, habrá 2 n combinaciones posibles con ceros y unos. Entonces, el valor de cada variable de salida depende de la combinación de variables de entrada. Entonces, cada variable de salida tendrá '1' para alguna combinación de variables de entrada y '0' para alguna otra combinación de variables de entrada.
Por tanto, podemos expresar cada variable de salida de dos formas siguientes.
- Formulario de SoP canónico
- Formulario de PoS canónico
Formulario de SoP canónico
La forma Canonical SoP significa la forma Canonical Sum of Products. De esta forma, cada término de producto contiene todos los literales. Entonces, estos términos de producto no son más que los términos mínimos. Por lo tanto, la forma canónica de SoP también se llama comosum of min terms formar.
Primero, identifique los términos mínimos para los cuales la variable de salida es uno y luego haga el OR lógico de esos términos mínimos para obtener la expresión (función) booleana correspondiente a esa variable de salida. Esta función booleana estará en forma de suma de términos mínimos.
Siga el mismo procedimiento para otras variables de salida también, si hay más de una variable de salida.
Ejemplo
Considera lo siguiente truth table.
| Entradas | Salida | ||
|---|---|---|---|
| p | q | r | f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Aquí, la salida (f) es '1' para cuatro combinaciones de entradas. Los términos mínimos correspondientes son p'qr, pq'r, pqr ', pqr. Haciendo OR lógico de estos cuatro términos mínimos, obtendremos la función booleana de la salida (f).
Por lo tanto, la función booleana de salida es f = p'qr + pq'r + pqr '+ pqr. Este es elcanonical SoP formde salida, f. También podemos representar esta función siguiendo dos notaciones.
$$f = m_{3}+m_{5}+m_{6}+m_{7}$$
$$f = \sum m\left ( 3,5,6,7 \right )$$
En una ecuación, representamos la función como la suma de los respectivos términos mínimos. En otra ecuación, usamos el símbolo para la suma de esos términos mínimos.
Formulario de PoS canónico
La forma Canonical PoS significa la forma Canonical Product of Sums. De esta forma, cada término de suma contiene todos los literales. Entonces, estos términos de suma no son más que los términos Max. Por lo tanto, la forma canónica de PoS también se llama comoproduct of Max terms formar.
Primero, identifique los términos Max para los cuales la variable de salida es cero y luego haga el AND lógico de esos términos Max para obtener la expresión booleana (función) correspondiente a esa variable de salida. Esta función booleana estará en forma de producto de términos máximos.
Siga el mismo procedimiento para otras variables de salida también, si hay más de una variable de salida.
Example
Considere la misma tabla de verdad del ejemplo anterior. Aquí, la salida (f) es '0' para cuatro combinaciones de entradas. Los términos Max correspondientes son p + q + r, p + q + r ', p + q' + r, p '+ q + r. Haciendo un AND lógico de estos cuatro términos Max, obtendremos la función booleana de la salida (f).
Por lo tanto, la función booleana de salida es f = (p + q + r). (P + q + r '). (P + q' + r). (P '+ q + r). Este es elcanonical PoS formde salida, f. También podemos representar esta función siguiendo dos notaciones.
$$f=M_{0}.M_{1}.M_{2}.M_{4}$$
$$f=\prod M\left ( 0,1,2,4 \right )$$
En una ecuación, representamos la función como el producto de los respectivos términos Max. En otra ecuación, usamos el símbolo para la multiplicación de esos términos máximos.
La función booleana, f = (p + q + r). (P + q + r '). (P + q' + r). (P '+ q + r) es el dual de la función booleana, f = p'qr + pq'r + pqr '+ pqr.
Por lo tanto, tanto las formas canónicas SoP como las PoS canónicas son Dualel uno al otro. Funcionalmente, estas dos formas son iguales. Según el requisito, podemos utilizar uno de estos dos formularios.
Formularios estándar de SoP y PoS
Discutimos dos formas canónicas de representar los resultados booleanos. De manera similar, hay dos formas estándar de representar los resultados booleanos. Éstas son la versión simplificada de las formas canónicas.
- Formulario estándar de SoP
- Formulario estándar de PoS
Discutiremos sobre las puertas lógicas en capítulos posteriores. El principaladvantagede las formas estándar es que se puede minimizar el número de entradas aplicadas a las puertas lógicas. A veces, habrá una reducción en el número total de puertas lógicas necesarias.
Formulario estándar de SoP
Forma estándar SoP significa Standard Sum of Productsformar. De esta forma, no es necesario que cada término de producto contenga todos los literales. Por lo tanto, los términos del producto pueden ser o no los términos mínimos. Por lo tanto, la forma SoP estándar es la forma simplificada de la forma SoP canónica.
Obtendremos la forma Standard SoP de la variable de salida en dos pasos.
- Obtener la forma canónica de SoP de la variable de salida
- Simplifique la función booleana anterior, que está en forma de SoP canónica.
Siga el mismo procedimiento para otras variables de salida también, si hay más de una variable de salida. A veces, puede que no sea posible simplificar el formulario de SoP canónico. En ese caso, los formularios SoP canónicos y estándar son iguales.
Example
Convierta la siguiente función booleana en formato SoP estándar.
f = p'qr + pq'r + pqr '+ pqr
La función booleana dada está en forma SoP canónica. Ahora, tenemos que simplificar esta función booleana para obtener la forma estándar de SoP.
Step 1 - Utilice el Boolean postulate, x + x = x. Eso significa que la operación O lógica con cualquier variable booleana 'n' veces será igual a la misma variable. Entonces, podemos escribir el último término pqr dos veces más.
⇒ f = p'qr + pq'r + pqr '+ pqr + pqr + pqr
Step 2 - utilizar Distributive lawpara 1 st y 4 th términos, 2 nd y 5 th términos, 3 rd y 6 th términos.
⇒ f = qr (p '+ p) + pr (q' + q) + pq (r '+ r)
Step 3 - utilizar Boolean postulate, x + x '= 1 para simplificar los términos presentes en cada paréntesis.
⇒ f = qr (1) + pr (1) + pq (1)
Step 4 - utilizar Boolean postulate, x.1 = x para simplificar los tres términos anteriores.
⇒ f = qr + pr + pq
⇒ f = pq + qr + pr
Esta es la función booleana simplificada. Por lo tanto, losstandard SoP form correspondiente a la forma de SoP canónica dada es f = pq + qr + pr
Formulario estándar de PoS
Forma estándar de PoS significa Standard Product of Sumsformar. De esta forma, no es necesario que cada término de suma contenga todos los literales. Por lo tanto, los términos de suma pueden ser o no los términos máximos. Por lo tanto, la forma estándar de PoS es la forma simplificada de la forma canónica de PoS.
Obtendremos la forma estándar de PoS de la variable de salida en dos pasos.
- Obtenga la forma canónica de PoS de variable de salida
- Simplifique la función booleana anterior, que está en forma canónica de PoS.
Siga el mismo procedimiento para otras variables de salida también, si hay más de una variable de salida. A veces, puede que no sea posible simplificar la forma canónica de PoS. En ese caso, las formas canónicas y estándar de PoS son iguales.
Example
Convierta la siguiente función booleana a la forma estándar de PoS.
f = (p + q + r). (p + q + r '). (p + q' + r). (p '+ q + r)
La función booleana dada está en forma canónica de PoS. Ahora, tenemos que simplificar esta función booleana para obtener la forma estándar de PoS.
Step 1 - Utilice el Boolean postulate, xx = x. Eso significa que la operación lógica AND con cualquier variable booleana 'n' veces será igual a la misma variable. Entonces, podemos escribir el primer término p + q + r dos veces más.
⇒ f = (p + q + r). (P + q + r). (P + q + r). (P + q + r '). (P + q' + r). (P '+ q + r)
Step 2 - utilizar Distributive law,x + (yz) = (x + y). (x + z) para 1 st y 4 º paréntesis, 2 nd y 5 º paréntesis, 3 rd y 6 º paréntesis.
⇒ f = (p + q + rr '). (P + r + qq'). (Q + r + pp ')
Step 3 - utilizar Boolean postulate, x.x '= 0 para simplificar los términos presentes en cada paréntesis.
⇒ f = (p + q + 0). (P + r + 0). (Q + r + 0)
Step 4 - utilizar Boolean postulate, x + 0 = x para simplificar los términos presentes en cada paréntesis
⇒ f = (p + q). (P + r). (Q + r)
⇒ f = (p + q). (Q + r). (P + r)
Esta es la función booleana simplificada. Por lo tanto, losstandard PoS form correspondiente a la forma canónica de PoS dada es f = (p + q).(q + r).(p + r). Este es eldual de la función booleana, f = pq + qr + pr.
Por lo tanto, los formularios Standard SoP y Standard PoS son duales entre sí.
En capítulos anteriores, hemos simplificado las funciones booleanas usando postulados y teoremas booleanos. Es un proceso que lleva mucho tiempo y tenemos que volver a escribir las expresiones simplificadas después de cada paso.
Para superar esta dificultad, Karnaughintrodujo un método para simplificar las funciones booleanas de una manera fácil. Este método se conoce como método de mapa de Karnaugh o método de mapa K. Es un método gráfico, que consta de 2 n celdas para 'n' variables. Las celdas adyacentes se diferencian solo en la posición de un solo bit.
K-Maps para 2 a 5 variables
El método K-Map es el más adecuado para minimizar las funciones booleanas de 2 variables a 5 variables. Ahora, hablemos de los K-Maps para 2 a 5 variables una por una.
2 K-Map variable
El número de celdas en 2 variables K-map es cuatro, ya que el número de variables es dos. La siguiente figura muestra2 variable K-Map.
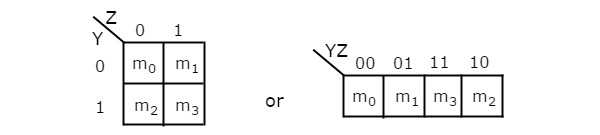
Solo existe una posibilidad de agrupar 4 términos mínimos adyacentes.
Las posibles combinaciones de agrupar 2 términos mínimos adyacentes son {(m 0 , m 1 ), (m 2 , m 3 ), (m 0 , m 2 ) y (m 1 , m 3 )}.
3 K-Map variable
El número de celdas en el mapa K de 3 variables es ocho, ya que el número de variables es tres. La siguiente figura muestra3 variable K-Map.
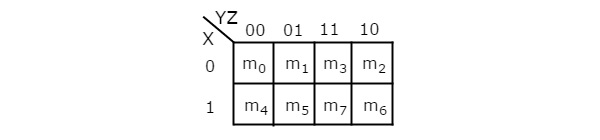
Solo existe una posibilidad de agrupar 8 términos mínimos adyacentes.
Las posibles combinaciones de agrupar 4 términos mínimos adyacentes son {(m 0 , m 1 , m 3 , m 2 ), (m 4 , m 5 , m 7 , m 6 ), (m 0 , m 1 , m 4 , m 5 ), (m 1 , m 3 , m 5 , m 7 ), (m 3 , m 2 , m 7 , m 6 ) y (m 2 , m 0 , m 6 , m 4 )}.
Las combinaciones posibles de agrupar 2 términos mínimos adyacentes son {(m 0 , m 1 ), (m 1 , m 3 ), (m 3 , m 2 ), (m 2 , m 0 ), (m 4 , m 5 ) , (m 5 , m 7 ), (m 7 , m 6 ), (m 6 , m 4 ), (m 0 , m 4 ), (m 1 , m 5 ), (m 3 , m 7 ) y ( m 2 , m 6 )}.
Si x = 0, entonces el mapa K de 3 variables se convierte en el mapa K de 2 variables.
4 K-Map variable
El número de celdas en el mapa K de 4 variables es dieciséis, ya que el número de variables es cuatro. La siguiente figura muestra4 variable K-Map.
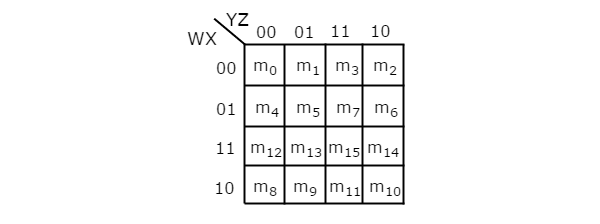
Solo existe una posibilidad de agrupar 16 términos mínimos adyacentes.
Deje que R 1 , R 2 , R 3 y R 4 representan los términos mínimos de la primera fila, segunda fila, tercera fila y cuarta fila respectivamente. De manera similar, C 1 , C 2 , C 3 y C 4 representan los términos mínimos de la primera columna, segunda columna, tercera columna y cuarta columna respectivamente. Las posibles combinaciones de agrupar 8 términos mínimos adyacentes son {(R 1 , R 2 ), (R 2 , R 3 ), (R 3 , R 4 ), (R 4 , R 1 ), (C 1 , C 2 ) , (C 2 , C 3 ), (C 3 , C 4 ), (C 4 , C 1 )}.
Si w = 0, entonces el mapa K de 4 variables se convierte en el mapa K de 3 variables.
5 K-Map variable
El número de celdas en el mapa K de 5 variables es treinta y dos, ya que el número de variables es 5. La siguiente figura muestra 5 variable K-Map.

Solo existe una posibilidad de agrupar 32 términos mínimos adyacentes.
Hay dos posibilidades de agrupar 16 términos mínimos adyacentes. es decir, agrupación de términos mínimos de m 0 a m 15 y m 16 a m 31 .
Si v = 0, el mapa K de 5 variables se convierte en el mapa K de 4 variables.
En todos los mapas K anteriores, usamos exclusivamente la notación de términos mínimos. Del mismo modo, puede utilizar exclusivamente la notación de términos Max.
Minimización de funciones booleanas usando K-Maps
Si consideramos la combinación de entradas para las que la función booleana es '1', obtendremos la función booleana, que está en standard sum of products formulario después de simplificar el K-map.
De manera similar, si consideramos la combinación de entradas para las que la función booleana es '0', obtendremos la función booleana, que está en standard product of sums formulario después de simplificar el K-map.
Siga estos rules for simplifying K-maps para obtener la forma estándar de suma de productos.
Seleccione el mapa K respectivo según el número de variables presentes en la función booleana.
Si la función booleana se da como suma de términos mínimos, coloque los unos en las respectivas celdas de término mínimo en el mapa K. Si la función booleana se da como suma de productos, coloque los unos en todas las celdas posibles de K-map para las que los términos de producto dados son válidos.
Verifique las posibilidades de agrupar el número máximo de adyacentes. Deberían ser potencias de dos. Empiece desde la potencia más alta de dos y hasta la potencia mínima de dos. La potencia más alta es igual al número de variables consideradas en el mapa K y la potencia mínima es cero.
Cada agrupación dará un término literal o de un producto. Es conocido comoprime implicant. Se dice que el principal implicante esessential prime implicant, si al menos un solo '1' no está cubierto con ninguna otra agrupación, sino solo esa agrupación cubre.
Anote todos los implicantes principales y los implicantes principales esenciales. La función booleana simplificada contiene todos los implicantes primos esenciales y solo los implicantes primos requeridos.
Note 1 - Si las salidas no están definidas para alguna combinación de entradas, esos valores de salida se representarán con don’t care symbol ‘x’. Eso significa que podemos considerarlos como '0' o '1'.
Note 2- Si los términos de indiferencia también están presentes, coloque la 'x' de indiferencia en las respectivas celdas de K-map. Considere solo las 'x' de no importa que sean útiles para agrupar el número máximo de adyacentes. En esos casos, trate el valor de no importa como '1'.
Ejemplo
Nos deja simplify la siguiente función booleana, f(W, X, Y, Z)= WX’Y’ + WY + W’YZ’ utilizando K-map.
La función booleana dada está en forma de suma de productos. Tiene 4 variables W, X, Y y Z. Por lo tanto, requerimos4 variable K-map. los4 variable K-map con los correspondientes a los términos del producto dados se muestra en la siguiente figura.
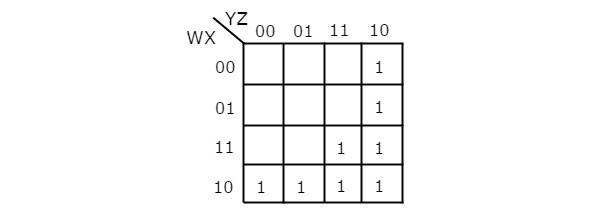
Aquí, los 1 se colocan en las siguientes celdas de K-map.
Las celdas, que son comunes a la intersección de la Fila 4 y las columnas 1 y 2, corresponden al término del producto, WX’Y’.
Las celdas, que son comunes a la intersección de las Filas 3 y 4 y las columnas 3 y 4 corresponden al término del producto, WY.
Las celdas, que son comunes a la intersección de las Filas 1 y 2 y la columna 4, corresponden al término del producto, W’YZ’.
No hay posibilidad de agrupar 16 adyacentes ni 8 adyacentes. Hay tres posibilidades de agrupar 4 adyacentes. Después de estas tres agrupaciones, no queda ninguna sin agrupar. Por lo tanto, no es necesario verificar la agrupación de 2 adyacentes. los4 variable K-map con estos tres groupings se muestra en la siguiente figura.

Aquí, tenemos tres implicantes principales WX ', WY e YZ'. Todos estos implicantes principales sonessential debido a las siguientes razones.
Dos unos (m8 & m9)de la agrupación de cuarta fila no están cubiertos por ninguna otra agrupación. Solo la agrupación de la cuarta fila cubre esos dos.
Solo uno (m15)de agrupación de forma cuadrada no está cubierta por ninguna otra agrupación. Solo la agrupación de forma cuadrada cubre ese.
Dos unos (m2 & m6)de los grupos de la cuarta columna no están cubiertos por ningún otro grupo. Solo el agrupamiento de la cuarta columna cubre esos dos.
Por lo tanto, los simplified Boolean function es
f = WX’ + WY + YZ’
Siga estos rules for simplifying K-maps para obtener un producto estándar en forma de sumas.
Seleccione el mapa K respectivo según el número de variables presentes en la función booleana.
Si la función booleana se da como producto de la forma de términos Max, coloque los ceros en las respectivas celdas de términos Max en el K-map. Si la función booleana se da como producto de sumas, coloque los ceros en todas las celdas posibles de K-map para las que los términos de suma dados son válidos.
Verifique las posibilidades de agrupar el número máximo de ceros adyacentes. Deberían ser potencias de dos. Empiece desde la potencia más alta de dos y hasta la potencia mínima de dos. La potencia más alta es igual al número de variables consideradas en el mapa K y la potencia mínima es cero.
Cada agrupación dará un término literal o de una suma. Es conocido comoprime implicant. Se dice que el principal implicante esessential prime implicant, si al menos un solo '0' no está cubierto por ninguna otra agrupación, sino solo por esa agrupación.
Anote todos los implicantes principales y los implicantes principales esenciales. La función booleana simplificada contiene todos los implicantes primos esenciales y solo los implicantes primos requeridos.
Note- Si los términos de indiferencia también están presentes, coloque la 'x' de indiferencia en las respectivas celdas de K-map. Considere solo las 'x' de no importa que sean útiles para agrupar el número máximo de ceros adyacentes. En esos casos, trate el valor de no importa como '0'.
Ejemplo
Nos deja simplify la siguiente función booleana, $f\left ( X,Y,Z \right )=\prod M\left ( 0,1,2,4 \right )$ utilizando K-map.
La función booleana dada está en forma de términos máximos. Tiene 3 variables X, Y y Z. Entonces, necesitamos 3 K-map variables. Los términos Max dados son M 0 , M 1 , M 2 y M 4 . Los 3variable K-map con ceros correspondientes a los términos Max dados se muestra en la siguiente figura.

No hay posibilidad de agrupar 8 ceros adyacentes ni 4 ceros adyacentes. Hay tres posibilidades de agrupar 2 ceros adyacentes. Después de estas tres agrupaciones, no queda un solo cero sin agrupar. los3 variable K-map con estos tres groupings se muestra en la siguiente figura.

Aquí, tenemos tres implicantes primos X + Y, Y + Z y Z + X. Todos estos implicantes primos son essential porque un cero en cada grupo no está cubierto por ningún otro grupo, excepto con sus grupos individuales.
Por lo tanto, los simplified Boolean function es
f = (X + Y).(Y + Z).(Z + X)
De esta manera, podemos simplificar fácilmente las funciones booleanas hasta 5 variables usando el método K-map. Para más de 5 variables, es difícil simplificar las funciones usando K-Maps. Porque, el número decells en K-map obtiene doubled incluyendo una nueva variable.
Debido a esta comprobación y agrupación de unos adyacentes (términos mínimos) o ceros adyacentes (términos máximos) será complicado. DiscutiremosTabular method en el próximo capítulo para superar las dificultades del método K-map.
En el capítulo anterior, discutimos el método K-map, que es un método conveniente para minimizar funciones booleanas hasta 5 variables. Pero es difícil simplificar las funciones booleanas que tienen más de 5 variables usando este método.
El método tabular de Quine-McClukey es un método tabular basado en el concepto de implicantes primos. Lo sabemosprime implicant es un término de producto (o suma), que no se puede reducir aún más mediante la combinación con cualquier otro término de producto (o suma) de la función booleana dada.
Este método tabular es útil para obtener los principales implicados mediante el uso repetido de la siguiente identidad booleana.
xy + xy '= x (y + y') = x.1 = x
Procedimiento del método tabular de Quine-McCluskey
Siga estos pasos para simplificar las funciones booleanas utilizando el método tabular de Quine-McClukey.
Step 1 - Organizar los términos mínimos dados en un ascending ordery hacer los grupos en función del número de unos presentes en sus representaciones binarias. Entonces, habráat most ‘n+1’ groups si hay 'n' variables booleanas en una función booleana o 'n' bits en el equivalente binario de términos mínimos.
Step 2 - Compare los términos mínimos presentes en successive groups. Si hay un cambio en la posición de un solo bit, entonces tome el par de esos dos términos mínimos. Coloque este símbolo '_' en la posición de bit diferente y mantenga los bits restantes como están.
Step 3 - Repita el paso 2 con términos recién formados hasta que obtengamos todos prime implicants.
Step 4 - Formular el prime implicant table. Consiste en un conjunto de filas y columnas. Los implicantes primos se pueden colocar en filas y los términos mínimos se pueden colocar en columnas. Coloque '1' en las celdas correspondientes a los términos mínimos que se cubren en cada implicante principal.
Step 5- Encontrar los implicantes primos esenciales observando cada columna. Si el término mínimo está cubierto solo por un implicante principal, entonces esessential prime implicant. Los implicantes primos esenciales formarán parte de la función booleana simplificada.
Step 6- Reducir la tabla de implicantes primos eliminando la fila de cada implicante primo esencial y las columnas correspondientes a los términos mínimos que se cubren en ese implicante primo esencial. Repita el paso 5 para la tabla de implicantes primos reducidos. Detenga este proceso cuando terminen todos los términos mínimos de la función booleana dada.
Ejemplo
Nos deja simplify la siguiente función booleana, $f\left ( W,X,Y,Z \right )=\sum m\left ( 2,6,8,9,10,11,14,15 \right )$ utilizando el método tabular de Quine-McClukey.
La función booleana dada está en sum of min termsformar. Tiene 4 variables W, X, Y y Z. Los términos mínimos dados son 2, 6, 8, 9, 10, 11, 14 y 15. El orden ascendente de estos términos mínimos se basa en el número de unos presentes en su equivalente binario es 2, 8, 6, 9, 10, 11, 14 y 15. La siguiente tabla muestra estosmin terms and their equivalent binary representaciones.
| Nombre del grupo | Términos mínimos | W | X | Y | Z |
|---|---|---|---|---|---|
| GA1 | 2 | 0 | 0 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | |
| GA2 | 6 | 0 | 1 | 1 | 0 |
| 9 | 1 | 0 | 0 | 1 | |
| 10 | 1 | 0 | 1 | 0 | |
| 11 | 1 | 0 | 1 | 1 | |
| 14 | 1 | 1 | 1 | 0 | |
| GA4 | 15 | 1 | 1 | 1 | 1 |
Los términos mínimos dados se organizan en 4 grupos según el número de unos presentes en sus equivalentes binarios. La siguiente tabla muestra los posiblesmerging of min terms de grupos adyacentes.
| Nombre del grupo | Términos mínimos | W | X | Y | Z |
|---|---|---|---|---|---|
| GB1 | 2,6 | 0 | - | 1 | 0 |
| 2,10 | - | 0 | 1 | 0 | |
| 8,9 | 1 | 0 | 0 | - | |
| 8,10 | 1 | 0 | - | 0 | |
| GB2 | 6,14 | - | 1 | 1 | 0 |
| 9,11 | 1 | 0 | - | 1 | |
| 10,11 | 1 | 0 | 1 | - | |
| 10,14 | 1 | - | 1 | 0 | |
| 11,15 | 1 | - | 1 | 1 | |
| 14,15 | 1 | 1 | 1 | - |
Se fusionan los términos mínimos, que se diferencian en sólo un bit de los grupos adyacentes. Ese bit diferente se representa con este símbolo, '-'. En este caso, hay tres grupos y cada grupo contiene combinaciones de dos términos mínimos. La siguiente tabla muestra los posiblesmerging of min term pairs de grupos adyacentes.
| Nombre del grupo | Términos mínimos | W | X | Y | Z |
|---|---|---|---|---|---|
| GB1 | 2,6,10,14 | - | - | 1 | 0 |
| 2,10,6,14 | - | - | 1 | 0 | |
| 8,9,10,11 | 1 | 0 | - | - | |
| 8,10,9,11 | 1 | 0 | - | - | |
| GB2 | 10,11,14,15 | 1 | - | 1 | - |
| 10,14,11,15 | 1 | - | 1 | - |
Se fusionan los grupos sucesivos de pares de términos mínimos, que se diferencian sólo en la posición de un bit. Ese bit diferente se representa con este símbolo, '-'. En este caso, hay dos grupos y cada grupo contiene combinaciones de cuatro términos mínimos. Aquí, estas combinaciones de términos de 4 minutos están disponibles en dos filas. Entonces, podemos eliminar las filas repetidas. La tabla reducida después de eliminar las filas redundantes se muestra a continuación.
| Nombre del grupo | Términos mínimos | W | X | Y | Z |
|---|---|---|---|---|---|
| GC1 | 2,6,10,14 | - | - | 1 | 0 |
| 8,9,10,11 | 1 | 0 | - | - | |
| GC2 | 10,11,14,15 | 1 | - | 1 | - |
No es posible una mayor fusión de las combinaciones de términos mínimos de grupos adyacentes, ya que se diferencian en más de una posición de un bit. Hay tres filas en la tabla anterior. Entonces, cada fila dará un implicante principal. Por lo tanto, losprime implicants son YZ ', WX' y WY.
los prime implicant table se muestra a continuación.
| Términos mínimos / Implicantes principales | 2 | 6 | 8 | 9 | 10 | 11 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|
| YZ’ | 1 | 1 | 1 | 1 | ||||
| WX’ | 1 | 1 | 1 | 1 | ||||
| WY | 1 | 1 | 1 | 1 |
Los implicantes principales se colocan en filas y los términos mínimos en columnas. Los 1 se colocan en las celdas comunes de las filas de implicantes primos y las correspondientes columnas de término mínimo.
Los términos mínimos 2 y 6 están cubiertos solo por un implicante principal YZ’. Entonces, es unessential prime implicant. Esto será parte de la función booleana simplificada. Ahora, elimine esta fila de implicantes primos y las columnas de término mínimo correspondientes. La tabla de implicantes primos reducidos se muestra a continuación.
| Términos mínimos / Implicantes principales | 8 | 9 | 11 | 15 |
|---|---|---|---|---|
| WX’ | 1 | 1 | 1 | |
| WY | 1 | 1 |
Los términos mínimos 8 y 9 están cubiertos solo por un implicante principal WX’. Entonces, es unessential prime implicant. Esto será parte de la función booleana simplificada. Ahora, elimine esta fila de implicantes primos y las columnas de término mínimo correspondientes. La tabla de implicantes primos reducidos se muestra a continuación.
| Términos mínimos / Implicantes principales | 15 |
|---|---|
| WY | 1 |
El término mínimo 15 está cubierto solo por un implicante principal WY. Entonces, es unessential prime implicant. Esto será parte de la función booleana simplificada.
En este problema de ejemplo, obtuvimos tres implicantes primos y los tres son esenciales. Por lo tanto, lossimplified Boolean function es
f(W,X,Y,Z) = YZ’ + WX’ + WY.
Los circuitos electrónicos digitales funcionan con voltajes de two logic levelsa saber, lógica baja y lógica alta. El rango de voltajes correspondiente a Logic Low se representa con '0'. De manera similar, el rango de voltajes correspondientes a Logic High se representa con '1'.
El circuito electrónico digital básico que tiene una o más entradas y una sola salida se conoce como Logic gate. Por lo tanto, las puertas lógicas son los componentes básicos de cualquier sistema digital. Podemos clasificar estas puertas lógicas en las siguientes tres categorías.
- Puertas básicas
- Puertas universales
- Puertas especiales
Ahora, hablemos de las puertas lógicas que se incluyen en cada categoría una por una.
Puertas básicas
En capítulos anteriores, aprendimos que las funciones booleanas se pueden representar en forma de suma de productos o en forma de producto de sumas según el requisito. Entonces, podemos implementar estas funciones booleanas usando puertas básicas. Las puertas básicas son las puertas Y, O y NO.
Y puerta
Una puerta AND es un circuito digital que tiene dos o más entradas y produce una salida, que es la logical ANDde todas esas entradas. Es opcional representar elLogical AND con el símbolo '.'.
La siguiente tabla muestra la truth table de puerta AND de 2 entradas.
| UN | segundo | Y = AB |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Aquí A, B son las entradas e Y es la salida de dos puertas Y de entrada. Si ambas entradas son '1', entonces solo la salida, Y es '1'. Para las combinaciones restantes de entradas, la salida, Y es '0'.
La siguiente figura muestra el symbol de una puerta AND, que tiene dos entradas A, B y una salida, Y.

Esta puerta AND produce una salida (Y), que es la logical ANDde dos entradas A, B. De manera similar, si hay 'n' entradas, entonces la puerta Y produce una salida, que es el Y lógico de todas esas entradas. Eso significa que la salida de la puerta AND será '1', cuando todas las entradas sean '1'.
Puerta OR
Una puerta OR es un circuito digital que tiene dos o más entradas y produce una salida, que es el OR lógico de todas esas entradas. Estalogical OR se representa con el símbolo '+'.
La siguiente tabla muestra la truth table de puerta OR de 2 entradas.
| UN | segundo | Y = A + B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Aquí A, B son las entradas e Y es la salida de dos puertas OR de entrada. Si ambas entradas son '0', entonces solo la salida, Y es '0'. Para las combinaciones restantes de entradas, la salida, Y es '1'.
La siguiente figura muestra el symbol de una puerta OR, que tiene dos entradas A, B y una salida, Y.

Esta puerta OR produce una salida (Y), que es la logical ORde dos entradas A, B. De manera similar, si hay 'n' entradas, entonces la puerta OR produce una salida, que es el OR lógico de todas esas entradas. Eso significa que la salida de una puerta OR será '1', cuando al menos una de esas entradas sea '1'.
NO puerta
Una puerta NOT es un circuito digital que tiene una sola entrada y una sola salida. La salida de la puerta NOT es lalogical inversionde entrada. Por lo tanto, la puerta NOT también se denomina inversor.
La siguiente tabla muestra la truth table de NO puerta.
| UN | Y = A ' |
|---|---|
| 0 | 1 |
| 1 | 0 |
Aquí A e Y son la entrada y salida de la puerta NOT respectivamente. Si la entrada, A es '0', entonces la salida, Y es '1'. De manera similar, si la entrada, A es '1', entonces la salida, Y es '0'.
La siguiente figura muestra el symbol de la puerta NOT, que tiene una entrada, A y una salida, Y.

Esta puerta NOT produce una salida (Y), que es la complement de entrada, A.
Puertas universales
Las puertas NAND y NOR se denominan universal gates. Porque podemos implementar cualquier función booleana, que está en forma de suma de productos utilizando solo puertas NAND. De manera similar, podemos implementar cualquier función booleana, que es producto de sumas utilizando solo puertas NOR.
Puerta NAND
La puerta NAND es un circuito digital que tiene dos o más entradas y produce una salida, que es la inversion of logical AND de todas esas entradas.
La siguiente tabla muestra la truth table de puerta NAND de 2 entradas.
| UN | segundo | Y = (AB) ' |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output of two input NAND gate. When both inputs are ‘1’, the output, Y is ‘0’. If at least one of the input is zero, then the output, Y is ‘1’. This is just opposite to that of two input AND gate operation.
The following image shows the symbol of NAND gate, which is having two inputs A, B and one output, Y.
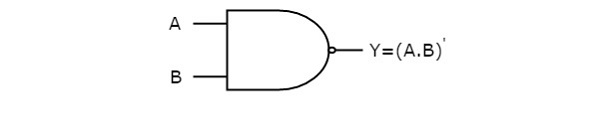
NAND gate operation is same as that of AND gate followed by an inverter. That’s why the NAND gate symbol is represented like that.
NOR gate
NOR gate is a digital circuit that has two or more inputs and produces an output, which is the inversion of logical OR of all those inputs.
The following table shows the truth table of 2-input NOR gate
| A | B | Y = (A+B)’ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output. If both inputs are ‘0’, then the output, Y is ‘1’. If at least one of the input is ‘1’, then the output, Y is ‘0’. This is just opposite to that of two input OR gate operation.
The following figure shows the symbol of NOR gate, which is having two inputs A, B and one output, Y.

NOR gate operation is same as that of OR gate followed by an inverter. That’s why the NOR gate symbol is represented like that.
Special Gates
Ex-OR & Ex-NOR gates are called as special gates. Because, these two gates are special cases of OR & NOR gates.
Ex-OR gate
The full form of Ex-OR gate is Exclusive-OR gate. Its function is same as that of OR gate except for some cases, when the inputs having even number of ones.
The following table shows the truth table of 2-input Ex-OR gate.
| A | B | Y = A⊕B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output of two input Ex-OR gate. The truth table of Ex-OR gate is same as that of OR gate for first three rows. The only modification is in the fourth row. That means, the output (Y) is zero instead of one, when both the inputs are one, since the inputs having even number of ones.
Therefore, the output of Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero, when both inputs are same.
Below figure shows the symbol of Ex-OR gate, which is having two inputs A, B and one output, Y.

Ex-OR gate operation is similar to that of OR gate, except for few combination(s) of inputs. That’s why the Ex-OR gate symbol is represented like that. The output of Ex-OR gate is ‘1’, when odd number of ones present at the inputs. Hence, the output of Ex-OR gate is also called as an odd function.
Ex-NOR gate
The full form of Ex-NOR gate is Exclusive-NOR gate. Its function is same as that of NOR gate except for some cases, when the inputs having even number of ones.
The following table shows the truth table of 2-input Ex-NOR gate.
| A | B | Y = A⊙B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Here A, B are the inputs and Y is the output. The truth table of Ex-NOR gate is same as that of NOR gate for first three rows. The only modification is in the fourth row. That means, the output is one instead of zero, when both the inputs are one.
Therefore, the output of Ex-NOR gate is ‘1’, when both inputs are same. And it is zero, when both the inputs are different.
The following figure shows the symbol of Ex-NOR gate, which is having two inputs A, B and one output, Y.

Ex-NOR gate operation is similar to that of NOR gate, except for few combination(s) of inputs. That’s why the Ex-NOR gate symbol is represented like that. The output of Ex-NOR gate is ‘1’, when even number of ones present at the inputs. Hence, the output of Ex-NOR gate is also called as an even function.
From the above truth tables of Ex-OR & Ex-NOR logic gates, we can easily notice that the Ex-NOR operation is just the logical inversion of Ex-OR operation.
The maximum number of levels that are present between inputs and output is two in two level logic. That means, irrespective of total number of logic gates, the maximum number of Logic gates that are present (cascaded) between any input and output is two in two level logic. Here, the outputs of first level Logic gates are connected as inputs of second level Logic gate(s).
Consider the four Logic gates AND, OR, NAND & NOR. Since, there are 4 Logic gates, we will get 16 possible ways of realizing two level logic. Those are AND-AND, AND-OR, ANDNAND, AND-NOR, OR-AND, OR-OR, OR-NAND, OR-NOR, NAND-AND, NAND-OR, NANDNAND, NAND-NOR, NOR-AND, NOR-OR, NOR-NAND, NOR-NOR.
These two level logic realizations can be classified into the following two categories.
- Degenerative form
- Non-degenerative form
Degenerative Form
If the output of two level logic realization can be obtained by using single Logic gate, then it is called as degenerative form. Obviously, the number of inputs of single Logic gate increases. Due to this, the fan-in of Logic gate increases. This is an advantage of degenerative form.
Only 6 combinations of two level logic realizations out of 16 combinations come under degenerative form. Those are AND-AND, AND-NAND, OR-OR, OR-NOR, NAND-NOR, NORNAND.
In this section, let us discuss some realizations. Assume, A, B, C & D are the inputs and Y is the output in each logic realization.
AND-AND Logic
In this logic realization, AND gates are present in both levels. Below figure shows an example for AND-AND logic realization.

We will get the outputs of first level logic gates as $Y_{1}=AB$ and $Y_{2}=CD$
These outputs, $Y_{1}$ and $Y_{2}$ are applied as inputs of AND gate that is present in second level. So, the output of this AND gate is
$$Y=Y_{1}Y_{2}$$
Substitute $Y_{1}$ and $Y_{2}$ values in the above equation.
$$Y=\left ( AB \right )\left ( CD \right )$$
$\Rightarrow Y=ABCD$
Therefore, the output of this AND-AND logic realization is ABCD. This Boolean function can be implemented by using a 4 input AND gate. Hence, it is degenerative form.
AND-NAND Logic
In this logic realization, AND gates are present in first level and NAND gate(s) are present in second level. The following figure shows an example for AND-NAND logic realization.
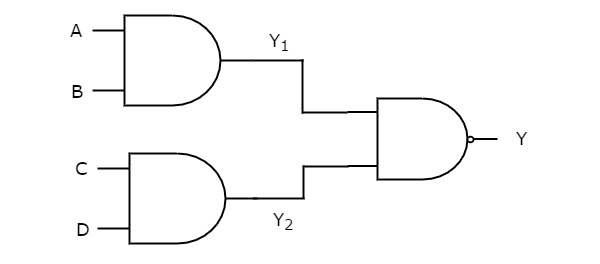
Anteriormente, obtuvimos las salidas de las puertas lógicas de primer nivel como $Y_{1} = AB$ y $Y_{2} = CD$
Estas salidas,$Y_{1}$ y $Y_{2}$se aplican como entradas de la puerta NAND que está presente en el segundo nivel. Entonces, la salida de esta puerta NAND es
$$Y={\left ( Y_{1}Y_{2} \right )}'$$
Sustituir $Y_{1}$ y $Y_{2}$ valores en la ecuación anterior.
$$Y={\left ( \left ( AB \right ) \left ( CD \right )\right )}'$$
$\Rightarrow Y={\left ( ABCD \right )}'$
Por lo tanto, la salida de esta realización lógica AND-NAND es ${\left ( ABCD \right )}'$. Esta función booleana se puede implementar utilizando una puerta NAND de 4 entradas. Por lo tanto, esdegenerative form.
Lógica OR-OR
En esta realización lógica, las puertas OR están presentes en ambos niveles. La siguiente figura muestra un ejemplo deOR-OR logic realización.
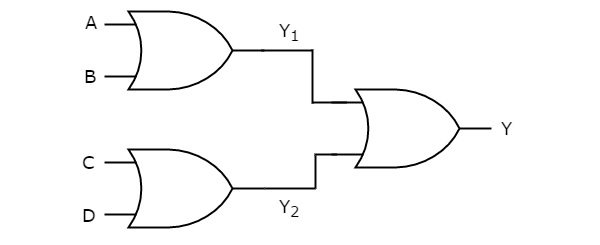
Obtendremos las salidas de las puertas lógicas de primer nivel como $Y_{1}=A+B$ y $Y_{2}=C+D$.
Estas salidas, $Y_{1}$ y $Y_{2}$se aplican como entradas de la puerta OR que está presente en el segundo nivel. Entonces, la salida de esta puerta OR es
$$Y=Y_{1}+Y_{2}$$
Sustituir $Y_{1}$ y $Y_{2}$ valores en la ecuación anterior.
$$Y=\left ( A+B \right )+\left ( C+D \right )$$
$\Rightarrow Y=A+B+C+D$
Por lo tanto, la salida de esta realización lógica OR-OR es A+B+C+D. Esta función booleana se puede implementar utilizando una puerta OR de 4 entradas. Por lo tanto, esdegenerative form.
Del mismo modo, puede verificar si las realizaciones restantes pertenecen a esta categoría o no.
Forma no degenerativa
Si la salida de la realización lógica de dos niveles no se puede obtener usando una puerta lógica única, entonces se llama como non-degenerative form.
El restante 10 combinationsde las realizaciones lógicas de dos niveles vienen bajo una forma no degenerativa. Esos son AND-OR, AND-NOR, OR-AND, OR-NAND, NAND-AND, NANDOR, NAND-NAND, NOR-AND, NOR-OR, NOR-NOR.
Ahora, analicemos algunas realizaciones. Suponga que A, B, C y D son las entradas e Y es la salida en cada realización lógica.
Lógica Y-O
En esta realización lógica, las puertas AND están presentes en el primer nivel y las puertas OR están presentes en el segundo nivel. La figura siguiente muestra un ejemplo deAND-OR logic realización.

Anteriormente, obtuvimos las salidas de las puertas lógicas de primer nivel como $Y_{1} = AB$ y $Y_{2} = CD$.
Estas salidas, Y1 e Y2 se aplican como entradas de la puerta OR que está presente en el segundo nivel. Entonces, la salida de esta puerta OR es
$$Y=Y_{1}+Y_{2}$$
Sustituir $Y_{1}$ y $Y_{2}$ valores en la ecuación anterior
$$Y=AB+CD$$
Por lo tanto, la salida de esta realización lógica AND-OR es AB+CD. Esta función booleana está enSum of Productsformar. Dado que no podemos implementarlo utilizando una puerta lógica única, esta realización lógica AND-OR es unanon-degenerative form.
Lógica AND-NOR
En esta realización lógica, las puertas AND están presentes en el primer nivel y las puertas NOR están presentes en el segundo nivel. La siguiente figura muestra un ejemplo deAND-NOR logic realización.

Conocemos las salidas de las puertas lógicas de primer nivel como $Y_{1} = AB$ y $Y_{2} = CD$
Estas salidas, Y1 e Y2 se aplican como entradas de la puerta NOR que está presente en el segundo nivel. Entonces, la salida de esta puerta NOR es
$$Y={\left ( Y_{1}+Y_{2} \right )}'$$
Sustituir $Y_{1}$ y $Y_{2}$ valores en la ecuación anterior.
$$Y={\left ( AB+CD \right )}'$$
Por lo tanto, la salida de esta realización lógica AND-NOR es ${\left ( AB+CD \right )}'$. Esta función booleana está enAND-OR-Invertformar. Dado que no podemos implementarlo mediante el uso de una puerta lógica única, esta realización lógica AND-NOR es unanon-degenerative form
Lógica OR-AND
En esta realización lógica, las puertas O están presentes en el primer nivel y las puertas Y están presentes en el segundo nivel. La siguiente figura muestra un ejemplo deOR-AND logic realización.

Anteriormente, obtuvimos las salidas de las puertas lógicas de primer nivel como $Y_{1}=A+B$ y $Y_{2}=C+D$.
Estas salidas, $Y_{1}$ y $Y_{2}$se aplican como entradas de la puerta Y que está presente en el segundo nivel. Entonces, la salida de esta puerta AND es
$$Y=Y_{1}Y_{2}$$
Sustituir $Y_{1}$ y $Y_{2}$ valores en la ecuación anterior.
$$Y = \left ( A+B \right )\left ( C+D \right )$$
Por lo tanto, la salida de esta realización lógica OR-AND es (A + B) (C + D). Esta función booleana está enProduct of Sumsformar. Dado que no podemos implementarlo utilizando una puerta lógica única, esta realización lógica O-Y es unanon-degenerative form.
Del mismo modo, puede verificar si las realizaciones restantes pertenecen a esta categoría o no.
Combinational circuitsconstan de puertas lógicas. Estos circuitos operan con valores binarios. La (s) salida (s) del circuito combinacional depende de la combinación de entradas presentes. La siguiente figura muestra elblock diagram de circuito combinacional.

Este circuito combinacional tiene 'n' variables de entrada y 'm' salidas. Cada combinación de variables de entrada afectará la (s) salida (s).
Procedimiento de diseño de circuitos combinacionales
Encuentre el número requerido de variables de entrada y salidas a partir de especificaciones dadas.
Formular el Truth table. Si hay 'n' variables de entrada, habrá 2n combinaciones posibles. Para cada combinación de entrada, encuentre los valores de salida.
Encuentra el Boolean expressionspara cada salida. Si es necesario, simplifique esas expresiones.
Implemente las expresiones booleanas anteriores correspondientes a cada salida usando Logic gates.
Convertidores de código
Hemos discutido varios códigos en el capítulo denominado códigos. Los convertidores, que convierten un código en otro código, se denominan comocode converters. Estos convertidores de código consisten básicamente en puertas lógicas.
Ejemplo
Conversor de código binario a código Gray
Implementemos un convertidor, que convierte un código binario de 4 bits WXYZ en su código Gray equivalente ABCD.
La siguiente tabla muestra la Truth table de un código binario de 4 bits a un convertidor de código Gray.
| Código binario WXYZ | WXYZ Código gris ABCD |
|---|---|
| 0000 | 0000 |
| 0001 | 0001 |
| 0010 | 0011 |
| 0011 | 0010 |
| 0100 | 0110 |
| 0101 | 0111 |
| 0110 | 0101 |
| 0111 | 0100 |
| 1000 | 1100 |
| 1001 | 1101 |
| 1010 | 1111 |
| 1011 | 1110 |
| 1100 | 1010 |
| 1101 | 1011 |
| 1110 | 1001 |
| 1111 | 1000 |
De la tabla de Verdad, podemos escribir el Boolean functions para cada bit de salida del código Gray como se muestra a continuación.
$$A=\sum m\left (8,9,10,11,12,13,14,15 \right )$$
$$B=\sum m\left (4,5,6,7,8,9,10,11 \right )$$
$$C=\sum m\left (2,3,4,5,10,11,12,13 \right )$$
$$D=\sum m\left (1,2,5,6,9,10,13,14 \right )$$
Simplifiquemos las funciones anteriores usando 4 K-Maps variables.
La siguiente figura muestra el 4 variable K-Map para simplificar Boolean function, A.

Al agrupar 8 adyacentes, obtuvimos $A=W$.
La siguiente figura muestra el 4 variable K-Map para simplificar Boolean function, B.

Hay dos grupos de 4 adyacentes. Después de agrupar, obtendremos B como
$$B={W}'X+W{X}'=W\oplus X $$
De manera similar, obtendremos las siguientes funciones booleanas para C & D después de simplificar.
$$C={X}'Y+X{Y}'=X \oplus Y$$
$$D={Y}'Z+Y{Z}'=Y \oplus Z$$
La siguiente figura muestra el circuit diagram de código binario de 4 bits a convertidor de código Gray.

Dado que las salidas dependen solo de las entradas presentes, este convertidor de código binario a código Gray de 4 bits es un circuito combinacional. Del mismo modo, puede implementar otros convertidores de código.
Generador de bits de paridad
Hay dos tipos de generadores de bits de paridad según el tipo de bit de paridad que se genera. Even parity generatorgenera un bit de paridad par. Similar,odd parity generator genera un bit de paridad impar.
Generador de paridad uniforme
Ahora, implementemos un generador de paridad par para una entrada binaria de 3 bits, WXY. Genera un bit de paridad par, P. Si hay un número impar de unos presentes en la entrada, entonces el bit de paridad par, P debería ser '1' para que la palabra resultante contenga un número par de unos. Para otras combinaciones de entrada, incluso el bit de paridad, P debe ser '0'. La siguiente tabla muestra laTruth table del generador de paridad par.
| Entrada binaria WXY | Paridad par bit P |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 1 |
| 011 | 0 |
| 100 | 1 |
| 101 | 0 |
| 110 | 0 |
| 111 | 1 |
De la tabla de Verdad anterior, podemos escribir el Boolean function para un bit de paridad uniforme como
$$P={W}'{X}'Y+{W}'X{Y}'+W{X}'{Y}'+WXY$$
$\Rightarrow P={W}'\left ( {X}'Y+X{Y}' \right )+W\left ({X}'{Y}'+XY \right )$
$\Rightarrow P={W}'\left ( X \oplus Y \right )+W{\left (X \oplus Y \right )}'=W \oplus X \oplus Y$
La siguiente figura muestra el circuit diagram del generador de paridad par.

Este circuito consta de dos Exclusive-OR gatesteniendo dos entradas cada uno. La primera puerta O exclusivo tiene dos entradas W y X y produce una salida W ⊕ X. Esta salida se da como una entrada de la segunda puerta O exclusivo. La otra entrada de esta segunda puerta OR exclusivo es Y y produce una salida de W ⊕ X ⊕ Y.
Generador de paridad impar
Si hay un número par de unos presentes en la entrada, entonces un bit de paridad impar, P debería ser '1' para que la palabra resultante contenga un número impar de unos. Para otras combinaciones de entrada, bit de paridad impar, P debe ser '0'.
Siga el mismo procedimiento del generador de paridad par para implementar el generador de paridad impar. loscircuit diagram del generador de paridad impar se muestra en la siguiente figura.

El diagrama de circuito anterior consta de una puerta Ex-OR en el primer nivel y una puerta Ex-NOR en el segundo nivel. Dado que la paridad impar es opuesta a la paridad par, podemos colocar un inversor en la salida del generador de paridad par. En ese caso, el primer y segundo nivel contienen una puerta ExOR en cada nivel y el tercer nivel consta de un inversor.
Comprobador de paridad
Hay dos tipos de verificadores de paridad según el tipo de paridad que se debe verificar. Even parity checkercomprueba el error en los datos transmitidos, que contienen bits de mensaje junto con paridad par. Similar,odd parity checker comprueba el error en los datos transmitidos, que contienen bits de mensaje junto con paridad impar.
Incluso el verificador de paridad
Ahora, implementemos un circuito de verificación de paridad par. Suponga una entrada binaria de 3 bits, WXY se transmite junto con un bit de paridad par, P. Entonces, la palabra (datos) resultante contiene 4 bits, que se recibirán como la entrada del verificador de paridad par.
Genera un even parity check bit, E. Este bit será cero si los datos recibidos contienen un número par de unos. Eso significa que no hay ningún error en los datos recibidos. Este bit de verificación de paridad par será uno, si los datos recibidos contienen un número impar de unos. Eso significa que hay un error en los datos recibidos.
La siguiente tabla muestra la Truth table de un verificador de paridad par.
| Datos recibidos de 4 bits WXYP | Bit de comprobación de paridad par E |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 1 |
| 0011 | 0 |
| 0100 | 1 |
| 0101 | 0 |
| 0110 | 0 |
| 0111 | 1 |
| 1000 | 1 |
| 1001 | 0 |
| 1010 | 0 |
| 1011 | 1 |
| 1100 | 0 |
| 1101 | 1 |
| 1110 | 1 |
| 1111 | 0 |
De la tabla de Verdad anterior, podemos observar que el valor del bit de verificación de paridad par es '1', cuando hay un número impar de unos presentes en los datos recibidos. Eso significa que la función booleana del bit de verificación de paridad par es unodd function. La función OR exclusivo satisface esta condición. Por tanto, podemos escribir directamente elBoolean function del bit de control de paridad par como
$$E=W \oplus X \oplus Y \oplus P$$
La siguiente figura muestra el circuit diagram del verificador de paridad par.

Este circuito consta de tres Exclusive-OR gatesteniendo dos entradas cada uno. Las puertas del primer nivel producen salidas de$W \oplus X$ Y $Y \oplus P$. La puerta O exclusivo, que está en el segundo nivel, produce una salida de$W \oplus X \oplus Y \oplus P$
Comprobador de paridad impar
Suponga una entrada binaria de 3 bits, WXY se transmite junto con el bit de paridad impar, P. Entonces, la palabra (datos) resultante contiene 4 bits, que se recibirán como la entrada del verificador de paridad impar.
Genera un odd parity check bit, E. Este bit será cero si los datos recibidos contienen un número impar de unos. Eso significa que no hay ningún error en los datos recibidos. Este bit de verificación de paridad impar será uno, si los datos recibidos contienen un número par de unos. Eso significa que hay un error en los datos recibidos.
Siga el mismo procedimiento de un verificador de paridad par para implementar un verificador de paridad impar. loscircuit diagram del verificador de paridad impar se muestra en la siguiente figura.

El diagrama de circuito anterior consta de puertas Ex-OR en el primer nivel y una puerta Ex-NOR en el segundo nivel. Dado que la paridad impar es opuesta a la paridad par, podemos colocar un inversor en la salida del verificador de paridad par. En ese caso, el primer, segundo y tercer nivel contienen dos puertas Ex-OR, una puerta Ex-OR y un inversor respectivamente.
Sumador binario
La operación aritmética más básica es la suma. El circuito, que realiza la suma de dos números binarios se conoce comoBinary adder. Primero, implementemos un sumador, que realiza la suma de dos bits.
Media víbora
El medio sumador es un circuito combinacional, que realiza la suma de dos números binarios A y B son de single bit. Produce dos salidas suma, S & carry, C.
los Truth table de Half sumador se muestra a continuación.
| Entradas | Salidas | ||
|---|---|---|---|
| UN | segundo | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Cuando hacemos la suma de dos bits, la suma resultante puede tener valores que van de 0 a 2 en decimal. Podemos representar los dígitos decimales 0 y 1 con un solo bit en binario. Pero no podemos representar el dígito decimal 2 con un solo bit en binario. Entonces, necesitamos dos bits para representarlo en binario.
Sea, sum, S es el bit menos significativo y lleve, C es el bit más significativo de la suma resultante. Para las primeras tres combinaciones de entradas, acarreo, C es cero y el valor de S será cero o uno según elnumber of onespresente en las entradas. Pero, para la última combinación de entradas, acarreo, C es uno y suma, S es cero, ya que la suma resultante es dos.
Desde la tabla de Verdad, podemos escribir directamente el Boolean functions para cada salida como
$$S=A \oplus B$$
$C=AB$
Podemos implementar las funciones anteriores con una puerta Ex-OR de 2 entradas y una puerta AND de 2 entradas. loscircuit diagram de Half sumador se muestra en la siguiente figura.

En el circuito anterior, una puerta Ex-OR de dos entradas y una puerta AND de dos entradas producen suma, S & acarreo, C respectivamente. Por tanto, Half-sumador realiza la suma de dos bits.
Sumador completo
El sumador completo es un circuito combinacional, que realiza el addition of three bitsA, B y C en . Donde, A y B son los dos bits significativos paralelos y C in es el bit de acarreo, que se genera a partir de la etapa anterior. Este sumador completo también produce dos salidas suma, S & carry, C out , que son similares al Half sumador.
los Truth table de sumador completo se muestra a continuación.
| Entradas | Salidas | |||
|---|---|---|---|---|
| A | B | Cin | Cout | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Cuando hacemos la suma de tres bits, la suma resultante puede tener valores que van de 0 a 3 en decimal. Podemos representar los dígitos decimales 0 y 1 con un solo bit en binario. Pero no podemos representar los dígitos decimales 2 y 3 con un solo bit en binario. Entonces, necesitamos dos bits para representar esos dos dígitos decimales en binario.
Sea, sum, S es el bit menos significativo y llevemos, C out es el bit más significativo de la suma resultante. Es fácil completar los valores de las salidas para todas las combinaciones de entradas en la tabla de verdad. Solo cuenta elnumber of onespresente en las entradas y escriba el número binario equivalente en las salidas. Si C in es igual a cero, la tabla de verdad del sumador completo es la misma que la tabla de verdad del sumador medio.
Obtendremos lo siguiente Boolean functions para cada salida después de la simplificación.
$$S=A \oplus B \oplus C_{in}$$
$c_{out} = AB + \left ( A \oplus B \right )c_{in}$
La suma, S es igual a uno, cuando hay un número impar de unos presentes en las entradas. Sabemos que la puerta Ex-OR produce una salida, que es una función extraña. Entonces, podemos usar dos compuertas Ex-OR de 2 entradas o una compuerta Ex-OR de 3 entradas para producir la suma, S. Podemos implementar el carry, C out usando dos compuertas AND de 2 entradas y una compuerta OR. loscircuit diagram de sumador completo se muestra en la siguiente figura.
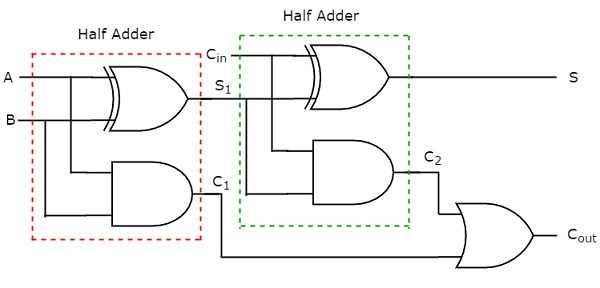
Este sumador se llama Full adderporque para implementar un sumador completo, necesitamos dos medios sumadores y una puerta OR. Si C in es cero, entonces el sumador completo se convierte en medio sumador. Podemos verificarlo fácilmente desde el diagrama de circuito anterior o desde las funciones booleanas de las salidas del sumador completo.
Sumador binario de 4 bits
El sumador binario de 4 bits realiza el addition of two 4-bit numbers. Deje que los números binarios de 4 bits,$A=A_{3}A_{2}A_{1}A_{0}$ y $B= B_{3}B_{2}B_{1}B_{0}$. Podemos implementar un sumador binario de 4 bits de una de las dos formas siguientes.
Utilice un Half sumador para hacer la suma de dos bits menos significativos y tres sumadores completos para hacer la suma de tres bits significativos más altos.
Utilice cuatro sumadores completos para uniformidad. Dado que, inicial carry C en es cero, el sumador completo que se utiliza para la adición de los bits menos significativos se convierte en medio sumador.
Por el momento, consideramos un segundo enfoque. losblock diagram del sumador binario de 4 bits se muestra en la siguiente figura.

Aquí, los 4 sumadores completos están en cascada. Cada sumador completo obtiene los bits respectivos de dos entradas paralelas A y B. La salida de acarreo de un sumador completo será la entrada de acarreo del sumador completo de orden superior posterior. Este sumador binario de 4 bits produce la suma resultante que tiene como máximo 5 bits. Por lo tanto, la última etapa completa, el sumador será el MSB.
De esta manera, podemos implementar cualquier sumador binario de orden superior simplemente conectando en cascada el número requerido de sumadores completos. Este sumador binario también se llama comoripple carry (binary) adder porque el acarreo se propaga (ondula) de una etapa a la siguiente.
Sustractor binario
El circuito, que realiza la resta de dos números binarios se conoce como Binary subtractor. Podemos implementar el restador binario siguiendo dos métodos.
- Restadores completos en cascada
- Método del complemento a 2
En el primer método, obtendremos un restador binario de n bits colocando en cascada 'n' restadores completos. Entonces, primero puede implementar Half sustractor y Full sustractor, similar a Half sumador y Sumador completo. Luego, puede implementar un sustractor binario de n bits, colocando en cascada 'n' sustractores completos. Entonces, tendremos dos circuitos separados para la suma y resta binaria de dos números binarios.
En el segundo método, podemos usar el mismo sumador binario para restar dos números binarios simplemente haciendo algunas modificaciones en la segunda entrada. Entonces, se lleva a cabo una operación de suma internamente binaria, pero la salida es una resta resultante.
Sabemos que la resta de dos números binarios A y B se puede escribir como,
$$A-B = A+\left ( {2}'s \: compliment \: of \: B \right )$$
$\Rightarrow A-B = A+\left ( {1}'s \: compliment \: of \: B \right )+1$
Sustractor binario de 4 bits
El restador binario de 4 bits produce el subtraction of two 4-bit numbers. Deje que los números binarios de 4 bits,$A=A_{3}A_{2}A_{1}A_{0}$ y $B= B_{3}B_{2}B_{1}B_{0}$. Internamente, la operación del restador binario de 4 bits es similar a la del sumador binario de 4 bits. Si los bits normales del número binario A, los bits complementados del número binario B y el acarreo inicial (prestado), C in como uno se aplican al sumador binario de 4 bits, entonces se convierte en un restador binario de 4 bits. losblock diagram del restador binario de 4 bits se muestra en la siguiente figura.

Este restador binario de 4 bits produce una salida que tiene como máximo 5 bits. Si el número binario A es mayor que el número binario B, entonces MSB de la salida es cero y los bits restantes tienen la magnitud de AB. Si el número binario A es menor que el número binario B, entonces el MSB de la salida es uno. Por lo tanto, tome el complemento a 2 de la salida para obtener la magnitud de AB.
De esta manera, podemos implementar cualquier resta binario de orden superior simplemente conectando en cascada el número requerido de sumadores completos con las modificaciones necesarias.
Sumador / restador binario
El circuito, que se puede utilizar para realizar sumas o restas de dos números binarios en cualquier momento, se conoce como Binary Adder / subtractor. Tanto el sumador binario como el restador binario contienen un conjunto de sumadores completos, que están en cascada. Los bits de entrada del número binario A se aplican directamente tanto en el sumador binario como en el restador binario.
Hay dos diferencias en las entradas de sumadores completos que están presentes en sumador binario y restador binario.
Los bits de entrada del número binario B se aplican directamente a los sumadores completos en el sumador binario, mientras que los bits complementados del número binario B se aplican a los sumadores completos en el restador binario.
El acarreo inicial, C 0 = 0 se aplica en el sumador binario de 4 bits, mientras que el acarreo inicial (préstamo), C 0 = 1 se aplica en el restador binario de 4 bits.
Sabemos que un 2-input Ex-OR gateproduce una salida, que es la misma que la de la primera entrada cuando la otra entrada es cero. De manera similar, produce una salida, que es complemento de la primera entrada cuando la otra entrada es una.
Por lo tanto, podemos aplicar los bits de entrada del número binario B a puertas Ex-OR de 2 entradas. La otra entrada a todas estas puertas Ex-OR es C 0 . Entonces, según el valor de C 0 , las puertas Ex-OR producen los bits normales o complementados del número binario B.
Sumador / restador binario de 4 bits
El sumador / restador binario de 4 bits produce la suma o la resta de dos números de 4 bits en función del valor del acarreo o préstamo inicial, 0 . Deje que los números binarios de 4 bits,$A=A_{3}A_{2}A_{1}A_{0}$ y $B= B_{3}B_{2}B_{1}B_{0}$. El funcionamiento del sumador / restador binario de 4 bits es similar al del sumador binario de 4 bits y del restador binario de 4 bits.
Aplicar los bits normales de los números binarios A y B y llevar o pedir prestado inicial, C 0 desde el exterior a un sumador binario de 4 bits. losblock diagram del sumador / restador binario de 4 bits se muestra en la siguiente figura.
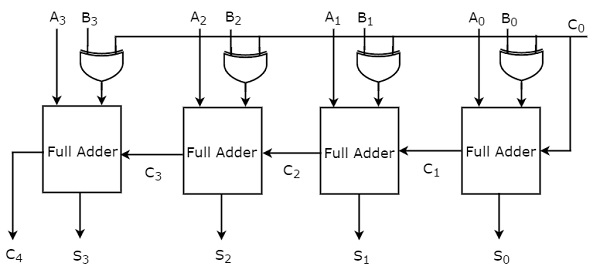
Si el acarreo inicial, 0 es cero, entonces cada sumador completo obtiene los bits normales de los números binarios A y B. Entonces, el sumador / restador binario de 4 bits produce una salida, que es laaddition of two binary numbers A y B.
Si el préstamo inicial, 0 es uno, entonces cada sumador completo obtiene los bits normales del número binario A y los bits complementados del número binario B. Entonces, el sumador / restador binario de 4 bits produce una salida, que es lasubtraction of two binary numbers A y B.
Por lo tanto, con la ayuda de compuertas Ex-OR adicionales, el mismo circuito se puede usar tanto para la suma como para la resta de dos números binarios.
Decoderes un circuito combinacional que tiene 'n' líneas de entrada y un máximo de 2 n líneas de salida. Una de estas salidas estará activa Alta en función de la combinación de entradas presentes, cuando el decodificador esté habilitado. Eso significa que el decodificador detecta un código en particular. Las salidas del decodificador no son más quemin terms de 'n' variables de entrada (líneas), cuando está habilitado.
Decodificador de 2 a 4
Deje 2 a 4 El decodificador tiene dos entradas A 1 y A 0 y cuatro salidas Y 3 , Y 2 , Y 1 e Y 0 . losblock diagram de 2 a 4 decodificadores se muestra en la siguiente figura.

Una de estas cuatro salidas será '1' para cada combinación de entradas cuando esté habilitada, E es '1'. losTruth table de 2 a 4 decodificadores se muestra a continuación.
| Habilitar | Entradas | Salidas | ||||
|---|---|---|---|---|---|---|
| E | A1 | A0 | Y3 | Y2 | Y1 | Y0 |
| 0 | X | X | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
De la tabla de Verdad, podemos escribir el Boolean functions para cada salida como
$$Y_{3}=E.A_{1}.A_{0}$$
$$ Y_{2}=E.A_{1}.{A_{0}}'$$
$$ Y_{1}=E.{A_{1}}'.A_{0}$$
$$ Y_{0}=E.{A_{1}}'.{A_{0}}'$$
Cada salida tiene un término de producto. Entonces, hay cuatro términos de producto en total. Podemos implementar estos cuatro términos de producto mediante el uso de cuatro puertas AND con tres entradas cada una y dos inversores. loscircuit diagram de 2 a 4 decodificadores se muestra en la siguiente figura.

Por lo tanto, las salidas de 2 a 4 decodificadores no son más que min termsde dos variables de entrada A 1 y A 0 , cuando se habilita, E es igual a uno. Si habilita, E es cero, entonces todas las salidas del decodificador serán iguales a cero.
De manera similar, el decodificador de 3 a 8 produce ocho términos mínimos de tres variables de entrada A 2 , A 1 y A 0 y el decodificador de 4 a 16 produce términos mínimos de cuatro variables de entrada A 3 , A 2 , A 1 y A 0 .
Implementación de decodificadores de orden superior
Ahora, implementemos los siguientes dos decodificadores de orden superior utilizando decodificadores de orden inferior.
- Decodificador de 3 a 8
- Decodificador 4 a 16
Decodificador de 3 a 8
En esta sección, implementemos 3 to 8 decoder using 2 to 4 decoders. Sabemos que el decodificador 2 a 4 tiene dos entradas, A 1 y A 0 y cuatro salidas, Y 3 a Y 0 . Mientras que el decodificador 3 a 8 tiene tres entradas A 2 , A 1 y A 0 y ocho salidas, Y 7 a Y 0 .
Podemos encontrar el número de decodificadores de orden inferior necesarios para implementar decodificadores de orden superior utilizando la siguiente fórmula.
$$Required \: number \: of \: lower \: order \: decoders=\frac{m_{2}}{m_{1}}$$
Dónde,
$m_{1}$ es el número de salidas del decodificador de orden inferior.
$m_{2}$ es el número de salidas del decodificador de orden superior.
Aquí, $m_{1}$ = 4 y $m_{2}$ = 8. Sustituya estos dos valores en la fórmula anterior.
$$Required \: number \: of \: 2 \: to \: 4 \: decoders=\frac{8}{4}=2$$
Por lo tanto, necesitamos dos decodificadores de 2 a 4 para implementar un decodificador de 3 a 8. losblock diagram de 3 a 8 decodificadores usando 2 a 4 decodificadores se muestra en la siguiente figura.

Las entradas paralelas A 1 y A 0 se aplican a cada decodificador de 2 a 4. El complemento de la entrada A 2 está conectado a Enable, E del decodificador inferior 2 a 4 para obtener las salidas, Y 3 a Y 0 . Estos son loslower four min terms. La entrada, A 2 se conecta directamente a Enable, E del decodificador superior 2 a 4 para obtener las salidas, Y 7 a Y 4 . Estos son loshigher four min terms.
Decodificador 4 a 16
En esta sección, implementemos 4 to 16 decoder using 3 to 8 decoders. Sabemos que 3 a 8 Decoder tiene tres entradas A 2 , A 1 y A 0 y ocho salidas, Y 7 a Y 0 . Considerando que, el decodificador 4 a 16 tiene cuatro entradas A 3 , A 2 , A 1 y A 0 y dieciséis salidas, Y 15 a Y 0
Conocemos la siguiente fórmula para encontrar el número de decodificadores de orden inferior necesarios.
$$Required \: number \: of \: lower \: order \: decoders=\frac{m_{2}}{m_{1}}$$
Sustituir, $m_{1}$ = 8 y $m_{2}$ = 16 en la fórmula anterior.
$$Required \: number \: of \: 3 \: to \: 8 decoders=\frac{16}{8}=2$$
Por lo tanto, necesitamos dos decodificadores de 3 a 8 para implementar un decodificador de 4 a 16. losblock diagram de 4 a 16 decodificadores usando 3 a 8 decodificadores se muestra en la siguiente figura.

Las entradas paralelas A 2 , A 1 y A 0 se aplican a cada decodificador de 3 a 8. El complemento de entrada A3 se conecta a Enable, E del decodificador inferior 3 a 8 para obtener las salidas Y 7 a Y 0 . Estos son loslower eight min terms. La entrada, A 3, se conecta directamente a Enable, E del decodificador superior 3 a 8 para obtener las salidas, Y 15 a Y 8 . Estos son loshigher eight min terms.
Un Encoderes un circuito combinacional que realiza la operación inversa del decodificador. Tiene un máximo de 2 n líneas de entrada y 'n' líneas de salida. Producirá un código binario equivalente a la entrada, que está activa Alta. Por lo tanto, el codificador codifica 2 n líneas de entrada con 'n' bits. Es opcional representar la señal de habilitación en codificadores.
Codificador 4 a 2
Deje 4 a 2 El codificador tiene cuatro entradas Y 3 , Y 2 , Y 1 e Y 0 y dos salidas A 1 y A 0 . losblock diagram de 4 a 2 Encoder se muestra en la siguiente figura.

En cualquier momento, solo una de estas 4 entradas puede ser '1' para obtener el código binario respectivo en la salida. losTruth table de 4 a 2 codificadores se muestra a continuación.
| Entradas | Salidas | ||||
|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
De la tabla de Verdad, podemos escribir el Boolean functions para cada salida como
$$A_{1}=Y_{3}+Y_{2}$$
$$A_{0}=Y_{3}+Y_{1}$$
Podemos implementar las dos funciones booleanas anteriores utilizando dos puertas OR de entrada. loscircuit diagram de 4 a 2 codificadores se muestra en la siguiente figura.

El diagrama de circuito anterior contiene dos puertas OR. Estas puertas OR codifican las cuatro entradas con dos bits
Codificador octal a binario
El codificador octal a binario tiene ocho entradas, Y 7 a Y 0 y tres salidas A 2 , A 1 y A 0 . El codificador octal a binario no es más que un codificador de 8 a 3. losblock diagram del codificador octal a binario se muestra en la siguiente figura.
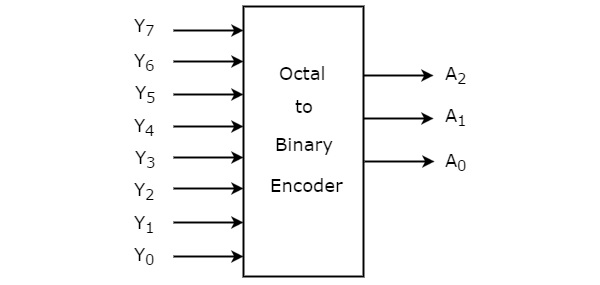
En cualquier momento, solo una de estas ocho entradas puede ser '1' para obtener el código binario respectivo. losTruth table del codificador octal a binario se muestra a continuación.
| Entradas | Salidas | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
De la tabla de Verdad, podemos escribir el Boolean functions para cada salida como
$$A_{2}=Y_{7}+Y_{6}+Y_{5}+Y_{4}$$
$$A_{1}=Y_{7}+Y_{6}+Y_{3}+Y_{2}$$
$$A_{0}=Y_{7}+Y_{5}+Y_{3}+Y_{1}$$
Podemos implementar las funciones booleanas anteriores utilizando cuatro puertas OR de entrada. loscircuit diagram del codificador octal a binario se muestra en la siguiente figura.

El diagrama de circuito anterior contiene tres puertas OR de 4 entradas. Estas puertas OR codifican las ocho entradas con tres bits.
Inconvenientes del codificador
Los siguientes son los inconvenientes del codificador normal.
Existe una ambigüedad cuando todas las salidas del codificador son iguales a cero. Porque, podría ser el código correspondiente a las entradas, cuando solo la entrada menos significativa es una o cuando todas las entradas son cero.
Si más de una entrada está activa High, entonces el codificador produce una salida, que puede no ser el código correcto. porexample, si tanto Y 3 como Y 6 son '1', entonces el codificador produce 111 en la salida. No es el código equivalente correspondiente a Y 3 , cuando es '1' ni el código equivalente correspondiente a Y 6 , cuando es '1'.
Entonces, para superar estas dificultades, debemos asignar prioridades a cada entrada del codificador. Entonces, la salida del codificador será el código (binario) correspondiente a las entradas altas activas, que tienen mayor prioridad. Este codificador se llamapriority encoder.
Codificador de prioridad
Un codificador de prioridad 4 a 2 tiene cuatro entradas Y 3 , Y 2 , Y 1 e Y 0 y dos salidas A 1 y A 0 . Aquí, la entrada Y 3 tiene la prioridad más alta, mientras que la entrada Y 0 tiene la prioridad más baja. En este caso, incluso si más de una entrada es '1' al mismo tiempo, la salida será el código (binario) correspondiente a la entrada, que tienehigher priority.
Consideramos uno más output, V para saber si el código disponible en las salidas es válido o no.
Si al menos una entrada del codificador es '1', entonces el código disponible en las salidas es válido. En este caso, la salida, V será igual a 1.
Si todas las entradas del codificador son '0', entonces el código disponible en las salidas no es válido. En este caso, la salida V será igual a 0.
los Truth table de codificador de prioridad 4 a 2 se muestra a continuación.
| Entradas | Salidas | |||||
|---|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 | V |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | X | 0 | 1 | 1 |
| 0 | 1 | X | X | 1 | 0 | 1 |
| 1 | X | X | X | 1 | 1 | 1 |
Utilizar 4 variable K-maps para obtener expresiones simplificadas para cada salida.
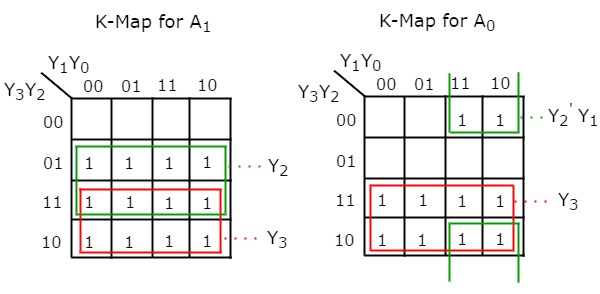
El simplificado Boolean functions son
$$A_{1}=Y_{3}+Y_{2}$$
$A_{0}=Y_{3}+{Y_{2}}'Y_{1}$
De manera similar, obtendremos la función booleana de salida, V como
$$V=Y_{3}+Y_{2}+Y_{1}+Y_{0}$$
Podemos implementar las funciones booleanas anteriores usando puertas lógicas. loscircuit diagram de codificador de prioridad 4 a 2 se muestra en la siguiente figura.

El diagrama de circuito anterior contiene dos puertas O de 2 entradas, una puerta O de 4 entradas, una puerta Y de 2 entradas y un inversor. Aquí, la combinación de puerta AND e inversor se utiliza para producir un código válido en las salidas, incluso cuando varias entradas son iguales a '1' al mismo tiempo. Por lo tanto, este circuito codifica las cuatro entradas con dos bits basados en elpriority asignado a cada entrada.
Multiplexeres un circuito combinacional que tiene un máximo de 2 n entradas de datos, 'n' líneas de selección y una sola línea de salida. Una de estas entradas de datos se conectará a la salida en función de los valores de las líneas de selección.
Dado que hay 'n' líneas de selección, habrá 2 n combinaciones posibles de ceros y unos. Entonces, cada combinación seleccionará solo una entrada de datos. El multiplexor también se llamaMux.
Multiplexor 4x1
El multiplexor 4x1 tiene cuatro entradas de datos I 3 , I 2 , I 1 & I 0 , dos líneas de selección s 1 & s 0 y una salida Y. Elblock diagram del multiplexor 4x1 se muestra en la siguiente figura.

Una de estas 4 entradas se conectará a la salida en base a la combinación de entradas presentes en estas dos líneas de selección. Truth table del multiplexor 4x1 se muestra a continuación.
| Líneas de selección | Salida | |
|---|---|---|
| S1 | S0 | Y |
| 0 | 0 | Yo 0 |
| 0 | 1 | Yo 1 |
| 1 | 0 | Yo 2 |
| 1 | 1 | Yo 3 |
Desde la tabla de Verdad, podemos escribir directamente el Boolean function para salida, Y como
$$Y={S_{1}}'{S_{0}}'I_{0}+{S_{1}}'S_{0}I_{1}+S_{1}{S_{0}}'I_{2}+S_{1}S_{0}I_{3}$$
Podemos implementar esta función booleana usando inversores, puertas Y y puerta OR. loscircuit diagram del multiplexor 4x1 se muestra en la siguiente figura.

Podemos entender fácilmente el funcionamiento del circuito anterior. De manera similar, puede implementar un multiplexor 8x1 y un multiplexor 16x1 siguiendo el mismo procedimiento.
Implementación de multiplexores de orden superior.
Ahora, implementemos los siguientes dos multiplexores de orden superior utilizando multiplexores de orden inferior.
- Multiplexor 8x1
- Multiplexor 16x1
Multiplexor 8x1
En esta sección, implementemos un multiplexor 8x1 usando multiplexores 4x1 y multiplexores 2x1. Sabemos que el multiplexor 4x1 tiene 4 entradas de datos, 2 líneas de selección y una salida. Considerando que, el multiplexor 8x1 tiene 8 entradas de datos, 3 líneas de selección y una salida.
Entonces, requerimos dos 4x1 Multiplexersen la primera etapa para obtener las 8 entradas de datos. Dado que cada multiplexor 4x1 produce una salida, necesitamos un2x1 Multiplexer en la segunda etapa considerando las salidas de la primera etapa como entradas y para producir la salida final.
Deje que el multiplexor 8x1 tenga ocho entradas de datos I 7 a I 0 , tres líneas de selección s 2 , s 1 & s0 y una salida Y. LaTruth table del multiplexor 8x1 se muestra a continuación.
| Entradas de selección | Salida | ||
|---|---|---|---|
| S2 | S1 | S0 | Y |
| 0 | 0 | 0 | Yo 0 |
| 0 | 0 | 1 | Yo 1 |
| 0 | 1 | 0 | Yo 2 |
| 0 | 1 | 1 | Yo 3 |
| 1 | 0 | 0 | Yo 4 |
| 1 | 0 | 1 | Yo 5 |
| 1 | 1 | 0 | Yo 6 |
| 1 | 1 | 1 | Yo 7 |
Podemos implementar un multiplexor 8x1 usando multiplexores de orden inferior fácilmente considerando la tabla de Verdad anterior. losblock diagram del multiplexor 8x1 se muestra en la siguiente figura.

Lo mismo selection lines, s1 & s0se aplican a ambos multiplexores 4x1. Las entradas de datos del multiplexor 4x1 superior son I 7 a I 4 y las entradas de datos del multiplexor 4x1 inferior son I 3 a I 0 . Por lo tanto, cada multiplexor 4x1 produce una salida basada en los valores de las líneas de selección, s 1 & s 0 .
Las salidas de los Multiplexores 4x1 de la primera etapa se aplican como entradas del Multiplexor 2x1 que está presente en la segunda etapa. El otroselection line, s2 se aplica al multiplexor 2x1.
Si s 2 es cero, entonces la salida del multiplexor 2x1 será una de las 4 entradas I 3 a I 0 según los valores de las líneas de selección s 1 & s 0 .
Si s 2 es uno, entonces la salida del multiplexor 2x1 será una de las 4 entradas I 7 a I 4 según los valores de las líneas de selección s 1 & s 0 .
Por lo tanto, la combinación general de dos multiplexores 4x1 y un multiplexor 2x1 funciona como un multiplexor 8x1.
Multiplexor 16x1
En esta sección, implementemos un multiplexor 16x1 usando multiplexores 8x1 y multiplexores 2x1. Sabemos que el multiplexor 8x1 tiene 8 entradas de datos, 3 líneas de selección y una salida. Considerando que, el multiplexor 16x1 tiene 16 entradas de datos, 4 líneas de selección y una salida.
Entonces, requerimos dos 8x1 Multiplexersen la primera etapa para obtener las 16 entradas de datos. Dado que cada multiplexor de 8x1 produce una salida, necesitamos un multiplexor de 2x1 en la segunda etapa considerando las salidas de la primera etapa como entradas y para producir la salida final.
Deje que el multiplexor 16x1 tenga dieciséis entradas de datos I 15 a I 0 , cuatro líneas de selección s 3 as 0 y una salida Y. LaTruth table del multiplexor 16x1 se muestra a continuación.
| Entradas de selección | Salida | |||
|---|---|---|---|---|
| S3 | S2 | S1 | S0 | Y |
| 0 | 0 | 0 | 0 | Yo 0 |
| 0 | 0 | 0 | 1 | Yo 1 |
| 0 | 0 | 1 | 0 | Yo 2 |
| 0 | 0 | 1 | 1 | Yo 3 |
| 0 | 1 | 0 | 0 | Yo 4 |
| 0 | 1 | 0 | 1 | Yo 5 |
| 0 | 1 | 1 | 0 | Yo 6 |
| 0 | 1 | 1 | 1 | Yo 7 |
| 1 | 0 | 0 | 0 | Yo 8 |
| 1 | 0 | 0 | 1 | Yo 9 |
| 1 | 0 | 1 | 0 | Yo 10 |
| 1 | 0 | 1 | 1 | Yo 11 |
| 1 | 1 | 0 | 0 | Yo 12 |
| 1 | 1 | 0 | 1 | Yo 13 |
| 1 | 1 | 1 | 0 | Yo 14 |
| 1 | 1 | 1 | 1 | Yo 15 |
Podemos implementar multiplexores 16x1 usando multiplexores de orden inferior fácilmente considerando la tabla de Verdad anterior. losblock diagram del multiplexor 16x1 se muestra en la siguiente figura.

los same selection lines, s2, s1 & s0se aplican a ambos multiplexores 8x1. Las entradas de datos del multiplexor 8x1 superior son I 15 a I 8 y las entradas de datos del multiplexor 8x1 inferior son I 7 a I 0 . Por lo tanto, cada multiplexor 8x1 produce una salida basada en los valores de las líneas de selección, s 2 , s 1 & s 0 .
Las salidas de los Multiplexores 8x1 de la primera etapa se aplican como entradas del Multiplexor 2x1 que está presente en la segunda etapa. El otroselection line, s3 se aplica al multiplexor 2x1.
Si s 3 es cero, entonces la salida del multiplexor 2x1 será una de las 8 entradas Is 7 a I 0 según los valores de las líneas de selección s 2 , s 1 & s 0 .
Si s 3 es uno, entonces la salida del multiplexor 2x1 será una de las 8 entradas I 15 a I 8 según los valores de las líneas de selección s 2 , s 1 & s 0 .
Por lo tanto, la combinación general de dos multiplexores 8x1 y un multiplexor 2x1 funciona como un multiplexor 16x1.
De-Multiplexeres un circuito combinacional que realiza la operación inversa del multiplexor. Tiene una sola entrada, 'n' líneas de selección y un máximo de 2 n salidas. La entrada se conectará a una de estas salidas en función de los valores de las líneas de selección.
Dado que hay 'n' líneas de selección, habrá 2 n combinaciones posibles de ceros y unos. Entonces, cada combinación puede seleccionar solo una salida. El demultiplexor también se denominaDe-Mux.
Desmultiplexor 1x4
El demultiplexor 1x4 tiene una entrada I, dos líneas de selección, s 1 & s 0 y cuatro salidas Y 3 , Y 2 , Y 1 e Y 0 . losblock diagram del demultiplexor 1x4 se muestra en la siguiente figura.

La entrada única 'I' se conectará a una de las cuatro salidas, Y 3 a Y 0 según los valores de las líneas de selección s 1 & s0. losTruth table del demultiplexor 1x4 se muestra a continuación.
| Entradas de selección | Salidas | ||||
|---|---|---|---|---|---|
| S1 | S0 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | I |
| 0 | 1 | 0 | 0 | I | 0 |
| 1 | 0 | 0 | I | 0 | 0 |
| 1 | 1 | I | 0 | 0 | 0 |
De la tabla de Verdad anterior, podemos escribir directamente el Boolean functions para cada salida como
$$Y_{3}=s_{1}s_{0}I$$
$$Y_{2}=s_{1}{s_{0}}'I$$
$$Y_{1}={s_{1}}'s_{0}I$$
$$Y_{0}={s_1}'{s_{0}}'I$$
Podemos implementar estas funciones booleanas usando inversores y puertas AND de 3 entradas. loscircuit diagram del demultiplexor 1x4 se muestra en la siguiente figura.

Podemos entender fácilmente el funcionamiento del circuito anterior. Del mismo modo, puede implementar De-Multiplexer 1x8 y De-Multiplexer 1x16 siguiendo el mismo procedimiento.
Implementación de demultiplexores de orden superior
Ahora, implementemos los siguientes dos demultiplexores de orden superior utilizando demultiplexores de orden inferior.
- Desmultiplexor 1x8
- Desmultiplexor 1x16
Desmultiplexor 1x8
En esta sección, implementemos el demultiplexor 1x8 usando demultiplexores 1x4 y demultiplexores 1x2. Sabemos que el demultiplexor 1x4 tiene una sola entrada, dos líneas de selección y cuatro salidas. Considerando que, 1x8 De-Multiplexer tiene una sola entrada, tres líneas de selección y ocho salidas.
Entonces, requerimos dos 1x4 De-Multiplexersen la segunda etapa para obtener las ocho salidas finales. Dado que el número de entradas en la segunda etapa es dos, requerimos1x2 DeMultiplexeren la primera etapa para que las salidas de la primera etapa sean las entradas de la segunda etapa. La entrada de este demultiplexor 1x2 será la entrada general del demultiplexor 1x8.
Deje que el demultiplexor 1x8 tenga una entrada I, tres líneas de selección s 2 , s 1 & s 0 y salidas Y 7 a Y 0 . losTruth table del demultiplexor 1x8 se muestra a continuación.
| Entradas de selección | Salidas | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| s2 | s1 | s0 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | I |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | I | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Podemos implementar fácilmente un demultiplexor 1x8 usando multiplexores de orden inferior considerando la tabla de Verdad anterior. losblock diagram del demultiplexor 1x8 se muestra en la siguiente figura.

Lo común selection lines, s1 & s0se aplican a ambos demultiplexores 1x4. Las salidas del demultiplexor 1x4 superior son Y 7 a Y 4 y las salidas del demultiplexor 1x4 inferior son Y 3 a Y 0 .
El otro selection line, s2se aplica al demultiplexor 1x2. Si s 2 es cero, entonces una de las cuatro salidas del demultiplexor 1x4 inferior será igual a la entrada, I, según los valores de las líneas de selección s 1 & s 0 . De manera similar, si s 2 es uno, entonces una de las cuatro salidas del DeMultiplexor 1x4 superior será igual a la entrada, I basado en los valores de las líneas de selección s 1 & s 0 .
Desmultiplexor 1x16
En esta sección, implementemos el demultiplexor 1x16 usando demultiplexores 1x8 y demultiplexor 1x2. Sabemos que el demultiplexor 1x8 tiene una sola entrada, tres líneas de selección y ocho salidas. Considerando que, 1x16 De-Multiplexer tiene una sola entrada, cuatro líneas de selección y dieciséis salidas.
Entonces, requerimos dos 1x8 De-Multiplexersen la segunda etapa para obtener las dieciséis salidas finales. Dado que el número de entradas en la segunda etapa es dos, requerimos1x2 DeMultiplexeren la primera etapa para que las salidas de la primera etapa sean las entradas de la segunda etapa. La entrada de este demultiplexor 1x2 será la entrada general del demultiplexor 1x16.
Deje que el demultiplexor 1x16 tenga una entrada I, cuatro líneas de selección s 3 , s 2 , s 1 & s 0 y salidas Y 15 a Y 0 . losblock diagram del demultiplexor 1x16 que utiliza multiplexores de orden inferior se muestra en la siguiente figura.
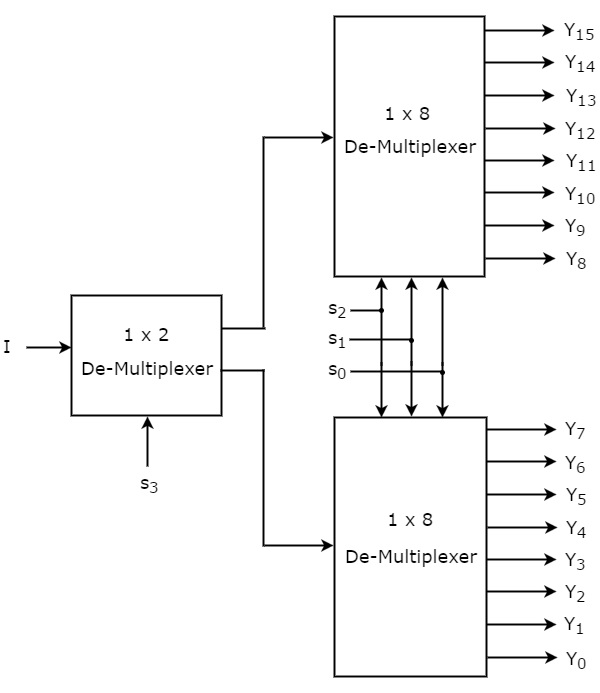
Lo común selection lines s2, s1 & s0se aplican a ambos demultiplexores 1x8. Las salidas del demultiplexor 1x8 superior son Y 15 a Y 8 y las salidas del demultiplexor 1x8 inferior son Y 7 a Y 0 .
El otro selection line, s3se aplica al demultiplexor 1x2. Si s 3 es cero, entonces una de las ocho salidas del De-Multiplexor 1x8 inferior será igual a la entrada, I basado en los valores de las líneas de selección s 2 , s 1 & s 0 . De manera similar, si s3 es uno, entonces una de las 8 salidas del demultiplexor 1x8 superior será igual a la entrada, I, según los valores de las líneas de selección s 2 , s 1 & s 0 .
Dispositivos lógicos programables (PLDs)son los circuitos integrados. Contienen una serie de puertas AND y otra serie de puertas OR. Hay tres tipos de PLD según el tipo de arreglo (s), que tiene una función programable.
- Memoria de sólo lectura programable
- Lógica de matriz programable
- Matriz lógica programable
El proceso de ingresar la información en estos dispositivos se conoce como programming. Básicamente, los usuarios pueden programar estos dispositivos o circuitos integrados eléctricamente para implementar las funciones booleanas según el requisito. Aquí, el término programación se refiere a la programación de hardware pero no a la programación de software.
Memoria programable de solo lectura (PROM)
La memoria de solo lectura (ROM) es un dispositivo de memoria que almacena la información binaria de forma permanente. Eso significa que no podemos cambiar esa información almacenada de ninguna manera más adelante. Si la ROM tiene una función programable, entonces se llama comoProgrammable ROM (PROM). El usuario tiene la flexibilidad de programar la información binaria eléctricamente una vez utilizando el programador PROM.
PROM es un dispositivo lógico programable que tiene una matriz AND fija y una matriz OR programable. losblock diagram de PROM se muestra en la siguiente figura.

Aquí, las entradas de las puertas AND no son de tipo programable. Por lo tanto, tenemos que generar 2 n términos de producto utilizando 2 n puertas Y con n entradas cada una. Podemos implementar estos términos de producto usando el decodificador nx2 n . Entonces, este decodificador genera 'n'min terms.
Aquí, las entradas de las puertas OR son programables. Eso significa que podemos programar cualquier cantidad de términos de producto requeridos, ya que todas las salidas de las puertas AND se aplican como entradas a cada puerta OR. Por lo tanto, las salidas de PROM estarán en forma desum of min terms.
Ejemplo
Implementemos lo siguiente Boolean functions utilizando PROM.
$$A(X,Y,Z)=\sum m\left ( 5,6,7 \right )$$
$$B(X,Y,Z)=\sum m\left ( 3,5,6,7 \right )$$
Las dos funciones dadas están en forma de suma de términos mínimos y cada función tiene tres variables X, Y y Z. Por lo tanto, necesitamos un decodificador de 3 a 8 y dos puertas OR programables para producir estas dos funciones. El correspondientePROM se muestra en la siguiente figura.

Aquí, el decodificador de 3 a 8 genera ocho términos mínimos. Las dos puertas OR programables tienen acceso a todos estos términos mínimos. Pero, solo los términos mínimos requeridos se programan para producir las funciones booleanas respectivas por cada puerta OR. El símbolo 'X' se utiliza para conexiones programables.
Lógica de matriz programable (PAL)
PAL es un dispositivo lógico programable que tiene una matriz Y programable y una matriz OR fija. La ventaja de PAL es que podemos generar solo los términos de producto requeridos de la función booleana en lugar de generar todos los términos mínimos mediante el uso de puertas AND programables. losblock diagram de PAL se muestra en la siguiente figura.

Aquí, las entradas de las puertas AND son programables. Eso significa que cada puerta AND tiene entradas de variables tanto normales como complementadas. Entonces, según el requisito, podemos programar cualquiera de esas entradas. Por lo tanto, podemos generar solo losproduct terms mediante el uso de estas puertas AND.
Aquí, las entradas de las puertas OR no son de tipo programable. Entonces, el número de entradas a cada puerta OR será de tipo fijo. Por lo tanto, aplique esos términos de producto requeridos a cada puerta OR como entradas. Por lo tanto, las salidas de PAL estarán en forma desum of products form.
Ejemplo
Implementemos lo siguiente Boolean functions utilizando PAL.
$$A=XY+X{Z}'$$
$$A=X{Y}'+Y{Z}'$$
Las dos funciones dadas están en forma de suma de productos. Hay dos términos de producto presentes en cada función booleana. Por lo tanto, necesitamos cuatro puertas Y programables y dos puertas O fijas para producir esas dos funciones. El correspondientePAL se muestra en la siguiente figura.

los programmable AND gatestener acceso a entradas de variables tanto normales como complementadas. En la figura anterior, las entradas X,${X}'$, Y, ${Y}'$, Z & ${Z}'$, están disponibles en las entradas de cada puerta AND. Por lo tanto, programe solo los literales requeridos para generar un término de producto por cada puerta AND. El símbolo 'X' se utiliza para conexiones programables.
Aquí, las entradas de las puertas OR son de tipo fijo. Entonces, los términos de producto necesarios están conectados a las entradas de cadaOR gate. Para que las puertas OR produzcan las respectivas funciones booleanas. El símbolo '.' se utiliza para conexiones fijas.
Matriz lógica programable (PLA)
PLA es un dispositivo lógico programable que tiene una matriz Y programable y una matriz OR programable. Por tanto, es el PLD más flexible. losblock diagram de PLA se muestra en la siguiente figura.

Aquí, las entradas de las puertas AND son programables. Eso significa que cada puerta AND tiene entradas de variables tanto normales como complementadas. Entonces, según el requisito, podemos programar cualquiera de esas entradas. Por lo tanto, podemos generar solo losproduct terms mediante el uso de estas puertas AND.
Aquí, las entradas de las puertas OR también son programables. Entonces, podemos programar cualquier cantidad de términos de producto requeridos, ya que todas las salidas de las puertas AND se aplican como entradas a cada puerta OR. Por lo tanto, las salidas de PAL estarán en forma desum of products form.
Ejemplo
Implementemos lo siguiente Boolean functions usando PLA.
$$A=XY+X{Z}'$$
$$B=X{Y}'+YZ+X{Z}'$$
Las dos funciones dadas están en forma de suma de productos. El número de términos de producto presentes en las funciones booleanas A y B dadas son dos y tres respectivamente. Un término de producto,${Z}'X$ es común en cada función.
Por lo tanto, necesitamos cuatro puertas Y programables y dos puertas O programables para producir esas dos funciones. El correspondientePLA se muestra en la siguiente figura.
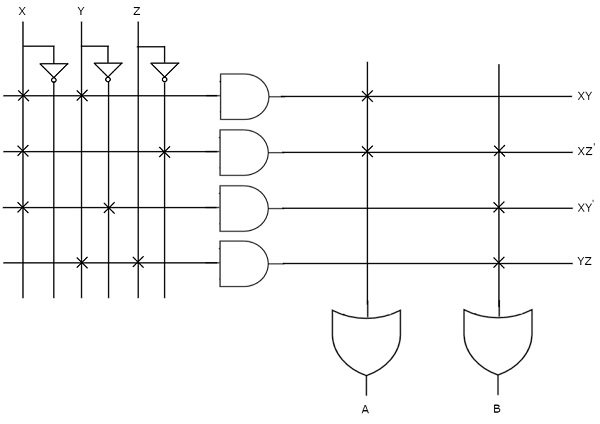
los programmable AND gatestener acceso a entradas de variables tanto normales como complementadas. En la figura anterior, las entradas X,${X}'$, Y, ${Y}'$, Z & ${Z}'$, están disponibles en las entradas de cada puerta AND. Por lo tanto, programe solo los literales requeridos para generar un término de producto por cada puerta AND.
Todos estos términos de producto están disponibles en las entradas de cada programmable OR gate. Pero, solo programe los términos de producto requeridos para producir las funciones booleanas respectivas por cada puerta OR. El símbolo 'X' se utiliza para conexiones programables.
En capítulos anteriores, hemos implementado varios circuitos combinacionales usando puertas lógicas. Excepto la puerta NO, todas las puertas lógicas restantes tienen al menos dos entradas y una salida. Del mismo modo, elthreshold gate también contiene al menos una entrada y solo una salida.
Además, contiene los pesos respectivos para cada entrada y un valor umbral. Los valores de estos pesos y umbrales podrían ser de cualquier número real finito.
Conceptos básicos de la puerta de umbral
Deje que las entradas de la puerta de umbral sean X 1 , X 2 , X 3 ,…, X n . Los pesos correspondientes de estas entradas son W 1 , W 2 , W 3 ,…, W n . lossymbol de la puerta de umbral se muestra en la siguiente figura.
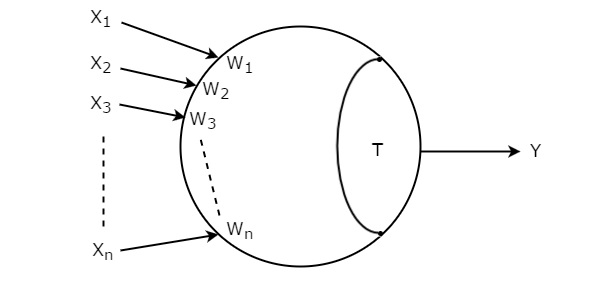
Threshold gatese representa con un círculo y tiene 'n' entradas, X 1 a X n y una sola salida, Y. Este círculo se divide en dos partes. Una parte representa los pesos correspondientes a las entradas y la otra parte representa el valor de umbral, T.
La suma de productos de insumos con pesos correspondientes se conoce como weighted sum. Si esta suma ponderada es mayor o igual que el valor de umbral, T entonces solo la salida, Y será igual a uno. De lo contrario, la salida Y será igual a cero.
Mathematically, podemos escribir esta relación entre las entradas y la salida de la puerta de umbral como se muestra a continuación.
$$Y=1, if \: \: W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{3}+...W_{n}X_{n}\geq T$$
= 0, de lo contrario.
Por lo tanto, podemos implementar varias puertas lógicas y funciones booleanas simplemente cambiando los valores de los pesos y / o el valor de umbral, T.
Ejemplo
Encontremos el simplified Boolean function para la siguiente puerta de umbral.

Esta puerta de umbral tiene tres entradas X 1 , X 2 , X 3 y una salida Y.
Los pesos correspondientes a las entradas X 1 , X 2 y X 3 son W 1 = 2, W 2 = 1 y W 3 = -4 respectivamente.
El valor de la puerta de umbral es T = -1.
los weighted sum de la puerta de umbral es
$$W=W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{3}$$
Sustituye los pesos dados en la ecuación anterior.
$$\Rightarrow W=2X_{1}+X_{2}-4X_{3}$$
La salida de la puerta de umbral, Y será '1' si W ≥ −1, de lo contrario será '0'.
El seguimiento table muestra la relación entre la entrada y la salida para todas las combinaciones posibles de entradas.
| Entradas | Suma ponderada | Salida | ||
|---|---|---|---|---|
| $X_{1}$ | $X_{2}$ | $X_{3}$ | $W=2X_{1}+X_{2}-4X_{3}$ | $Y$ |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | -4 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | -3 | 0 |
| 1 | 0 | 0 | 2 | 1 |
| 1 | 0 | 1 | -2 | 0 |
| 1 | 1 | 0 | 3 | 1 |
| 1 | 1 | 1 | -1 | 1 |
De la tabla anterior, podemos escribir el Boolean function para salida, Y como
$$Y= \sum m\left ( 0,2,4,6,7 \right )$$
La simplificación de esta función booleana usando 3 variable K-Map se muestra en la siguiente figura.

Por lo tanto, los simplified Boolean function para la puerta de umbral dada es $Y={X_{3}'}+X_{1}X_{2}$.
Síntesis de funciones de umbral
La puerta de umbral también se llama como universal gateporque podemos implementar cualquier función booleana usando compuertas de umbral. Algunas veces, puede que no sea posible implementar pocas puertas lógicas y funciones booleanas utilizando una única puerta de umbral. En ese caso, es posible que necesitemos varias puertas de umbral.
Siga estos steps para implementar una función booleana utilizando una única puerta de umbral.
Step 1 - Formular un Truth table para una función booleana dada.
Step 2 - En la tabla de Verdad anterior, agregue (incluya) una columna más, que da la relación entre weighted sums y Threshold value.
Step 3 - Escriba la relación entre las sumas ponderadas y el umbral para cada combinación de entradas como se menciona a continuación.
Si la salida de la función booleana es 1, entonces la suma ponderada será mayor o igual al valor de umbral para esa combinación de entradas.
Si la salida de la función booleana es 0, entonces la suma ponderada será menor que el valor de umbral para esa combinación de entradas.
Step 4 - Elija los valores de pesos y umbral de tal forma que satisfagan todas las relaciones presentes en la última columna de la tabla anterior.
step 5 - Dibuja el symbol de la puerta de umbral con esos pesos y valor de umbral.
Ejemplo
Implementemos lo siguiente Boolean function utilizando una puerta de umbral única.
$$Y\left ( X_{1},X_{2},X_{3} \right )=\sum m\left ( 0,2,4,6,7 \right )$$
La función booleana dada es una función de tres variables, que se representa en forma de suma de términos mínimos. losTruth table de esta función se muestra a continuación.
| Entradas | Salida | ||
|---|---|---|---|
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Ahora, agreguemos (incluyamos) una columna más a la tabla de Verdad anterior. Esta última columna contiene las relaciones entreweighted sums (W) and Threshold valor (T) para cada combinación de entradas.
| Entradas | Salida | Relaciones entre W & T | ||
|---|---|---|---|---|
| X1 | X2 | X3 | Y | |
| 0 | 0 | 0 | 1 | 0 ≥T |
| 0 | 0 | 1 | 0 | W 3 <T |
| 0 | 1 | 0 | 1 | W 2 ≥ T |
| 0 | 1 | 1 | 0 | W 2 + W 3 <T |
| 1 | 0 | 0 | 1 | W 1 ≥ T |
| 1 | 0 | 1 | 0 | W 1 + W 3 <T |
| 1 | 1 | 0 | 1 | W 1 + W 2 ≥ T |
| 1 | 1 | 1 | 1 | W 1 + W 2 + W 3 ≥ T |
A continuación se presentan las conclusiones de la tabla anterior.
El valor de Threshold debe ser cero o negativo según la primera relación.
El valor de W 3 debe ser negativo según la primera y la segunda relación.
Los valores de W 1 y W 2 deben ser mayores o iguales al valor de umbral basado en la quinta y tercera relaciones.
W 2 debe ser mayor que W 3 según la cuarta relación.
Podemos elegir los siguientes valores para pesos y umbrales basados en las conclusiones anteriores.
W 1 = 2, W 2 = 1, W 3 = -4 y T = -1
los symbol de la puerta de umbral con los valores anteriores se muestra a continuación.

Por lo tanto, esta puerta de umbral implementa el Boolean function, $Y\left ( X_{1}, X_{2},X_{3} \right )=\sum m\left ( 0,2,4,6,7 \right )$.
Discutimos varios circuitos combinacionales en capítulos anteriores. Todos estos circuitos tienen un conjunto de salidas, que dependen únicamente de la combinación de las entradas presentes. La siguiente figura muestra elblock diagram de circuito secuencial.
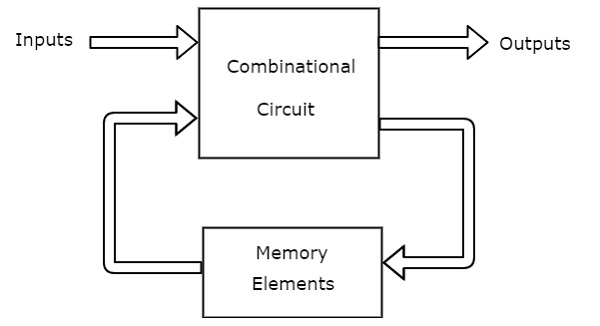
Este circuito secuencial contiene un conjunto de entradas y salidas. La (s) salida (s) del circuito secuencial depende no solo de la combinación de las entradas actuales sino también de las salidas anteriores. La salida anterior no es más que lapresent state. Por lo tanto, los circuitos secuenciales contienen circuitos combinacionales junto con elementos de memoria (almacenamiento). Algunos circuitos secuenciales pueden no contener circuitos combinacionales, sino solo elementos de memoria.
La siguiente tabla muestra differences entre circuitos combinacionales y circuitos secuenciales.
| Circuitos combinacionales | Circuitos secuenciales |
|---|---|
| Las salidas dependen solo de las entradas presentes. | Las salidas dependen tanto de las entradas actuales como del estado actual. |
| La ruta de retroalimentación no está presente. | La ruta de retroalimentación está presente. |
| No se requieren elementos de memoria. | Se requieren elementos de memoria. |
| No se requiere señal de reloj. | Se requiere señal de reloj. |
| Fácil de diseñar. | Difícil de diseñar. |
Tipos de circuitos secuenciales
A continuación se muestran los dos tipos de circuitos secuenciales:
- Circuitos secuenciales asincrónicos
- Circuitos secuenciales sincrónicos
Circuitos secuenciales asincrónicos
Si algunas o todas las salidas de un circuito secuencial no cambian (afectan) con respecto a la transición activa de la señal de reloj, entonces ese circuito secuencial se denomina como Asynchronous sequential circuit. Eso significa que todas las salidas de los circuitos secuenciales asíncronos no cambian (afectan) al mismo tiempo. Por lo tanto, la mayoría de las salidas de los circuitos secuenciales asíncronos sonnot in synchronous con solo bordes positivos o solo bordes negativos de la señal de reloj.
Circuitos secuenciales sincrónicos
Si todas las salidas de un circuito secuencial cambian (afectan) con respecto a la transición activa de la señal de reloj, entonces ese circuito secuencial se denomina como Synchronous sequential circuit. Eso significa que todas las salidas de los circuitos secuenciales síncronos cambian (afectan) al mismo tiempo. Por lo tanto, las salidas de los circuitos secuenciales síncronos están sincronizadas con solo bordes positivos o solo bordes negativos de la señal de reloj.
Señal de reloj y activación
En esta sección, analicemos sobre la señal del reloj y los tipos de activación uno por uno.
Señal de reloj
La señal del reloj es una señal periódica y su tiempo de ENCENDIDO y APAGADO no tiene por qué ser el mismo. Podemos representar la señal del reloj comosquare wave, cuando tanto el tiempo de ENCENDIDO como el de APAGADO son iguales. Esta señal de reloj se muestra en la siguiente figura.

En la figura anterior, la onda cuadrada se considera una señal de reloj. Esta señal permanece en lógica alta (5 V) durante algún tiempo y permanece en lógica baja (0 V) durante la misma cantidad de tiempo. Este patrón se repite con algún período de tiempo. En este caso, eltime period será igual al doble de tiempo de ENCENDIDO o al doble de tiempo de APAGADO.
Podemos representar la señal del reloj como train of pulses, cuando la hora ON y OFF no son iguales. Esta señal de reloj se muestra en la siguiente figura.

En la figura anterior, el tren de pulsos se considera una señal de reloj. Esta señal permanece en lógica alta (5 V) durante algún tiempo y permanece en lógica baja (0 V) durante otro tiempo. Este patrón se repite con algún período de tiempo. En este caso, eltime period será igual a la suma del tiempo de encendido y apagado.
El recíproco del período de tiempo de la señal del reloj se conoce como frequencyde la señal del reloj. Todos los circuitos secuenciales funcionan con señal de reloj. Por lo tanto, debe elegirse la frecuencia a la que los circuitos secuenciales pueden funcionar de acuerdo con la frecuencia de la señal de reloj.
Tipos de activación
A continuación se muestran los dos tipos posibles de activación que se utilizan en circuitos secuenciales.
- Activación de nivel
- Disparo de borde
Activación de nivel
Hay dos niveles, a saber, lógica alta y lógica baja en la señal de reloj. Los siguientes son los dostypes of level triggering.
- Activación de nivel positivo
- Activación de nivel negativo
Si el circuito secuencial se opera con la señal de reloj cuando está en Logic High, ese tipo de activación se conoce como Positive level triggering. Está resaltado en la siguiente figura.
Si el circuito secuencial se opera con la señal de reloj cuando está en Logic Low, ese tipo de activación se conoce como Negative level triggering. Está resaltado en la siguiente figura.

Disparo de borde
Hay dos tipos de transiciones que ocurren en la señal de reloj. Eso significa que la señal del reloj cambia de Lógica baja a Lógica alta o Lógica alta a Lógica baja.
Los siguientes son los dos types of edge triggering basado en las transiciones de la señal del reloj.
- Disparo por flanco positivo
- Disparo por flanco negativo
Si el circuito secuencial se opera con la señal de reloj que está pasando de Lógica baja a Lógica alta, entonces ese tipo de activación se conoce como Positive edge triggering. También se denomina activación por flanco ascendente. Se muestra en la siguiente figura.

Si el circuito secuencial se opera con la señal de reloj que está pasando de lógica alta a lógica baja, entonces ese tipo de activación se conoce como Negative edge triggering. También se denomina activación por flanco descendente. Se muestra en la siguiente figura.

En los próximos capítulos, analizaremos varios circuitos secuenciales en función del tipo de activación que se puede utilizar en él.
Hay dos tipos de elementos de memoria según el tipo de disparo que sea adecuado para operarlo.
- Latches
- Flip-flops
Los pestillos funcionan con la señal de habilitación, que es level sensitive. Mientras que las chanclas son sensibles a los bordes. Discutiremos sobre chanclas en el próximo capítulo. Ahora, hablemos sobre SR Latch & D Latch uno por uno.
SR Latch
SR Latch también se llama Set Reset Latch. Este pestillo afecta a las salidas siempre que la habilitación, E se mantenga en '1'. loscircuit diagram de SR Latch se muestra en la siguiente figura.
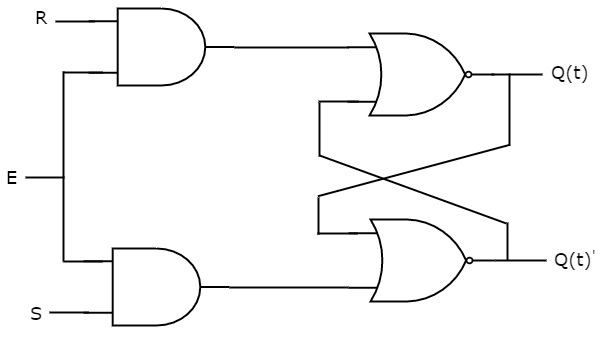
Este circuito tiene dos entradas S y R y dos salidas Q (t) y Q (t) '. losupper NOR gate tiene dos entradas R & complemento del estado actual, Q (t) 'y produce el siguiente estado, Q (t + 1) cuando se habilita, E es' 1 '.
Del mismo modo, el lower NOR gate tiene dos entradas S & estado presente, Q (t) y produce complemento del siguiente estado, Q (t + 1) 'cuando se habilita, E es' 1 '.
Sabemos que un 2-input NOR gateproduce una salida, que es el complemento de otra entrada cuando una de las entradas es '0'. De manera similar, produce una salida '0', cuando una de las entradas es '1'.
Si S = 1, entonces el siguiente estado Q (t + 1) será igual a '1' independientemente del estado actual, los valores de Q (t).
Si R = 1, entonces el siguiente estado Q (t + 1) será igual a '0' independientemente del estado actual, los valores de Q (t).
En cualquier momento, solo de esas dos entradas debe ser '1'. Si ambas entradas son '1', entonces el siguiente valor del estado Q (t + 1) no está definido.
La siguiente tabla muestra la state table del pestillo SR.
| S | R | Q (t + 1) |
|---|---|---|
| 0 | 0 | Q (t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | - |
Por lo tanto, SR Latch realiza tres tipos de funciones como Hold, Set & Reset según las condiciones de entrada.
D Pestillo
Hay un inconveniente de SR Latch. Ese es el siguiente valor de estado que no se puede predecir cuando ambas entradas S y R son una. Entonces, podemos superar esta dificultad con D Latch. También se denomina Data Latch. loscircuit diagram de D Latch se muestra en la siguiente figura.

Este circuito tiene una sola entrada D y dos salidas Q (t) y Q (t) '. D Latch se obtiene de SR Latch colocando un inversor entre las entradas S amp; & R y conectando la entrada D a S. Eso significa que eliminamos que las combinaciones de S & R tienen el mismo valor.
Si D = 0 → S = 0 & R = 1, entonces el siguiente estado Q (t + 1) será igual a '0' independientemente del estado actual, los valores de Q (t). Esto corresponde a la segunda fila de la tabla de estado SR Latch.
Si D = 1 → S = 1 & R = 0, entonces el siguiente estado Q (t + 1) será igual a '1' independientemente del estado actual, los valores de Q (t). Esto corresponde a la tercera fila de la tabla de estado SR Latch.
La siguiente tabla muestra la state table del pestillo D.
| re | Q (t + 1) |
|---|---|
| 0 | 0 |
| 1 | 1 |
Por lo tanto, D Latch Retiene la información que está disponible en la entrada de datos, D. Eso significa que la salida de D Latch es sensible a los cambios en la entrada, D siempre que la habilitación sea Alta.
En este capítulo, implementamos varios pestillos proporcionando el acoplamiento cruzado entre las puertas NOR. Del mismo modo, puede implementar estos pestillos utilizando puertas NAND.
En el capítulo anterior, hablamos sobre los cierres. Esos son los componentes básicos de las chanclas. Podemos implementar flip-flops en dos métodos.
En el primer método, cascade two latchesde tal manera que el primer pestillo se habilita para cada pulso de reloj positivo y el segundo pestillo se habilita para cada pulso de reloj negativo. Para que la combinación de estos dos pestillos se convierta en un flip-flop.
En el segundo método, podemos implementar directamente el flip-flop, que es sensible a los bordes. En este capítulo, analicemos lo siguienteflip-flops utilizando el segundo método.
- SR Flip-Flop
- D Flip-Flop
- Chanclas JK
- T Flip-Flop
SR Flip-Flop
El flip-flop SR funciona solo con transiciones de reloj positivas o transiciones de reloj negativas. Considerando que, SR latch opera con señal de habilitación. loscircuit diagram del flip-flop SR se muestra en la siguiente figura.

Este circuito tiene dos entradas S y R y dos salidas Q (t) y Q (t) '. El funcionamiento del flipflop SR es similar al SR Latch. Pero este flip-flop afecta las salidas solo cuando se aplica una transición positiva de la señal de reloj en lugar de la habilitación activa.
La siguiente tabla muestra la state table de SR flip-flop.
| S | R | Q (t + 1) |
|---|---|---|
| 0 | 0 | Q (t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | - |
Aquí, Q (t) y Q (t + 1) son el estado presente y el siguiente estado respectivamente. Por lo tanto, el flip-flop SR se puede usar para una de estas tres funciones, como Hold, Reset & Set según las condiciones de entrada, cuando se aplica la transición positiva de la señal de reloj. La siguiente tabla muestra lacharacteristic table de SR flip-flop.
| Entradas presentes | Estado actual | Estado siguiente | |
|---|---|---|---|
| S | R | Q(t) | Q(t + 1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | X |
| 1 | 1 | 1 | X |
Al usar tres K-Map variables, podemos obtener la expresión simplificada para el siguiente estado, Q (t + 1). losthree variable K-Map para el siguiente estado, Q (t + 1) se muestra en la siguiente figura.

Las agrupaciones máximas posibles de adyacentes ya se muestran en la figura. Por lo tanto, lossimplified expression para el siguiente estado Q (t + 1) es
$Q\left ( t+1 \right )=S+{R}'Q\left ( t \right )$
D Flip-Flop
El flip-flop D funciona solo con transiciones de reloj positivas o transiciones de reloj negativas. Considerando que, el pestillo D opera con señal de habilitación. Eso significa que la salida del flip-flop D es insensible a los cambios en la entrada, D excepto por la transición activa de la señal de reloj. loscircuit diagram del flip-flop D se muestra en la siguiente figura.

Este circuito tiene una sola entrada D y dos salidas Q (t) y Q (t) '. El funcionamiento del flip-flop D es similar al del D Latch. Pero este flip-flop afecta las salidas solo cuando se aplica una transición positiva de la señal de reloj en lugar de la habilitación activa.
La siguiente tabla muestra la state table de D flip-flop.
| re | Qt + 1t + 1 |
|---|---|
| 0 | 0 |
| 1 | 1 |
Por lo tanto, D flip-flop siempre contiene la información, que está disponible en la entrada de datos, D de la transición positiva anterior de la señal de reloj. De la tabla de estado anterior, podemos escribir directamente la siguiente ecuación de estado como
Q (t + 1) = D
El siguiente estado del flip-flop D es siempre igual a la entrada de datos, D para cada transición positiva de la señal de reloj. Por lo tanto, los flip-flops D se pueden usar en registros,shift registers y algunos de los contadores.
Chanclas JK
El flip-flop JK es la versión modificada del flip-flop SR. Opera solo con transiciones de reloj positivas o transiciones de reloj negativas. loscircuit diagram del flip-flop JK se muestra en la siguiente figura.
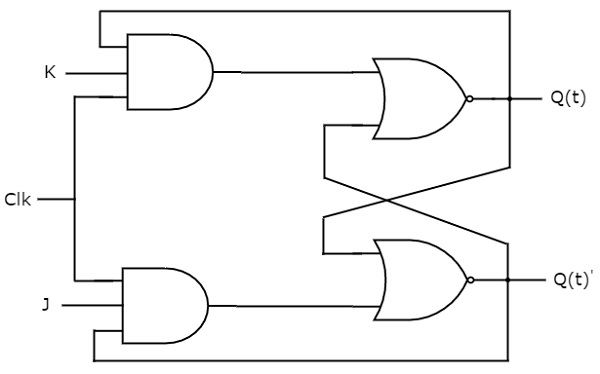
Este circuito tiene dos entradas J y K y dos salidas Q (t) y Q (t) '. El funcionamiento del flip-flop JK es similar al del flip-flop SR. Aquí, consideramos las entradas del flip-flop SR comoS = J Q(t)’ y R = KQ(t) para utilizar el flip-flop SR modificado para 4 combinaciones de entradas.
La siguiente tabla muestra la state table del flip-flop JK.
| J | K | Q (t + 1) |
|---|---|---|
| 0 | 0 | Q (t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | Q (t) ' |
Aquí, Q (t) y Q (t + 1) son el estado presente y el siguiente estado respectivamente. Por lo tanto, el flip-flop JK se puede utilizar para una de estas cuatro funciones, como Mantener, Restablecer, Establecer y Complementar el estado actual según las condiciones de entrada, cuando se aplica la transición positiva de la señal de reloj. La siguiente tabla muestra lacharacteristic table del flip-flop JK.
| Entradas presentes | Estado actual | Estado siguiente | |
|---|---|---|---|
| J | K | Q(t) | Q(t+1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Al usar tres K-Map variables, podemos obtener la expresión simplificada para el siguiente estado, Q (t + 1). Three variable K-Map para el siguiente estado, Q (t + 1) se muestra en la siguiente figura.

Las agrupaciones máximas posibles de adyacentes ya se muestran en la figura. Por lo tanto, lossimplified expression para el siguiente estado Q (t + 1) es
$$Q\left ( t+1 \right )=J{Q\left ( t \right )}'+{K}'Q\left ( t \right )$$
T Flip-Flop
T flip-flop es la versión simplificada del flip-flop JK. Se obtiene conectando la misma entrada 'T' a ambas entradas del flip-flop JK. Opera solo con transiciones de reloj positivas o transiciones de reloj negativas. loscircuit diagram de T flip-flop se muestra en la siguiente figura.

Este circuito tiene una sola entrada T y dos salidas Q (t) y Q (t) '. El funcionamiento del flip-flop T es el mismo que el del flip-flop JK. Aquí, consideramos las entradas del flip-flop JK comoJ = T y K = Tpara utilizar el flip-flop JK modificado para 2 combinaciones de entradas. Entonces, eliminamos las otras dos combinaciones de J & K, para las cuales esos dos valores se complementan entre sí en T flip-flop.
La siguiente tabla muestra la state table de T flip-flop.
| re | Q (t + 1) |
|---|---|
| 0 | Q (t) |
| 1 | Q (t) ' |
Aquí, Q (t) y Q (t + 1) son el estado presente y el siguiente estado respectivamente. Por lo tanto, el flip-flop T se puede utilizar para una de estas dos funciones, como Retener y Complementar el estado actual según las condiciones de entrada, cuando se aplica la transición positiva de la señal de reloj. La siguiente tabla muestra lacharacteristic table de T flip-flop.
| Entradas | Estado actual | Estado siguiente |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
De la tabla de características anterior, podemos escribir directamente el next state equation como
$$Q\left ( t+1 \right )={T}'Q\left ( t \right )+TQ{\left ( t \right )}'$$
$$\Rightarrow Q\left ( t+1 \right )=T\oplus Q\left ( t \right )$$
La salida del flip-flop T siempre cambia para cada transición positiva de la señal de reloj, cuando la entrada T permanece en lógica alta (1). Por lo tanto, T flip-flop se puede utilizar encounters.
En este capítulo, implementamos varios flip-flops al proporcionar el acoplamiento cruzado entre puertas NOR. Del mismo modo, puede implementar estos flip-flops utilizando puertas NAND.
En el capítulo anterior, discutimos los cuatro flip-flops, a saber, flip-flop SR, flip-flop D, flip-flop JK y flip-flop T. Podemos convertir un flip-flop en los tres flip-flops restantes al incluir algo de lógica adicional. Entonces, habrá un total de doceflip-flop conversions.
Siga estos steps para convertir un flip-flop en otro.
Considera el characteristic table del flip-flop deseado.
Complete los valores de excitación (entradas) de un flip-flop dado para cada combinación de estado actual y estado siguiente. losexcitation table para todos los flip-flops se muestra a continuación.
| Estado actual | Estado siguiente | Entradas SR flip-flop | Entrada flip-flop D | Entradas flip-flop JK | T entrada flip-flop | ||
|---|---|---|---|---|---|---|---|
| Q(t) | Q(t+1) | S | R | D | J | K | T |
| 0 | 0 | 0 | X | 0 | 0 | X | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | X | 1 |
| 1 | 0 | 0 | 1 | 0 | X | 1 | 1 |
| 1 | 1 | X | 0 | 1 | X | 0 | 0 |
Consigue el simplified expressionspara cada entrada de excitación. Si es necesario, use Kmaps para simplificar.
Dibuja el circuit diagram del flip-flop deseado de acuerdo con las expresiones simplificadas utilizando el flip-flop dado y las puertas lógicas necesarias.
Ahora, convierta algunas chanclas en otras. Siga el mismo proceso para las conversiones flip-flop restantes.
SR Flip-Flop a otras conversiones Flip-Flop
A continuación se muestran las tres posibles conversiones de flip-flop SR a otros flip-flops.
- Flip-flop SR a flip-flop D
- Flip-flop SR a flip-flop JK
- SR flip-flop a T flip-flop
Conversión de flip-flop SR a flip-flop D
Aquí, el flip-flop dado es el flip-flop SR y el flip-flop deseado es el flip-flop D. Por lo tanto, considere lo siguientecharacteristic table de D flip-flop.
| Entrada flip-flop D | Estado actual | Estado siguiente |
|---|---|---|
| D | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Sabemos que el flip-flop SR tiene dos entradas S y R. Por lo tanto, escriba los valores de excitación del flip-flop SR para cada combinación de valores del estado actual y del siguiente estado. La siguiente tabla muestra la tabla de características del flip-flop D junto con elexcitation inputs de SR flip-flop.
| Entrada flip-flop D | Estado actual | Estado siguiente | Entradas SR flip-flop | |
|---|---|---|---|---|
| D | Q(t) | Q(t + 1) | S | R |
| 0 | 0 | 0 | 0 | X |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | X | 0 |
De la tabla anterior, podemos escribir el Boolean functions para cada entrada como se muestra a continuación.
$$S=m_{2}+d_{3}$$
$$R=m_{1}+d_{0}$$
Podemos usar 2 K-Maps variables para obtener expresiones simplificadas para estas entradas. losk-Maps para S & R se muestran a continuación.

Entonces, obtuvimos S = D & R = D 'después de simplificar. loscircuit diagram del flip-flop D se muestra en la siguiente figura.

Este circuito consta de un flip-flop SR y un inversor. Este inversor produce una salida, que es un complemento de la entrada, D. Entonces, el circuito general tiene una sola entrada, D y dos salidas Q (t) y Q (t) '. Por tanto, es unD flip-flop. Del mismo modo, puede realizar otras dos conversiones.
D Flip-Flop a otras conversiones Flip-Flop
A continuación se muestran las tres posibles conversiones de flip-flop D a otros flip-flops.
- D flip-flop a T flip-flop
- Flip-flop D a flip-flop SR
- Flip-flop D a flip-flop JK
Conversión de flip-flop D a flip-flop T
Aquí, el flip-flop dado es D flip-flop y el flip-flop deseado es T flip-flop. Por lo tanto, considere lo siguientecharacteristic table de T flip-flop.
| T entrada flip-flop | Estado actual | Estado siguiente |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Sabemos que el flip-flop D tiene una sola entrada D. Por lo tanto, anote los valores de excitación del flip-flop D para cada combinación de valores del estado actual y del siguiente estado. La siguiente tabla muestra la tabla característica de T flip-flop junto con elexcitation input de D flip-flop.
| T entrada flip-flop | Estado actual | Estado siguiente | Entrada flip-flop D |
|---|---|---|---|
| T | Q(t) | Q(t + 1) | D |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
De la tabla anterior, podemos escribir directamente el Boolean function de D como se muestra a continuación.
$$D=T\oplus Q\left ( t \right )$$
Por lo tanto, necesitamos una puerta OR exclusivo de dos entradas junto con un flip-flop D. loscircuit diagram de T flip-flop se muestra en la siguiente figura.

Este circuito consta de un flip-flop D y una puerta OR exclusivo. Esta puerta OR exclusivo produce una salida, que es Ex-OR de T y Q (t). Entonces, el circuito general tiene una sola entrada, T y dos salidas Q (t) y Q (t) '. Por tanto, es unT flip-flop. Del mismo modo, puede realizar otras dos conversiones.
JK Flip-Flop a otras conversiones Flip-Flop
A continuación se muestran las tres posibles conversiones de flip-flop JK a otros flip-flops.
- Flip-flop JK a flip-flop T
- Flip-flop JK a flip-flop D
- Flip-flop JK a flip-flop SR
Conversión de flip-flop JK a flip-flop T
Aquí, el flip-flop dado es el flip-flop JK y el flip-flop deseado es el flip-flop T. Por lo tanto, considere lo siguientecharacteristic table de T flip-flop.
| T entrada flip-flop | Estado actual | Estado siguiente |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Sabemos que el flip-flop JK tiene dos entradas J y K. Por lo tanto, escriba los valores de excitación del flip-flop JK para cada combinación de valores del estado actual y del estado siguiente. La siguiente tabla muestra la tabla característica de T flip-flop junto con elexcitation inputs de flipflop JK.
| T entrada flip-flop | Estado actual | Estado siguiente | Entradas flip-flop JK | |
|---|---|---|---|---|
| T | Q(t) | Q(t + 1) | J | K |
| 0 | 0 | 0 | 0 | X |
| 0 | 1 | 1 | X | 0 |
| 1 | 0 | 1 | 1 | X |
| 1 | 1 | 0 | X | 1 |
De la tabla anterior, podemos escribir el Boolean functions para cada entrada como se muestra a continuación.
$$J=m_{2}+d_{1}+d_{3}$$
$$K=m_{3}+d_{0}+d_{2}$$
Podemos usar 2 K-Maps variables para obtener expresiones simplificadas para estas dos entradas. losk-Maps para J & K se muestran a continuación.

Entonces, obtuvimos, J = T & K = T después de simplificar. loscircuit diagram de T flip-flop se muestra en la siguiente figura.

Este circuito consta de flip-flop JK únicamente. No requiere ninguna otra puerta. Simplemente conecte la misma entrada T a J y K. Por lo tanto, el circuito general tiene una sola entrada, T y dos salidas Q (t) y Q (t) '. Por tanto, es unT flip-flop. Del mismo modo, puede realizar otras dos conversiones.
T Flip-Flop a otras conversiones Flip-Flop
A continuación se muestran las tres posibles conversiones de T flip-flop a otros flip-flops.
- T flip-flop a D flip-flop
- T flip-flop a SR flip-flop
- T flip-flop a JK flip-flop
Conversión de flip-flop T a flip-flop D
Aquí, el flip-flop dado es T flip-flop y el flip-flop deseado es D flip-flop. Por lo tanto, considere la tabla de características del flip-flop D y anote los valores de excitación del flip-flop T para cada combinación de valores del estado actual y del estado siguiente. La siguiente tabla muestra lacharacteristic table del flip-flop D junto con el excitation input de T flip-flop.
| Entrada flip-flop D | Estado actual | Estado siguiente | T entrada flip-flop | |
|---|---|---|---|---|
| D | Q(t) | Q(t + 1) | T | |
| 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | |
De la tabla anterior, podemos escribir directamente la función booleana de T como se muestra a continuación.
$$T=D\oplus Q\left ( t \right )$$
Por lo tanto, necesitamos una puerta OR exclusivo de dos entradas junto con un flip-flop T. loscircuit diagram del flip-flop D se muestra en la siguiente figura.

Este circuito consta de un flip-flop T y una puerta OR exclusivo. Esta puerta OR exclusivo produce una salida, que es Ex-OR de D y Q (t). Entonces, el circuito general tiene una sola entrada, D y dos salidas Q (t) y Q (t) '. Por tanto, es unD flip-flop. Del mismo modo, puede realizar otras dos conversiones.
Sabemos que un flip-flop puede almacenar un bit de información. Para almacenar varios bits de información, necesitamos varios flip-flops. El grupo de flip-flops, que se utilizan para almacenar (almacenar) los datos binarios, se conoce comoregister.
Si el registro es capaz de desplazar bits hacia el lado derecho o hacia el lado izquierdo, se conoce como shift register. Un registro de desplazamiento de bit 'N' contiene 'N' flip-flops. A continuación se muestran los cuatro tipos de registros de desplazamiento basados en la aplicación de entradas y el acceso a las salidas.
- Registro de desplazamiento de entrada en serie - salida en serie
- Registro de desplazamiento de entrada en serie - salida en paralelo
- Registro de desplazamiento de entrada paralela - salida serie
- Paralelo de entrada - registro de desplazamiento paralelo de salida
Registro de cambios de entrada en serie - salida en serie (SISO)
El registro de desplazamiento, que permite la entrada en serie y produce una salida en serie, se conoce como Entrada serie - Salida serie (SISO)registro de desplazamiento. losblock diagram del registro de desplazamiento SISO de 3 bits se muestra en la siguiente figura.

Este diagrama de bloques consta de tres flip-flops D, que son cascaded. Eso significa que la salida de un flip-flop D está conectada como la entrada del siguiente flip-flop D. Todos estos flip-flops están sincronizados entre sí, ya que a cada uno se le aplica la misma señal de reloj.
En este registro de desplazamiento, podemos enviar los bits en serie desde la entrada del flip-flop D más a la izquierda. Por lo tanto, esta entrada también se denominaserial input. Por cada disparo de flanco positivo de la señal de reloj, los datos se desplazan de una etapa a la siguiente. Entonces, podemos recibir los bits en serie desde la salida del flip-flop D más derecho. Por lo tanto, esta salida también se denomina comoserial output.
Ejemplo
Veamos el funcionamiento del registro de desplazamiento SISO de 3 bits enviando la información binaria “011” de LSB a MSB en serie en la entrada.
Suponga que el estado inicial de los flip-flops D desde el extremo izquierdo al extremo derecho es $Q_{2}Q_{1}Q_{0}=000$. Podemos entender elworking of 3-bit SISO shift register de la siguiente tabla.
| No de borde positivo del reloj | Entrada serial | Q 2 | Q 1 | Q 0 |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1 (LSB) | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 0 (MSB) | 0 | 1 | 1 (LSB) |
| 4 | - | - | 0 | 1 |
| 5 | - | - | - | 0 (MSB) |
El estado inicial de los flip-flops D en ausencia de señal de reloj es $Q_{2}Q_{1}Q_{0}=000$. Aquí, la salida en serie proviene de$Q_{0}$. Por lo tanto, el LSB (1) se recibe en 3 rd flanco positivo del reloj y el MSB (0) se recibe en 5 º flanco positivo del reloj.
Por lo tanto, el registro de desplazamiento SISO de 3 bits requiere cinco pulsos de reloj para producir una salida válida. Del mismo modo, elN-bit SISO shift register requiere 2N-1 pulsos de reloj para cambiar la información de bits 'N'.
Registro de cambios de entrada en serie - salida en paralelo (SIPO)
El registro de desplazamiento, que permite la entrada en serie y produce una salida en paralelo, se conoce como Serial In - Parallel Out (SIPO)registro de desplazamiento. losblock diagram del registro de desplazamiento SIPO de 3 bits se muestra en la siguiente figura.
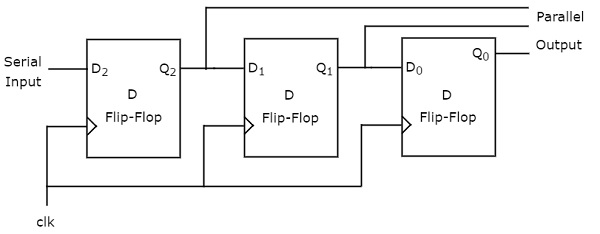
Este circuito consta de tres flip-flops D, que están en cascada. Eso significa que la salida de un flip-flop D está conectada como la entrada del siguiente flip-flop D. Todos estos flip-flops están sincronizados entre sí, ya que a cada uno se le aplica la misma señal de reloj.
En este registro de desplazamiento, podemos enviar los bits en serie desde la entrada del flip-flop D más a la izquierda. Por lo tanto, esta entrada también se denominaserial input. Por cada disparo de flanco positivo de la señal de reloj, los datos se desplazan de una etapa a la siguiente. En este caso, podemos acceder a las salidas de cada flip-flop D en paralelo. Entonces, obtendremosparallel outputs de este registro de desplazamiento.
Ejemplo
Veamos el funcionamiento del registro de desplazamiento SIPO de 3 bits enviando la información binaria “011” de LSB a MSB en serie en la entrada.
Suponga que el estado inicial de los flip-flops D desde el extremo izquierdo al extremo derecho es $Q_{2}Q_{1}Q_{0}=000$. Aquí,$Q_{2}$ Y $Q_{0}$son MSB y LSB respectivamente. Podemos entender elworking of 3-bit SIPO shift register de la siguiente tabla.
| No de borde positivo del reloj | Entrada serial | Q 2 (MSB) | Q 1 | Q 0 (LSB) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1 (LSB) | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 0 (MSB) | 0 | 1 | 1 |
El estado inicial de los flip-flops D en ausencia de señal de reloj es $Q_{2}Q_{1}Q_{0}=000$. La información binaria“011” se obtiene en paralelo en las salidas de los flip-flops D para el tercer flanco positivo del reloj.
Por lo tanto, el registro de desplazamiento SIPO de 3 bits requiere tres pulsos de reloj para producir una salida válida. Del mismo modo, elN-bit SIPO shift register requiere N pulsos de reloj para cambiar la información de bits 'N'.
Registro de cambios de entrada paralela - salida serie (PISO)
El registro de desplazamiento, que permite la entrada en paralelo y produce una salida en serie, se conoce como entrada paralela - salida en serie. (PISO)registro de desplazamiento. losblock diagram del registro de desplazamiento PISO de 3 bits se muestra en la siguiente figura.

Este circuito consta de tres flip-flops D, que están en cascada. Eso significa que la salida de un flip-flop D está conectada como la entrada del siguiente flip-flop D. Todos estos flip-flops están sincronizados entre sí, ya que a cada uno se le aplica la misma señal de reloj.
En este registro de desplazamiento, podemos aplicar el parallel inputsa cada flip-flop D haciendo Preset Enable en 1. Para cada disparo de flanco positivo de la señal del reloj, los datos cambian de una etapa a la siguiente. Entonces, obtendremos elserial output desde el flip-flop más a la derecha.
Ejemplo
Veamos el funcionamiento del registro de desplazamiento PISO de 3 bits aplicando la información binaria “011” en paralelo a través de entradas preestablecidas.
Dado que las entradas preestablecidas se aplican antes del borde positivo del reloj, el estado inicial de los flip-flops D de la izquierda a la derecha será $Q_{2}Q_{1}Q_{0}=011$. Podemos entender elworking of 3-bit PISO shift register de la siguiente tabla.
| No de borde positivo del reloj | Q 2 | Q 1 | Q 0 |
|---|---|---|---|
| 0 | 0 | 1 | 1 (LSB) |
| 1 | - | 0 | 1 |
| 2 | - | - | 0 (LSB) |
Aquí, la salida en serie proviene de $Q_{0}$. Por lo tanto, el LSB (1) es recibido antes de aplicar el flanco positivo del reloj y el MSB (0) se recibe en 2 nd flanco positivo del reloj.
Por lo tanto, el registro de desplazamiento PISO de 3 bits requiere dos pulsos de reloj para producir una salida válida. Del mismo modo, elN-bit PISO shift register requiere N-1 pulsos de reloj para cambiar la información de bits 'N'.
Registro de cambios de entrada paralela - salida paralela (PIPO)
El registro de desplazamiento, que permite la entrada en paralelo y produce una salida en paralelo, se conoce como Parallel In - Parallel Out (PIPO)registro de desplazamiento. losblock diagram del registro de desplazamiento PIPO de 3 bits se muestra en la siguiente figura.

Este circuito consta de tres flip-flops D, que están en cascada. Eso significa que la salida de un flip-flop D está conectada como la entrada del siguiente flip-flop D. Todos estos flip-flops están sincronizados entre sí, ya que a cada uno se le aplica la misma señal de reloj.
En este registro de desplazamiento, podemos aplicar el parallel inputsa cada flip-flop D haciendo Preset Enable en 1. Podemos aplicar las entradas paralelas a través de preset o clear. Estas dos son entradas asincrónicas. Eso significa que los flip-flops producen las salidas correspondientes, basadas en los valores de las entradas asincrónicas. En este caso, el efecto de las salidas es independiente de la transición del reloj. Entonces, obtendremos elparallel outputs de cada flip-flop D.
Ejemplo
Veamos el funcionamiento del registro de desplazamiento PIPO de 3 bits aplicando la información binaria “011” en paralelo a través de entradas preestablecidas.
Dado que las entradas preestablecidas se aplican antes del borde positivo del reloj, el estado inicial de los flip-flops D de la izquierda a la derecha será $Q_{2}Q_{1}Q_{0}=011$. Entonces, la información binaria“011” se obtiene en paralelo en las salidas de los flip-flops D antes de aplicar el flanco positivo del reloj.
Por lo tanto, el registro de desplazamiento PIPO de 3 bits requiere cero pulsos de reloj para producir una salida válida. Del mismo modo, elN-bit PIPO shift register no requiere ningún pulso de reloj para cambiar la información de bits 'N'.
En el capítulo anterior, discutimos cuatro tipos de registros de desplazamiento. Según el requisito, podemos utilizar uno de esos registros de desplazamiento. A continuación se muestran las aplicaciones de los registros de turnos.
El registro de cambio se utiliza como Parallel to serial converter, que convierte los datos en paralelo en datos en serie. Se utiliza en la sección del transmisor después del bloque Convertidor analógico a digital (ADC).
El registro de cambio se utiliza como Serial to parallel converter, que convierte los datos en serie en datos en paralelo. Se utiliza en la sección del receptor antes del bloque del convertidor digital a analógico (DAC).
El registro de desplazamiento junto con algunas puertas adicionales generan la secuencia de ceros y unos. Por tanto, se utiliza comosequence generator.
Los registros de desplazamiento también se utilizan como counters. Hay dos tipos de contadores según el tipo de salida de la mayoría de los flip-flop D conectados a la entrada en serie. Esos son el contador Ring y el contador Johnson Ring.
En este capítulo, analicemos estos dos contadores uno por uno.
Contador de anillo
En el capítulo anterior, discutimos el funcionamiento de Serial In - Parallel Out (SIPO)registro de desplazamiento. Acepta los datos del exterior en forma de serie y requiere "N" pulsos de reloj para cambiar "N" datos de bits.
Similar, ‘N’ bit Ring counterrealiza una operación similar. Pero, la única diferencia es que la salida del flip-flop D más a la derecha se da como entrada del flip-flop D más a la izquierda en lugar de aplicar datos desde el exterior. Por lo tanto, el contador de anillo produce una secuencia de estados (patrón de ceros y unos) y se repite para cada‘N’ clock cycles.
los block diagram del contador de anillo de 3 bits se muestra en la siguiente figura.
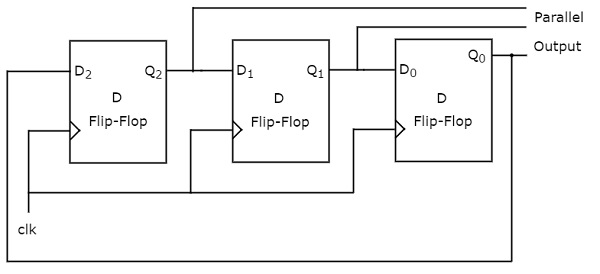
El contador de anillo de 3 bits contiene solo un registro de desplazamiento SIPO de 3 bits. La salida del flip-flop D más a la derecha está conectada a la entrada serial del flip-flop D más a la izquierda.
Suponga que el estado inicial de los flip-flops D desde el extremo izquierdo al extremo derecho es $Q_{2}Q_{1}Q_{0}=001$. Aquí,$Q_{2}$ Y $Q_{0}$son MSB y LSB respectivamente. Podemos entender elworking of Ring counter de la siguiente tabla.
| No de borde positivo del reloj | Entrada serial = Q 0 | Q 2 (MSB) | Q 1 | Q 0 (LSB) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 |
El estado inicial de los flip-flops D en ausencia de señal de reloj es $Q_{2}Q_{1}Q_{0}=001$. Este estado se repite por cada tres transiciones de flanco positivo de la señal de reloj.
Por lo tanto, lo siguiente operations tienen lugar para cada flanco positivo de la señal del reloj.
La entrada en serie del primer flip-flop D obtiene la salida anterior del tercer flip-flop. Entonces, la salida actual del primer flip-flop D es igual a la salida anterior del tercer flip-flop.
Las salidas anteriores del primer y segundo flip-flops D se desplazan a la derecha un bit. Eso significa que las salidas actuales del segundo y tercer flip-flops D son iguales a las salidas anteriores del primer y segundo flip-flops D.
Contador de anillos Johnson
La operación de Johnson Ring counteres similar a la del contador Ring. Pero, la única diferencia es que la salida complementada del flip-flop D más a la derecha se da como entrada del flip-flop D más a la izquierda en lugar de la salida normal. Por lo tanto, el contador Johnson Ring de 'N' bits produce una secuencia de estados (patrón de ceros y unos) y se repite para cada‘2N’ clock cycles.
El contador Johnson Ring también se llama Twisted Ring countere interruptor contador de anillo de cola. losblock diagram del contador Johnson Ring de 3 bits se muestra en la siguiente figura.

El contador Johnson Ring de 3 bits también contiene solo un registro de desplazamiento SIPO de 3 bits. La salida complementada del flip-flop D más a la derecha está conectada a la entrada en serie del flip-flop D más a la izquierda.
Supongamos que inicialmente todos los flip-flops D se borran. Entonces,$Q_{2}Q_{1}Q_{0}=000$. Aquí,$Q_{2}$ Y $Q_{0}$son MSB y LSB respectivamente. Podemos entender elworking del contador Johnson Ring de la siguiente tabla.
| No de borde positivo del reloj | Entrada serial = Q 0 | Q 2 (MSB) | Q 1 | Q 0 (LSB) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 1 | 1 | 1 | 1 |
| 4 | 0 | 0 | 1 | 1 |
| 5 | 0 | 0 | 0 | 1 |
| 6 | 0 | 0 | 0 | 0 |
El estado inicial de los flip-flops D en ausencia de señal de reloj es $Q_{2}Q_{1}Q_{0}=000$. Este estado se repite por cada seis transiciones de flanco positivo de la señal de reloj.
Por lo tanto, lo siguiente operations tienen lugar para cada flanco positivo de la señal del reloj.
La entrada en serie del primer flip-flop D obtiene la salida complementada anterior del tercer flip-flop. Entonces, la salida actual del primer flip-flop D es igual a la salida complementada anterior del tercer flip-flop.
Las salidas anteriores del primer y segundo flip-flops D se desplazan a la derecha un bit. Eso significa que las salidas actuales del segundo y tercer flip-flops D son iguales a las salidas anteriores del primer y segundo flip-flops D.
En los dos capítulos anteriores, discutimos varios registros de desplazamiento y counters using D flipflops. Ahora, analicemos varios contadores que usan chanclas T. Sabemos que T flip-flop alterna la salida para cada borde positivo de la señal de reloj o para el borde negativo de la señal de reloj.
Un contador binario de 'N' bits consta de 'N' T flip-flops. Si el contador cuenta de 0 a 2 - 1, entonces se llama binario up counter. Del mismo modo, si el contador cuenta atrás desde 2 - 1 a 0, entonces se llama binario down counter.
Hay dos types of counters basado en los flip-flops que están conectados en sincronía o no.
- Contadores asincrónicos
- Contadores síncronos
Contadores asincrónicos
Si los flip-flops no reciben la misma señal de reloj, ese contador se llama como Asynchronous counter. La salida del reloj del sistema se aplica como señal de reloj solo al primer flip-flop. Los flip-flops restantes reciben la señal de reloj de la salida de su flip-flop de etapa anterior. Por lo tanto, las salidas de todos los flip-flops no cambian (afectan) al mismo tiempo.
Ahora, analicemos los siguientes dos contadores uno por uno.
- Contador progresivo binario asincrónico
- Contador regresivo binario asincrónico
Contador ascendente binario asíncrono
Un contador progresivo binario asíncrono de 'N' bit consta de flip-flops 'N' T. Cuenta de 0 a 2 - 1. El block diagram del contador progresivo binario asíncrono de 3 bits se muestra en la siguiente figura.

El contador ascendente binario asíncrono de 3 bits contiene tres flip-flops T y la entrada T de todos los flip-flops está conectada a '1'. Todos estos flip-flops se activan por flanco negativo, pero las salidas cambian de forma asincrónica. La señal de reloj se aplica directamente al primer flip-flop T. Entonces, la salida del primer flip-flop Ttoggles por cada flanco negativo de la señal del reloj.
La salida del primer flip-flop T se aplica como señal de reloj para el segundo flip-flop T. Entonces, la salida del segundo flip-flop T cambia para cada borde negativo de la salida del primer flip-flop T. De manera similar, la salida del tercer flip-flop T cambia para cada borde negativo de la salida del segundo flip-flop T, ya que la salida del segundo flip-flop T actúa como la señal de reloj para el tercer flip-flop T.
Suponga que el estado inicial de los flip-flops T desde el extremo derecho al extremo izquierdo es $Q_{2}Q_{1}Q_{0}=000$. Aquí,$Q_{2}$ Y $Q_{0}$son MSB y LSB respectivamente. Podemos entender elworking del contador binario asíncrono de 3 bits de la siguiente tabla.
| No de borde negativo del reloj | Q 0 (LSB) | Q 1 | Q 2 (MSB) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 1 | 1 | 0 |
| 4 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 |
| 7 | 1 | 1 | 1 |
aquí $Q_{0}$ alterna para cada borde negativo de la señal del reloj. $Q_{1}$ alternado para cada $Q_{0}$que va de 1 a 0, de lo contrario permanece en el estado anterior. Similar,$Q_{2}$ alternado para cada $Q_{1}$ que va de 1 a 0, de lo contrario permanece en el estado anterior.
El estado inicial de los flip-flops T en ausencia de señal de reloj es $Q_{2}Q_{1}Q_{0}=000$. Esto se incrementa en uno por cada flanco negativo de la señal de reloj y alcanza el valor máximo a 7 º flanco negativo de la señal de reloj. Este patrón se repite cuando se aplican más bordes negativos de la señal de reloj.
Contador regresivo binario asíncrono
Un contador regresivo binario asíncrono bit 'N' consta de flip-flops 'N' T. Cuenta desde 2 - 1 a 0. El block diagram del contador regresivo binario asíncrono de 3 bits se muestra en la siguiente figura.

El diagrama de bloques del contador progresivo binario asíncrono de 3 bits es similar al diagrama de bloques del contador progresivo binario asíncrono de 3 bits. Pero, la única diferencia es que en lugar de conectar las salidas normales del flip-flop de una etapa como señal de reloj para el flip-flop de la siguiente etapa, conecte elcomplemented outputsdel flip-flop de una etapa como señal de reloj para el flip-flop de la siguiente etapa. La salida complementada va de 1 a 0 es la misma que la salida normal va de 0 a 1.
Suponga que el estado inicial de los flip-flops T desde el extremo derecho al extremo izquierdo es $Q_{2}Q_{1}Q_{0}=000$. Aquí,$Q_{2}$ Y $Q_{0}$son MSB y LSB respectivamente. Podemos entender elworking del contador regresivo binario asíncrono de 3 bits de la siguiente tabla.
| No de borde negativo del reloj | Q 0 (LSB) | Q 1 | Q 2 (MSB) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 0 | 1 | 1 |
| 3 | 1 | 0 | 1 |
| 4 | 0 | 0 | 1 |
| 5 | 1 | 1 | 0 |
| 6 | 0 | 1 | 0 |
| 7 | 1 | 0 | 0 |
aquí $Q_{0}$ alterna para cada borde negativo de la señal del reloj. $Q_{1}$ alternado para cada $Q_{0}$que va de 0 a 1, de lo contrario permanece en el estado anterior. Similar,$Q_{2}$ alternado para cada $Q_{1}$ que va de 0 a 1, de lo contrario permanece en el estado anterior.
El estado inicial de los flip-flops T en ausencia de señal de reloj es $Q_{2}Q_{1}Q_{0}=000$. Esto se decrementa en uno por cada flanco negativo de la señal de reloj y alcanza el mismo valor en 8 º flanco negativo de la señal de reloj. Este patrón se repite cuando se aplican más bordes negativos de la señal de reloj.
Contadores síncronos
Si todos los flip-flops reciben la misma señal de reloj, entonces ese contador se llama como Synchronous counter. Por lo tanto, las salidas de todos los flip-flops cambian (afectan) al mismo tiempo.
Ahora, analicemos los siguientes dos contadores uno por uno.
- Contador progresivo binario síncrono
- Contador regresivo binario síncrono
Contador progresivo binario síncrono
Un contador progresivo binario síncrono de 'N' bit consta de flip-flops 'N' T. Cuenta de 0 a 2 - 1. El block diagram del contador progresivo binario síncrono de 3 bits se muestra en la siguiente figura.

El contador progresivo binario síncrono de 3 bits contiene tres flip-flops T y una puerta AND de 2 entradas. Todos estos flip-flops se activan por flanco negativo y las salidas de los flip-flops cambian (afectan) sincrónicamente. Las entradas T del primer, segundo y tercer flip-flops son 1,$Q_{0}$ Y $Q_{1}Q_{0}$ respectivamente.
La salida del primer flip-flop T togglespor cada flanco negativo de la señal del reloj. La salida del segundo flip-flop T cambia para cada borde negativo de la señal de reloj si$Q_{0}$ es 1. La salida del tercer flip-flop T cambia para cada borde negativo de la señal de reloj si ambos $Q_{0}$ Y $Q_{1}$ son 1.
Contador regresivo binario síncrono
Un contador regresivo binario síncrono de 'N' bit consta de flip-flops 'N' T. Cuenta desde 2 - 1 a 0. El block diagram del contador regresivo binario síncrono de 3 bits se muestra en la siguiente figura.

El contador regresivo binario síncrono de 3 bits contiene tres flip-flops T y una puerta AND de 2 entradas. Todos estos flip-flops se activan por flanco negativo y las salidas de los flip-flops cambian (afectan) sincrónicamente. Las entradas T del primer, segundo y tercer flip-flops son 1,${Q_{0}}'$ & ' ${Q_{1}}'$${Q_ {0}} '$ respectivamente.
La salida del primer flip-flop T togglespor cada flanco negativo de la señal del reloj. La salida del segundo flip-flop T cambia para cada borde negativo de la señal del reloj si $ {Q_ {0}} '$ is 1. The output of third T flip-flop toggles for every negative edge of clock signal if both ${Q_ {1}} '$ & ${Q_ {0}} '$ son 1.
Sabemos que los circuitos secuenciales síncronos cambian (afectan) sus estados para cada transición positiva (o negativa) de la señal de reloj basada en la entrada. Entonces, este comportamiento de los circuitos secuenciales síncronos se puede representar en forma gráfica y se conoce comostate diagram.
Un circuito secuencial síncrono también se denomina como Finite State Machine(FSM), si tiene un número finito de estados. Hay dos tipos de FSM.
- Máquina de estado harinosa
- Máquina de estado de Moore
Ahora, analicemos estas dos máquinas de estado una por una.
Máquina de estado harinosa
Se dice que una máquina de estados finitos es una máquina de estados Mealy, si las salidas dependen tanto de las entradas actuales como de los estados presentes. losblock diagram de la máquina de estado Mealy se muestra en la siguiente figura.
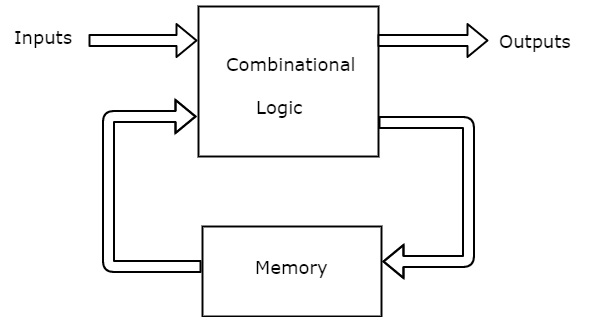
Como se muestra en la figura, hay dos partes presentes en la máquina de estado Mealy. Esos son la lógica y la memoria combinacionales. La memoria es útil para proporcionar algunos o parte de los resultados anteriores.(present states) como entradas de lógica combinacional.
Entonces, en base a las entradas actuales y los estados presentes, la máquina de estado Mealy produce salidas. Por lo tanto, las salidas serán válidas solo en la transición positiva (o negativa) de la señal de reloj.
los state diagram de la máquina de estado Mealy se muestra en la siguiente figura.
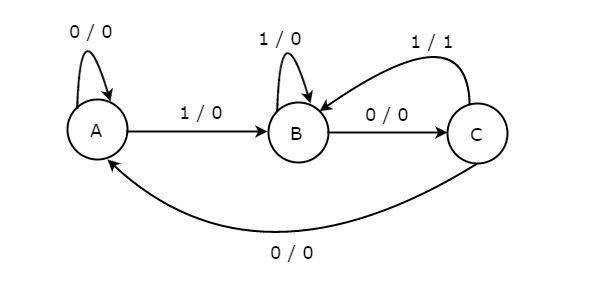
En la figura anterior, hay tres estados, a saber, A, B y C. Estos estados están etiquetados dentro de los círculos y cada círculo corresponde a un estado. Las transiciones entre estos estados se representan con líneas dirigidas. Aquí, 0/0, 1/0 y 1/1 denotainput / output. En la figura anterior, hay dos transiciones de cada estado según el valor de la entrada, x.
En general, el número de estados requeridos en la máquina de estados Mealy es menor o igual que el número de estados requeridos en la máquina de estados de Moore. Hay una máquina de estado de Moore equivalente para cada máquina de estado de Mealy.
Máquina de estado de Moore
Se dice que una máquina de estados finitos es una máquina de estados de Moore, si las salidas dependen solo de los estados presentes. losblock diagram de la máquina de estado de Moore se muestra en la siguiente figura.

Como se muestra en la figura, hay dos partes presentes en la máquina de estado de Moore. Esos son la lógica y la memoria combinacionales. En este caso, las entradas actuales y los estados presentes determinan los siguientes estados. Entonces, según los siguientes estados, la máquina de estados de Moore produce los resultados. Por lo tanto, las salidas serán válidas solo después de la transición del estado.
los state diagram de la máquina de estado de Moore se muestra en la siguiente figura.

En la figura anterior, hay cuatro estados, a saber, A, B, C y D. Estos estados y las salidas respectivas están etiquetados dentro de los círculos. Aquí, solo el valor de entrada está etiquetado en cada transición. En la figura anterior, hay dos transiciones de cada estado según el valor de la entrada, x.
En general, la cantidad de estados requeridos en la máquina de estados de Moore es mayor o igual que la cantidad de estados requeridos en la máquina de estados Mealy. Hay una máquina de estado Mealy equivalente para cada máquina de estado de Moore. Entonces, según el requisito, podemos usar uno de ellos.
Cada digital systemse puede dividir en dos partes. Esos son circuitos de ruta de datos (digitales) y circuitos de control. Los circuitos de ruta de datos realizan funciones como el almacenamiento de información binaria (datos) y la transferencia de datos de un sistema al otro. Considerando que, los circuitos de control determinan el flujo de operaciones de los circuitos digitales.
Es difícil describir el comportamiento de las grandes máquinas de estado utilizando diagramas de estado. Para superar esta dificultad, se pueden utilizar gráficos de máquina de estado algorítmica (ASM).ASM chartsson similares a los diagramas de flujo. Se utilizan para representar el flujo de tareas que deben realizar los circuitos de ruta de datos y los circuitos de control.
Componentes básicos de los gráficos ASM
A continuación se muestran los tres componentes básicos de los gráficos ASM.
- Cuadro de estado
- Cuadro de decisión
- Caja de salida condicional
Cuadro de estado
El cuadro de estado se representa en forma rectangular. Cada cuadro de estado representa un estado del circuito secuencial. lossymbol del cuadro de estado se muestra en la siguiente figura.
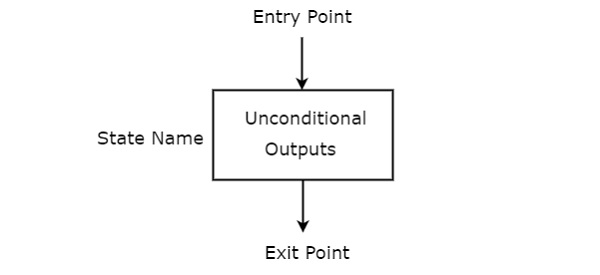
Tiene un punto de entrada y un punto de salida. El nombre del estado se coloca a la izquierda del cuadro de estado. Las salidas incondicionales correspondientes a ese estado se pueden colocar dentro del cuadro de estado.Moore Las salidas de la máquina de estado también se pueden colocar dentro del cuadro de estado.
Cuadro de decisión
El cuadro de decisión está representado en forma de diamante. lossymbol del cuadro de decisión se muestra en la siguiente figura.

Tiene un punto de entrada y dos caminos de salida. Las entradas o expresiones booleanas se pueden colocar dentro del cuadro de decisión, que se debe verificar si son verdaderas o falsas. Si la condición es verdadera, entonces preferirá path1. De lo contrario, preferirá path2.
Caja de salida condicional
El cuadro de salida condicional se representa en forma ovalada. lossymbol del cuadro de salida condicional se muestra en la siguiente figura.

También tiene un punto de entrada y un punto de salida similar al cuadro de estado. Las salidas condicionales se pueden colocar dentro del cuadro de estado. En general,MealyLas salidas de la máquina de estado se representan dentro del cuadro de salida condicional. Entonces, según el requisito, podemos usar los componentes anteriores correctamente para dibujar gráficos ASM.