Guía rápida

Los instrumentos que se utilizan para medir cualquier cantidad se conocen como instrumentos de medida. Este tutorial cubre principalmente loselectronic instruments, que son útiles para medir magnitudes o parámetros eléctricos.

A continuación se muestran los instrumentos electrónicos más utilizados.

• Voltmeter
• Ammeter
• Ohmmeter
• Multimeter

Ahora, analicemos brevemente estos instrumentos.

Voltímetro

Como el nombre sugiere, voltmeteres un instrumento de medición que mide el voltaje en dos puntos cualesquiera de un circuito eléctrico. Hay dos tipos de voltímetros: voltímetro de CC y voltímetro de CA.

El voltímetro de CC mide el voltaje de CC en dos puntos cualesquiera de un circuito eléctrico, mientras que el voltímetro de CA mide el voltaje de CA en dos puntos cualesquiera de un circuito eléctrico. Un ejemplo depractical DC voltmeter se muestra en la siguiente figura.

El voltímetro de CC que se muestra en la figura anterior es un $(0-100)V$ DC voltmeter. Por lo tanto, se puede utilizar para medir los voltajes de CC desde cero voltios hasta 10 voltios.

Amperímetro

Como el nombre sugiere, ammeteres un instrumento de medición que mide la corriente que fluye a través de dos puntos cualesquiera de un circuito eléctrico. Hay dos tipos de amperímetros: amperímetro de CC y amperímetro de CA.

El amperímetro de CC mide la corriente CC que fluye a través de dos puntos cualesquiera de un circuito eléctrico. Considerando que, el amperímetro de CA mide la corriente CA que fluye a través de dos puntos cualesquiera de un circuito eléctrico. Un ejemplo depractical AC ammeter se muestra en la siguiente figura -

El amperímetro de CA que se muestra en la figura anterior es un $(0-100)A \:$ AC ammeter. Por lo tanto, se puede utilizar para medir las corrientes de CA desde cero amperios hasta 100 amperios.

Ohmímetro

Ohmmeterse utiliza para medir el valor de la resistencia entre dos puntos cualesquiera de un circuito eléctrico. También se puede utilizar para encontrar el valor de una resistencia desconocida. Hay dos tipos de ohmímetros: ohmímetro en serie y ohmímetro en derivación.

En el ohmímetro de tipo serie, la resistencia cuyo valor se desconoce y que se va a medir debe conectarse en serie con el ohmímetro. Es útil para medirhigh values of resistances.

En el ohmímetro de tipo shunt, la resistencia cuyo valor se desconoce y que se va a medir debe conectarse en paralelo (shunt) con el ohmímetro. Es útil para medirlow values of resistances.

Un ejemplo de practical shunt ohmmeterse muestra en la figura anterior. El ohmímetro que se muestra en la figura anterior es un$(0-100)\Omega$ shunt ohmmeter. Por lo tanto, se puede utilizar para medir los valores de resistencia desde cero ohmios hasta 100 ohmios.

Multimetro

Multimeteres un instrumento electrónico que se utiliza para medir cantidades tales como voltaje, corriente y resistencia una a la vez. Se puede utilizar para medir voltajes CC y CA, corrientes CC y CA y resistencias de varios rangos. Un práctico multímetro se muestra en la siguiente figura:

Como se muestra en la figura, este multímetro se puede utilizar para medir varias resistencias altas, bajas resistencias, voltajes de CC, voltajes de CA, corrientes de CC y corrientes de CA. Las diferentes escalas y rango de valores para cada una de estas cantidades están marcadas en la figura anterior.

Los instrumentos que consideramos en este capítulo son de indicating type instruments, ya que los indicadores de estos instrumentos se desvían y apuntan a un valor particular. Discutiremos sobre estos instrumentos de medición electrónicos en detalle en capítulos posteriores.

Las características de los instrumentos de medición que son útiles para conocer el desempeño del instrumento y ayudar a medir cualquier cantidad o parámetro, se conocen como Performance Characteristics.

Tipos de características de rendimiento

Las características de rendimiento de los instrumentos se pueden clasificar en las siguientes two types.

• Características estáticas
• Características dinámicas

Ahora, analicemos estos dos tipos de características una por una.

Características estáticas

Las características de los instrumentos de medida de magnitudes o parámetros que do not varycon respecto al tiempo se denominan características estáticas. A veces, estas cantidades o parámetros pueden variar lentamente con respecto al tiempo. A continuación se muestra la lista destatic characteristics.

• Accuracy
• Precision
• Sensitivity
• Resolution
• Error estático

Ahora, analicemos estas características estáticas una por una.

Exactitud

La diferencia algebraica entre el valor indicado de un instrumento, $ A_ {i} $ y el valor verdadero, $ A_ {t} $ se conoce como accuracy. Matemáticamente, se puede representar como:

$$ Precisión = A_ {i} - A_ {t} $$

El término precisión significa cuánto el valor indicado de un instrumento, $ A_ {i} $ está más cerca del valor real, $ A_ {t} $.

Error estático

La diferencia entre el valor real, $ A_ {t} $ de la cantidad que no varía con respecto al tiempo y el valor indicado de un instrumento, $ A_ {i} $ se conoce como static error, $ e_ {s} $. Matemáticamente, se puede representar como:

$$ e_ {s} = A_ {t} - A_ {i} $$

El término error estático significa la inexactitud del instrumento. Si el error estático se representa en términos de porcentaje, entonces se llamapercentage of static error. Matemáticamente, se puede representar como:

$$ \% e_ {s} = \ frac {e_ {s}} {A_ {t}} \ veces 100 $$

Sustituya, el valor de $ e_ {s} $ en el lado derecho de la ecuación anterior -

$$ \% e_ {s} = \ frac {A_ {t} - A_ {i}} {A_ {t}} \ veces 100 $$

Dónde,

$ \% e_ {s} $ es el porcentaje de error estático.

Precisión

Si un instrumento indica el mismo valor repetidamente cuando se usa para medir la misma cantidad en las mismas circunstancias por cualquier número de veces, entonces podemos decir que el instrumento tiene un alto precision.

Sensibilidad

La relación de cambio en la salida, $ \ Delta A_ {out} $ de un instrumento para un cambio dado en la entrada, $ \ Delta A_ {in} $ que se va a medir se llama sensitivity, S. Matemáticamente se puede representar como -

$$ S = \ frac {\ Delta A_ {out}} {\ Delta A_ {in}} $$

El término sensibilidad significa el cambio más pequeño en la entrada medible que se requiere para que un instrumento responda.

• Si la curva de calibracin es linear, entonces la sensibilidad del instrumento será constante y será igual a la pendiente de la curva de calibración.

• Si la curva de calibracin es non-linear, entonces la sensibilidad del instrumento no será constante y variará con respecto a la entrada.

Resolución

Si la salida de un instrumento cambiará solo cuando hay un incremento específico de la entrada, entonces ese incremento de la entrada se llama Resolution. Eso significa que el instrumento es capaz de medir la entrada de manera efectiva, cuando hay una resolución de la entrada.

Características dinámicas

Las características de los instrumentos, que se utilizan para medir las cantidades o parámetros que varían muy rápidamente con respecto al tiempo, se denominan características dinámicas. A continuación se muestra la lista dedynamic characteristics.

• Rapidez de respuesta
• Error dinámico
• Fidelity
• Lag

Ahora, analicemos estas características dinámicas una por una.

Rapidez de respuesta

La velocidad a la que responde el instrumento siempre que hay algún cambio en la cantidad a medir se denomina speed of response. Indica qué tan rápido es el instrumento.

Retraso

La cantidad de retraso presente en la respuesta de un instrumento siempre que haya un cambio en la cantidad a medir se llama retraso de medición. También se llama simplementelag.

Error dinámico

La diferencia entre el valor real, $ A_ {t} $ de la cantidad que varía con respecto al tiempo y el valor indicado de un instrumento, $ A_ {i} $ se conoce como error dinámico, $ e_ {d} $.

Fidelidad

El grado en que un instrumento indica cambios en la cantidad medida sin ningún error dinámico se conoce como Fidelity

Los errores que ocurren durante la medición se conocen como measurement errors. En este capítulo, analicemos los tipos de errores de medición.

Tipos de errores de medición

Podemos clasificar los errores de medición en los siguientes tres tipos.

• Errores graves
• Errores aleatorios
• Errores sistemáticos

Ahora, analicemos estos tres tipos de errores de medición uno por uno.

Errores graves

Los errores, que ocurren debido a la falta de experiencia del observador al tomar los valores de medición, se conocen como gross errors. Los valores de los errores brutos variarán de un observador a otro. A veces, los errores graves también pueden ocurrir debido a una selección incorrecta del instrumento. Podemos minimizar los errores graves siguiendo estos dos pasos.

• Elija el instrumento más adecuado, en función del rango de valores a medir.
• Anote las lecturas con cuidado

Errores sistemáticos

Si el instrumento produce un error, el cual es de una desviación uniforme constante durante su operación se conoce como systematic error. Los errores sistemáticos ocurren debido a las características de los materiales utilizados en el instrumento.

Types of Systematic Errors

Los errores sistemáticos se pueden clasificar en los siguientes three types.

• Instrumental Errors - Este tipo de errores se producen por deficiencias de instrumentos y efectos de carga.

• Environmental Errors - Este tipo de errores se producen debido a cambios en el entorno, como cambios de temperatura, presión, etc.

• observational Errors - Este tipo de errores ocurren debido a que el observador toma las lecturas del medidor. Parallax errors pertenecen a este tipo de errores.

Errores aleatorios

Los errores, que ocurren debido a fuentes desconocidas durante el tiempo de medición, se conocen como random errors. Por tanto, no es posible eliminar o minimizar estos errores. Pero, si queremos obtener los valores de medición más precisos sin ningún error aleatorio, entonces es posible siguiendo estos dos pasos.

• Step1 - Realizar más lecturas por diferentes observadores.

• Step2 - Realizar análisis estadístico de las lecturas obtenidas en el Paso 1.

A continuación se muestran los parámetros que se utilizan en el análisis estadístico.

• Mean
• Median
• Variance
• Deviation
• Desviación Estándar

Ahora, hablemos de estos statistical parameters.

Media

Deje que $ x_ {1}, x_ {2}, x_ {3}, ...., x_ {N} $ son las lecturas de $ N $ de una medida en particular. La media oaverage value de estas lecturas se pueden calcular utilizando la siguiente fórmula.

$$ m = \ frac {x_ {1} + x_ {2} + x_ {3} + .... + x_ {N}} {N} $$

Donde, $ m $ es el valor medio o promedio.

Si el número de lecturas de una medida en particular es mayor, entonces el valor medio o promedio será aproximadamente igual a true value

Mediana

Si el número de lecturas de una medida en particular es mayor, entonces es difícil calcular el valor medio o promedio. Aquí, calcula elmedian value y será aproximadamente igual al valor medio.

Para calcular el valor mediano, primero tenemos que organizar las lecturas de una medida particular en un ascending order. Podemos calcular el valor mediano usando la siguiente fórmula, cuando el número de lecturas es unodd number.

$$ M = x _ {\ left (\ frac {N + 1} {2} \ right)} $$

Podemos calcular el valor mediano usando la siguiente fórmula, cuando el número de lecturas es un even number.

$$ M = \ frac {x _ {\ left (N / 2 \ right)} + x_ \ left (\ left [N / 2 \ right] +1 \ right)} {2} $$

Desviación de la media

La diferencia entre la lectura de una medición en particular y el valor medio se conoce como desviación de la media . En resumen, se llama desviación . Matemáticamente, se puede representar como

$$ d_ {i} = x_ {i} -m $$

Dónde,

$ d_ {i} $ es la desviación de $ i ^ {th} $ lectura de la media.

$ x_ {i} $ es el valor de $ i ^ {th} $ lectura.

$ m $ es el valor medio o promedio.

Desviación Estándar

La raíz cuadrada media de la desviación se llama standard deviation. Matemáticamente, se puede representar como

$$ \ sigma = \ sqrt {\ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + { d_ {N}} ^ {2}} {N}} $$

La fórmula anterior es válida si el número de lecturas, N es mayor o igual que 20. Podemos usar la siguiente fórmula para la desviación estándar, cuando el número de lecturas, N es menor que 20.

$$ \ sigma = \ sqrt {\ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + { d_ {N}} ^ {2}} {N-1}} $$

Dónde,

$ \ sigma $ es la desviación estándar

$ d_ {1}, d_ {2}, d_ {3},…, d_ {N} $ son las desviaciones de la primera, segunda, tercera,…, $ N ^ {th} $ lecturas de la media respectivamente.

Note - Si el valor de la desviación estándar es pequeño, habrá más precisión en los valores de lectura de la medición.

Diferencia

El cuadrado de la desviación estándar se llama variance. Matemáticamente, se puede representar como

$$ V = \ sigma ^ {2} $$

Dónde,

$ V $ es la variación

$ \ sigma $ es la desviación estándar

El cuadrado medio de la desviación también se llama variance. Matemáticamente, se puede representar como

$$ V = \ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + {d_ {N} } ^ {2}} {N} $$

La fórmula anterior es válida si el número de lecturas, N es mayor o igual que 20. Podemos usar la siguiente fórmula para la varianza cuando el número de lecturas, N es menor que 20.

$$ V = \ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + {d_ {N} } ^ {2}} {N-1} $$

Dónde,

$ V $ es la variación

$ d_ {1}, d_ {2}, d_ {3},…, d_ {N} $ son las desviaciones de la primera, segunda, tercera,…, $ N ^ {th} $ lecturas de la media respectivamente.

Entonces, con la ayuda de parámetros estadísticos, podemos analizar las lecturas de una medida en particular. De esta forma, obtendremos valores de medición más precisos.

Los instrumentos utilizados para medir cualquier cantidad se conocen como measuring instruments. Si los instrumentos pueden medir las cantidades eléctricas básicas, como el voltaje y la corriente, se conocen comobasic measuring instruments.

Tipos de instrumentos de medida básicos

Podemos clasificar los instrumentos de medición básicos en los dos tipos siguientes.

• Voltmeters
• Ammeters

Analicemos brevemente estos dos instrumentos de medición básicos.

Voltímetros

Como el nombre sugiere, voltmeteres un instrumento de medición que mide el voltaje en dos puntos cualesquiera de un circuito eléctrico. Las unidades de voltaje son voltios y el instrumento de medida es metro. Por lo tanto, la palabra "voltímetro" se obtiene combinando las dos palabras“volt” y “meter”.

Podemos clasificar los voltímetros en los siguientes two types basado en el tipo de voltaje que puede medir.

• Voltímetros DC
• Voltímetros CA

Voltímetro DC

Como sugiere el nombre, el voltímetro de CC mide el DC voltagea través de dos puntos cualesquiera de un circuito eléctrico. En la siguiente figura se muestra un práctico voltímetro de CC.

El voltímetro de CC que se muestra en la figura es un $(0-10)V$ DC voltmeter. Por lo tanto, se puede utilizar para medir los voltajes de CC desde cero voltios hasta 10 voltios.

Voltímetro AC

Como sugiere el nombre, el voltímetro de CA mide la AC voltagea través de dos puntos cualesquiera de un circuito eléctrico. En la siguiente figura se muestra un práctico voltímetro de CA.

El voltímetro de CA que se muestra en la figura anterior es un $(0-250)V$ AC voltmeter. Por lo tanto, se puede utilizar para medir los voltajes de CA desde cero voltios hasta 250 voltios.

Amperímetros

Como el nombre sugiere, ammeteres un instrumento de medición que mide la corriente que fluye a través de dos puntos cualesquiera de un circuito eléctrico. La unidad de corriente es el amperio y el instrumento de medida es el metro. La palabra "amperímetro" se obtiene combinando“am” de amperio con “meter”.

Podemos clasificar los amperímetros en los siguientes two types basado en el tipo de corriente que puede medir.

• Amperímetros DC
• Amperímetros CA

Amperímetro DC

Como sugiere el nombre, el amperímetro de CC mide el DC currentque fluye a través de dos puntos cualesquiera de un circuito eléctrico. En la figura se muestra un práctico amperímetro de CC.

El amperímetro de CC que se muestra en la figura anterior es un $(0-50)A$ DC ammeter. Por lo tanto, se puede utilizar para medir las corrientes de CC desde cero amperios hasta 50 amperios.

Amperímetro de CA

Como sugiere el nombre, el amperímetro de CA mide el AC currentque fluye a través de dos puntos cualesquiera de un circuito eléctrico. En la siguiente figura se muestra un práctico amperímetro de CA.

El amperímetro de CA que se muestra en la figura anterior es un $(0-100)A$ AC ammeter. Por lo tanto, se puede utilizar para medir las corrientes de CA desde cero amperios hasta 100 amperios.

Discutiremos sobre varios voltímetros y amperímetros en detalle en los siguientes capítulos

El voltímetro de CC es un instrumento de medición que se utiliza para medir el voltaje de CC en dos puntos cualesquiera del circuito eléctrico. Si colocamos una resistencia en serie con el galvanómetro de bobina móvil de imán permanente (PMMC), entonces toda la combinación actúa comoDC voltmeter.

La resistencia en serie, que se utiliza en el voltímetro de CC, también se denomina resistencia de multiplicador en serie o simplemente multiplicador. Básicamente, limita la cantidad de corriente que fluye a través del galvanómetro para evitar que la corriente del medidor exceda el valor de deflexión de escala completa. loscircuit diagram del voltímetro de CC se muestra en la siguiente figura.

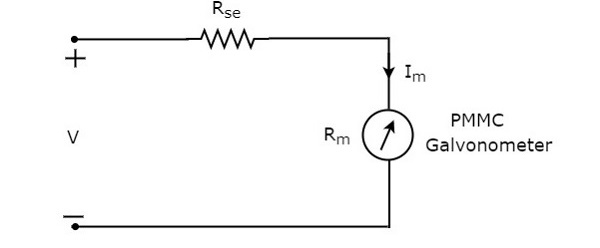
Tenemos que colocar este voltímetro de CC en los dos puntos de un circuito eléctrico, donde se medirá el voltaje de CC.

Aplicar KVL alrededor del bucle del circuito anterior.

$ V-I_ {m} R_ {se} -I_ {m} R_ {m} = 0 $ (Ecuación 1)

$$ \ Rightarrow V-I_ {m} R_ {m} = I_ {m} R_ {se} $$

$$ \ Rightarrow R_ {se} = \ frac {V-I_ {m} R_ {m}} {I_ {m}} $$

$ \ Rightarrow R_ {se} = \ frac {V} {I_ {m}} - R_ {m} $ (Ecuación 2)

Dónde,

$ R_ {se} $ es la resistencia del multiplicador de la serie

$ V $ es el voltaje de CC de rango completo que se va a medir

$ I_ {m} $ es la corriente de deflexión de escala completa

$ R_ {m} $ es la resistencia interna del galvanómetro

La relación entre el voltaje de CC de rango completo que se va a medir, $ V $ y la caída de voltaje de CC en el galvanómetro, $ V_ {m} $ se conoce como multiplying factor, m. Matemáticamente, se puede representar como

$ m = \ frac {V} {V_ {m}} $ (Ecuación 3)

De la Ecuación 1, obtendremos la siguiente ecuación para full range DC voltage que se va a medir, $ V $.

$ V = I_ {m} R_ {se} + I_ {m} R_ {m} $ (Ecuación 4)

los DC voltage dropa lo largo del galvanómetro, $ V_ {m} $ es el producto de la corriente de deflexión de escala completa, $ I_ {m} $ y la resistencia interna del galvanómetro, $ R_ {m} $. Matemáticamente, se puede escribir como

$ V_ {m} = I_ {m} R_ {m} $ (Ecuación 5)

Substitute, Ecuación 4 y Ecuación 5 en Ecuación 3.

$$ m = \ frac {I_ {m} R_ {se} + I_ {m} R_ {m}} {I_ {m} R_ {m}} $$

$ \ Flecha derecha m = \ frac {R_ {se}} {R_ {m}} + 1 $

$ \ Flecha derecha m-1 = \ frac {R_ {se}} {R_ {m}} $

$ R_ {se} = R_ {m} \ left (m-1 \ right) $ (Ecuación 6)

Podemos encontrar el value of series multiplier resistance utilizando la Ecuación 2 o la Ecuación 6 según los datos disponibles.

Voltímetro de CC de rango múltiple

En la sección anterior, habíamos discutido el voltímetro de CC, que se obtiene colocando una resistencia multiplicadora en serie con el galvanómetro PMMC. Este voltímetro de CC se puede utilizar para medir unparticular range de tensiones CC.

Si queremos utilizar el voltímetro de CC para medir los voltajes de CC de multiple ranges, entonces tenemos que usar múltiples resistencias multiplicadoras paralelas en lugar de una sola resistencia multiplicadora y toda esta combinación de resistencias está en serie con el galvanómetro PMMC. loscircuit diagram del voltímetro de CC de rango múltiple se muestra en la siguiente figura.

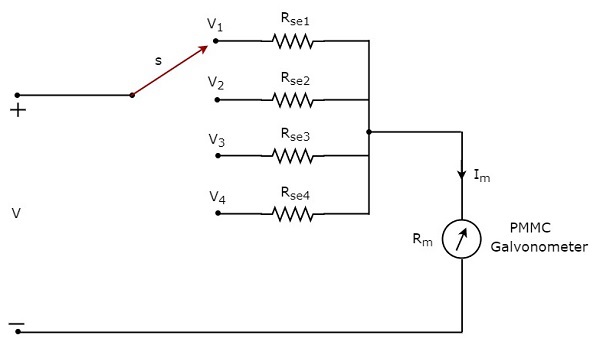
Tenemos que colocar esto multi range DC voltmetera través de los dos puntos de un circuito eléctrico, donde se medirá el voltaje de CC del rango requerido. Podemos elegir el rango deseado de voltajes conectando los interruptores a la respectiva resistencia multiplicadora.

Sea, $ m_ {1}, m_ {2}, m_ {2} $ y $ m_ {4} $ son los multiplying factorsdel voltímetro de CC cuando consideramos que los voltajes de CC de rango completo se miden como $ V_ {1}, V_ {2}, V_ {3} $ y $ V_ {4} $ respectivamente. A continuación se muestran las fórmulas correspondientes a cada factor multiplicador.

$$ m_ {1} = \ frac {V_ {1}} {V_ {m}} $$

$$ m_ {2} = \ frac {V_ {2}} {V_ {m}} $$

$$ m_ {3} = \ frac {V_ {3}} {V_ {m}} $$

$$ m_ {4} = \ frac {V_ {4}} {V_ {m}} $$

En el circuito anterior, hay cuatro series multiplier resistors, $ R_ {se1}, R_ {se2}, R_ {se3} $ y $ R_ {se4} $. A continuación se muestran las fórmulas correspondientes a estas cuatro resistencias.

$$ R_ {se1} = R_ {m} \ left (m_ {1} -1 \ right) $$

$$ R_ {se2} = R_ {m} \ left (m_ {2} -1 \ right) $$

$$ R_ {se3} = R_ {m} \ left (m_ {3} -1 \ right) $$

$$ R_ {se4} = R_ {m} \ left (m_ {4} -1 \ right) $$

Entonces, podemos encontrar los valores de resistencia de cada resistencia multiplicadora de serie usando las fórmulas anteriores.

El instrumento, que se utiliza para medir el voltaje de CA en dos puntos cualesquiera del circuito eléctrico se llama AC voltmeter. Si el voltímetro de CA consta de un rectificador, entonces se dice que es un voltímetro de CA basado en un rectificador.

El voltímetro de CC mide solo voltajes de CC. Si queremos usarlo para medir voltajes AC, entonces tenemos que seguir estos dos pasos.

• Step1 - Convierta la señal de voltaje CA en una señal de voltaje CC utilizando un rectificador.

• Step2 - Mida la CC o el valor medio de la señal de salida del rectificador.

Obtenemos Rectifier based AC voltmeter, simplemente incluyendo el circuito rectificador al voltímetro de CC básico. Este capítulo trata sobre voltímetros de CA basados ​​en rectificadores.

Tipos de voltímetros de CA basados ​​en rectificador

Los siguientes son los two types de voltímetros de CA basados ​​en rectificador.

• Voltímetro de CA con rectificador de media onda
• Voltímetro de CA con rectificador de onda completa

Ahora, hablemos sobre estos dos voltímetros de CA uno por uno.

Voltímetro de CA con rectificador de media onda

Si se conecta un rectificador de media onda por delante del voltímetro de CC, entonces toda la combinación se llama voltímetro de CA utilizando un rectificador de media onda. losblock diagram del voltímetro de CA con rectificador de media onda se muestra en la siguiente figura.

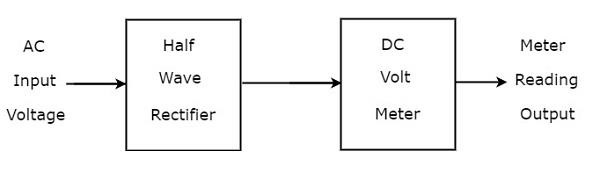
El diagrama de bloques anterior consta de dos bloques: rectificador de media onda y voltímetro de CC. Obtendremos el diagrama de circuito correspondiente, simplemente reemplazando cada bloque con los componentes respectivos en el diagrama de bloques anterior. Entonces elcircuit diagram del voltímetro de CA utilizando un rectificador de media onda se verá como se muestra en la siguiente figura.

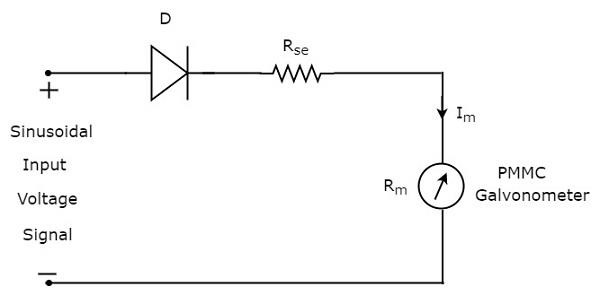
los rms value de la señal de voltaje de entrada sinusoidal (CA) es

$$ V_ {rms} = \ frac {V_ {m}} {\ sqrt {2}} $$

$$ \ Rightarrow V_ {m} = \ sqrt {2} V_ {rms} $$

$$ \ Rightarrow V_ {m} = 1.414 V_ {rms} $$

Dónde,

$ V_ {m} $ es el valor máximo de la señal de voltaje de entrada sinusoidal (CA).

los DC o el valor medio de la señal de salida del rectificador de media onda es

$$ V_ {dc} = \ frac {V_ {m}} {\ pi} $$

Substitute, el valor de $ V_ {m} $ en la ecuación anterior.

$$ V_ {dc} = \ frac {1.414 V_ {rms}} {\ pi} $$

$$ V_ {dc} = 0.45 V_ {rms} $$

Por lo tanto, el voltímetro de CA produce un voltaje de salida, que es igual a 0.45 multiplicado por el valor eficaz de la señal de tensión de entrada sinusoidal (CA)

Voltímetro de CA con rectificador de onda completa

Si se conecta un rectificador de onda completa antes del voltímetro de CC, entonces toda la combinación se llama voltímetro de CA que usa un rectificador de onda completa. losblock diagram del voltímetro de CA con rectificador de onda completa se muestra en la siguiente figura

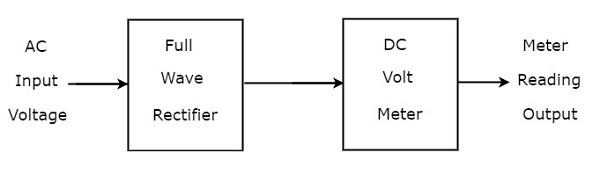
El diagrama de bloques anterior consta de dos bloques: rectificador de onda completa y voltímetro de CC. Obtendremos el diagrama de circuito correspondiente simplemente reemplazando cada bloque con los componentes respectivos en el diagrama de bloques anterior.

Entonces el circuit diagram del voltímetro de CA con rectificador de onda completa se verá como se muestra en la siguiente figura.

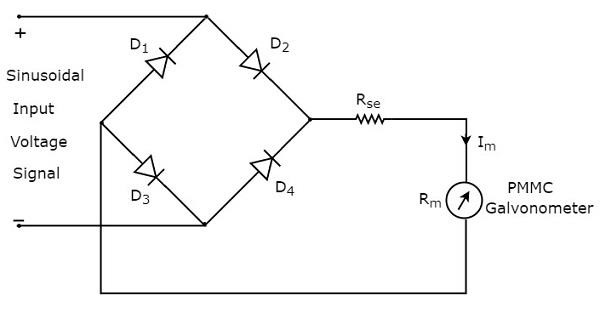
los rms value de la señal de voltaje de entrada sinusoidal (CA) es

$$ V_ {rms} = \ frac {V_ {m}} {\ sqrt {2}} $$

$$ \ Flecha derecha V_ {m} = \ sqrt {2} \: V_ {rms} $$

$$ \ Rightarrow V_ {m} = 1.414 V_ {rms} $$

Dónde,

$ V_ {m} $ es el valor máximo de la señal de voltaje de entrada sinusoidal (CA).

los DC o el valor medio de la señal de salida del rectificador de onda completa es

$$ V_ {dc} = \ frac {2V_ {m}} {\ pi} $$

Substitute, el valor de $ V_ {m} $ en la ecuación anterior

$$ V_ {dc} = \ frac {2 \ times 1.414 \: V_ {rms}} {\ pi} $$

$$ V_ {dc} = 0.9 \: V_ {rms} $$

Por lo tanto, el voltímetro de CA produce un voltaje de salida, que es igual a 0.9 multiplicado por el valor eficaz de la señal de tensión de entrada sinusoidal (CA).

En el capítulo anterior, discutimos acerca de los voltímetros de CA basados ​​en rectificadores. Este capítulo cubre los siguientes dos tipos de voltímetros de CA.

• Voltímetro de CA de respuesta máxima
• Voltímetro de CA de respuesta eficaz verdadero

Ahora, analicemos estos dos tipos de voltímetros de CA uno por uno.

Voltímetro de CA de respuesta máxima

Como sugiere el nombre, el voltímetro de CA de respuesta máxima responde a peak valuesde la señal de voltaje CA. Eso significa que este voltímetro mide los valores máximos de los voltajes de CA. loscircuit diagram del voltímetro de CA de respuesta máxima se muestra a continuación:

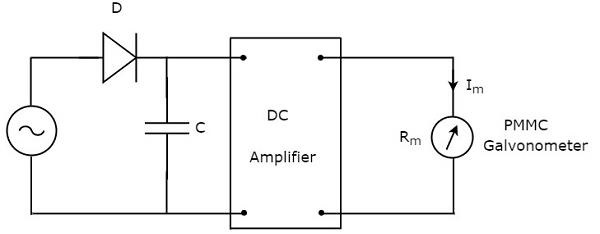
El circuito anterior consta de un diodo, condensador, amplificador de CC y galvanómetro PMMC. El diodo presente en el circuito anterior se utiliza para fines de rectificación. Entonces, el diodo convierte la señal de voltaje CA en una señal de voltaje CC. El condensador se carga al valor máximo de esta señal de voltaje de CC.

Durante positive half cyclede la señal de voltaje de CA, el diodo conduce y el condensador se carga al valor máximo de la señal de voltaje de CA. Cuando el valor de la señal de voltaje de CA es menor que este valor, el diodo tendrá polarización inversa.

Por lo tanto, el condensador se descargará a través de la resistencia del amplificador de CC hasta el próximo semiciclo positivo de la señal de voltaje de CA. Cuando el valor de la señal de voltaje de CA es mayor que el voltaje del capacitor, el diodo conduce y el proceso se repetirá.

Debemos seleccionar los valores de los componentes de tal manera que el capacitor se cargue rápidamente y se descargue lentamente. Como resultado, el medidor siempre responde a este voltaje del capacitor, es decir, elpeak value of AC voltage.

Voltímetro de CA de respuesta eficaz verdadero

Como sugiere el nombre, el verdadero voltímetro de CA de respuesta eficaz responde a los valores eficaces verdaderos de la señal de voltaje de CA. Este voltímetro mide valores RMS de voltajes de CA. loscircuit diagram del voltímetro de CA de respuesta eficaz verdadero se muestra en la siguiente figura.

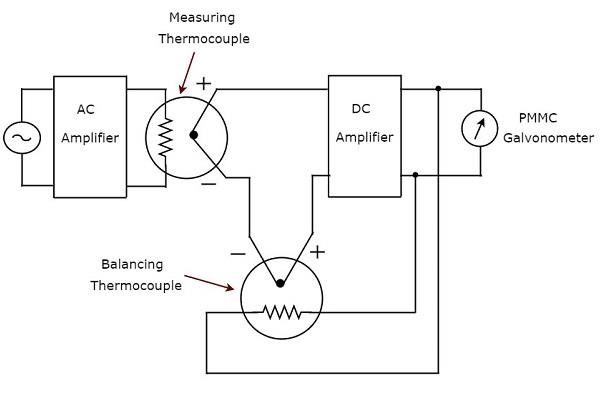
El circuito anterior consta de un amplificador de CA, dos termopares, un amplificador de CC y un galvanómetro PMMC. El amplificador de CA amplifica la señal de voltaje de CA. Dos termopares que se utilizan en el circuito anterior son un termopar de medición y un termopar de equilibrio.Measuring thermocouple produce un voltaje de salida, que es proporcional al valor RMS de la señal de voltaje de CA.

Cualquier termopar convierte un cuadrado de una cantidad de entrada en una cantidad normal. Esto significa que existe una relación no lineal entre la salida y la entrada de un termopar. El efecto del comportamiento no lineal de un termopar puede despreciarse utilizando otro termopar en el circuito de retroalimentación. El termopar que se utiliza para este propósito en el circuito anterior se conoce comobalancing thermocouple.

Los dos termopares, a saber, el termopar de medición y el termopar de equilibrio juntos forman una novia en la entrada del amplificador de CC. Como resultado, el medidor siempre responde a latrue RMS value de la señal de voltaje CA.

La corriente es la tasa de flujo de la carga eléctrica. Si esta carga eléctrica fluye solo en una dirección, entonces la corriente resultante se llama Corriente continua (CC). El instrumento, que se utiliza para medir la corriente continua llamadoDC ammeter.

Si colocamos una resistencia en paralelo con el galvanómetro de bobina móvil de imán permanente (PMMC), entonces toda la combinación actúa como amperímetro de CC. La resistencia paralela, que se utiliza en el amperímetro de CC, también se llama resistencia en derivación o simplemente,shunt. El valor de esta resistencia debe considerarse pequeño para medir la corriente CC de gran valor.

los circuit diagram del amperímetro de CC se muestra en la siguiente figura.

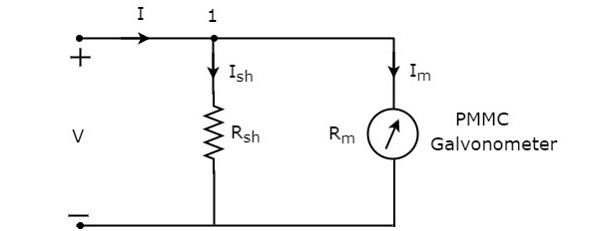
Tenemos que colocar esto DC ammeteren serie con la rama de un circuito eléctrico, donde se medirá la corriente continua. El voltaje entre los elementos, que están conectados en paralelo, es el mismo. Entonces, el voltaje a través de la resistencia de derivación, $ R_ {sh} $ y el voltaje a través de la resistencia del galvanómetro, $ R_ {m} $ es el mismo, ya que esos dos elementos están conectados en paralelo en el circuito anterior.Mathematically, se puede escribir como

$$ I_ {sh} R_ {sh} = I_ {m} R_ {m} $$

$ \ Flecha derecha R_ {sh} = \ frac {I_ {m} R_ {m}} {I_ {sh}} $ (Ecuación 1)

los KCL equation en el nodo 1 es

$$ - I + I_ {sh} + I_ {m} = 0 $$

$$ \ Flecha derecha I_ {sh} = I-I_ {m} $$

Substitute el valor de $ I_ {sh} $ en la Ecuación 1.

$ R_ {sh} = \ frac {I_ {m} R_ {m}} {I-I_ {m}} $ (Ecuación 2)

Tome, $ I_ {m} $ como común en el término denominador, que está presente en el lado derecho de la Ecuación 2

$$ R_ {sh} = \ frac {I_ {m} R_ {m}} {I_ {m} (\ frac {1} {I_ {m}} - 1)} $$

$ \ Flecha derecha R_ {sh} = \ frac {R_ {m}} {\ frac {I} {I_ {m}} - 1} $ (Ecuación 3)

Dónde,

$ R_ {sh} $ es la resistencia de derivación

$ R_ {m} $ es la resistencia interna del galvanómetro

$ I $ es la corriente continua total que se va a medir

$ I_ {m} $ es la corriente de deflexión de escala completa

La relación de la corriente continua total que se va a medir, $ I $ y la corriente de deflexión de escala completa del galvanómetro, $ I_ {m} $ se conoce como multiplying factor, m. Matemáticamente, se puede representar como

$ m = \ frac {I} {I_ {m}} $ (Ecuación 4)

$ R_ {sh} = \ frac {R_ {m}} {m-1} $ (Ecuación 5)

Podemos encontrar el value of shunt resistance utilizando la Ecuación 2 o la Ecuación 5 según los datos disponibles.

Amperímetro de CC de rango múltiple

En la sección anterior, discutimos sobre el amperímetro de CC que se obtiene colocando una resistencia en paralelo con el galvanómetro PMMC. Este amperímetro de CC se puede utilizar para medir unparticular range de Corrientes Directas.

Si queremos utilizar el amperímetro de CC para medir las corrientes directas de multiple ranges, entonces tenemos que usar múltiples resistencias en paralelo en lugar de una resistencia única y toda esta combinación de resistencias está en paralelo al galvanómetro PMMC. loscircuit diagram del amperímetro de CC de rango múltiple se muestra en la siguiente figura.

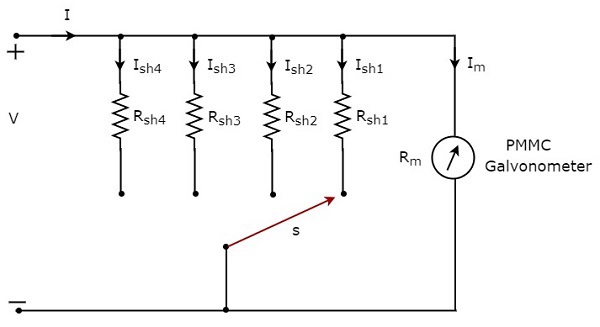
Coloque este amperímetro de CC de rango múltiple en serie con la rama de un circuito eléctrico, donde se medirá la corriente continua del rango requerido. El rango de corrientes deseado se elige conectando el interruptor, sa la respectiva resistencia de derivación.

Sea, $ m_ {1}, m_ {2}, m_ {3} $ y $ m_ {4} $ son los multiplying factorsdel amperímetro de CC cuando consideramos que las corrientes directas totales se miden como $ I_ {1}, I_ {2}, I_ {3} $ y $ I_ {4} $ respectivamente. A continuación se muestran las fórmulas correspondientes a cada factor multiplicador.

$$ m_ {1} = \ frac {I_ {1}} {I_ {m}} $$

$$ m_ {2} = \ frac {I_ {2}} {I_ {m}} $$

$$ m_ {3} = \ frac {I_ {3}} {I_ {m}} $$

$$ m_ {4} = \ frac {I_ {4}} {I_ {m}} $$

En el circuito anterior, hay cuatro shunt resistors, $ R_ {sh1}, R_ {sh2}, R_ {sh2} $ y $ R_ {sh4} $. A continuación se muestran las fórmulas correspondientes a estas cuatro resistencias.

$$ R_ {sh1} = \ frac {R_ {m}} {m_ {1} -1} $$

$$ R_ {sh2} = \ frac {R_ {m}} {m_ {2} -1} $$

$$ R_ {sh3} = \ frac {R_ {m}} {m_ {3} -1} $$

$$ R_ {sh4} = \ frac {R_ {m}} {m_ {4} -1} $$

Las fórmulas anteriores nos ayudarán a encontrar los valores de resistencia de cada resistencia en derivación.

La corriente es la tasa de flujo de la carga eléctrica. Si la dirección de esta carga eléctrica cambia regularmente, entonces la corriente resultante se llamaAlternating Current (AC).

El instrumento, que se utiliza para medir la corriente alterna que fluye a través de cualquier rama del circuito eléctrico se llama AC ammeter.

Example - Amperímetro AC tipo termopar.

Ahora, hablemos sobre el amperímetro de CA tipo termopar.

Amperímetro de CA tipo termopar

Si se conecta un termopar antes del galvanómetro PMMC, entonces toda esa combinación se denomina amperímetro de CA de tipo termopar. losblock diagram del amperímetro de CA tipo termopar se muestra en la siguiente figura.

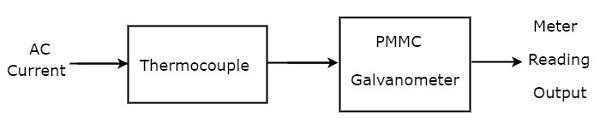
El diagrama de bloques anterior consta principalmente de dos bloques: un termopar y un galvanómetro PMMC. Obtendremos el diagrama de circuito correspondiente, simplemente reemplazando cada bloque con los componentes respectivos en el diagrama de bloques anterior. Entonces elcircuit diagram del amperímetro de CA de tipo termopar se verá como se muestra en la siguiente figura.

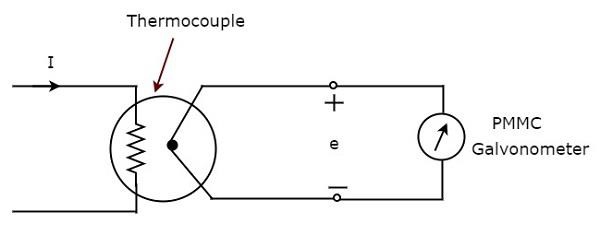
El termopar genera un EMF, $ e $, siempre que la corriente alterna, I fluya a través del elemento calefactor. Este EMF, $ e $ es directamente proporcional al valor rms de la corriente, I que fluye a través del elemento calefactor. Entonces, tenemos que calibrar la escala del instrumento PMMC para leerrms values of current.

Entonces, con este capítulo hemos completado todos los instrumentos de medición básicos como voltímetros de CC, voltímetros de CA, amperímetros de CC y amperímetros de CA. En el próximo capítulo, analicemos sobre los medidores o instrumentos de medición, que miden el valor de resistencia.

El instrumento, que se utiliza para medir el valor de la resistencia entre dos puntos cualesquiera en un circuito eléctrico se llama ohmmeter. También se puede usar para encontrar el valor de una resistencia desconocida. Las unidades de resistencia son ohmios y el instrumento de medida es metro. Entonces, la palabra "ohmímetro" se obtiene combinando las palabras“ohm” y “meter”.

Tipos de ohmímetros

Los siguientes son los two types de ohmímetros.

• Ohmímetro serie
• Ohmímetro de derivación

Ahora, analicemos estos dos tipos de ohmímetros uno por uno.

Ohmímetro serie

Si el valor de la resistencia es desconocido y tiene que medirse colocándolo en serie con el ohmímetro, entonces ese ohmímetro se llama ohmímetro en serie. loscircuit diagram del ohmímetro de la serie se muestra en la siguiente figura.

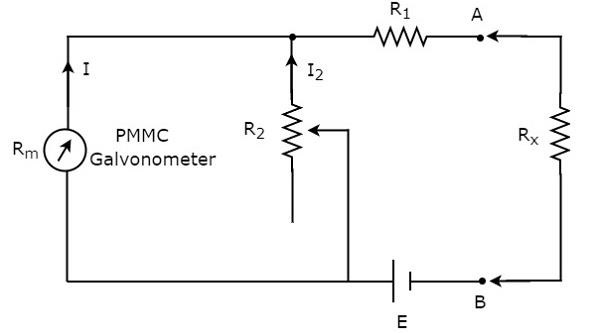
La parte del circuito, que está al lado izquierdo de los terminales A y B es series ohmmeter. Entonces, podemos medir el valor de la resistencia desconocida colocándolo en el lado derecho de las terminales A y B. Ahora, analicemos sobre elcalibration scale del ohmímetro de serie.

• Si $ R_ {x} = 0 \: \ Omega $, entonces las terminales A y B se cortocircuitarán entre sí. Entonces, la corriente del medidor se divide entre las resistencias, $ R_ {1} $ y $ R_ {2} $. Ahora, varíe el valor de la resistencia, $ R_ {2} $ de tal manera que toda la corriente del medidor fluya a través de la resistencia, $ R_ {1} $ solamente. En este caso, el medidor muestra llenoscale deflection current. Por lo tanto, esta corriente de deflexión de escala completa del medidor se puede representar como $ 0 \: \ Omega $.

• Si $ R_ {x} = \ infty \: \ Omega $, entonces las terminales A y B estarán en circuito abierto entre sí. Entonces, no fluye corriente a través del resistor $ R_ {1} $. En este caso, el medidor muestra una corriente de deflexión nula. Por lo tanto, esta desviación nula del medidor se puede representar como $ \ infty \ Omega $.

• De esta manera, al considerar diferentes valores de $ R_ {x} $, el medidor muestra diferentes deflexiones. Entonces, en consecuencia, podemos representar esas deflexiones con el valor de resistencia correspondiente.

El ohmímetro de la serie consta de una escala de calibración. Tiene las indicaciones de 0 $ \ Omega $ y $ \ infty \: \ Omega $ en los puntos finales de la mano derecha e izquierda de la escala, respectivamente. El ohmímetro de serie es útil para medirhigh values of resistances.

Ohmímetro de derivación

Si se desconoce el valor de la resistencia y se debe medir colocándolo en paralelo (derivación) con el ohmímetro, entonces ese ohmímetro se llama ohmímetro de derivación. loscircuit diagram del ohmímetro de derivación se muestra en la siguiente figura.

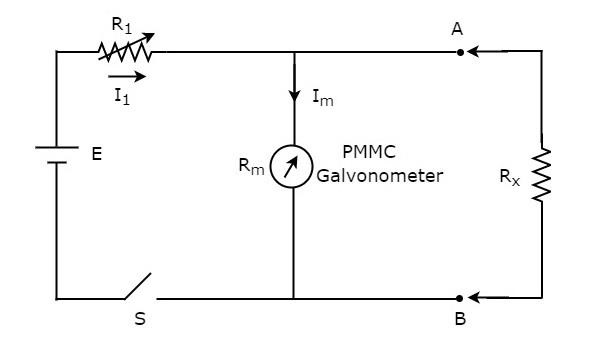
La parte del circuito, que está al lado izquierdo de los terminales A y B es shunt ohmmeter. Entonces, podemos medir el valor de la resistencia desconocida colocándolo en el lado derecho de las terminales A y B.

Ahora, hablemos sobre el calibration scaledel ohmímetro de derivación. Cierre el interruptor S del circuito anterior mientras esté en uso.

• Si $ R_ {x} = 0 \: \ Omega $, entonces las terminales A y B se cortocircuitarán entre sí. Debido a esto, toda la corriente $ I_ {1} $ fluye a través de las terminales A y B. En este caso, no fluye corriente a través del galvanómetro PMMC. Por lo tanto, lanull deflection del galvanómetro PMMC se puede representar como $ 0 \: \ Omega $.

• Si $ R_ {x} = \ infty \: \ Omega $, entonces las terminales A y B estarán en circuito abierto entre sí. Entonces, no fluye corriente a través de las terminales A y B. En este caso, toda la corriente, $ I_ {1} $ fluye a través del galvanómetro PMMC. Si es necesario, varíe (ajuste) el valor de la resistencia, $ R_ {1} $ hasta que el galvanómetro PMMC muestre la corriente de deflexión de escala completa. Por lo tanto, estefull scale deflection La corriente del galvanómetro PMMC se puede representar como $ \ infty \: \ Omega $

• De esta manera, al considerar diferentes valores de $ R_ {x} $, el medidor muestra diferentes deflexiones. Entonces, en consecuencia, podemos representar esas deflexiones con los valores de resistencia correspondientes.

El ohmímetro de derivación consta de una escala de calibración. Tiene las indicaciones de $ 0 \: \ Omega $ y $ \ infty \: \ Omega $ en los puntos finales de la mano izquierda y derecha de la escala, respectivamente.

El ohmímetro de derivación es útil para medir low values of resistances. Por lo tanto, podemos usar un ohmímetro en serie o un ohmímetro en derivación en función de los valores de las resistencias que se van a medir, es decir, alta o baja.

En capítulos anteriores, discutimos sobre voltímetros, amperímetros y ohmímetros. Estos instrumentos de medición se utilizan para medir voltaje, corriente y resistencia respectivamente. Eso significa que tenemosseparate measuring instruments para medir voltaje, corriente y resistencia.

Supongamos que, si se puede usar un solo instrumento de medición para medir las cantidades como voltaje, corriente y resistencia una a la vez, entonces se dice que es multimeter. Tiene el nombre de multímetro, ya que puede medir múltiples cantidades eléctricas una a la vez.

Mediciones con multímetro

Multimeteres un instrumento utilizado para medir voltajes CC y CA, corrientes CC y CA y resistencias de varios rangos. También se llama Multímetro electrónico o Ohmímetro de voltaje (VOM).

Medida de voltaje DC

La parte del circuit diagram del multímetro, que se puede utilizar para medir el voltaje de CC, se muestra en la siguiente figura.

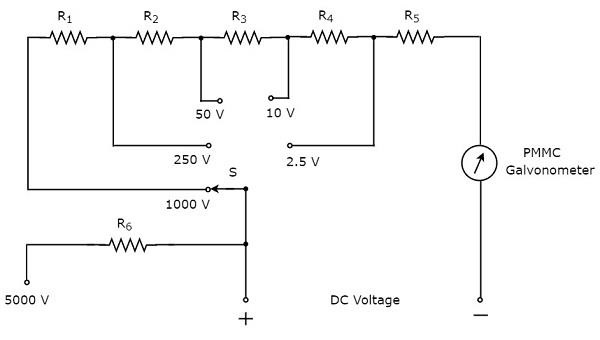
El circuito anterior parece un voltímetro de CC de rango múltiple. La combinación de una resistencia en serie con un galvanómetro PMMC es unaDC voltmeter. Por lo tanto, se puede utilizar para medir voltajes de CC hasta cierto valor.

Podemos aumentar el rango de voltajes de CC que se pueden medir con el mismo voltímetro de CC aumentando el valor de resistencia. el valor de la resistencia equivalente aumenta, cuando conectamos las resistencias están enseries.

En el circuito anterior, podemos medir los voltajes de CC hasta 2.5Vusando la combinación de resistencia, $ R_ {5} $ en serie con el galvanómetro PMMC. Al conectar una resistencia, $ R_ {4} $ en serie con el circuito anterior, podemos medir los voltajes de CC hasta10V. De esta manera, podemos aumentar el rango de voltajes de CC, simplemente conectando una resistencia en serie con el circuito anterior (anterior).

Podemos medir el voltaje de CC en dos puntos cualesquiera de un circuito eléctrico, conectando el interruptor, S al rango de voltaje deseado.

Medida de corriente DC

La parte del circuit diagram del multímetro, que se puede utilizar para medir la corriente CC, se muestra en la siguiente figura.

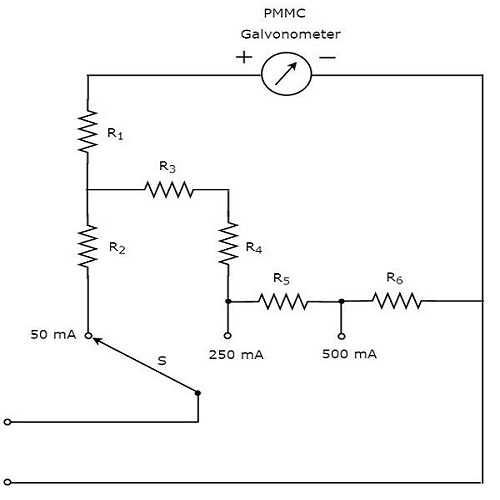
El circuito anterior parece un amperímetro de CC de rango múltiple. la combinación de una resistencia en paralelo con el galvanómetro PMMC es unDC ammeter. Por lo tanto, se puede utilizar para medir corrientes de CC hasta cierto valor.

Podemos obtener different rangesde corrientes CC medidas con el mismo amperímetro CC colocando las resistencias en paralelo con la resistencia anterior. En el circuito anterior, la resistencia $ R_ {1} $ está conectada en serie con el galvanómetro PMMC para evitar que el medidor se dañe debido a una gran corriente.

Podemos medir la corriente CC que fluye a través de dos puntos cualesquiera de un circuito eléctrico, conectando el interruptor, S al rango de corriente deseado

Medición de voltaje CA

La parte del circuit diagram del multímetro, que se puede utilizar para medir el voltaje de CA, se muestra en la siguiente figura.

El circuito anterior parece un multi range AC voltmeter. Sabemos que obtendremos un voltímetro de CA simplemente colocando el rectificador en serie (cascada) con el voltímetro de CC. El circuito anterior fue creado simplemente colocando la combinación de diodos y la resistencia, $ R_ {6} $ entre la resistencia, $ R_ {5} $ y el galvanómetro PMMC.

Podemos medir el voltaje de CA en dos puntos cualesquiera de un circuito eléctrico, conectando el interruptor, S al rango de voltaje deseado.

Medida de resistencia

La parte del circuit diagram del multímetro, que se puede utilizar para medir la resistencia, se muestra en la siguiente figura.

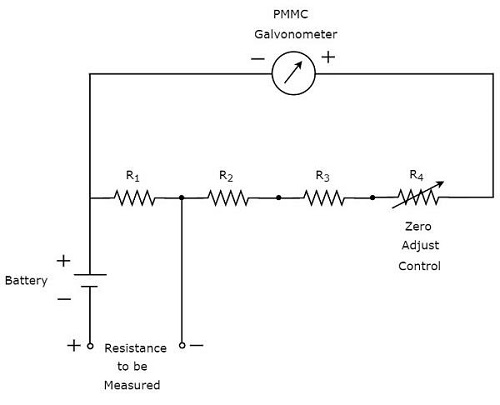
Tenemos que hacer las siguientes dos tareas antes de realizar cualquier medición.

• Cortocircuito el instrumento
• Varíe el control de ajuste a cero hasta que el medidor muestre la corriente de escala completa. Eso significa que el medidor indica un valor de resistencia cero.

Ahora, el circuito anterior se comporta como un ohmímetro de derivación y tiene la multiplicación de escala de 1, es decir, 10 ⁰ . También podemos considerar potencias de orden superior de 10 como multiplicaciones de escala para medir altas resistencias.

Signal generator es un equipo electrónico que proporciona señales de prueba estándar como onda sinusoidal, onda cuadrada, onda triangular, etc. También se le llama oscilador, ya que produce señales periódicas.

El generador de señal, que produce la señal periódica que tiene una frecuencia de rango de frecuencia de audio (AF) se llama AF signal generator. el rango de frecuencias de audio es de 20 Hz a 20 KHz.

Generador de ondas cuadradas y sinusoidales AF

El generador de señal AF, que genera una onda sinusoidal o una onda cuadrada en el rango de frecuencias de audio según el requisito, se denomina generador de ondas AF sinusoidal y cuadrada. Susblock diagramse muestra en la siguiente figura.

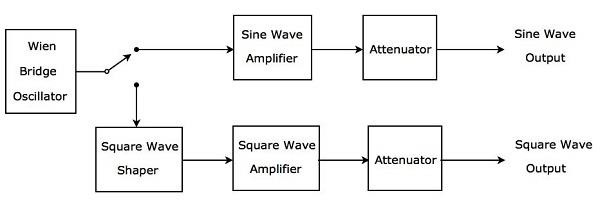
El diagrama de bloques anterior consta principalmente de two paths. Esos son el camino superior y el camino inferior. La ruta superior se usa para producir una onda sinusoidal AF y la ruta inferior se usa para producir una onda cuadrada AF.

Wien bridge oscillatorproducirá una onda sinusoidal en el rango de frecuencias de audio. Según el requisito, podemos conectar la salida del oscilador de puente de Wien a la ruta superior o inferior mediante un interruptor.

La ruta superior consta de bloques como amplificador y atenuador de onda sinusoidal. Si el interruptor se usa para conectar la salida del oscilador de puente de Wien a la ruta superior, producirá unAF sine wave en la salida del camino superior.

La ruta inferior consta de los siguientes bloques: formador de onda cuadrada, amplificador de onda cuadrada y atenuador. El modelador de onda cuadrada convierte la onda sinusoidal en una onda cuadrada. Si el interruptor se utiliza para conectar la salida del oscilador de puente de Wien a la ruta inferior, producirá unAF square waveen la salida del camino inferior. De esta manera, el diagrama de bloques que consideramos se puede utilizar para producir una onda sinusoidal AF o una onda cuadrada AF según el requisito.

Generador de funciones

El generador de funciones es un generador de señales que genera tres o más ondas periódicas. Considera lo siguienteblock diagram de un generador de funciones, que producirá ondas periódicas como onda triangular, onda cuadrada y onda sinusoidal.

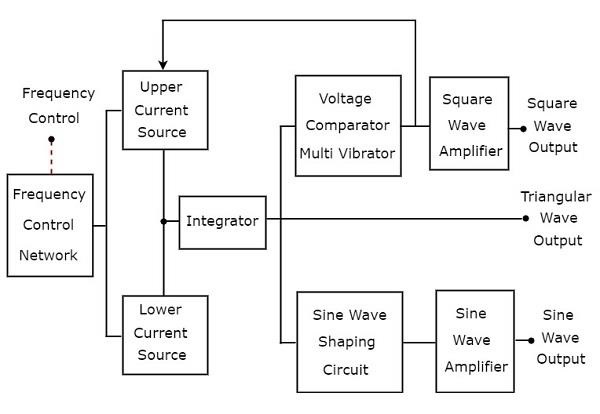
Hay dos current sources, a saber, fuente de corriente superior y fuente de corriente inferior en el diagrama de bloques anterior. Estas dos fuentes de corriente están reguladas por la tensión controlada por frecuencia.

Onda triangular

Integratorpresente en el diagrama de bloques anterior, obtiene corriente constante alternativamente de fuentes de corriente superior e inferior durante la misma cantidad de tiempo repetidamente. Entonces, el integrador producirá dos tipos de salida al mismo tiempo repetidamente:

• El voltaje de salida de un integrador. increases linearly con respecto al tiempo para el período durante el cual el integrador obtiene corriente de la fuente de corriente superior.

• El voltaje de salida de un integrador. decreases linearly con respecto al tiempo para el período durante el cual el integrador obtiene corriente de una fuente de corriente más baja.

De esta manera, el integrador presente en el diagrama de bloques anterior producirá un triangular wave.

Onda cuadrada y onda sinusoidal

La salida del integrador, es decir, la onda triangular se aplica como entrada a otros dos bloques, como se muestra en el diagrama de bloques anterior, para obtener la onda cuadrada y la onda sinusoidal respectivamente. Discutamos sobre estos dos uno por uno.

Ola cuadrada

La onda triangular tiene pendiente positiva y pendiente negativa alternativamente durante la misma cantidad de tiempo repetidamente. Entonces elvoltage comparator multi vibrator presente en el diagrama de bloques anterior producirá los siguientes dos tipos de salida durante la misma cantidad de tiempo repetidamente.

• Un tipo de constante (higher) voltage en la salida del multivibrador comparador de voltaje durante el período durante el cual el multivibrador comparador de voltaje obtiene la pendiente positiva de la onda triangular.

• Otro tipo de constante (lower) voltage en la salida del multivibrador comparador de voltaje durante el período durante el cual el multivibrador comparador de voltaje obtiene la pendiente negativa de la onda triangular.

El multivibrador comparador de voltaje presente en el diagrama de bloques anterior producirá un square wave. Si la amplitud de la onda cuadrada que se produce en la salida del multivibrador comparador de voltaje no es suficiente, entonces se puede amplificar al valor requerido utilizando un amplificador de onda cuadrada.

Onda sinusoidal

los sine wave shaping circuitproducirá una salida de onda sinusoidal a partir de la onda de entrada triangular. Básicamente, este circuito consta de una red de resistencias de diodos. Si la amplitud de la onda sinusoidal producida en la salida del circuito de conformación de la onda sinusoidal es insuficiente, entonces se puede amplificar al valor requerido utilizando un amplificador de onda sinusoidal.

El instrumento electrónico utilizado para analizar ondas se llama wave analyzer. También se le llama analizador de señales, ya que los términos señal y onda pueden usarse indistintamente con frecuencia.

Podemos representar el periodic signal como suma de los dos términos siguientes.

• Componente DC
• Serie de armónicos sinusoidales

Entonces, el análisis de una señal periódica es el análisis de los componentes armónicos presentes en ella.

Analizador de ondas básico

El analizador de ondas básico consta principalmente de tres bloques: el detector primario, el rectificador de onda completa y el galvanómetro PMMC. losblock diagram del analizador de ondas básico se muestra en la siguiente figura:

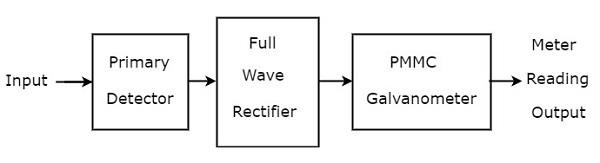
los function de cada bloque presente en el analizador de ondas básico se menciona a continuación.

• Primary Detector- Consta de un circuito LC. Podemos ajustar los valores de inductor, L y capacitor, C de tal manera que solo permita la componente de frecuencia armónica deseada que se va a medir.

• Full Wave Rectifier - Convierte la entrada de CA en una salida de CC.

• PMMC Galvanometer - Muestra el valor pico de la señal, que se obtiene a la salida del rectificador de onda completa.

Obtendremos el diagrama de circuito correspondiente, simplemente reemplazando cada bloque con el componente o componentes respectivos en el diagrama de bloques anterior del analizador de ondas básico. Entonces elcircuit diagram del analizador de ondas básico se verá como se muestra en la siguiente figura:

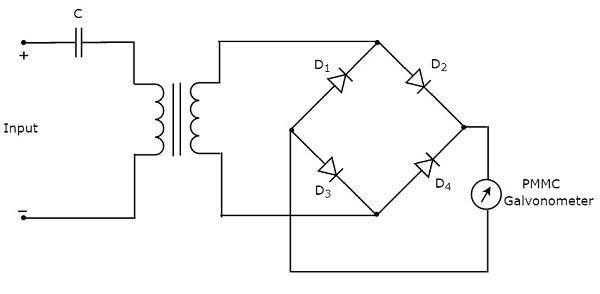
Este analizador de ondas básico se puede utilizar para analizar todos y cada uno de los componentes de frecuencia armónica de una señal periódica.

Tipos de analizadores de ondas

Los analizadores de ondas se pueden clasificar en los siguientes two types.

• Analizador de ondas selectivas de frecuencia
• Analizador de ondas superheterodinas

Ahora, hablemos de estos dos analizadores de ondas uno por uno.

Analizador de ondas selectivas de frecuencia

El analizador de ondas, que se utiliza para analizar las señales del rango AF, se denomina analizador de ondas selectivo de frecuencia. losblock diagram del analizador de ondas selectivas de frecuencia se muestra en la siguiente figura.

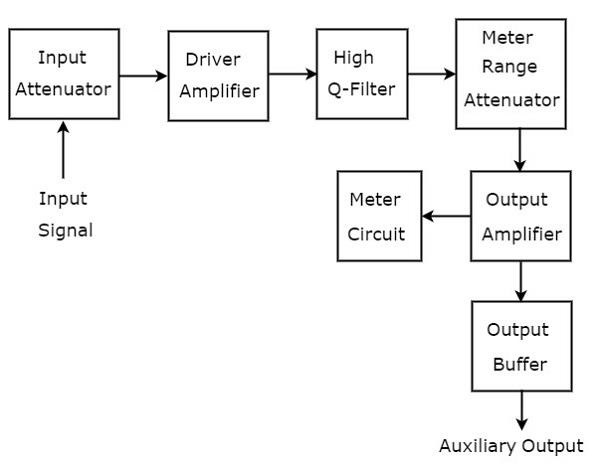
El analizador de ondas selectivo de frecuencia consta de un conjunto de bloques. losfunction de cada bloque se menciona a continuación.

• Input Attenuator- La señal AF que se va a analizar se aplica al atenuador de entrada. Si la amplitud de la señal es demasiado grande, puede atenuarse mediante un atenuador de entrada.

• Driver Amplifier - Amplifica la señal recibida siempre que sea necesario.

• High Q-filter- Se utiliza para seleccionar la frecuencia deseada y rechazar frecuencias no deseadas. Consiste en dos secciones RC y dos amplificadores de filtro y todos estos están conectados en cascada entre sí. Podemos variar los valores de capacitancia para cambiar el rango de frecuencias en potencias de 10. De manera similar, podemos variar los valores de resistencia para cambiar la frecuencia dentro de un rango seleccionado.

• Meter Range Attenuator - Obtiene la señal AF seleccionada como entrada y produce una salida atenuada, siempre que sea necesario.

• Output Amplifier - Amplifica la señal AF seleccionada si es necesario.

• Output Buffer - Se utiliza para proporcionar la señal AF seleccionada a los dispositivos de salida.

• Meter Circuit- Muestra la lectura de la señal AF seleccionada. Podemos elegir la lectura del medidor en rango de voltios o rango de decibelios.

Analizador de ondas superheterodinas

El analizador de ondas, que se utiliza para analizar las señales de rango de RF, se denomina analizador de ondas superheterodinas. La siguiente figura muestra elblock diagram del analizador de ondas superheterodinas.

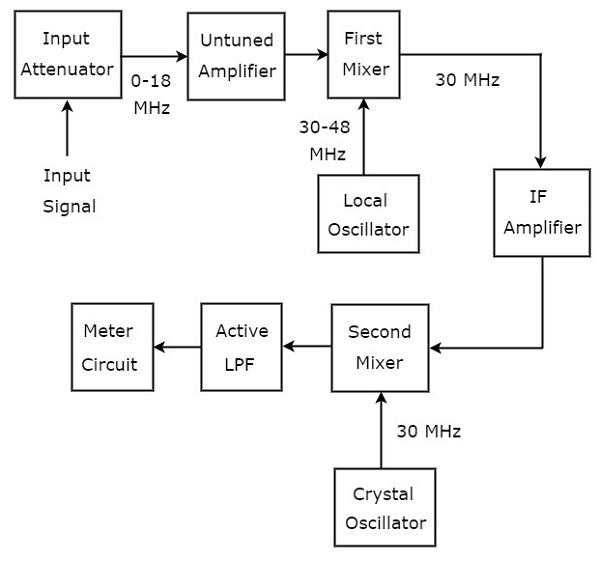
los working del analizador de ondas superheterodinas se menciona a continuación.

• La señal de RF que se va a analizar se aplica al atenuador de entrada. Si la amplitud de la señal es demasiado grande, entonces puede atenuarse medianteinput attenuator.

• Untuned amplifier amplifica la señal de RF siempre que sea necesario y se aplica al primer mezclador.

• Los rangos de frecuencia de la señal de RF y la salida del oscilador local son 0-18 MHz y 30-48 MHz respectivamente. Entonces,first mixerproduce una salida, que tiene una frecuencia de 30 MHz. Esta es la diferencia de frecuencias de las dos señales que se le aplican.

• IF amplifieramplifica la señal de frecuencia intermedia (IF), es decir, la salida del primer mezclador. La señal de FI amplificada se aplica al segundo mezclador.

• Las frecuencias de la señal de IF amplificada y la salida del oscilador Crystal son iguales e iguales a 30MHz. Entonces elsecond mixerproduce una salida, que tiene una frecuencia de 0 Hz. Esta es la diferencia de frecuencias de las dos señales que se le aplican.

• La frecuencia de corte de Active Low Pass Filter (LPF)se elige como 1500 Hz. Por lo tanto, este filtro permite la señal de salida del segundo mezclador.

• Meter Circuitmuestra la lectura de la señal de RF. Podemos elegir la lectura del medidor en rango de voltios o rango de decibelios.

Entonces, podemos elegir un analizador de ondas en particular en función del rango de frecuencia de la señal que se va a analizar.

El instrumento electrónico, utilizado para analizar ondas en el dominio de la frecuencia se llama spectrum analyzer. Básicamente, muestra la distribución de energía de una señal en su pantalla CRT. Aquí, el eje x representa la frecuencia y el eje y representa la amplitud.

Tipos de analizadores de espectro

Podemos clasificar los analizadores de espectro en los siguientes two types.

• Analizador de espectro de banco de filtros
• Analizador de espectro superheterodino

Ahora, hablemos de estos dos analizadores de espectro uno por uno.

Analizador de espectro de banco de filtros

El analizador de espectro, que se utiliza para analizar las señales del rango AF, se denomina analizador de espectro de banco de filtros, o real time spectrum analyzer porque muestra (muestra) cualquier variación en todas las frecuencias de entrada.

La siguiente figura muestra el block diagram del analizador de espectro del banco de filtros.

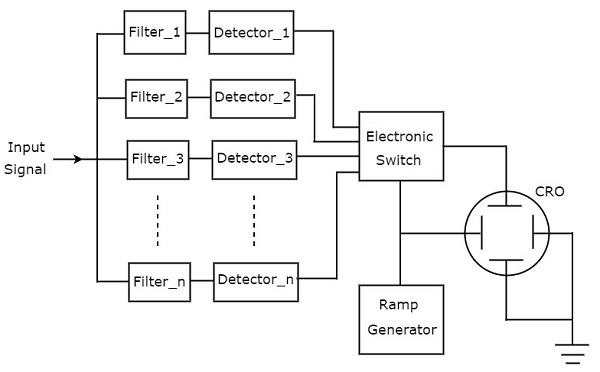
los working del analizador de espectro del banco de filtros se menciona a continuación.

• Tiene un conjunto de filtros de paso de banda y cada uno está diseñado para permitir una banda de frecuencias específica. La salida de cada filtro de paso de banda se envía a un detector correspondiente.

• Todas las salidas del detector están conectadas al interruptor electrónico. Este interruptor permite que el detector salga secuencialmente a la placa de deflexión vertical de CRO. Entonces, CRO muestra la frecuenciaspectrum of AF signal en su pantalla CRT.

Analizador de espectro superheterodino

El analizador de espectro, que se utiliza para analizar las señales que son de rango de RF se denomina superheterodyne spectrum analyzer. Susblock diagram se muestra en la siguiente figura.

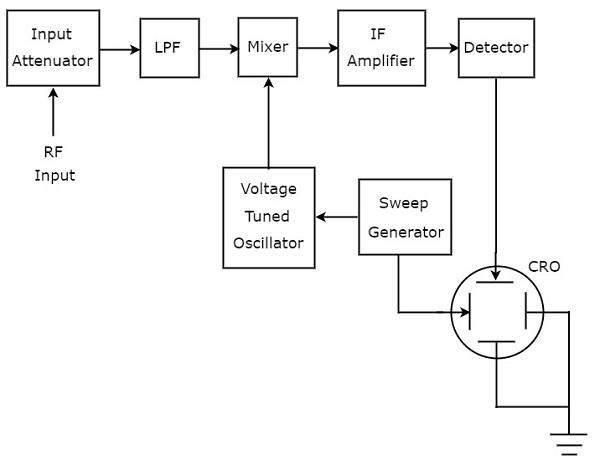
los working del analizador de espectro superheterodino se menciona a continuación.

• La señal de RF que se va a analizar se aplica al atenuador de entrada. Si la amplitud de la señal es demasiado grande, puede atenuarse mediante uninput attenuator.

• Low Pass Filter (LPF) permite solo los componentes de frecuencia que son menores que la frecuencia de corte.

• Mixerobtiene las entradas del filtro de paso bajo y del oscilador sintonizado por voltaje. Produce una salida, que es la diferencia de frecuencias de las dos señales que se le aplican.

• IF amplifieramplifica la señal de frecuencia intermedia (IF), es decir, la salida del mezclador. La señal de FI amplificada se aplica al detector.

La salida del detector se da a la placa de deflexión vertical de CRO. Entonces, CRO muestra la frecuenciaspectrum of RF signal en su pantalla CRT.

Entonces, podemos elegir un analizador de espectro en particular en función del rango de frecuencia de la señal que se va a analizar.

Oscilloscopees un equipo electrónico que muestra una forma de onda de voltaje. Entre los osciloscopios, el osciloscopio de rayos catódicos (CRO) es el básico y muestra una señal o forma de onda que varía en el tiempo.

En este capítulo, analicemos sobre el diagrama de bloques de CRO y las medidas de algunos parámetros utilizando CRO.

Diagrama de bloques de CRO

El osciloscopio de rayos catódicos (CRO) consta de un conjunto de bloques. Estos son amplificador vertical, línea de retardo, circuito de disparo, generador de base de tiempo, amplificador horizontal, tubo de rayos catódicos (CRT) y fuente de alimentación. losblock diagram de CRO se muestra en la siguiente figura.

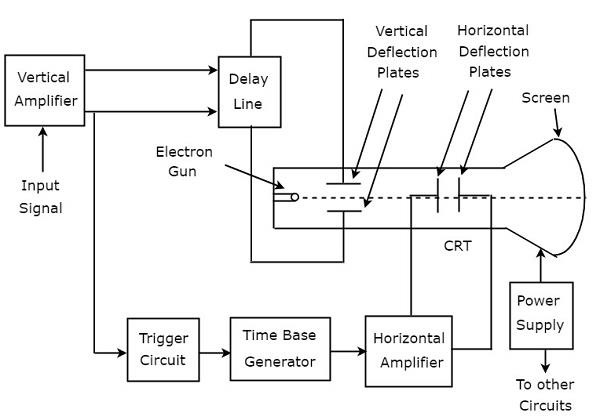
los function de cada bloque de CRO se menciona a continuación.

• Vertical Amplifier - Amplifica la señal de entrada, que se mostrará en la pantalla del CRT.

• Delay Line- Proporciona cierta cantidad de retraso a la señal, que se obtiene a la salida del amplificador vertical. Esta señal retardada se aplica luego a las placas de deflexión vertical de CRT.

• Trigger Circuit - Produce una señal de activación para sincronizar las deflexiones horizontales y verticales del haz de electrones.

• Time base Generator - Produce una señal de diente de sierra, que es útil para la desviación horizontal del haz de electrones.

• Horizontal Amplifier - Amplifica la señal de diente de sierra y luego la conecta a las placas deflectoras horizontales del CRT.

• Power supply- Produce voltajes tanto altos como bajos. El alto voltaje negativo y el voltaje bajo positivo se aplican al CRT y a otros circuitos, respectivamente.

• Cathode Ray Tube (CRT)- Es el bloque más importante de CRO y consta principalmente de cuatro partes. Estos son cañón de electrones, placas de deflexión vertical, placas de deflexión horizontal y pantalla fluorescente.

El haz de electrones, que es producido por un cañón de electrones, se desvía tanto en dirección vertical como horizontal por un par de placas de desviación verticales y un par de placas de desviación horizontales, respectivamente. Finalmente, el rayo desviado aparecerá como un punto en la pantalla fluorescente.

De esta manera, CRO mostrará la señal de entrada aplicada en la pantalla de CRT. Entonces, podemos analizar las señales en el dominio del tiempo usando CRO

Medidas usando CRO

Podemos hacer las siguientes medidas usando CRO.

• Medida de amplitud
• Medición del período de tiempo
• Medida de frecuencia

Ahora, analicemos estas medidas una por una.

Medida de amplitud

CRO muestra la señal de voltaje en función del tiempo en su pantalla. losamplitude de esa señal de voltaje es constante, pero podemos variar el número de divisiones que cubren la señal de voltaje en dirección vertical variando volt/divisionperilla en el panel CRO. Por lo tanto, obtendremos elamplitude de la señal, que está presente en la pantalla de CRO utilizando la siguiente fórmula.

$$ A = j \ veces n_ {v} $$

Dónde,

$ A $ es la amplitud

$ j $ es el valor de voltio / división

$ n_ {v} $ es el número de divisiones que cubren la señal en dirección vertical.

Medición del período de tiempo

CRO muestra la señal de voltaje en función del tiempo en su pantalla. losTime period de esa señal de voltaje periódica es constante, pero podemos variar el número de divisiones que cubren un ciclo completo de señal de voltaje en dirección horizontal variando time/division perilla en el panel CRO.

Por lo tanto, obtendremos el Time period de la señal, que está presente en la pantalla de CRO utilizando la siguiente fórmula.

$$ T = k \ veces n_ {h} $$

Dónde,

$ T $ es el período de tiempo

$ j $ es el valor del tiempo / división

$ n_ {v} $ es el número de divisiones que cubren un ciclo completo de la señal periódica en dirección horizontal.

Medida de frecuencia

La frecuencia, f de una señal periódica es el recíproco del período de tiempo, T. Mathematically, se puede representar como

$$ f = \ frac {1} {T} $$

Entonces, podemos encontrar la frecuencia, f de una señal periódica siguiendo estos dos pasos.

• Step1 - Encuentra el Time period de señal periódica

• Step2 - tomar reciprocal del período de tiempo de la señal periódica, que se obtiene en el Paso 1

Discutiremos sobre osciloscopios de propósito especial en el próximo capítulo.

En el capítulo anterior, hablamos sobre el osciloscopio de rayos catódicos (CRO), que es un osciloscopio básico. Obtendremos osciloscopios de propósito especial con solo incluir algunos bloques adicionales al osciloscopio básico según el requisito.

Los siguientes son los special purpose oscilloscopes.

• Osciloscopio de doble haz
• Osciloscopio de seguimiento dual
• Osciloscopio de almacenamiento digital

Ahora, hablemos sobre estos osciloscopios de propósito especial uno por uno.

Osciloscopio de doble haz

El osciloscopio, que muestra dos formas de onda de voltaje, se denomina osciloscopio de doble haz. Susblock diagram se muestra en la siguiente figura.

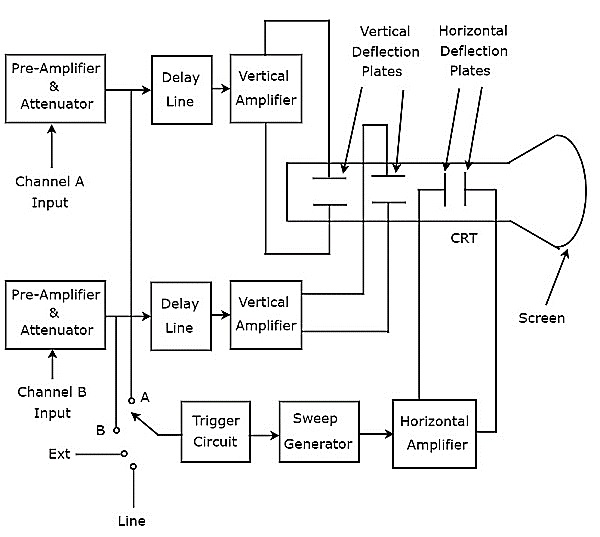
Como se muestra en la figura anterior, el CRT del osciloscopio de doble haz consta de dos juegos de placas de deflexión vertical y un juego de placas de deflexión horizontal.

La combinación de los siguientes bloques juntos se llama channel.

• Preamplificador y atenuador
• Línea de retardo
• Amplificador vertical
• Un conjunto de placas de deflexión vertical

Hay dos canales en el osciloscopio de doble haz. Entonces, podemos aplicar las dos señales, a saber, A y B como entrada del canal A y el canal B respectivamente. Podemos elegir cualquiera de estas cuatro señales comotrigger inputal circuito de disparo mediante el uso de un interruptor. Estas son las señales de entrada A y B, la señal externa (Ext) y la entrada de línea.

Este osciloscopio producirá dos haces de deflexión vertical, ya que hay dos pares de placas de deflexión vertical. En este osciloscopio, los bloques que son útiles para desviar el haz en dirección horizontal son comunes para ambas señales de entrada. Finalmente, este osciloscopio producirá eltwo input signals simultáneamente en la pantalla del CRT.

Osciloscopio de seguimiento dual

El osciloscopio, que produce dos trazos en su pantalla, se llama osciloscopio de doble trazo. Susblock diagram se muestra en la siguiente figura.

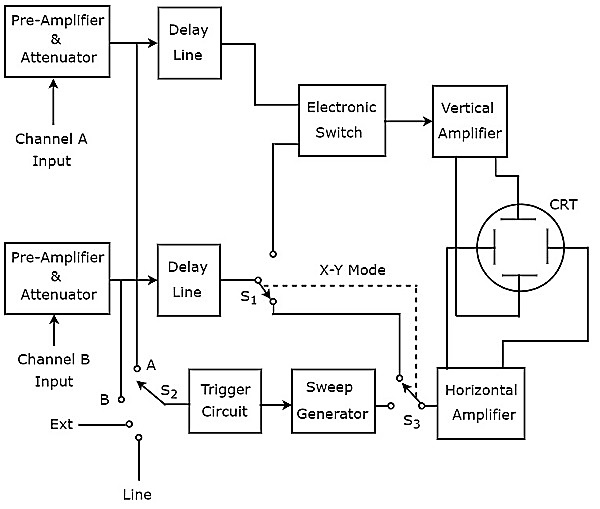
Como se muestra en la figura anterior, el CRT del osciloscopio de seguimiento dual consta de un conjunto de placas de deflexión vertical y otro conjunto de placas de deflexión horizontal. El canal consta de cuatro bloques, es decir, preamplificador y atenuador, línea de retardo, amplificador vertical y placas de deflexión vertical.

En el diagrama de bloques anterior, los dos primeros bloques están presentes por separado en ambos canales. Los dos últimos bloques son comunes a ambos canales. Por tanto, con la ayuda deelectronic switch podemos conectar la salida de la línea de retardo de un canal específico al amplificador vertical.

Podemos elegir cualquiera de estas cuatro señales como entrada de disparo al trigger circuitusando un interruptor. Estas son las señales de entrada A y B, la señal externa (Ext) y la entrada de línea.

Este osciloscopio usa el mismo haz de electrones para desviar las señales de entrada A y B en dirección vertical usando un interruptor electrónico, y produce two traces. los bloques que desvían el haz horizontalmente son comunes para ambas señales de entrada.

Osciloscopio de almacenamiento digital

El osciloscopio, que almacena la forma de onda digitalmente, se conoce como osciloscopio de almacenamiento digital. losblock diagram del osciloscopio de almacenamiento (digital) está por debajo de -

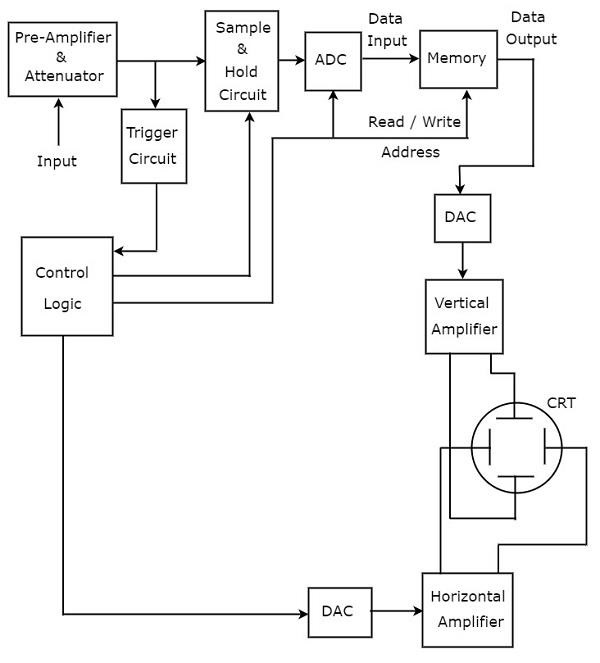
Los bloques adicionales necesarios para el almacenamiento de datos digitales se agregan a un osciloscopio básico para convertirlo en un osciloscopio de almacenamiento digital. Los bloques que se requieren parastoring of digital dataSe encuentran entre el preamplificador y atenuador y el amplificador vertical en el osciloscopio de almacenamiento digital. Estos son circuito de muestreo y retención, convertidor analógico a digital (ADC), convertidor de memoria y digital a analógico.

Control logiccontrola los primeros tres bloques enviando varias señales de control. Los bloques como la lógica de control y el convertidor de digital a analógico están presentes entre el circuito de disparo y el amplificador horizontal en el osciloscopio de almacenamiento digital.

El osciloscopio de almacenamiento digital stores the dataen digital antes de que muestre la forma de onda en la pantalla. Considerando que, el osciloscopio básico no tiene esta característica.

Lissajous figurees el patrón que se muestra en la pantalla, cuando se aplican señales sinusoidales a las placas de deflexión horizontal y vertical de CRO. Estos patrones variarán en función de las amplitudes, frecuencias y diferencias de fase de las señales sinusoidales, que se aplican a las placas de deflexión horizontal y vertical de CRO.

La siguiente figura muestra un example de la figura de Lissajous.

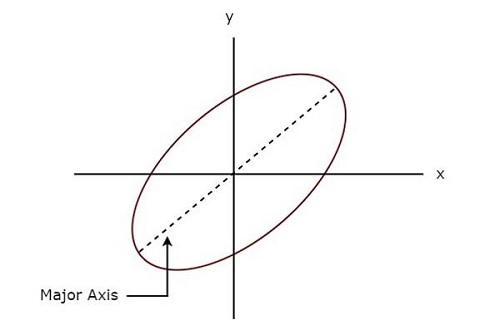
La figura de Lissajous anterior está en elliptical shape y su eje mayor tiene algún ángulo de inclinación con eje x positivo.

Medidas usando figuras de Lissajous

Podemos hacer lo siguiente two measurements de una figura de Lissajous.

• Frecuencia de la señal sinusoidal
• Diferencia de fase entre dos señales sinusoidales

Ahora, analicemos estas dos medidas una por una.

Medida de frecuencia

La figura de Lissajous se mostrará en la pantalla, cuando las señales sinusoidales se apliquen a las placas de deflexión horizontal y vertical de CRO. Por lo tanto, aplique la señal sinusoidal, que tiene estándarknown frequencya las placas de deflexión horizontal de CRO. Del mismo modo, aplique la señal sinusoidal, cuyafrequency es unknown a las placas de deflexión vertical de CRO

Sea, $ f_ {H} $ y $ f_ {V} $ son las frecuencias de las señales sinusoidales, que se aplican a las placas de deflexión horizontal y vertical de CRO respectivamente. La relación entre $ f_ {H} $ y $ f_ {V} $ puede sermathematically representado como se muestra a continuación.

$$ \ frac {f_ {V}} {f_ {H}} = \ frac {n_ {H}} {n_ {V}} $$

De la relación anterior, obtendremos la frecuencia de la señal sinusoidal, que se aplica a las placas de deflexión vertical de CRO como

$ f_ {V} = \ left (\ frac {n_ {H}} {n_ {V}} \ right) f_ {H} $ (Ecuación 1)

Dónde,

$ n_ {H} $ es el número de tangencias horizontales

$ n_ {V} $ es el número de tangencias verticales

Podemos encontrar los valores de $ n_ {H} $ y $ n_ {V} $ de la figura de Lissajous. Entonces, al sustituir los valores de $ n_ {H} $, $ n_ {V} $ y $ f_ {H} $ en la Ecuación 1, obtendremos el valor de$f_{V}$, es decir, el frequency of sinusoidal signal que se aplica a las placas de deflexión vertical de CRO.

Medida de la diferencia de fase

Se muestra una figura de Lissajous en la pantalla cuando se aplican señales sinusoidales a las placas de deflexión horizontal y vertical de CRO. Por lo tanto, aplique las señales sinusoidales, que tienensame amplitude and frequency a las placas deflectoras horizontales y verticales de CRO.

Para algunas figuras de Lissajous basadas en su forma, podemos decir directamente la diferencia de fase entre las dos señales sinusoidales.

• Si la figura de Lissajous es un straight line con una inclinación de $ 45 ^ {\ circ} $ con eje x positivo, entonces el phase differenceentre las dos señales sinusoidales estará $ 0 ^ {\ circ} $. Eso significa que no hay diferencia de fase entre esas dos señales sinusoidales.

• Si la figura de Lissajous es un straight line con una inclinación de $ 135 ^ {\ circ} $ con eje x positivo, entonces el phase differenceentre las dos señales sinusoidales será $ 180 ^ {\ circ} $. Eso significa que esas dos señales sinusoidales están desfasadas.

• Si la figura de Lissajous está en circular shape, entonces la diferencia de fase entre las dos señales sinusoidales será $ 90 ^ {\ circ} $ o $ 270 ^ {\ circ} $.

Podemos calcular la diferencia de fase entre las dos señales sinusoidales usando fórmulas, cuando las cifras de Lissajous son de elliptical shape.

• Si el eje mayor de una figura de Lissajous de forma elíptica que tiene un ángulo de inclinación se encuentra entre $ 0 ^ {\ circ} $ y $ 90 ^ {\ circ} $ con eje x positivo, entonces la diferencia de fase entre las dos señales sinusoidales será.

$$ \ phi = \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = \ sin ^ {- 1} \ left (\ frac {y_ {1} } {y_ {2}} \ right) $$

• Si el eje mayor de una figura de Lissajous de forma elíptica que tiene un ángulo de inclinación se encuentra entre $ 90 ^ {\ circ} $ y $ 180 ^ {\ circ} $ con eje x positivo, entonces la diferencia de fase entre las dos señales sinusoidales será.

$$ \ phi = 180 - \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = 180 - \ sin ^ {- 1} \ left (\ frac { y_ {1}} {y_ {2}} \ right) $$

Where,

$ x_ {1} $ es la distancia desde el origen hasta el punto en el eje x, donde se cruza la figura de Lissajous de forma elíptica

$ x_ {2} $ es la distancia desde el origen hasta la tangente vertical de la figura de Lissajous de forma elíptica

$ y_ {1} $ es la distancia desde el origen hasta el punto en el eje y, donde la figura de Lissajous de forma elíptica se cruza

$ y_ {2} $ es la distancia desde el origen a la tangente horizontal de la figura de Lissajous de forma elíptica

En este capítulo, aprendimos cómo encontrar la frecuencia de una señal sinusoidal desconocida y la diferencia de fase entre dos señales sinusoidales de figuras de Lissajous usando fórmulas.

Podemos conectar cualquier circuito de prueba a un osciloscopio a través de una sonda. Como CRO es un osciloscopio básico, la sonda que está conectada a él también se llamaCRO probe.

Debemos seleccionar la sonda de tal manera que no cree problemas de carga con el circuito de prueba. Para que podamos analizar el circuito de prueba con las señales correctamente en la pantalla CRO.

Las sondas CRO deben tener lo siguiente characteristics.

• Alta impedancia
• Alto ancho de banda

los block diagram de la sonda CRO se muestra en la siguiente figura.

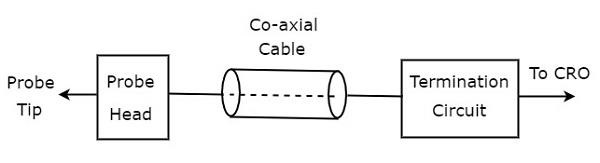
Como se muestra en la figura, la sonda CRO consta principalmente de tres bloques. Estos son el cabezal de la sonda, el cable coaxial y el circuito de terminación. El cable coaxial simplemente conecta el cabezal de la sonda y el circuito de terminación.

Tipos de sondas CRO

Las sondas CRO se pueden clasificar en las siguientes two types.

• Sondas pasivas
• Sondas activas

Ahora, analicemos estos dos tipos de sondas una por una.

Sondas pasivas

Si el cabezal de la sonda consta de elementos pasivos, entonces se llama passive probe. El diagrama del circuito de la sonda pasiva se muestra en la siguiente figura.

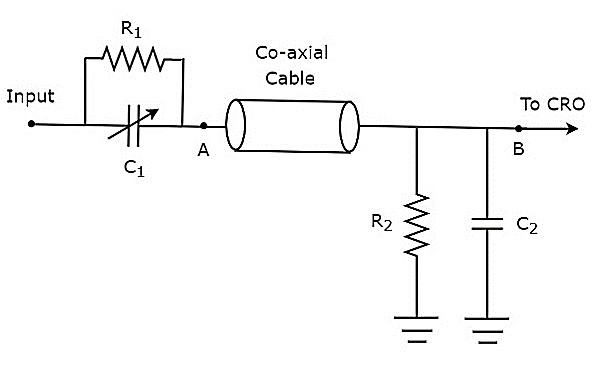
Como se muestra en la figura, el cabezal de la sonda consta de una combinación en paralelo de resistencia, $ R_ {1} $ y un condensador variable, $ C_ {1} $. De manera similar, el circuito de terminación consta de una combinación en paralelo de resistencia, $ R_ {2} $ y capacitor, $ C_ {2} $.

El diagrama de circuito anterior se modifica en forma de bridge circuit y se muestra en la siguiente figura.

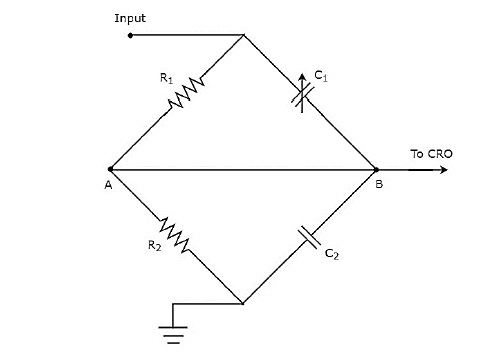
Podemos equilibrar el puente, ajustando el valor del condensador variable, $ c_ {1} $. Discutiremos el concepto de puentes en los siguientes capítulos. Por el momento, considere lo siguientebalancing condition of AC bridge.

$$ Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $$

Substitute, las impedancias $ Z_ {1}, Z_ {2}, Z_ {3} $ y $ Z_ {4} $ como $ R_ {1}, \ frac {1} {j \ omega C_ {1}}, R_ { 2} $ y $ \ frac {1} {j \ omega C_ {2}} $ respectivamente en la ecuación anterior.

$$ R_ {1} \ left (\ frac {1} {j \ omega C_ {2}} \ right) = \ left (\ frac {1} {j \ omega C_ {1}} \ right) R_ {2 } $$

$ \ Rightarrow R_ {1} C_ {1} = R_ {2} C_ {2} $ Ecuación 1

Por el principio de división de voltaje, obtendremos el voltage across resistor, $R_{2}$ como

$$ V_ {0} = V_ {i} \ left (\ frac {R_ {2}} {R_ {1} + R_ {2}} \ right) $$

attenuation factores la relación entre el voltaje de entrada, $ V_ {i} $ y el voltaje de salida, $ V_ {0} $. Entonces, de la ecuación anterior obtendremos el factor de atenuación, $ \ alpha $ como

$$ \ alpha = \ frac {V_ {i}} {V_ {0}} = \ frac {R_ {1} + R_ {2}} {R_ {2}} $$

$ \ Flecha derecha \ alpha = 1+ \ frac {R_ {1}} {R_ {2}} $

$ \ Flecha derecha \ alpha-1 = \ frac {R_ {1}} {R_ {2}} $

$ \ Rightarrow R_ {1} = \ left (\ alpha-1 \ right) R_ {2} $ Ecuación 2

De la Ecuación 2, podemos concluir que el valor de $ R_ {1} $ es mayor o igual que el valor de ð ?? '… 2 para valores enteros de $ \: \ alpha> 1 $.

Sustituya la ecuación 2 en la ecuación 1.

$$ \ left (\ alpha-1 \ right) R_ {2} C_ {1} = R_ {2} C_ {2} $$

$ \ Flecha derecha \ izquierda (\ alpha-1 \ derecha) C_ {1} = C_ {2} $

$ \ Rightarrow C_ {1} = \ frac {C_ {2}} {\ left (\ alpha-1 \ right)} $ Ecuación 3

De la ecuación 3, podemos concluir que el valor de $ C_ {1} $ es menor o igual que el valor de $ C_ {2} $ para valores enteros de $ \ alpha> 1 $

Example

Encontremos los valores de $ R_ {1} $ y $ C_ {1} $ de una sonda que tiene un factor de atenuación, $ \ alpha $ como 10. Supongamos, $ R_ {2} = 1 M \ Omega $ y $ C_ {2} = 18pF $.

• Step1 - Obtendremos el valor de $ R_ {1} $ sustituyendo los valores de $ \ alpha $ y $ R_ {2} $ en la Ecuación 2.

$$ R_ {1} = \ left (10-1 \ right) \ times 1 \ times 10 ^ {6} $$

$$ \ Rightarrow R_ {1} = 9 \ times 10 ^ {6} $$

$$ \ Flecha derecha R_ {1} = 9 M \ Omega $$

Step 2 - Obtendremos el valor de $ C_ {1} $ sustituyendo los valores de $ \ alpha $ y $ C_ {2} $ en la Ecuación 3.

$$ C_ {1} = \ frac {18 \ times10 ^ {- 12}} {\ left (10-1 \ right)} $$

$$ \ Rightarrow C_ {1} = 2 \ times 10 ^ {- 12} $$

$$ \ Flecha derecha C_ {1} = 2 pF $$

Por lo tanto, los valores de $ R_ {1} $ y $ C_ {1} $ de una sonda serán $ 9M \ Omega $ y $ 2pF $ respectivamente para las especificaciones dadas.

Sondas activas

Si el cabezal de la sonda consta de componentes electrónicos activos, entonces se llama active probe. El diagrama de bloques de la sonda activa se muestra en la siguiente figura.

Como se muestra en la figura, el cabezal de la sonda consta de un seguidor de fuente FET en cascada con seguidor de emisor BJT. El seguidor de fuente FET proporciona alta impedancia de entrada y baja impedancia de salida. Considerando que, el propósito del seguidor de emisor BJT es que evita o elimina el desajuste de impedancia.

Las otras dos partes, como el cable coaxial y el circuito de terminación, siguen siendo las mismas en las sondas activas y pasivas.

Si los componentes eléctricos están dispuestos en forma de puente o estructura de anillo, entonces ese circuito eléctrico se llama un bridge. En general, el puente forma un bucle con un conjunto de cuatro brazos o ramas. Cada rama puede contener uno o dos componentes eléctricos.

Tipos de puentes

Podemos clasificar los circuitos puente o puentes en las siguientes dos categorías en función de la señal de voltaje con la que se pueden operar.

• Puentes DC
• Puentes AC

Ahora, hablemos brevemente sobre estos dos puentes.

Puentes DC

Si el circuito puente se puede operar solo con una señal de voltaje CC, entonces es un circuito puente CC o simplemente DC bridge. Los puentes de CC se utilizan para medir el valor de la resistencia desconocida. loscircuit diagram del puente de CC se ve como se muestra en la siguiente figura.

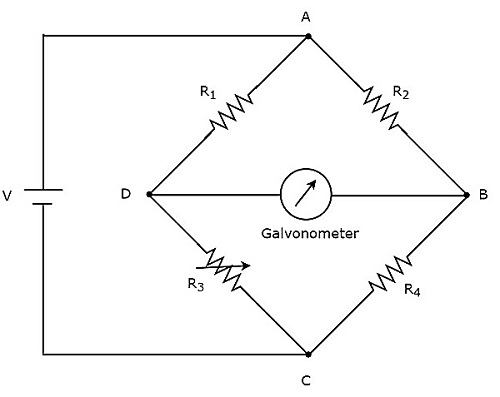
El puente de CC anterior tiene four armsy cada brazo consta de una resistencia. Entre los cuales, dos resistencias tienen valores de resistencia fijos, una resistencia es una resistencia variable y la otra tiene un valor de resistencia desconocido.

El circuito de puente de CC anterior se puede excitar con un DC voltage sourcecolocándolo en una diagonal. El galvanómetro se coloca en otra diagonal del puente de CC. Muestra cierta desviación siempre que el puente esté desequilibrado.

Varíe el valor de resistencia de la resistencia variable hasta que el galvanómetro muestre una deflexión nula (cero). Ahora, se dice que el puente de CC anterior es equilibrado. Entonces, podemos encontrar el valor deunknown resistance utilizando ecuaciones nodales.

Puentes AC

Si el circuito de puente se puede operar solo con una señal de voltaje de CA, entonces se dice que es un circuito de puente de CA o simplemente AC bridge. Los puentes de CA se utilizan para medir el valor de inductancia, capacitancia y frecuencia desconocidas.

los circuit diagram del puente de CA se ve como se muestra en la siguiente figura.

El diagrama de circuito del puente de CA es similar al del puente de CC. El puente de CA anterior tienefour armsy cada brazo consta de cierta impedancia. Eso significa que cada brazo tendrá uno o una combinación de elementos pasivos como resistencia, inductor y condensador.

Entre las cuatro impedancias, dos impedancias tienen valores fijos, una impedancia es variable y la otra es una impedancia desconocida.

El circuito de puente de CA anterior se puede excitar con un AC voltage sourcecolocándolo en una diagonal. Se coloca un detector en otra diagonal del puente de CA. Muestra cierta desviación siempre que el puente esté desequilibrado.

El circuito de puente de CA anterior se puede excitar con un AC voltage sourcecolocándolo en una diagonal. Se coloca un detector en otra diagonal del puente de CA. Muestra cierta desviación siempre que el puente esté desequilibrado.

Varíe el valor de impedancia de la impedancia variable hasta que el detector muestre una deflexión nula (cero). Ahora, se dice que el puente de CA anterior es equilibrado. Entonces, podemos encontrar el valor deunknown impedance mediante el uso de condiciones equilibradas.

DC bridgesse puede operar solo con señal de voltaje CC. Los puentes de CC son útiles para medir el valor de resistencia desconocida, que está presente en el puente. El puente de Wheatstone es un ejemplo de puente DC.

Ahora, hablemos sobre Wheatstone’s Bridge para encontrar el valor de la resistencia desconocida.

Puente de Wheatstone

El puente de Wheatstone es un simple puente de CC, que tiene principalmente cuatro brazos. Estos cuatro brazos forman un rombo o forma cuadrada y cada brazo consta de una resistencia.

Para encontrar el valor de la resistencia desconocida, necesitamos el galvanómetro y la fuente de voltaje de CC. Por lo tanto, uno de estos dos se coloca en una diagonal del puente de Wheatstone y el otro se coloca en otra diagonal del puente de Wheatstone.

El puente de Wheatstone se utiliza para medir el valor de la resistencia media. loscircuit diagram del puente de Wheatstone se muestra en la siguiente figura.

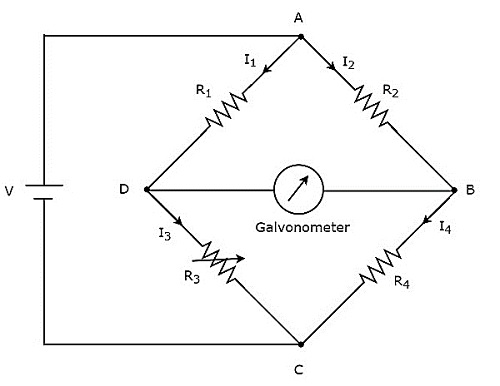
En el circuito anterior, los brazos AB, BC, CD y DA juntos forman un rhombuso forma cuadrada. Consisten en resistencias $ R_ {2} $, $ R_ {4} $, $ R_ {3} $ y $ R_ {1} $ respectivamente. Deje que la corriente que fluye a través de estos brazos de resistencia sea $ I_ {2} $, $ I_ {4} $, $ I_ {3} $ y $ I_ {1} $ respectivamente y las direcciones de estas corrientes se muestran en la figura.

Los brazos diagonales DB y AC constan de un galvanómetro y una fuente de voltaje de CC de V voltios respectivamente. Aquí, la resistencia $ R_ {3} $ es una resistencia variable estándar y la resistencia $ R_ {4} $ es una resistencia desconocida. Podemosbalance the bridge, variando el valor de resistencia del resistor, $ R_ {3} $.

El circuito de puente anterior está equilibrado cuando no fluye corriente a través del brazo diagonal, DB. Eso significa que hayno deflection en el galvanómetro, cuando el puente está equilibrado.

El puente estará equilibrado, cuando lo siguiente two conditions estan satisfechos.

• El voltaje en el brazo AD es igual al voltaje en el brazo AB. es decir,

$$ V_ {AD} = V_ {AB} $$

$ \ Rightarrow I_ {1} R_ {1} = I_ {2} R_ {2} $ Ecuación 1

• El voltaje en el brazo DC es igual al voltaje en el brazo BC. es decir,

$$ V_ {DC} = V_ {BC} $$

$ \ Flecha derecha I_ {3} R_ {3} = I_ {4} R_ {4} $ Ecuación 2

De las dos condiciones de equilibrio anteriores, obtendremos lo siguiente two conclusions.

• La corriente que fluye a través del brazo AD será igual a la del brazo DC. es decir,

$$ I_ {1} = I_ {3} $$

• La corriente que fluye a través del brazo AB será igual a la del brazo BC. es decir,

$$ I_ {2} = I_ {4} $$

Calcula la razón de la Ecuación 1 y la Ecuación 2.

$ \ frac {I_ {1} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {2} R_ {2}} {I_ {4} R_ {4}} $ Ecuación 3

Sustituya, $ I_ {1} = I_ {3} $ y $ I_ {2} = I_ {4} $ en la Ecuación 3.

$$ \ frac {I_ {3} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {4} R_ {2}} {I_ {4} R_ {4}} $$

$$ \ Flecha derecha \ frac {R_ {1}} {R_ {3}} = \ frac {R_ {2}} {R_ {4}} $$

$$ \ Flecha derecha R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$

Sustituyendo los valores conocidos de las resistencias $ R_ {1} $, $ R_ {2} $ y $ R_ {3} $ en la ecuación anterior, obtendremos el value of resistor,$R_{4}$.

En este capítulo, analicemos los puentes de CA, que se pueden utilizar para medir la inductancia. Los puentes de CA funcionan solo con una señal de voltaje de CA. loscircuit diagram del puente de CA se muestra en la siguiente figura.

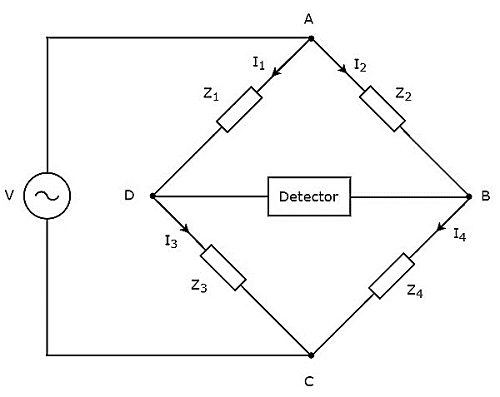
Como se muestra en la figura anterior, el puente de CA consta principalmente de cuatro brazos, que están conectados en rombo o square shape. Todos estos brazos constan de cierta impedancia.

El detector y la fuente de voltaje de CA también son necesarios para encontrar el valor de impedancia desconocida. Por lo tanto, uno de estos dos se coloca en una diagonal del puente de CA y el otro se coloca en la otra diagonal del puente de CA. La condición de equilibrio del puente de Wheatstone como:

$$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$

Obtendremos el balancing condition of AC bridge, simplemente reemplazando R con Z en la ecuación anterior.

$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$

$ \ Flecha derecha Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $

Aquí, $ Z_ {1} $ y $ Z_ {2} $ son impedancias fijas. Mientras que $ Z_ {3} $ es una impedancia variable estándar y $ Z_ {4} $ es una impedancia desconocida.

Note - Podemos elegir dos de esas cuatro impedancias como impedancias fijas, una impedancia como impedancia variable estándar y la otra impedancia como una impedancia desconocida según la aplicación.

A continuación se muestran los dos puentes de CA, que se pueden utilizar para medir inductance.

• Puente de Maxwell
• Puente del heno

Ahora, hablemos de estos dos puentes de CA uno por uno.

Puente de Maxwell

El puente de Maxwell es un puente de CA que tiene cuatro brazos, que están conectados en forma de rombo o square shape. Dos brazos de este puente consisten en una sola resistencia, un brazo consiste en una combinación en serie de resistor e inductor y el otro brazo consiste en una combinación en paralelo de resistor y capacitor.

Se utiliza un detector de CA y una fuente de voltaje de CA para encontrar el valor de impedancia desconocida. Por lo tanto, uno de estos dos se coloca en una diagonal del puente de Maxwell y el otro se coloca en otra diagonal del puente de Maxwell.

El puente de Maxwell se utiliza para medir el valor de la inductancia media. loscircuit diagram del puente de Maxwell se muestra en la siguiente figura.

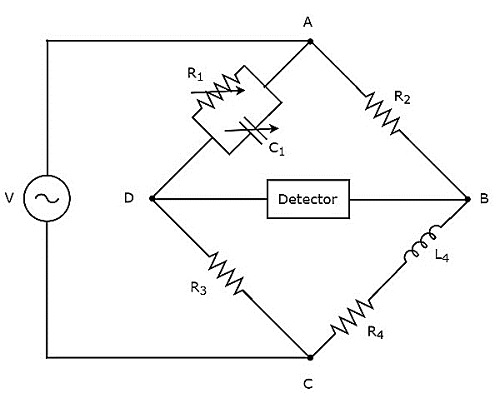
En el circuito anterior, los brazos AB, BC, CD y DA juntos forman un rombo o forma cuadrada. Los brazos AB y CD constan de resistencias, $ R_ {2} $ y $ R_ {3} $ respectivamente. El brazo BC consta de una combinación en serie de resistencia, $ R_ {4} $ e inductor, $ L_ {4} $. El brazo, DA consta de una combinación en paralelo de resistencia, $ R_ {1} $ y condensador, $ C_ {1} $.

Sea, $ Z_ {1}, Z_ {2}, Z_ {3} $ y $ Z_ {4} $ son las impedancias de los brazos DA, AB, CD y BC respectivamente. losvalues of these impedances estarán

$$ Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $$

$$ \ Flecha derecha Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $$

$ Z_ {2} = R_ {2} $

$ Z_ {3} = R_ {3} $

$ Z_ {4} = R_ {4} + j \ omega L_ {4} $

Substitute estos valores de impedancia en la siguiente condición de equilibrio del puente de CA.

$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$

$$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left ({\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} \ right)} $$

$ \ Flecha derecha R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ { 1}} $

$ \ Flecha derecha R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + \ frac {j \ omega R_ {1} C_ {1} R_ {2} R_ {3}} {R_ {1}} $

$ \ Flecha derecha R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + j \ omega C_ {1} R_ {2} R_ {3} PS

Por comparing los respectivos términos reales e imaginarios de la ecuación anterior, obtendremos

$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $ Ecuación 1

$ L_ {4} = C_ {1} R_ {2} R_ {3} $ Ecuación 2

Sustituyendo los valores de las resistencias $ R_ {1} $, $ R_ {2} $ y $ R_ {3} $ en la Ecuación 1, obtendremos el valor de la resistencia, $ R_ {4} $. De manera similar, sustituyendo el valor del capacitor, $ C_ {1} $ y los valores de las resistencias, $ R_ {2} $ y $ R_ {3} $ en la Ecuación 2, obtendremos el valor del inductor, $ L_ {4 PS

los advantage del puente de Maxwell es que tanto los valores de la resistencia, $ R_ {4} $ como de un inductor, $ L_ {4} $ son independientes del valor de la frecuencia.

Puente del heno

El puente de Hay es una versión modificada del puente de Maxwell, que obtenemos modificando el brazo, que consiste en una combinación en paralelo de resistencia y capacitor en el brazo, que consiste en una combinación en serie de resistencia y capacitor en el puente de Maxwell.

El puente de Hay se utiliza para medir el valor de alta inductancia. loscircuit diagram del puente de Hay se muestra en la siguiente figura.

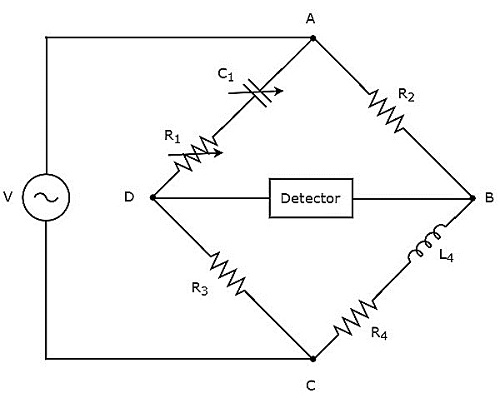
En el circuito anterior, los brazos AB, BC, CD y DA juntos forman un rombo o forma cuadrada. Los brazos, AB y CD constan de resistencias, $ R_ {2} $ y $ R_ {3} $ respectivamente. El brazo BC consta de una combinación en serie de resistencia, $ R_ {4} $ e inductor, $ L_ {4} $. El brazo, DA consta de una combinación en serie de resistencia, $ R_ {1} $ y condensador, $ C_ {1} $.

Sea, $ Z_ {1}, Z_ {2}, Z_ {3} $ y $ Z_ {4} $ son las impedancias de los brazos DA, AB, CD y BC respectivamente. losvalues of these impedances estarán

$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$

$ \ Flecha derecha Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $

$ Z_ {2} = R_ {2} $

$ Z_ {3} = R_ {3} $

$ Z_ {4} = R_ {4} + j \ omega L_ {4} $

Substitute estos valores de impedancia en la siguiente condición de equilibrio del puente de CA.

$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$

$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} \ right)} $

$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ {1} \ right)} $

Multiplica el numerador y el denominador del término del lado derecho de la ecuación anterior con $ 1 - j \ omega R_ {1} C_ {1} $.

$ \ Flecha derecha R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ { 1} \ right)} \ times \ frac {\ left (1 - j \ omega R_ {1} C_ {1} \ right)} {\ left (1 - j \ omega R_ {1} C_ {1} \ right PS

$ \ Flecha derecha R_ {4} + j \ omega L_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3} + j \ omega R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} PS

Por comparing los respectivos términos reales e imaginarios de la ecuación anterior, obtendremos

$ R_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ Ecuación 3

$ L_ {4} = \ frac {R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ Ecuación 4

Sustituyendo los valores de $ R_ {1}, R_ {2}, R_ {3}, C_ {1} $ y $ \ omega $ en la Ecuación 3 y la Ecuación 4, obtendremos los valores de la resistencia, $ R_ {4 } $ e inductor, $ L_ {4} $.

En el capítulo anterior, discutimos sobre dos puentes de CA que se pueden usar para medir la inductancia. En este capítulo, analicemos lo siguientetwo AC bridges.

• Puente de Schering
• Puente de Viena

Estos dos puentes se pueden utilizar para medir capacitancia y frecuencia respectivamente.

Puente de Schering

El puente de Schering es un puente de CA que tiene cuatro brazos, que están conectados en forma de rombo o square shape, cuyo brazo consiste en una sola resistencia, un brazo consiste en una combinación en serie de resistencia y capacitor, un brazo consiste en un solo capacitor y el otro brazo consiste en una combinación en paralelo de resistencia y capacitor.

El detector de CA y la fuente de voltaje de CA también se utilizan para encontrar el valor de impedancia desconocida, por lo tanto, uno de ellos se coloca en una diagonal del puente Schering y el otro se coloca en la otra diagonal del puente Schering.

El puente de Schering se utiliza para medir el valor de la capacitancia. loscircuit diagram del puente Schering se muestra en la siguiente figura.

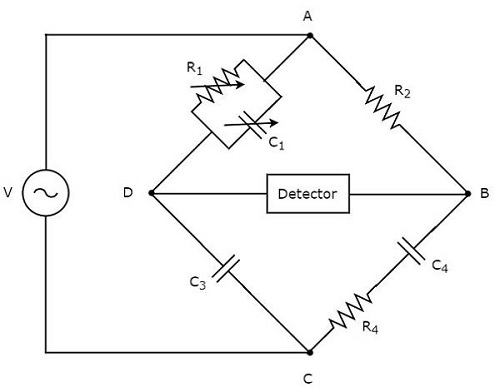
En el circuito anterior, los brazos AB, BC, CD y DA juntos forman un rombo o square shape. El brazo AB consta de una resistencia, $ R_ {2} $. El brazo BC consta de una combinación en serie de resistencia, $ R_ {4} $ y condensador, $ C_ {4} $. El brazo CD consta de un condensador, $ C_ {3} $. El brazo DA consta de una combinación en paralelo de resistencia, $ R_ {1} $ y condensador, $ C_ {1} $.

Sea, $ Z_ {1} $, $ Z_ {2} $, $ Z_ {3} $ y $ Z_ {4} $ son las impedancias de los brazos DA, AB, CD y BC respectivamente. losvalues of these impedances estarán

$ Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $

$ \ Flecha derecha Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $

$ Z_ {2} = R_ {2} $

$ Z_ {3} = \ frac {1} {j \ omega C_ {3}} $

$ Z_ {4} = R_ {4} + \ frac {1} {j \ omega C_ {4}} $

$ \ Flecha derecha Z_ {4} = \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} $

Substitute estos valores de impedancia en la siguiente condición de equilibrio del puente de CA.

$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$

$$ \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left (\ frac {1} {j \ omega C_ { 3}} \ right)} {\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} $$

$ \ Flecha derecha \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {j \ omega R_ {1} C_ {3}} $

$ \ Flecha derecha \ frac {1 + j \ omega R_ {4} C_ {4}} {C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ {1} C_ {3}} $

$ \ Flecha derecha \ frac {1} {C_ {4}} + j \ omega R_ {4} = \ frac {R_ {2}} {R_ {1} C_ {3}} + \ frac {j \ omega C_ { 1} R_ {2}} {C_ {3}} $

Por comparing los respectivos términos reales e imaginarios de la ecuación anterior, obtendremos

$ C_ {4} = \ frac {R_ {1} C_ {3}} {R_ {2}} $ Ecuación 1

$ R_ {4} = \ frac {C_ {1} R_ {2}} {C_ {3}} $ Ecuación 2

Sustituyendo los valores de $ R_ {1}, R_ {2} $ y $ C_ {3} $ en la Ecuación 1, obtendremos el valor del capacitor, $ C_ {4} $. De manera similar, sustituyendo los valores de $ R_ {2}, C_ {1} $ y $ C_ {3} $ en la Ecuación 2, obtendremos el valor de la resistencia, $ R_ {4} $.

los advantage del puente de Schering es que tanto los valores de la resistencia, $ R_ {4} $ como del condensador, $ C_ {4} $ son independientes del valor de la frecuencia.

Puente de Viena

Wien’s bridgees un puente de CA que tiene cuatro brazos, que están conectados en forma de rombo o cuadrado. Entre dos brazos constan de una sola resistencia, un brazo consta de una combinación en paralelo de resistencia y condensador y el otro brazo consta de una combinación en serie de resistencia y condensador.

El detector de CA y la fuente de voltaje de CA también son necesarios para encontrar el valor de la frecuencia. Por lo tanto, uno de estos dos se coloca en una diagonal del puente de Wien y el otro se coloca en otra diagonal del puente de Wien.

los circuit diagram del puente de Wien se muestra en la siguiente figura.

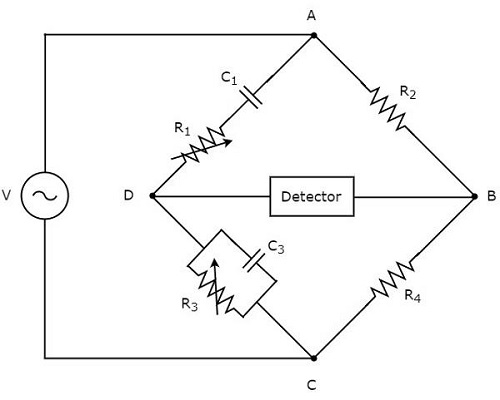
En el circuito anterior, los brazos AB, BC, CD y DA juntos forman un rombo o square shape. Los brazos, AB y BC constan de resistencias, $ R_ {2} $ y $ R_ {4} $ respectivamente. El brazo, CD, consta de una combinación en paralelo de resistencia, $ R_ {3} $ y condensador, $ C_ {3} $. El brazo, DA consta de una combinación en serie de resistencia, $ R_ {1} $ y condensador, $ C_ {1} $.

Sea, $ Z_ {1}, Z_ {2}, Z_ {3} $ y $ Z_ {4} $ son las impedancias de los brazos DA, AB, CD y BC respectivamente. losvalues of these impedances estarán

$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$

$$ \ Flecha derecha Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $$

$ Z_ {2} = R_ {2} $

$$ Z_ {3} = \ frac {R_ {3} \ left (\ frac {1} {j \ omega C_ {3}} \ right)} {R_ {3} + \ frac {1} {j \ omega C_ {3}}} $$

$$ \ Flecha derecha Z_ {3} = \ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} $$

$ Z_ {4} = R_ {4} $

Substitute estos valores de impedancia en la siguiente condición de equilibrio del puente de CA.

$$ Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $$

$$ \ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} \ right) R_ {4} = R_ {2} \ left (\ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} \ right) $$

$ \ Flecha derecha \ izquierda (1 + j \ omega R_ {1} C_ {1} \ derecha) \ izquierda (1 + j \ omega R_ {3} C_ {3} \ derecha) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3} $

$ \ Flecha derecha \ izquierda (1 + j \ omega R_ {3} C_ {3} + j \ omega R_ {1} C_ {1} - \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3} $

$ \ Flecha derecha R_ {4} \ izquierda (\ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ derecha) + j \ omega R_ {4} \ izquierda (R_ {3} C_ {3} + R_ {1} C_ {1} \ right) = j \ omega C_ {1} R_ {2} R_ {3} $

Equate el respectivo real terms de la ecuación anterior.

$$ R_ {4} \ left (1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) = 0 $$

$ \ Flecha derecha 1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} = 0 $

$ \ Flecha derecha 1 = \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} $

$ \ omega = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $

Substitute, $ \ omega = 2 \ pi f $ en la ecuación anterior.

$$ \ Flecha derecha 2 \ pi f = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $$

$ \ Flecha derecha f = \ frac {1} {2 \ pi \ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $

Podemos encontrar el valor de la frecuencia, $ f $ de la fuente de voltaje de CA sustituyendo los valores de $ R_ {1}, R_ {3}, C_ {1} $ y $ C_ {3} $ en la ecuación anterior.

Si $ R_ {1} = R_ {3} = R $ y $ C_ {1} = C_ {3} = C $, entonces podemos encontrar el valor de la frecuencia, $ f $ de la fuente de voltaje CA usando la siguiente fórmula .

$$ f = \ frac {1} {2 \ pi RC} $$

El puente de Wein se utiliza principalmente para encontrar el frequency value del rango AF.

Básicamente, Transducer convierte una forma de energía en otra forma de energía. El transductor, que convierte una forma de energía no eléctrica en una forma eléctrica de energía, se conoce comoelectrical transducer. losblock diagram del transductor eléctrico se muestra en la siguiente figura.

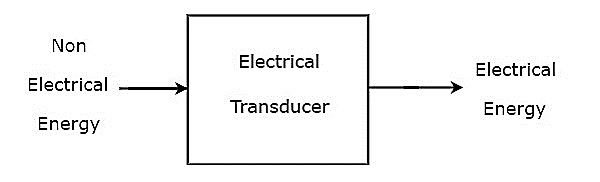
Como se muestra en la figura, el transductor eléctrico producirá una salida que tiene energía eléctrica. La salida del transductor eléctrico es equivalente a la entrada, que tiene energía no eléctrica.

Tipos de transductores eléctricos

Básicamente, los transductores eléctricos se pueden clasificar en los siguientes two types.

• Transductores activos
• Transductores pasivos

Ahora, analicemos brevemente estos dos tipos de transductores.

Transductores activos

El transductor, que puede producir una de las magnitudes eléctricas, como voltaje y corriente, se conoce como active transducer. También se denomina transductor autogenerador, ya que no requiere ninguna fuente de alimentación externa.

los block diagram del transductor activo se muestra en la siguiente figura.

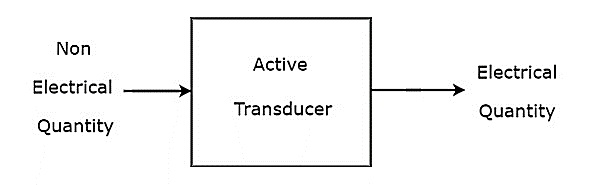
Como se muestra en la figura, el transductor activo producirá una cantidad eléctrica (o señal), que es equivalente a la cantidad de entrada no eléctrica (o señal).

Examples

A continuación se muestran ejemplos de transductores activos.

• Transductor piezoeléctrico
• Foto transductor eléctrico
• Transductor termoeléctrico

Hablaremos de estos transductores activos en el próximo capítulo.

Transductores pasivos

El transductor, que no puede producir cantidades eléctricas como voltaje y corriente, se conoce como passive transducer. Pero, produce la variación en uno de los elementos pasivos como resistencia (R), inductor (L) y condensador (C). El transductor pasivo requiere una fuente de alimentación externa.

los block diagram del transductor pasivo se muestra en la siguiente figura.

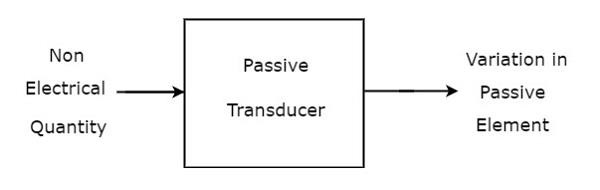
Como se muestra en la figura, el transductor pasivo producirá una variación en el elemento pasivo de acuerdo con la variación en la cantidad de entrada no eléctrica (o señal).

Examples

A continuación se muestran ejemplos de transductores pasivos.

• Transductor resistivo
• Transductor inductivo
• Transductor capacitivo

Hablaremos de estos transductores pasivos en capítulos posteriores.

Active transduceres un transductor, que convierte la cantidad no eléctrica en una cantidad eléctrica. Consideremos las magnitudes no eléctricas como la presión, la iluminación de la luz y la temperatura. Por tanto, obtendremos los siguientes tres transductores activos en función de la cantidad no eléctrica que elijamos.

• Transductor piezoeléctrico
• Foto transductor eléctrico
• Transductor termoeléctrico

Ahora, hablemos de estos tres transductores activos uno por uno.

Transductor piezoeléctrico

Se dice que un transductor activo es piezo electric transducer, cuando produce una cantidad eléctrica equivalente a la entrada de presión. Las siguientes tres sustancias exhiben un efecto piezoeléctrico.

• Quartz
• Sales de Rochelle
• Tourmaline

El efecto piezoeléctrico exhibido por estas tres sustancias es las sales de Turmalina, Cuarzo y Rochelle, en este orden ascendente. El orden ascendente de resistencia mecánica que tienen estas tres sustancias es sales de Rochelle, Cuarzo, Turmalina.

Quartz se utiliza como transductor piezoeléctrico, ya que exhibe el efecto piezoeléctrico moderado y tiene una resistencia mecánica moderada entre esas tres sustancias piezoeléctricas.

Transductor de cuarzo

los circuit diagramdel transductor de cuarzo se muestra en la siguiente figura. Como se muestra en la figura, el cristal de cuarzo se coloca entre la base y el miembro sumador de fuerzas. El voltaje de salida se puede medir a través de los electrodos metálicos, que se colocan en dos lados del cristal de cuarzo.

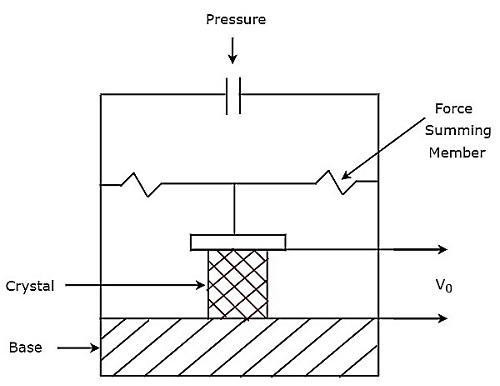
los output voltage, $ V_ {0} $ del transductor de presión anterior será

$$ V_ {0} = \ frac {Q} {C} $$

Foto transductor eléctrico

Se dice que un transductor activo es un transductor fotoeléctrico, cuando produce una cantidad eléctrica equivalente a la iluminación de la entrada de luz. loscircuit diagram del transductor fotoeléctrico se muestra en la siguiente figura.

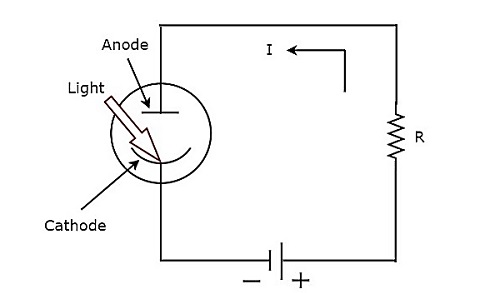
los working del foto transductor eléctrico se menciona a continuación.

• Step1 - El transductor fotoeléctrico libera electrones, cuando la luz incide sobre su cátodo.

• Step2 - El transductor fotoeléctrico produce una corriente I en el circuito debido a la atracción de electrones hacia el ánodo.

Podemos encontrar el sensitivity de transductor fotoeléctrico utilizando la siguiente fórmula.

$$ S = \ frac {I} {i} $$

Dónde,

$ S $ es la sensibilidad del foto transductor eléctrico

$ I $ es la corriente de salida del foto transductor eléctrico

$ i $ es la iluminación de la entrada de luz del transductor fotoeléctrico

Transductor termoeléctrico

Se dice que un transductor activo es thermo electric transducer, cuando produce una cantidad eléctrica equivalente a la entrada de temperatura. Los siguientes dos transductores son ejemplos de transductores termoeléctricos.

• Transductor de termistor
• Transductor de termopar

Ahora, hablemos de estos dos transductores uno por uno.

Transductor de termistor

La resistencia, que depende de la temperatura, se llama resistencia térmica. En resumen, se llamaThermistor. El coeficiente de temperatura del termistor es negativo. Eso significa que, a medida que aumenta la temperatura, la resistencia del termistor disminuye.

Mathematically, la relación entre la resistencia del termistor y la temperatura se puede representar como

$$ R_ {1} = R_ {2} e ^ \ left (\ beta \ left [\ frac {1} {T_ {1}} - \ frac {1} {T_ {2}} \ right] \ right) $$

Where,

$ R_ {1} $ es la resistencia del termistor a la temperatura $ {T_ {1}} ^ {0} K $

$ R_ {2} $ es la resistencia del termistor a la temperatura $ {T_ {2}} ^ {0} K $

$ \ beta $ es la constante de temperatura

los advantage del transductor termistor es que producirá una respuesta rápida y estable.

Transductor de termopar

El transductor de termopar produce un voltaje de salida para un cambio correspondiente de temperatura en la entrada. Si dos alambres de diferentes metales se unen para crear dos uniones, entonces toda esa configuración se llamaThermocouple. El diagrama de circuito del termopar básico se muestra a continuación:

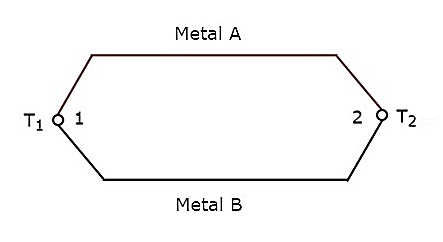
El termopar anterior tiene dos metales, A y B y dos uniones, 1 y 2. Considere una temperatura de referencia constante, $ T_ {2} $ en el cruce 2. Sea la temperatura en el cruce, 1 $ T_ {1} $. El termopar genera unemf (fuerza electromotriz), siempre que los valores de $ T_ {1} $ y $ T_ {2} $ sean diferentes.

Eso significa que el termopar genera una fem, siempre que haya una diferencia de temperatura entre las dos uniones, 1 y 2, y es directamente proporcional a la diferencia de temperatura entre esas dos uniones. Mathematically, se puede representar como

$$ e \ alpha \ left (T_ {1} -T_ {2} \ right) $$

Dónde,

$ e $ es la fem generada por el termopar

El circuito de termopar anterior se puede representar como se muestra en la figura siguiente para aplicaciones prácticas.

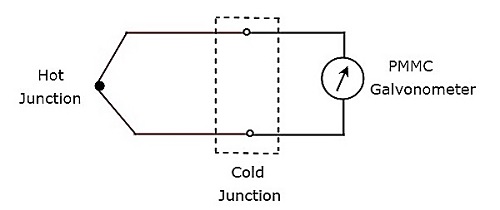
La parte del circuito que se encuentra entre las uniones frías y calientes, incluidas esas dos uniones, es un modelo equivalente de termopar básico. Un galvanómetro PMMC está conectado a través de la unión fría y se desvía de acuerdo con la fem generada a través de la unión fría.Thermocouple transducer es el transductor termoeléctrico más utilizado.

passive transduceres un transductor, que produce la variación en elemento pasivo. Consideraremos los elementos pasivos como resistencia, inductor y condensador. Por tanto, obtendremos los siguientes tres transductores pasivos en función del elemento pasivo que elijamos.

• Transductor resistivo
• Transductor inductivo
• Transductor capacitivo

Ahora, hablemos de estos tres transductores pasivos uno por uno.

Transductor resistivo

Se dice que un transductor pasivo es un resistive transducer, cuando produce la variación (cambio) en el valor de resistencia. la siguiente fórmula pararesistance, R de un conductor metálico.

$$ R = \ frac {\ rho \: l} {A} $$

Dónde,

$ \ rho $ es la resistividad del conductor

$ l $ es la longitud del conductor

$ A $ es el área de la sección transversal del conductor

El valor de la resistencia depende de los tres parámetros $ \ rho, l $ & $ A $. Entonces, podemos hacerresistive transducersbasado en la variación en uno de los tres parámetros $ \ rho, l $ & $ A $. La variación en cualquiera de esos tres parámetros cambia el valor de resistencia.

• Resistencia, R es directamente proporcional a la resistivitydel conductor, $ \ rho $. Entonces, a medida que la resistividad del conductor, $ \ rho $ aumenta el valor de la resistencia, R también aumenta. De manera similar, a medida que la resistividad del conductor, $ \ rho $ disminuye el valor de la resistencia, R también disminuye.

• Resistencia, R es directamente proporcional a la lengthde conductor, $ l $. Entonces, a medida que la longitud del conductor, $ l $ aumenta el valor de la resistencia, R también aumenta. De manera similar, a medida que la longitud del conductor, $ l $ disminuye el valor de la resistencia, R también disminuye.

• Resistencia, R es inversamente proporcional a la cross sectional areadel director, $ A $. Entonces, a medida que el área de la sección transversal del conductor, $ A $ aumenta el valor de la resistencia, R disminuye. De manera similar, a medida que el área de la sección transversal del conductor, $ A $ disminuye el valor de la resistencia, R aumenta.

Transductor inductivo

Se dice que un transductor pasivo es un inductive transducer, cuando produce la variación (cambio) en el valor de inductancia. la siguiente fórmula parainductance, L de un inductor.

$ L = \ frac {N ^ {2}} {S} $ Ecuación 1

Dónde,

$ N $ es el número de vueltas de la bobina

$ S $ es el número de vueltas de la bobina

la siguiente fórmula para reluctance, S de bobina.

$ S = \ frac {l} {\ mu A} $ Ecuación 2

Dónde,

$ l $ es la longitud del circuito magnético

$ \ mu $ es la permeabilidad del núcleo

$ A $ es el área del circuito magnético a través del cual fluye el flujo

Sustituya la Ecuación 2 en la Ecuación 1.

$$ L = \ frac {N ^ {2}} {\ left (\ frac {l} {\ mu A} \ right)} $$

$ \ Flecha derecha L = \ frac {N ^ {2} \ mu A} {l} $ Ecuación 3

De la Ecuación 1 y la Ecuación 3, podemos concluir que el valor de la inductancia depende de los tres parámetros $ N, S $ & $ \ mu $. Entonces, podemos hacerinductive transducersbasado en la variación en uno de los tres parámetros $ N, S $ & $ \ mu $. Porque, la variación en cualquiera de esos tres parámetros cambia el valor de inductancia.

• Inductancia, L es directamente proporcional al cuadrado de la number of turns of coil. Entonces, a medida que el número de vueltas de la bobina, $ N $ aumenta el valor de la inductancia, $ L $ también aumenta. De manera similar, a medida que el número de vueltas de la bobina, $ N $ disminuye el valor de la inductancia, $ L $ también disminuye.

• Inductancia, $ L $ es inversamente proporcional a reluctance of coil, $ S $. Entonces, a medida que la resistencia de la bobina, $ S $ aumenta el valor de la inductancia, $ L $ disminuye. De manera similar, a medida que la resistencia de la bobina, $ S $ disminuye el valor de la inductancia, $ L $ aumenta.

• Inductancia, L es directamente proporcional a permeability of core, $ \ mu $. Entonces, a medida que la permeabilidad del núcleo, $ \ mu $ aumenta el valor de la inductancia, L también aumenta. De manera similar, a medida que la permeabilidad del núcleo, $ \ mu $ disminuye el valor de la inductancia, L también disminuye.

Transductor capacitivo

Se dice que un transductor pasivo es un capacitive transducer, cuando produce la variación (cambio) en el valor de capacitancia. la siguiente fórmula paracapacitance, C de un condensador de placas paralelas.

$$ C = \ frac {\ varepsilon A} {d} $$

Dónde,

$ \ varepsilon $ es la permitividad o la constante dieléctrica

$ A $ es el área efectiva de dos placas

$ d $ es el área efectiva de dos placas

El valor de capacitancia depende de los tres parámetros $ \ varepsilon, A $ & $ d $. Entonces, podemos hacercapacitive transducersbasado en la variación en uno de los tres parámetros $ \ varepsilon, A $ & $ d $. Porque, la variación en cualquiera de esos tres parámetros cambia el valor de capacitancia.

• Capacitancia, C es directamente proporcional a permittivity, $ \ varepsilon $. Entonces, a medida que la permitividad, $ \ varepsilon $ aumenta el valor de la capacitancia, C también aumenta. De manera similar, a medida que la permitividad, $ \ varepsilon $ disminuye el valor de la capacitancia, C también disminuye.

• La capacitancia, C es directamente proporcional a la effective area of two plates, $ A $. Entonces, a medida que el área efectiva de dos placas, $ A $ aumenta el valor de la capacitancia, C también aumenta. De manera similar, a medida que el área efectiva de dos placas, $ A $ disminuye el valor de la capacitancia, C también disminuye.

• La capacitancia, C es inversamente proporcional a la distance between two plates, $ d $. Entonces, a medida que la distancia entre dos placas, $ d $ aumenta el valor de la capacitancia, C disminuye. De manera similar, a medida que la distancia entre dos placas, $ d $ disminuye el valor de la capacitancia, C aumenta.

En este capítulo, discutimos sobre tres transductores pasivos. En el próximo capítulo, analicemos un ejemplo para cada transductor pasivo.

los physical quantitiescomo el desplazamiento, la velocidad, la fuerza, la temperatura, etc., son todas magnitudes no eléctricas. El transductor activo convierte la cantidad física en una señal eléctrica. Considerando que, el transductor pasivo convierte la cantidad física en la variación del elemento pasivo.

Entonces, según el requisito, podemos elegir entre transductor activo o transductor pasivo. En este capítulo, analicemos cómo medir el desplazamiento utilizando un transductor pasivo. Si un cuerpo que se mueve de un punto a otro en línea recta, entonces la longitud entre esos dos puntos se llamadisplacement.

Tenemos lo siguiente three passive transducers

• Transductor resistivo
• Transductor inductivo
• Transductor capacitivo

Ahora, hablemos sobre la medición del desplazamiento con estos tres transductores pasivos uno por uno.

Medición de desplazamiento mediante transductor resistivo

los circuit diagram del transductor resistivo, que se utiliza para medir el desplazamiento, se muestra en la siguiente figura.

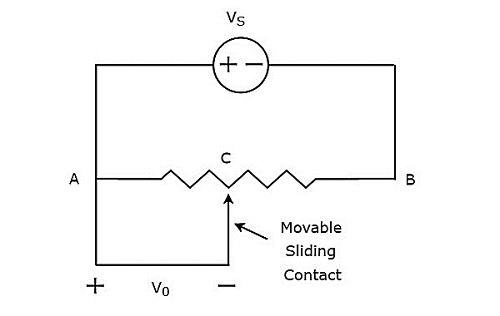
El circuito anterior consta de un potenciómetro y una fuente de voltaje, $ V_ {S} $. Podemos decir que estos dos están conectados en paralelo con respecto a los puntos A y B. El potenciómetro tiene un contacto deslizante, que se puede variar. Entonces, el punto C es variable. En el circuito anterior, eloutput voltage, $ V_ {0} $ se mide en los puntos A y C.

Mathematically, la relación entre los voltajes y las distancias se puede representar como

$$ \ frac {V_ {0}} {V_ {S}} = \ frac {AC} {AB} $$

Por tanto, debemos conectar el cuerpo cuyo desplazamiento se va a medir al contacto deslizante. Entonces, siempre que el cuerpo se mueve en línea recta, el punto C también varía. Debido a esto, el voltaje de salida, $ V_ {0} $ también cambia en consecuencia.

En este caso, podemos encontrar el desplazamiento midiendo el voltaje de salida, $ V_ {0} $.

Medición de desplazamiento mediante transductor inductivo

los circuit diagram del transductor inductivo, que se utiliza para medir el desplazamiento, se muestra en la siguiente figura.

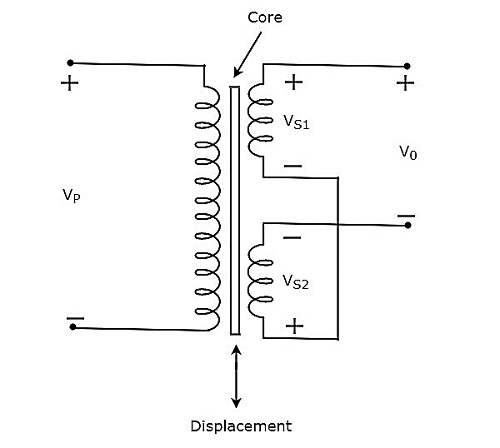
El transformador presente en el circuito anterior tiene un devanado primario y dos devanados secundarios. Aquí, los puntos finales de dos devanados secundarios se unen. Entonces, podemos decir que estos dos devanados secundarios están conectados enseries opposition.

El voltaje, $ V_ {P} $ se aplica a través del devanado primario del transformador. Sea, el voltaje desarrollado a través de cada devanado secundario es ð ?? '‰ ð ??' † 1 y ð ?? '‰ ð ??' † 2. El voltaje de salida, $ V_ {0} $ se toma a través de los puntos de inicio de dos devanados secundarios.

Mathematically, el voltaje de salida, ð ?? '‰ 0 se puede escribir como

$$ V_ {0} = V_ {S1} -V_ {S2} $$

El transformador presente en el circuito anterior se llama differential transformer, ya que produce un voltaje de salida, que es la diferencia entre $ V_ {S1} $ y $ V_ {S2} $.

• Si el núcleo está en la posición central, entonces el voltaje de salida, $ V_ {0} $ será igual a cero. Porque, las respectivas magnitudes y fases de $ V_ {S1} $ y $ V_ {S2} $ son las mismas.

• Si el núcleo no está en la posición central, entonces el voltaje de salida, $ V_ {0} $ tendrá alguna magnitud y fase. Porque, las respectivas magnitudes y fases de $ V_ {S1} $ y $ V_ {S2} $ no son iguales.

Por tanto, debemos conectar el cuerpo cuyo desplazamiento se va a medir al núcleo central. Entonces, siempre que el cuerpo se mueve en línea recta, la posición central del núcleo varía. Debido a esto, el voltaje de salida, $ V_ {0} $ también cambia en consecuencia.

En este caso, podemos encontrar el displacementmidiendo el voltaje de salida, $ V_ {0} $. La magnitud y la fase del voltaje de salida, $ V_ {0} $ representa el desplazamiento del cuerpo y su dirección respectivamente.

Medición de desplazamiento mediante transductor capacitivo

los circuit diagram del transductor capacitivo, que se utiliza para medir el desplazamiento, se muestra en la siguiente figura.

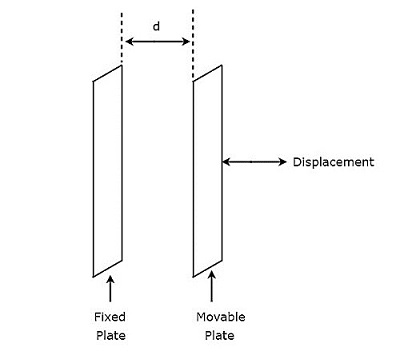
los capacitor, que está presente en el circuito anterior tiene dos placas paralelas. Entre los cuales, una placa es fija y la otra placa es móvil. Debido a esto, el espacio entre estas dos placas también variará. el valor de la capacitancia cambia a medida que cambia el espacio entre dos placas de condensador.

Por tanto, debemos conectar el cuerpo cuyo displacementdebe medirse en la placa móvil de un condensador. Entonces, siempre que el cuerpo se mueve en línea recta, el espacio entre las dos placas del capacitor varía. Debido a esto, el valor de capacitancia cambia.

Los sistemas utilizados para la adquisición de datos se conocen como data acquisition systems. Estos sistemas de adquisición de datos realizarán tareas tales como conversión de datos, almacenamiento de datos, transmisión de datos y procesamiento de datos.

Los sistemas de adquisición de datos consideran lo siguiente analog signals.

• Señales analógicas, que se obtienen de la medición directa de magnitudes eléctricas como tensiones CC y CA, corrientes CC y CA, resistencias, etc.

• Señales analógicas, que se obtienen de transductores como LVDT, termopar, etc.

Tipos de sistemas de adquisición de datos

Los sistemas de adquisición de datos se pueden clasificar en los siguientes two types.

• Sistemas de adquisición de datos analógicos
• Sistemas de adquisición de datos digitales

Ahora, analicemos estos dos tipos de sistemas de adquisición de datos uno por uno.

Sistemas de adquisición de datos analógicos

Los sistemas de adquisición de datos que pueden funcionar con señales analógicas se conocen como analog data acquisition systems. A continuación se muestran los bloques de los sistemas de adquisición de datos analógicos.

• Transducer - Convierte magnitudes físicas en señales eléctricas.

• Signal conditioner - Realiza funciones como amplificación y selección de la porción deseada de la señal.

• Display device - Muestra las señales de entrada con fines de monitoreo.

• Graphic recording instruments - Estos se pueden utilizar para hacer el registro de datos de entrada de forma permanente.

• Magnetic tape instrumentation - Se utiliza para adquirir, almacenar y reproducir datos de entrada.

Sistemas de adquisición de datos digitales

Los sistemas de adquisición de datos, que pueden funcionar con señales digitales, se conocen como digital data acquisition systems. Por tanto, utilizan componentes digitales para almacenar o mostrar la información.

Principalmente, lo siguiente operations tienen lugar en la adquisición de datos digitales.

• Adquisición de señales analógicas
• Conversión de señales analógicas en señales digitales o datos digitales
• Procesamiento de señales digitales o datos digitales

Los siguientes son los bloques de Digital data acquisition systems.

• Transducer - Convierte magnitudes físicas en señales eléctricas.

• Signal conditioner - Realiza funciones como amplificación y selección de la porción deseada de la señal.

• Multiplexer- conecta una de las múltiples entradas a la salida. Entonces, actúa como un convertidor paralelo a serie.

• Analog to Digital Converter - Convierte la entrada analógica en su salida digital equivalente.

• Display device - Muestra los datos en formato digital.

• Digital Recorder - Se utiliza para registrar los datos en formato digital.

Los sistemas de adquisición de datos se utilizan en diversas aplicaciones, como la biomédica y la aeroespacial. Por lo tanto, podemos elegir sistemas de adquisición de datos analógicos o sistemas de adquisición de datos digitales según los requisitos.