MATLAB - Guía rápida

MATLAB (laboratorio de matrices) es un lenguaje de programación de alto nivel de cuarta generación y un entorno interactivo para cálculo numérico, visualización y programación.

MATLAB es desarrollado por MathWorks.

Permite manipulaciones matriciales; trazado de funciones y datos; implementación de algoritmos; creación de interfaces de usuario; interactuar con programas escritos en otros lenguajes, incluidos C, C ++, Java y FORTRAN; analizar datos; desarrollar algoritmos; y crear modelos y aplicaciones.

Tiene numerosos comandos integrados y funciones matemáticas que lo ayudan en los cálculos matemáticos, la generación de gráficos y la ejecución de métodos numéricos.

El poder de las matemáticas computacionales de MATLAB

MATLAB se utiliza en todas las facetas de las matemáticas computacionales. A continuación se muestran algunos cálculos matemáticos de uso común donde se usa con más frecuencia:

• Tratar con matrices y matrices
• Trazado y gráficos 2-D y 3-D
• Álgebra lineal
• Ecuaciones algebraicas
• Funciones no lineales
• Statistics
• Análisis de los datos
• Cálculo y ecuaciones diferenciales
• Cálculos numéricos
• Integration
• Transforms
• Ajuste de curvas
• Varias otras funciones especiales

Características de MATLAB

Las siguientes son las características básicas de MATLAB:

• Es un lenguaje de alto nivel para cálculo numérico, visualización y desarrollo de aplicaciones.

• También proporciona un entorno interactivo para la exploración, el diseño y la resolución de problemas iterativos.

• Proporciona una amplia biblioteca de funciones matemáticas para álgebra lineal, estadística, análisis de Fourier, filtrado, optimización, integración numérica y resolución de ecuaciones diferenciales ordinarias.

• Proporciona gráficos integrados para visualizar datos y herramientas para crear gráficos personalizados.

• La interfaz de programación de MATLAB proporciona herramientas de desarrollo para mejorar el mantenimiento de la calidad del código y maximizar el rendimiento.

• Proporciona herramientas para crear aplicaciones con interfaces gráficas personalizadas.

• Proporciona funciones para integrar algoritmos basados ​​en MATLAB con aplicaciones y lenguajes externos como C, Java, .NET y Microsoft Excel.

Usos de MATLAB

MATLAB se utiliza ampliamente como herramienta computacional en ciencia e ingeniería que abarca los campos de la física, la química, las matemáticas y todas las corrientes de ingeniería. Se utiliza en una variedad de aplicaciones que incluyen:

• Procesamiento de señales y comunicaciones
• Procesamiento de imagen y video
• Sistemas de control
• Prueba y Medida
• Finanzas Computacionales
• Biología Computacional

Configuración del entorno local

La configuración del entorno MATLAB es cuestión de unos pocos clics. El instalador se puede descargar desde aquí .

MathWorks proporciona el producto con licencia, una versión de prueba y también una versión para estudiantes. Debe iniciar sesión en el sitio y esperar un poco su aprobación.

Después de descargar el instalador, el software se puede instalar con unos pocos clics.

Comprensión del entorno MATLAB

El IDE de desarrollo de MATLAB se puede iniciar desde el icono creado en el escritorio. La ventana de trabajo principal en MATLAB se llama escritorio. Cuando se inicia MATLAB, el escritorio aparece en su diseño predeterminado:

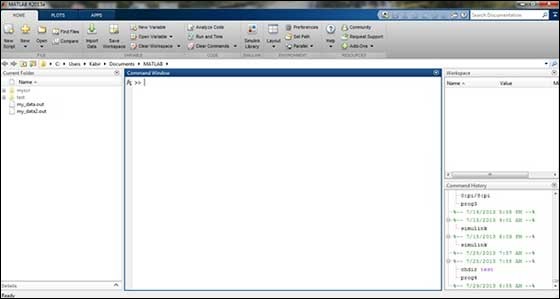
El escritorio tiene los siguientes paneles:

• Current Folder - Este panel le permite acceder a las carpetas y archivos del proyecto.



• Command Window- Esta es el área principal donde se pueden ingresar comandos en la línea de comandos. Se indica mediante el símbolo del sistema (>>).



• Workspace - El espacio de trabajo muestra todas las variables creadas y / o importadas desde archivos.



• Command History - Este panel muestra o devuelve comandos que se ingresan en la línea de comando.

Configurar GNU Octave

Si está dispuesto a utilizar Octave en su máquina (Linux, BSD, OS X o Windows), descargue la última versión de Descargar GNU Octave . Puede consultar las instrucciones de instalación proporcionadas para su máquina.

El entorno MATLAB se comporta como una calculadora supercompleja. Puede ingresar comandos en la línea de comandos >>.

MATLAB es un entorno interpretado. En otras palabras, da un comando y MATLAB lo ejecuta de inmediato.

Práctica práctica

Escriba una expresión válida, por ejemplo,

5 + 5

Y presione ENTER

Cuando hace clic en el botón Ejecutar, o escribe Ctrl + E, MATLAB lo ejecuta inmediatamente y el resultado devuelto es:

ans = 10

Tomemos algunos ejemplos más:

3 ^ 2	       % 3 raised to the power of 2

Cuando hace clic en el botón Ejecutar, o escribe Ctrl + E, MATLAB lo ejecuta inmediatamente y el resultado devuelto es:

ans = 9

Otro ejemplo,

sin(pi /2)	  % sine of angle 90o

Cuando hace clic en el botón Ejecutar, o escribe Ctrl + E, MATLAB lo ejecuta inmediatamente y el resultado devuelto es:

ans = 1

Otro ejemplo,

7/0		      % Divide by zero

Cuando hace clic en el botón Ejecutar, o escribe Ctrl + E, MATLAB lo ejecuta inmediatamente y el resultado devuelto es:

ans = Inf
warning: division by zero

Otro ejemplo,

732 * 20.3

Cuando hace clic en el botón Ejecutar, o escribe Ctrl + E, MATLAB lo ejecuta inmediatamente y el resultado devuelto es:

ans =  1.4860e+04

MATLAB proporciona algunas expresiones especiales para algunos símbolos matemáticos, como pi para π, Inf para ∞, i (y j) para √-1, etc. Nan significa 'no es un número'.

Uso de punto y coma (;) en MATLAB

El punto y coma (;) indica el final de la declaración. Sin embargo, si desea suprimir y ocultar la salida de MATLAB para una expresión, agregue un punto y coma después de la expresión.

Por ejemplo,

x = 3;
y = x + 5

Cuando hace clic en el botón Ejecutar, o escribe Ctrl + E, MATLAB lo ejecuta inmediatamente y el resultado devuelto es:

y =  8

Agregar comentarios

El símbolo de porcentaje (%) se utiliza para indicar una línea de comentario. Por ejemplo,

x = 9	     % assign the value 9 to x

También puede escribir un bloque de comentarios utilizando los operadores de comentarios de bloque% {y%}.

El editor MATLAB incluye herramientas y elementos de menú contextual para ayudarlo a agregar, eliminar o cambiar el formato de los comentarios.

Operadores y caracteres especiales de uso común

MATLAB admite los siguientes operadores y caracteres especiales de uso común:

Operador	Propósito
+	Más; operador de adición.
-	Menos; operador de resta.
*	Operador de multiplicación escalar y matricial.
.*	Operador de multiplicación de matrices.
^	Operador de exponenciación escalar y matricial.
.^	Operador de exponenciación de matriz.
\	Operador de división a la izquierda.
/	Operador de división a la derecha.
.\	Operador de división a la izquierda de matriz.
./	Operador de división por la derecha de matriz.
:	Colon; genera elementos espaciados regularmente y representa una fila o columna completa.
( )	Paréntesis; encierra argumentos de función e índices de matriz; anula la precedencia.
[ ]	Soportes; elementos de matriz de recintos.
.	Punto decimal.
…	Elipsis; operador de continuación de línea
,	Coma; separa declaraciones y elementos en una fila
;	Punto y coma; separa columnas y suprime la visualización.
%	Signo de porcentaje; designa un comentario y especifica el formato.
_	Cotizar signo y transponer operador.
._	Operador de transposición no conjugado.
=	Operador de asignación.

Variables y constantes especiales

MATLAB admite las siguientes variables y constantes especiales:

Nombre	Sentido
ans	Respuesta más reciente.
eps	Exactitud de precisión de punto flotante.
i,j	La unidad imaginaria √-1.
Inf	Infinito.
NaN	Resultado numérico indefinido (no un número).
pi	El número π

Nombrar variables

Los nombres de las variables consisten en una letra seguida de cualquier número de letras, dígitos o guiones bajos.

MATLAB es case-sensitive.

Los nombres de las variables pueden tener cualquier longitud, sin embargo, MATLAB usa solo los primeros N caracteres, donde N viene dado por la función namelengthmax.

Guardar su trabajo

los save El comando se usa para guardar todas las variables en el espacio de trabajo, como un archivo con extensión .mat, en el directorio actual.

Por ejemplo,

save myfile

Puede volver a cargar el archivo en cualquier momento utilizando el load mando.

load myfile

En el entorno MATLAB, cada variable es una matriz o matriz.

Puede asignar variables de forma sencilla. Por ejemplo,

x = 3	       % defining x and initializing it with a value

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

x = 3

Crea una matriz de 1 por 1 llamada x y almacena el valor 3 en su elemento. Veamos otro ejemplo,

x = sqrt(16) 	% defining x and initializing it with an expression

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

x = 4

Tenga en cuenta que -

• Una vez que se ingresa una variable en el sistema, puede consultarla más tarde.

• Las variables deben tener valores antes de usarse.

• Cuando una expresión devuelve un resultado que no está asignado a ninguna variable, el sistema lo asigna a una variable llamada ans, que se puede usar más adelante.

Por ejemplo,

sqrt(78)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =  8.8318

Puedes usar esta variable ans -

sqrt(78);
9876/ans

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =  1118.2

Veamos otro ejemplo:

x = 7 * 8;
y = x * 7.89

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

y =  441.84

Varias asignaciones

Puede tener varias asignaciones en la misma línea. Por ejemplo,

a = 2; b = 7; c = a * b

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

c = 14

¡He olvidado las Variables!

los who El comando muestra todos los nombres de variables que ha utilizado.

who

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

Your variables are:
a    ans  b    c

los whos el comando muestra poco más sobre las variables -

• Variables actualmente en memoria
• Tipo de cada variable
• Memoria asignada a cada variable
• Si son variables complejas o no

whos

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

Attr Name        Size        Bytes      Class
==== ====        ====        ====       ===== 
   a             1x1           8        double
   ans           1x70         757        cell
   b             1x1           8        double
   c             1x1           8        double

Total is 73 elements using 781 bytes

los clear comando borra todas las variables (o las especificadas) de la memoria.

clear x     % it will delete x, won't display anything
clear       % it will delete all variables in the workspace
            %  peacefully and unobtrusively

Asignaciones largas

Las asignaciones largas se pueden extender a otra línea usando puntos suspensivos (...). Por ejemplo,

initial_velocity = 0;
acceleration = 9.8;
time = 20;
final_velocity = initial_velocity + acceleration * time

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

final_velocity = 196

El comando de formato

De forma predeterminada, MATLAB muestra números con cuatro valores de posición decimales. Esto se conoce comoshort format.

Sin embargo, si desea más precisión, debe utilizar el format mando.

los format long El comando muestra 16 dígitos después del decimal.

Por ejemplo

format long
x = 7 + 10/3 + 5 ^ 1.2

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

x = 17.2319816406394

Otro ejemplo,

format short
x = 7 + 10/3 + 5 ^ 1.2

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

x = 17.232

los format bankEl comando redondea los números a dos decimales. Por ejemplo,

format bank
daily_wage = 177.45;
weekly_wage = daily_wage * 6

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

weekly_wage = 1064.70

MATLAB muestra números grandes usando notación exponencial.

los format short e El comando permite mostrar en forma exponencial con cuatro lugares decimales más el exponente.

Por ejemplo,

format short e
4.678 * 4.9

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans = 2.2922e+01

los format long eEl comando permite mostrar en forma exponencial con cuatro lugares decimales más el exponente. Por ejemplo,

format long e
x = pi

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

x = 3.141592653589793e+00

los format ratEl comando da la expresión racional más cercana resultante de un cálculo. Por ejemplo,

format rat
4.678 * 4.9

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans = 34177/1491

Crear vectores

Un vector es una matriz unidimensional de números. MATLAB permite crear dos tipos de vectores:

• Vectores de fila
• Vectores de columna

Row vectors se crean encerrando el conjunto de elementos entre corchetes, utilizando espacio o coma para delimitar los elementos.

Por ejemplo,

r = [7 8 9 10 11]

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

r =

   7    8    9   10   11

Otro ejemplo,

r = [7 8 9 10 11];
t = [2, 3, 4, 5, 6];
res = r + t

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

res =

         9         11         13         15         17

Column vectors se crean encerrando el conjunto de elementos entre corchetes, utilizando punto y coma (;) para delimitar los elementos.

c = [7;  8;  9;  10; 11]

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

c =
       7       
       8       
       9       
      10       
      11

Creando Matrices

Una matriz es una matriz bidimensional de números.

En MATLAB, se crea una matriz ingresando cada fila como una secuencia de elementos separados por espacios o comas, y el final de una fila está demarcado por un punto y coma. Por ejemplo, creemos una matriz de 3 por 3 como:

m = [1 2 3; 4 5 6; 7 8 9]

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

m =
       1              2              3       
       4              5              6       
       7              8              9

MATLAB es un programa interactivo para el cálculo numérico y la visualización de datos. Puede ingresar un comando escribiéndolo en el indicador de MATLAB '>>' en elCommand Window.

En esta sección, proporcionaremos listas de comandos generales de MATLAB de uso común.

Comandos para administrar una sesión

MATLAB proporciona varios comandos para administrar una sesión. La siguiente tabla proporciona todos estos comandos:

Mando	Propósito
clc	Borra la ventana de comandos.
claro	Elimina variables de la memoria.
existe	Verifica la existencia de archivo o variable.
global	Declara que las variables son globales.
ayuda	Busca un tema de ayuda.
buscar	Busca entradas de ayuda para una palabra clave.
dejar	Detiene MATLAB.
OMS	Enumera las variables actuales.
quien	Enumera las variables actuales (visualización larga).

Comandos para trabajar con el sistema

MATLAB proporciona varios comandos útiles para trabajar con el sistema, como guardar el trabajo actual en el espacio de trabajo como un archivo y cargar el archivo más tarde.

También proporciona varios comandos para otras actividades relacionadas con el sistema, como mostrar la fecha, listar archivos en el directorio, mostrar el directorio actual, etc.

La siguiente tabla muestra algunos comandos relacionados con el sistema de uso común:

Mando	Propósito
discos compactos	Cambia el directorio actual.
fecha	Muestra la fecha actual.
Eliminar	Elimina un archivo.
diario	Activa / desactiva la grabación de archivos de diario.
dir	Muestra todos los archivos del directorio actual.
carga	Carga variables de espacio de trabajo desde un archivo.
camino	Muestra la ruta de búsqueda.
pwd	Muestra el directorio actual.
salvar	Guarda las variables del espacio de trabajo en un archivo.
tipo	Muestra el contenido de un archivo.
qué	Muestra todos los archivos MATLAB en el directorio actual.
wklread	Lee el archivo de hoja de cálculo .wk1.

Comandos de entrada y salida

MATLAB proporciona los siguientes comandos relacionados con la entrada y la salida:

Mando	Propósito
disp	Muestra el contenido de una matriz o cadena.
fscanf	Leer datos formateados de un archivo.
formato	Controla el formato de visualización de la pantalla.
fprintf	Realiza escrituras formateadas en pantalla o archivo.
entrada	Muestra mensajes y espera una entrada.
;	Suprime la serigrafía.

los fscanf y fprintfLos comandos se comportan como las funciones C scanf y printf. Admiten los siguientes códigos de formato:

Código de formato	Propósito
%s	Formatee como una cadena.
%d	Formatee como un número entero.
%f	Formatee como valor de coma flotante.
%e	Formatee como valor de coma flotante en notación científica.
%g	Formatee en la forma más compacta:% fo% e.
\n	Inserte una nueva línea en la cadena de salida.
\t	Inserte una pestaña en la cadena de salida.

La función de formato tiene las siguientes formas que se utilizan para la visualización numérica:

Función de formato	Mostrar hasta
formato corto	Cuatro dígitos decimales (predeterminado).
formato largo	16 dígitos decimales.
formato corto e	Cinco dígitos más exponente.
formato largo e	16 dígitos más exponentes.
banco de formato	Dos dígitos decimales.
formato +	Positivo, negativo o cero.
formato de rata	Aproximación racional.
formato compacto	Suprime algunos avances de línea.
formato suelto	Se restablece al modo de visualización menos compacto.

Comandos de vector, matriz y arreglo

La siguiente tabla muestra varios comandos utilizados para trabajar con matrices, matrices y vectores:

Mando	Propósito
gato	Concatena matrices.
encontrar	Encuentra índices de elementos distintos de cero.
longitud	Calcula el número de elementos.
linspace	Crea un vector espaciado regularmente.
espacio de registro	Crea un vector espaciado logarítmicamente.
max	Devuelve el elemento más grande.
min	Devuelve el elemento más pequeño.
pinchar	Producto de cada columna.
remodelar	Cambia de tamaño.
Talla	Calcula el tamaño de la matriz.
ordenar	Ordena cada columna.
suma	Suma cada columna.
ojo	Crea una matriz de identidad.
unos	Crea una matriz de unos.
ceros	Crea una matriz de ceros.
cruzar	Calcula productos cruzados de matriz.
punto	Calcula productos escalares matriciales.
det	Calcula el determinante de una matriz.
inv	Calcula la inversa de una matriz.
pinv	Calcula la pseudoinversa de una matriz.
rango	Calcula el rango de una matriz.
rref	Calcula la forma escalonada reducida de las filas.
celda	Crea una matriz de celdas.
celldisp	Muestra la matriz de celdas.
trama celular	Muestra una representación gráfica de la matriz de celdas.
num2cell	Convierte una matriz numérica en una matriz de celdas.
acuerdo	Coincide con listas de entrada y salida.
iscell	Identifica la matriz de celdas.

Comandos de trazado

MATLAB proporciona numerosos comandos para trazar gráficos. La siguiente tabla muestra algunos de los comandos más utilizados para trazar:

Mando	Propósito
eje	Establece límites de eje.
fplot	Trazado inteligente de funciones.
cuadrícula	Muestra líneas de cuadrícula.
trama	Genera un gráfico xy.
impresión	Imprime el trazado o guarda el trazado en un archivo.
título	Coloca el texto en la parte superior del gráfico.
xlabel	Agrega una etiqueta de texto al eje x.
etiqueta	Agrega una etiqueta de texto al eje y.
ejes	Crea objetos de ejes.
cerca	Cierra la trama actual.
cierra todo	Cierra todas las parcelas.
figura	Abre una nueva ventana de figura.
gtext	Permite la colocación de etiquetas con el mouse.
sostener	Congela la trama actual.
leyenda	Colocación de la leyenda con el mouse.
actualizar	Vuelve a dibujar la ventana de la figura actual.
conjunto	Especifica propiedades de objetos como ejes.
subtrama	Crea gráficos en subventanas.
texto	Coloca la cuerda en la figura.
bar	Crea un gráfico de barras.
registro	Crea una gráfica logarítmica.
polar	Crea un diagrama polar.
semilogx	Crea un gráfico semilogarítmico. (abscisa logarítmica).
semilogía	Crea un gráfico semilogarítmico. (ordenada logarítmica).
escalera	Crea trama de escaleras.
vástago	Crea un diagrama de tallo.

Hasta ahora, hemos utilizado el entorno MATLAB como calculadora. Sin embargo, MATLAB también es un poderoso lenguaje de programación, así como un entorno computacional interactivo.

En capítulos anteriores, aprendió cómo ingresar comandos desde el símbolo del sistema de MATLAB. MATLAB también le permite escribir una serie de comandos en un archivo y ejecutar el archivo como una unidad completa, como escribir una función y llamarla.

Los archivos M

MATLAB permite escribir dos tipos de archivos de programa:

• Scripts - los archivos de script son archivos de programa con .m extension. En estos archivos, escribe una serie de comandos que desea ejecutar juntos. Los scripts no aceptan entradas y no devuelven ninguna salida. Operan con datos en el espacio de trabajo.

• Functions - los archivos de funciones también son archivos de programa con .m extension. Las funciones pueden aceptar entradas y devolver salidas. Las variables internas son locales a la función.

Puede utilizar el editor MATLAB o cualquier otro editor de texto para crear su .marchivos. En esta sección, discutiremos los archivos de script. Un archivo de secuencia de comandos contiene varias líneas secuenciales de comandos y llamadas a funciones de MATLAB. Puede ejecutar un script escribiendo su nombre en la línea de comando.

Crear y ejecutar un archivo de script

Para crear archivos de secuencias de comandos, debe utilizar un editor de texto. Puede abrir el editor MATLAB de dos formas:

• Usando el símbolo del sistema
• Usando el IDE

Si está utilizando el símbolo del sistema, escriba editen el símbolo del sistema. Esto abrirá el editor. Puede escribir directamenteedit y luego el nombre del archivo (con extensión .m)

edit 
Or
edit <filename>

El comando anterior creará el archivo en el directorio MATLAB predeterminado. Si desea almacenar todos los archivos de programa en una carpeta específica, deberá proporcionar la ruta completa.

Creemos una carpeta llamada progs. Escriba los siguientes comandos en el símbolo del sistema (>>) -

mkdir progs    % create directory progs under default directory
chdir progs    % changing the current directory to progs
edit  prog1.m  % creating an m file named prog1.m

Si está creando el archivo por primera vez, MATLAB le pedirá que lo confirme. Haga clic en Sí.

Alternativamente, si está utilizando el IDE, elija NUEVO -> Script. Esto también abre el editor y crea un archivo llamado Sin título. Puede nombrar y guardar el archivo después de escribir el código.

Escriba el siguiente código en el editor:

NoOfStudents = 6000;
TeachingStaff = 150;
NonTeachingStaff = 20;
Total = NoOfStudents + TeachingStaff ...
   + NonTeachingStaff;
disp(Total);

Después de crear y guardar el archivo, puede ejecutarlo de dos formas:

• Haciendo clic en el Run en la ventana del editor o

• Simplemente escribiendo el nombre del archivo (sin extensión) en el símbolo del sistema: >> prog1

El indicador de la ventana de comando muestra el resultado:

6170

Ejemplo

Cree un archivo de secuencia de comandos y escriba el siguiente código:

a = 5; b = 7;
c = a + b
d = c + sin(b)
e = 5 * d
f = exp(-d)

Cuando el código anterior se compila y ejecuta, produce el siguiente resultado:

c =  12
d =  12.657
e =  63.285
f =    3.1852e-06

MATLAB no requiere ninguna declaración de tipo o declaración de dimensión. Siempre que MATLAB encuentra un nuevo nombre de variable, crea la variable y asigna el espacio de memoria apropiado.

Si la variable ya existe, MATLAB reemplaza el contenido original con contenido nuevo y asigna nuevo espacio de almacenamiento, cuando sea necesario.

Por ejemplo,

Total = 42

La declaración anterior crea una matriz de 1 por 1 denominada 'Total' y almacena el valor 42 en ella.

Tipos de datos disponibles en MATLAB

MATLAB proporciona 15 tipos de datos fundamentales. Cada tipo de datos almacena datos en forma de matriz o arreglo. El tamaño de esta matriz o matriz es un mínimo de 0 por 0 y esto puede crecer hasta una matriz o matriz de cualquier tamaño.

La siguiente tabla muestra los tipos de datos más utilizados en MATLAB:

No Señor.	Tipo de datos y descripción
1	int8 Entero de 8 bits con signo
2	uint8 Entero sin signo de 8 bits
3	int16 Entero de 16 bits con signo
4	uint16 Entero sin signo de 16 bits
5	int32 Entero de 32 bits con signo
6	uint32 Entero sin signo de 32 bits
7	int64 Entero de 64 bits con signo
8	uint64 Entero sin signo de 64 bits
9	single datos numéricos de precisión simple
10	double datos numéricos de doble precisión
11	logical valores lógicos de 1 o 0, representan verdadero y falso respectivamente
12	char datos de caracteres (las cadenas se almacenan como vector de caracteres)
13	cell array Matriz de celdas indexadas, cada una capaz de almacenar una matriz de diferente dimensión y tipo de datos.
14	structure Estructuras similares a C, cada estructura tiene campos con nombre capaces de almacenar una matriz de una dimensión y tipo de datos diferentes
15	function handle puntero a una función
dieciséis	user classes objetos construidos a partir de una clase definida por el usuario
17	java classes objetos construidos a partir de una clase Java

Ejemplo

Cree un archivo de script con el siguiente código:

str = 'Hello World!'
n = 2345
d = double(n)
un = uint32(789.50)
rn = 5678.92347
c = int32(rn)

Cuando el código anterior se compila y ejecuta, produce el siguiente resultado:

str = Hello World!
n =  2345
d =  2345
un = 790
rn = 5678.9
c =  5679

Conversión de tipo de datos

MATLAB proporciona varias funciones para convertir un valor de un tipo de datos a otro. La siguiente tabla muestra las funciones de conversión de tipos de datos:

Función	Propósito
carbonizarse	Convertir a matriz de caracteres (cadena)
int2str	Convertir datos enteros en cadenas
mat2str	Convertir matriz en cadena
num2str	Convertir número en cadena
str2double	Convertir cadena en valor de doble precisión
str2num	Convertir cadena en número
native2unicode	Convertir bytes numéricos a caracteres Unicode
unicode2native	Convertir caracteres Unicode en bytes numéricos
base2dec	Convierta la cadena de números base N a un número decimal
bin2dec	Convertir una cadena de números binarios en un número decimal
dec2base	Convertir decimal a base N número en cadena
dec2bin	Convertir decimal a binario en una cadena
dec2hex	Convertir decimal a número hexadecimal en cadena
hex2dec	Convierta la cadena numérica hexadecimal en un número decimal
hex2num	Convierta la cadena numérica hexadecimal en un número de doble precisión
num2hex	Convierta sencillos y dobles en cadenas hexadecimales IEEE
cell2mat	Convertir matriz de celdas en matriz numérica
cell2struct	Convertir matriz de celdas en matriz de estructura
celltr	Cree una matriz de celdas de cadenas a partir de una matriz de caracteres
mat2cell	Convierta una matriz en una matriz de celdas con celdas de tamaño potencialmente diferente
num2cell	Convierta una matriz en una matriz de celdas con celdas de tamaño uniforme
struct2cell	Convertir estructura en matriz de celdas

Determinación de tipos de datos

MATLAB proporciona varias funciones para identificar el tipo de datos de una variable.

La siguiente tabla proporciona las funciones para determinar el tipo de datos de una variable:

Función	Propósito
es	Detectar estado
es un	Determinar si la entrada es un objeto de la clase especificada
iscell	Determinar si la entrada es una matriz de celdas
iscellstr	Determinar si la entrada es una matriz de cadenas de celdas
ischar	Determinar si el elemento es una matriz de caracteres
isfield	Determinar si la entrada es un campo de matriz de estructura
isfloat	Determinar si la entrada es una matriz de punto flotante
ishghandle	Verdadero para identificadores de objetos de gráficos de manejo
isinteger	Determinar si la entrada es una matriz de enteros
isjava	Determinar si la entrada es un objeto Java
isologico	Determinar si la entrada es una matriz lógica
isnumérico	Determinar si la entrada es una matriz numérica
isobjeto	Determinar si la entrada es un objeto MATLAB
es real	Verifique si la entrada es una matriz real
isscalar	Determinar si la entrada es escalar
isstr	Determinar si la entrada es una matriz de caracteres
isstruct	Determinar si la entrada es una matriz de estructura
isvector	Determine si la entrada es vectorial
clase	Determinar la clase de objeto
validar atributos	Verificar la validez de la matriz
quien	Lista de variables en el espacio de trabajo, con tamaños y tipos

Ejemplo

Cree un archivo de script con el siguiente código:

x = 3
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
 
x = 23.54
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
 
x = [1 2 3]
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
 
x = 'Hello'
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)

Cuando ejecuta el archivo, produce el siguiente resultado:

x = 3
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x = 23.540
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x =

          1          2          3

ans = 0
ans = 1
ans = 1
ans = 0
x = Hello
ans = 0
ans = 0
ans = 1
ans = 0
ans = 0

Un operador es un símbolo que le dice al compilador que realice manipulaciones matemáticas o lógicas específicas. MATLAB está diseñado para operar principalmente en matrices y arreglos completos. Por lo tanto, los operadores de MATLAB funcionan tanto con datos escalares como no escalares. MATLAB permite los siguientes tipos de operaciones elementales:

• Operadores aritméticos
• Operadores relacionales
• Operadores logicos
• Operaciones bit a bit
• Establecer operaciones

Operadores aritméticos

MATLAB permite dos tipos diferentes de operaciones aritméticas:

• Operaciones aritméticas matriciales
• Operaciones aritméticas de matrices

Las operaciones aritméticas matriciales son las mismas que se definen en álgebra lineal. Las operaciones de matriz se ejecutan elemento por elemento, tanto en una matriz unidimensional como multidimensional.

Los operadores de matriz y los operadores de matriz se diferencian por el símbolo de punto (.). Sin embargo, como la operación de suma y resta es la misma para matrices y arreglos, el operador es el mismo para ambos casos. La siguiente tabla ofrece una breve descripción de los operadores:

Mostrar ejemplos

No Señor.	Operador y descripción
1	+ Adición o plus unario. A + B suma los valores almacenados en las variables A y B. A y B deben tener el mismo tamaño, a menos que uno sea un escalar. Se puede agregar un escalar a una matriz de cualquier tamaño.
2	- Resta o menos unario. AB resta el valor de B de A. A y B deben tener el mismo tamaño, a menos que uno sea un escalar. Un escalar se puede restar de una matriz de cualquier tamaño.
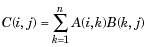
3	* Multiplicación de matrices. C = A * B es el producto algebraico lineal de las matrices A y B. Más precisamente, Para A y B no escalares, el número de columnas de A debe ser igual al número de filas de B. Un escalar puede multiplicar una matriz de cualquier tamaño.
4	.* Multiplicación de matrices. A. * B es el producto elemento por elemento de las matrices A y B. A y B deben tener el mismo tamaño, a menos que uno de ellos sea un escalar.
5	/ División derecha de barra o matriz. B / A es aproximadamente lo mismo que B * inv (A). Más precisamente, B / A = (A '\ B') '.
6	./ Matriz de división a la derecha. A./B es la matriz con elementos A (i, j) / B (i, j). A y B deben tener el mismo tamaño, a menos que uno de ellos sea un escalar.
7	\ Barra invertida o división de matriz a la izquierda. Si A es una matriz cuadrada, A \ B es aproximadamente lo mismo que inv (A) * B, excepto que se calcula de una manera diferente. Si A es un n-por-n matriz y B es un vector columna con n componentes, o una matriz con varias de estas columnas, entonces X = A \ B es la solución a la ecuación AX = B . Se muestra un mensaje de advertencia si A tiene una escala incorrecta o es casi singular.
8	.\ Array división izquierda. A. \ B es la matriz con elementos B (i, j) / A (i, j). A y B deben tener el mismo tamaño, a menos que uno de ellos sea un escalar.
9	^ Poder de la matriz. X ^ p es X elevado a p, si p es un escalar. Si p es un número entero, la potencia se calcula elevando al cuadrado repetidamente. Si el número entero es negativo, X se invierte primero. Para otros valores de p, el cálculo involucra valores propios y vectores propios, de modo que si [V, D] = eig (X), entonces X ^ p = V * D. ^ p / V.
10	.^ Poder de matriz. A. ^ B es la matriz con elementos A (i, j) a la potencia B (i, j). A y B deben tener el mismo tamaño, a menos que uno de ellos sea un escalar.
11	' Transposición de matriz. A 'es la transpuesta algebraica lineal de A. Para matrices complejas, esta es la transpuesta conjugada compleja.
12	.' Transposición de matriz. UN.' es la transposición de la matriz de A. Para matrices complejas, esto no implica conjugación.

Operadores relacionales

Los operadores relacionales también pueden trabajar con datos escalares y no escalares. Los operadores relacionales para matrices realizan comparaciones elemento por elemento entre dos matrices y devuelven una matriz lógica del mismo tamaño, con elementos configurados en 1 lógico (verdadero) donde la relación es verdadera y elementos configurados en 0 lógico (falso) donde es no.

La siguiente tabla muestra los operadores relacionales disponibles en MATLAB:

Mostrar ejemplos

No Señor.	Operador y descripción
1	< Menos que
2	<= Menos que o igual a
3	> Mas grande que
4	>= Mayor qué o igual a
5	== Igual a
6	~= No igual a

Operadores logicos

MATLAB ofrece dos tipos de funciones y operadores lógicos:

• En cuanto a elementos: estos operadores operan en elementos correspondientes de matrices lógicas.

• Cortocircuito: estos operadores operan en expresiones escalares y lógicas.

Los operadores lógicos de elementos operan elemento por elemento en matrices lógicas. Los símbolos &, | y ~ son los operadores de matriz lógica AND, OR y NOT.

Los operadores lógicos de cortocircuito permiten el cortocircuito en operaciones lógicas. Los símbolos && y || son los operadores lógicos de cortocircuito AND y OR.

Mostrar ejemplos

Operaciones bit a bit

Los operadores bit a bit trabajan en bits y realizan operaciones bit a bit. Las tablas de verdad para &, | y ^ son las siguientes:

pags	q	p & q	p | q	p ^ q
0	0	0	0	0
0	1	0	1	1
1	1	1	1	0
1	0	0	1	1

Suponga si A = 60; y B = 13; Ahora en formato binario serán los siguientes:

A = 0011 1100

B = 0000 1101

-----------------

A&B = 0000 1100

A | B = 0011 1101

A ^ B = 0011 0001

~ A = 1100 0011

MATLAB proporciona varias funciones para operaciones bit a bit como operaciones 'bit a bit y', 'bit a bit o' y 'bit a bit no', operación de desplazamiento, etc.

La siguiente tabla muestra las operaciones bit a bit más utilizadas:

Mostrar ejemplos

Función	Propósito
bitand (a, b)	AND de bits de enteros una y b
bitcmp (a)	Complemento bit a bit de un
bitget (a, pos)	Obtener el bit en la posición especificada pos , en la matriz de enteros a
mordedor (a, b)	Bit a bit OR de enteros una y b
bitset (a, pos)	Bit activado en ubicación específica pos de una
desplazamiento de bits (a, k)	Devuelve un desplazado a la izquierda por k bits, equivalente a multiplicar por 2 k . Los valores negativos de k corresponden a desplazar bits a la derecha o dividir por 2 | k | y redondeando al número entero más cercano hacia el infinito negativo. Los bits de desbordamiento se truncan.
bitxor (a, b)	XOR bit a bit de los enteros una y b
swapbytes	Intercambiar orden de bytes

Establecer operaciones

MATLAB proporciona varias funciones para operaciones de conjuntos, como unión, intersección y prueba para pertenencia a conjuntos, etc.

La siguiente tabla muestra algunas operaciones de conjuntos de uso común:

Mostrar ejemplos

No Señor.	Función descriptiva
1	intersect(A,B) Establecer la intersección de dos matrices; devuelve los valores comunes a A y B. Los valores devueltos están ordenados.
2	intersect(A,B,'rows') Trata cada fila de A y cada fila de B como entidades únicas y devuelve las filas comunes a A y B. Las filas de la matriz devuelta están ordenadas.
3	ismember(A,B) Devuelve una matriz del mismo tamaño que A, que contiene 1 (verdadero) donde los elementos de A se encuentran en B. En otros lugares, devuelve 0 (falso).
4	ismember(A,B,'rows') Trata cada fila de A y cada fila de B como entidades individuales y devuelve un vector que contiene 1 (verdadero) donde las filas de la matriz A también son filas de B. En otros lugares, devuelve 0 (falso).
5	issorted(A) Devuelve un 1 lógico (verdadero) si los elementos de A están ordenados y un 0 lógico (falso) en caso contrario. La entrada A puede ser un vector o una matriz de cadenas de celdas de N-por-1 o 1-por-N.A is considered to be sorted if A y la salida del tipo (A) son iguales.
6	issorted(A, 'rows') Devuelve un 1 lógico (verdadero) si las filas de la matriz bidimensional A están ordenadas y un 0 lógico (falso) en caso contrario. Matrix A is considered to be sorted if A y la salida de sortrows (A) son iguales.
7	setdiff(A,B) Establece la diferencia de dos matrices; devuelve los valores de A que no están en B. Los valores de la matriz devuelta están ordenados.
8	setdiff(A,B,'rows') Trata cada fila de A y cada fila de B como entidades únicas y devuelve las filas de A que no están en B. Las filas de la matriz devuelta están ordenadas. La opción 'filas' no admite matrices de celdas.
9	setxor Establece OR exclusivo de dos matrices
10	union Establece la unión de dos matrices
11	unique Unique values in array

Decision making structures require that the programmer should specify one or more conditions to be evaluated or tested by the program, along with a statement or statements to be executed if the condition is determined to be true, and optionally, other statements to be executed if the condition is determined to be false.

Following is the general form of a typical decision making structure found in most of the programming languages −

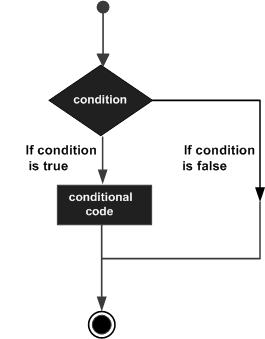
MATLAB provides following types of decision making statements. Click the following links to check their detail −

Sr.No.	Statement & Description
1	if ... end statement An if ... end statement consists of a boolean expression followed by one or more statements.
2	if...else...end statement An if statement can be followed by an optional else statement, which executes when the boolean expression is false.
3	If... elseif...elseif...else...end statements An if statement can be followed by one (or more) optional elseif... and an else statement, which is very useful to test various conditions.
4	nested if statements You can use one if or elseif statement inside another if or elseif statement(s).
5	switch statement A switch statement allows a variable to be tested for equality against a list of values.
6	nested switch statements You can use one switch statement inside another switch statement(s).

There may be a situation when you need to execute a block of code several number of times. In general, statements are executed sequentially. The first statement in a function is executed first, followed by the second, and so on.

Programming languages provide various control structures that allow for more complicated execution paths.

A loop statement allows us to execute a statement or group of statements multiple times and following is the general form of a loop statement in most of the programming languages −

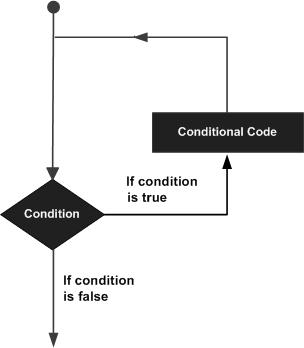
MATLAB provides following types of loops to handle looping requirements. Click the following links to check their detail −

Sr.No.	Loop Type & Description
1	while loop Repeats a statement or group of statements while a given condition is true. It tests the condition before executing the loop body.
2	for loop Executes a sequence of statements multiple times and abbreviates the code that manages the loop variable.
3	nested loops You can use one or more loops inside any another loop.

Loop Control Statements

Loop control statements change execution from its normal sequence. When execution leaves a scope, all automatic objects that were created in that scope are destroyed.

MATLAB supports the following control statements. Click the following links to check their detail.

Sr.No.	Control Statement & Description
1	break statement Terminates the loop statement and transfers execution to the statement immediately following the loop.
2	continue statement Causes the loop to skip the remainder of its body and immediately retest its condition prior to reiterating.

A vector is a one-dimensional array of numbers. MATLAB allows creating two types of vectors −

• Row vectors
• Column vectors

Row Vectors

Row vectors are created by enclosing the set of elements in square brackets, using space or comma to delimit the elements.

r = [7 8 9 10 11]

MATLAB will execute the above statement and return the following result −

r =

   7    8    9   10   11

Column Vectors

Column vectors are created by enclosing the set of elements in square brackets, using semicolon to delimit the elements.

c = [7;  8;  9;  10; 11]

MATLAB will execute the above statement and return the following result −

c =
      7       
      8       
      9       
      10       
      11

Referencing the Elements of a Vector

You can reference one or more of the elements of a vector in several ways. The i^th component of a vector v is referred as v(i). For example −

v = [ 1; 2; 3; 4; 5; 6];	% creating a column vector of 6 elements
v(3)

MATLAB will execute the above statement and return the following result −

ans =  3

When you reference a vector with a colon, such as v(:), all the components of the vector are listed.

v = [ 1; 2; 3; 4; 5; 6];	% creating a column vector of 6 elements
v(:)

MATLAB will execute the above statement and return the following result −

ans =
     1
     2
     3
     4
     5
     6

MATLAB allows you to select a range of elements from a vector.

For example, let us create a row vector rv of 9 elements, then we will reference the elements 3 to 7 by writing rv(3:7) and create a new vector named sub_rv.

rv = [1 2 3 4 5 6 7 8 9];
sub_rv = rv(3:7)

MATLAB will execute the above statement and return the following result −

sub_rv =

   3   4   5   6   7

Vector Operations

In this section, let us discuss the following vector operations −

• Addition and Subtraction of Vectors

• Scalar Multiplication of Vectors

• Transpose of a Vector

• Appending Vectors

• Magnitude of a Vector

• Vector Dot Product

• Vectors with Uniformly Spaced Elements

A matrix is a two-dimensional array of numbers.

In MATLAB, you create a matrix by entering elements in each row as comma or space delimited numbers and using semicolons to mark the end of each row.

For example, let us create a 4-by-5 matrix a −

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]

MATLAB will execute the above statement and return the following result −

a =
      1     2     3     4     5
      2     3     4     5     6
      3     4     5     6     7
      4     5     6     7     8

Referencing the Elements of a Matrix

To reference an element in the m^th row and n^th column, of a matrix mx, we write −

mx(m, n);

Por ejemplo, para hacer referencia al elemento en la ^2ª fila y la ^5ª columna, de la matriz a , como se creó en la última sección, escribimos -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(2,5)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =  6

Para hacer referencia a todos los elementos de la m ^ésima columna, escribimos A (:, m).

Vamos a crear un vector columna V, a partir de los elementos de la 4 ^ª fila de la matriz A -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
v = a(:,4)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

v =
      4
      5
      6
      7

También puede seleccionar los elementos de la m ^ésima a la n ^ésima columna, para esto escribimos -

a(:,m:n)

Creemos una matriz más pequeña tomando los elementos de la segunda y tercera columnas -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =
      2     3
      3     4
      4     5
      5     6

De la misma manera, puede crear una submatriz tomando una subparte de una matriz.

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =
      2     3
      3     4
      4     5
      5     6

De la misma manera, puede crear una submatriz tomando una subparte de una matriz.

Por ejemplo, creemos una submatriz sa tomando la subparte interna de a -

3     4     5     
4     5     6

Para hacer esto, escriba -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
sa = a(2:3,2:4)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

sa =
      3     4     5
      4     5     6

Eliminar una fila o una columna en una matriz

Puede eliminar una fila o columna completa de una matriz asignando un conjunto vacío de llaves [] a esa fila o columna. Básicamente, [] denota una matriz vacía.

Por ejemplo, eliminemos la cuarta fila de un -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a( 4 , : ) = []

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

a =
      1     2     3     4     5
      2     3     4     5     6
      3     4     5     6     7

A continuación, eliminemos la quinta columna de un -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(: , 5)=[]

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

a =
      1     2     3     4
      2     3     4     5
      3     4     5     6
      4     5     6     7

Ejemplo

En este ejemplo, creemos una matriz m de 3 por 3, luego copiaremos la segunda y tercera filas de esta matriz dos veces para crear una matriz de 4 por 3.

Cree un archivo de script con el siguiente código:

a = [ 1 2 3 ; 4 5 6; 7 8 9];
new_mat = a([2,3,2,3],:)

Cuando ejecuta el archivo, muestra el siguiente resultado:

new_mat =
      4     5     6
      7     8     9
      4     5     6
      7     8     9

Operaciones de matriz

En esta sección, analicemos las siguientes operaciones matriciales básicas y de uso común:

• Suma y resta de matrices

• División de matrices

• Operaciones escalares de matrices

• Transposición de una matriz

• Matrices de concatenación

• Multiplicación de matrices

• Determinante de una matriz

• Inversa de una matriz

Todas las variables de todos los tipos de datos en MATLAB son matrices multidimensionales. Un vector es una matriz unidimensional y una matriz es una matriz bidimensional.

Ya hemos hablado de vectores y matrices. En este capítulo, analizaremos las matrices multidimensionales. Sin embargo, antes de eso, analicemos algunos tipos especiales de matrices.

Matrices especiales en MATLAB

En esta sección, discutiremos algunas funciones que crean algunas matrices especiales. Para todas estas funciones, un solo argumento crea una matriz cuadrada, los argumentos dobles crean una matriz rectangular.

los zeros() la función crea una matriz de todos los ceros -

Por ejemplo

zeros(5)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =
      0     0     0     0     0
      0     0     0     0     0
      0     0     0     0     0
      0     0     0     0     0
      0     0     0     0     0

los ones() la función crea una matriz de todos unos -

Por ejemplo

ones(4,3)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =
      1     1     1
      1     1     1
      1     1     1
      1     1     1

los eye() La función crea una matriz de identidad.

Por ejemplo

eye(4)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =
      1     0     0     0
      0     1     0     0
      0     0     1     0
      0     0     0     1

los rand() La función crea una matriz de números aleatorios distribuidos uniformemente en (0,1) -

Por ejemplo

rand(3, 5)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =
   0.8147    0.9134    0.2785    0.9649    0.9572
   0.9058    0.6324    0.5469    0.1576    0.4854
   0.1270    0.0975    0.9575    0.9706    0.8003

Un cuadrado mágico

UN magic square es un cuadrado que produce la misma suma, cuando sus elementos se agregan en filas, columnas o diagonalmente.

los magic()La función crea una matriz cuadrada mágica. Se necesita un argumento singular que da el tamaño del cuadrado. El argumento debe ser un escalar mayor o igual a 3.

magic(4)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =
   16     2     3    13
   5    11    10     8
   9     7     6    12
   4    14    15     1

Matrices multidimensionales

Una matriz que tiene más de dos dimensiones se denomina matriz multidimensional en MATLAB. Las matrices multidimensionales en MATLAB son una extensión de la matriz bidimensional normal.

Generalmente, para generar una matriz multidimensional, primero creamos una matriz bidimensional y la ampliamos.

Por ejemplo, creemos una matriz bidimensional a.

a = [7 9 5; 6 1 9; 4 3 2]

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

a =
   7     9     5
   6     1     9
   4     3     2

La matriz a es una matriz de 3 por 3; podemos agregar una tercera dimensión a a , proporcionando valores como -

a(:, :, 2)= [ 1 2 3; 4 5 6; 7 8 9]

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

a =

ans(:,:,1) =

   0   0   0
   0   0   0
   0   0   0

ans(:,:,2) =

   1   2   3
   4   5   6
   7   8   9

También podemos crear matrices multidimensionales usando las funciones unos (), ceros () o rand ().

Por ejemplo,

b = rand(4,3,2)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

b(:,:,1) =
   0.0344    0.7952    0.6463
   0.4387    0.1869    0.7094
   0.3816    0.4898    0.7547
   0.7655    0.4456    0.2760

b(:,:,2) =
   0.6797    0.4984    0.2238
   0.6551    0.9597    0.7513
   0.1626    0.3404    0.2551
   0.1190    0.5853    0.5060

También podemos utilizar el cat()función para construir matrices multidimensionales. Concatena una lista de matrices a lo largo de una dimensión especificada:

La sintaxis de la función cat () es -

B = cat(dim, A1, A2...)

Dónde,

• B es la nueva matriz creada

• A1 , A2 , ... son las matrices que se van a concatenar

• dim es la dimensión a lo largo de la cual concatenar las matrices

Ejemplo

Cree un archivo de script y escriba el siguiente código en él:

a = [9 8 7; 6 5 4; 3 2 1];
b = [1 2 3; 4 5 6; 7 8 9];
c = cat(3, a, b, [ 2 3 1; 4 7 8; 3 9 0])

Cuando ejecuta el archivo, muestra:

c(:,:,1) =
      9     8     7
      6     5     4
      3     2     1
c(:,:,2) =
      1     2     3
      4     5     6
      7     8     9
c(:,:,3) =
      2     3     1
      4     7     8
      3     9     0

Funciones de matriz

MATLAB proporciona las siguientes funciones para ordenar, rotar, permutar, remodelar o cambiar el contenido de la matriz.

Función	Propósito
longitud	Longitud del vector o dimensión de matriz más grande
ndims	Número de dimensiones de la matriz
numel	Número de elementos de la matriz
Talla	Dimensiones de la matriz
iscolumn	Determina si la entrada es un vector de columna
esta vacio	Determina si la matriz está vacía
ismatrix	Determina si la entrada es matriz
isrow	Determina si la entrada es un vector de fila
isscalar	Determina si la entrada es escalar
isvector	Determina si la entrada es vectorial
blkdiag	Construye una matriz diagonal de bloques a partir de argumentos de entrada
circshift	Cambia la matriz circularmente
ctranspose	Transposición conjugada compleja
diag	Matrices diagonales y diagonales de matriz
flipdim	Voltea la matriz a lo largo de la dimensión especificada
fliplr	Voltea la matriz de izquierda a derecha
flipud	Voltea la matriz de arriba a abajo
permutar	Invierte las dimensiones de permutación de la matriz ND
permutar	Reorganiza las dimensiones de la matriz ND
repmat	Replicaciones y matriz de mosaicos
remodelar	Matriz de remodelaciones
rot90	Gira la matriz 90 grados
shiftdim	Cambia las dimensiones
clasificado	Determina si los elementos del conjunto están ordenados
ordenar	Ordena los elementos de la matriz en orden ascendente o descendente
sortrows	Ordena las filas en orden ascendente
exprimir	Elimina dimensiones singleton
transponer	Transponer
vectorizar	Vectoriza la expresión

Ejemplos

Los siguientes ejemplos ilustran algunas de las funciones mencionadas anteriormente.

Length, Dimension and Number of elements −

Cree un archivo de script y escriba el siguiente código en él:

x = [7.1, 3.4, 7.2, 28/4, 3.6, 17, 9.4, 8.9];
length(x)      % length of x vector
y = rand(3, 4, 5, 2);
ndims(y)       % no of dimensions in array y
s = ['Zara', 'Nuha', 'Shamim', 'Riz', 'Shadab'];
numel(s)       % no of elements in s

Cuando ejecuta el archivo, muestra el siguiente resultado:

ans =  8
ans =  4
ans =  23

Circular Shifting of the Array Elements −

Cree un archivo de script y escriba el siguiente código en él:

a = [1 2 3; 4 5 6; 7 8 9]  % the original array a
b = circshift(a,1)         %  circular shift first dimension values down by 1.
c = circshift(a,[1 -1])    % circular shift first dimension values % down by 1 
                           % and second dimension values to the left % by 1.

Cuando ejecuta el archivo, muestra el siguiente resultado:

a =
   1     2     3
   4     5     6
   7     8     9

b =
   7     8     9
   1     2     3
   4     5     6

c =
   8     9     7
   2     3     1
   5     6     4

Ordenación de matrices

Cree un archivo de script y escriba el siguiente código en él:

v = [ 23 45 12 9 5 0 19 17]  % horizontal vector
sort(v)                      % sorting v
m = [2 6 4; 5 3 9; 2 0 1]    % two dimensional array
sort(m, 1)                   % sorting m along the row
sort(m, 2)                   % sorting m along the column

Cuando ejecuta el archivo, muestra el siguiente resultado:

v =
   23    45    12     9     5     0    19    17
ans =
   0     5     9    12    17    19    23    45
m =
   2     6     4
   5     3     9
   2     0     1
ans =
   2     0     1
   2     3     4
   5     6     9
ans =
   2     4     6
   3     5     9
   0     1     2

Matriz de celdas

Las matrices de celdas son matrices de celdas indexadas donde cada celda puede almacenar una matriz de diferentes dimensiones y tipos de datos.

los cellLa función se utiliza para crear una matriz de celdas. La sintaxis de la función de celda es:

C = cell(dim)
C = cell(dim1,...,dimN)
D = cell(obj)

Dónde,

• C es la matriz de celdas;

• dim es un entero escalar o vector de enteros que especifica las dimensiones de la matriz de celdas C;

• dim1, ..., dimN son números enteros escalares que especifican las dimensiones de C;

• obj es uno de los siguientes:

  • Matriz u objeto de Java
  • Matriz .NET de tipo System.String o System.Object

Ejemplo

Cree un archivo de script y escriba el siguiente código en él:

c = cell(2, 5);
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5}

Cuando ejecuta el archivo, muestra el siguiente resultado:

c = 
{
   [1,1] = Red
   [2,1] =  1
   [1,2] = Blue
   [2,2] =  2
   [1,3] = Green
   [2,3] =  3
   [1,4] = Yellow
   [2,4] =  4
   [1,5] = White
   [2,5] =  5
}

Acceso a datos en matrices de celdas

Hay dos formas de hacer referencia a los elementos de una matriz de celdas:

• Incluyendo los índices en el primer corchete (), para hacer referencia a conjuntos de celdas
• Incluir los índices entre llaves {}, para hacer referencia a los datos dentro de celdas individuales

Cuando encierra los índices en el primer corchete, se refiere al conjunto de celdas.

Los índices de matriz de celdas entre paréntesis suaves se refieren a conjuntos de celdas.

Por ejemplo

c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c(1:2,1:2)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans = 
{
   [1,1] = Red
   [2,1] =  1
   [1,2] = Blue
   [2,2] =  2
}

También puede acceder al contenido de las celdas indexando con llaves.

Por ejemplo

c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c{1, 2:4}

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans = Blue
ans = Green
ans = Yellow

los colon(:)es uno de los operadores más útiles en MATLAB. Se utiliza para crear vectores, matrices de subíndices yspecify for iterations.

Si desea crear un vector de fila, que contenga números enteros del 1 al 10, escriba:

1:10

MATLAB ejecuta la declaración y devuelve un vector de fila que contiene los números enteros del 1 al 10 -

ans =                                                                           
                                                                                
   1    2    3    4    5    6    7    8    9   10

Si desea especificar un valor de incremento que no sea uno, por ejemplo:

100: -5: 50

MATLAB ejecuta la declaración y devuelve el siguiente resultado:

ans =
   100    95    90    85    80    75    70    65    60    55    50

Tomemos otro ejemplo:

0:pi/8:pi

MATLAB ejecuta la declaración y devuelve el siguiente resultado:

ans =
   Columns 1 through 7
      0    0.3927    0.7854    1.1781    1.5708    1.9635    2.3562
   Columns 8 through 9
      2.7489    3.1416

Puede utilizar el operador de dos puntos para crear un vector de índices para seleccionar filas, columnas o elementos de matrices.

La siguiente tabla describe su uso para este propósito (tengamos una matriz A) -

Formato	Propósito
A(:,j)	es la j-ésima columna de A.
A(i,:)	es la i-ésima fila de A.
A(:,:)	es la matriz bidimensional equivalente. Para matrices, esto es lo mismo que A.
A(j:k)	es A (j), A (j + 1), ..., A (k).
A(:,j:k)	es A (:, j), A (:, j + 1), ..., A (:, k).
A(:,:,k)	es la k- ésima página de la matriz tridimensional A.
A(i,j,k,:)	es un vector en una matriz A de cuatro dimensiones. El vector incluye A (i, j, k, 1), A (i, j, k, 2), A (i, j, k, 3), y así sucesivamente.
A(:)	son todos los elementos de A, considerados como una sola columna. En el lado izquierdo de una instrucción de asignación, A (:) llena A, conservando su forma de antes. En este caso, el lado derecho debe contener el mismo número de elementos que A.

Ejemplo

Cree un archivo de secuencia de comandos y escriba el siguiente código en él:

A = [1 2 3 4; 4 5 6 7; 7 8 9 10]
A(:,2)      % second column of A
A(:,2:3)    % second and third column of A
A(2:3,2:3)  % second and third rows and second and third columns

Cuando ejecuta el archivo, muestra el siguiente resultado:

A =
      1     2     3     4
      4     5     6     7
      7     8     9    10

ans =
      2
      5
      8

ans =
      2     3
      5     6
      8     9

ans =
      5     6
      8     9

MATLAB admite varias clases numéricas que incluyen números enteros con y sin signo y números de punto flotante de precisión simple y doble. De forma predeterminada, MATLAB almacena todos los valores numéricos como números de punto flotante de doble precisión.

Puede optar por almacenar cualquier número o matriz de números como enteros o como números de precisión simple.

Todos los tipos numéricos admiten operaciones básicas de matriz y operaciones matemáticas.

Conversión a varios tipos de datos numéricos

MATLAB proporciona las siguientes funciones para convertir a varios tipos de datos numéricos:

Función	Propósito
doble	Convierte en número de doble precisión
soltero	Convierte a un número de precisión simple
int8	Convierte a un entero de 8 bits con signo
int16	Convierte a un entero de 16 bits con signo
int32	Convierte a un entero de 32 bits con signo
int64	Convierte a un entero de 64 bits con signo
uint8	Convierte a un entero sin signo de 8 bits
uint16	Convierte a un entero sin signo de 16 bits
uint32	Convierte en un entero sin signo de 32 bits
uint64	Convierte en un entero sin signo de 64 bits

Ejemplo

Cree un archivo de secuencia de comandos y escriba el siguiente código:

x = single([5.32 3.47 6.28]) .* 7.5
x = double([5.32 3.47 6.28]) .* 7.5
x = int8([5.32 3.47 6.28]) .* 7.5
x = int16([5.32 3.47 6.28]) .* 7.5
x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5

Cuando ejecuta el archivo, muestra el siguiente resultado:

x =

   39.900   26.025   47.100

x =

   39.900   26.025   47.100

x =

   38  23  45

x =

   38  23  45

x =

   38  23  45

x =

   38  23  45

Ejemplo

Extendamos un poco más el ejemplo anterior. Cree un archivo de secuencia de comandos y escriba el siguiente código:

x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5
x = num2cell(x)

Cuando ejecuta el archivo, muestra el siguiente resultado:

x =

   38  23  45

x =

   38  23  45

x = 
{
   [1,1] = 38
   [1,2] = 23
   [1,3] = 45
}

Enteros más pequeños y más grandes

Las funciones intmax() y intmin() devuelve los valores máximo y mínimo que se pueden representar con todos los tipos de números enteros.

Ambas funciones toman el tipo de datos entero como argumento, por ejemplo, intmax (int8) o intmin (int64) y devuelven los valores máximo y mínimo que puede representar con el tipo de datos entero.

Ejemplo

El siguiente ejemplo ilustra cómo obtener los valores más pequeños y más grandes de números enteros. Cree un archivo de script y escriba el siguiente código en él:

% displaying the smallest and largest signed integer data
str = 'The range for int8 is:\n\t%d to %d ';
sprintf(str, intmin('int8'), intmax('int8'))
str = 'The range for int16 is:\n\t%d to %d ';
sprintf(str, intmin('int16'), intmax('int16'))
str = 'The range for int32 is:\n\t%d to %d ';
sprintf(str, intmin('int32'), intmax('int32'))
str = 'The range for int64 is:\n\t%d to %d ';
sprintf(str, intmin('int64'), intmax('int64'))
 
% displaying the smallest and largest unsigned integer data
str = 'The range for uint8 is:\n\t%d to %d ';
sprintf(str, intmin('uint8'), intmax('uint8'))
str = 'The range for uint16 is:\n\t%d to %d ';
sprintf(str, intmin('uint16'), intmax('uint16'))
str = 'The range for uint32 is:\n\t%d to %d ';
sprintf(str, intmin('uint32'), intmax('uint32'))
str = 'The range for uint64 is:\n\t%d to %d ';
sprintf(str, intmin('uint64'), intmax('uint64'))

Cuando ejecuta el archivo, muestra el siguiente resultado:

ans = The range for int8 is:
	-128 to 127 
ans = The range for int16 is:
	-32768 to 32767 
ans = The range for int32 is:
	-2147483648 to 2147483647 
ans = The range for int64 is:
	0 to 0 
ans = The range for uint8 is:
	0 to 255 
ans = The range for uint16 is:
	0 to 65535 
ans = The range for uint32 is:
	0 to -1 
ans = The range for uint64 is:
	0 to 18446744073709551616

Números de punto flotante más pequeños y más grandes

Las funciones realmax() y realmin() devuelve los valores máximo y mínimo que se pueden representar con números de coma flotante.

Ambas funciones, cuando se llaman con el argumento 'single', devuelven los valores máximo y mínimo que puede representar con el tipo de datos de precisión simple y cuando se llaman con el argumento 'double', devuelven los valores máximo y mínimo que puede representar con el tipo de datos de doble precisión.

Ejemplo

El siguiente ejemplo ilustra cómo obtener los números de coma flotante más pequeños y más grandes. Cree un archivo de script y escriba el siguiente código en él:

% displaying the smallest and largest single-precision 
% floating point number
str = 'The range for single is:\n\t%g to %g and\n\t %g to  %g';
sprintf(str, -realmax('single'), -realmin('single'), ...
   realmin('single'), realmax('single'))

% displaying the smallest and largest double-precision 
% floating point number
str = 'The range for double is:\n\t%g to %g and\n\t %g to  %g';
sprintf(str, -realmax('double'), -realmin('double'), ...
   realmin('double'), realmax('double'))

Cuando ejecuta el archivo, muestra el siguiente resultado:

ans = The range for single is:                                                  
        -3.40282e+38 to -1.17549e-38 and                                        
         1.17549e-38 to  3.40282e+38                                            
ans = The range for double is:                                                  
        -1.79769e+308 to -2.22507e-308 and                                      
         2.22507e-308 to  1.79769e+308

Crear una cadena de caracteres es bastante simple en MATLAB. De hecho, lo hemos usado muchas veces. Por ejemplo, escribe lo siguiente en el símbolo del sistema:

my_string = 'Tutorials Point'

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

my_string = Tutorials Point

MATLAB considera todas las variables como matrices y las cadenas se consideran matrices de caracteres. Usemos elwhos comando para verificar la variable creada anteriormente -

whos

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

Name           Size            Bytes  Class    Attributes
my_string      1x16               32  char

Curiosamente, puede utilizar funciones de conversión numérica como uint8 o uint16para convertir los caracteres de la cadena a sus códigos numéricos. loschar función convierte el vector entero de nuevo a caracteres -

Ejemplo

Cree un archivo de script y escriba el siguiente código en él:

my_string = 'Tutorial''s Point';
str_ascii = uint8(my_string)        % 8-bit ascii values
str_back_to_char= char(str_ascii)  
str_16bit = uint16(my_string)       % 16-bit ascii values
str_back_to_char = char(str_16bit)

Cuando ejecuta el archivo, muestra el siguiente resultado:

str_ascii =

   84  117  116  111  114  105   97  108   39  115   32   80  111  105  110  116

str_back_to_char = Tutorial's Point
str_16bit =

   84  117  116  111  114  105   97  108   39  115   32   80  111  105  110  116

str_back_to_char = Tutorial's Point

Matriz de caracteres rectangulares

Las cadenas que hemos discutido hasta ahora son matrices de caracteres unidimensionales; sin embargo, necesitamos almacenar más que eso. Necesitamos almacenar datos textuales más dimensionales en nuestro programa. Esto se logra mediante la creación de matrices de caracteres rectangulares.

La forma más sencilla de crear una matriz de caracteres rectangular es concatenando dos o más matrices de caracteres unidimensionales, ya sea vertical u horizontalmente, según sea necesario.

Puede combinar cadenas verticalmente de cualquiera de las siguientes formas:

• Usando el operador de concatenación de MATLAB []y separando cada fila con un punto y coma (;). Tenga en cuenta que en este método cada fila debe contener el mismo número de caracteres. Para cadenas con diferentes longitudes, debe rellenar con caracteres de espacio según sea necesario.

• Utilizando el charfunción. Si las cadenas tienen diferentes longitudes, char rellena las cadenas más cortas con espacios en blanco al final para que cada fila tenga el mismo número de caracteres.

Ejemplo

Cree un archivo de script y escriba el siguiente código en él:

doc_profile = ['Zara Ali                             '; ...
               'Sr. Surgeon                          '; ...
               'R N Tagore Cardiology Research Center']
doc_profile = char('Zara Ali', 'Sr. Surgeon', ...
                  'RN Tagore Cardiology Research Center')

Cuando ejecuta el archivo, muestra el siguiente resultado:

doc_profile =
Zara Ali                             
Sr. Surgeon                          
R N Tagore Cardiology Research Center
doc_profile =
Zara Ali                            
Sr. Surgeon                         
RN Tagore Cardiology Research Center

Puede combinar cadenas horizontalmente de cualquiera de las siguientes formas:

• Usando el operador de concatenación de MATLAB, []y separando las cadenas de entrada con una coma o un espacio. Este método conserva los espacios finales en las matrices de entrada.

• Usando la función de concatenación de cadenas, strcat. Este método elimina los espacios finales en las entradas.

Ejemplo

Cree un archivo de script y escriba el siguiente código en él:

name =     'Zara Ali                             ';
position = 'Sr. Surgeon                          '; 
worksAt =  'R N Tagore Cardiology Research Center';
profile = [name ', ' position ', ' worksAt]
profile = strcat(name, ', ', position, ', ', worksAt)

Cuando ejecuta el archivo, muestra el siguiente resultado:

profile = Zara Ali      , Sr. Surgeon      , R N Tagore Cardiology Research Center
profile = Zara Ali,Sr. Surgeon,R N Tagore Cardiology Research Center

Combinar cadenas en una matriz de celdas

De nuestra discusión anterior, está claro que combinar cadenas con diferentes longitudes podría ser una molestia, ya que todas las cadenas de la matriz deben tener la misma longitud. Hemos utilizado espacios en blanco al final de las cadenas para igualar su longitud.

Sin embargo, una forma más eficaz de combinar las cadenas es convertir la matriz resultante en una matriz de celdas.

La matriz de celdas de MATLAB puede contener diferentes tamaños y tipos de datos en una matriz. Las matrices de celdas proporcionan una forma más flexible de almacenar cadenas de longitud variable.

los cellstr La función convierte una matriz de caracteres en una matriz de celdas de cadenas.

Ejemplo

Cree un archivo de script y escriba el siguiente código en él:

name =     'Zara Ali                             ';
position = 'Sr. Surgeon                          '; 
worksAt =  'R N Tagore Cardiology Research Center';
profile = char(name, position, worksAt);
profile = cellstr(profile);
disp(profile)

Cuando ejecuta el archivo, muestra el siguiente resultado:

{                                                                               
   [1,1] = Zara Ali                                                              
   [2,1] = Sr. Surgeon                                                           
   [3,1] = R N Tagore Cardiology Research Center                                 
}

Funciones de cadena en MATLAB

MATLAB proporciona numerosas funciones de cadenas para crear, combinar, analizar, comparar y manipular cadenas.

La siguiente tabla proporciona una breve descripción de las funciones de cadena en MATLAB:

Función	Propósito
Funciones para almacenar texto en matrices de caracteres, combinar matrices de caracteres, etc.
espacios en blanco	Crea una cadena de caracteres en blanco
celltr	Cree una matriz de celdas de cadenas a partir de una matriz de caracteres
carbonizarse	Convertir a matriz de caracteres (cadena)
iscellstr	Determinar si la entrada es una matriz de cadenas de celdas
ischar	Determinar si el elemento es una matriz de caracteres
sprintf	Dar formato a los datos en una cadena
strcat	Concatenar cadenas horizontalmente
strjoin	Unir cadenas en una matriz de celdas en una sola cadena
Funciones para identificar partes de cadenas, buscar y reemplazar subcadenas
ischar	Determinar si el elemento es una matriz de caracteres
isletter	Elementos de matriz que son letras alfabéticas
espacio	Elementos de matriz que son caracteres espaciales
isstrprop	Determinar si la cadena pertenece a la categoría especificada
sscanf	Leer datos formateados de una cadena
strfind	Encuentra una cuerda dentro de otra
strrep	Buscar y reemplazar subcadena
strsplit	Dividir cadena en el delimitador especificado
strtok	Partes seleccionadas de la cuerda
validatestring	Verificar la validez de la cadena de texto
symvar	Determinar variables simbólicas en expresión
regexp	Coincidir con expresión regular (distingue entre mayúsculas y minúsculas)
regexpi	Coincidir con expresión regular (no distingue entre mayúsculas y minúsculas)
regexprep	Reemplazar cadena usando expresión regular
regexptranslate	Traducir cadena a expresión regular
Funciones para la comparación de cadenas
strcmp	Comparar cadenas (distingue entre mayúsculas y minúsculas)
strcmpi	Comparar cadenas (no distingue entre mayúsculas y minúsculas)
strncmp	Comparar los primeros n caracteres de cadenas (distingue entre mayúsculas y minúsculas)
strncmpi	Comparar los primeros n caracteres de cadenas (no distingue entre mayúsculas y minúsculas)
Funciones para cambiar cadenas a mayúsculas o minúsculas, crear o eliminar espacios en blanco
deblank	Pele los espacios en blanco finales del final de la cuerda
strtrim	Eliminar los espacios en blanco iniciales y finales de la cadena
inferior	Convertir cadena a minúscula
Superior	Convertir cadena a mayúscula
strjust	Justificar la matriz de caracteres

Ejemplos

Los siguientes ejemplos ilustran algunas de las funciones de cadena mencionadas anteriormente:

Formateo de cadenas

Cree un archivo de script y escriba el siguiente código en él:

A = pi*1000*ones(1,5);
sprintf(' %f \n %.2f \n %+.2f \n %12.2f \n %012.2f \n', A)

Cuando ejecuta el archivo, muestra el siguiente resultado:

ans =  3141.592654 
   3141.59 
   +3141.59 
      3141.59 
   000003141.59

Unir cadenas

Cree un archivo de script y escriba el siguiente código en él:

%cell array of strings
str_array = {'red','blue','green', 'yellow', 'orange'};

% Join strings in cell array into single string
str1 = strjoin(str_array, "-")
str2 = strjoin(str_array, ",")

Cuando ejecuta el archivo, muestra el siguiente resultado:

str1 = red-blue-green-yellow-orange
str2 = red,blue,green,yellow,orange

Encontrar y reemplazar cadenas

Cree un archivo de script y escriba el siguiente código en él:

students = {'Zara Ali', 'Neha Bhatnagar', ...
            'Monica Malik', 'Madhu Gautam', ...
            'Madhu Sharma', 'Bhawna Sharma',...
            'Nuha Ali', 'Reva Dutta', ...
            'Sunaina Ali', 'Sofia Kabir'};
 
% The strrep function searches and replaces sub-string.
new_student = strrep(students(8), 'Reva', 'Poulomi')
% Display first names
first_names = strtok(students)

Cuando ejecuta el archivo, muestra el siguiente resultado:

new_student = 
{
   [1,1] = Poulomi Dutta
}
first_names = 
{
   [1,1] = Zara
   [1,2] = Neha
   [1,3] = Monica
   [1,4] = Madhu
   [1,5] = Madhu
   [1,6] = Bhawna
   [1,7] = Nuha
   [1,8] = Reva
   [1,9] = Sunaina
   [1,10] = Sofia
}

Comparación de cadenas

Cree un archivo de script y escriba el siguiente código en él:

str1 = 'This is test'
str2 = 'This is text'
if (strcmp(str1, str2))
   sprintf('%s and %s are equal', str1, str2)
else
   sprintf('%s and %s are not equal', str1, str2)
end

Cuando ejecuta el archivo, muestra el siguiente resultado:

str1 = This is test
str2 = This is text
ans = This is test and This is text are not equal

Una función es un grupo de declaraciones que juntas realizan una tarea. En MATLAB, las funciones se definen en archivos separados. El nombre del archivo y de la función debe ser el mismo.

Las funciones operan en variables dentro de su propio espacio de trabajo, que también se llama local workspace, separado del espacio de trabajo al que accede en el símbolo del sistema de MATLAB, que se llama base workspace.

Las funciones pueden aceptar más de un argumento de entrada y pueden devolver más de un argumento de salida.

La sintaxis de una declaración de función es:

function [out1,out2, ..., outN] = myfun(in1,in2,in3, ..., inN)

Ejemplo

La siguiente función llamada mymax debe escribirse en un archivo llamado mymax.m . Toma cinco números como argumento y devuelve el máximo de números.

Cree un archivo de función, llamado mymax.m y escriba el siguiente código en él:

function max = mymax(n1, n2, n3, n4, n5)

%This function calculates the maximum of the
% five numbers given as input
max =  n1;
if(n2 > max)
   max = n2;
end
if(n3 > max)
   max = n3;
end
if(n4 > max)
   max = n4;
end
if(n5 > max)
   max = n5;
end

La primera línea de una función comienza con la palabra clave function. Da el nombre de la función y el orden de los argumentos. En nuestro ejemplo, la función mymax tiene cinco argumentos de entrada y un argumento de salida.

Las líneas de comentarios que vienen inmediatamente después de la declaración de función proporcionan el texto de ayuda. Estas líneas se imprimen cuando escribe:

help mymax

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

This function calculates the maximum of the
   five numbers given as input

Puede llamar a la función como -

mymax(34, 78, 89, 23, 11)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans = 89

Funciones anónimas

Una función anónima es como una función en línea en los lenguajes de programación tradicionales, definida dentro de una sola declaración de MATLAB. Consiste en una sola expresión MATLAB y cualquier número de argumentos de entrada y salida.

Puede definir una función anónima directamente en la línea de comandos de MATLAB o dentro de una función o script.

De esta manera puede crear funciones simples sin tener que crear un archivo para ellas.

La sintaxis para crear una función anónima a partir de una expresión es

f = @(arglist)expression

Ejemplo

En este ejemplo, escribiremos una función anónima llamada potencia, que tomará dos números como entrada y devolverá el primer número elevado a la potencia del segundo número.

Cree un archivo de secuencia de comandos y escriba el siguiente código en él:

power = @(x, n) x.^n;
result1 = power(7, 3)
result2 = power(49, 0.5)
result3 = power(10, -10)
result4 = power (4.5, 1.5)

Cuando ejecuta el archivo, muestra:

result1 =  343
result2 =  7
result3 =  1.0000e-10
result4 =  9.5459

Funciones primarias y secundarias

Cualquier función que no sea una función anónima debe definirse dentro de un archivo. Cada archivo de función contiene una función primaria requerida que aparece primero y cualquier número de subfunciones opcionales que vienen después de la función primaria y son utilizadas por esta.

Las funciones primarias se pueden llamar desde fuera del archivo que las define, ya sea desde la línea de comandos o desde otras funciones, pero las subfunciones no se pueden llamar desde la línea de comandos u otras funciones, fuera del archivo de funciones.

Las subfunciones son visibles solo para la función principal y otras subfunciones dentro del archivo de función que las define.

Ejemplo

Escribamos una función llamada cuadrática que calcularía las raíces de una ecuación cuadrática. La función tomaría tres entradas, el coeficiente cuadrático, el coeficiente lineal y el término constante. Devolvería las raíces.

El archivo de función quadratic.m contendrá la función principal cuadrática y el disco de subfunción , que calcula el discriminante.

Cree un archivo de función quadratic.m y escriba el siguiente código en él:

function [x1,x2] = quadratic(a,b,c)

%this function returns the roots of 
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficients of x2, x and the 
%constant term
% It returns the roots
d = disc(a,b,c); 
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end   % end of quadratic

function dis = disc(a,b,c) 
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end   % end of sub-function

Puede llamar a la función anterior desde el símbolo del sistema como:

quadratic(2,4,-4)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans = 0.7321

Funciones anidadas

Puede definir funciones dentro del cuerpo de otra función. Se denominan funciones anidadas. Una función anidada contiene alguno o todos los componentes de cualquier otra función.

Las funciones anidadas se definen dentro del alcance de otra función y comparten el acceso al espacio de trabajo de la función que las contiene.

Una función anidada sigue la siguiente sintaxis:

function x = A(p1, p2)
...
B(p2)
   function y = B(p3)
   ...
   end
...
end

Ejemplo

Reescribamos la función cuadrática , del ejemplo anterior, sin embargo, esta vez la función de disco será una función anidada.

Cree un archivo de función quadratic2.m y escriba el siguiente código en él:

function [x1,x2] = quadratic2(a,b,c)
function disc  % nested function
d = sqrt(b^2 - 4*a*c);
end   % end of function disc

disc;
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end   % end of function quadratic2

Puede llamar a la función anterior desde el símbolo del sistema como:

quadratic2(2,4,-4)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =  0.73205

Funciones privadas

Una función privada es una función principal que solo es visible para un grupo limitado de otras funciones. Si no desea exponer la implementación de una función, puede crearlas como funciones privadas.

Las funciones privadas residen en subfolders con el nombre especial private.

Solo son visibles para las funciones de la carpeta principal.

Ejemplo

Reescribamos la función cuadrática . Esta vez, sin embargo, la función de disco que calcula el discriminante será una función privada.

Cree una subcarpeta denominada privada en el directorio de trabajo. Almacene el siguiente archivo de función disc.m en él:

function dis = disc(a,b,c) 
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end      % end of sub-function

Cree una función quadratic3.m en su directorio de trabajo y escriba el siguiente código en ella:

function [x1,x2] = quadratic3(a,b,c)

%this function returns the roots of 
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficient of x2, x and the 
%constant term
% It returns the roots
d = disc(a,b,c); 

x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end      % end of quadratic3

Puede llamar a la función anterior desde el símbolo del sistema como:

quadratic3(2,4,-4)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =  0.73205

Variables globales

Las variables globales pueden ser compartidas por más de una función. Para ello, debe declarar la variable como global en todas las funciones.

Si desea acceder a esa variable desde el espacio de trabajo base, declare la variable en la línea de comando.

La declaración global debe ocurrir antes de que la variable se use realmente en una función. Es una buena práctica utilizar letras mayúsculas para los nombres de las variables globales para distinguirlas de otras variables.

Ejemplo

Creemos un archivo de función llamado average.m y escriba el siguiente código en él:

function avg = average(nums)
global TOTAL
avg = sum(nums)/TOTAL;
end

Cree un archivo de secuencia de comandos y escriba el siguiente código en él:

global TOTAL;
TOTAL = 10;
n = [34, 45, 25, 45, 33, 19, 40, 34, 38, 42];
av = average(n)

Cuando ejecute el archivo, mostrará el siguiente resultado:

av =  35.500

Importar datos en MATLAB significa cargar datos desde un archivo externo. losimportdataLa función permite cargar varios archivos de datos de diferentes formatos. Tiene las siguientes cinco formas:

No Señor.	Función descriptiva
1	A = importdata(filename) Carga datos en la matriz A desde el archivo indicado por el nombre de archivo .
2	A = importdata('-pastespecial') Carga datos del portapapeles del sistema en lugar de un archivo.
3	A = importdata(___, delimiterIn) Interpreta delimiterIn como el separador de columna en el archivo ASCII, el nombre del archivo o los datos del portapapeles. Puede usar delimiterIn con cualquiera de los argumentos de entrada en las sintaxis anteriores.
4	A = importdata(___, delimiterIn, headerlinesIn) Carga datos desde el archivo ASCII, el nombre del archivo o el portapapeles, leyendo datos numéricos a partir de la línea de encabezadoIn + 1 .
5	[A, delimiterOut, headerlinesOut] = importdata(___) Devuelve el carácter delimitador detectado para el archivo ASCII de entrada en delimiterOut y el número detectado de líneas de encabezado en headerlinesOut , utilizando cualquiera de los argumentos de entrada en las sintaxis anteriores.

De forma predeterminada, Octave no tiene soporte para la función importdata () , por lo que tendrá que buscar e instalar este paquete para que los siguientes ejemplos funcionen con su instalación de Octave.

Ejemplo 1

Carguemos y visualicemos un archivo de imagen. Cree un archivo de secuencia de comandos y escriba el siguiente código en él:

filename = 'smile.jpg';
A = importdata(filename);
image(A);

Cuando ejecuta el archivo, MATLAB muestra el archivo de imagen. Sin embargo, debe almacenarlo en el directorio actual.

Ejemplo 2

En este ejemplo, importamos un archivo de texto y especificamos Delimitador y Encabezado de columna. Creemos un archivo ASCII delimitado por espacios con encabezados de columna, llamado WeeklyData.txt .

Nuestro archivo de texto semanaldata.txt se ve así:

SunDay  MonDay  TuesDay  WednesDay  ThursDay  FriDay  SaturDay
95.01   76.21   61.54    40.57       55.79    70.28   81.53
73.11   45.65   79.19    93.55       75.29    69.87   74.68
60.68   41.85   92.18    91.69       81.32    90.38   74.51
48.60   82.14   73.82    41.03       0.99     67.22   93.18
89.13   44.47   57.63    89.36       13.89    19.88   46.60

Cree un archivo de secuencia de comandos y escriba el siguiente código en él:

filename = 'weeklydata.txt';
delimiterIn = ' ';
headerlinesIn = 1;
A = importdata(filename,delimiterIn,headerlinesIn);

% View data
for k = [1:7]
   disp(A.colheaders{1, k})
   disp(A.data(:, k))
   disp(' ')
end

Cuando ejecuta el archivo, muestra el siguiente resultado:

SunDay
   95.0100
   73.1100
   60.6800
   48.6000
   89.1300
 
MonDay
   76.2100
   45.6500
   41.8500
   82.1400
   44.4700
 
TuesDay
   61.5400
   79.1900
   92.1800
   73.8200
   57.6300

WednesDay
   40.5700
   93.5500
   91.6900
   41.0300
   89.3600
 
ThursDay
   55.7900
   75.2900
   81.3200
   0.9900
   13.8900
 
FriDay
   70.2800
   69.8700
   90.3800
   67.2200
   19.8800

SaturDay
   81.5300
   74.6800
   74.5100
   93.1800
   46.6000

Ejemplo 3

En este ejemplo, vamos a importar datos desde el portapapeles.

Copie las siguientes líneas en el portapapeles:

Mathematics is simple

Cree un archivo de secuencia de comandos y escriba el siguiente código:

A = importdata('-pastespecial')

Cuando ejecuta el archivo, muestra el siguiente resultado:

A = 
   'Mathematics is simple'

E / S de archivos de bajo nivel

La función importdata es una función de alto nivel. Las funciones de E / S de archivo de bajo nivel en MATLAB permiten el mayor control sobre la lectura o escritura de datos en un archivo. Sin embargo, estas funciones necesitan información más detallada sobre su archivo para funcionar de manera eficiente.

MATLAB proporciona las siguientes funciones para operaciones de lectura y escritura en el nivel de bytes o caracteres:

Función	Descripción
fcerrar	Cerrar uno o todos los archivos abiertos
feof	Prueba de fin de archivo
ferror	Información sobre errores de E / S de archivos
fgetl	Leer línea del archivo, eliminar caracteres de nueva línea
fgets	Leer línea desde archivo, manteniendo caracteres de nueva línea
fopen	Abrir archivo u obtener información sobre archivos abiertos
fprintf	Escribir datos en un archivo de texto
fread	Leer datos de un archivo binario
frewind	Mover el indicador de posición del archivo al comienzo del archivo abierto
fscanf	Leer datos del archivo de texto
fseek	Mover a la posición especificada en el archivo
ftell	Posición en archivo abierto
escribir	Escribir datos en un archivo binario

Importar archivos de datos de texto con E / S de bajo nivel

MATLAB proporciona las siguientes funciones para la importación a bajo nivel de archivos de datos de texto:

• los fscanf La función lee datos formateados en un archivo de texto o ASCII.

• los fgetl y fgets las funciones leen una línea de un archivo a la vez, donde un carácter de nueva línea separa cada línea.

• los fread La función lee un flujo de datos a nivel de bytes o bits.

Ejemplo

Tenemos un archivo de datos de texto 'myfile.txt' guardado en nuestro directorio de trabajo. El archivo almacena datos de lluvia durante tres meses; Junio, julio y agosto para el año 2012.

Los datos en myfile.txt contienen conjuntos repetidos de mediciones de tiempo, mes y lluvia en cinco lugares. Los datos del encabezado almacenan el número de meses M; por lo que tenemos M conjuntos de medidas.

El archivo tiene este aspecto:

Rainfall Data
Months: June, July, August
 
M = 3
12:00:00
June-2012
17.21  28.52  39.78  16.55 23.67
19.15  0.35   17.57  NaN   12.01
17.92  28.49  17.40  17.06 11.09
9.59   9.33   NaN    0.31  0.23 
10.46  13.17  NaN    14.89 19.33
20.97  19.50  17.65  14.45 14.00
18.23  10.34  17.95  16.46 19.34
09:10:02
July-2012
12.76  16.94  14.38  11.86 16.89
20.46  23.17  NaN    24.89 19.33
30.97  49.50  47.65  24.45 34.00
18.23  30.34  27.95  16.46 19.34
30.46  33.17  NaN    34.89  29.33
30.97  49.50  47.65  24.45 34.00
28.67  30.34  27.95  36.46 29.34
15:03:40
August-2012
17.09  16.55  19.59  17.25 19.22
17.54  11.45  13.48  22.55 24.01
NaN    21.19  25.85  25.05 27.21
26.79  24.98  12.23  16.99 18.67
17.54  11.45  13.48  22.55 24.01
NaN    21.19  25.85  25.05 27.21
26.79  24.98  12.23  16.99 18.67

Importaremos datos de este archivo y mostraremos estos datos. Siga los siguientes pasos:

• Abra el archivo con fopen función y obtener el identificador de archivo.

• Describe los datos del archivo con format specifiers, como '%s'por una cuerda,'%d'para un número entero, o'%f'para un número de coma flotante.

• Para omitir caracteres literales en el archivo, inclúyalos en la descripción del formato. Para omitir un campo de datos, use un asterisco ('*') en el especificador.

  Por ejemplo, para leer los encabezados y devolver el valor único de M, escribimos:

  M = fscanf(fid, '%*s %*s\n%*s %*s %*s %*s\nM=%d\n\n', 1);

• Por defecto, fscanflee los datos de acuerdo con nuestra descripción de formato hasta que no encuentra ninguna coincidencia con los datos, o llega al final del archivo. Aquí usaremos for loop para leer 3 conjuntos de datos y cada vez leerá 7 filas y 5 columnas.

• Crearemos una estructura denominada mydata en el espacio de trabajo para almacenar los datos leídos del archivo. Esta estructura tiene tres campos: hora , mes y matriz de datos de lluvia .

Cree un archivo de secuencia de comandos y escriba el siguiente código en él:

filename = '/data/myfile.txt';
rows = 7;
cols = 5;
 
% open the file
fid = fopen(filename);
 
% read the file headers, find M (number of months)
M = fscanf(fid, '%*s %*s\n%*s %*s %*s %*s\nM=%d\n\n', 1);
 
% read each set of measurements
for n = 1:M
   mydata(n).time = fscanf(fid, '%s', 1);
   mydata(n).month = fscanf(fid, '%s', 1);
 
   % fscanf fills the array in column order,
   % so transpose the results
   mydata(n).raindata  = ...
      fscanf(fid, '%f', [rows, cols]);
end
for n = 1:M
   disp(mydata(n).time), disp(mydata(n).month)
   disp(mydata(n).raindata)
end
 
% close the file
fclose(fid);

Cuando ejecuta el archivo, muestra el siguiente resultado:

12:00:00
June-2012
   17.2100   17.5700   11.0900   13.1700   14.4500
   28.5200       NaN    9.5900       NaN   14.0000
   39.7800   12.0100    9.3300   14.8900   18.2300
   16.5500   17.9200       NaN   19.3300   10.3400
   23.6700   28.4900    0.3100   20.9700   17.9500
   19.1500   17.4000    0.2300   19.5000   16.4600
   0.3500   17.0600   10.4600   17.6500   19.3400

09:10:02
July-2012
   12.7600       NaN   34.0000   33.1700   24.4500
   16.9400   24.8900   18.2300       NaN   34.0000
   14.3800   19.3300   30.3400   34.8900   28.6700
   11.8600   30.9700   27.9500   29.3300   30.3400
   16.8900   49.5000   16.4600   30.9700   27.9500
   20.4600   47.6500   19.3400   49.5000   36.4600
   23.1700   24.4500   30.4600   47.6500   29.3400

15:03:40
August-2012
   17.0900   13.4800   27.2100   11.4500   25.0500
   16.5500   22.5500   26.7900   13.4800   27.2100
   19.5900   24.0100   24.9800   22.5500   26.7900
   17.2500       NaN   12.2300   24.0100   24.9800
   19.2200   21.1900   16.9900       NaN   12.2300
   17.5400   25.8500   18.6700   21.1900   16.9900
   11.4500   25.0500   17.5400   25.8500   18.6700

La exportación (o salida) de datos en MATLAB significa escribir en archivos. MATLAB le permite utilizar sus datos en otra aplicación que lee archivos ASCII. Para ello, MATLAB proporciona varias opciones de exportación de datos.

Puede crear los siguientes tipos de archivos:

• Archivo de datos ASCII delimitado y rectangular de una matriz.

• Archivo diario (o registro) de pulsaciones de teclas y la salida de texto resultante.

• Archivo ASCII especializado que utiliza funciones de bajo nivel como fprintf.

• MEX-file para acceder a su rutina C / C ++ o Fortran que escribe en un formato de archivo de texto particular.

Aparte de esto, también puede exportar datos a hojas de cálculo.

Hay dos formas de exportar una matriz numérica como un archivo de datos ASCII delimitado:

• Utilizando el save función y especificando el -ascii Calificatorio

• Utilizando el dlmwrite función

La sintaxis para usar la función de guardar es:

save my_data.out num_array -ascii

donde my_data.out es el archivo de datos ASCII delimitado creado, num_array es una matriz numérica y−ascii es el especificador.

Sintaxis para usar el dlmwrite la función es -

dlmwrite('my_data.out', num_array, 'dlm_char')

donde my_data.out es el archivo de datos ASCII delimitado creado, num_array es una matriz numérica y dlm_char es el carácter delimitador.

Ejemplo

El siguiente ejemplo demuestra el concepto. Cree un archivo de secuencia de comandos y escriba el siguiente código:

num_array = [ 1 2 3 4 ; 4 5 6 7; 7 8 9 0];
save array_data1.out num_array -ascii;
type array_data1.out
dlmwrite('array_data2.out', num_array, ' ');
type array_data2.out

Cuando ejecuta el archivo, muestra el siguiente resultado:

1.0000000e+00   2.0000000e+00   3.0000000e+00   4.0000000e+00
   4.0000000e+00   5.0000000e+00   6.0000000e+00   7.0000000e+00
   7.0000000e+00   8.0000000e+00   9.0000000e+00   0.0000000e+00

1 2 3 4
4 5 6 7
7 8 9 0

Tenga en cuenta que el comando save -ascii y la función dlmwrite no funcionan con matrices de celdas como entrada. Para crear un archivo ASCII delimitado a partir del contenido de una matriz de celdas, puede

• O convierta la matriz de celdas en una matriz usando el cell2mat función

• O exporte la matriz de celdas utilizando funciones de E / S de archivos de bajo nivel.

Si usa el save función para escribir una matriz de caracteres en un archivo ASCII, escribe el equivalente ASCII de los caracteres en el archivo.

Por ejemplo, escribamos la palabra 'hola' en un archivo -

h = 'hello';
save textdata.out h -ascii
type textdata.out

MATLAB ejecuta las declaraciones anteriores y muestra el siguiente resultado. que son los caracteres de la cadena 'hola' en formato ASCII de 8 dígitos.

1.0400000e+02   1.0100000e+02   1.0800000e+02   1.0800000e+02   1.1100000e+02

Escribir en archivos de diario

Los archivos de diario son registros de actividad de su sesión de MATLAB. La función de diario crea una copia exacta de su sesión en un archivo de disco, sin incluir gráficos.

Para activar la función de diario, escriba -

diary

Opcionalmente, puede dar el nombre del archivo de registro, por ejemplo:

diary logdata.out

Para desactivar la función de diario:

diary off

Puede abrir el archivo del diario en un editor de texto.

Exportación de datos a archivos de datos de texto con E / S de bajo nivel

Hasta ahora, hemos exportado matrices numéricas. Sin embargo, es posible que deba crear otros archivos de texto, incluidas combinaciones de datos numéricos y de caracteres, archivos de salida no rectangulares o archivos con esquemas de codificación no ASCII. Para estos fines, MATLAB proporciona el nivel bajofprintf función.

Al igual que en las actividades de archivo de E / S de bajo nivel, antes de exportar, debe abrir o crear un archivo con el fopenfunción y obtener el identificador de archivo. De forma predeterminada, fopen abre un archivo para acceso de solo lectura. Debe especificar el permiso para escribir o agregar, como 'w' o 'a'.

Después de procesar el archivo, debe cerrarlo con fclose(fid) función.

El siguiente ejemplo demuestra el concepto:

Ejemplo

Cree un archivo de secuencia de comandos y escriba el siguiente código en él:

% create a matrix y, with two rows
x = 0:10:100;
y = [x; log(x)];
 
% open a file for writing
fid = fopen('logtable.txt', 'w');
 
% Table Header
fprintf(fid, 'Log     Function\n\n');
 
% print values in column order
% two values appear on each row of the file
fprintf(fid, '%f    %f\n', y);
fclose(fid);

% display the file created
type logtable.txt

Cuando ejecuta el archivo, muestra el siguiente resultado:

Log         Function

0.000000    -Inf
10.000000    2.302585
20.000000    2.995732
30.000000    3.401197
40.000000    3.688879
50.000000    3.912023
60.000000    4.094345
70.000000    4.248495
80.000000    4.382027
90.000000    4.499810
100.000000    4.605170

Para trazar la gráfica de una función, debe seguir los siguientes pasos:

• Definir x, especificando el range of values para la variable x, para el cual se trazará la función

• Definir la función, y = f(x)

• Llama a plot comando, como plot(x, y)

El siguiente ejemplo demostraría el concepto. Tracemos la función simpley = x para el rango de valores de x de 0 a 100, con un incremento de 5.

Cree un archivo de secuencia de comandos y escriba el siguiente código:

x = [0:5:100];
y = x;
plot(x, y)

Cuando ejecuta el archivo, MATLAB muestra el siguiente gráfico:

Tomemos un ejemplo más para graficar la función y = x ² . En este ejemplo dibujaremos dos gráficos con la misma función, pero en la segunda vez reduciremos el valor de incremento. Tenga en cuenta que a medida que disminuimos el incremento, el gráfico se vuelve más suave.

Cree un archivo de secuencia de comandos y escriba el siguiente código:

x = [1 2 3 4 5 6 7 8 9 10];
x = [-100:20:100];
y = x.^2;
plot(x, y)

Cuando ejecuta el archivo, MATLAB muestra el siguiente gráfico:

Cambie un poco el archivo de código, reduzca el incremento a 5 -

x = [-100:5:100];
y = x.^2;
plot(x, y)

MATLAB dibuja un gráfico más suave:

Agregar título, etiquetas, líneas de cuadrícula y escala en el gráfico

MATLAB le permite agregar títulos, etiquetas a lo largo del eje xy del eje y, líneas de cuadrícula y también ajustar los ejes para arreglar el gráfico.

• los xlabel y ylabel Los comandos generan etiquetas a lo largo de los ejes X e Y.

• los title El comando le permite poner un título en el gráfico.

• los grid on El comando le permite poner las líneas de la cuadrícula en el gráfico.

• los axis equal El comando permite generar el diagrama con los mismos factores de escala y los espacios en ambos ejes.

• los axis square El comando genera un diagrama cuadrado.

Ejemplo

Cree un archivo de secuencia de comandos y escriba el siguiente código:

x = [0:0.01:10];
y = sin(x);
plot(x, y), xlabel('x'), ylabel('Sin(x)'), title('Sin(x) Graph'),
grid on, axis equal

MATLAB genera el siguiente gráfico:

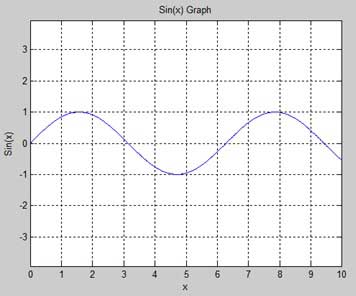
Dibujar varias funciones en el mismo gráfico

Puede dibujar varios gráficos en el mismo gráfico. El siguiente ejemplo demuestra el concepto:

Ejemplo

Cree un archivo de secuencia de comandos y escriba el siguiente código:

x = [0 : 0.01: 10];
y = sin(x);
g = cos(x);
plot(x, y, x, g, '.-'), legend('Sin(x)', 'Cos(x)')

MATLAB genera el siguiente gráfico:

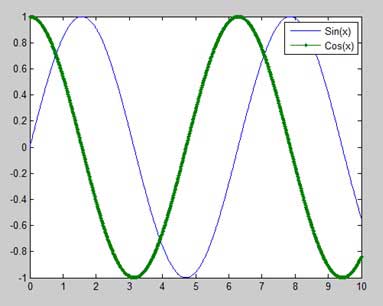
Establecer colores en el gráfico

MATLAB proporciona ocho opciones de color básicas para dibujar gráficos. La siguiente tabla muestra los colores y sus códigos:

Código	Color
w	Blanco
k	Negro
segundo	Azul
r	rojo
C	Cian
gramo	Verde
metro	Magenta
y	Amarillo

Ejemplo

Dibujemos la gráfica de dos polinomios

• f (x) = 3x ⁴ + 2x ³ + 7x ² + 2x + 9 y

• g (x) = 5x ³ + 9x + 2

Cree un archivo de secuencia de comandos y escriba el siguiente código:

x = [-10 : 0.01: 10];
y = 3*x.^4 + 2 * x.^3 + 7 * x.^2 + 2 * x + 9;
g = 5 * x.^3 + 9 * x + 2;
plot(x, y, 'r', x, g, 'g')

Cuando ejecuta el archivo, MATLAB genera el siguiente gráfico:

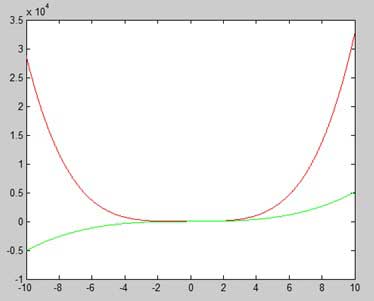
Configuración de escalas de eje

los axisEl comando le permite establecer las escalas de los ejes. Puede proporcionar valores mínimos y máximos para los ejes xey utilizando el comando de eje de la siguiente manera:

axis ( [xmin xmax ymin ymax] )

El siguiente ejemplo muestra esto:

Ejemplo

Cree un archivo de secuencia de comandos y escriba el siguiente código:

x = [0 : 0.01: 10];
y = exp(-x).* sin(2*x + 3);
plot(x, y), axis([0 10 -1 1])

Cuando ejecuta el archivo, MATLAB genera el siguiente gráfico:

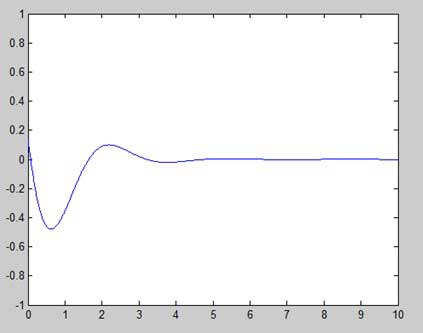
Generación de subparcelas

Cuando crea una matriz de parcelas en la misma figura, cada una de estas parcelas se denomina subtrama. lossubplot El comando se usa para crear subtramas.

La sintaxis del comando es:

subplot(m, n, p)

donde, m y n son el número de filas y columnas de la matriz de trama y p especifica dónde colocar una trama particular.

Cada gráfico creado con el comando subplot puede tener sus propias características. El siguiente ejemplo demuestra el concepto:

Ejemplo

Generemos dos gráficos:

y = e ^−1.5x sin (10x)

y = e ^−2x sin (10x)

Cree un archivo de secuencia de comandos y escriba el siguiente código:

x = [0:0.01:5];
y = exp(-1.5*x).*sin(10*x);
subplot(1,2,1)
plot(x,y), xlabel('x'),ylabel('exp(–1.5x)*sin(10x)'),axis([0 5 -1 1])
y = exp(-2*x).*sin(10*x);
subplot(1,2,2)
plot(x,y),xlabel('x'),ylabel('exp(–2x)*sin(10x)'),axis([0 5 -1 1])

Cuando ejecuta el archivo, MATLAB genera el siguiente gráfico:

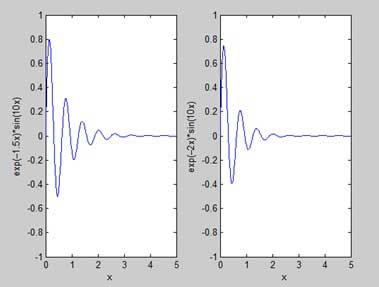
Este capítulo continuará explorando las capacidades de trazado y gráficos de MATLAB. Discutiremos -

• Dibujar gráficos de barras
• Dibujar contornos
• Parcelas tridimensionales

Dibujar gráficos de barras

los barEl comando dibuja un gráfico de barras bidimensional. Tomemos un ejemplo para demostrar la idea.

Ejemplo

Tengamos un aula imaginaria con 10 alumnos. Sabemos que el porcentaje de calificaciones obtenidas por estos estudiantes es 75, 58, 90, 87, 50, 85, 92, 75, 60 y 95. Dibujaremos la gráfica de barras para estos datos.

Cree un archivo de secuencia de comandos y escriba el siguiente código:

x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.eps

Cuando ejecuta el archivo, MATLAB muestra el siguiente gráfico de barras:

Dibujar contornos

Una línea de contorno de una función de dos variables es una curva a lo largo de la cual la función tiene un valor constante. Las curvas de nivel se utilizan para crear mapas de curvas de nivel uniendo puntos de igual elevación por encima de un nivel determinado, como el nivel medio del mar.

MATLAB proporciona una contour función para dibujar mapas de contorno.

Ejemplo

Generemos un mapa de curvas de nivel que muestre las curvas de nivel para una función dada g = f (x, y). Esta función tiene dos variables. Entonces, tendremos que generar dos variables independientes, es decir, dos conjuntos de datos xey. Esto se hace llamando almeshgrid mando.

los meshgrid El comando se usa para generar una matriz de elementos que dan el rango sobre xey junto con la especificación del incremento en cada caso.

Grafiquemos nuestra función g = f (x, y), donde −5 ≤ x ≤ 5, −3 ≤ y ≤ 3. Tomemos un incremento de 0.1 para ambos valores. Las variables se establecen como -

[x,y] = meshgrid(–5:0.1:5, –3:0.1:3);

Por último, necesitamos asignar la función. Sea nuestra función: x ² + y ²

Cree un archivo de secuencia de comandos y escriba el siguiente código:

[x,y] = meshgrid(-5:0.1:5,-3:0.1:3);   %independent variables
g = x.^2 + y.^2;                       % our function
contour(x,y,g)                         % call the contour function
print -deps graph.eps

Cuando ejecuta el archivo, MATLAB muestra el siguiente mapa de contorno:

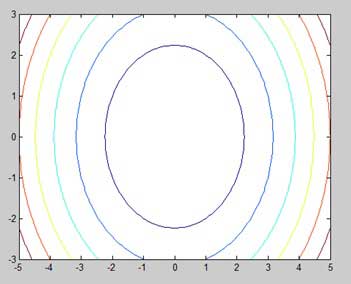
Modifiquemos un poco el código para arreglar el mapa

[x,y] = meshgrid(-5:0.1:5,-3:0.1:3);   %independent variables
g = x.^2 + y.^2;                       % our function
[C, h] = contour(x,y,g);               % call the contour function
set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)
print -deps graph.eps

Cuando ejecuta el archivo, MATLAB muestra el siguiente mapa de contorno:

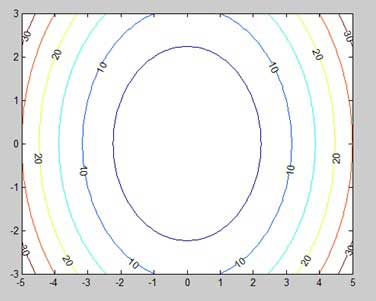
Gráficos tridimensionales

Las gráficas tridimensionales básicamente muestran una superficie definida por una función en dos variables, g = f (x, y).

Como antes, para definir g, primero creamos un conjunto de (x, y) puntos sobre el dominio de la función usando el meshgridmando. A continuación, asignamos la función en sí. Finalmente, usamos elsurf comando para crear un gráfico de superficie.

El siguiente ejemplo demuestra el concepto:

Ejemplo

Creemos un mapa de superficie 3D para la función g = xe ^{- (x 2 + y 2 )}

Cree un archivo de secuencia de comandos y escriba el siguiente código:

[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.eps

Cuando ejecuta el archivo, MATLAB muestra el siguiente mapa 3D:

También puede utilizar el meshcomando para generar una superficie tridimensional. sin embargo, elsurf El comando muestra tanto las líneas de conexión como las caras de la superficie en color, mientras que el mesh El comando crea una superficie de estructura alámbrica con líneas de colores que conectan los puntos de definición.

Hasta ahora, hemos visto que todos los ejemplos funcionan en MATLAB así como en su GNU, alternativamente llamado Octave. Pero para resolver ecuaciones algebraicas básicas, tanto MATLAB como Octave son un poco diferentes, por lo que intentaremos cubrir MATLAB y Octave en secciones separadas.

También discutiremos la factorización y simplificación de expresiones algebraicas.

Resolver ecuaciones algebraicas básicas en MATLAB

los solveLa función se usa para resolver ecuaciones algebraicas. En su forma más simple, la función de resolución toma la ecuación entre comillas como argumento.

Por ejemplo, despejemos x en la ecuación x-5 = 0

solve('x-5=0')

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =
   5

También puede llamar a la función de resolución como -

y = solve('x-5 = 0')

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

y =
   5

Incluso puede que no incluya el lado derecho de la ecuación:

solve('x-5')

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =
   5

Si la ecuación involucra varios símbolos, entonces MATLAB de forma predeterminada asume que está resolviendo para x, sin embargo, la función de resolución tiene otra forma:

solve(equation, variable)

donde, también puede mencionar la variable.

Por ejemplo, resuelva la ecuación v - u - 3t ² = 0, para v. En este caso, deberíamos escribir -

solve('v-u-3*t^2=0', 'v')

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =
   3*t^2 + u

Resolver ecuaciones algebraicas básicas en octava

los roots La función se usa para resolver ecuaciones algebraicas en Octave y puede escribir los ejemplos anteriores de la siguiente manera:

Por ejemplo, despejemos x en la ecuación x-5 = 0

roots([1, -5])

Octave ejecutará la declaración anterior y devolverá el siguiente resultado:

ans = 5

También puede llamar a la función de resolución como -

y = roots([1, -5])

Octave ejecutará la declaración anterior y devolverá el siguiente resultado:

y = 5

Resolver ecuaciones cuadráticas en MATLAB

los solveLa función también puede resolver ecuaciones de orden superior. A menudo se usa para resolver ecuaciones cuadráticas. La función devuelve las raíces de la ecuación en una matriz.

El siguiente ejemplo resuelve la ecuación cuadrática x ² -7x +12 = 0. Cree un archivo de secuencia de comandos y escriba el siguiente código:

eq = 'x^2 -7*x + 12 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));

Cuando ejecuta el archivo, muestra el siguiente resultado:

The first root is: 
   3
The second root is: 
   4

Resolver ecuaciones cuadráticas en octava

El siguiente ejemplo resuelve la ecuación cuadrática x ² -7x 12 = 0 en Octave. Cree un archivo de secuencia de comandos y escriba el siguiente código:

s = roots([1, -7, 12]);

disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));

Cuando ejecuta el archivo, muestra el siguiente resultado:

The first root is: 
   4
The second root is: 
   3

Resolver ecuaciones de orden superior en MATLAB

los solveLa función también puede resolver ecuaciones de orden superior. Por ejemplo, resuelva una ecuación cúbica como (x-3) ² (x-7) = 0

solve('(x-3)^2*(x-7)=0')

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =
   3
   3
   7

En el caso de ecuaciones de orden superior, las raíces son largas y contienen muchos términos. Puede obtener el valor numérico de dichas raíces convirtiéndolas al doble. El siguiente ejemplo resuelve la ecuación de cuarto orden x ⁴ - 7x ³ + 3x ² - 5x + 9 = 0.

Cree un archivo de secuencia de comandos y escriba el siguiente código:

eq = 'x^4 - 7*x^3 + 3*x^2 - 5*x + 9 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));
disp('The third root is: '), disp(s(3));
disp('The fourth root is: '), disp(s(4));

% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));

Cuando ejecuta el archivo, devuelve el siguiente resultado:

The first root is: 
6.630396332390718431485053218985
 The second root is: 
1.0597804633025896291682772499885
 The third root is: 
- 0.34508839784665403032666523448675 - 1.0778362954630176596831109269793*i
 The fourth root is: 
- 0.34508839784665403032666523448675 + 1.0778362954630176596831109269793*i
Numeric value of first root
   6.6304
Numeric value of second root
   1.0598
Numeric value of third root
   -0.3451 - 1.0778i
Numeric value of fourth root
   -0.3451 + 1.0778i

Tenga en cuenta que las dos últimas raíces son números complejos.

Resolver ecuaciones de orden superior en octava

El siguiente ejemplo resuelve la ecuación de cuarto orden x ⁴ - 7x ³ + 3x ² - 5x + 9 = 0.

Cree un archivo de secuencia de comandos y escriba el siguiente código:

v = [1, -7,  3, -5, 9];
s = roots(v);

% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));

Cuando ejecuta el archivo, devuelve el siguiente resultado:

Numeric value of first root
 6.6304
Numeric value of second root
-0.34509 + 1.07784i
Numeric value of third root
-0.34509 - 1.07784i
Numeric value of fourth root
 1.0598

Resolver sistema de ecuaciones en MATLAB

los solveLa función también se puede usar para generar soluciones de sistemas de ecuaciones que involucran más de una variable. Tomemos un ejemplo sencillo para demostrar este uso.

Resolvamos las ecuaciones -

5x + 9y = 5

3x - 6y = 4

Cree un archivo de secuencia de comandos y escriba el siguiente código:

s = solve('5*x + 9*y = 5','3*x - 6*y = 4');
s.x
s.y

Cuando ejecuta el archivo, muestra el siguiente resultado:

ans =
   22/19
ans =
   -5/57

De la misma manera, puede resolver sistemas lineales más grandes. Considere el siguiente conjunto de ecuaciones:

x + 3y -2z = 5

3x + 5y + 6z = 7

2x + 4y + 3z = 8

Resolver sistema de ecuaciones en octava

Tenemos un enfoque un poco diferente para resolver un sistema de 'n' ecuaciones lineales en 'n' incógnitas. Tomemos un ejemplo sencillo para demostrar este uso.

Resolvamos las ecuaciones -

5x + 9y = 5

3x - 6y = 4

Dicho sistema de ecuaciones lineales se puede escribir como la ecuación de matriz única Ax = b, donde A es la matriz de coeficientes, b es el vector de columna que contiene el lado derecho de las ecuaciones lineales yx es el vector de columna que representa la solución como mostrado en el programa siguiente -

Cree un archivo de secuencia de comandos y escriba el siguiente código:

A = [5, 9; 3, -6];
b = [5;4];
A \ b

Cuando ejecuta el archivo, muestra el siguiente resultado:

ans =

   1.157895
  -0.087719

De la misma manera, puede resolver sistemas lineales más grandes como se indica a continuación:

x + 3y -2z = 5

3x + 5y + 6z = 7

2x + 4y + 3z = 8

Ampliación y recopilación de ecuaciones en MATLAB

los expand y el collectLa función expande y recopila una ecuación respectivamente. El siguiente ejemplo demuestra los conceptos:

Cuando trabaja con muchas funciones simbólicas, debe declarar que sus variables son simbólicas.

Cree un archivo de secuencia de comandos y escriba el siguiente código:

syms x   %symbolic variable x
syms y   %symbolic variable x
% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(sin(2*x))
expand(cos(x+y))
 
% collecting equations
collect(x^3 *(x-7))
collect(x^4*(x-3)*(x-5))

Cuando ejecuta el archivo, muestra el siguiente resultado:

ans =
   x^2 + 4*x - 45
ans =
   x^4 + x^3 - 43*x^2 + 23*x + 210
ans =
   2*cos(x)*sin(x)
ans =
   cos(x)*cos(y) - sin(x)*sin(y)
ans =
   x^4 - 7*x^3
ans =
   x^6 - 8*x^5 + 15*x^4

Ampliación y recopilación de ecuaciones en octava

Necesitas tener symbolic paquete, que proporciona expand y el collectfunción para expandir y recopilar una ecuación, respectivamente. El siguiente ejemplo demuestra los conceptos:

Cuando trabaja con muchas funciones simbólicas, debe declarar que sus variables son simbólicas, pero Octave tiene un enfoque diferente para definir variables simbólicas. Observe el uso deSin y Cos, que también se definen en paquete simbólico.

Cree un archivo de secuencia de comandos y escriba el siguiente código:

% first of all load the package, make sure its installed.
pkg load symbolic

% make symbols module available
symbols

% define symbolic variables
x = sym ('x');
y = sym ('y');
z = sym ('z');

% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(Sin(2*x))
expand(Cos(x+y))
 
% collecting equations
collect(x^3 *(x-7), z)
collect(x^4*(x-3)*(x-5), z)

Cuando ejecuta el archivo, muestra el siguiente resultado:

ans =

-45.0+x^2+(4.0)*x
ans =

210.0+x^4-(43.0)*x^2+x^3+(23.0)*x
ans =

sin((2.0)*x)
ans =

cos(y+x)
ans =

x^(3.0)*(-7.0+x)
ans =

(-3.0+x)*x^(4.0)*(-5.0+x)

Factorización y simplificación de expresiones algebraicas

los factor función factoriza una expresión y la simplifyfunción simplifica una expresión. El siguiente ejemplo demuestra el concepto:

Ejemplo

Cree un archivo de secuencia de comandos y escriba el siguiente código:

syms x
syms y
factor(x^3 - y^3)
factor([x^2-y^2,x^3+y^3])
simplify((x^4-16)/(x^2-4))

Cuando ejecuta el archivo, muestra el siguiente resultado:

ans =
   (x - y)*(x^2 + x*y + y^2)
ans =
   [ (x - y)*(x + y), (x + y)*(x^2 - x*y + y^2)]
ans =
   x^2 + 4

MATLAB proporciona varias formas de resolver problemas de cálculo diferencial e integral, resolución de ecuaciones diferenciales de cualquier grado y cálculo de límites. Lo mejor de todo es que puede trazar fácilmente las gráficas de funciones complejas y verificar máximos, mínimos y otros puntos de papelería en una gráfica resolviendo la función original, así como su derivada.

Este capítulo se ocupará de los problemas de cálculo. En este capítulo, discutiremos conceptos previos al cálculo, es decir, calcular límites de funciones y verificar las propiedades de los límites.

En el próximo capítulo Diferencial , calcularemos la derivada de una expresión y encontraremos los máximos y mínimos locales en una gráfica. También discutiremos la resolución de ecuaciones diferenciales.

Finalmente, en el capítulo Integración , discutiremos el cálculo integral.

Calcular límites

MATLAB proporciona la limitfunción para calcular límites. En su forma más básica, ellimit La función toma la expresión como argumento y encuentra el límite de la expresión cuando la variable independiente llega a cero.

Por ejemplo, calculemos el límite de una función f (x) = (x ³ + 5) / (x ⁴ + 7), ya que x tiende a cero.

syms x
limit((x^3 + 5)/(x^4 + 7))

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =
   5/7

La función límite cae en el ámbito de la computación simbólica; necesitas usar elsymsfunción para decirle a MATLAB qué variables simbólicas está utilizando. También puede calcular el límite de una función, ya que la variable tiende a algún número distinto de cero. Para calcular lim _{x-> a} (f (x)), usamos el comando limit con argumentos. El primero es la expresión y el segundo es el número, al que x se acerca, aquí es a .

Por ejemplo, calculemos el límite de una función f (x) = (x-3) / (x-1), ya que x tiende a 1.

limit((x - 3)/(x-1),1)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =
   NaN

Tomemos otro ejemplo,

limit(x^2 + 5, 3)

MATLAB ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =
   14

Calcular límites usando una octava

A continuación se muestra la versión Octave del ejemplo anterior usando symbolic paquete, intente ejecutar y comparar el resultado -

pkg load symbolic
symbols

x = sym("x");
subs((x^3+5)/(x^4+7),x,0)

Octave ejecutará la declaración anterior y devolverá el siguiente resultado:

ans =
   0.7142857142857142857

Verificación de las propiedades básicas de los límites

El teorema algebraico del límite proporciona algunas propiedades básicas de los límites. Estos son los siguientes:

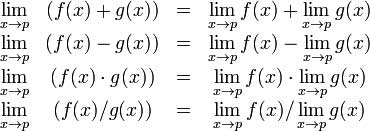
Consideremos dos funciones:

• f (x) = (3x + 5) / (x - 3)
• g (x) = x ² + 1.

Calculemos los límites de las funciones cuando x tiende a 5, de ambas funciones y verifiquemos las propiedades básicas de los límites usando estas dos funciones y MATLAB.

Ejemplo

Cree un archivo de script y escriba el siguiente código en él:

syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)

Cuando ejecuta el archivo, muestra:

l1 =
   17
  
l2 =
   17
  
lAdd =
   34
 
lSub =
   0
  
lMult =
   289
  
lDiv =
   1

Verificación de las propiedades básicas de los límites usando Octave

A continuación se muestra la versión Octave del ejemplo anterior usando symbolic paquete, intente ejecutar y comparar el resultado -

pkg load symbolic
symbols

x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;

l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)

Octave ejecutará la declaración anterior y devolverá el siguiente resultado:

l1 =
   17.0
l2 =
   17.0
lAdd =
   34.0
lSub =
   0.0
lMult =
   289.0
lDiv =
   1.0

Límites de los lados izquierdo y derecho

Cuando una función tiene una discontinuidad para algún valor particular de la variable, el límite no existe en ese punto. En otras palabras, los límites de una función f (x) tiene discontinuidad en x = a, cuando el valor del límite, cuando x se acerca a x desde el lado izquierdo, no es igual al valor del límite cuando x se acerca desde el lado derecho.

Esto lleva al concepto de límites para diestros y zurdos. Un límite a la izquierda se define como el límite cuando x -> a, desde la izquierda, es decir, x se acerca a a, para valores de x <a. Un límite a la derecha se define como el límite cuando x -> a, desde la derecha, es decir, x se acerca a a, para valores de x> a. Cuando el límite para zurdos y el límite para diestros no son iguales, el límite no existe.

Consideremos una función -

f(x) = (x - 3)/|x - 3|

Demostraremos que lím _{x-> 3} f (x) no existe. MATLAB nos ayuda a establecer este hecho de dos formas:

• Trazando la gráfica de la función y mostrando la discontinuidad.
• Calculando los límites y mostrando que ambos son diferentes.

Los límites para zurdos y diestros se calculan pasando las cadenas de caracteres 'izquierda' y 'derecha' al comando de límite como último argumento.

Ejemplo

Cree un archivo de script y escriba el siguiente código en él:

f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')

Cuando ejecuta el archivo, MATLAB dibuja la siguiente gráfica

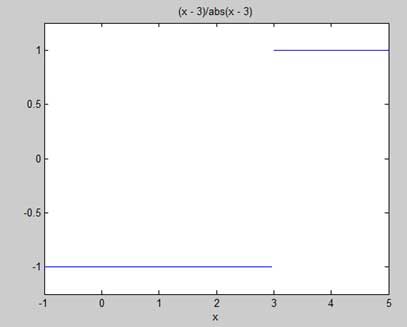
Después de que se muestre la siguiente salida:

l =
   -1
  
r =
   1

MATLAB proporciona la diffcomando para calcular derivadas simbólicas. En su forma más simple, pasa la función que desea diferenciar al comando diff como argumento.

Por ejemplo, calculemos la derivada de la función f (t) = 3t ² + 2t ^-2

Ejemplo

Cree un archivo de script y escriba el siguiente código en él:

syms t
f = 3*t^2 + 2*t^(-2);
diff(f)

Cuando el código anterior se compila y ejecuta, produce el siguiente resultado:

ans =
6*t - 4/t^3

A continuación se muestra el equivalente en octava del cálculo anterior:

pkg load symbolic
symbols

t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)

Octave ejecuta el código y devuelve el siguiente resultado:

ans =
   -(4.0)*t^(-3.0)+(6.0)*t

Verificación de reglas elementales de diferenciación

Enunciemos brevemente varias ecuaciones o reglas para la diferenciación de funciones y verifiquemos estas reglas. Para este propósito, escribiremos f '(x) para una derivada de primer orden y f "(x) para una derivada de segundo orden.

Las siguientes son las reglas para la diferenciación:

Regla 1

Para cualquier función f y g y cualquier número real a y b son la derivada de la función -

h(x) = af(x) + bg(x) con respecto ax está dado por -

h'(x) = af'(x) + bg'(x)

Regla 2

los sum y subtraction Las reglas establecen que si f y g son dos funciones, f 'y g' son sus derivadas respectivamente, entonces,

(f + g)' = f' + g'

(f - g)' = f' - g'

Regla 3

los product La regla establece que si f y g son dos funciones, f 'y g' son sus derivadas respectivamente, entonces,

(f.g)' = f'.g + g'.f

Regla 4

los quotient La regla establece que si f y g son dos funciones, f 'y g' son sus derivadas respectivamente, entonces,

(f/g)' = (f'.g - g'.f)/g²

Regla 5

los polynomial o la regla de poder elemental establece que, si y = f(x) = xⁿ, luego f' = n. x^(n-1)

Un resultado directo de esta regla es que la derivada de cualquier constante es cero, es decir, si y = k, cualquier constante, entonces

f' = 0

Regla 6

los chain La regla establece que, derivada de la función de una función h(x) = f(g(x)) con respecto ax es,

h'(x)= f'(g(x)).g'(x)

Ejemplo

Cree un archivo de script y escriba el siguiente código en él:

syms x
syms t

f = (x + 2)*(x^2 + 3)
der1 = diff(f)
f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)
f = (x^2 + 1)^17
der5 = diff(f)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)

Cuando ejecuta el archivo, MATLAB muestra el siguiente resultado:

f =
   (x^2 + 3)*(x + 2)
 
   der1 =
   2*x*(x + 2) + x^2 + 3
  
f =
   (t^(1/2) + t^3)*(t^2 + 3)
 
   der2 =
   (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)
  
f =
   (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
  
der3 =
   (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)
 
f =
   (2*x^2 + 3*x)/(x^3 + 1)
  
der4 =
   (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2
  
f =
   (x^2 + 1)^17
  
der5 =
   34*x*(x^2 + 1)^16
  
f =
   1/(t^3 + 3*t^2 + 5*t - 9)^6
  
der6 =
   -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7

A continuación se muestra el equivalente en octava del cálculo anterior:

pkg load symbolic
symbols

x = sym("x");
t = sym("t");
f = (x + 2)*(x^2 + 3) 
der1 = differentiate(f,x) 
f = (t^2 + 3)*(t^(1/2) + t^3) 
der2 = differentiate(f,t) 
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) 
der3 = differentiate(f,x) 
f = (2*x^2 + 3*x)/(x^3 + 1) 
der4 = differentiate(f,x) 
f = (x^2 + 1)^17 
der5 = differentiate(f,x) 
f = (t^3 + 3* t^2 + 5*t -9)^(-6) 
der6 = differentiate(f,t)

Octave ejecuta el código y devuelve el siguiente resultado:

f =

(2.0+x)*(3.0+x^(2.0))
der1 =

3.0+x^(2.0)+(2.0)*(2.0+x)*x
f =

(t^(3.0)+sqrt(t))*(3.0+t^(2.0))
der2 =

(2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0))
f =

(1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))
der3 =

(-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x)
f =

(1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x)
der4 =

(1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x)
f =

(1.0+x^(2.0))^(17.0)
der5 =

(34.0)*(1.0+x^(2.0))^(16.0)*x
f =

(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0)
der6 =

-(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)

Derivadas de funciones exponenciales, logarítmicas y trigonométricas

La siguiente tabla proporciona las derivadas de funciones exponenciales, logarítmicas y trigonométricas de uso común:

Función	Derivado
ca.x	c a.x .ln ca (ln es el logaritmo natural)
ex	e x
ln x	1 / x
lncx	1 / x.ln c
xx	x x . (1 + ln x)
sin(x)	cos (x)
cos(x)	-pecado (x)
tan(x)	seg 2 (x), o 1 / cos 2 (x), o 1 + tan 2 (x)
cot(x)	-csc 2 (x), o -1 / sin 2 (x), o - (1 + cot 2 (x))
sec(x)	sec (x) .tan (x)
csc(x)	-csc (x) .cot (x)

Ejemplo

Cree un archivo de script y escriba el siguiente código en él:

syms x
y = exp(x)
diff(y)
y = x^9
diff(y)
y = sin(x)
diff(y)
y = tan(x)
diff(y)
y = cos(x)
diff(y)
y = log(x)
diff(y)
y = log10(x)
diff(y)
y = sin(x)^2
diff(y)
y = cos(3*x^2 + 2*x + 1)
diff(y)
y = exp(x)/sin(x)
diff(y)

Cuando ejecuta el archivo, MATLAB muestra el siguiente resultado:

y =
   exp(x)
   ans =
   exp(x)

y =
   x^9
   ans =
   9*x^8
  
y =
   sin(x)
   ans =
   cos(x)
  
y =
   tan(x)
   ans =
   tan(x)^2 + 1
 
y =
   cos(x)
   ans =
   -sin(x)
  
y =
   log(x)
   ans =
   1/x
  
y =
   log(x)/log(10)
   ans =
   1/(x*log(10))
 
y =
   sin(x)^2
   ans =
   2*cos(x)*sin(x)
 
y =
   cos(3*x^2 + 2*x + 1)
   ans =
   -sin(3*x^2 + 2*x + 1)*(6*x + 2)
  
y =
   exp(x)/sin(x)
   ans =
   exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2

A continuación se muestra el equivalente en octava del cálculo anterior:

pkg load symbolic
symbols

x = sym("x");
y = Exp(x)
differentiate(y,x)

y = x^9
differentiate(y,x)

y = Sin(x)
differentiate(y,x)

y = Tan(x)
differentiate(y,x)

y = Cos(x)
differentiate(y,x)

y = Log(x)
differentiate(y,x)

% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)

y = Sin(x)^2
differentiate(y,x)

y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)

y = Exp(x)/Sin(x)
differentiate(y,x)

Octave ejecuta el código y devuelve el siguiente resultado:

y =

exp(x)
ans =

exp(x)
y =

x^(9.0)
ans =

(9.0)*x^(8.0)
y =

sin(x)
ans =

cos(x)
y =

tan(x)
ans =

1+tan(x)^2
y =

cos(x)
ans =

-sin(x)
y =

log(x)
ans =

x^(-1)
y =

sin(x)^(2.0)
ans =

(2.0)*sin(x)*cos(x)
y =

cos(1.0+(2.0)*x+(3.0)*x^(2.0))
ans =

-(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0))
y =

sin(x)^(-1)*exp(x)
ans =

sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)

Cálculo de derivados de orden superior

Para calcular derivadas más altas de una función f, usamos la sintaxis diff(f,n).

Calculemos la segunda derivada de la función y = f (x) = x .e ^-3x

f = x*exp(-3*x);
diff(f, 2)

MATLAB ejecuta el código y devuelve el siguiente resultado:

ans =
9*x*exp(-3*x) - 6*exp(-3*x)

A continuación se muestra el equivalente en octava del cálculo anterior:

pkg load symbolic
symbols

x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)

Octave ejecuta el código y devuelve el siguiente resultado:

ans =

(9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)

Ejemplo

En este ejemplo, solucionemos un problema. Dado que una funcióny = f(x) = 3 sin(x) + 7 cos(5x). Tendremos que averiguar si la ecuaciónf" + f = -5cos(2x) se mantiene cierto.

Cree un archivo de script y escriba el siguiente código en él:

syms x
y = 3*sin(x)+7*cos(5*x);  % defining the function
lhs = diff(y,2)+y;        %evaluting the lhs of the equation
rhs = -5*cos(2*x);        %rhs of the equation
if(isequal(lhs,rhs))
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

Cuando ejecuta el archivo, muestra el siguiente resultado:

No, the equation does not hold true
Value of LHS is: 
-168*cos(5*x)

A continuación se muestra el equivalente en octava del cálculo anterior:

pkg load symbolic
symbols

x = sym("x");
y = 3*Sin(x)+7*Cos(5*x);           % defining the function
lhs = differentiate(y, x, 2) + y;  %evaluting the lhs of the equation
rhs = -5*Cos(2*x);                 %rhs of the equation

if(lhs == rhs)
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

Octave ejecuta el código y devuelve el siguiente resultado:

No, the equation does not hold true
Value of LHS is: 
-(168.0)*cos((5.0)*x)

Encontrar los máximos y mínimos de una curva

Si buscamos los máximos y mínimos locales para un gráfico, básicamente buscamos los puntos más altos o más bajos en el gráfico de la función en una localidad en particular, o para un rango particular de valores de la variable simbólica.

Para una función y = f (x) los puntos en el gráfico donde el gráfico tiene pendiente cero se llaman stationary points. En otras palabras, los puntos estacionarios son donde f '(x) = 0.

Para encontrar los puntos estacionarios de una función que diferenciamos, necesitamos igualar la derivada a cero y resolver la ecuación.

Ejemplo

Encontremos los puntos estacionarios de la función f (x) = 2x ³ + 3x ² - 12x + 17

Siga los siguientes pasos:

First let us enter the function and plot its graph.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y)

MATLAB ejecuta el código y devuelve el siguiente gráfico:

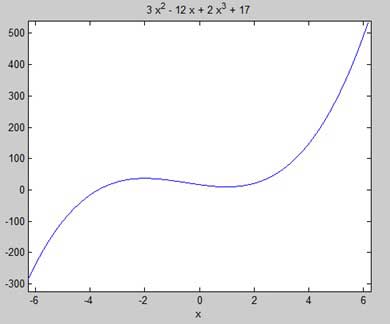
Aquí está el código equivalente de Octave para el ejemplo anterior:

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y)
print -deps graph.eps

Our aim is to find some local maxima and minima on the graph, so let us find the local maxima and minima for the interval [-2, 2] on the graph.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y, [-2, 2])

MATLAB ejecuta el código y devuelve el siguiente gráfico:

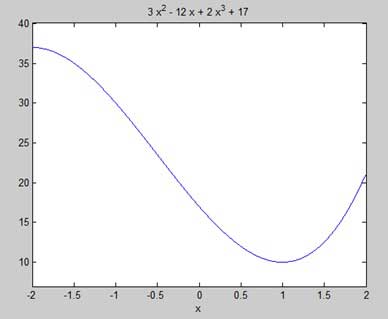
Aquí está el código equivalente de Octave para el ejemplo anterior:

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y, [-2, 2])
print -deps graph.eps

Next, let us compute the derivative.

g = diff(y)

MATLAB ejecuta el código y devuelve el siguiente resultado:

g =
   6*x^2 + 6*x - 12

Aquí está el equivalente en octava del cálculo anterior:

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

Octave ejecuta el código y devuelve el siguiente resultado:

g =
   -12.0+(6.0)*x+(6.0)*x^(2.0)

Let us solve the derivative function, g, to get the values where it becomes zero.

s = solve(g)

MATLAB ejecuta el código y devuelve el siguiente resultado:

s =
   1
   -2

A continuación se muestra el equivalente en octava del cálculo anterior:

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])

Octave ejecuta el código y devuelve el siguiente resultado:

g =

-12.0+(6.0)*x^(2.0)+(6.0)*x
ans =

  -2
   1

This agrees with our plot. So let us evaluate the function f at the critical points x = 1, -2. Podemos sustituir un valor en una función simbólica usando el subs mando.

subs(y, 1), subs(y, -2)

MATLAB ejecuta el código y devuelve el siguiente resultado:

ans =
   10
ans =
   37

A continuación se muestra el equivalente en octava del cálculo anterior:

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)

ans =
   10.0
ans =
   37.0-4.6734207789940138748E-18*I

Por lo tanto, los valores mínimo y máximo de la función f (x) = 2x ³ + 3x ² - 12x + 17, en el intervalo [-2,2] son ​​10 y 37.

Resolver ecuaciones diferenciales

MATLAB proporciona la dsolve comando para resolver ecuaciones diferenciales simbólicamente.

La forma más básica del dsolve El comando para encontrar la solución a una sola ecuación es

dsolve('eqn')

donde eqn es una cadena de texto utilizada para ingresar la ecuación.

Devuelve una solución simbólica con un conjunto de constantes arbitrarias que MATLAB etiqueta C1, C2, etc.

También puede especificar las condiciones iniciales y de contorno para el problema, como una lista delimitada por comas siguiendo la ecuación como -

dsolve('eqn','cond1', 'cond2',…)

Con el fin de utilizar el comando dsolve, derivatives are indicated with a D. Por ejemplo, una ecuación como f '(t) = -2 * f + costo (t) se ingresa como -

'Df = -2*f + cos(t)'

Las derivadas más altas se indican siguiendo a D por el orden de la derivada.

Por ejemplo, la ecuación f "(x) + 2f '(x) = 5sin3x debe ingresarse como -

'D2y + 2Dy = 5*sin(3*x)'

Tomemos un ejemplo simple de una ecuación diferencial de primer orden: y '= 5y.

s = dsolve('Dy = 5*y')

MATLAB ejecuta el código y devuelve el siguiente resultado:

s =
   C2*exp(5*t)

Tomemos otro ejemplo de una ecuación diferencial de segundo orden como: y "- y = 0, y (0) = -1, y '(0) = 2.

dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')

MATLAB ejecuta el código y devuelve el siguiente resultado:

ans =
   exp(t)/2 - (3*exp(-t))/2

La integración se ocupa de dos tipos de problemas esencialmente diferentes.

• En el primer tipo, se da la derivada de una función y queremos encontrar la función. Por tanto, básicamente invertimos el proceso de diferenciación. Este proceso inverso se conoce como anti-diferenciación, o encontrar la función primitiva, o encontrar unaindefinite integral.

• El segundo tipo de problemas implica sumar un número muy grande de cantidades muy pequeñas y luego tomar un límite cuando el tamaño de las cantidades se acerca a cero, mientras que el número de términos tiende a infinito. Este proceso conduce a la definición deldefinite integral.

Las integrales definidas se utilizan para encontrar área, volumen, centro de gravedad, momento de inercia, trabajo realizado por una fuerza y ​​en muchas otras aplicaciones.

Encontrar integrales indefinidas con MATLAB

Por definición, si la derivada de una función f (x) es f '(x), entonces decimos que una integral indefinida de f' (x) con respecto a x es f (x). Por ejemplo, dado que la derivada (con respecto a x) de x ² es 2x, podemos decir que una integral indefinida de 2x es x ² .

En símbolos -

f'(x²) = 2x, por lo tanto,

∫ 2xdx = x².

La integral indefinida no es única, porque la derivada de x ² + c, para cualquier valor de una constante c, también será 2x.

Esto se expresa en símbolos como:

∫ 2xdx = x² + c.

Donde, c se llama una 'constante arbitraria'.

MATLAB proporciona una intcomando para calcular la integral de una expresión. Para derivar una expresión para la integral indefinida de una función, escribimos:

int(f);

Por ejemplo, de nuestro ejemplo anterior:

syms x 
int(2*x)

MATLAB ejecuta la declaración anterior y devuelve el siguiente resultado:

ans =
   x^2

Ejemplo 1

En este ejemplo, busquemos la integral de algunas expresiones de uso común. Cree un archivo de secuencia de comandos y escriba el siguiente código en él:

syms x n

int(sym(x^n))
f = 'sin(n*t)'
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)

Cuando ejecuta el archivo, muestra el siguiente resultado:

ans =
   piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
   -cos(n*t)/n
   ans =
   (a*sin(pi*t))/pi
   ans =
   a^x/log(a)

Ejemplo 2

Cree un archivo de secuencia de comandos y escriba el siguiente código en él:

syms x n
int(cos(x))
int(exp(x))
int(log(x))
int(x^-1)
int(x^5*cos(5*x))
pretty(int(x^5*cos(5*x)))
int(x^-5)
int(sec(x)^2)
pretty(int(1 - 10*x + 9 * x^2))
int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))

Tenga en cuenta que el pretty La función devuelve una expresión en un formato más legible.

Cuando ejecuta el archivo, muestra el siguiente resultado:

ans =
   sin(x)
 
ans =
   exp(x)
 
ans =
   x*(log(x) - 1)
 
ans =
   log(x)
 
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
                                    2             4 
   24 cos(5 x)   24 x sin(5 x)   12 x  cos(5 x)   x  cos(5 x) 
   ----------- + ------------- - -------------- + ------------ 
      3125            625             125              5 
   
        3             5 
 
   4 x  sin(5 x)   x  sin(5 x) 
   ------------- + ----------- 
         25              5
 
ans =
-1/(4*x^4)
 
ans =
tan(x)
        2 
  x (3 x  - 5 x + 1)
 
ans = 
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
 
      6      5      4    3 
    7 x    3 x    5 x    x 
  - ---- - ---- + ---- + -- 
     12     5      8     2

Encontrar integrales definidas usando MATLAB

Por definición, la integral definida es básicamente el límite de una suma. Usamos integrales definidas para encontrar áreas como el área entre una curva y el eje xy el área entre dos curvas. Las integrales definidas también se pueden usar en otras situaciones, donde la cantidad requerida se puede expresar como el límite de una suma.

los int La función se puede utilizar para una integración definida pasando los límites sobre los que desea calcular la integral.

Calcular

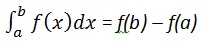
nosotros escribimos,

int(x, a, b)

Por ejemplo, para calcular el valor de

escribimos:

int(x, 4, 9)

MATLAB ejecuta la declaración anterior y devuelve el siguiente resultado:

ans =
   65/2

A continuación se muestra el equivalente en octava del cálculo anterior:

pkg load symbolic
symbols

x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);

a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));

Octave ejecuta el código y devuelve el siguiente resultado:

Area: 

   32.500

Se puede dar una solución alternativa usando la función quad () proporcionada por Octave de la siguiente manera:

pkg load symbolic
symbols

f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);

display('Area: '), disp(double(a));

Octave ejecuta el código y devuelve el siguiente resultado:

Area: 
   32.500

Ejemplo 1

Calculemos el área encerrada entre el eje x, y la curva y = x ³ −2x + 5 y las ordenadas x = 1 y x = 2.

El área requerida viene dada por:

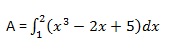
Cree un archivo de secuencia de comandos y escriba el siguiente código:

f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));

Cuando ejecuta el archivo, muestra el siguiente resultado:

a =
23/4
Area: 
   5.7500

A continuación se muestra el equivalente en octava del cálculo anterior:

pkg load symbolic
symbols

x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);

a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));

Octave ejecuta el código y devuelve el siguiente resultado:

Area: 

   5.7500

Se puede dar una solución alternativa usando la función quad () proporcionada por Octave de la siguiente manera:

pkg load symbolic
symbols

x = sym("x");
f = inline("x^3 - 2*x +5");

[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));

Octave ejecuta el código y devuelve el siguiente resultado:

Area: 
   5.7500

Ejemplo 2

Encuentre el área bajo la curva: f (x) = x ² cos (x) para −4 ≤ x ≤ 9.

Cree un archivo de script y escriba el siguiente código:

f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));

Cuando ejecuta el archivo, MATLAB traza el gráfico:

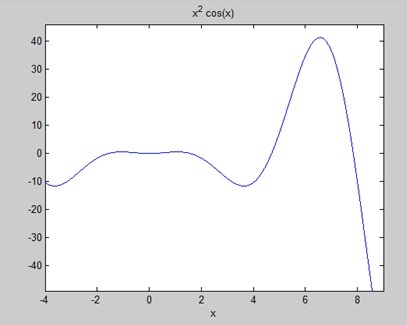
La salida se da a continuación:

a = 
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
 
Area: 
   0.3326

A continuación se muestra el equivalente en octava del cálculo anterior:

pkg load symbolic
symbols

x = sym("x");
f = inline("x^2*cos(x)");

ezplot(f, [-4,9])
print -deps graph.eps

[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));

MATLAB representa polinomios como vectores de fila que contienen coeficientes ordenados por potencias descendentes. Por ejemplo, la ecuación P (x) = x ⁴ + 7x ³ - 5x + 9 podría representarse como -

p = [1 7 0 -5 9];

Evaluación de polinomios

los polyvalLa función se utiliza para evaluar un polinomio en un valor especificado. Por ejemplo, para evaluar nuestro polinomio anteriorp, en x = 4, escriba -

p = [1 7 0  -5 9];
polyval(p,4)

MATLAB ejecuta las declaraciones anteriores y devuelve el siguiente resultado:

ans = 693

MATLAB también proporciona polyvalmfunción para evaluar un polinomio matricial. Un polinomio matricial es unpolynomial con matrices como variables.

Por ejemplo, creemos una matriz cuadrada X y evaluemos el polinomio p, en X -

p = [1 7 0  -5 9];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
polyvalm(p, X)

MATLAB ejecuta las declaraciones anteriores y devuelve el siguiente resultado:

ans =
      2307       -1769        -939        4499
      2314       -2376        -249        4695
      2256       -1892        -549        4310
      4570       -4532       -1062        9269

Encontrar las raíces de los polinomios

los rootsLa función calcula las raíces de un polinomio. Por ejemplo, para calcular las raíces de nuestro polinomio p, escriba -

p = [1 7 0  -5 9];
r = roots(p)

MATLAB ejecuta las declaraciones anteriores y devuelve el siguiente resultado:

r =
   -6.8661 + 0.0000i
   -1.4247 + 0.0000i
   0.6454 + 0.7095i
   0.6454 - 0.7095i

La función polyes una función inversa de la función de raíces y vuelve a los coeficientes del polinomio. Por ejemplo

p2 = poly(r)

MATLAB ejecuta las declaraciones anteriores y devuelve el siguiente resultado:

p2 =

   Columns 1 through 3:

      1.00000 + 0.00000i   7.00000 + 0.00000i   0.00000 + 0.00000i

   Columns 4 and 5:

      -5.00000 - 0.00000i   9.00000 + 0.00000i

Ajuste de curva polinomial

los polyfitLa función encuentra los coeficientes de un polinomio que se ajusta a un conjunto de datos en un sentido de mínimos cuadrados. Si xey son dos vectores que contienen los datos xey que se van a ajustar a un polinomio de n grados, entonces obtenemos el polinomio que ajusta los datos escribiendo:

p = polyfit(x,y,n)

Ejemplo

Cree un archivo de secuencia de comandos y escriba el siguiente código:

x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67];   %data
p = polyfit(x,y,4)   %get the polynomial

% Compute the values of the polyfit estimate over a finer range, 
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;          
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid on

Cuando ejecuta el archivo, MATLAB muestra el siguiente resultado:

p =
   4.1056  -47.9607  222.2598 -362.7453  191.1250

Y traza el siguiente gráfico:

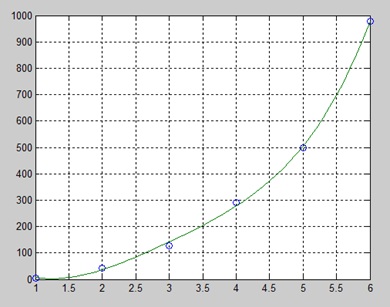
MATLAB proporciona comandos para trabajar con transformaciones, como las transformadas de Laplace y Fourier. Las transformaciones se utilizan en ciencia e ingeniería como una herramienta para simplificar el análisis y observar los datos desde otro ángulo.

Por ejemplo, la transformada de Fourier nos permite convertir una señal representada en función del tiempo en función de la frecuencia. La transformada de Laplace nos permite convertir una ecuación diferencial en una ecuación algebraica.

MATLAB proporciona la laplace, fourier y fft comandos para trabajar con transformadas de Laplace, Fourier y Fast Fourier.

La Transformada de Laplace

La transformada de Laplace de una función del tiempo f (t) viene dada por la siguiente integral:

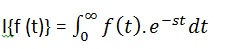
La transformada de Laplace también se denota como transformada de f (t) en F (s). Puede ver que este proceso de transformación o integración convierte f (t), una función de la variable simbólica t, en otra función F (s), con otra variable s.

La transformada de Laplace convierte las ecuaciones diferenciales en algebraicas. Para calcular una transformada de Laplace de una función f (t), escriba -

laplace(f(t))

Ejemplo

En este ejemplo, calcularemos la transformada de Laplace de algunas funciones de uso común.

Cree un archivo de secuencia de comandos y escriba el siguiente código:

syms s t a b w

laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))

Cuando ejecuta el archivo, muestra el siguiente resultado:

ans =
   1/s^2

ans =
   2/s^3

ans =
   362880/s^10

ans =
   1/(b + s)
  
ans =
   w/(s^2 + w^2)
  
ans =
   s/(s^2 + w^2)

La transformada inversa de Laplace

MATLAB nos permite calcular la transformada inversa de Laplace usando el comando ilaplace.

Por ejemplo,

ilaplace(1/s^3)

MATLAB ejecutará la declaración anterior y mostrará el resultado:

ans =
   t^2/2

Ejemplo

Cree un archivo de secuencia de comandos y escriba el siguiente código:

syms s t a b w

ilaplace(1/s^7)
ilaplace(2/(w+s))
ilaplace(s/(s^2+4))
ilaplace(exp(-b*t))
ilaplace(w/(s^2 + w^2))
ilaplace(s/(s^2 + w^2))

Cuando ejecuta el archivo, muestra el siguiente resultado:

ans =
   t^6/720

ans =
   2*exp(-t*w)

ans =
   cos(2*t)

ans =
   ilaplace(exp(-b*t), t, x)

ans =
   sin(t*w)

ans =
   cos(t*w)

Las transformadas de Fourier

La transformada de Fourier comúnmente transforma una función matemática del tiempo, f (t), en una nueva función, a veces denotada por o F, cuyo argumento es la frecuencia con unidades de ciclos / s (hercios) o radianes por segundo. La nueva función se conoce entonces como la transformada de Fourier y / o el espectro de frecuencia de la función f.

Ejemplo

Cree un archivo de secuencia de comandos y escriba el siguiente código en él:

syms x 
f = exp(-2*x^2);     %our function
ezplot(f,[-2,2])     % plot of our function
FT = fourier(f)      % Fourier transform

Cuando ejecuta el archivo, MATLAB traza el siguiente gráfico:

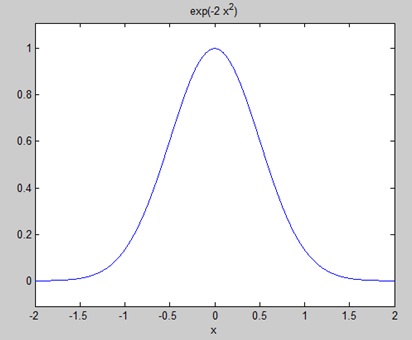
Se muestra el siguiente resultado:

FT =
   (2^(1/2)*pi^(1/2)*exp(-w^2/8))/2

Trazando la transformada de Fourier como -

ezplot(FT)

Da el siguiente gráfico:

Transformadas inversas de Fourier

MATLAB proporciona la ifouriercomando para calcular la transformada de Fourier inversa de una función. Por ejemplo,

f = ifourier(-2*exp(-abs(w)))

MATLAB ejecutará la declaración anterior y mostrará el resultado:

f =
   -2/(pi*(x^2 + 1))

GNU Octave es un lenguaje de programación de alto nivel como MATLAB y es principalmente compatible con MATLAB. También se utiliza para cálculos numéricos.

Octave tiene las siguientes características comunes con MATLAB:

• las matrices son tipos de datos fundamentales
• tiene soporte incorporado para números complejos
• tiene funciones matemáticas y bibliotecas integradas
• admite funciones definidas por el usuario

GNU Octave también es un software de libre distribución. Puede redistribuirlo y / o modificarlo según los términos de la Licencia Pública General GNU (GPL) publicada por la Free Software Foundation.

MATLAB vs Octava

La mayoría de los programas de MATLAB se ejecutan en Octave, pero es posible que algunos de los programas de Octave no se ejecuten en MATLAB porque Octave permite cierta sintaxis que MATLAB no permite.

Por ejemplo, MATLAB solo admite comillas simples, pero Octave admite comillas simples y dobles para definir cadenas. Si está buscando un tutorial sobre Octave, lea este tutorial desde el principio, que cubre tanto MATLAB como Octave.

Ejemplos compatibles

Casi todos los ejemplos cubiertos en este tutorial son compatibles con MATLAB y con Octave. Intentemos seguir el ejemplo en MATLAB y Octave que produce el mismo resultado sin ningún cambio de sintaxis:

Este ejemplo crea un mapa de superficie 3D para la función g = xe ^{- (x 2 + y 2 )} . Cree un archivo de secuencia de comandos y escriba el siguiente código:

[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.eps

Cuando ejecuta el archivo, MATLAB muestra el siguiente mapa 3D:

Ejemplos no compatibles

Aunque toda la funcionalidad principal de MATLAB está disponible en Octave, hay algunas funcionalidades, por ejemplo, Cálculo diferencial y de integración, que no coincide exactamente en ambos lenguajes. Este tutorial ha intentado dar ambos tipos de ejemplos en los que diferían en su sintaxis.

Considere el siguiente ejemplo donde MATLAB y Octave hacen uso de diferentes funciones para obtener el área de una curva: f (x) = x ² cos (x) para −4 ≤ x ≤ 9. A continuación se muestra la versión MATLAB del código:

f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));

Cuando ejecuta el archivo, MATLAB traza el gráfico:

Se muestra el siguiente resultado

a =
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
 
Area: 
   0.3326

Pero para dar un área de la misma curva en una octava, tendrá que hacer uso de symbolic paquete de la siguiente manera -

pkg load symbolic
symbols

x = sym("x");
f = inline("x^2*cos(x)");

ezplot(f, [-4,9])
print -deps graph.eps

[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));

Simulink es un entorno de diseño basado en modelos y simulación para sistemas dinámicos e integrados, integrado con MATLAB. Simulink, también desarrollado por MathWorks, es una herramienta de lenguaje de programación gráfica de flujo de datos para modelar, simular y analizar sistemas dinámicos multidominio. Básicamente es una herramienta gráfica de diagrama de bloques con un conjunto personalizable de bibliotecas de bloques.

Le permite incorporar algoritmos de MATLAB en modelos, así como exportar los resultados de la simulación a MATLAB para su posterior análisis.

Soportes de Simulink -

• diseño a nivel de sistema
• simulation
• generación automática de código
• prueba y verificación de sistemas integrados

Hay varios otros productos complementarios proporcionados por MathWorks y productos de hardware y software de terceros que están disponibles para su uso con Simulink.

La siguiente lista ofrece una breve descripción de algunos de ellos:

• Stateflow permite desarrollar máquinas de estados y diagramas de flujo.

• Simulink Coder permite la generación de código fuente C para la implementación de sistemas en tiempo real de forma automática.

• xPC Target Juntos con x86-based real-time systems proporcionar un entorno para simular y probar modelos de Simulink y Stateflow en tiempo real en el sistema físico.

• Embedded Coder admite objetivos integrados específicos.

• HDL Coder permite generar automáticamente VHDL y Verilog sintetizables.

• SimEvents proporciona una biblioteca de bloques de construcción gráficos para modelar sistemas de cola.

Simulink es capaz de realizar una verificación y validación sistemática de modelos mediante la verificación del estilo de modelado, la trazabilidad de requisitos y el análisis de cobertura del modelo.

Simulink Design Verifier le permite identificar errores de diseño y generar escenarios de casos de prueba para la verificación de modelos.

Usando Simulink

Para abrir Simulink, escriba en el espacio de trabajo de MATLAB:

simulink

Simulink abre con el Library Browser. El navegador de biblioteca se utiliza para crear modelos de simulación.

En el panel de la ventana del lado izquierdo, encontrará varias bibliotecas categorizadas según varios sistemas, al hacer clic en cada una se mostrarán los bloques de diseño en el panel de la ventana de la derecha.

La construcción de modelos

Para crear un nuevo modelo, haga clic en el Newen la barra de herramientas del navegador de la biblioteca. Esto abre una nueva ventana de modelo sin título.

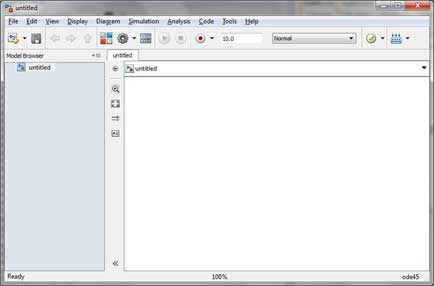
Un modelo de Simulink es un diagrama de bloques.

Los elementos del modelo se agregan seleccionando los elementos apropiados del navegador de la biblioteca y arrastrándolos a la ventana del modelo.

Alternativamente, puede copiar los elementos del modelo y pegarlos en la ventana del modelo.

Ejemplos

Arrastre y suelte elementos de la biblioteca de Simulink para crear su proyecto.

A los efectos de este ejemplo, se utilizarán dos bloques para la simulación: A Source (una señal) y un Sink(un alcance). Un generador de señales (la fuente) genera una señal analógica, que luego será visualizada gráficamente por el osciloscopio (el sumidero).

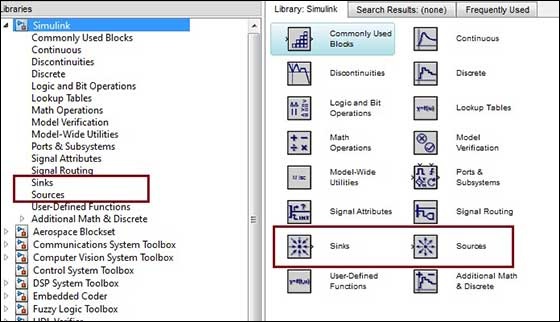
Comience arrastrando los bloques necesarios desde la biblioteca a la ventana del proyecto. Luego, conecte los bloques entre sí, lo que se puede hacer arrastrando los conectores desde los puntos de conexión de un bloque a los de otro.

Arrastremos un bloque 'Sine Wave' en el modelo.

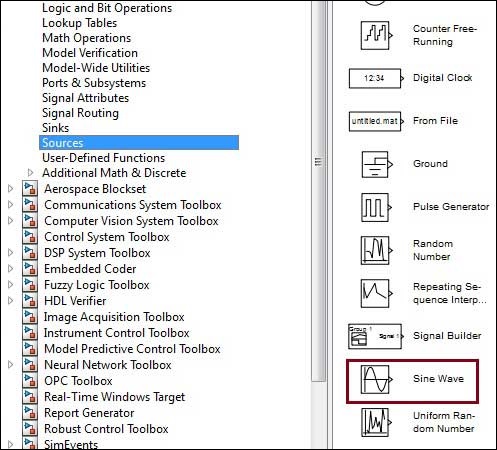
Seleccione 'Fregaderos' de la biblioteca y arrastre un bloque 'Alcance' en el modelo.

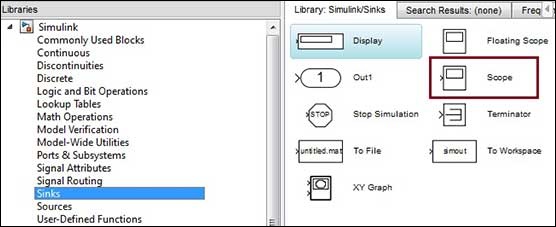
Arrastre una línea de señal desde la salida del bloque Sine Wave hasta la entrada del bloque Scope.

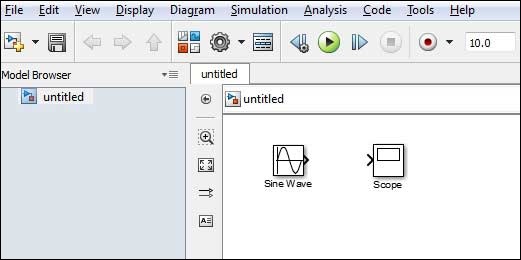
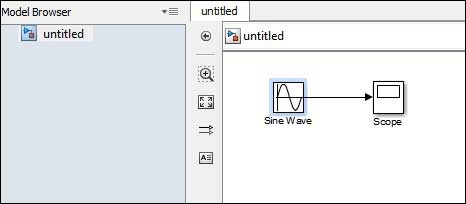
Ejecute la simulación presionando el botón 'Run', manteniendo todos los parámetros predeterminados (puede cambiarlos desde el menú Simulación)

Debería obtener el siguiente gráfico del alcance.