Algoritmo paralelo - Guía rápida

Un algorithmes una secuencia de pasos que toman entradas del usuario y luego de algunos cálculos, producen una salida. UNparallel algorithm es un algoritmo que puede ejecutar varias instrucciones simultáneamente en diferentes dispositivos de procesamiento y luego combinar todas las salidas individuales para producir el resultado final.

Procesamiento concurrente

La fácil disponibilidad de las computadoras junto con el crecimiento de Internet ha cambiado la forma en que almacenamos y procesamos los datos. Vivimos en una época en la que los datos están disponibles en abundancia. Todos los días tratamos con grandes volúmenes de datos que requieren una computación compleja y eso también, en poco tiempo. A veces, necesitamos obtener datos de eventos similares o interrelacionados que ocurren simultáneamente. Aquí es donde requerimosconcurrent processing que puede dividir una tarea compleja y procesarla en varios sistemas para producir la salida en un tiempo rápido.

El procesamiento simultáneo es esencial cuando la tarea implica procesar una gran cantidad de datos complejos. Los ejemplos incluyen: acceso a grandes bases de datos, pruebas de aeronaves, cálculos astronómicos, física atómica y nuclear, análisis biomédico, planificación económica, procesamiento de imágenes, robótica, pronóstico del tiempo, servicios basados ​​en la web, etc.

¿Qué es el paralelismo?

Parallelismes el proceso de procesar varios conjuntos de instrucciones simultáneamente. Reduce el tiempo computacional total. El paralelismo se puede implementar usandoparallel computers,es decir, una computadora con muchos procesadores. Las computadoras paralelas requieren algoritmos paralelos, lenguajes de programación, compiladores y sistemas operativos que admitan la multitarea.

En este tutorial, discutiremos solo sobre parallel algorithms. Antes de seguir adelante, analicemos primero los algoritmos y sus tipos.

¿Qué es un algoritmo?

Un algorithmes una secuencia de instrucciones que se siguen para resolver un problema. Al diseñar un algoritmo, debemos considerar la arquitectura de la computadora en la que se ejecutará el algoritmo. Según la arquitectura, hay dos tipos de computadoras:

• Computadora secuencial
• Computadora paralela

Dependiendo de la arquitectura de las computadoras, tenemos dos tipos de algoritmos:

• Sequential Algorithm - Un algoritmo en el que se ejecutan algunos pasos consecutivos de instrucciones en orden cronológico para resolver un problema.

• Parallel Algorithm- El problema se divide en subproblemas y se ejecutan en paralelo para obtener salidas individuales. Posteriormente, estas salidas individuales se combinan para obtener la salida final deseada.

No es fácil dividir un gran problema en sub-problems. Los subproblemas pueden tener dependencia de datos entre ellos. Por lo tanto, los procesadores deben comunicarse entre sí para resolver el problema.

Se ha descubierto que el tiempo que necesitan los procesadores para comunicarse entre sí es mayor que el tiempo real de procesamiento. Por lo tanto, al diseñar un algoritmo paralelo, se debe considerar la utilización adecuada de la CPU para obtener un algoritmo eficiente.

Para diseñar un algoritmo correctamente, debemos tener una idea clara de los model of computation en una computadora paralela.

Modelo de Computación

Tanto las computadoras secuenciales como las paralelas operan en un conjunto (flujo) de instrucciones llamadas algoritmos. Este conjunto de instrucciones (algoritmo) instruye a la computadora sobre lo que tiene que hacer en cada paso.

Según el flujo de instrucciones y el flujo de datos, las computadoras se pueden clasificar en cuatro categorías:

• Computadoras de flujo de instrucción único, flujo de datos único (SISD)
• Computadoras de flujo de instrucciones único, flujo de datos múltiples (SIMD)
• Computadoras de flujo de instrucciones múltiples, flujo de datos único (MISD)
• Computadoras de flujo de instrucciones múltiples, flujo de datos múltiples (MIMD)

Computadoras SISD

Las computadoras del SISD contienen one control unit, one processing unit, y one memory unit.

En este tipo de computadoras, el procesador recibe un único flujo de instrucciones de la unidad de control y opera con un único flujo de datos de la unidad de memoria. Durante el cálculo, en cada paso, el procesador recibe una instrucción de la unidad de control y opera con un solo dato recibido de la unidad de memoria.

Computadoras SIMD

Las computadoras SIMD contienen one control unit, multiple processing units, y shared memory or interconnection network.

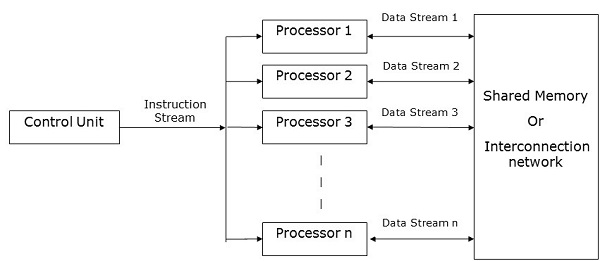
Aquí, una sola unidad de control envía instrucciones a todas las unidades de procesamiento. Durante el cálculo, en cada paso, todos los procesadores reciben un único conjunto de instrucciones de la unidad de control y operan con diferentes conjuntos de datos de la unidad de memoria.

Cada una de las unidades de procesamiento tiene su propia unidad de memoria local para almacenar tanto datos como instrucciones. En las computadoras SIMD, los procesadores necesitan comunicarse entre ellos. Esto es hecho porshared memory o por interconnection network.

Mientras algunos de los procesadores ejecutan un conjunto de instrucciones, los procesadores restantes esperan su siguiente conjunto de instrucciones. Las instrucciones de la unidad de control deciden qué procesador seactive (ejecutar instrucciones) o inactive (espere la siguiente instrucción).

Computadoras de MISD

Como sugiere el nombre, las computadoras de MISD contienen multiple control units, multiple processing units, y one common memory unit.

Aquí, cada procesador tiene su propia unidad de control y comparten una unidad de memoria común. Todos los procesadores reciben instrucciones individualmente de su propia unidad de control y operan en un solo flujo de datos según las instrucciones que han recibido de sus respectivas unidades de control. Este procesador funciona simultáneamente.

Ordenadores MIMD

Las computadoras MIMD tienen multiple control units, multiple processing units, y un shared memory o interconnection network.

Aquí, cada procesador tiene su propia unidad de control, unidad de memoria local y unidad aritmética y lógica. Reciben diferentes conjuntos de instrucciones de sus respectivas unidades de control y operan con diferentes conjuntos de datos.

Nota

• Una computadora MIMD que comparte una memoria común se conoce como multiprocessors, mientras que aquellos que utilizan una red de interconexión se conocen como multicomputers.

• Según la distancia física de los procesadores, los multicomputadoras son de dos tipos:

  • Multicomputer - Cuando todos los procesadores están muy cerca unos de otros (por ejemplo, en la misma habitación).

  • Distributed system - Cuando todos los procesadores están lejos unos de otros (por ejemplo, en las diferentes ciudades)

El análisis de un algoritmo nos ayuda a determinar si el algoritmo es útil o no. Generalmente, un algoritmo se analiza en función de su tiempo de ejecución.(Time Complexity) y la cantidad de espacio (Space Complexity) Requiere.

Dado que tenemos sofisticados dispositivos de memoria disponibles a un costo razonable, el espacio de almacenamiento ya no es un problema. Por tanto, no se le da tanta importancia a la complejidad del espacio.

Los algoritmos paralelos están diseñados para mejorar la velocidad de cálculo de una computadora. Para analizar un algoritmo paralelo, normalmente consideramos los siguientes parámetros:

• Complejidad del tiempo (tiempo de ejecución),
• Número total de procesadores utilizados y
• Coste total.

Complejidad del tiempo

La razón principal detrás del desarrollo de algoritmos paralelos fue reducir el tiempo de cálculo de un algoritmo. Por lo tanto, evaluar el tiempo de ejecución de un algoritmo es extremadamente importante para analizar su eficiencia.

El tiempo de ejecución se mide sobre la base del tiempo que tarda el algoritmo en resolver un problema. El tiempo total de ejecución se calcula desde el momento en que el algoritmo comienza a ejecutarse hasta el momento en que se detiene. Si todos los procesadores no inician o finalizan la ejecución al mismo tiempo, entonces el tiempo total de ejecución del algoritmo es el momento en que el primer procesador inició su ejecución hasta el momento en que el último procesador detiene su ejecución.

La complejidad temporal de un algoritmo se puede clasificar en tres categorías:

• Worst-case complexity - Cuando la cantidad de tiempo requerida por un algoritmo para una entrada dada es maximum.

• Average-case complexity - Cuando la cantidad de tiempo requerida por un algoritmo para una entrada dada es average.

• Best-case complexity - Cuando la cantidad de tiempo requerida por un algoritmo para una entrada dada es minimum.

Análisis asintótico

La complejidad o eficiencia de un algoritmo es el número de pasos ejecutados por el algoritmo para obtener el resultado deseado. El análisis asintótico se realiza para calcular la complejidad de un algoritmo en su análisis teórico. En el análisis asintótico, se utiliza una gran longitud de entrada para calcular la función de complejidad del algoritmo.

Note - Asymptotices una condición en la que una línea tiende a encontrarse con una curva, pero no se cruzan. Aquí la línea y la curva son asintóticas entre sí.

La notación asintótica es la forma más sencilla de describir el tiempo de ejecución más rápido y más lento posible para un algoritmo que utiliza límites altos y límites bajos de velocidad. Para esto, usamos las siguientes notaciones:

• Notación Big O
• Notación omega
• Notación theta

Notación Big O

En matemáticas, la notación Big O se usa para representar las características asintóticas de las funciones. Representa el comportamiento de una función para grandes entradas en un método simple y preciso. Es un método para representar el límite superior del tiempo de ejecución de un algoritmo. Representa la mayor cantidad de tiempo que podría tardar el algoritmo en completar su ejecución. La función -

f (n) = O (g (n))

si existen constantes positivas c y n₀ tal que f(n) ≤ c * g(n) para todos n dónde n ≥ n₀.

Notación omega

La notación Omega es un método para representar el límite inferior del tiempo de ejecución de un algoritmo. La función -

f (n) = Ω (g (n))

si existen constantes positivas c y n₀ tal que f(n) ≥ c * g(n) para todos n dónde n ≥ n₀.

Notación theta

La notación theta es un método para representar tanto el límite inferior como el límite superior del tiempo de ejecución de un algoritmo. La función -

f (n) = θ (g (n))

si existen constantes positivas c₁, c₂, y n₀ tal que c1 * g (n) ≤ f (n) ≤ c2 * g (n) para todos n dónde n ≥ n₀.

Aceleración de un algoritmo

El rendimiento de un algoritmo paralelo se determina calculando su speedup. La aceleración se define como la relación entre el tiempo de ejecución del peor caso del algoritmo secuencial más rápido conocido para un problema particular y el tiempo de ejecución del peor caso del algoritmo paralelo.

Número de procesadores utilizados

El número de procesadores utilizados es un factor importante en el análisis de la eficiencia de un algoritmo paralelo. Se calcula el costo de compra, mantenimiento y funcionamiento de las computadoras. Cuanto mayor sea el número de procesadores que utiliza un algoritmo para resolver un problema, más costoso se vuelve el resultado obtenido.

Coste total

El costo total de un algoritmo paralelo es el producto de la complejidad del tiempo y el número de procesadores usados ​​en ese algoritmo en particular.

Costo total = Complejidad de tiempo × Número de procesadores utilizados

Por lo tanto, los efficiency de un algoritmo paralelo es -

El modelo de un algoritmo paralelo se desarrolla considerando una estrategia para dividir los datos y el método de procesamiento y aplicando una estrategia adecuada para reducir las interacciones. En este capítulo, discutiremos los siguientes modelos de algoritmos paralelos:

• Modelo paralelo de datos
• Modelo de gráfico de tareas
• Modelo de piscina de trabajo
• Modelo maestro esclavo
• Productor consumidor o modelo de canalización
• Modelo híbrido

Paralelo de datos

En el modelo paralelo de datos, las tareas se asignan a los procesos y cada tarea realiza tipos similares de operaciones en diferentes datos. Data parallelism es una consecuencia de operaciones únicas que se aplican a varios elementos de datos.

El modelo paralelo de datos se puede aplicar en espacios de direcciones compartidas y paradigmas de paso de mensajes. En el modelo paralelo de datos, los gastos generales de interacción se pueden reducir seleccionando una localidad que preserve la descomposición, utilizando rutinas de interacción colectiva optimizadas o superponiendo el cálculo y la interacción.

La característica principal de los problemas de modelos paralelos de datos es que la intensidad del paralelismo de datos aumenta con el tamaño del problema, lo que a su vez hace posible utilizar más procesos para resolver problemas más grandes.

Example - Multiplicación de matrices densas.

Modelo de gráfico de tareas

En el modelo de gráfico de tareas, el paralelismo se expresa mediante un task graph. Un gráfico de tareas puede ser trivial o no trivial. En este modelo, la correlación entre las tareas se utiliza para promover la localidad o minimizar los costos de interacción. Este modelo se aplica para resolver problemas en los que la cantidad de datos asociados con las tareas es enorme en comparación con la cantidad de cálculos asociados con ellas. Las tareas se asignan para ayudar a mejorar el costo del movimiento de datos entre las tareas.

Examples - Clasificación rápida en paralelo, factorización de matriz dispersa y algoritmos paralelos derivados mediante el enfoque de dividir y conquistar.

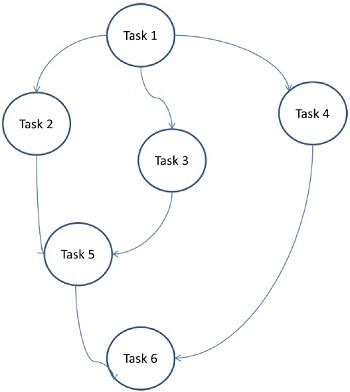
Aquí, los problemas se dividen en tareas atómicas y se implementan como un gráfico. Cada tarea es una unidad de trabajo independiente que tiene dependencias en una o más tareas precedentes. Después de completar una tarea, el resultado de una tarea anterior se pasa a la tarea dependiente. Una tarea con tarea antecedente comienza a ejecutarse solo cuando se completa toda su tarea antecedente. El resultado final del gráfico se recibe cuando se completa la última tarea dependiente (Tarea 6 en la figura anterior).

Modelo de piscina de trabajo

En el modelo de grupo de trabajo, las tareas se asignan dinámicamente a los procesos para equilibrar la carga. Por lo tanto, cualquier proceso puede ejecutar potencialmente cualquier tarea. Este modelo se utiliza cuando la cantidad de datos asociados con las tareas es comparativamente menor que el cálculo asociado con las tareas.

No existe una asignación previa deseada de tareas a los procesos. La asignación de tareas está centralizada o descentralizada. Los punteros a las tareas se guardan en una lista compartida físicamente, en una cola de prioridad o en una tabla o árbol hash, o podrían guardarse en una estructura de datos distribuida físicamente.

La tarea puede estar disponible al principio o puede generarse dinámicamente. Si la tarea se genera dinámicamente y se realiza una asignación descentralizada de la tarea, entonces se requiere un algoritmo de detección de terminación para que todos los procesos puedan detectar la finalización de todo el programa y dejar de buscar más tareas.

Example - Búsqueda de árbol paralelo

Modelo maestro-esclavo

En el modelo maestro-esclavo, uno o más procesos maestros generan tareas y las asignan a procesos esclavos. Las tareas pueden asignarse de antemano si:

• el maestro puede estimar el volumen de las tareas, o
• una asignación aleatoria puede hacer un trabajo satisfactorio de equilibrio de carga, o
• a los esclavos se les asignan tareas más pequeñas en diferentes momentos.

Este modelo es generalmente igualmente adecuado para shared-address-space o message-passing paradigms, ya que la interacción es naturalmente de dos formas.

En algunos casos, es posible que sea necesario completar una tarea en fases, y la tarea de cada fase debe completarse antes de que se pueda generar la tarea de las siguientes fases. El modelo maestro-esclavo se puede generalizar ahierarchical o multi-level master-slave model en el que el maestro de nivel superior alimenta la gran parte de las tareas al maestro de segundo nivel, quien subdivide aún más las tareas entre sus propios esclavos y puede realizar una parte de la tarea en sí.

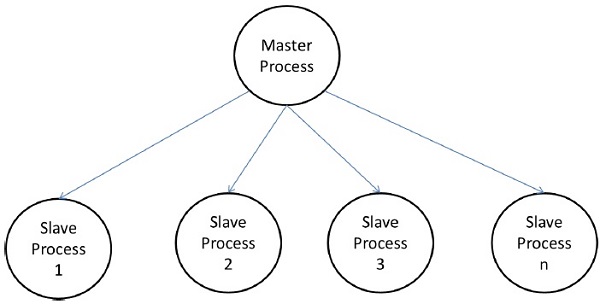
Precauciones al usar el modelo maestro-esclavo

Se debe tener cuidado para asegurar que el maestro no se convierta en un punto de congestión. Puede suceder si las tareas son demasiado pequeñas o los trabajadores son comparativamente rápidos.

Las tareas deben seleccionarse de manera que el costo de realizar una tarea domine el costo de la comunicación y el costo de la sincronización.

La interacción asincrónica puede ayudar a superponer la interacción y el cálculo asociado con la generación de trabajo por parte del maestro.

Modelo de canalización

También se conoce como producer-consumer model. Aquí, un conjunto de datos se transmite a través de una serie de procesos, cada uno de los cuales realiza alguna tarea en él. Aquí, la llegada de nuevos datos genera la ejecución de una nueva tarea por un proceso en la cola. Los procesos podrían formar una cola en forma de matrices lineales o multidimensionales, árboles o gráficos generales con o sin ciclos.

Este modelo es una cadena de productores y consumidores. Cada proceso en la cola puede ser considerado como consumidor de una secuencia de ítems de datos para el proceso que lo precede en la cola y como productor de datos para el proceso que lo sigue en la cola. No es necesario que la cola sea una cadena lineal; puede ser un gráfico dirigido. La técnica de minimización de interacciones más común aplicable a este modelo es la interacción superpuesta con la computación.

Example - Algoritmo de factorización LU en paralelo.

Modelos híbridos

Se requiere un modelo de algoritmo híbrido cuando se puede necesitar más de un modelo para resolver un problema.

Un modelo híbrido puede estar compuesto por múltiples modelos aplicados jerárquicamente o múltiples modelos aplicados secuencialmente a diferentes fases de un algoritmo paralelo.

Example - Clasificación rápida paralela

Parallel Random Access Machines (PRAM)es un modelo, que se considera para la mayoría de los algoritmos paralelos. Aquí, varios procesadores están conectados a un solo bloque de memoria. Un modelo PRAM contiene:

• Un conjunto de procesadores de tipo similar.

• Todos los procesadores comparten una unidad de memoria común. Los procesadores pueden comunicarse entre sí a través de la memoria compartida únicamente.

• Una unidad de acceso a memoria (MAU) conecta los procesadores con la única memoria compartida.

Aquí, n número de procesadores puede realizar operaciones independientes en nnúmero de datos en una unidad de tiempo particular. Esto puede resultar en el acceso simultáneo de diferentes procesadores a la misma ubicación de memoria.

Para resolver este problema, se han aplicado las siguientes restricciones en el modelo PRAM:

• Exclusive Read Exclusive Write (EREW) - Aquí no se permite que dos procesadores lean o escriban en la misma ubicación de memoria al mismo tiempo.

• Exclusive Read Concurrent Write (ERCW) - Aquí no se permite que dos procesadores lean desde la misma ubicación de memoria al mismo tiempo, pero sí pueden escribir en la misma ubicación de memoria al mismo tiempo.

• Concurrent Read Exclusive Write (CREW) - Aquí todos los procesadores pueden leer desde la misma ubicación de memoria al mismo tiempo, pero no pueden escribir en la misma ubicación de memoria al mismo tiempo.

• Concurrent Read Concurrent Write (CRCW) - Todos los procesadores pueden leer o escribir en la misma ubicación de memoria al mismo tiempo.

Hay muchos métodos para implementar el modelo PRAM, pero los más destacados son:

• Modelo de memoria compartida
• Modelo de paso de mensajes
• Modelo paralelo de datos

Modelo de memoria compartida

La memoria compartida enfatiza en control parallelism que en data parallelism. En el modelo de memoria compartida, varios procesos se ejecutan en diferentes procesadores de forma independiente, pero comparten un espacio de memoria común. Debido a cualquier actividad del procesador, si hay algún cambio en cualquier ubicación de la memoria, es visible para el resto de los procesadores.

A medida que varios procesadores acceden a la misma ubicación de memoria, puede suceder que en un momento determinado, más de un procesador acceda a la misma ubicación de memoria. Suponga que uno está leyendo esa ubicación y el otro está escribiendo en esa ubicación. Puede crear confusión. Para evitar esto, algún mecanismo de control, comolock / semaphore, se implementa para garantizar la exclusión mutua.

La programación de memoria compartida se ha implementado en lo siguiente:

• Thread libraries- La biblioteca de subprocesos permite múltiples subprocesos de control que se ejecutan simultáneamente en la misma ubicación de memoria. La biblioteca de subprocesos proporciona una interfaz que admite subprocesos múltiples a través de una biblioteca de subrutinas. Contiene subrutinas para

  • Creando y destruyendo hilos
  • Programación de la ejecución del hilo
  • pasar datos y mensajes entre hilos
  • guardar y restaurar contextos de hilo

Entre los ejemplos de bibliotecas de subprocesos se incluyen: subprocesos de SolarisTM para Solaris, subprocesos POSIX implementados en Linux, subprocesos Win32 disponibles en Windows NT y Windows 2000 y subprocesos de JavaTM como parte del JavaTM Development Kit (JDK) estándar.

• Distributed Shared Memory (DSM) Systems- Los sistemas DSM crean una abstracción de la memoria compartida en una arquitectura débilmente acoplada para implementar la programación de la memoria compartida sin soporte de hardware. Implementan bibliotecas estándar y utilizan las funciones avanzadas de administración de memoria a nivel de usuario presentes en los sistemas operativos modernos. Los ejemplos incluyen Tread Marks System, Munin, IVY, Shasta, Brazos y Cashmere.

• Program Annotation Packages- Esto se implementa en las arquitecturas que tienen características uniformes de acceso a memoria. El ejemplo más notable de paquetes de anotaciones de programas es OpenMP. OpenMP implementa el paralelismo funcional. Se centra principalmente en la paralelización de bucles.

El concepto de memoria compartida proporciona un control de bajo nivel del sistema de memoria compartida, pero tiende a ser tedioso y erróneo. Es más aplicable a la programación de sistemas que a la programación de aplicaciones.

Méritos de la programación de memoria compartida

• El espacio de direcciones global brinda un enfoque de programación fácil de usar para la memoria.

• Debido a la cercanía de la memoria a la CPU, el intercambio de datos entre procesos es rápido y uniforme.

• No es necesario especificar claramente la comunicación de datos entre procesos.

• La sobrecarga de comunicación del proceso es insignificante.

• Es muy fácil de aprender.

Deméritos de la programación de memoria compartida

• No es portátil.
• La gestión de la localidad de datos es muy difícil.

Modelo de paso de mensajes

El paso de mensajes es el enfoque de programación paralela más utilizado en los sistemas de memoria distribuida. Aquí, el programador tiene que determinar el paralelismo. En este modelo, todos los procesadores tienen su propia unidad de memoria local e intercambian datos a través de una red de comunicación.

Los procesadores utilizan bibliotecas de paso de mensajes para comunicarse entre ellos. Junto con los datos que se envían, el mensaje contiene los siguientes componentes:

• La dirección del procesador desde el que se envía el mensaje;

• Dirección de inicio de la ubicación de la memoria de los datos en el procesador de envío;

• Tipo de datos de los datos de envío;

• Tamaño de los datos de envío;

• La dirección del procesador al que se envía el mensaje;

• Dirección de inicio de la ubicación de la memoria para los datos en el procesador receptor.

Los procesadores pueden comunicarse entre sí mediante cualquiera de los siguientes métodos:

• Comunicación punto a punto
• Comunicación colectiva
• Interfaz de paso de mensajes

Comunicación punto a punto

La comunicación punto a punto es la forma más sencilla de transmitir mensajes. Aquí, se puede enviar un mensaje desde el procesador de envío a un procesador de recepción mediante cualquiera de los siguientes modos de transferencia:

• Synchronous mode - El siguiente mensaje se envía solo después de recibir una confirmación de que su mensaje anterior ha sido entregado, para mantener la secuencia del mensaje.

• Asynchronous mode - Para enviar el siguiente mensaje, no se requiere el recibo de la confirmación de la entrega del mensaje anterior.

Comunicación colectiva

La comunicación colectiva involucra más de dos procesadores para el paso de mensajes. Los siguientes modos permiten comunicaciones colectivas:

• Barrier - El modo barrera es posible si todos los procesadores incluidos en las comunicaciones ejecutan un bloque en particular (conocido como barrier block) para el paso de mensajes.

• Broadcast - La radiodifusión es de dos tipos -

  • One-to-all - Aquí, un procesador con una sola operación envía el mismo mensaje a todos los demás procesadores.

  • All-to-all - Aquí, todos los procesadores envían mensajes a todos los demás procesadores.

Los mensajes transmitidos pueden ser de tres tipos:

• Personalized - Los mensajes únicos se envían a todos los demás procesadores de destino.

• Non-personalized - Todos los procesadores de destino reciben el mismo mensaje.

• Reduction - En la transmisión de reducción, un procesador del grupo recopila todos los mensajes de todos los demás procesadores del grupo y los combina en un solo mensaje al que pueden acceder todos los demás procesadores del grupo.

Méritos de la transmisión de mensajes

• Proporciona un control de paralelismo de bajo nivel;
• Es portátil;
• Menos propenso a errores;
• Menos gastos generales en sincronización paralela y distribución de datos.

Deméritos de la transmisión de mensajes

• En comparación con el código de memoria compartida en paralelo, el código de paso de mensajes generalmente necesita más software.

Bibliotecas de paso de mensajes

Hay muchas bibliotecas de paso de mensajes. Aquí, discutiremos dos de las bibliotecas de paso de mensajes más utilizadas:

• Interfaz de paso de mensajes (MPI)
• Máquina virtual paralela (PVM)

Interfaz de paso de mensajes (MPI)

Es un estándar universal para proporcionar comunicación entre todos los procesos concurrentes en un sistema de memoria distribuida. La mayoría de las plataformas de computación paralela comúnmente utilizadas proporcionan al menos una implementación de interfaz de paso de mensajes. Se ha implementado como la colección de funciones predefinidas llamadaslibrary y se puede llamar desde lenguajes como C, C ++, Fortran, etc. Los MPI son rápidos y portátiles en comparación con otras bibliotecas de paso de mensajes.

Merits of Message Passing Interface

• Se ejecuta solo en arquitecturas de memoria compartida o arquitecturas de memoria distribuida;

• Cada procesador tiene sus propias variables locales;

• En comparación con las computadoras grandes con memoria compartida, las computadoras con memoria distribuida son menos costosas.

Demerits of Message Passing Interface

• Se requieren más cambios de programación para el algoritmo paralelo;
• A veces es difícil de depurar; y
• No funciona bien en la red de comunicación entre los nodos.

Máquina virtual paralela (PVM)

PVM es un sistema de paso de mensajes portátil, diseñado para conectar máquinas host heterogéneas separadas para formar una sola máquina virtual. Es un único recurso informático paralelo manejable. Los grandes problemas computacionales como los estudios de superconductividad, las simulaciones de dinámica molecular y los algoritmos matriciales pueden resolverse de manera más rentable utilizando la memoria y la potencia agregada de muchas computadoras. Gestiona todo el enrutamiento de mensajes, conversión de datos, programación de tareas en la red de arquitecturas informáticas incompatibles.

Features of PVM

• Muy fácil de instalar y configurar;
• Varios usuarios pueden utilizar PVM al mismo tiempo;
• Un usuario puede ejecutar varias aplicaciones;
• Es un paquete pequeño;
• Soporta C, C ++, Fortran;
• Para una ejecución determinada de un programa PVM, los usuarios pueden seleccionar el grupo de máquinas;
• Es un modelo de transmisión de mensajes,
• Computación basada en procesos;
• Soporta arquitectura heterogénea.

Programación en paralelo de datos

El enfoque principal del modelo de programación en paralelo de datos es realizar operaciones en un conjunto de datos simultáneamente. El conjunto de datos está organizado en una estructura como una matriz, hipercubo, etc. Los procesadores realizan operaciones colectivamente en la misma estructura de datos. Cada tarea se realiza en una partición diferente de la misma estructura de datos.

Es restrictivo, ya que no todos los algoritmos se pueden especificar en términos de paralelismo de datos. Ésta es la razón por la que el paralelismo de datos no es universal.

Los lenguajes paralelos de datos ayudan a especificar la descomposición de datos y la asignación a los procesadores. También incluye declaraciones de distribución de datos que permiten al programador tener control sobre los datos, por ejemplo, qué datos irán a qué procesador, para reducir la cantidad de comunicación dentro de los procesadores.

Para aplicar cualquier algoritmo correctamente, es muy importante que seleccione una estructura de datos adecuada. Esto se debe a que una operación particular realizada en una estructura de datos puede llevar más tiempo en comparación con la misma operación realizada en otra estructura de datos.

Example- Para acceder al i- ^ésimo elemento de un conjunto usando una matriz, puede tomar un tiempo constante, pero al usar una lista vinculada, el tiempo requerido para realizar la misma operación puede convertirse en un polinomio.

Por tanto, la selección de una estructura de datos debe hacerse considerando la arquitectura y el tipo de operaciones a realizar.

Las siguientes estructuras de datos se utilizan comúnmente en la programación paralela:

• Lista enlazada
• Arrays
• Red de hipercubo

Lista enlazada

Una lista enlazada es una estructura de datos que tiene cero o más nodos conectados por punteros. Los nodos pueden ocupar o no ubicaciones de memoria consecutivas. Cada nodo tiene dos o tres partes: unadata part que almacena los datos y los otros dos son link fieldsque almacenan la dirección del nodo anterior o siguiente. La dirección del primer nodo se almacena en un puntero externo llamadohead. El último nodo, conocido comotail, generalmente no contiene ninguna dirección.

Hay tres tipos de listas vinculadas:

• Lista individualmente vinculada
• Lista doblemente vinculada
• Lista enlazada circular

Lista individualmente vinculada

Un nodo de una lista enlazada individualmente contiene datos y la dirección del siguiente nodo. Un puntero externo llamadohead almacena la dirección del primer nodo.

Lista doblemente vinculada

Un nodo de una lista doblemente enlazada contiene datos y la dirección tanto del nodo anterior como del siguiente. Un puntero externo llamadohead almacena la dirección del primer nodo y el puntero externo llamado tail almacena la dirección del último nodo.

Lista enlazada circular

Una lista enlazada circular es muy similar a la lista enlazada individual, excepto por el hecho de que el último nodo guardó la dirección del primer nodo.

Matrices

Una matriz es una estructura de datos donde podemos almacenar tipos de datos similares. Puede ser unidimensional o multidimensional. Las matrices se pueden crear de forma estática o dinámica.

• En statically declared arrays, la dimensión y el tamaño de las matrices se conocen en el momento de la compilación.

• En dynamically declared arrays, la dimensión y el tamaño de la matriz se conocen en tiempo de ejecución.

Para la programación de memoria compartida, las matrices se pueden usar como una memoria común y para la programación paralela de datos, se pueden usar particionando en submatrices.

Red de hipercubo

La arquitectura de hipercubo es útil para aquellos algoritmos paralelos donde cada tarea tiene que comunicarse con otras tareas. La topología de hipercubo puede incrustar fácilmente otras topologías como anillo y malla. También se conoce como n-cubos, dondenes el número de dimensiones. Un hipercubo se puede construir de forma recursiva.

Seleccionar una técnica de diseño adecuada para un algoritmo paralelo es la tarea más difícil e importante. La mayoría de los problemas de programación paralela pueden tener más de una solución. En este capítulo, discutiremos las siguientes técnicas de diseño para algoritmos paralelos:

• Divide y conquistaras
• Método codicioso
• Programación dinámica
• Backtracking
• Rama y atado
• Programación lineal

Método de dividir y conquistar

En el enfoque de divide y vencerás, el problema se divide en varios subproblemas pequeños. Luego, los subproblemas se resuelven de forma recursiva y se combinan para obtener la solución del problema original.

El enfoque de divide y vencerás implica los siguientes pasos en cada nivel:

• Divide - El problema original se divide en subproblemas.

• Conquer - Los subproblemas se resuelven de forma recursiva.

• Combine - Las soluciones de los subproblemas se combinan para obtener la solución del problema original.

El enfoque de divide y vencerás se aplica en los siguientes algoritmos:

• Búsqueda binaria
• Ordenación rápida
• Combinar ordenación
• Multiplicación de enteros
• Inversión de matriz
• Multiplicación de matrices

Método codicioso

En el codicioso algoritmo de optimización de la solución, se elige la mejor solución en cualquier momento. Un algoritmo codicioso es muy fácil de aplicar a problemas complejos. Decide qué paso proporcionará la solución más precisa en el siguiente paso.

Este algoritmo se llama greedyporque cuando se proporciona la solución óptima para la instancia más pequeña, el algoritmo no considera el programa total como un todo. Una vez que se considera una solución, el algoritmo codicioso nunca vuelve a considerar la misma solución.

Un algoritmo codicioso funciona de forma recursiva creando un grupo de objetos a partir de las partes componentes más pequeñas posibles. La recursividad es un procedimiento para resolver un problema en el que la solución a un problema específico depende de la solución de la instancia más pequeña de ese problema.

Programación dinámica

La programación dinámica es una técnica de optimización, que divide el problema en subproblemas más pequeños y después de resolver cada subproblema, la programación dinámica combina todas las soluciones para obtener la solución definitiva. A diferencia del método de divide y vencerás, la programación dinámica reutiliza la solución a los subproblemas muchas veces.

El algoritmo recursivo para la serie Fibonacci es un ejemplo de programación dinámica.

Algoritmo de retroceso

El retroceso es una técnica de optimización para resolver problemas de combinación. Se aplica a problemas tanto programáticos como de la vida real. El problema de las ocho reinas, el Sudoku y atravesar un laberinto son ejemplos populares en los que se utiliza un algoritmo de retroceso.

En retroceso, comenzamos con una posible solución, que satisface todas las condiciones requeridas. Luego pasamos al siguiente nivel y si ese nivel no produce una solución satisfactoria, regresamos un nivel hacia atrás y comenzamos con una nueva opción.

Rama y atado

Un algoritmo de ramificación y enlace es una técnica de optimización para obtener una solución óptima al problema. Busca la mejor solución para un problema dado en todo el espacio de la solución. Los límites de la función a optimizar se fusionan con el valor de la mejor solución más reciente. Permite que el algoritmo encuentre partes del espacio de la solución por completo.

El propósito de una búsqueda de bifurcaciones y límites es mantener la ruta de menor costo hacia un objetivo. Una vez que se encuentra una solución, puede seguir mejorando la solución. La búsqueda de bifurcaciones y límites se implementa en la búsqueda limitada en profundidad y la búsqueda en profundidad primero.

Programación lineal

La programación lineal describe una amplia clase de trabajo de optimización donde tanto el criterio de optimización como las restricciones son funciones lineales. Es una técnica para obtener el mejor resultado, como la máxima ganancia, el camino más corto o el costo más bajo.

En esta programación, tenemos un conjunto de variables y tenemos que asignarles valores absolutos para satisfacer un conjunto de ecuaciones lineales y maximizar o minimizar una función objetivo lineal dada.

Una matriz es un conjunto de datos numéricos y no numéricos dispuestos en un número fijo de filas y columnas. La multiplicación de matrices es un diseño de multiplicación importante en el cálculo paralelo. Aquí, discutiremos la implementación de la multiplicación de matrices en varias redes de comunicación como malla e hipercubo. La malla y el hipercubo tienen una mayor conectividad de red, por lo que permiten un algoritmo más rápido que otras redes como la red en anillo.

Red de malla

Una topología en la que un conjunto de nodos forma una cuadrícula p-dimensional se denomina topología de malla. Aquí, todos los bordes son paralelos al eje de la cuadrícula y todos los nodos adyacentes pueden comunicarse entre sí.

Número total de nodos = (número de nodos en fila) × (número de nodos en columna)

Una red de malla se puede evaluar utilizando los siguientes factores:

• Diameter
• Ancho de bisección

Diameter - En una red de malla, la más larga distanceentre dos nodos es su diámetro. Una red de malla p-dimensional que tienekP nodos tiene un diámetro de p(k–1).

Bisection width - El ancho de bisección es el número mínimo de bordes necesarios que se deben eliminar de una red para dividir la red de malla en dos mitades.

Multiplicación de matrices utilizando una red de malla

Hemos considerado un modelo SIMD de red de malla 2D que tiene conexiones envolventes. Diseñaremos un algoritmo para multiplicar dos matrices n × n usando n ² procesadores en una cantidad de tiempo particular.

Las matrices A y B tienen elementos a _ij y b _ij respectivamente. El elemento de procesamiento PE _ij representa a _ij y b _ij . Disponga las matrices A y B de tal forma que cada procesador tenga un par de elementos para multiplicar. Los elementos de la matriz A se moverán hacia la izquierda y los elementos de la matriz B se moverán hacia arriba. Estos cambios en la posición de los elementos en la matriz A y B presentan a cada elemento de procesamiento, PE, un nuevo par de valores a multiplicar.

Pasos en el algoritmo

• Alterne dos matrices.
• Calcule todos los productos, a _ik × b _kj
• Calcule las sumas cuando termine el paso 2.

Algoritmo

Procedure MatrixMulti

Begin
   for k = 1 to n-1
	
   for all Pij; where i and j ranges from 1 to n
      ifi is greater than k then
         rotate a in left direction
      end if
		
   if j is greater than k then
      rotate b in the upward direction
   end if
	
   for all Pij ; where i and j lies between 1 and n
      compute the product of a and b and store it in c
   for k= 1 to n-1 step 1
   for all Pi;j where i and j ranges from 1 to n
      rotate a in left direction
      rotate b in the upward direction
      c=c+aXb
End

Red de hipercubo

Un hipercubo es una construcción n-dimensional donde los bordes son perpendiculares entre sí y tienen la misma longitud. Un hipercubo de n dimensiones también se conoce como un cubo de n o un cubo de n dimensiones.

Características de Hypercube con nodo 2 ^k

• Diámetro = k
• Ancho de bisección = 2 ^{k – 1}
• Número de aristas = k

Multiplicación de matrices mediante Hypercube Network

Especificación general de las redes Hypercube -

• Dejar N = 2^msea ​​el número total de procesadores. Sean los procesadores P _0, P ₁ … ..P _N-1 .

• Sean i y i ^b dos números enteros, 0 <i, i ^b <N-1 y su representación binaria difiera sólo en la posición b, 0 <b <k – 1.

• Consideremos dos matrices n × n, la matriz A y la matriz B.

• Step 1- Los elementos de la matriz A y la matriz B se asignan a los n ³ procesadores de manera que el procesador en la posición i, j, k tendrá a _ji y b _ik .

• Step 2 - Todo el procesador en posición (i, j, k) calcula el producto

  C (yo, j, k) = A (yo, j, k) × B (yo, j, k)

• Step 3 - La suma C (0, j, k) = ΣC (i, j, k) para 0 ≤ i ≤ n-1, donde 0 ≤ j, k <n – 1.

Matriz de bloques

Block Matrix o matriz particionada es una matriz donde cada elemento en sí mismo representa una matriz individual. Estas secciones individuales se conocen comoblock o sub-matrix.

Ejemplo

En la Figura (a), X es una matriz de bloques donde A, B, C, D son matrices ellos mismos. La figura (f) muestra la matriz total.

Multiplicación de matriz de bloques

Cuando dos matrices de bloque son matrices cuadradas, entonces se multiplican de la misma manera que realizamos la multiplicación de matrices simple. Por ejemplo,

La clasificación es un proceso de organizar elementos en un grupo en un orden particular, es decir, orden ascendente, orden descendente, orden alfabético, etc. Aquí discutiremos lo siguiente:

• Orden de enumeración
• Orden de transposición pares-impares
• Orden de fusión en paralelo
• Clasificación hiperrápida

Ordenar una lista de elementos es una operación muy común. Un algoritmo de clasificación secuencial puede no ser lo suficientemente eficiente cuando tenemos que clasificar un gran volumen de datos. Por lo tanto, se utilizan algoritmos paralelos en la clasificación.

Orden de enumeración

El ordenamiento por enumeración es un método para organizar todos los elementos en una lista al encontrar la posición final de cada elemento en una lista ordenada. Se hace comparando cada elemento con todos los demás elementos y encontrando el número de elementos que tienen un valor menor.

Por lo tanto, para dos elementos cualesquiera, a _i y a _j cualquiera de los siguientes casos debe ser verdadero:

• a _i <a _j
• a _i > a _j
• a _yo = a _j

Algoritmo

procedure ENUM_SORTING (n)

begin
   for each process P1,j do
      C[j] := 0;
		
   for each process Pi, j do
	
      if (A[i] < A[j]) or A[i] = A[j] and i < j) then
         C[j] := 1;
      else
         C[j] := 0;
			
   for each process P1, j do
      A[C[j]] := A[j];
		
end ENUM_SORTING

Orden de transposición pares-impares

La clasificación por transposición de pares pares e impares se basa en la técnica de clasificación de burbujas. Compara dos números adyacentes y los cambia, si el primer número es mayor que el segundo número para obtener una lista en orden ascendente. El caso contrario se aplica a una serie de orden descendente. La ordenación por transposición pares-impares opera en dos fases:odd phase y even phase. En ambas fases, los procesos intercambian números con su número adyacente a la derecha.

Algoritmo

procedure ODD-EVEN_PAR (n) 

begin 
   id := process's label 
	
   for i := 1 to n do 
   begin 
	
      if i is odd and id is odd then 
         compare-exchange_min(id + 1); 
      else 
         compare-exchange_max(id - 1);
			
      if i is even and id is even then 
         compare-exchange_min(id + 1); 
      else 
         compare-exchange_max(id - 1);
			
   end for
	
end ODD-EVEN_PAR

Orden de fusión en paralelo

Merge sort primero divide la lista sin clasificar en sublistas más pequeñas posibles, la compara con la lista adyacente y la fusiona en un orden ordenado. Implementa el paralelismo muy bien siguiendo el algoritmo divide y vencerás.

Algoritmo

procedureparallelmergesort(id, n, data, newdata)

begin
   data = sequentialmergesort(data)
	
      for dim = 1 to n
         data = parallelmerge(id, dim, data)
      endfor
		
   newdata = data
end

Clasificación hiperrápida

La ordenación hiperrápida es una implementación de la ordenación rápida en hipercubo. Sus pasos son los siguientes:

• Divida la lista sin clasificar entre cada nodo.
• Ordene cada nodo localmente.
• Desde el nodo 0, difunda el valor mediano.
• Divida cada lista localmente, luego intercambie las mitades en la dimensión más alta.
• Repita los pasos 3 y 4 en paralelo hasta que la dimensión llegue a 0.

Algoritmo

procedure HYPERQUICKSORT (B, n)
begin

   id := process’s label;
	
   for i := 1 to d do
      begin
      x := pivot;
      partition B into B1 and B2 such that B1 ≤ x < B2;
      if ith bit is 0 then
		
      begin
         send B2 to the process along the ith communication link;
         C := subsequence received along the ith communication link;
         B := B1 U C;
      endif
      
      else
         send B1 to the process along the ith communication link;
         C := subsequence received along the ith communication link;
         B := B2 U C;
         end else
      end for
		
   sort B using sequential quicksort;
	
end HYPERQUICKSORT

La búsqueda es una de las operaciones fundamentales en informática. Se usa en todas las aplicaciones donde necesitamos encontrar si un elemento está en la lista dada o no. En este capítulo, discutiremos los siguientes algoritmos de búsqueda:

• Divide y conquistaras
• Búsqueda en profundidad
• Búsqueda primero en amplitud
• Mejor búsqueda primero

Divide y conquistaras

En el enfoque de divide y vencerás, el problema se divide en varios subproblemas pequeños. Luego, los subproblemas se resuelven de forma recursiva y se combinan para obtener la solución del problema original.

El enfoque de divide y vencerás implica los siguientes pasos en cada nivel:

• Divide - El problema original se divide en subproblemas.

• Conquer - Los subproblemas se resuelven de forma recursiva.

• Combine - Las soluciones de los subproblemas se combinan para obtener la solución del problema original.

La búsqueda binaria es un ejemplo de algoritmo de divide y vencerás.

Pseudocódigo

Binarysearch(a, b, low, high)

if low < high then
   return NOT FOUND
else
   mid ← (low+high) / 2
   if b = key(mid) then
      return key(mid)
   else if b < key(mid) then
      return BinarySearch(a, b, low, mid−1)
   else
   
      return BinarySearch(a, b, mid+1, high)

Búsqueda en profundidad

La búsqueda en profundidad primero (o DFS) es un algoritmo para buscar un árbol o una estructura de datos de gráfico no dirigida. Aquí, el concepto es comenzar desde el nodo inicial conocido como elrooty atravesar lo más lejos posible en el mismo ramal. Si obtenemos un nodo sin nodo sucesor, regresamos y continuamos con el vértice, que aún no se ha visitado.

Pasos de la búsqueda en profundidad

• Considere un nodo (raíz) que no se visitó anteriormente y márquelo como visitado.

• Visite el primer nodo sucesor adyacente y márquelo como visitado.

• Si todos los nodos sucesores del nodo considerado ya están visitados o no tiene más nodos sucesores, regrese a su nodo padre.

Pseudocódigo

Dejar v ser el vértice donde comienza la búsqueda en Graph G.

DFS(G,v)

   Stack S := {};
	
   for each vertex u, set visited[u] := false;
   push S, v;
   while (S is not empty) do
     u := pop S;
	  
      if (not visited[u]) then
         visited[u] := true;
         for each unvisited neighbour w of u
            push S, w;
      end if
		
   end while
   
END DFS()

Búsqueda primero en amplitud

Breadth-First Search (o BFS) es un algoritmo para buscar un árbol o una estructura de datos de gráficos no dirigida. Aquí, comenzamos con un nodo y luego visitamos todos los nodos adyacentes en el mismo nivel y luego pasamos al nodo sucesor adyacente en el siguiente nivel. Esto también se conoce comolevel-by-level search.

Pasos de la búsqueda primero en amplitud

• Comience con el nodo raíz, márquelo como visitado.
• Como el nodo raíz no tiene ningún nodo en el mismo nivel, pase al siguiente nivel.
• Visite todos los nodos adyacentes y márquelos como visitados.
• Vaya al siguiente nivel y visite todos los nodos adyacentes no visitados.
• Continúe este proceso hasta que se visiten todos los nodos.

Pseudocódigo

Dejar v ser el vértice donde comienza la búsqueda en Graph G.

BFS(G,v)

   Queue Q := {};
	
   for each vertex u, set visited[u] := false;
   insert Q, v;
   while (Q is not empty) do
      u := delete Q;
		
      if (not visited[u]) then
         visited[u] := true;
         for each unvisited neighbor w of u
            insert Q, w;
      end if
		
   end while
   
END BFS()

Mejor búsqueda primero

Best-First Search es un algoritmo que atraviesa un gráfico para alcanzar un objetivo en la ruta más corta posible. A diferencia de BFS y DFS, Best-First Search sigue una función de evaluación para determinar qué nodo es el más apropiado para atravesar a continuación.

Pasos de la búsqueda "Mejor primero"

• Comience con el nodo raíz, márquelo como visitado.
• Busque el siguiente nodo apropiado y márquelo como visitado.
• Vaya al siguiente nivel y busque el nodo apropiado y márquelo como visitado.
• Continúe este proceso hasta alcanzar el objetivo.

Pseudocódigo

BFS( m )

   Insert( m.StartNode )
   Until PriorityQueue is empty
      c ← PriorityQueue.DeleteMin
      If c is the goal
      Exit
   Else
   
      Foreach neighbor n of c
         If n "Unvisited"
            Mark n "Visited"
            Insert( n )
      Mark c "Examined"
      
End procedure

Un gráfico es una notación abstracta que se utiliza para representar la conexión entre pares de objetos. Un gráfico consta de:

• Vertices- Los objetos interconectados en un gráfico se denominan vértices. Los vértices también se conocen comonodes.

• Edges - Los bordes son los enlaces que conectan los vértices.

Hay dos tipos de gráficos:

• Directed graph - En un gráfico dirigido, las aristas tienen dirección, es decir, las aristas van de un vértice a otro.

• Undirected graph - En un gráfico no dirigido, los bordes no tienen dirección.

Gráfico para colorear

La coloración de gráficos es un método para asignar colores a los vértices de un gráfico de modo que no haya dos vértices adyacentes del mismo color. Algunos problemas de coloración de gráficos son:

• Vertex coloring - Una forma de colorear los vértices de un gráfico para que no haya dos vértices adyacentes que compartan el mismo color.

• Edge Coloring - Es el método de asignar un color a cada borde para que no haya dos bordes adyacentes del mismo color.

• Face coloring - Asigna un color a cada cara o región de un gráfico plano para que dos caras que comparten un límite común no tengan el mismo color.

Número cromático

El número cromático es el número mínimo de colores necesarios para colorear un gráfico. Por ejemplo, el número cromático del siguiente gráfico es 3.

El concepto de coloración gráfica se aplica en la preparación de horarios, asignación de radiofrecuencia móvil, Suduku, asignación de registros y coloración de mapas.

Pasos para colorear gráficos

• Establezca el valor inicial de cada procesador en la matriz n-dimensional en 1.

• Ahora, para asignar un color particular a un vértice, determine si ese color ya está asignado a los vértices adyacentes o no.

• Si un procesador detecta el mismo color en los vértices adyacentes, establece su valor en la matriz en 0.

• Después de hacer n ² comparaciones, si cualquier elemento de la matriz es 1, entonces es un color válido.

Pseudocódigo para colorear gráficos

begin

   create the processors P(i0,i1,...in-1) where 0_iv < m, 0 _ v < n
   status[i0,..in-1] = 1
	
   for j varies from 0 to n-1 do
      begin
		
         for k varies from 0 to n-1 do
         begin
            if aj,k=1 and ij=ikthen
            status[i0,..in-1] =0
         end
			
      end
      ok = ΣStatus
		
   if ok > 0, then display valid coloring exists
   else
      display invalid coloring
      
end

Árbol de expansión mínimo

Un árbol de expansión cuya suma de peso (o longitud) de todos sus bordes es menor que todos los demás árboles de expansión posibles del gráfico G se conoce como minimal spanning tree o minimum cost spanningárbol. La siguiente figura muestra un gráfico conectado ponderado.

Algunos árboles de expansión posibles del gráfico anterior se muestran a continuación:

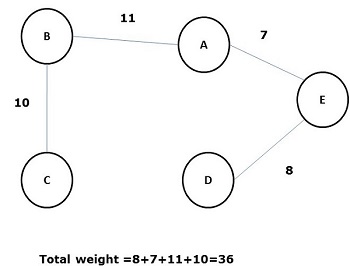
Entre todos los árboles de expansión anteriores, la figura (d) es el árbol de expansión mínimo. El concepto de árbol de expansión de costo mínimo se aplica en el problema del viajante de comercio, el diseño de circuitos electrónicos, el diseño de redes eficientes y el diseño de algoritmos de enrutamiento eficientes.

Para implementar el árbol de costo mínimo, se utilizan los siguientes dos métodos:

• Algoritmo de Prim
• Algoritmo de Kruskal

Algoritmo de Prim

El algoritmo de Prim es un algoritmo codicioso, que nos ayuda a encontrar el árbol de expansión mínimo para un gráfico no dirigido ponderado. Primero selecciona un vértice y encuentra una arista con el peso más bajo que incide en ese vértice.

Pasos del algoritmo de Prim

• Seleccione cualquier vértice, digamos v ₁ del Gráfico G.

• Seleccione una arista, digamos e ₁ de G tal que e ₁ = v ₁ v ₂ y v ₁ ≠ v ₂ ye ₁ tenga un peso mínimo entre las aristas que inciden en v ₁ en el gráfico G.

• Ahora, siguiendo el paso 2, seleccione el incidente de borde ponderado mínimo en v ₂ .

• Continúe esto hasta que se hayan elegido n – 1 aristas. aquín es el número de vértices.

El árbol de expansión mínimo es:

Algoritmo de Kruskal

El algoritmo de Kruskal es un algoritmo codicioso, que nos ayuda a encontrar el árbol de expansión mínimo para un gráfico ponderado conectado, agregando arcos de costos crecientes en cada paso. Es un algoritmo de árbol de expansión mínimo que encuentra un borde del menor peso posible que conecta dos árboles cualesquiera en el bosque.

Pasos del algoritmo de Kruskal

• Seleccione un borde de peso mínimo; digamos que e ₁ del Gráfico G ye ₁ no es un bucle.

• Seleccione el siguiente borde ponderado mínimo conectado a e ₁ .

• Continúe esto hasta que se hayan elegido n – 1 aristas. aquín es el número de vértices.

El árbol de expansión mínimo del gráfico anterior es:

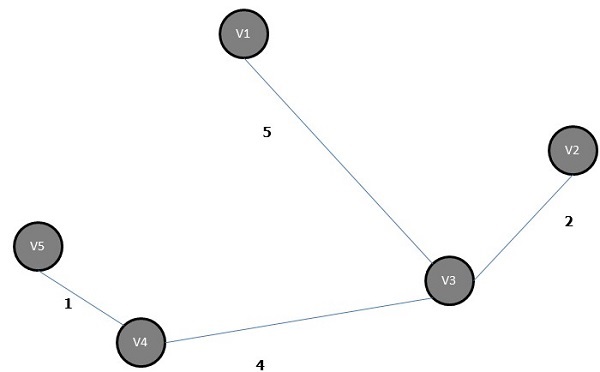
Algoritmo de ruta más corta

El algoritmo de ruta más corta es un método para encontrar la ruta de menor costo desde el nodo de origen (S) hasta el nodo de destino (D). Aquí, discutiremos el algoritmo de Moore, también conocido como algoritmo de búsqueda primero de amplitud.

Algoritmo de Moore

• Etiquetar el vértice de origen, S y etiquetarlo i y establecer i=0.

• Encuentra todos los vértices sin etiquetar adyacentes al vértice etiquetado i. Si no hay vértices conectados al vértice, S, entonces el vértice, D, no está conectado a S. Si hay vértices conectados a S, etiquételosi+1.

• Si D está etiquetado, vaya al paso 4; de lo contrario, vaya al paso 2 para aumentar i = i + 1.

• Deténgase después de encontrar la longitud del camino más corto.