Física - Lentes esféricas
Introducción
Un material transparente (normalmente vidrio) unido por dos superficies, de las cuales una o ambas superficies son esféricas, se conoce como "lente esférica".

Lentes convexas
Una lente puede tener dos superficies esféricas, abultadas hacia afuera (como se muestra en la imagen que se muestra a continuación), lo que se conoce como lente convexa o lente convexa doble.
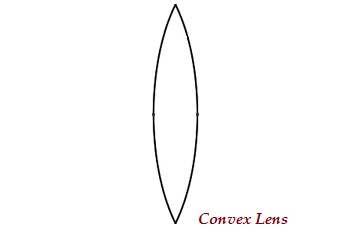
La parte media de esta lente está abultada (más gruesa) y en ambos extremos, es estrecha.
La lente convexa converge los rayos de luz; por lo tanto, también se conoce comoconverging lens.
Lente cóncava
Una lente puede tener dos superficies esféricas, curvadas hacia adentro (como se muestra en la imagen que se muestra a continuación), se conoce como lente cóncava o lente cóncava doble.
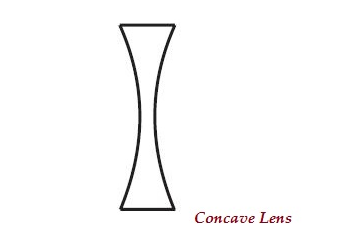
La parte media de esta lente es estrecha (curvada hacia adentro) y ambos bordes son más gruesos.
La lente cóncava diverge los rayos de luz; por lo tanto, también se conoce comodiverging lens.
Una lente, ya sea cóncava o convexa, tiene dos superficies esféricas y cada una de estas superficies forma parte de la esfera. Los centros de estas esferas se conocen comocenters of curvature, representado por letra inglesa 'C.
Como hay dos centros de curvatura, por lo tanto, representados como 'C 1 ' y 'C 2 '.
Una línea recta imaginaria, que pasa por ambos centros de curvatura de una lente, se conoce como principal axis.
El centro óptico es el punto central de una lente. Está representado por 'O.
Una apertura es el diámetro real del contorno circular de una lente esférica.
El foco principal de la lente está representado por 'F.
Una lente tiene generalmente dos focos representados como F 1 y F 2 .
Focal lengthes la distancia entre el foco principal y el centro óptico de una lente. Está representado por 'f.
La siguiente tabla ilustra la naturaleza y posición de las imágenes formadas por una lente convexa:
| Posición del objeto | Posición de la imagen | Tamaño de imagen | Naturaleza de la imagen | Imagen |
|---|---|---|---|---|
| En el infinito | En el foco F 2 | Muy disminuido, puntiagudo | Real e invertido |
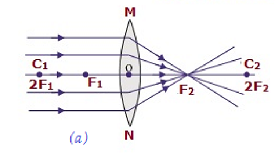
|
| Más allá de 2F 1 | Blanco y negro F 2 y 2F 2 | Disminuido | Real e invertido |
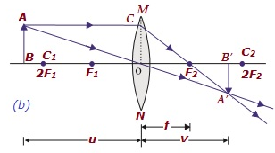
|
| En 2F 1 | En 2F 2 | Mismo tamaño | Real e invertido |
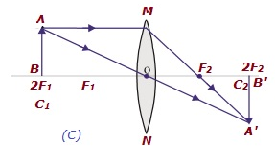
|
| B / w F 1 y 2F 1 | Más allá de 2F 2 | Engrandecido | Real e invertido |

|
| En el foco F 1 | En el infinito | Infinitamente grande o muy agrandado | Real e inverte d |
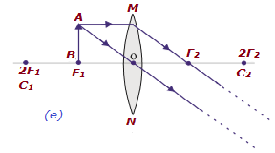
|
| Enfoque B / n F 1 y centro óptico O | En el mismo lado de la lente que el objeto | Engrandecido | Virtual y erecto |
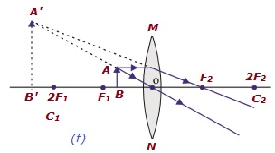
|
La siguiente tabla ilustra la naturaleza y posición de las imágenes formadas por una lente cóncava:
| Posición del objeto | Posición de la imagen | Tamaño relativo de imagen | Naturaleza de la imagen | Imagen |
|---|---|---|---|---|
| En el infinito | En el foco F 1 | Muy disminuido, puntiagudo | Virtual y erecto |
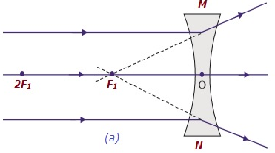
|
| Infinito en blanco y negro y centro óptico O de la lente | B / w F 1 y centro óptico O | Diminishe d | Virtual y erecto |
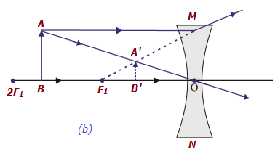
|
Fórmula de la lente
La fórmula se expresa como -
La fórmula de la lente expresa las relaciones entre la distancia del objeto (es decir, u), distancia de la imagen (es decir v) y la distancia focal (es decir, f) de una lente.
$$ \ frac {1} {v} - \ frac {1} {u} = \ frac {1} {f} $$