Electrónica de potencia: parámetros de rendimiento

Es importante determinar los parámetros de rendimiento para diferentes convertidores cuyas topologías pueden ser monofásicas o multifásicas.

Supuestos

• Los dispositivos utilizados son ideales, es decir, no tienen pérdidas.
• Los dispositivos tienen cargas resistivas

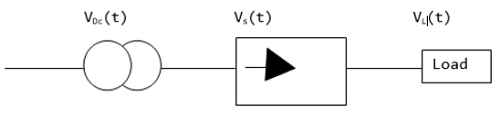
Voltaje DC en carga

$$ V_ {DC} = \ frac {1} {T} \ int_ {0} ^ {T} V_ {L} \ left (t \ right) dt $$

Voltaje RMS en carga

$$ V_ {L} = \ sqrt {\ frac {1} {T}} \ int_ {0} ^ {T} V_ {L} ^ {2} \ left (t \ right) dt $$

Factor de forma

$$ FF = \ frac {V_ {L}} {V_ {DC}} $$

Factor de ondulación

$$ RF = \ frac {\ sqrt {V_ {L} ^ {2} -V_ {DC} ^ {2}}} {V_ {DC}} = \ sqrt {FF ^ {2} -1} $$

Eficiencia (factor de rectificación)

$$ \ eta = \ frac {P_ {DC}} {P_ {L} + P_ {D}} $$

Donde lo anterior se define como:

$ P_ {DC} = V_ {DC} \ veces I_ {DC} $

$ P_ {L} = V_ {L} \ veces I_ {L} $

$ P_ {D} = R_ {D} \ times I_ {L} ^ {2} $ ($ P_ {D} $ son las pérdidas del rectificador y $ R_ {D} $ la resistencia)

$$ \ eta = \ frac {V_ {DC} I_ {DC}} {\ izquierda (V_ {L} I_ {L} \ derecha) + \ izquierda (R_ {D} I_ {L} ^ {2} \ derecha )} = \ frac {V_ {DC} ^ {2}} {V_ {L} ^ {2}} \ times \ frac {1} {1+ \ frac {R_ {D}} {R_ {L}}} $$

Pero $ R_ {D} = 0 $

Por lo tanto,

$$ \ eta = \ left (\ frac {V_ {DC}} {V_ {L}} \ right) ^ {2} = \ left (\ frac {1} {FF} \ right) ^ {2} $$

Factor de utilización del transformador

$$ TUF = \ frac {P_ {DC}} {VA \: Clasificación \: de \: el \: Transformador} = \ frac {P_ {DC}} {\ frac {VA_ {p} + VA_ {s}} {2}} $$

VA _p y VA _s son las clasificaciones de potencia primaria y secundaria del transformador.