Modulación de pulsos
Hasta ahora, hemos hablado de la modulación de onda continua. Ahora es el momento de las señales discretas. losPulse modulationtécnicas, se ocupa de señales discretas. Veamos cómo convertir una señal continua en discreta. El proceso llamado Muestreo nos ayuda con esto.
Muestreo
El proceso de convertir señales de tiempo continuas en señales de tiempo discretas equivalentes, puede denominarse como Sampling. Un determinado instante de datos se muestrea continuamente en el proceso de muestreo.
La siguiente figura indica una señal de tiempo continuo x(t) y una señal muestreada xs(t). Cuandox(t) se multiplica por un tren de impulsos periódico, la señal muestreada xs(t) es obtenido.
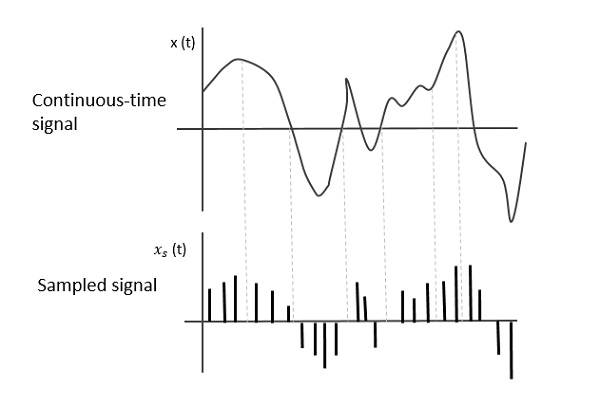
UN sampling signal es un tren periódico de pulsos, que tiene unit amplitude, muestreados a intervalos de tiempo iguales Ts, que se llama como Sampling time. Estos datos se transmiten en los instantes de tiempoTs y la señal portadora se transmite en el tiempo restante.
Tasa de muestreo
Para discretizar las señales, se debe arreglar el espacio entre las muestras. Esa brecha puede denominarsesampling period Ts.
$$ Muestreo \: Frecuencia = \ frac {1} {T_s} = f_s $$
Dónde,
Ts = el tiempo de muestreo
fs = la frecuencia de muestreo o la frecuencia de muestreo
Teorema de muestreo
Al considerar la frecuencia de muestreo, se debe considerar un punto importante con respecto a cuánto debe ser la frecuencia. losrate of sampling debe ser tal que los datos de la señal del mensaje no se pierdan ni se superpongan.
los sampling theorem establece que, "una señal se puede reproducir exactamente si se muestrea a la velocidad fs que es mayor o igual al doble de la frecuencia máxima W. "
Para decirlo en palabras más simples, para la reproducción efectiva de la señal original, la frecuencia de muestreo debe ser el doble de la frecuencia más alta.
Lo que significa,
$$ f_s \ geq 2W $$
Dónde,
fs = la frecuencia de muestreo
W es la frecuencia más alta
Esta tasa de muestreo se denomina Nyquist rate.
El teorema de muestreo, que también se llama Nyquist theorem, ofrece la teoría de una frecuencia de muestreo suficiente en términos de ancho de banda para la clase de funciones con limitación de banda.
Para la señal de tiempo continuo x(t), la señal de banda limitada en el dominio de la frecuencia, se puede representar como se muestra en la siguiente figura.
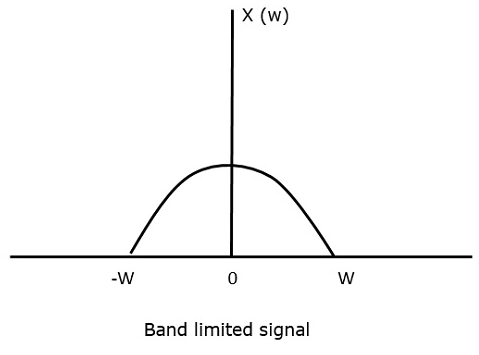
Si la señal se muestrea por encima de la tasa de Nyquist, se puede recuperar la señal original. La siguiente figura explica una señal, si se muestrea a una velocidad superior a 2w en el dominio de la frecuencia.
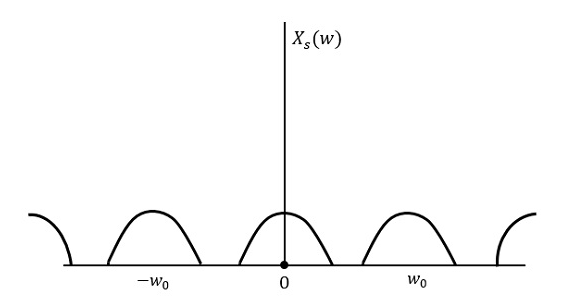
Si se muestrea la misma señal a una velocidad menor a 2w, entonces la señal muestreada se vería como la siguiente figura.
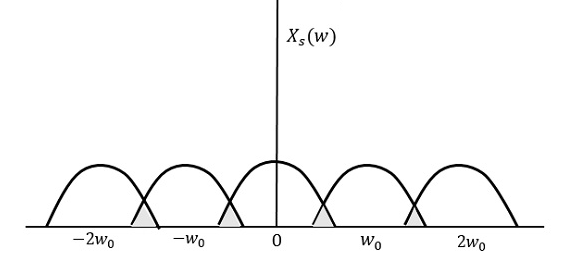
Podemos observar a partir del patrón anterior que se realiza el solapamiento de información, lo que conduce a confusión y pérdida de información. Este fenómeno no deseado de superposición se denomina comoAliasing.
El aliasing se puede denominar "el fenómeno de un componente de alta frecuencia en el espectro de una señal, que adquiere la identidad de un componente de baja frecuencia en el espectro de su versión muestreada".
Por lo tanto, el muestreo de la señal se elige a la tasa de Nyquist, como se estableció en el teorema de muestreo. Si la frecuencia de muestreo es igual al doble de la frecuencia más alta (2W).
Eso significa,
$$ f_s = 2W $$
Dónde,
fs = la frecuencia de muestreo
W es la frecuencia más alta

El resultado será el que se muestra en la figura anterior. La información se reemplaza sin pérdida alguna. Por tanto, esta es una buena frecuencia de muestreo.