Aprendizaje profundo de Python - Guía rápida

El aprendizaje estructurado profundo o el aprendizaje jerárquico o el aprendizaje profundo en resumen es parte de la familia de métodos de aprendizaje automático que son en sí mismos un subconjunto del campo más amplio de la inteligencia artificial.

El aprendizaje profundo es una clase de algoritmos de aprendizaje automático que utilizan varias capas de unidades de procesamiento no lineales para la extracción y transformación de características. Cada capa sucesiva utiliza la salida de la capa anterior como entrada.

Las redes neuronales profundas, las redes de creencias profundas y las redes neuronales recurrentes se han aplicado a campos como la visión por computadora, el reconocimiento de voz, el procesamiento del lenguaje natural, el reconocimiento de audio, el filtrado de redes sociales, la traducción automática y la bioinformática, donde produjeron resultados comparables y en algunos casos. mejor que los expertos humanos.

Algoritmos y redes de aprendizaje profundo -

• se basan en el aprendizaje no supervisado de múltiples niveles de características o representaciones de los datos. Las características de nivel superior se derivan de las características de nivel inferior para formar una representación jerárquica.

• use alguna forma de descenso de gradiente para entrenar.

En este capítulo, aprenderemos sobre el entorno configurado para Python Deep Learning. Tenemos que instalar el siguiente software para realizar algoritmos de aprendizaje profundo.

• Python 2.7+
• Scipy con Numpy
• Matplotlib
• Theano
• Keras
• TensorFlow

Se recomienda encarecidamente que Python, NumPy, SciPy y Matplotlib se instalen a través de la distribución Anaconda. Viene con todos esos paquetes.

Necesitamos asegurarnos de que los diferentes tipos de software estén instalados correctamente.

Vayamos a nuestro programa de línea de comandos y escriba el siguiente comando:

$ python
Python 3.6.3 |Anaconda custom (32-bit)| (default, Oct 13 2017, 14:21:34)
[GCC 7.2.0] on linux

A continuación, podemos importar las bibliotecas necesarias e imprimir sus versiones:

import numpy
print numpy.__version__

Salida

1.14.2

Instalación de Theano, TensorFlow y Keras

Antes de comenzar con la instalación de los paquetes: Theano, TensorFlow y Keras, debemos confirmar si el pipesta instalado. El sistema de administración de paquetes en Anaconda se llama pip.

Para confirmar la instalación de pip, escriba lo siguiente en la línea de comando:

$ pip

Una vez que se confirma la instalación de pip, podemos instalar TensorFlow y Keras ejecutando el siguiente comando:

$pip install theano $pip install tensorflow
$pip install keras

Confirme la instalación de Theano ejecutando la siguiente línea de código:

$python –c “import theano: print (theano.__version__)”

Salida

1.0.1

Confirme la instalación de Tensorflow ejecutando la siguiente línea de código:

$python –c “import tensorflow: print tensorflow.__version__”

Salida

1.7.0

Confirme la instalación de Keras ejecutando la siguiente línea de código:

$python –c “import keras: print keras.__version__”
Using TensorFlow backend

Salida

2.1.5

La Inteligencia Artificial (IA) es cualquier código, algoritmo o técnica que permite a una computadora imitar el comportamiento cognitivo o la inteligencia humana. El aprendizaje automático (ML) es un subconjunto de la IA que utiliza métodos estadísticos para permitir que las máquinas aprendan y mejoren con la experiencia. El aprendizaje profundo es un subconjunto del aprendizaje automático, que hace posible el cálculo de redes neuronales multicapa. El aprendizaje automático se considera un aprendizaje superficial, mientras que el aprendizaje profundo se considera un aprendizaje jerárquico con abstracción.

El aprendizaje automático se ocupa de una amplia gama de conceptos. Los conceptos se enumeran a continuación:

• supervised
• unsupervised
• aprendizaje reforzado
• regresión lineal
• funciones de costo
• overfitting
• under-fitting
• hiperparámetro, etc.

En el aprendizaje supervisado, aprendemos a predecir valores a partir de datos etiquetados. Una técnica de ML que ayuda aquí es la clasificación, donde los valores objetivo son valores discretos; por ejemplo, perros y gatos. Otra técnica de aprendizaje automático que podría resultar útil es la regresión. La regresión funciona sobre los valores objetivo. Los valores objetivo son valores continuos; por ejemplo, los datos del mercado de valores se pueden analizar mediante Regresión.

En el aprendizaje no supervisado, hacemos inferencias a partir de los datos de entrada que no están etiquetados ni estructurados. Si tenemos un millón de registros médicos y tenemos que darle sentido, encontrar la estructura subyacente, los valores atípicos o detectar anomalías, usamos la técnica de agrupación para dividir los datos en grupos amplios.

Los conjuntos de datos se dividen en conjuntos de entrenamiento, conjuntos de prueba, conjuntos de validación, etc.

Un gran avance en 2012 llevó a la prominencia el concepto de Deep Learning. Un algoritmo clasificó 1 millón de imágenes en 1000 categorías con éxito utilizando 2 GPU y las últimas tecnologías como Big Data.

Relacionar el aprendizaje profundo y el aprendizaje automático tradicional

Uno de los principales desafíos que se encuentran en los modelos tradicionales de aprendizaje automático es un proceso llamado extracción de características. El programador debe ser específico y decirle a la computadora las características que debe buscar. Estas características ayudarán a tomar decisiones.

La introducción de datos sin procesar en el algoritmo rara vez funciona, por lo que la extracción de características es una parte fundamental del flujo de trabajo de aprendizaje automático tradicional.

Esto coloca una gran responsabilidad en el programador, y la eficiencia del algoritmo depende en gran medida de la inventiva del programador. Para problemas complejos como el reconocimiento de objetos o el reconocimiento de escritura a mano, este es un problema enorme.

El aprendizaje profundo, con la capacidad de aprender múltiples capas de representación, es uno de los pocos métodos que nos ha ayudado con la extracción automática de características. Se puede suponer que las capas inferiores realizan la extracción automática de características, lo que requiere poca o ninguna orientación del programador.

La red neuronal artificial, o simplemente la red neuronal para abreviar, no es una idea nueva. Ha existido durante unos 80 años.

No fue hasta 2011, cuando las redes neuronales profundas se hicieron populares con el uso de nuevas técnicas, una gran disponibilidad de conjuntos de datos y computadoras potentes.

Una red neuronal imita a una neurona, que tiene dendritas, un núcleo, un axón y un axón terminal.

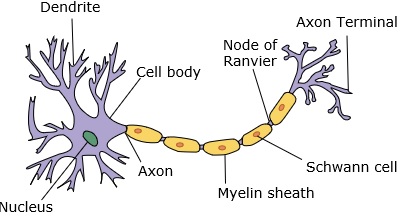
Para una red, necesitamos dos neuronas. Estas neuronas transfieren información a través de sinapsis entre las dendritas de una y el axón terminal de otra.

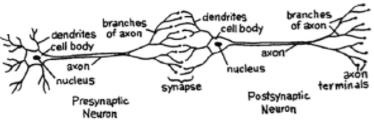
Un modelo probable de una neurona artificial se ve así:

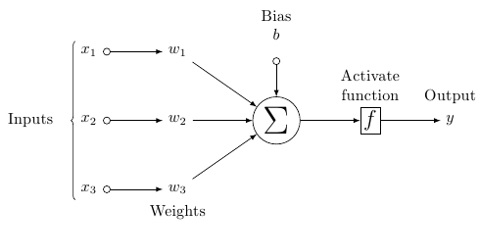
Una red neuronal se verá como se muestra a continuación:

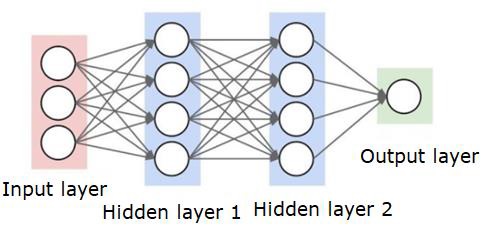
Los círculos son neuronas o nodos, con sus funciones en los datos y las líneas / bordes que los conectan son los pesos / información que se transmite.

Cada columna es una capa. La primera capa de sus datos es la capa de entrada. Entonces, todas las capas entre la capa de entrada y la capa de salida son las capas ocultas.

Si tiene una o varias capas ocultas, entonces tiene una red neuronal poco profunda. Si tiene muchas capas ocultas, entonces tiene una red neuronal profunda.

En este modelo, tiene datos de entrada, los pondera y los pasa a través de la función en la neurona que se llama función de umbral o función de activación.

Básicamente, es la suma de todos los valores después de compararlo con un valor determinado. Si dispara una señal, entonces el resultado es (1) apagado, o no se dispara nada, entonces (0). Luego se pondera y se pasa a la siguiente neurona, y se ejecuta el mismo tipo de función.

Podemos tener una función sigmoidea (en forma de s) como función de activación.

En cuanto a los pesos, son aleatorios para comenzar y son únicos por entrada en el nodo / neurona.

En un típico "feed forward", el tipo más básico de red neuronal, usted hace que su información pase directamente a través de la red que creó y compara la salida con lo que esperaba que hubiera estado usando sus datos de muestra.

Desde aquí, debe ajustar los pesos para ayudarlo a que su salida coincida con la salida deseada.

El acto de enviar datos directamente a través de una red neuronal se denomina feed forward neural network.

Nuestros datos van desde la entrada a las capas, en orden, luego a la salida.

Cuando retrocedemos y comenzamos a ajustar los pesos para minimizar la pérdida / costo, esto se llama back propagation.

Esto es un optimization problem. Con la red neuronal, en la práctica real, tenemos que lidiar con cientos de miles de variables, o millones, o más.

La primera solución fue utilizar el descenso de gradiente estocástico como método de optimización. Ahora, hay opciones como AdaGrad, Adam Optimizer, etc. De cualquier manera, esta es una operación computacional masiva. Es por eso que las redes neuronales se dejaron en la estantería durante más de medio siglo. Fue solo muy recientemente que incluso teníamos la potencia y la arquitectura en nuestras máquinas para considerar siquiera realizar estas operaciones, y los conjuntos de datos del tamaño adecuado para coincidir.

Para tareas de clasificación simples, la red neuronal tiene un rendimiento relativamente similar al de otros algoritmos simples como K Vecinos más cercanos. La utilidad real de las redes neuronales se realiza cuando tenemos datos mucho más grandes y preguntas mucho más complejas, las cuales superan a otros modelos de aprendizaje automático.

Una red neuronal profunda (DNN) es una ANN con múltiples capas ocultas entre las capas de entrada y salida. De manera similar a las ANN poco profundas, las DNN pueden modelar relaciones complejas no lineales.

El propósito principal de una red neuronal es recibir un conjunto de entradas, realizar cálculos progresivamente complejos sobre ellas y dar salida para resolver problemas del mundo real como la clasificación. Nos limitamos a alimentar redes neuronales.

Tenemos una entrada, una salida y un flujo de datos secuenciales en una red profunda.

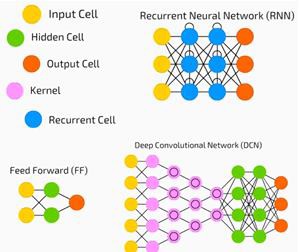
Las redes neuronales se utilizan ampliamente en problemas de aprendizaje supervisado y aprendizaje reforzado. Estas redes se basan en un conjunto de capas conectadas entre sí.

En el aprendizaje profundo, la cantidad de capas ocultas, en su mayoría no lineales, puede ser grande; digamos unas 1000 capas.

Los modelos DL producen resultados mucho mejores que las redes ML normales.

Usamos principalmente el método de descenso de gradiente para optimizar la red y minimizar la función de pérdida.

Podemos usar el Imagenet, un repositorio de millones de imágenes digitales para clasificar un conjunto de datos en categorías como gatos y perros. Las redes DL se utilizan cada vez más para imágenes dinámicas, además de las estáticas, y para series de tiempo y análisis de texto.

El entrenamiento de los conjuntos de datos forma una parte importante de los modelos de Deep Learning. Además, la retropropagación es el algoritmo principal en el entrenamiento de modelos DL.

DL se ocupa del entrenamiento de grandes redes neuronales con transformaciones complejas de entrada y salida.

Un ejemplo de DL es la asignación de una foto al nombre de la (s) persona (s) en la foto como lo hacen en las redes sociales y describir una imagen con una frase es otra aplicación reciente de DL.

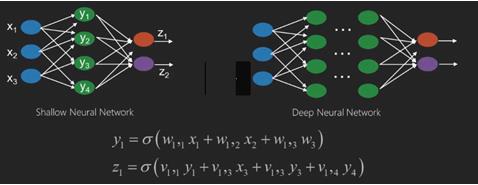
Las redes neuronales son funciones que tienen entradas como x1, x2, x3… que se transforman en salidas como z1, z2, z3 y así sucesivamente en dos (redes poco profundas) o varias operaciones intermedias también llamadas capas (redes profundas).

Los pesos y sesgos cambian de una capa a otra. 'w' y 'v' son los pesos o sinapsis de capas de las redes neuronales.

El mejor caso de uso del aprendizaje profundo es el problema del aprendizaje supervisado. Aquí, tenemos un gran conjunto de entradas de datos con un conjunto deseado de salidas.

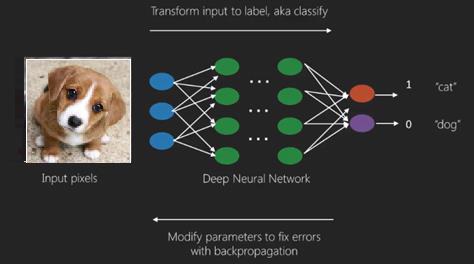
Aquí aplicamos el algoritmo de retropropagación para obtener una predicción de salida correcta.

El conjunto de datos más básico de aprendizaje profundo es el MNIST, un conjunto de datos de dígitos escritos a mano.

Podemos entrenar en profundidad una red neuronal convolucional con Keras para clasificar imágenes de dígitos escritos a mano de este conjunto de datos.

El disparo o activación de un clasificador de red neuronal produce una puntuación. Por ejemplo, para clasificar a los pacientes como enfermos y sanos, consideramos parámetros como la altura, el peso y la temperatura corporal, la presión arterial, etc.

Una puntuación alta significa que el paciente está enfermo y una puntuación baja significa que está sano.

Cada nodo en las capas de salida y ocultas tiene sus propios clasificadores. La capa de entrada toma entradas y pasa sus puntuaciones a la siguiente capa oculta para una mayor activación y esto continúa hasta que se alcanza la salida.

Este progreso de entrada a salida de izquierda a derecha en la dirección de avance se llama forward propagation.

La ruta de asignación de crédito (CAP) en una red neuronal es la serie de transformaciones que comienzan desde la entrada hasta la salida. Los CAP elaboran conexiones causales probables entre la entrada y la salida.

La profundidad de CAP para una red neuronal de alimentación directa determinada o la profundidad de CAP es el número de capas ocultas más una, ya que se incluye la capa de salida. Para las redes neuronales recurrentes, donde una señal puede propagarse a través de una capa varias veces, la profundidad de CAP puede ser potencialmente ilimitada.

Redes profundas y redes poco profundas

No existe un umbral claro de profundidad que separe el aprendizaje superficial del aprendizaje profundo; pero la mayoría está de acuerdo en que para el aprendizaje profundo que tiene múltiples capas no lineales, CAP debe ser mayor que dos.

El nodo básico en una red neuronal es una percepción que imita una neurona en una red neuronal biológica. Luego tenemos Perception multicapa o MLP. Cada conjunto de entradas se modifica mediante un conjunto de pesos y sesgos; cada borde tiene un peso único y cada nodo tiene un sesgo único.

La predicción accuracy de una red neuronal depende de su weights and biases.

El proceso de mejora de la precisión de la red neuronal se llama training. La salida de una red de apoyo hacia adelante se compara con ese valor que se sabe que es correcto.

los cost function or the loss function es la diferencia entre la salida generada y la salida real.

El objetivo del entrenamiento es hacer que el costo del entrenamiento sea lo más pequeño posible en millones de ejemplos de entrenamiento. Para hacer esto, la red ajusta los pesos y los sesgos hasta que la predicción coincide con el resultado correcto.

Una vez entrenada bien, una red neuronal tiene el potencial de hacer una predicción precisa en todo momento.

Cuando el patrón se vuelve complejo y desea que su computadora los reconozca, debe optar por redes neuronales. En escenarios de patrones tan complejos, la red neuronal supera a todos los demás algoritmos competidores.

Ahora hay GPU que pueden entrenarlos más rápido que nunca. Las redes neuronales profundas ya están revolucionando el campo de la IA

Las computadoras han demostrado ser buenas para realizar cálculos repetitivos y seguir instrucciones detalladas, pero no tan buenas para reconocer patrones complejos.

Si existe el problema del reconocimiento de patrones simples, una máquina de vectores de soporte (svm) o un clasificador de regresión logística pueden hacer bien el trabajo, pero a medida que aumenta la complejidad del patrón, no hay más remedio que optar por redes neuronales profundas.

Por lo tanto, para patrones complejos como un rostro humano, las redes neuronales superficiales fallan y no tienen otra alternativa que optar por redes neuronales profundas con más capas. Las redes profundas pueden hacer su trabajo descomponiendo los patrones complejos en patrones más simples. Por ejemplo, rostro humano; Una red profunda usaría bordes para detectar partes como labios, nariz, ojos, oídos, etc. y luego los volvería a combinar para formar un rostro humano.

La precisión de la predicción correcta se ha vuelto tan precisa que recientemente, en un Desafío de reconocimiento de patrones de Google, una red profunda venció a un humano.

Esta idea de una red de perceptrones en capas ha existido durante algún tiempo; en esta área, las redes profundas imitan el cerebro humano. Pero una desventaja de esto es que tardan mucho en entrenarse, una restricción de hardware

Sin embargo, las GPU de alto rendimiento recientes han podido entrenar redes tan profundas en menos de una semana; mientras que las CPU rápidas podrían haber tardado semanas o quizás meses en hacer lo mismo.

Elegir una red profunda

¿Cómo elegir una red profunda? Tenemos que decidir si estamos construyendo un clasificador o si estamos tratando de encontrar patrones en los datos y si vamos a utilizar el aprendizaje no supervisado. Para extraer patrones de un conjunto de datos sin etiquetar, utilizamos una máquina Boltzman restringida o un codificador automático.

Considere los siguientes puntos al elegir una red profunda:

• Para el procesamiento de texto, análisis de sentimientos, análisis sintáctico y reconocimiento de entidades de nombres, utilizamos una red recurrente o una red de tensor neuronal recursiva o RNTN;

• Para cualquier modelo de lenguaje que opere a nivel de personaje, usamos la red recurrente.

• Para el reconocimiento de imágenes, utilizamos una red de creencias profundas DBN o una red convolucional.

• Para el reconocimiento de objetos, utilizamos un RNTN o una red convolucional.

• Para el reconocimiento de voz, utilizamos la red recurrente.

En general, las redes de creencias profundas y los perceptrones multicapa con unidades lineales rectificadas o RELU son buenas opciones para la clasificación.

Para el análisis de series de tiempo, siempre se recomienda utilizar la red recurrente.

Las redes neuronales existen desde hace más de 50 años; pero solo ahora han cobrado importancia. La razón es que son difíciles de entrenar; cuando tratamos de entrenarlos con un método llamado propagación hacia atrás, nos encontramos con un problema llamado gradientes que desaparecen o explotan. Cuando eso sucede, el entrenamiento lleva más tiempo y la precisión pasa a un segundo plano. Cuando entrenamos un conjunto de datos, calculamos constantemente la función de costo, que es la diferencia entre la producción prevista y la producción real de un conjunto de datos de entrenamiento etiquetados. Luego, la función de costo se minimiza ajustando los valores de pesos y sesgos hasta el valor más bajo. es obtenido. El proceso de entrenamiento utiliza un gradiente, que es la tasa a la que cambiará el costo con respecto al cambio en los valores de peso o sesgo.

Autoencoders o redes Boltzman restringidas - RBN

En 2006, se logró un gran avance al abordar el problema de los gradientes que desaparecen. Geoff Hinton ideó una estrategia novedosa que condujo al desarrollo deRestricted Boltzman Machine - RBM, una red poco profunda de dos capas.

La primera capa es la visible capa y la segunda capa es la hiddencapa. Cada nodo de la capa visible está conectado a cada nodo de la capa oculta. La red se conoce como restringida, ya que no se permite que dos capas dentro de la misma capa compartan una conexión.

Los codificadores automáticos son redes que codifican datos de entrada como vectores. Crean una representación oculta o comprimida de los datos sin procesar. Los vectores son útiles en la reducción de dimensionalidad; el vector comprime los datos brutos en un número menor de dimensiones esenciales. Los autocodificadores están emparejados con decodificadores, lo que permite la reconstrucción de datos de entrada en función de su representación oculta.

RBM es el equivalente matemático de un traductor bidireccional. Un pase directo toma entradas y las traduce en un conjunto de números que codifica las entradas. Mientras tanto, un pase hacia atrás toma este conjunto de números y los vuelve a traducir en entradas reconstruidas. Una red bien entrenada realiza el apoyo de la espalda con un alto grado de precisión.

En cualquiera de los pasos, las ponderaciones y los sesgos tienen un papel fundamental; ayudan al RBM a decodificar las interrelaciones entre las entradas y a decidir qué entradas son esenciales para detectar patrones. A través de pasadas hacia adelante y hacia atrás, el RBM está capacitado para reconstruir la entrada con diferentes pesos y sesgos hasta que la entrada y la construcción estén lo más cerca posible. Un aspecto interesante de la GBR es que no es necesario etiquetar los datos. Esto resulta ser muy importante para conjuntos de datos del mundo real como fotos, videos, voces y datos de sensores, todos los cuales tienden a no estar etiquetados. En lugar de etiquetar manualmente los datos por humanos, la RBM clasifica automáticamente los datos; Al ajustar correctamente los pesos y los sesgos, una GBR puede extraer características importantes y reconstruir la entrada. RBM es parte de la familia de redes neuronales de extracción de características, que están diseñadas para reconocer patrones inherentes en los datos. También se denominan codificadores automáticos porque tienen que codificar su propia estructura.

Redes de creencias profundas - DBN

Las redes de creencias profundas (DBN) se forman combinando RBM e introduciendo un método de entrenamiento inteligente. Tenemos un nuevo modelo que finalmente resuelve el problema del gradiente de fuga. Geoff Hinton inventó los RBM y también las Deep Belief Nets como alternativa a la propagación inversa.

Un DBN es similar en estructura a un MLP (perceptrón multicapa), pero muy diferente cuando se trata de entrenamiento. es la formación que permite a los DBN superar a sus homólogos superficiales

Una DBN se puede visualizar como una pila de RBM donde la capa oculta de una RBM es la capa visible de la RBM por encima de ella. El primer RBM está capacitado para reconstruir su entrada con la mayor precisión posible.

La capa oculta de la primera RBM se toma como la capa visible de la segunda RBM y la segunda RBM se entrena utilizando las salidas de la primera RBM. Este proceso se repite hasta que se entrena cada capa de la red.

En un DBN, cada RBM aprende toda la entrada. Un DBN funciona globalmente ajustando toda la entrada en sucesión a medida que el modelo mejora lentamente como una lente de cámara enfocando lentamente una imagen. Una pila de RBM supera a una sola RBM como un perceptrón multicapa MLP supera a un solo perceptrón.

En esta etapa, las GBR han detectado patrones inherentes en los datos pero sin ningún nombre ni etiqueta. Para terminar el entrenamiento del DBN, tenemos que introducir etiquetas a los patrones y afinar la red con aprendizaje supervisado.

Necesitamos un conjunto muy pequeño de muestras etiquetadas para que las características y los patrones puedan asociarse con un nombre. Este conjunto de datos con etiquetas pequeñas se utiliza para el entrenamiento. Este conjunto de datos etiquetados puede ser muy pequeño en comparación con el conjunto de datos original.

Los pesos y sesgos se alteran ligeramente, lo que resulta en un pequeño cambio en la percepción de la red de los patrones y, a menudo, un pequeño aumento en la precisión total.

El entrenamiento también se puede completar en un período de tiempo razonable utilizando GPU que brindan resultados muy precisos en comparación con las redes poco profundas y también vemos una solución al problema del gradiente que desaparece.

Redes generativas antagónicas - GAN

Las redes generativas adversarias son redes neuronales profundas que comprenden dos redes, enfrentadas una contra la otra, de ahí el nombre de “adversario”.

Las GAN se introdujeron en un artículo publicado por investigadores de la Universidad de Montreal en 2014. El experto en inteligencia artificial de Facebook, Yann LeCun, en referencia a las GAN, calificó el entrenamiento contradictorio como "la idea más interesante de los últimos 10 años en ML".

El potencial de las GAN es enorme, ya que el escaneo de red aprende a imitar cualquier distribución de datos. A los GAN se les puede enseñar a crear mundos paralelos sorprendentemente similares al nuestro en cualquier dominio: imágenes, música, habla, prosa. Son artistas de robots en cierto modo, y su producción es bastante impresionante.

En una GAN, una red neuronal, conocida como generador, genera nuevas instancias de datos, mientras que la otra, el discriminador, evalúa su autenticidad.

Digamos que estamos tratando de generar números escritos a mano como los que se encuentran en el conjunto de datos MNIST, que se toman del mundo real. El trabajo del discriminador, cuando se muestra una instancia del verdadero conjunto de datos MNIST, es reconocerlos como auténticos.

Ahora considere los siguientes pasos de la GAN:

• La red del generador toma la entrada en forma de números aleatorios y devuelve una imagen.

• Esta imagen generada se proporciona como entrada a la red discriminadora junto con un flujo de imágenes tomadas del conjunto de datos real.

• El discriminador toma imágenes tanto reales como falsas y devuelve probabilidades, un número entre 0 y 1, donde 1 representa una predicción de autenticidad y 0 representa falso.

• Entonces tienes un ciclo de retroalimentación doble:

  • El discriminador está en un circuito de retroalimentación con la verdad fundamental de las imágenes, que conocemos.

  • El generador está en un circuito de retroalimentación con el discriminador.

Redes neuronales recurrentes - RNN

RNNSon redes neuronales en las que los datos pueden fluir en cualquier dirección. Estas redes se utilizan para aplicaciones como modelado de lenguaje o procesamiento de lenguaje natural (NLP).

El concepto básico que subyace a las RNN es utilizar información secuencial. En una red neuronal normal, se supone que todas las entradas y salidas son independientes entre sí. Si queremos predecir la siguiente palabra en una oración, tenemos que saber qué palabras vinieron antes.

Los RNN se denominan recurrentes porque repiten la misma tarea para cada elemento de una secuencia, y el resultado se basa en los cálculos anteriores. Por tanto, se puede decir que los RNN tienen una "memoria" que captura información sobre lo que se ha calculado previamente. En teoría, los RNN pueden usar información en secuencias muy largas, pero en realidad, solo pueden mirar hacia atrás unos pocos pasos.

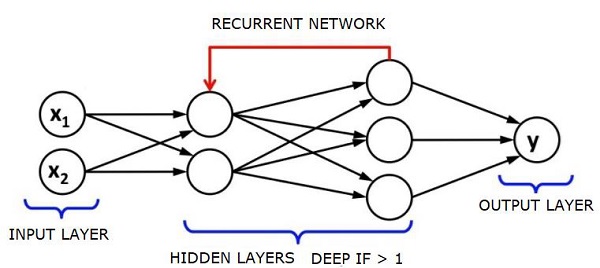
Las redes de memoria a largo plazo a corto plazo (LSTM) son las RNN más utilizadas.

Junto con las redes neuronales convolucionales, las RNN se han utilizado como parte de un modelo para generar descripciones de imágenes sin etiquetar. Es bastante sorprendente lo bien que parece funcionar.

Redes neuronales profundas convolucionales - CNN

Si aumentamos el número de capas en una red neuronal para hacerla más profunda, aumenta la complejidad de la red y nos permite modelar funciones que son más complicadas. Sin embargo, el número de ponderaciones y sesgos aumentará exponencialmente. De hecho, aprender problemas tan difíciles puede resultar imposible para las redes neuronales normales. Esto conduce a una solución, las redes neuronales convolucionales.

Las CNN se utilizan ampliamente en visión por computadora; También se han aplicado en el modelado acústico para el reconocimiento automático de voz.

La idea detrás de las redes neuronales convolucionales es la idea de un "filtro en movimiento" que atraviesa la imagen. Este filtro móvil, o convolución, se aplica a un cierto vecindario de nodos que, por ejemplo, pueden ser píxeles, donde el filtro aplicado es 0.5 x el valor del nodo -

El destacado investigador Yann LeCun fue pionero en las redes neuronales convolucionales. Facebook como software de reconocimiento facial usa estas redes. CNN ha sido la solución ideal para proyectos de visión artificial. Hay muchas capas en una red convolucional. En el desafío Imagenet, una máquina pudo vencer a un humano en el reconocimiento de objetos en 2015.

En pocas palabras, las redes neuronales convolucionales (CNN) son redes neuronales multicapa. Las capas a veces tienen hasta 17 o más y asumen que los datos de entrada son imágenes.

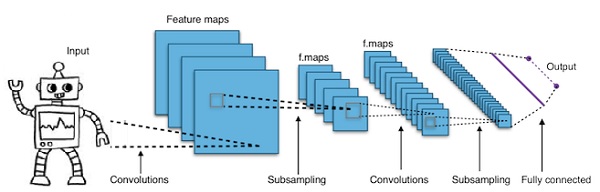
Las CNN reducen drásticamente la cantidad de parámetros que deben ajustarse. Por lo tanto, las CNN manejan eficientemente la alta dimensionalidad de las imágenes sin procesar.

En este capítulo, analizaremos los fundamentos de Python Deep Learning.

Modelos / algoritmos de aprendizaje profundo

Aprendamos ahora sobre los diferentes modelos / algoritmos de aprendizaje profundo.

Algunos de los modelos populares dentro del aprendizaje profundo son los siguientes:

• Redes neuronales convolucionales
• Redes neuronales recurrentes
• Redes de creencias profundas
• Redes generativas de confrontación
• Auto-codificadores y así sucesivamente

Las entradas y salidas se representan como vectores o tensores. Por ejemplo, una red neuronal puede tener entradas donde los valores RGB de píxeles individuales en una imagen se representan como vectores.

Las capas de neuronas que se encuentran entre la capa de entrada y la capa de salida se denominan capas ocultas. Aquí es donde ocurre la mayor parte del trabajo cuando la red neuronal intenta resolver problemas. Una mirada más cercana a las capas ocultas puede revelar mucho sobre las características que la red ha aprendido a extraer de los datos.

Se forman diferentes arquitecturas de redes neuronales eligiendo qué neuronas conectar con las otras neuronas en la siguiente capa.

Pseudocódigo para calcular la salida

A continuación se muestra el pseudocódigo para calcular la salida de Forward-propagating Neural Network -

• # nodo []: = matriz de nodos ordenados topológicamente
• # Una arista de a a b significa que a está a la izquierda de b
• # Si la red neuronal tiene entradas R y salidas S,
• # entonces los primeros nodos R son nodos de entrada y los últimos nodos S son nodos de salida.
• # entrantes [x]: = nodos conectados al nodo x
• # peso [x]: = pesos de los bordes entrantes ax

Para cada neurona x, de izquierda a derecha:

• si x <= R: no hacer nada # es un nodo de entrada
• entradas [x] = [salida [i] para i en entrante [x]]
• suma_ponderada = producto_punto (pesos [x], entradas [x])
• salida [x] = Función_activación (suma_ponderada)

Ahora aprenderemos a entrenar una red neuronal. También aprenderemos el algoritmo de propagación hacia atrás y el paso hacia atrás en Python Deep Learning.

Tenemos que encontrar los valores óptimos de los pesos de una red neuronal para obtener el resultado deseado. Para entrenar una red neuronal, utilizamos el método de descenso de gradiente iterativo. Comenzamos inicialmente con la inicialización aleatoria de los pesos. Después de la inicialización aleatoria, hacemos predicciones sobre algún subconjunto de los datos con el proceso de propagación hacia adelante, calculamos la función de costo correspondiente C y actualizamos cada peso w en una cantidad proporcional a dC / dw, es decir, la derivada de las funciones de costo wrt el peso. La constante de proporcionalidad se conoce como tasa de aprendizaje.

Los gradientes se pueden calcular de manera eficiente utilizando el algoritmo de retropropagación. La observación clave de la propagación hacia atrás o apoyo hacia atrás es que debido a la regla de diferenciación de la cadena, el gradiente en cada neurona en la red neuronal se puede calcular utilizando el gradiente en las neuronas, tiene bordes de salida hacia. Por lo tanto, calculamos los degradados hacia atrás, es decir, primero calculamos los degradados de la capa de salida, luego la capa superior más oculta, seguida de la capa oculta anterior, y así sucesivamente, terminando en la capa de entrada.

El algoritmo de retropropagación se implementa principalmente utilizando la idea de un gráfico computacional, donde cada neurona se expande a muchos nodos en el gráfico computacional y realiza una operación matemática simple como suma, multiplicación. El gráfico computacional no tiene pesos en los bordes; todos los pesos se asignan a los nodos, por lo que los pesos se convierten en sus propios nodos. El algoritmo de propagación hacia atrás se ejecuta luego en el gráfico computacional. Una vez que se completa el cálculo, solo se requieren los gradientes de los nodos de peso para la actualización. El resto de gradientes se pueden descartar.

Técnica de optimización del descenso de gradientes

Una función de optimización de uso común que ajusta los pesos de acuerdo con el error que causaron se llama "descenso de gradiente".

Gradiente es otro nombre para pendiente, y la pendiente, en un gráfico xy, representa cómo dos variables se relacionan entre sí: la elevación durante la carrera, el cambio en la distancia durante el cambio en el tiempo, etc. En este caso, la pendiente es la relación entre el error de la red y un solo peso; es decir, cómo cambia el error a medida que se varía el peso.

Para decirlo con mayor precisión, queremos encontrar qué peso produce el menor error. Queremos encontrar el peso que represente correctamente las señales contenidas en los datos de entrada y las traduzca a una clasificación correcta.

A medida que una red neuronal aprende, ajusta lentamente muchos pesos para que puedan asignar la señal al significado correctamente. La relación entre el error de red y cada uno de esos pesos es una derivada, dE / dw, que calcula hasta qué punto un ligero cambio en un peso provoca un ligero cambio en el error.

Cada peso es solo un factor en una red profunda que involucra muchas transformaciones; la señal del peso pasa a través de activaciones y sumas en varias capas, por lo que usamos la regla de la cadena de cálculo para trabajar a través de las activaciones y salidas de la red, lo que nos lleva al peso en cuestión y su relación con el error general.

Dadas dos variables, error y peso, están mediadas por una tercera variable, activation, a través del cual pasa el peso. Podemos calcular cómo un cambio en el peso afecta un cambio en el error calculando primero cómo un cambio en la activación afecta un cambio en el Error, y cómo un cambio en el peso afecta un cambio en la activación.

La idea básica en el aprendizaje profundo no es más que eso: ajustar los pesos de un modelo en respuesta al error que produce, hasta que ya no se pueda reducir el error.

La red profunda se entrena lentamente si el valor del gradiente es pequeño y rápido si el valor es alto. Cualquier inexactitud en la formación conduce a resultados inexactos. El proceso de entrenamiento de las redes desde la salida hasta la entrada se llama propagación hacia atrás o apoyo hacia atrás. Sabemos que la propagación hacia adelante comienza con la entrada y funciona hacia adelante. El apoyo trasero hace lo contrario / opuesto calculando el gradiente de derecha a izquierda.

Cada vez que calculamos un gradiente, usamos todos los gradientes anteriores hasta ese punto.

Comencemos en un nodo en la capa de salida. El borde usa el degradado en ese nodo. A medida que volvemos a las capas ocultas, se vuelve más complejo. El producto de dos números entre 0 y 1 le da un número menor. El valor del gradiente se vuelve cada vez más pequeño y, como resultado, el apoyo trasero lleva mucho tiempo para entrenar y la precisión se ve afectada.

Desafíos en los algoritmos de aprendizaje profundo

Existen ciertos desafíos tanto para las redes neuronales superficiales como para las redes neuronales profundas, como el sobreajuste y el tiempo de cálculo. Los DNN se ven afectados por el sobreajuste debido al uso de capas adicionales de abstracción que les permiten modelar dependencias raras en los datos de entrenamiento.

RegularizationDurante el entrenamiento se aplican métodos como el abandono, la detención anticipada, el aumento de datos y el aprendizaje por transferencia para combatir el sobreajuste. La regularización de abandono omite aleatoriamente las unidades de las capas ocultas durante el entrenamiento, lo que ayuda a evitar dependencias raras. Los DNN toman en consideración varios parámetros de entrenamiento como el tamaño, es decir, el número de capas y el número de unidades por capa, la tasa de aprendizaje y los pesos iniciales. Encontrar parámetros óptimos no siempre es práctico debido al alto costo de tiempo y recursos computacionales. Varios trucos, como el procesamiento por lotes, pueden acelerar el cálculo. La gran potencia de procesamiento de las GPU ha ayudado significativamente al proceso de entrenamiento, ya que los cálculos matriciales y vectoriales requeridos están bien ejecutados en las GPU.

Abandonar

La deserción es una técnica de regularización popular para redes neuronales. Las redes neuronales profundas son particularmente propensas a sobreajustarse.

Veamos ahora qué es la deserción y cómo funciona.

En palabras de Geoffrey Hinton, uno de los pioneros del aprendizaje profundo, 'si tiene una red neuronal profunda y no está sobreajustada, probablemente debería usar una más grande y usar abandono'.

La deserción es una técnica en la que durante cada iteración de descenso de gradiente, soltamos un conjunto de nodos seleccionados al azar. Esto significa que ignoramos algunos nodos al azar como si no existieran.

Cada neurona se mantiene con una probabilidad de q y se elimina aleatoriamente con una probabilidad de 1-q. El valor q puede ser diferente para cada capa de la red neuronal. Un valor de 0,5 para las capas ocultas y 0 para la capa de entrada funciona bien en una amplia gama de tareas.

Durante la evaluación y la predicción, no se utiliza ningún abandono. La salida de cada neurona se multiplica por q para que la entrada a la siguiente capa tenga el mismo valor esperado.

La idea detrás de la deserción es la siguiente: en una red neuronal sin regularización de la deserción, las neuronas desarrollan una codependencia entre sí que conduce a un sobreajuste.

Truco de implementación

El abandono se implementa en bibliotecas como TensorFlow y Pytorch manteniendo la salida de las neuronas seleccionadas al azar en 0. Es decir, aunque la neurona existe, su salida se sobrescribe como 0.

Parada anticipada

Entrenamos redes neuronales utilizando un algoritmo iterativo llamado descenso de gradiente.

La idea detrás de la parada temprana es intuitiva; dejamos de entrenar cuando el error comienza a aumentar. Aquí, por error, nos referimos al error medido en los datos de validación, que es la parte de los datos de entrenamiento que se utilizan para ajustar los hiperparámetros. En este caso, el hiperparámetro es el criterio de parada.

Aumento de datos

El proceso en el que aumentamos la cantidad de datos que tenemos o la aumentamos mediante el uso de datos existentes y la aplicación de algunas transformaciones en ellos. Las transformaciones exactas utilizadas dependen de la tarea que pretendamos realizar. Además, las transformaciones que ayudan a la red neuronal dependen de su arquitectura.

Por ejemplo, en muchas tareas de visión por computadora, como la clasificación de objetos, una técnica de aumento de datos efectiva es agregar nuevos puntos de datos que son versiones recortadas o traducidas de los datos originales.

Cuando una computadora acepta una imagen como entrada, toma una matriz de valores de píxeles. Digamos que toda la imagen se desplaza a la izquierda 15 píxeles. Aplicamos muchos cambios diferentes en diferentes direcciones, lo que da como resultado un conjunto de datos aumentado muchas veces el tamaño del conjunto de datos original.

Transferir aprendizaje

El proceso de tomar un modelo previamente entrenado y "afinar" el modelo con nuestro propio conjunto de datos se llama aprendizaje de transferencia. Hay varias formas de hacer esto, algunas se describen a continuación:

• Entrenamos el modelo previamente entrenado en un gran conjunto de datos. Luego, eliminamos la última capa de la red y la reemplazamos con una nueva capa con pesos aleatorios.

• Luego congelamos los pesos de todas las demás capas y entrenamos la red normalmente. Aquí congelar las capas no cambia los pesos durante el descenso u optimización del gradiente.

El concepto detrás de esto es que el modelo previamente entrenado actuará como un extractor de características y solo la última capa será entrenada en la tarea actual.

La retropropagación se implementa en marcos de aprendizaje profundo como Tensorflow, Torch, Theano, etc., mediante el uso de gráficos computacionales. Más significativamente, la comprensión de la retropropagación en gráficos computacionales combina varios algoritmos diferentes y sus variaciones, como backprop a través del tiempo y backprop con pesos compartidos. Una vez que todo se convierte en un gráfico computacional, siguen siendo el mismo algoritmo, solo retropropagación en gráficos computacionales.

¿Qué es el gráfico computacional?

Un gráfico computacional se define como un gráfico dirigido donde los nodos corresponden a operaciones matemáticas. Los gráficos computacionales son una forma de expresar y evaluar una expresión matemática.

Por ejemplo, aquí hay una ecuación matemática simple:

$$p = x+y$$

Podemos dibujar un gráfico computacional de la ecuación anterior de la siguiente manera.

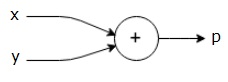
El gráfico computacional anterior tiene un nodo de suma (nodo con el signo "+") con dos variables de entrada xey y una salida q.

Tomemos otro ejemplo, un poco más complejo. Tenemos la siguiente ecuación.

$$g = \left (x+y \right ) \ast z $$

La ecuación anterior está representada por el siguiente gráfico computacional.

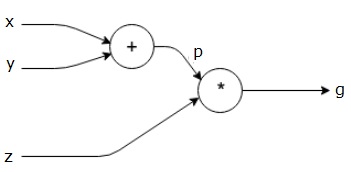
Gráficos computacionales y retropropagación

Los gráficos computacionales y la retropropagación son conceptos centrales importantes en el aprendizaje profundo para el entrenamiento de redes neuronales.

Pase adelantado

El pase hacia adelante es el procedimiento para evaluar el valor de la expresión matemática representada por gráficos computacionales. Hacer un pase hacia adelante significa que estamos pasando el valor de las variables en la dirección hacia adelante desde la izquierda (entrada) hacia la derecha donde está la salida.

Consideremos un ejemplo dando algún valor a todas las entradas. Supongamos que se dan los siguientes valores a todas las entradas.

$$x=1, y=3, z=−3$$

Al dar estos valores a las entradas, podemos realizar un pase hacia adelante y obtener los siguientes valores para las salidas en cada nodo.

Primero, usamos el valor de x = 1 e y = 3, para obtener p = 4.

Luego usamos p = 4 yz = -3 para obtener g = -12. Vamos de izquierda a derecha, hacia adelante.

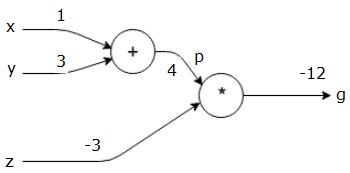
Objetivos de Backward Pass

En el paso hacia atrás, nuestra intención es calcular los gradientes para cada entrada con respecto a la salida final. Estos gradientes son esenciales para entrenar la red neuronal mediante el descenso de gradientes.

Por ejemplo, deseamos los siguientes gradientes.

Gradientes deseados

$$\frac{\partial x}{\partial f}, \frac{\partial y}{\partial f}, \frac{\partial z}{\partial f}$$

Pase hacia atrás (propagación hacia atrás)

Comenzamos el pase hacia atrás encontrando la derivada de la salida final con respecto a la salida final (¡en sí misma!). Por lo tanto, dará como resultado la derivación de identidad y el valor es igual a uno.

$$\frac{\partial g}{\partial g} = 1$$

Nuestro gráfico computacional ahora se ve como se muestra a continuación:

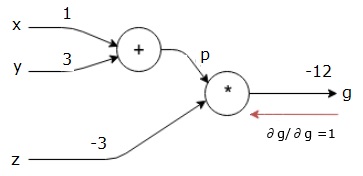
A continuación, haremos el paso hacia atrás mediante la operación "*". Calcularemos los gradientes en py z. Dado que g = p * z, sabemos que -

$$\frac{\partial g}{\partial z} = p$$

$$\frac{\partial g}{\partial p} = z$$

Ya conocemos los valores de zyp del pase hacia adelante. Por lo tanto, obtenemos -

$$\frac{\partial g}{\partial z} = p = 4$$

y

$$\frac{\partial g}{\partial p} = z = -3$$

Queremos calcular los gradientes en xey -

$$\frac{\partial g}{\partial x}, \frac{\partial g}{\partial y}$$

Sin embargo, queremos hacer esto de manera eficiente (aunque xyg están a solo dos saltos de distancia en este gráfico, imagina que están muy lejos uno del otro). Para calcular estos valores de manera eficiente, usaremos la regla de diferenciación de la cadena. De la regla de la cadena, tenemos:

$$\frac{\partial g}{\partial x}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial x}$$

$$\frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial y}$$

Pero ya sabemos que dg / dp = -3, dp / dx y dp / dy son fáciles ya que p depende directamente de xey. Tenemos -

$$p=x+y\Rightarrow \frac{\partial x}{\partial p} = 1, \frac{\partial y}{\partial p} = 1$$

Por lo tanto, obtenemos -

$$\frac{\partial g} {\partial f} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial x} = \left ( -3 \right ).1 = -3$$

Además, para la entrada y -

$$\frac{\partial g} {\partial y} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial y} = \left ( -3 \right ).1 = -3$$

La razón principal para hacer esto al revés es que cuando tuvimos que calcular el gradiente en x, solo usamos valores ya calculados y dq / dx (derivada de la salida del nodo con respecto a la entrada del mismo nodo). Usamos información local para calcular un valor global.

Pasos para entrenar una red neuronal

Siga estos pasos para entrenar una red neuronal:

• Para el punto de datos x en el conjunto de datos, pasamos adelante con x como entrada y calculamos el costo c como salida.

• Hacemos un pase hacia atrás comenzando en cy calculamos los gradientes para todos los nodos en el gráfico. Esto incluye nodos que representan los pesos de la red neuronal.

• Luego, actualizamos los pesos haciendo W = W - tasa de aprendizaje * gradientes.

• Repetimos este proceso hasta que se cumplan los criterios de parada.

El aprendizaje profundo ha producido buenos resultados para algunas aplicaciones, como visión por computadora, traducción de idiomas, subtítulos de imágenes, transcripción de audio, biología molecular, reconocimiento de voz, procesamiento de lenguaje natural, automóviles sin conductor, detección de tumores cerebrales, traducción de voz en tiempo real, música. composición, juego automático y así sucesivamente.

El aprendizaje profundo es el siguiente gran salto después del aprendizaje automático con una implementación más avanzada. Actualmente, se dirige a convertirse en un estándar de la industria, lo que brinda una fuerte promesa de cambiar las reglas del juego cuando se trata de datos no estructurados sin procesar.

El aprendizaje profundo es actualmente uno de los mejores proveedores de soluciones para una amplia gama de problemas del mundo real. Los desarrolladores están creando programas de inteligencia artificial que, en lugar de usar reglas dadas previamente, aprenden de ejemplos para resolver tareas complicadas. Dado que muchos científicos de datos utilizan el aprendizaje profundo, las redes neuronales más profundas están proporcionando resultados cada vez más precisos.

La idea es desarrollar redes neuronales profundas aumentando el número de capas de entrenamiento para cada red; la máquina aprende más sobre los datos hasta que sean lo más precisos posible. Los desarrolladores pueden utilizar técnicas de aprendizaje profundo para implementar tareas complejas de aprendizaje automático y entrenar redes de IA para que tengan altos niveles de reconocimiento perceptivo.

El aprendizaje profundo encuentra su popularidad en la visión por computadora. Aquí una de las tareas que se logran es la clasificación de imágenes donde las imágenes de entrada dadas se clasifican como gato, perro, etc. o como una clase o etiqueta que mejor describe la imagen. Nosotros, como seres humanos, aprendemos a realizar esta tarea muy temprano en nuestras vidas y tenemos estas habilidades para reconocer patrones rápidamente, generalizar a partir de conocimientos previos y adaptarnos a diferentes entornos de imágenes.

En este capítulo, relacionaremos el aprendizaje profundo con las diferentes bibliotecas y marcos.

Aprendizaje profundo y Theano

Si queremos comenzar a codificar una red neuronal profunda, es mejor que tengamos una idea de cómo funcionan diferentes marcos como Theano, TensorFlow, Keras, PyTorch, etc.

Theano es una biblioteca de Python que proporciona un conjunto de funciones para construir redes profundas que entrenan rápidamente en nuestra máquina.

Theano se desarrolló en la Universidad de Montreal, Canadá, bajo el liderazgo de Yoshua Bengio, un pionero de la red profunda.

Theano nos permite definir y evaluar expresiones matemáticas con vectores y matrices que son matrices rectangulares de números.

Desde el punto de vista técnico, tanto las redes neuronales como los datos de entrada se pueden representar como matrices y todas las operaciones de red estándar se pueden redefinir como operaciones matriciales. Esto es importante ya que las computadoras pueden realizar operaciones matriciales muy rápidamente.

Podemos procesar múltiples valores de matrices en paralelo y si construimos una red neuronal con esta estructura subyacente, podemos usar una sola máquina con una GPU para entrenar redes enormes en un período de tiempo razonable.

Sin embargo, si usamos Theano, tenemos que construir la red profunda desde cero. La biblioteca no proporciona una funcionalidad completa para crear un tipo específico de red profunda.

En cambio, tenemos que codificar todos los aspectos de la red profunda como el modelo, las capas, la activación, el método de entrenamiento y cualquier método especial para detener el sobreajuste.

Sin embargo, la buena noticia es que Theano permite construir nuestra implementación sobre una parte superior de funciones vectorizadas, lo que nos proporciona una solución altamente optimizada.

Hay muchas otras bibliotecas que amplían la funcionalidad de Theano. TensorFlow y Keras se pueden usar con Theano como backend.

Aprendizaje profundo con TensorFlow

Googles TensorFlow es una biblioteca de Python. Esta biblioteca es una excelente opción para crear aplicaciones de aprendizaje profundo de grado comercial.

TensorFlow surgió de otra biblioteca, DistBelief V2, que formaba parte de Google Brain Project. Esta biblioteca tiene como objetivo ampliar la portabilidad del aprendizaje automático para que los modelos de investigación puedan aplicarse a aplicaciones de nivel comercial.

Al igual que la biblioteca Theano, TensorFlow se basa en gráficos computacionales donde un nodo representa datos persistentes u operaciones matemáticas y los bordes representan el flujo de datos entre nodos, que es una matriz o tensor multidimensional; de ahí el nombre TensorFlow

La salida de una operación o un conjunto de operaciones se alimenta como entrada a la siguiente.

Aunque TensorFlow fue diseñado para redes neuronales, funciona bien para otras redes donde la computación se puede modelar como un gráfico de flujo de datos.

TensorFlow también usa varias características de Theano, como eliminación común y de subexpresión, diferenciación automática, variables compartidas y simbólicas.

Se pueden construir diferentes tipos de redes profundas usando TensorFlow como redes convolucionales, codificadores automáticos, RNTN, RNN, RBM, DBM / MLP, etc.

Sin embargo, no hay soporte para la configuración de hiperparámetros en TensorFlow. Para esta funcionalidad, podemos usar Keras.

Aprendizaje profundo y Keras

Keras es una potente biblioteca de Python fácil de usar para desarrollar y evaluar modelos de aprendizaje profundo.

Tiene un diseño minimalista que nos permite construir una red capa a capa; entrenarlo y ejecutarlo.

Envuelve las eficientes bibliotecas de cálculo numérico Theano y TensorFlow y nos permite definir y entrenar modelos de redes neuronales en unas pocas líneas cortas de código.

Es una API de red neuronal de alto nivel que ayuda a hacer un uso amplio del aprendizaje profundo y la inteligencia artificial. Se ejecuta sobre una serie de bibliotecas de nivel inferior, incluidas TensorFlow, Theano, etc. El código de Keras es portátil; podemos implementar una red neuronal en Keras usando Theano o TensorFlow como back-end sin ningún cambio en el código.

En esta implementación de aprendizaje profundo, nuestro objetivo es predecir la pérdida de clientes o los datos agitados para un determinado banco, qué clientes es probable que abandonen este servicio bancario. El conjunto de datos utilizado es relativamente pequeño y contiene 10000 filas con 14 columnas. Estamos utilizando la distribución de Anaconda y marcos como Theano, TensorFlow y Keras. Keras se basa en Tensorflow y Theano, que funcionan como backends.

# Artificial Neural Network
# Installing Theano
pip install --upgrade theano

# Installing Tensorflow
pip install –upgrade tensorflow

# Installing Keras
pip install --upgrade keras

Paso 1: preprocesamiento de datos

In[]:

# Importing the libraries
   import numpy as np
   import matplotlib.pyplot as plt
   import pandas as pd
 
# Importing the database
   dataset = pd.read_csv('Churn_Modelling.csv')

Paso 2

Creamos matrices de las características del conjunto de datos y la variable objetivo, que es la columna 14, etiquetada como "Salido".

El aspecto inicial de los datos es el que se muestra a continuación:

In[]:
X = dataset.iloc[:, 3:13].values
Y = dataset.iloc[:, 13].values
X

Salida

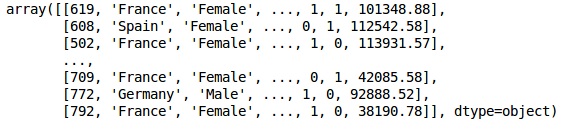
Paso 3

Y

Salida

array([1, 0, 1, ..., 1, 1, 0], dtype = int64)

Etapa 4

Simplificamos el análisis codificando variables de cadena. Estamos usando la función ScikitLearn 'LabelEncoder' para codificar automáticamente las diferentes etiquetas en las columnas con valores entre 0 y n_classes-1.

from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder_X_1 = LabelEncoder() 
X[:,1] = labelencoder_X_1.fit_transform(X[:,1]) 
labelencoder_X_2 = LabelEncoder() 
X[:, 2] = labelencoder_X_2.fit_transform(X[:, 2])
X

Salida

En el resultado anterior, los nombres de los países se reemplazan por 0, 1 y 2; mientras que macho y hembra se reemplazan por 0 y 1.

Paso 5

Labelling Encoded Data

Usamos lo mismo ScikitLearn biblioteca y otra función llamada OneHotEncoder simplemente pasar el número de columna creando una variable ficticia.

onehotencoder = OneHotEncoder(categorical features = [1])
X = onehotencoder.fit_transform(X).toarray()
X = X[:, 1:]
X

Ahora, las dos primeras columnas representan el país y la cuarta columna representa el género.

Salida

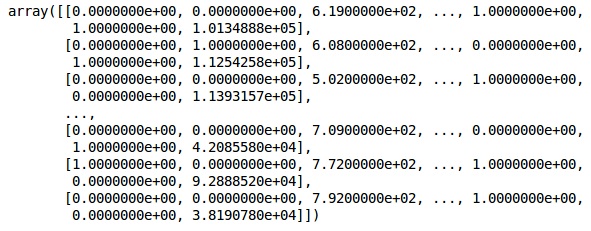
Siempre dividimos nuestros datos en parte de entrenamiento y prueba; entrenamos nuestro modelo en datos de entrenamiento y luego verificamos la precisión de un modelo en datos de prueba que ayudan a evaluar la eficiencia del modelo.

Paso 6

Estamos usando ScikitLearn's train_test_splitfunción para dividir nuestros datos en conjunto de entrenamiento y conjunto de prueba. Mantenemos la relación de división de tren a prueba en 80:20.

#Splitting the dataset into the Training set and the Test Set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)

Algunas variables tienen valores en miles, mientras que otras tienen valores en decenas o unidades. Escalamos los datos para que sean más representativos.

Paso 7

En este código, estamos ajustando y transformando los datos de entrenamiento usando el StandardScalerfunción. Estandarizamos nuestro escalado para que usemos el mismo método ajustado para transformar / escalar datos de prueba.

# Feature Scaling

fromsklearn.preprocessing import StandardScaler 
sc = StandardScaler() 
X_train = sc.fit_transform(X_train) 
X_test = sc.transform(X_test)

Salida

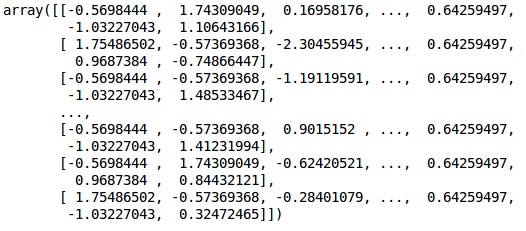
Los datos ahora se escalan correctamente. Finalmente, hemos terminado con nuestro procesamiento previo de datos. Ahora, comenzaremos con nuestro modelo.

Paso 8

Importamos los módulos necesarios aquí. Necesitamos el módulo secuencial para inicializar la red neuronal y el módulo denso para agregar las capas ocultas.

# Importing the Keras libraries and packages 
import keras 
from keras.models import Sequential 
from keras.layers import Dense

Paso 9

Nombraremos el modelo como Clasificador ya que nuestro objetivo es clasificar la rotación de clientes. Luego usamos el módulo Sequential para la inicialización.

#Initializing Neural Network 
classifier = Sequential()

Paso 10

Agregamos las capas ocultas una por una usando la función densa. En el código siguiente, veremos muchos argumentos.

Nuestro primer parámetro es output_dim. Es la cantidad de nodos que agregamos a esta capa.inites la inicialización del estocástico gradiente decente. En una red neuronal asignamos pesos a cada nodo. En la inicialización, los pesos deben estar cerca de cero e inicializamos aleatoriamente los pesos usando la función uniforme. losinput_dimEl parámetro es necesario solo para la primera capa, ya que el modelo no conoce el número de nuestras variables de entrada. Aquí el número total de variables de entrada es 11. En la segunda capa, el modelo conoce automáticamente el número de variables de entrada de la primera capa oculta.

Ejecute la siguiente línea de código para agregar la capa de entrada y la primera capa oculta:

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu', input_dim = 11))

Ejecute la siguiente línea de código para agregar la segunda capa oculta:

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu'))

Ejecute la siguiente línea de código para agregar la capa de salida:

classifier.add(Dense(units = 1, kernel_initializer = 'uniform', 
activation = 'sigmoid'))

Paso 11

Compiling the ANN

Hemos agregado múltiples capas a nuestro clasificador hasta ahora. Ahora los compilaremos usando elcompilemétodo. Los argumentos agregados en el control de compilación final completan la red neuronal, por lo que debemos tener cuidado en este paso.

Aquí hay una breve explicación de los argumentos.

El primer argumento es OptimizerEste es un algoritmo que se utiliza para encontrar el conjunto óptimo de pesos. Este algoritmo se llamaStochastic Gradient Descent (SGD). Aquí estamos usando uno entre varios tipos, llamado 'optimizador de Adam'. El SGD depende de la pérdida, por lo que nuestro segundo parámetro es la pérdida. Si nuestra variable dependiente es binaria, usamos la función de pérdida logarítmica llamada‘binary_crossentropy’, y si nuestra variable dependiente tiene más de dos categorías en la salida, usamos ‘categorical_crossentropy’. Queremos mejorar el rendimiento de nuestra red neuronal basándonos enaccuracy, entonces agregamos metrics como precisión.

# Compiling Neural Network 
classifier.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])

Paso 12

Es necesario ejecutar varios códigos en este paso.

Adaptación de la ANN al conjunto de entrenamiento

Ahora entrenamos nuestro modelo con los datos de entrenamiento. Usamos elfitmétodo para adaptarse a nuestro modelo. También optimizamos los pesos para mejorar la eficiencia del modelo. Para ello, tenemos que actualizar los pesos.Batch size es el número de observaciones después de las cuales actualizamos los pesos. Epoches el número total de iteraciones. Los valores de tamaño de lote y época se eligen mediante el método de prueba y error.

classifier.fit(X_train, y_train, batch_size = 10, epochs = 50)

Hacer predicciones y evaluar el modelo

# Predicting the Test set results
y_pred = classifier.predict(X_test)
y_pred = (y_pred > 0.5)

Predecir una única observación nueva

# Predicting a single new observation
"""Our goal is to predict if the customer with the following data will leave the bank:
Geography: Spain
Credit Score: 500
Gender: Female
Age: 40
Tenure: 3
Balance: 50000
Number of Products: 2
Has Credit Card: Yes
Is Active Member: Yes

Paso 13

Predicting the test set result

El resultado de la predicción le dará la probabilidad de que el cliente deje la empresa. Convertiremos esa probabilidad en 0 y 1 binarios.

# Predicting the Test set results 
y_pred = classifier.predict(X_test) 
y_pred = (y_pred > 0.5)

new_prediction = classifier.predict(sc.transform
(np.array([[0.0, 0, 500, 1, 40, 3, 50000, 2, 1, 1, 40000]])))
new_prediction = (new_prediction > 0.5)

Paso 14

Este es el último paso en el que evaluamos el rendimiento de nuestro modelo. Ya tenemos resultados originales y, por lo tanto, podemos construir una matriz de confusión para verificar la precisión de nuestro modelo.

Making the Confusion Matrix

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
print (cm)

Salida

loss: 0.3384 acc: 0.8605
[ [1541 54]
[230 175] ]

A partir de la matriz de confusión, la precisión de nuestro modelo se puede calcular como:

Accuracy = 1541+175/2000=0.858

We achieved 85.8% accuracy, lo que es bueno.

El algoritmo de propagación hacia adelante

En esta sección, aprenderemos cómo escribir código para realizar la propagación (predicción) hacia adelante para una red neuronal simple:

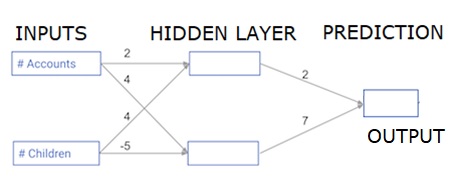
Cada punto de datos es un cliente. La primera entrada es cuántas cuentas tienen y la segunda entrada es cuántos hijos tienen. El modelo predecirá cuántas transacciones realizará el usuario durante el próximo año.

Los datos de entrada se cargan previamente como datos de entrada y los pesos están en un diccionario llamado pesos. La matriz de pesos para el primer nodo en la capa oculta está en pesos ['nodo_0'], y para el segundo nodo en la capa oculta está en pesos ['nodo_1'] respectivamente.

Los pesos que ingresan al nodo de salida están disponibles en pesos.

La función de activación lineal rectificada

Una "función de activación" es una función que trabaja en cada nodo. Transforma la entrada del nodo en alguna salida.

La función de activación lineal rectificada (llamada ReLU ) se usa ampliamente en redes de muy alto rendimiento. Esta función toma un solo número como entrada, devolviendo 0 si la entrada es negativa y entrada como salida si la entrada es positiva.

A continuación se muestran algunos ejemplos:

• relu (4) = 4
• relu (-2) = 0

Completamos la definición de la función relu ()

• Usamos la función max () para calcular el valor de la salida de relu ().
• Aplicamos la función relu () a node_0_input para calcular node_0_output.
• Aplicamos la función relu () a node_1_input para calcular node_1_output.

import numpy as np
input_data = np.array([-1, 2])
weights = {
   'node_0': np.array([3, 3]),
   'node_1': np.array([1, 5]),
   'output': np.array([2, -1])
}
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = np.tanh(node_0_input)
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = np.tanh(node_1_input)
hidden_layer_output = np.array(node_0_output, node_1_output)
output =(hidden_layer_output * weights['output']).sum()
print(output)

def relu(input):
   '''Define your relu activation function here'''
   # Calculate the value for the output of the relu function: output
   output = max(input,0)
      # Return the value just calculated
   return(output)
# Calculate node 0 value: node_0_output
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = relu(node_0_input)

# Calculate node 1 value: node_1_output
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = relu(node_1_input)

# Put node values into array: hidden_layer_outputs
hidden_layer_outputs = np.array([node_0_output, node_1_output])

# Calculate model output (do not apply relu)
odel_output = (hidden_layer_outputs * weights['output']).sum()
print(model_output)# Print model output

Salida

0.9950547536867305
-3

Aplicar la red a muchas observaciones / filas de datos

En esta sección, aprenderemos cómo definir una función llamada predict_with_network (). Esta función generará predicciones para múltiples observaciones de datos, tomadas de la red anterior como input_data. Se están utilizando los pesos dados en la red anterior. También se está utilizando la definición de la función relu ().

Definamos una función llamada predict_with_network () que acepta dos argumentos, input_data_row y weights, y devuelve una predicción de la red como salida.

Calculamos los valores de entrada y salida para cada nodo, almacenándolos como: node_0_input, node_0_output, node_1_input y node_1_output.

Para calcular el valor de entrada de un nodo, multiplicamos las matrices relevantes y calculamos su suma.

Para calcular el valor de salida de un nodo, aplicamos la función relu () al valor de entrada del nodo. Usamos un 'bucle for' para iterar sobre input_data -

También usamos nuestro predict_with_network () para generar predicciones para cada fila de input_data - input_data_row. También adjuntamos cada predicción a los resultados.

# Define predict_with_network()
def predict_with_network(input_data_row, weights):
   # Calculate node 0 value
   node_0_input = (input_data_row * weights['node_0']).sum()
   node_0_output = relu(node_0_input)
   
   # Calculate node 1 value
   node_1_input = (input_data_row * weights['node_1']).sum()
   node_1_output = relu(node_1_input)
   
   # Put node values into array: hidden_layer_outputs
   hidden_layer_outputs = np.array([node_0_output, node_1_output])
   
   # Calculate model output
   input_to_final_layer = (hidden_layer_outputs*weights['output']).sum()
   model_output = relu(input_to_final_layer)
# Return model output
   return(model_output)

# Create empty list to store prediction results
results = []
for input_data_row in input_data:
   # Append prediction to results
   results.append(predict_with_network(input_data_row, weights))
print(results)# Print results

Salida

[0, 12]

Aquí hemos utilizado la función relu donde relu (26) = 26 y relu (-13) = 0 y así sucesivamente.

Redes neuronales profundas de múltiples capas

Aquí estamos escribiendo código para hacer propagación hacia adelante para una red neuronal con dos capas ocultas. Cada capa oculta tiene dos nodos. Los datos de entrada se han precargado comoinput_data. Los nodos de la primera capa oculta se denominan nodo_0_0 y nodo_0_1.

Sus pesos están precargados como pesos ['nodo_0_0'] y pesos ['nodo_0_1'] respectivamente.

Los nodos de la segunda capa oculta se denominan node_1_0 and node_1_1. Sus pesos están precargados comoweights['node_1_0'] y weights['node_1_1'] respectivamente.

Luego creamos una salida de modelo a partir de los nodos ocultos usando pesos precargados como weights['output'].

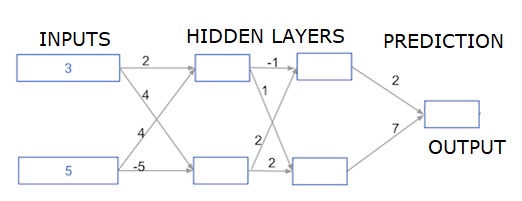
Calculamos node_0_0_input usando sus pesos ponderaciones ['node_0_0'] y los input_data dados. Luego aplique la función relu () para obtener node_0_0_output.

Hacemos lo mismo que el anterior para node_0_1_input para obtener node_0_1_output.

Calculamos node_1_0_input usando sus pesos ponderaciones ['node_1_0'] y las salidas de la primera capa oculta: hidden_0_outputs. Luego aplicamos la función relu () para obtener node_1_0_output.

Hacemos lo mismo que el anterior para node_1_1_input para obtener node_1_1_output.

Calculamos model_output usando pesos ['output'] y los resultados de la segunda capa oculta hidden_1_outputs array. No aplicamos la función relu () a esta salida.

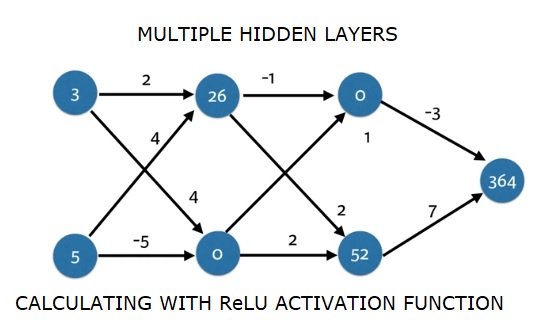
import numpy as np
input_data = np.array([3, 5])
weights = {
   'node_0_0': np.array([2, 4]),
   'node_0_1': np.array([4, -5]),
   'node_1_0': np.array([-1, 1]),
   'node_1_1': np.array([2, 2]),
   'output': np.array([2, 7])
}
def predict_with_network(input_data):
   # Calculate node 0 in the first hidden layer
   node_0_0_input = (input_data * weights['node_0_0']).sum()
   node_0_0_output = relu(node_0_0_input)
   
   # Calculate node 1 in the first hidden layer
   node_0_1_input = (input_data*weights['node_0_1']).sum()
   node_0_1_output = relu(node_0_1_input)
   
   # Put node values into array: hidden_0_outputs
   hidden_0_outputs = np.array([node_0_0_output, node_0_1_output])
   
   # Calculate node 0 in the second hidden layer
   node_1_0_input = (hidden_0_outputs*weights['node_1_0']).sum()
   node_1_0_output = relu(node_1_0_input)
   
   # Calculate node 1 in the second hidden layer
   node_1_1_input = (hidden_0_outputs*weights['node_1_1']).sum()
   node_1_1_output = relu(node_1_1_input)
   
   # Put node values into array: hidden_1_outputs
   hidden_1_outputs = np.array([node_1_0_output, node_1_1_output])
   
   # Calculate model output: model_output
   model_output = (hidden_1_outputs*weights['output']).sum()
      # Return model_output
   return(model_output)
output = predict_with_network(input_data)
print(output)

Salida

364