R - Guía rápida
R es un lenguaje de programación y un entorno de software para análisis estadístico, representación gráfica e informes. R fue creado por Ross Ihaka y Robert Gentleman en la Universidad de Auckland, Nueva Zelanda, y actualmente está desarrollado por R Development Core Team.
El núcleo de R es un lenguaje informático interpretado que permite ramificaciones y bucles, así como programación modular utilizando funciones. R permite la integración con los procedimientos escritos en los lenguajes C, C ++, .Net, Python o FORTRAN para mayor eficiencia.
R está disponible gratuitamente bajo la Licencia Pública General GNU, y se proporcionan versiones binarias precompiladas para varios sistemas operativos como Linux, Windows y Mac.
R es software libre distribuido bajo una copia estilo GNU izquierda, y una parte oficial del proyecto GNU llamado GNU S.
Evolución de R
R fue escrito inicialmente por Ross Ihaka y Robert Gentlemanen el Departamento de Estadística de la Universidad de Auckland en Auckland, Nueva Zelanda. R hizo su primera aparición en 1993.
Un gran grupo de personas ha contribuido a R enviando códigos e informes de errores.
Desde mediados de 1997 ha habido un grupo principal (el "Equipo principal de R") que puede modificar el archivo de código fuente de R.
Características de R
Como se indicó anteriormente, R es un lenguaje de programación y un entorno de software para análisis estadístico, representación de gráficos e informes. Las siguientes son las características importantes de R:
R es un lenguaje de programación bien desarrollado, simple y efectivo que incluye condicionales, bucles, funciones recursivas definidas por el usuario e instalaciones de entrada y salida.
R tiene una instalación efectiva de manejo y almacenamiento de datos,
R proporciona un conjunto de operadores para cálculos en matrices, listas, vectores y matrices.
R proporciona una colección amplia, coherente e integrada de herramientas para el análisis de datos.
R proporciona funciones gráficas para el análisis de datos y la visualización, ya sea directamente en la computadora o imprimiendo en los periódicos.
Como conclusión, R es el lenguaje de programación de estadísticas más utilizado en el mundo. Es la elección número uno de los científicos de datos y está respaldada por una comunidad de colaboradores vibrante y talentosa. R se enseña en universidades y se implementa en aplicaciones comerciales de misión crítica. Este tutorial le enseñará a programar en R junto con ejemplos adecuados en pasos simples y sencillos.
Configuración del entorno local
Si todavía está dispuesto a configurar su entorno para R, puede seguir los pasos que se indican a continuación.
Instalación de Windows
Puede descargar la versión del instalador de Windows de R de R-3.2.2 para Windows (32/64 bits) y guardarla en un directorio local.
Como es un instalador de Windows (.exe) con un nombre "R-version-win.exe". Puede simplemente hacer doble clic y ejecutar el instalador aceptando la configuración predeterminada. Si su Windows es una versión de 32 bits, instala la versión de 32 bits. Pero si su Windows es de 64 bits, entonces instala las versiones de 32 y 64 bits.
Después de la instalación, puede ubicar el icono para ejecutar el programa en una estructura de directorio "R \ R3.2.2 \ bin \ i386 \ Rgui.exe" en los archivos de programa de Windows. Al hacer clic en este icono, aparece la R-GUI, que es la consola R para realizar la programación R.
Instalación de Linux
R está disponible como binario para muchas versiones de Linux en la ubicación R Binaries .
Las instrucciones para instalar Linux varían de un sabor a otro. Estos pasos se mencionan en cada tipo de versión de Linux en el enlace mencionado. Sin embargo, si tiene prisa, puede usaryum comando para instalar R de la siguiente manera:
$ yum install REl comando anterior instalará la funcionalidad central de la programación R junto con los paquetes estándar, aún necesita un paquete adicional, luego puede iniciar el indicador R de la siguiente manera:
$ R
R version 3.2.0 (2015-04-16) -- "Full of Ingredients"
Copyright (C) 2015 The R Foundation for Statistical Computing
Platform: x86_64-redhat-linux-gnu (64-bit)
R is free software and comes with ABSOLUTELY NO WARRANTY.
You are welcome to redistribute it under certain conditions.
Type 'license()' or 'licence()' for distribution details.
R is a collaborative project with many contributors.
Type 'contributors()' for more information and
'citation()' on how to cite R or R packages in publications.
Type 'demo()' for some demos, 'help()' for on-line help, or
'help.start()' for an HTML browser interface to help.
Type 'q()' to quit R.
>Ahora puede usar el comando de instalación en el indicador de R para instalar el paquete requerido. Por ejemplo, se instalará el siguiente comandoplotrix paquete que se requiere para gráficos 3D.
> install.packages("plotrix")Como convención, comenzaremos a aprender programación en R escribiendo un "¡Hola, mundo!" programa. Dependiendo de las necesidades, puede programar en el símbolo del sistema de R o puede usar un archivo de script de R para escribir su programa. Revisemos ambos uno por uno.
Símbolo del sistema R
Una vez que tenga la configuración del entorno R, entonces es fácil iniciar su símbolo del sistema de R simplemente escribiendo el siguiente comando en su símbolo del sistema:
$ REsto iniciará el intérprete de R y obtendrá un mensaje> donde puede comenzar a escribir su programa de la siguiente manera:
> myString <- "Hello, World!"
> print ( myString)
[1] "Hello, World!"Aquí la primera declaración define una variable de cadena myString, donde asignamos una cadena "¡Hola, mundo!" y luego la siguiente instrucción print () se usa para imprimir el valor almacenado en la variable myString.
Archivo de script R
Por lo general, hará su programación escribiendo sus programas en archivos de script y luego ejecutará esos scripts en su símbolo del sistema con la ayuda del intérprete de R llamado Rscript. Así que comencemos escribiendo el siguiente código en un archivo de texto llamado test.R como en -
# My first program in R Programming
myString <- "Hello, World!"
print ( myString)Guarde el código anterior en un archivo test.R y ejecútelo en el símbolo del sistema de Linux como se indica a continuación. Incluso si está utilizando Windows u otro sistema, la sintaxis seguirá siendo la misma.
$ Rscript test.RCuando ejecutamos el programa anterior, produce el siguiente resultado.
[1] "Hello, World!"Comentarios
Los comentarios son como texto de ayuda en su programa R y el intérprete los ignora mientras ejecuta su programa real. El comentario único se escribe usando # al principio de la declaración de la siguiente manera:
# My first program in R ProgrammingR no admite comentarios de varias líneas, pero puede realizar un truco que es el siguiente:
if(FALSE) {
"This is a demo for multi-line comments and it should be put inside either a
single OR double quote"
}
myString <- "Hello, World!"
print ( myString)[1] "Hello, World!"Aunque los comentarios anteriores serán ejecutados por el intérprete de R, no interferirán con su programa real. Debe poner dichos comentarios dentro, ya sea entre comillas simples o dobles.
Por lo general, al programar en cualquier lenguaje de programación, debe utilizar varias variables para almacenar información diversa. Las variables no son más que ubicaciones de memoria reservadas para almacenar valores. Esto significa que, cuando crea una variable, reserva algo de espacio en la memoria.
Es posible que desee almacenar información de varios tipos de datos como carácter, carácter ancho, entero, punto flotante, punto flotante doble, booleano, etc. En función del tipo de datos de una variable, el sistema operativo asigna memoria y decide qué se puede almacenar en el memoria reservada.
A diferencia de otros lenguajes de programación como C y java en R, las variables no se declaran como algún tipo de datos. Las variables se asignan con R-Objects y el tipo de datos del objeto R se convierte en el tipo de datos de la variable. Hay muchos tipos de objetos R. Los de uso frecuente son:
- Vectors
- Lists
- Matrices
- Arrays
- Factors
- Marcos de datos
El más simple de estos objetos es el vector objecty hay seis tipos de datos de estos vectores atómicos, también denominados seis clases de vectores. Los otros objetos R se basan en los vectores atómicos.
| Tipo de datos | Ejemplo | Verificar |
|---|---|---|
| Lógico | VERDADERO FALSO |
produce el siguiente resultado: |
| Numérico | 12,3, 5, 999 |
produce el siguiente resultado: |
| Entero | 2L, 34L, 0L |
produce el siguiente resultado: |
| Complejo | 3 + 2i |
produce el siguiente resultado: |
| Personaje | 'a', '"bueno", "VERDADERO", '23 .4' |
produce el siguiente resultado: |
| Crudo | "Hola" se almacena como 48 65 6c 6c 6f |
produce el siguiente resultado: |
En la programación R, los tipos de datos muy básicos son los objetos R llamados vectorsque contienen elementos de diferentes clases como se muestra arriba. Tenga en cuenta que en R el número de clases no se limita solo a los seis tipos anteriores. Por ejemplo, podemos usar muchos vectores atómicos y crear una matriz cuya clase se convertirá en matriz.
Vectores
Cuando desee crear un vector con más de un elemento, debe usar c() función que significa combinar los elementos en un vector.
# Create a vector.
apple <- c('red','green',"yellow")
print(apple)
# Get the class of the vector.
print(class(apple))Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] "red" "green" "yellow"
[1] "character"Liza
Una lista es un objeto R que puede contener muchos tipos diferentes de elementos dentro de ella, como vectores, funciones e incluso otra lista dentro de ella.
# Create a list.
list1 <- list(c(2,5,3),21.3,sin)
# Print the list.
print(list1)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[[1]]
[1] 2 5 3
[[2]]
[1] 21.3
[[3]]
function (x) .Primitive("sin")Matrices
Una matriz es un conjunto de datos rectangulares bidimensionales. Se puede crear usando una entrada de vector a la función matricial.
# Create a matrix.
M = matrix( c('a','a','b','c','b','a'), nrow = 2, ncol = 3, byrow = TRUE)
print(M)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[,1] [,2] [,3]
[1,] "a" "a" "b"
[2,] "c" "b" "a"Matrices
Si bien las matrices se limitan a dos dimensiones, las matrices pueden tener cualquier número de dimensiones. La función de matriz toma un atributo tenue que crea el número requerido de dimensión. En el siguiente ejemplo, creamos una matriz con dos elementos que son matrices de 3x3 cada uno.
# Create an array.
a <- array(c('green','yellow'),dim = c(3,3,2))
print(a)Cuando ejecutamos el código anterior, produce el siguiente resultado:
, , 1
[,1] [,2] [,3]
[1,] "green" "yellow" "green"
[2,] "yellow" "green" "yellow"
[3,] "green" "yellow" "green"
, , 2
[,1] [,2] [,3]
[1,] "yellow" "green" "yellow"
[2,] "green" "yellow" "green"
[3,] "yellow" "green" "yellow"Factores
Los factores son los objetos r que se crean usando un vector. Almacena el vector junto con los valores distintos de los elementos en el vector como etiquetas. Las etiquetas son siempre de caracteres, independientemente de si son numéricas o de caracteres o booleanas, etc. en el vector de entrada. Son útiles en el modelado estadístico.
Los factores se crean utilizando el factor()función. losnlevels funciones da el recuento de niveles.
# Create a vector.
apple_colors <- c('green','green','yellow','red','red','red','green')
# Create a factor object.
factor_apple <- factor(apple_colors)
# Print the factor.
print(factor_apple)
print(nlevels(factor_apple))Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] green green yellow red red red green
Levels: green red yellow
[1] 3Marcos de datos
Los marcos de datos son objetos de datos tabulares. A diferencia de una matriz en un marco de datos, cada columna puede contener diferentes modos de datos. La primera columna puede ser numérica, mientras que la segunda columna puede ser de caracteres y la tercera columna puede ser lógica. Es una lista de vectores de igual longitud.
Los marcos de datos se crean utilizando el data.frame() función.
# Create the data frame.
BMI <- data.frame(
gender = c("Male", "Male","Female"),
height = c(152, 171.5, 165),
weight = c(81,93, 78),
Age = c(42,38,26)
)
print(BMI)Cuando ejecutamos el código anterior, produce el siguiente resultado:
gender height weight Age
1 Male 152.0 81 42
2 Male 171.5 93 38
3 Female 165.0 78 26Una variable nos proporciona un almacenamiento con nombre que nuestros programas pueden manipular. Una variable en R puede almacenar un vector atómico, un grupo de vectores atómicos o una combinación de muchos Robjects. Un nombre de variable válido consta de letras, números y el punto o el subrayado. El nombre de la variable comienza con una letra o el punto no seguido de un número.
| Nombre de la variable | Validez | Razón |
|---|---|---|
| var_name2. | válido | Tiene letras, números, puntos y subrayado. |
| var_name% | Inválido | Tiene el carácter '%'. Solo se permiten puntos (.) Y guiones bajos. |
| 2var_name | inválido | Comienza con un número |
.var_name, var.name |
válido | Puede comenzar con un punto (.) Pero el punto (.) No debe ir seguido de un número. |
| .2var_name | inválido | El punto inicial va seguido de un número que lo invalida. |
| _var_name | inválido | Empieza por _ que no es válido |
Asignación variable
A las variables se les pueden asignar valores usando el operador hacia la izquierda, hacia la derecha e igual a. Los valores de las variables se pueden imprimir usandoprint() o cat()función. loscat() La función combina varios elementos en una salida de impresión continua.
# Assignment using equal operator.
var.1 = c(0,1,2,3)
# Assignment using leftward operator.
var.2 <- c("learn","R")
# Assignment using rightward operator.
c(TRUE,1) -> var.3
print(var.1)
cat ("var.1 is ", var.1 ,"\n")
cat ("var.2 is ", var.2 ,"\n")
cat ("var.3 is ", var.3 ,"\n")Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 0 1 2 3
var.1 is 0 1 2 3
var.2 is learn R
var.3 is 1 1Note- El vector c (VERDADERO, 1) tiene una mezcla de clase lógica y numérica. Entonces, la clase lógica se coacciona a la clase numérica, lo que hace que sea VERDADERO como 1.
Tipo de datos de una variable
En R, una variable en sí no se declara de ningún tipo de datos, sino que obtiene el tipo de datos del objeto R que se le asigna. Entonces, R se llama lenguaje de tipado dinámico, lo que significa que podemos cambiar el tipo de datos de una variable de la misma variable una y otra vez cuando la usamos en un programa.
var_x <- "Hello"
cat("The class of var_x is ",class(var_x),"\n")
var_x <- 34.5
cat(" Now the class of var_x is ",class(var_x),"\n")
var_x <- 27L
cat(" Next the class of var_x becomes ",class(var_x),"\n")Cuando ejecutamos el código anterior, produce el siguiente resultado:
The class of var_x is character
Now the class of var_x is numeric
Next the class of var_x becomes integerEncontrar variables
Para conocer todas las variables disponibles actualmente en el espacio de trabajo usamos el ls()función. Además, la función ls () puede usar patrones para hacer coincidir los nombres de las variables.
print(ls())Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] "my var" "my_new_var" "my_var" "var.1"
[5] "var.2" "var.3" "var.name" "var_name2."
[9] "var_x" "varname"Note - Es una salida de muestra dependiendo de qué variables se declaran en su entorno.
La función ls () puede usar patrones para hacer coincidir los nombres de las variables.
# List the variables starting with the pattern "var".
print(ls(pattern = "var"))Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] "my var" "my_new_var" "my_var" "var.1"
[5] "var.2" "var.3" "var.name" "var_name2."
[9] "var_x" "varname"Las variables que comienzan con dot(.) están ocultos, se pueden listar usando el argumento "all.names = TRUE" para la función ls ().
print(ls(all.name = TRUE))Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] ".cars" ".Random.seed" ".var_name" ".varname" ".varname2"
[6] "my var" "my_new_var" "my_var" "var.1" "var.2"
[11]"var.3" "var.name" "var_name2." "var_x"Borrar variables
Las variables se pueden eliminar utilizando el rm()función. A continuación borramos la variable var.3. Al imprimir se lanza el valor de la variable error.
rm(var.3)
print(var.3)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] "var.3"
Error in print(var.3) : object 'var.3' not foundTodas las variables se pueden eliminar utilizando el rm() y ls() Funcionan juntos.
rm(list = ls())
print(ls())Cuando ejecutamos el código anterior, produce el siguiente resultado:
character(0)Un operador es un símbolo que le dice al compilador que realice manipulaciones matemáticas o lógicas específicas. El lenguaje R es rico en operadores integrados y proporciona los siguientes tipos de operadores.
Tipos de operadores
Tenemos los siguientes tipos de operadores en la programación R:
- Operadores aritméticos
- Operadores relacionales
- Operadores logicos
- Operadores de Asignación
- Operadores varios
Operadores aritméticos
La siguiente tabla muestra los operadores aritméticos compatibles con el lenguaje R. Los operadores actúan sobre cada elemento del vector.
| Operador | Descripción | Ejemplo |
|---|---|---|
| + | Agrega dos vectores |
produce el siguiente resultado: |
| - | Resta el segundo vector del primero |
produce el siguiente resultado: |
| * | Multiplica ambos vectores |
produce el siguiente resultado: |
| / | Divide el primer vector con el segundo |
Cuando ejecutamos el código anterior, produce el siguiente resultado: |
| %% | Dar el resto del primer vector con el segundo |
produce el siguiente resultado: |
| % /% | El resultado de la división del primer vector con el segundo (cociente) |
produce el siguiente resultado: |
| ^ | El primer vector elevado al exponente del segundo vector |
produce el siguiente resultado: |
Operadores relacionales
La siguiente tabla muestra los operadores relacionales compatibles con el lenguaje R. Cada elemento del primer vector se compara con el elemento correspondiente del segundo vector. El resultado de la comparación es un valor booleano.
| Operador | Descripción | Ejemplo |
|---|---|---|
| > | Comprueba si cada elemento del primer vector es mayor que el elemento correspondiente del segundo vector. |
produce el siguiente resultado: |
| < | Comprueba si cada elemento del primer vector es menor que el elemento correspondiente del segundo vector. |
produce el siguiente resultado: |
| == | Comprueba si cada elemento del primer vector es igual al elemento correspondiente del segundo vector. |
produce el siguiente resultado: |
| <= | Comprueba si cada elemento del primer vector es menor o igual que el elemento correspondiente del segundo vector. |
produce el siguiente resultado: |
| > = | Comprueba si cada elemento del primer vector es mayor o igual que el elemento correspondiente del segundo vector. |
produce el siguiente resultado: |
| ! = | Comprueba si cada elemento del primer vector es diferente al elemento correspondiente del segundo vector. |
produce el siguiente resultado: |
Operadores logicos
La siguiente tabla muestra los operadores lógicos compatibles con el lenguaje R. Es aplicable solo a vectores de tipo lógico, numérico o complejo. Todos los números mayores que 1 se consideran valor lógico VERDADERO.
Cada elemento del primer vector se compara con el elemento correspondiente del segundo vector. El resultado de la comparación es un valor booleano.
| Operador | Descripción | Ejemplo |
|---|---|---|
| Y | Se llama operador AND lógico por elementos. Combina cada elemento del primer vector con el elemento correspondiente del segundo vector y da una salida VERDADERA si ambos elementos son VERDADEROS. |
produce el siguiente resultado: |
| | | Se llama operador OR lógico basado en elementos. Combina cada elemento del primer vector con el elemento correspondiente del segundo vector y da una salida VERDADERO si uno de los elementos es VERDADERO. |
produce el siguiente resultado: |
| ! | Se llama operador NOT lógico. Toma cada elemento del vector y da el valor lógico opuesto. |
produce el siguiente resultado: |
El operador lógico && y || considera solo el primer elemento de los vectores y da un vector de un solo elemento como salida.
| Operador | Descripción | Ejemplo |
|---|---|---|
| && | Operador llamado lógico AND. Toma el primer elemento de ambos vectores y da el VERDADERO solo si ambos son VERDADEROS. |
produce el siguiente resultado: |
| || | Operador OR lógico llamado. Toma el primer elemento de ambos vectores y da el VERDADERO si uno de ellos es VERDADERO. |
produce el siguiente resultado: |
Operadores de Asignación
Estos operadores se utilizan para asignar valores a los vectores.
| Operador | Descripción | Ejemplo |
|---|---|---|
| <- o = o << - |
Asignación llamada izquierda |
produce el siguiente resultado: |
| -> o - >> |
Asignación derecha llamada |
produce el siguiente resultado: |
Operadores varios
Estos operadores se utilizan para fines específicos y no para cálculos matemáticos o lógicos generales.
| Operador | Descripción | Ejemplo |
|---|---|---|
| : | Operador de colon. Crea la serie de números en secuencia para un vector. |
produce el siguiente resultado: |
| %en% | Este operador se utiliza para identificar si un elemento pertenece a un vector. |
produce el siguiente resultado: |
| % *% | Este operador se usa para multiplicar una matriz con su transposición. |
produce el siguiente resultado: |
Las estructuras de toma de decisiones requieren que el programador especifique una o más condiciones para ser evaluadas o probadas por el programa, junto con una declaración o declaraciones que se ejecutarán si se determina que la condición es truey, opcionalmente, otras sentencias que se ejecutarán si se determina que la condición es false.
A continuación se muestra la forma general de una estructura de toma de decisiones típica que se encuentra en la mayoría de los lenguajes de programación:
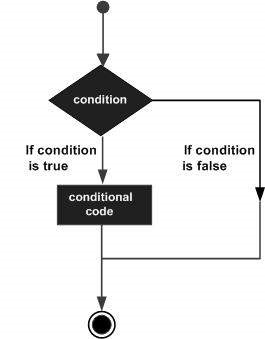
R proporciona los siguientes tipos de declaraciones para la toma de decisiones. Haga clic en los siguientes enlaces para verificar su detalle.
| No Señor. | Declaración y descripción |
|---|---|
| 1 | si declaración Un if declaración consta de una expresión booleana seguida de una o más declaraciones. |
| 2 | declaración if ... else Un if La declaración puede ir seguida de una else declaración, que se ejecuta cuando la expresión booleana es falsa. |
| 3 | declaración de cambio UN switch La declaración permite probar la igualdad de una variable con una lista de valores. |
Puede haber una situación en la que necesite ejecutar un bloque de código varias veces. En general, las declaraciones se ejecutan de forma secuencial. La primera instrucción de una función se ejecuta primero, seguida de la segunda, y así sucesivamente.
Los lenguajes de programación proporcionan varias estructuras de control que permiten rutas de ejecución más complicadas.
Una declaración de bucle nos permite ejecutar una declaración o grupo de declaraciones varias veces y la siguiente es la forma general de una declaración de bucle en la mayoría de los lenguajes de programación:
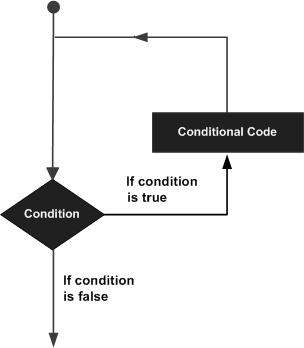
El lenguaje de programación R proporciona los siguientes tipos de bucle para manejar los requisitos de bucle. Haga clic en los siguientes enlaces para verificar su detalle.
| No Señor. | Tipo de bucle y descripción |
|---|---|
| 1 | repetir bucle Ejecuta una secuencia de declaraciones varias veces y abrevia el código que administra la variable de ciclo. |
| 2 | while loop Repite una declaración o un grupo de declaraciones mientras una condición determinada es verdadera. Prueba la condición antes de ejecutar el cuerpo del bucle. |
| 3 | en bucle Como una instrucción while, excepto que prueba la condición al final del cuerpo del bucle. |
Declaraciones de control de bucle
Las sentencias de control de bucle cambian la ejecución de su secuencia normal. Cuando la ejecución abandona un ámbito, todos los objetos automáticos que se crearon en ese ámbito se destruyen.
R admite las siguientes declaraciones de control. Haga clic en los siguientes enlaces para verificar su detalle.
| No Señor. | Declaración de control y descripción |
|---|---|
| 1 | declaración de ruptura Termina el loop instrucción y transfiere la ejecución a la instrucción que sigue inmediatamente al ciclo. |
| 2 | Siguiente declaración los next declaración simula el comportamiento del interruptor R. |
Una función es un conjunto de declaraciones organizadas juntas para realizar una tarea específica. R tiene una gran cantidad de funciones integradas y el usuario puede crear sus propias funciones.
En R, una función es un objeto, por lo que el intérprete de R puede pasar el control a la función, junto con los argumentos que pueden ser necesarios para que la función realice las acciones.
La función, a su vez, realiza su tarea y devuelve el control al intérprete, así como cualquier resultado que pueda almacenarse en otros objetos.
Definición de función
Una función R se crea usando la palabra clave function. La sintaxis básica de la definición de una función R es la siguiente:
function_name <- function(arg_1, arg_2, ...) {
Function body
}Componentes de funciones
Las diferentes partes de una función son:
Function Name- Este es el nombre real de la función. Se almacena en el entorno R como un objeto con este nombre.
Arguments- Un argumento es un marcador de posición. Cuando se invoca una función, se pasa un valor al argumento. Los argumentos son opcionales; es decir, una función puede no contener argumentos. Además, los argumentos pueden tener valores predeterminados.
Function Body - El cuerpo de la función contiene una colección de declaraciones que define lo que hace la función.
Return Value - El valor de retorno de una función es la última expresión en el cuerpo de la función que se evaluará.
R tiene muchos in-builtfunciones que se pueden llamar directamente en el programa sin definirlas primero. También podemos crear y utilizar nuestras propias funciones denominadasuser defined funciones.
Función incorporada
Ejemplos simples de funciones integradas son seq(), mean(), max(), sum(x) y paste(...)etc. Son llamados directamente por programas escritos por el usuario. Puede consultar las funciones R más utilizadas.
# Create a sequence of numbers from 32 to 44.
print(seq(32,44))
# Find mean of numbers from 25 to 82.
print(mean(25:82))
# Find sum of numbers frm 41 to 68.
print(sum(41:68))Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 32 33 34 35 36 37 38 39 40 41 42 43 44
[1] 53.5
[1] 1526Función definida por el usuario
Podemos crear funciones definidas por el usuario en R. Son específicas de lo que quiere un usuario y, una vez creadas, pueden usarse como las funciones integradas. A continuación se muestra un ejemplo de cómo se crea y se usa una función.
# Create a function to print squares of numbers in sequence.
new.function <- function(a) {
for(i in 1:a) {
b <- i^2
print(b)
}
}Llamar a una función
# Create a function to print squares of numbers in sequence.
new.function <- function(a) {
for(i in 1:a) {
b <- i^2
print(b)
}
}
# Call the function new.function supplying 6 as an argument.
new.function(6)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 1
[1] 4
[1] 9
[1] 16
[1] 25
[1] 36Llamar a una función sin un argumento
# Create a function without an argument.
new.function <- function() {
for(i in 1:5) {
print(i^2)
}
}
# Call the function without supplying an argument.
new.function()Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 1
[1] 4
[1] 9
[1] 16
[1] 25Llamar a una función con valores de argumento (por posición y por nombre)
Los argumentos de una llamada de función se pueden proporcionar en la misma secuencia que se define en la función o se pueden proporcionar en una secuencia diferente pero asignados a los nombres de los argumentos.
# Create a function with arguments.
new.function <- function(a,b,c) {
result <- a * b + c
print(result)
}
# Call the function by position of arguments.
new.function(5,3,11)
# Call the function by names of the arguments.
new.function(a = 11, b = 5, c = 3)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 26
[1] 58Llamar a una función con argumento predeterminado
Podemos definir el valor de los argumentos en la definición de la función y llamar a la función sin proporcionar ningún argumento para obtener el resultado predeterminado. Pero también podemos llamar a tales funciones proporcionando nuevos valores del argumento y obteniendo un resultado no predeterminado.
# Create a function with arguments.
new.function <- function(a = 3, b = 6) {
result <- a * b
print(result)
}
# Call the function without giving any argument.
new.function()
# Call the function with giving new values of the argument.
new.function(9,5)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 18
[1] 45Evaluación perezosa de la función
Los argumentos de las funciones se evalúan de forma perezosa, lo que significa que solo se evalúan cuando el cuerpo de la función los necesita.
# Create a function with arguments.
new.function <- function(a, b) {
print(a^2)
print(a)
print(b)
}
# Evaluate the function without supplying one of the arguments.
new.function(6)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 36
[1] 6
Error in print(b) : argument "b" is missing, with no defaultCualquier valor escrito dentro de un par de comillas simples o dobles en R se trata como una cadena. Internamente, R almacena cada cadena entre comillas dobles, incluso cuando las crea con comillas simples.
Reglas aplicadas en la construcción de cadenas
Las comillas al principio y al final de una cadena deben ser comillas dobles o comillas simples. No se pueden mezclar.
Se pueden insertar comillas dobles en una cadena que comience y termine con comillas simples.
Se pueden insertar comillas simples en una cadena que comience y termine con comillas dobles.
No se pueden insertar comillas dobles en una cadena que comience y termine con comillas dobles.
Las comillas simples no se pueden insertar en una cadena que comience y termine con comillas simples.
Ejemplos de cadenas válidas
Los siguientes ejemplos aclaran las reglas sobre la creación de una cadena en R.
a <- 'Start and end with single quote'
print(a)
b <- "Start and end with double quotes"
print(b)
c <- "single quote ' in between double quotes"
print(c)
d <- 'Double quotes " in between single quote'
print(d)Cuando se ejecuta el código anterior, obtenemos el siguiente resultado:
[1] "Start and end with single quote"
[1] "Start and end with double quotes"
[1] "single quote ' in between double quote"
[1] "Double quote \" in between single quote"Ejemplos de cadenas no válidas
e <- 'Mixed quotes"
print(e)
f <- 'Single quote ' inside single quote'
print(f)
g <- "Double quotes " inside double quotes"
print(g)Cuando ejecutamos el script, falla dando los siguientes resultados.
Error: unexpected symbol in:
"print(e)
f <- 'Single"
Execution haltedManipulación de cuerdas
Concatenación de cadenas - función paste ()
Muchas cadenas en R se combinan usando el paste()función. Pueden ser necesarios varios argumentos para combinarlos.
Sintaxis
La sintaxis básica para la función de pegar es:
paste(..., sep = " ", collapse = NULL)A continuación se muestra la descripción de los parámetros utilizados:
... representa cualquier número de argumentos a combinar.
seprepresenta cualquier separador entre los argumentos. Es opcional.
collapsese utiliza para eliminar el espacio entre dos cadenas. Pero no el espacio entre dos palabras de una cadena.
Ejemplo
a <- "Hello"
b <- 'How'
c <- "are you? "
print(paste(a,b,c))
print(paste(a,b,c, sep = "-"))
print(paste(a,b,c, sep = "", collapse = ""))Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] "Hello How are you? "
[1] "Hello-How-are you? "
[1] "HelloHoware you? "Formateo de números y cadenas - función format ()
Los números y las cadenas se pueden formatear a un estilo específico usando format() función.
Sintaxis
La sintaxis básica para la función de formato es:
format(x, digits, nsmall, scientific, width, justify = c("left", "right", "centre", "none"))A continuación se muestra la descripción de los parámetros utilizados:
x es la entrada del vector.
digits es el número total de dígitos mostrados.
nsmall es el número mínimo de dígitos a la derecha del punto decimal.
scientific se establece en TRUE para mostrar la notación científica.
width indica el ancho mínimo que se mostrará rellenando espacios en blanco al principio.
justify es la visualización de la cadena a la izquierda, derecha o centro.
Ejemplo
# Total number of digits displayed. Last digit rounded off.
result <- format(23.123456789, digits = 9)
print(result)
# Display numbers in scientific notation.
result <- format(c(6, 13.14521), scientific = TRUE)
print(result)
# The minimum number of digits to the right of the decimal point.
result <- format(23.47, nsmall = 5)
print(result)
# Format treats everything as a string.
result <- format(6)
print(result)
# Numbers are padded with blank in the beginning for width.
result <- format(13.7, width = 6)
print(result)
# Left justify strings.
result <- format("Hello", width = 8, justify = "l")
print(result)
# Justfy string with center.
result <- format("Hello", width = 8, justify = "c")
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] "23.1234568"
[1] "6.000000e+00" "1.314521e+01"
[1] "23.47000"
[1] "6"
[1] " 13.7"
[1] "Hello "
[1] " Hello "Contando el número de caracteres en una cadena - función nchar ()
Esta función cuenta el número de caracteres incluidos los espacios en una cadena.
Sintaxis
La sintaxis básica de la función nchar () es:
nchar(x)A continuación se muestra la descripción de los parámetros utilizados:
x es la entrada del vector.
Ejemplo
result <- nchar("Count the number of characters")
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 30Cambiar el caso: funciones toupper () y tolower ()
Estas funciones cambian el caso de los caracteres de una cadena.
Sintaxis
La sintaxis básica para la función toupper () y tolower () es -
toupper(x)
tolower(x)A continuación se muestra la descripción de los parámetros utilizados:
x es la entrada del vector.
Ejemplo
# Changing to Upper case.
result <- toupper("Changing To Upper")
print(result)
# Changing to lower case.
result <- tolower("Changing To Lower")
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] "CHANGING TO UPPER"
[1] "changing to lower"Extraer partes de una cadena - función substring ()
Esta función extrae partes de una cadena.
Sintaxis
La sintaxis básica de la función substring () es:
substring(x,first,last)A continuación se muestra la descripción de los parámetros utilizados:
x es la entrada del vector de caracteres.
first es la posición del primer carácter que se va a extraer.
last es la posición del último carácter que se va a extraer.
Ejemplo
# Extract characters from 5th to 7th position.
result <- substring("Extract", 5, 7)
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] "act"Los vectores son los objetos de datos R más básicos y existen seis tipos de vectores atómicos. Son lógicos, enteros, dobles, complejos, de carácter y crudos.
Creación de vectores
Vector de elemento único
Incluso cuando escribe solo un valor en R, se convierte en un vector de longitud 1 y pertenece a uno de los tipos de vectores anteriores.
# Atomic vector of type character.
print("abc");
# Atomic vector of type double.
print(12.5)
# Atomic vector of type integer.
print(63L)
# Atomic vector of type logical.
print(TRUE)
# Atomic vector of type complex.
print(2+3i)
# Atomic vector of type raw.
print(charToRaw('hello'))Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] "abc"
[1] 12.5
[1] 63
[1] TRUE
[1] 2+3i
[1] 68 65 6c 6c 6fVector de elementos múltiples
Using colon operator with numeric data
# Creating a sequence from 5 to 13.
v <- 5:13
print(v)
# Creating a sequence from 6.6 to 12.6.
v <- 6.6:12.6
print(v)
# If the final element specified does not belong to the sequence then it is discarded.
v <- 3.8:11.4
print(v)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 5 6 7 8 9 10 11 12 13
[1] 6.6 7.6 8.6 9.6 10.6 11.6 12.6
[1] 3.8 4.8 5.8 6.8 7.8 8.8 9.8 10.8Using sequence (Seq.) operator
# Create vector with elements from 5 to 9 incrementing by 0.4.
print(seq(5, 9, by = 0.4))Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 5.0 5.4 5.8 6.2 6.6 7.0 7.4 7.8 8.2 8.6 9.0Using the c() function
Los valores que no son caracteres están sujetos al tipo de carácter si uno de los elementos es un carácter.
# The logical and numeric values are converted to characters.
s <- c('apple','red',5,TRUE)
print(s)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] "apple" "red" "5" "TRUE"Acceso a elementos vectoriales
Se accede a los elementos de un vector mediante indexación. los[ ] bracketsse utilizan para indexar. La indexación comienza con la posición 1. Dar un valor negativo en el índice elimina ese elemento del resultado.TRUE, FALSE o 0 y 1 también se puede utilizar para indexar.
# Accessing vector elements using position.
t <- c("Sun","Mon","Tue","Wed","Thurs","Fri","Sat")
u <- t[c(2,3,6)]
print(u)
# Accessing vector elements using logical indexing.
v <- t[c(TRUE,FALSE,FALSE,FALSE,FALSE,TRUE,FALSE)]
print(v)
# Accessing vector elements using negative indexing.
x <- t[c(-2,-5)]
print(x)
# Accessing vector elements using 0/1 indexing.
y <- t[c(0,0,0,0,0,0,1)]
print(y)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] "Mon" "Tue" "Fri"
[1] "Sun" "Fri"
[1] "Sun" "Tue" "Wed" "Fri" "Sat"
[1] "Sun"Manipulación de vectores
Aritmética vectorial
Se pueden sumar, restar, multiplicar o dividir dos vectores de la misma longitud dando el resultado como una salida vectorial.
# Create two vectors.
v1 <- c(3,8,4,5,0,11)
v2 <- c(4,11,0,8,1,2)
# Vector addition.
add.result <- v1+v2
print(add.result)
# Vector subtraction.
sub.result <- v1-v2
print(sub.result)
# Vector multiplication.
multi.result <- v1*v2
print(multi.result)
# Vector division.
divi.result <- v1/v2
print(divi.result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 7 19 4 13 1 13
[1] -1 -3 4 -3 -1 9
[1] 12 88 0 40 0 22
[1] 0.7500000 0.7272727 Inf 0.6250000 0.0000000 5.5000000Reciclaje de elementos vectoriales
Si aplicamos operaciones aritméticas a dos vectores de longitud desigual, entonces los elementos del vector más corto se reciclan para completar las operaciones.
v1 <- c(3,8,4,5,0,11)
v2 <- c(4,11)
# V2 becomes c(4,11,4,11,4,11)
add.result <- v1+v2
print(add.result)
sub.result <- v1-v2
print(sub.result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 7 19 8 16 4 22
[1] -1 -3 0 -6 -4 0Clasificación de elementos vectoriales
Los elementos en un vector se pueden ordenar usando el sort() función.
v <- c(3,8,4,5,0,11, -9, 304)
# Sort the elements of the vector.
sort.result <- sort(v)
print(sort.result)
# Sort the elements in the reverse order.
revsort.result <- sort(v, decreasing = TRUE)
print(revsort.result)
# Sorting character vectors.
v <- c("Red","Blue","yellow","violet")
sort.result <- sort(v)
print(sort.result)
# Sorting character vectors in reverse order.
revsort.result <- sort(v, decreasing = TRUE)
print(revsort.result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] -9 0 3 4 5 8 11 304
[1] 304 11 8 5 4 3 0 -9
[1] "Blue" "Red" "violet" "yellow"
[1] "yellow" "violet" "Red" "Blue"Las listas son los objetos R que contienen elementos de diferentes tipos como: números, cadenas, vectores y otra lista dentro. Una lista también puede contener una matriz o una función como sus elementos. La lista se crea usandolist() función.
Crear una lista
A continuación se muestra un ejemplo para crear una lista que contenga cadenas, números, vectores y valores lógicos.
# Create a list containing strings, numbers, vectors and a logical
# values.
list_data <- list("Red", "Green", c(21,32,11), TRUE, 51.23, 119.1)
print(list_data)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[[1]]
[1] "Red"
[[2]]
[1] "Green"
[[3]]
[1] 21 32 11
[[4]]
[1] TRUE
[[5]]
[1] 51.23
[[6]]
[1] 119.1Elementos de la lista de nombres
Los elementos de la lista pueden recibir nombres y se puede acceder a ellos utilizando estos nombres.
# Create a list containing a vector, a matrix and a list.
list_data <- list(c("Jan","Feb","Mar"), matrix(c(3,9,5,1,-2,8), nrow = 2),
list("green",12.3))
# Give names to the elements in the list.
names(list_data) <- c("1st Quarter", "A_Matrix", "A Inner list")
# Show the list.
print(list_data)Cuando ejecutamos el código anterior, produce el siguiente resultado:
$`1st_Quarter` [1] "Jan" "Feb" "Mar" $A_Matrix
[,1] [,2] [,3]
[1,] 3 5 -2
[2,] 9 1 8
$A_Inner_list $A_Inner_list[[1]]
[1] "green"
$A_Inner_list[[2]]
[1] 12.3Acceder a los elementos de la lista
Se puede acceder a los elementos de la lista mediante el índice del elemento en la lista. En el caso de listas con nombre, también se puede acceder utilizando los nombres.
Continuamos usando la lista en el ejemplo anterior:
# Create a list containing a vector, a matrix and a list.
list_data <- list(c("Jan","Feb","Mar"), matrix(c(3,9,5,1,-2,8), nrow = 2),
list("green",12.3))
# Give names to the elements in the list.
names(list_data) <- c("1st Quarter", "A_Matrix", "A Inner list")
# Access the first element of the list.
print(list_data[1])
# Access the thrid element. As it is also a list, all its elements will be printed.
print(list_data[3])
# Access the list element using the name of the element.
print(list_data$A_Matrix)Cuando ejecutamos el código anterior, produce el siguiente resultado:
$`1st_Quarter` [1] "Jan" "Feb" "Mar" $A_Inner_list
$A_Inner_list[[1]] [1] "green" $A_Inner_list[[2]]
[1] 12.3
[,1] [,2] [,3]
[1,] 3 5 -2
[2,] 9 1 8Manipular elementos de lista
Podemos agregar, eliminar y actualizar elementos de la lista como se muestra a continuación. Podemos agregar y eliminar elementos solo al final de una lista. Pero podemos actualizar cualquier elemento.
# Create a list containing a vector, a matrix and a list.
list_data <- list(c("Jan","Feb","Mar"), matrix(c(3,9,5,1,-2,8), nrow = 2),
list("green",12.3))
# Give names to the elements in the list.
names(list_data) <- c("1st Quarter", "A_Matrix", "A Inner list")
# Add element at the end of the list.
list_data[4] <- "New element"
print(list_data[4])
# Remove the last element.
list_data[4] <- NULL
# Print the 4th Element.
print(list_data[4])
# Update the 3rd Element.
list_data[3] <- "updated element"
print(list_data[3])Cuando ejecutamos el código anterior, produce el siguiente resultado:
[[1]]
[1] "New element"
$<NA> NULL $`A Inner list`
[1] "updated element"Fusión de listas
Puede fusionar muchas listas en una lista colocando todas las listas dentro de una función list ().
# Create two lists.
list1 <- list(1,2,3)
list2 <- list("Sun","Mon","Tue")
# Merge the two lists.
merged.list <- c(list1,list2)
# Print the merged list.
print(merged.list)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[[1]]
[1] 1
[[2]]
[1] 2
[[3]]
[1] 3
[[4]]
[1] "Sun"
[[5]]
[1] "Mon"
[[6]]
[1] "Tue"Conversión de lista en vector
Una lista se puede convertir en un vector para que los elementos del vector se puedan usar para una manipulación posterior. Todas las operaciones aritméticas sobre vectores se pueden aplicar después de que la lista se convierta en vectores. Para hacer esta conversión, usamos elunlist()función. Toma la lista como entrada y produce un vector.
# Create lists.
list1 <- list(1:5)
print(list1)
list2 <-list(10:14)
print(list2)
# Convert the lists to vectors.
v1 <- unlist(list1)
v2 <- unlist(list2)
print(v1)
print(v2)
# Now add the vectors
result <- v1+v2
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[[1]]
[1] 1 2 3 4 5
[[1]]
[1] 10 11 12 13 14
[1] 1 2 3 4 5
[1] 10 11 12 13 14
[1] 11 13 15 17 19Las matrices son los objetos R en los que los elementos están dispuestos en un diseño rectangular bidimensional. Contienen elementos de los mismos tipos atómicos. Aunque podemos crear una matriz que contenga solo caracteres o solo valores lógicos, no son de mucha utilidad. Usamos matrices que contienen elementos numéricos para ser usados en cálculos matemáticos.
Se crea una matriz utilizando el matrix() función.
Sintaxis
La sintaxis básica para crear una matriz en R es:
matrix(data, nrow, ncol, byrow, dimnames)A continuación se muestra la descripción de los parámetros utilizados:
data es el vector de entrada que se convierte en los elementos de datos de la matriz.
nrow es el número de filas que se crearán.
ncol es el número de columnas que se crearán.
byrowes una pista lógica. Si es TRUE, los elementos del vector de entrada están ordenados por filas.
dimname son los nombres asignados a las filas y columnas.
Ejemplo
Cree una matriz tomando un vector de números como entrada.
# Elements are arranged sequentially by row.
M <- matrix(c(3:14), nrow = 4, byrow = TRUE)
print(M)
# Elements are arranged sequentially by column.
N <- matrix(c(3:14), nrow = 4, byrow = FALSE)
print(N)
# Define the column and row names.
rownames = c("row1", "row2", "row3", "row4")
colnames = c("col1", "col2", "col3")
P <- matrix(c(3:14), nrow = 4, byrow = TRUE, dimnames = list(rownames, colnames))
print(P)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[,1] [,2] [,3]
[1,] 3 4 5
[2,] 6 7 8
[3,] 9 10 11
[4,] 12 13 14
[,1] [,2] [,3]
[1,] 3 7 11
[2,] 4 8 12
[3,] 5 9 13
[4,] 6 10 14
col1 col2 col3
row1 3 4 5
row2 6 7 8
row3 9 10 11
row4 12 13 14Acceso a elementos de una matriz
Se puede acceder a los elementos de una matriz utilizando el índice de fila y columna del elemento. Consideramos la matriz P anterior para encontrar los elementos específicos a continuación.
# Define the column and row names.
rownames = c("row1", "row2", "row3", "row4")
colnames = c("col1", "col2", "col3")
# Create the matrix.
P <- matrix(c(3:14), nrow = 4, byrow = TRUE, dimnames = list(rownames, colnames))
# Access the element at 3rd column and 1st row.
print(P[1,3])
# Access the element at 2nd column and 4th row.
print(P[4,2])
# Access only the 2nd row.
print(P[2,])
# Access only the 3rd column.
print(P[,3])Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 5
[1] 13
col1 col2 col3
6 7 8
row1 row2 row3 row4
5 8 11 14Cálculos matriciales
Se realizan varias operaciones matemáticas en las matrices utilizando los operadores R. El resultado de la operación también es una matriz.
Las dimensiones (número de filas y columnas) deben ser las mismas para las matrices involucradas en la operación.
Suma y resta de matrices
# Create two 2x3 matrices.
matrix1 <- matrix(c(3, 9, -1, 4, 2, 6), nrow = 2)
print(matrix1)
matrix2 <- matrix(c(5, 2, 0, 9, 3, 4), nrow = 2)
print(matrix2)
# Add the matrices.
result <- matrix1 + matrix2
cat("Result of addition","\n")
print(result)
# Subtract the matrices
result <- matrix1 - matrix2
cat("Result of subtraction","\n")
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[,1] [,2] [,3]
[1,] 3 -1 2
[2,] 9 4 6
[,1] [,2] [,3]
[1,] 5 0 3
[2,] 2 9 4
Result of addition
[,1] [,2] [,3]
[1,] 8 -1 5
[2,] 11 13 10
Result of subtraction
[,1] [,2] [,3]
[1,] -2 -1 -1
[2,] 7 -5 2Multiplicación y división de matrices
# Create two 2x3 matrices.
matrix1 <- matrix(c(3, 9, -1, 4, 2, 6), nrow = 2)
print(matrix1)
matrix2 <- matrix(c(5, 2, 0, 9, 3, 4), nrow = 2)
print(matrix2)
# Multiply the matrices.
result <- matrix1 * matrix2
cat("Result of multiplication","\n")
print(result)
# Divide the matrices
result <- matrix1 / matrix2
cat("Result of division","\n")
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[,1] [,2] [,3]
[1,] 3 -1 2
[2,] 9 4 6
[,1] [,2] [,3]
[1,] 5 0 3
[2,] 2 9 4
Result of multiplication
[,1] [,2] [,3]
[1,] 15 0 6
[2,] 18 36 24
Result of division
[,1] [,2] [,3]
[1,] 0.6 -Inf 0.6666667
[2,] 4.5 0.4444444 1.5000000Las matrices son los objetos de datos R que pueden almacenar datos en más de dos dimensiones. Por ejemplo, si creamos una matriz de dimensión (2, 3, 4), entonces crea 4 matrices rectangulares cada una con 2 filas y 3 columnas. Las matrices solo pueden almacenar tipos de datos.
Una matriz se crea usando el array()función. Toma vectores como entrada y usa los valores en eldim parámetro para crear una matriz.
Ejemplo
El siguiente ejemplo crea una matriz de dos matrices 3x3 cada una con 3 filas y 3 columnas.
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
# Take these vectors as input to the array.
result <- array(c(vector1,vector2),dim = c(3,3,2))
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
, , 1
[,1] [,2] [,3]
[1,] 5 10 13
[2,] 9 11 14
[3,] 3 12 15
, , 2
[,1] [,2] [,3]
[1,] 5 10 13
[2,] 9 11 14
[3,] 3 12 15Nombrar columnas y filas
Podemos dar nombres a las filas, columnas y matrices en la matriz usando el dimnames parámetro.
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
column.names <- c("COL1","COL2","COL3")
row.names <- c("ROW1","ROW2","ROW3")
matrix.names <- c("Matrix1","Matrix2")
# Take these vectors as input to the array.
result <- array(c(vector1,vector2),dim = c(3,3,2),dimnames = list(row.names,column.names,
matrix.names))
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
, , Matrix1
COL1 COL2 COL3
ROW1 5 10 13
ROW2 9 11 14
ROW3 3 12 15
, , Matrix2
COL1 COL2 COL3
ROW1 5 10 13
ROW2 9 11 14
ROW3 3 12 15Acceso a elementos de matriz
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
column.names <- c("COL1","COL2","COL3")
row.names <- c("ROW1","ROW2","ROW3")
matrix.names <- c("Matrix1","Matrix2")
# Take these vectors as input to the array.
result <- array(c(vector1,vector2),dim = c(3,3,2),dimnames = list(row.names,
column.names, matrix.names))
# Print the third row of the second matrix of the array.
print(result[3,,2])
# Print the element in the 1st row and 3rd column of the 1st matrix.
print(result[1,3,1])
# Print the 2nd Matrix.
print(result[,,2])Cuando ejecutamos el código anterior, produce el siguiente resultado:
COL1 COL2 COL3
3 12 15
[1] 13
COL1 COL2 COL3
ROW1 5 10 13
ROW2 9 11 14
ROW3 3 12 15Manipulación de elementos de matriz
Como la matriz está formada por matrices en múltiples dimensiones, las operaciones sobre los elementos de la matriz se realizan accediendo a elementos de las matrices.
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
# Take these vectors as input to the array.
array1 <- array(c(vector1,vector2),dim = c(3,3,2))
# Create two vectors of different lengths.
vector3 <- c(9,1,0)
vector4 <- c(6,0,11,3,14,1,2,6,9)
array2 <- array(c(vector1,vector2),dim = c(3,3,2))
# create matrices from these arrays.
matrix1 <- array1[,,2]
matrix2 <- array2[,,2]
# Add the matrices.
result <- matrix1+matrix2
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[,1] [,2] [,3]
[1,] 10 20 26
[2,] 18 22 28
[3,] 6 24 30Cálculos entre elementos de matriz
Podemos hacer cálculos a través de los elementos en una matriz usando el apply() función.
Sintaxis
apply(x, margin, fun)A continuación se muestra la descripción de los parámetros utilizados:
x es una matriz.
margin es el nombre del conjunto de datos utilizado.
fun es la función que se aplicará a los elementos de la matriz.
Ejemplo
Usamos la función apply () a continuación para calcular la suma de los elementos en las filas de una matriz en todas las matrices.
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
# Take these vectors as input to the array.
new.array <- array(c(vector1,vector2),dim = c(3,3,2))
print(new.array)
# Use apply to calculate the sum of the rows across all the matrices.
result <- apply(new.array, c(1), sum)
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
, , 1
[,1] [,2] [,3]
[1,] 5 10 13
[2,] 9 11 14
[3,] 3 12 15
, , 2
[,1] [,2] [,3]
[1,] 5 10 13
[2,] 9 11 14
[3,] 3 12 15
[1] 56 68 60Los factores son los objetos de datos que se utilizan para categorizar los datos y almacenarlos como niveles. Pueden almacenar tanto cadenas como enteros. Son útiles en las columnas que tienen un número limitado de valores únicos. Como "Masculino," Femenino "y Verdadero, Falso, etc. Son útiles en el análisis de datos para el modelado estadístico.
Los factores se crean utilizando el factor () función tomando un vector como entrada.
Ejemplo
# Create a vector as input.
data <- c("East","West","East","North","North","East","West","West","West","East","North")
print(data)
print(is.factor(data))
# Apply the factor function.
factor_data <- factor(data)
print(factor_data)
print(is.factor(factor_data))Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] "East" "West" "East" "North" "North" "East" "West" "West" "West" "East" "North"
[1] FALSE
[1] East West East North North East West West West East North
Levels: East North West
[1] TRUEFactores en el marco de datos
Al crear cualquier marco de datos con una columna de datos de texto, R trata la columna de texto como datos categóricos y crea factores en ella.
# Create the vectors for data frame.
height <- c(132,151,162,139,166,147,122)
weight <- c(48,49,66,53,67,52,40)
gender <- c("male","male","female","female","male","female","male")
# Create the data frame.
input_data <- data.frame(height,weight,gender)
print(input_data)
# Test if the gender column is a factor.
print(is.factor(input_data$gender)) # Print the gender column so see the levels. print(input_data$gender)Cuando ejecutamos el código anterior, produce el siguiente resultado:
height weight gender
1 132 48 male
2 151 49 male
3 162 66 female
4 139 53 female
5 166 67 male
6 147 52 female
7 122 40 male
[1] TRUE
[1] male male female female male female male
Levels: female maleCambiar el orden de los niveles
El orden de los niveles en un factor se puede cambiar aplicando la función del factor nuevamente con un nuevo orden de los niveles.
data <- c("East","West","East","North","North","East","West",
"West","West","East","North")
# Create the factors
factor_data <- factor(data)
print(factor_data)
# Apply the factor function with required order of the level.
new_order_data <- factor(factor_data,levels = c("East","West","North"))
print(new_order_data)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] East West East North North East West West West East North
Levels: East North West
[1] East West East North North East West West West East North
Levels: East West NorthGeneración de niveles de factor
Podemos generar niveles de factores usando el gl()función. Toma dos enteros como entrada que indica cuántos niveles y cuántas veces cada nivel.
Sintaxis
gl(n, k, labels)A continuación se muestra la descripción de los parámetros utilizados:
n es un número entero que indica el número de niveles.
k es un número entero que indica el número de repeticiones.
labels es un vector de etiquetas para los niveles de factor resultantes.
Ejemplo
v <- gl(3, 4, labels = c("Tampa", "Seattle","Boston"))
print(v)Cuando ejecutamos el código anterior, produce el siguiente resultado:
Tampa Tampa Tampa Tampa Seattle Seattle Seattle Seattle Boston
[10] Boston Boston Boston
Levels: Tampa Seattle BostonUn marco de datos es una tabla o una estructura bidimensional similar a una matriz en la que cada columna contiene valores de una variable y cada fila contiene un conjunto de valores de cada columna.
A continuación se muestran las características de un marco de datos.
- Los nombres de las columnas no deben estar vacíos.
- Los nombres de las filas deben ser únicos.
- Los datos almacenados en un marco de datos pueden ser de tipo numérico, factorial o de carácter.
- Cada columna debe contener el mismo número de elementos de datos.
Crear marco de datos
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Print the data frame.
print(emp.data)Cuando ejecutamos el código anterior, produce el siguiente resultado:
emp_id emp_name salary start_date
1 1 Rick 623.30 2012-01-01
2 2 Dan 515.20 2013-09-23
3 3 Michelle 611.00 2014-11-15
4 4 Ryan 729.00 2014-05-11
5 5 Gary 843.25 2015-03-27Obtenga la estructura del marco de datos
La estructura del marco de datos se puede ver usando str() función.
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Get the structure of the data frame.
str(emp.data)Cuando ejecutamos el código anterior, produce el siguiente resultado:
'data.frame': 5 obs. of 4 variables:
$ emp_id : int 1 2 3 4 5 $ emp_name : chr "Rick" "Dan" "Michelle" "Ryan" ...
$ salary : num 623 515 611 729 843 $ start_date: Date, format: "2012-01-01" "2013-09-23" "2014-11-15" "2014-05-11" ...Resumen de datos en el marco de datos
El resumen estadístico y la naturaleza de los datos se pueden obtener aplicando summary() función.
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Print the summary.
print(summary(emp.data))Cuando ejecutamos el código anterior, produce el siguiente resultado:
emp_id emp_name salary start_date
Min. :1 Length:5 Min. :515.2 Min. :2012-01-01
1st Qu.:2 Class :character 1st Qu.:611.0 1st Qu.:2013-09-23
Median :3 Mode :character Median :623.3 Median :2014-05-11
Mean :3 Mean :664.4 Mean :2014-01-14
3rd Qu.:4 3rd Qu.:729.0 3rd Qu.:2014-11-15
Max. :5 Max. :843.2 Max. :2015-03-27Extraer datos del marco de datos
Extraiga una columna específica de un marco de datos utilizando el nombre de la columna.
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01","2013-09-23","2014-11-15","2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Extract Specific columns.
result <- data.frame(emp.data$emp_name,emp.data$salary)
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
emp.data.emp_name emp.data.salary
1 Rick 623.30
2 Dan 515.20
3 Michelle 611.00
4 Ryan 729.00
5 Gary 843.25Extraiga las dos primeras filas y luego todas las columnas
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Extract first two rows.
result <- emp.data[1:2,]
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
emp_id emp_name salary start_date
1 1 Rick 623.3 2012-01-01
2 2 Dan 515.2 2013-09-23Extraiga la 3ª y 5ª fila con la 2ª y 4ª columna
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Extract 3rd and 5th row with 2nd and 4th column.
result <- emp.data[c(3,5),c(2,4)]
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
emp_name start_date
3 Michelle 2014-11-15
5 Gary 2015-03-27Expandir marco de datos
Un marco de datos se puede expandir agregando columnas y filas.
Añadir columna
Simplemente agregue el vector de columna con un nuevo nombre de columna.
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Add the "dept" coulmn.
emp.data$dept <- c("IT","Operations","IT","HR","Finance")
v <- emp.data
print(v)Cuando ejecutamos el código anterior, produce el siguiente resultado:
emp_id emp_name salary start_date dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 5 Gary 843.25 2015-03-27 FinanceAñadir fila
Para agregar más filas permanentemente a un marco de datos existente, necesitamos traer las nuevas filas en la misma estructura que el marco de datos existente y usar el rbind() función.
En el siguiente ejemplo, creamos un marco de datos con nuevas filas y lo fusionamos con el marco de datos existente para crear el marco de datos final.
# Create the first data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
dept = c("IT","Operations","IT","HR","Finance"),
stringsAsFactors = FALSE
)
# Create the second data frame
emp.newdata <- data.frame(
emp_id = c (6:8),
emp_name = c("Rasmi","Pranab","Tusar"),
salary = c(578.0,722.5,632.8),
start_date = as.Date(c("2013-05-21","2013-07-30","2014-06-17")),
dept = c("IT","Operations","Fianance"),
stringsAsFactors = FALSE
)
# Bind the two data frames.
emp.finaldata <- rbind(emp.data,emp.newdata)
print(emp.finaldata)Cuando ejecutamos el código anterior, produce el siguiente resultado:
emp_id emp_name salary start_date dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 5 Gary 843.25 2015-03-27 Finance
6 6 Rasmi 578.00 2013-05-21 IT
7 7 Pranab 722.50 2013-07-30 Operations
8 8 Tusar 632.80 2014-06-17 FiananceLos paquetes R son una colección de funciones R, código compilado y datos de muestra. Se almacenan en un directorio llamado"library"en el entorno R. De forma predeterminada, R instala un conjunto de paquetes durante la instalación. Se agregan más paquetes más adelante, cuando se necesitan para algún propósito específico. Cuando iniciamos la consola R, solo los paquetes predeterminados están disponibles de forma predeterminada. Otros paquetes que ya están instalados deben cargarse explícitamente para que los utilice el programa R que los va a utilizar.
Todos los paquetes disponibles en lenguaje R se enumeran en Paquetes R.
A continuación se muestra una lista de comandos que se utilizarán para comprobar, verificar y utilizar los paquetes R.
Ver paquetes R disponibles
Obtener ubicaciones de bibliotecas que contienen paquetes R
.libPaths()Cuando ejecutamos el código anterior, produce el siguiente resultado. Puede variar según la configuración local de su PC.
[2] "C:/Program Files/R/R-3.2.2/library"Obtenga la lista de todos los paquetes instalados
library()Cuando ejecutamos el código anterior, produce el siguiente resultado. Puede variar según la configuración local de su PC.
Packages in library ‘C:/Program Files/R/R-3.2.2/library’:
base The R Base Package
boot Bootstrap Functions (Originally by Angelo Canty
for S)
class Functions for Classification
cluster "Finding Groups in Data": Cluster Analysis
Extended Rousseeuw et al.
codetools Code Analysis Tools for R
compiler The R Compiler Package
datasets The R Datasets Package
foreign Read Data Stored by 'Minitab', 'S', 'SAS',
'SPSS', 'Stata', 'Systat', 'Weka', 'dBase', ...
graphics The R Graphics Package
grDevices The R Graphics Devices and Support for Colours
and Fonts
grid The Grid Graphics Package
KernSmooth Functions for Kernel Smoothing Supporting Wand
& Jones (1995)
lattice Trellis Graphics for R
MASS Support Functions and Datasets for Venables and
Ripley's MASS
Matrix Sparse and Dense Matrix Classes and Methods
methods Formal Methods and Classes
mgcv Mixed GAM Computation Vehicle with GCV/AIC/REML
Smoothness Estimation
nlme Linear and Nonlinear Mixed Effects Models
nnet Feed-Forward Neural Networks and Multinomial
Log-Linear Models
parallel Support for Parallel computation in R
rpart Recursive Partitioning and Regression Trees
spatial Functions for Kriging and Point Pattern
Analysis
splines Regression Spline Functions and Classes
stats The R Stats Package
stats4 Statistical Functions using S4 Classes
survival Survival Analysis
tcltk Tcl/Tk Interface
tools Tools for Package Development
utils The R Utils PackageObtenga todos los paquetes cargados actualmente en el entorno R
search()Cuando ejecutamos el código anterior, produce el siguiente resultado. Puede variar según la configuración local de su PC.
[1] ".GlobalEnv" "package:stats" "package:graphics"
[4] "package:grDevices" "package:utils" "package:datasets"
[7] "package:methods" "Autoloads" "package:base"Instalar un paquete nuevo
Hay dos formas de agregar nuevos paquetes R. Uno está instalando directamente desde el directorio CRAN y otro es descargar el paquete a su sistema local e instalarlo manualmente.
Instalar directamente desde CRAN
El siguiente comando obtiene los paquetes directamente de la página web de CRAN e instala el paquete en el entorno R. Es posible que se le solicite que elija un espejo más cercano. Elija el apropiado para su ubicación.
install.packages("Package Name")
# Install the package named "XML".
install.packages("XML")Instalar el paquete manualmente
Vaya al enlace Paquetes R para descargar el paquete necesario. Guarde el paquete como.zip archivo en una ubicación adecuada en el sistema local.
Ahora puede ejecutar el siguiente comando para instalar este paquete en el entorno R.
install.packages(file_name_with_path, repos = NULL, type = "source")
# Install the package named "XML"
install.packages("E:/XML_3.98-1.3.zip", repos = NULL, type = "source")Cargar paquete en la biblioteca
Antes de que se pueda utilizar un paquete en el código, se debe cargar en el entorno actual de R. También debe cargar un paquete que ya esté instalado anteriormente pero que no esté disponible en el entorno actual.
Un paquete se carga usando el siguiente comando:
library("package Name", lib.loc = "path to library")
# Load the package named "XML"
install.packages("E:/XML_3.98-1.3.zip", repos = NULL, type = "source")La remodelación de datos en R consiste en cambiar la forma en que los datos se organizan en filas y columnas. La mayor parte del tiempo, el procesamiento de datos en R se realiza tomando los datos de entrada como un marco de datos. Es fácil extraer datos de las filas y columnas de un marco de datos, pero hay situaciones en las que necesitamos el marco de datos en un formato diferente al formato en el que lo recibimos. R tiene muchas funciones para dividir, fusionar y cambiar las filas a columnas y viceversa en un marco de datos.
Unir columnas y filas en un marco de datos
Podemos unir múltiples vectores para crear un marco de datos usando el cbind()función. También podemos fusionar dos marcos de datos usandorbind() función.
# Create vector objects.
city <- c("Tampa","Seattle","Hartford","Denver")
state <- c("FL","WA","CT","CO")
zipcode <- c(33602,98104,06161,80294)
# Combine above three vectors into one data frame.
addresses <- cbind(city,state,zipcode)
# Print a header.
cat("# # # # The First data frame\n")
# Print the data frame.
print(addresses)
# Create another data frame with similar columns
new.address <- data.frame(
city = c("Lowry","Charlotte"),
state = c("CO","FL"),
zipcode = c("80230","33949"),
stringsAsFactors = FALSE
)
# Print a header.
cat("# # # The Second data frame\n")
# Print the data frame.
print(new.address)
# Combine rows form both the data frames.
all.addresses <- rbind(addresses,new.address)
# Print a header.
cat("# # # The combined data frame\n")
# Print the result.
print(all.addresses)Cuando ejecutamos el código anterior, produce el siguiente resultado:
# # # # The First data frame
city state zipcode
[1,] "Tampa" "FL" "33602"
[2,] "Seattle" "WA" "98104"
[3,] "Hartford" "CT" "6161"
[4,] "Denver" "CO" "80294"
# # # The Second data frame
city state zipcode
1 Lowry CO 80230
2 Charlotte FL 33949
# # # The combined data frame
city state zipcode
1 Tampa FL 33602
2 Seattle WA 98104
3 Hartford CT 6161
4 Denver CO 80294
5 Lowry CO 80230
6 Charlotte FL 33949Fusionar marcos de datos
Podemos fusionar dos marcos de datos usando el merge()función. Los marcos de datos deben tener los mismos nombres de columna en los que ocurre la fusión.
En el siguiente ejemplo, consideramos los conjuntos de datos sobre la diabetes en mujeres indias pima disponibles en los nombres de la biblioteca "MASS". fusionamos los dos conjuntos de datos en función de los valores de la presión arterial ("pb") y el índice de masa corporal ("bmi"). Al elegir estas dos columnas para fusionar, los registros donde los valores de estas dos variables coinciden en ambos conjuntos de datos se combinan para formar un solo marco de datos.
library(MASS)
merged.Pima <- merge(x = Pima.te, y = Pima.tr,
by.x = c("bp", "bmi"),
by.y = c("bp", "bmi")
)
print(merged.Pima)
nrow(merged.Pima)Cuando ejecutamos el código anterior, produce el siguiente resultado:
bp bmi npreg.x glu.x skin.x ped.x age.x type.x npreg.y glu.y skin.y ped.y
1 60 33.8 1 117 23 0.466 27 No 2 125 20 0.088
2 64 29.7 2 75 24 0.370 33 No 2 100 23 0.368
3 64 31.2 5 189 33 0.583 29 Yes 3 158 13 0.295
4 64 33.2 4 117 27 0.230 24 No 1 96 27 0.289
5 66 38.1 3 115 39 0.150 28 No 1 114 36 0.289
6 68 38.5 2 100 25 0.324 26 No 7 129 49 0.439
7 70 27.4 1 116 28 0.204 21 No 0 124 20 0.254
8 70 33.1 4 91 32 0.446 22 No 9 123 44 0.374
9 70 35.4 9 124 33 0.282 34 No 6 134 23 0.542
10 72 25.6 1 157 21 0.123 24 No 4 99 17 0.294
11 72 37.7 5 95 33 0.370 27 No 6 103 32 0.324
12 74 25.9 9 134 33 0.460 81 No 8 126 38 0.162
13 74 25.9 1 95 21 0.673 36 No 8 126 38 0.162
14 78 27.6 5 88 30 0.258 37 No 6 125 31 0.565
15 78 27.6 10 122 31 0.512 45 No 6 125 31 0.565
16 78 39.4 2 112 50 0.175 24 No 4 112 40 0.236
17 88 34.5 1 117 24 0.403 40 Yes 4 127 11 0.598
age.y type.y
1 31 No
2 21 No
3 24 No
4 21 No
5 21 No
6 43 Yes
7 36 Yes
8 40 No
9 29 Yes
10 28 No
11 55 No
12 39 No
13 39 No
14 49 Yes
15 49 Yes
16 38 No
17 28 No
[1] 17Fundición y Fundición
Uno de los aspectos más interesantes de la programación en R es cambiar la forma de los datos en varios pasos para obtener la forma deseada. Las funciones utilizadas para hacer esto se llamanmelt() y cast().
Consideramos el conjunto de datos llamados barcos presentes en la biblioteca llamada "MASS".
library(MASS)
print(ships)Cuando ejecutamos el código anterior, produce el siguiente resultado:
type year period service incidents
1 A 60 60 127 0
2 A 60 75 63 0
3 A 65 60 1095 3
4 A 65 75 1095 4
5 A 70 60 1512 6
.............
.............
8 A 75 75 2244 11
9 B 60 60 44882 39
10 B 60 75 17176 29
11 B 65 60 28609 58
............
............
17 C 60 60 1179 1
18 C 60 75 552 1
19 C 65 60 781 0
............
............Derretir los datos
Ahora fusionamos los datos para organizarlos, convirtiendo todas las columnas que no sean tipo y año en varias filas.
molten.ships <- melt(ships, id = c("type","year"))
print(molten.ships)Cuando ejecutamos el código anterior, produce el siguiente resultado:
type year variable value
1 A 60 period 60
2 A 60 period 75
3 A 65 period 60
4 A 65 period 75
............
............
9 B 60 period 60
10 B 60 period 75
11 B 65 period 60
12 B 65 period 75
13 B 70 period 60
...........
...........
41 A 60 service 127
42 A 60 service 63
43 A 65 service 1095
...........
...........
70 D 70 service 1208
71 D 75 service 0
72 D 75 service 2051
73 E 60 service 45
74 E 60 service 0
75 E 65 service 789
...........
...........
101 C 70 incidents 6
102 C 70 incidents 2
103 C 75 incidents 0
104 C 75 incidents 1
105 D 60 incidents 0
106 D 60 incidents 0
...........
...........Lanza los datos fundidos
Podemos convertir los datos fundidos en una nueva forma donde se crea el agregado de cada tipo de barco para cada año. Se hace usando elcast() función.
recasted.ship <- cast(molten.ships, type+year~variable,sum)
print(recasted.ship)Cuando ejecutamos el código anterior, produce el siguiente resultado:
type year period service incidents
1 A 60 135 190 0
2 A 65 135 2190 7
3 A 70 135 4865 24
4 A 75 135 2244 11
5 B 60 135 62058 68
6 B 65 135 48979 111
7 B 70 135 20163 56
8 B 75 135 7117 18
9 C 60 135 1731 2
10 C 65 135 1457 1
11 C 70 135 2731 8
12 C 75 135 274 1
13 D 60 135 356 0
14 D 65 135 480 0
15 D 70 135 1557 13
16 D 75 135 2051 4
17 E 60 135 45 0
18 E 65 135 1226 14
19 E 70 135 3318 17
20 E 75 135 542 1En R, podemos leer datos de archivos almacenados fuera del entorno R. También podemos escribir datos en archivos que serán almacenados y accesibles por el sistema operativo. R puede leer y escribir en varios formatos de archivo como csv, excel, xml, etc.
En este capítulo, aprenderemos a leer datos de un archivo csv y luego escribir datos en un archivo csv. El archivo debe estar presente en el directorio de trabajo actual para que R pueda leerlo. Por supuesto, también podemos configurar nuestro propio directorio y leer archivos desde allí.
Obtener y configurar el directorio de trabajo
Puede comprobar a qué directorio apunta el espacio de trabajo de R utilizando el getwd()función. También puede configurar un nuevo directorio de trabajo usandosetwd()función.
# Get and print current working directory.
print(getwd())
# Set current working directory.
setwd("/web/com")
# Get and print current working directory.
print(getwd())Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] "/web/com/1441086124_2016"
[1] "/web/com"Este resultado depende de su sistema operativo y su directorio actual donde está trabajando.
Entrada como archivo CSV
El archivo csv es un archivo de texto en el que los valores de las columnas están separados por una coma. Consideremos los siguientes datos presentes en el archivo llamadoinput.csv.
Puede crear este archivo usando el bloc de notas de Windows copiando y pegando estos datos. Guarde el archivo comoinput.csv usando la opción guardar como todos los archivos (*. *) en el bloc de notas.
id,name,salary,start_date,dept
1,Rick,623.3,2012-01-01,IT
2,Dan,515.2,2013-09-23,Operations
3,Michelle,611,2014-11-15,IT
4,Ryan,729,2014-05-11,HR
5,Gary,843.25,2015-03-27,Finance
6,Nina,578,2013-05-21,IT
7,Simon,632.8,2013-07-30,Operations
8,Guru,722.5,2014-06-17,FinanceLeer un archivo CSV
A continuación se muestra un ejemplo sencillo de read.csv() función para leer un archivo CSV disponible en su directorio de trabajo actual -
data <- read.csv("input.csv")
print(data)Cuando ejecutamos el código anterior, produce el siguiente resultado:
id, name, salary, start_date, dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
6 6 Nina 578.00 2013-05-21 IT
7 7 Simon 632.80 2013-07-30 Operations
8 8 Guru 722.50 2014-06-17 FinanceAnalizando el archivo CSV
Por defecto el read.csv()La función da la salida como un marco de datos. Esto se puede comprobar fácilmente de la siguiente manera. También podemos comprobar el número de columnas y filas.
data <- read.csv("input.csv")
print(is.data.frame(data))
print(ncol(data))
print(nrow(data))Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] TRUE
[1] 5
[1] 8Una vez que leemos los datos en un marco de datos, podemos aplicar todas las funciones aplicables a los marcos de datos como se explica en la sección siguiente.
Obtén el salario máximo
# Create a data frame.
data <- read.csv("input.csv")
# Get the max salary from data frame.
sal <- max(data$salary)
print(sal)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 843.25Obtenga los detalles de la persona con salario máximo
Podemos buscar filas que cumplan con criterios de filtro específicos similares a una cláusula where de SQL.
# Create a data frame.
data <- read.csv("input.csv")
# Get the max salary from data frame.
sal <- max(data$salary)
# Get the person detail having max salary.
retval <- subset(data, salary == max(salary))
print(retval)Cuando ejecutamos el código anterior, produce el siguiente resultado:
id name salary start_date dept
5 NA Gary 843.25 2015-03-27 FinanceHaga que todas las personas trabajen en el departamento de TI
# Create a data frame.
data <- read.csv("input.csv")
retval <- subset( data, dept == "IT")
print(retval)Cuando ejecutamos el código anterior, produce el siguiente resultado:
id name salary start_date dept
1 1 Rick 623.3 2012-01-01 IT
3 3 Michelle 611.0 2014-11-15 IT
6 6 Nina 578.0 2013-05-21 ITConsiga las personas del departamento de TI cuyo salario sea superior a 600
# Create a data frame.
data <- read.csv("input.csv")
info <- subset(data, salary > 600 & dept == "IT")
print(info)Cuando ejecutamos el código anterior, produce el siguiente resultado:
id name salary start_date dept
1 1 Rick 623.3 2012-01-01 IT
3 3 Michelle 611.0 2014-11-15 ITObtenga las personas que se unieron a partir de 2014
# Create a data frame.
data <- read.csv("input.csv")
retval <- subset(data, as.Date(start_date) > as.Date("2014-01-01"))
print(retval)Cuando ejecutamos el código anterior, produce el siguiente resultado:
id name salary start_date dept
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
8 8 Guru 722.50 2014-06-17 FinanceEscribir en un archivo CSV
R puede crear un archivo csv a partir de un marco de datos existente. loswrite.csv()La función se utiliza para crear el archivo csv. Este archivo se crea en el directorio de trabajo.
# Create a data frame.
data <- read.csv("input.csv")
retval <- subset(data, as.Date(start_date) > as.Date("2014-01-01"))
# Write filtered data into a new file.
write.csv(retval,"output.csv")
newdata <- read.csv("output.csv")
print(newdata)Cuando ejecutamos el código anterior, produce el siguiente resultado:
X id name salary start_date dept
1 3 3 Michelle 611.00 2014-11-15 IT
2 4 4 Ryan 729.00 2014-05-11 HR
3 5 NA Gary 843.25 2015-03-27 Finance
4 8 8 Guru 722.50 2014-06-17 FinanceAquí la columna X proviene del conjunto de datos newper. Esto se puede eliminar utilizando parámetros adicionales mientras se escribe el archivo.
# Create a data frame.
data <- read.csv("input.csv")
retval <- subset(data, as.Date(start_date) > as.Date("2014-01-01"))
# Write filtered data into a new file.
write.csv(retval,"output.csv", row.names = FALSE)
newdata <- read.csv("output.csv")
print(newdata)Cuando ejecutamos el código anterior, produce el siguiente resultado:
id name salary start_date dept
1 3 Michelle 611.00 2014-11-15 IT
2 4 Ryan 729.00 2014-05-11 HR
3 NA Gary 843.25 2015-03-27 Finance
4 8 Guru 722.50 2014-06-17 FinanceMicrosoft Excel es el programa de hoja de cálculo más utilizado que almacena datos en formato .xls o .xlsx. R puede leer directamente de estos archivos usando algunos paquetes específicos de Excel. Pocos de estos paquetes son: XLConnect, xlsx, gdata, etc. Usaremos el paquete xlsx. R también puede escribir en un archivo de Excel usando este paquete.
Instalar paquete xlsx
Puede utilizar el siguiente comando en la consola de R para instalar el paquete "xlsx". Puede solicitar la instalación de algunos paquetes adicionales de los que depende este paquete. Siga el mismo comando con el nombre del paquete requerido para instalar los paquetes adicionales.
install.packages("xlsx")Verificar y cargar el paquete "xlsx"
Utilice el siguiente comando para verificar y cargar el paquete "xlsx".
# Verify the package is installed.
any(grepl("xlsx",installed.packages()))
# Load the library into R workspace.
library("xlsx")Cuando se ejecuta el script, obtenemos el siguiente resultado.
[1] TRUE
Loading required package: rJava
Loading required package: methods
Loading required package: xlsxjarsEntrada como archivo xlsx
Abra Microsoft Excel. Copie y pegue los siguientes datos en la hoja de trabajo denominada sheet1.
id name salary start_date dept
1 Rick 623.3 1/1/2012 IT
2 Dan 515.2 9/23/2013 Operations
3 Michelle 611 11/15/2014 IT
4 Ryan 729 5/11/2014 HR
5 Gary 43.25 3/27/2015 Finance
6 Nina 578 5/21/2013 IT
7 Simon 632.8 7/30/2013 Operations
8 Guru 722.5 6/17/2014 FinanceTambién copie y pegue los siguientes datos en otra hoja de trabajo y cambie el nombre de esta hoja de trabajo a "ciudad".
name city
Rick Seattle
Dan Tampa
Michelle Chicago
Ryan Seattle
Gary Houston
Nina Boston
Simon Mumbai
Guru DallasGuarde el archivo de Excel como "input.xlsx". Debe guardarlo en el directorio de trabajo actual del espacio de trabajo de R.
Leer el archivo de Excel
El input.xlsx se lee usando el read.xlsx()funciona como se muestra a continuación. El resultado se almacena como un marco de datos en el entorno R.
# Read the first worksheet in the file input.xlsx.
data <- read.xlsx("input.xlsx", sheetIndex = 1)
print(data)Cuando ejecutamos el código anterior, produce el siguiente resultado:
id, name, salary, start_date, dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
6 6 Nina 578.00 2013-05-21 IT
7 7 Simon 632.80 2013-07-30 Operations
8 8 Guru 722.50 2014-06-17 FinanceUn archivo binario es un archivo que contiene información almacenada solo en forma de bits y bytes (0 y 1). No son legibles por humanos, ya que los bytes que contienen se traducen en caracteres y símbolos que contienen muchos otros caracteres no imprimibles. Intentar leer un archivo binario usando cualquier editor de texto mostrará caracteres como Ø y ð.
El archivo binario debe ser leído por programas específicos para que sea utilizable. Por ejemplo, el archivo binario de un programa de Microsoft Word se puede leer en un formato legible por humanos solo mediante el programa de Word. Lo que indica que, además del texto legible por humanos, hay mucha más información como formateo de caracteres y números de página, etc., que también se almacenan junto con caracteres alfanuméricos. Y finalmente un archivo binario es una secuencia continua de bytes. El salto de línea que vemos en un archivo de texto es un carácter que une la primera línea a la siguiente.
A veces, los datos generados por otros programas deben ser procesados por R como un archivo binario. También se requiere R para crear archivos binarios que se pueden compartir con otros programas.
R tiene dos funciones WriteBin() y readBin() para crear y leer archivos binarios.
Sintaxis
writeBin(object, con)
readBin(con, what, n )A continuación se muestra la descripción de los parámetros utilizados:
con es el objeto de conexión para leer o escribir el archivo binario.
object es el archivo binario que se va a escribir.
what es el modo como carácter, entero, etc. que representa los bytes a leer.
n es el número de bytes para leer del archivo binario.
Ejemplo
Consideramos los datos incorporados R "mtcars". Primero creamos un archivo csv a partir de él, lo convertimos en un archivo binario y lo almacenamos como un archivo del sistema operativo. A continuación, leemos este archivo binario creado en R.
Escribir el archivo binario
Leemos el marco de datos "mtcars" como un archivo csv y luego lo escribimos como un archivo binario en el sistema operativo.
# Read the "mtcars" data frame as a csv file and store only the columns
"cyl", "am" and "gear".
write.table(mtcars, file = "mtcars.csv",row.names = FALSE, na = "",
col.names = TRUE, sep = ",")
# Store 5 records from the csv file as a new data frame.
new.mtcars <- read.table("mtcars.csv",sep = ",",header = TRUE,nrows = 5)
# Create a connection object to write the binary file using mode "wb".
write.filename = file("/web/com/binmtcars.dat", "wb")
# Write the column names of the data frame to the connection object.
writeBin(colnames(new.mtcars), write.filename)
# Write the records in each of the column to the file.
writeBin(c(new.mtcars$cyl,new.mtcars$am,new.mtcars$gear), write.filename)
# Close the file for writing so that it can be read by other program.
close(write.filename)Leyendo el archivo binario
El archivo binario creado anteriormente almacena todos los datos como bytes continuos. Entonces lo leeremos eligiendo los valores apropiados de los nombres de las columnas, así como los valores de las columnas.
# Create a connection object to read the file in binary mode using "rb".
read.filename <- file("/web/com/binmtcars.dat", "rb")
# First read the column names. n = 3 as we have 3 columns.
column.names <- readBin(read.filename, character(), n = 3)
# Next read the column values. n = 18 as we have 3 column names and 15 values.
read.filename <- file("/web/com/binmtcars.dat", "rb")
bindata <- readBin(read.filename, integer(), n = 18)
# Print the data.
print(bindata)
# Read the values from 4th byte to 8th byte which represents "cyl".
cyldata = bindata[4:8]
print(cyldata)
# Read the values form 9th byte to 13th byte which represents "am".
amdata = bindata[9:13]
print(amdata)
# Read the values form 9th byte to 13th byte which represents "gear".
geardata = bindata[14:18]
print(geardata)
# Combine all the read values to a dat frame.
finaldata = cbind(cyldata, amdata, geardata)
colnames(finaldata) = column.names
print(finaldata)Cuando ejecutamos el código anterior, produce el siguiente resultado y gráfico:
[1] 7108963 1728081249 7496037 6 6 4
[7] 6 8 1 1 1 0
[13] 0 4 4 4 3 3
[1] 6 6 4 6 8
[1] 1 1 1 0 0
[1] 4 4 4 3 3
cyl am gear
[1,] 6 1 4
[2,] 6 1 4
[3,] 4 1 4
[4,] 6 0 3
[5,] 8 0 3Como podemos ver, recuperamos los datos originales leyendo el archivo binario en R.
XML es un formato de archivo que comparte tanto el formato de archivo como los datos en la World Wide Web, intranets y en otros lugares utilizando texto ASCII estándar. Significa Extensible Markup Language (XML). Al igual que HTML, contiene etiquetas de marcado. Pero a diferencia del HTML donde la etiqueta de marcado describe la estructura de la página, en xml las etiquetas de marcado describen el significado de los datos contenidos en el archivo.
Puede leer un archivo xml en R usando el paquete "XML". Este paquete se puede instalar usando el siguiente comando.
install.packages("XML")Los datos de entrada
Cree un archivo XMl copiando los datos a continuación en un editor de texto como el bloc de notas. Guarde el archivo con un.xml extensión y elegir el tipo de archivo como all files(*.*).
<RECORDS>
<EMPLOYEE>
<ID>1</ID>
<NAME>Rick</NAME>
<SALARY>623.3</SALARY>
<STARTDATE>1/1/2012</STARTDATE>
<DEPT>IT</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>2</ID>
<NAME>Dan</NAME>
<SALARY>515.2</SALARY>
<STARTDATE>9/23/2013</STARTDATE>
<DEPT>Operations</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>3</ID>
<NAME>Michelle</NAME>
<SALARY>611</SALARY>
<STARTDATE>11/15/2014</STARTDATE>
<DEPT>IT</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>4</ID>
<NAME>Ryan</NAME>
<SALARY>729</SALARY>
<STARTDATE>5/11/2014</STARTDATE>
<DEPT>HR</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>5</ID>
<NAME>Gary</NAME>
<SALARY>843.25</SALARY>
<STARTDATE>3/27/2015</STARTDATE>
<DEPT>Finance</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>6</ID>
<NAME>Nina</NAME>
<SALARY>578</SALARY>
<STARTDATE>5/21/2013</STARTDATE>
<DEPT>IT</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>7</ID>
<NAME>Simon</NAME>
<SALARY>632.8</SALARY>
<STARTDATE>7/30/2013</STARTDATE>
<DEPT>Operations</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>8</ID>
<NAME>Guru</NAME>
<SALARY>722.5</SALARY>
<STARTDATE>6/17/2014</STARTDATE>
<DEPT>Finance</DEPT>
</EMPLOYEE>
</RECORDS>Leer archivo XML
R lee el archivo xml usando la función xmlParse(). Se almacena como una lista en R.
# Load the package required to read XML files.
library("XML")
# Also load the other required package.
library("methods")
# Give the input file name to the function.
result <- xmlParse(file = "input.xml")
# Print the result.
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
1
Rick
623.3
1/1/2012
IT
2
Dan
515.2
9/23/2013
Operations
3
Michelle
611
11/15/2014
IT
4
Ryan
729
5/11/2014
HR
5
Gary
843.25
3/27/2015
Finance
6
Nina
578
5/21/2013
IT
7
Simon
632.8
7/30/2013
Operations
8
Guru
722.5
6/17/2014
FinanceObtener el número de nodos presentes en el archivo XML
# Load the packages required to read XML files.
library("XML")
library("methods")
# Give the input file name to the function.
result <- xmlParse(file = "input.xml")
# Exract the root node form the xml file.
rootnode <- xmlRoot(result)
# Find number of nodes in the root.
rootsize <- xmlSize(rootnode)
# Print the result.
print(rootsize)Cuando ejecutamos el código anterior, produce el siguiente resultado:
output
[1] 8Detalles del primer nodo
Veamos el primer registro del archivo analizado. Nos dará una idea de los distintos elementos presentes en el nodo de nivel superior.
# Load the packages required to read XML files.
library("XML")
library("methods")
# Give the input file name to the function.
result <- xmlParse(file = "input.xml")
# Exract the root node form the xml file.
rootnode <- xmlRoot(result)
# Print the result.
print(rootnode[1])Cuando ejecutamos el código anterior, produce el siguiente resultado:
$EMPLOYEE
1
Rick
623.3
1/1/2012
IT
attr(,"class")
[1] "XMLInternalNodeList" "XMLNodeList"Obtener diferentes elementos de un nodo
# Load the packages required to read XML files.
library("XML")
library("methods")
# Give the input file name to the function.
result <- xmlParse(file = "input.xml")
# Exract the root node form the xml file.
rootnode <- xmlRoot(result)
# Get the first element of the first node.
print(rootnode[[1]][[1]])
# Get the fifth element of the first node.
print(rootnode[[1]][[5]])
# Get the second element of the third node.
print(rootnode[[3]][[2]])Cuando ejecutamos el código anterior, produce el siguiente resultado:
1
IT
MichelleXML a marco de datos
Para manejar los datos de manera efectiva en archivos grandes, leemos los datos en el archivo xml como un marco de datos. Luego procese el marco de datos para el análisis de datos.
# Load the packages required to read XML files.
library("XML")
library("methods")
# Convert the input xml file to a data frame.
xmldataframe <- xmlToDataFrame("input.xml")
print(xmldataframe)Cuando ejecutamos el código anterior, produce el siguiente resultado:
ID NAME SALARY STARTDATE DEPT
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
6 6 Nina 578.00 2013-05-21 IT
7 7 Simon 632.80 2013-07-30 Operations
8 8 Guru 722.50 2014-06-17 FinanceComo los datos ahora están disponibles como un marco de datos, podemos usar la función relacionada con el marco de datos para leer y manipular el archivo.
El archivo JSON almacena datos como texto en formato legible por humanos. Json son las siglas de JavaScript Object Notation. R puede leer archivos JSON usando el paquete rjson.
Instalar el paquete rjson
En la consola de R, puede ejecutar el siguiente comando para instalar el paquete rjson.
install.packages("rjson")Los datos de entrada
Cree un archivo JSON copiando los datos a continuación en un editor de texto como el bloc de notas. Guarde el archivo con un.json extensión y elegir el tipo de archivo como all files(*.*).
{
"ID":["1","2","3","4","5","6","7","8" ],
"Name":["Rick","Dan","Michelle","Ryan","Gary","Nina","Simon","Guru" ],
"Salary":["623.3","515.2","611","729","843.25","578","632.8","722.5" ],
"StartDate":[ "1/1/2012","9/23/2013","11/15/2014","5/11/2014","3/27/2015","5/21/2013",
"7/30/2013","6/17/2014"],
"Dept":[ "IT","Operations","IT","HR","Finance","IT","Operations","Finance"]
}Leer el archivo JSON
R lee el archivo JSON usando la función de JSON(). Se almacena como una lista en R.
# Load the package required to read JSON files.
library("rjson")
# Give the input file name to the function.
result <- fromJSON(file = "input.json")
# Print the result.
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
$ID
[1] "1" "2" "3" "4" "5" "6" "7" "8"
$Name [1] "Rick" "Dan" "Michelle" "Ryan" "Gary" "Nina" "Simon" "Guru" $Salary
[1] "623.3" "515.2" "611" "729" "843.25" "578" "632.8" "722.5"
$StartDate [1] "1/1/2012" "9/23/2013" "11/15/2014" "5/11/2014" "3/27/2015" "5/21/2013" "7/30/2013" "6/17/2014" $Dept
[1] "IT" "Operations" "IT" "HR" "Finance" "IT"
"Operations" "Finance"Convertir JSON en un marco de datos
Podemos convertir los datos extraídos arriba en un marco de datos R para un análisis adicional utilizando el as.data.frame() función.
# Load the package required to read JSON files.
library("rjson")
# Give the input file name to the function.
result <- fromJSON(file = "input.json")
# Convert JSON file to a data frame.
json_data_frame <- as.data.frame(result)
print(json_data_frame)Cuando ejecutamos el código anterior, produce el siguiente resultado:
id, name, salary, start_date, dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
6 6 Nina 578.00 2013-05-21 IT
7 7 Simon 632.80 2013-07-30 Operations
8 8 Guru 722.50 2014-06-17 FinanceMuchos sitios web proporcionan datos para el consumo de sus usuarios. Por ejemplo, la Organización Mundial de la Salud (OMS) proporciona informes sobre información médica y de salud en forma de archivos CSV, txt y XML. Con los programas R, podemos extraer mediante programación datos específicos de dichos sitios web. Algunos paquetes en R que se utilizan para eliminar datos de la web son: "RCurl", XML "y" stringr ". Se utilizan para conectarse a las URL, identificar los enlaces necesarios para los archivos y descargarlos en el entorno local.
Instalar paquetes R
Los siguientes paquetes son necesarios para procesar las URL y los enlaces a los archivos. Si no están disponibles en su entorno R, puede instalarlos usando los siguientes comandos.
install.packages("RCurl")
install.packages("XML")
install.packages("stringr")
install.packages("plyr")Los datos de entrada
Visitaremos la URL de datos meteorológicos y descargaremos los archivos CSV usando R para el año 2015.
Ejemplo
Usaremos la función getHTMLLinks()para recopilar las URL de los archivos. Entonces usaremos la funcióndownload.file()para guardar los archivos en el sistema local. Como aplicaremos el mismo código una y otra vez para varios archivos, crearemos una función que se llamará varias veces. Los nombres de archivo se pasan como parámetros en forma de un objeto de lista R a esta función.
# Read the URL.
url <- "http://www.geos.ed.ac.uk/~weather/jcmb_ws/"
# Gather the html links present in the webpage.
links <- getHTMLLinks(url)
# Identify only the links which point to the JCMB 2015 files.
filenames <- links[str_detect(links, "JCMB_2015")]
# Store the file names as a list.
filenames_list <- as.list(filenames)
# Create a function to download the files by passing the URL and filename list.
downloadcsv <- function (mainurl,filename) {
filedetails <- str_c(mainurl,filename)
download.file(filedetails,filename)
}
# Now apply the l_ply function and save the files into the current R working directory.
l_ply(filenames,downloadcsv,mainurl = "http://www.geos.ed.ac.uk/~weather/jcmb_ws/")Verificar la descarga del archivo
Después de ejecutar el código anterior, puede ubicar los siguientes archivos en el directorio de trabajo actual de R.
"JCMB_2015.csv" "JCMB_2015_Apr.csv" "JCMB_2015_Feb.csv" "JCMB_2015_Jan.csv"
"JCMB_2015_Mar.csv"Los datos son Los sistemas de bases de datos relacionales se almacenan en un formato normalizado. Entonces, para llevar a cabo la computación estadística necesitaremos consultas Sql muy avanzadas y complejas. Pero R puede conectarse fácilmente a muchas bases de datos relacionales como MySql, Oracle, servidor Sql, etc. y obtener registros de ellas como un marco de datos. Una vez que los datos están disponibles en el entorno R, se convierten en un conjunto de datos R normal y pueden manipularse o analizarse utilizando todos los potentes paquetes y funciones.
En este tutorial usaremos MySql como nuestra base de datos de referencia para conectarnos a R.
Paquete RMySQL
R tiene un paquete integrado llamado "RMySQL" que proporciona conectividad nativa con la base de datos MySql. Puede instalar este paquete en el entorno R usando el siguiente comando.
install.packages("RMySQL")Conectando R a MySql
Una vez que el paquete está instalado, creamos un objeto de conexión en R para conectarnos a la base de datos. Toma el nombre de usuario, la contraseña, el nombre de la base de datos y el nombre del host como entrada.
# Create a connection Object to MySQL database.
# We will connect to the sampel database named "sakila" that comes with MySql installation.
mysqlconnection = dbConnect(MySQL(), user = 'root', password = '', dbname = 'sakila',
host = 'localhost')
# List the tables available in this database.
dbListTables(mysqlconnection)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] "actor" "actor_info"
[3] "address" "category"
[5] "city" "country"
[7] "customer" "customer_list"
[9] "film" "film_actor"
[11] "film_category" "film_list"
[13] "film_text" "inventory"
[15] "language" "nicer_but_slower_film_list"
[17] "payment" "rental"
[19] "sales_by_film_category" "sales_by_store"
[21] "staff" "staff_list"
[23] "store"Consultar las tablas
Podemos consultar las tablas de la base de datos en MySql usando la función dbSendQuery(). La consulta se ejecuta en MySql y el conjunto de resultados se devuelve usando Rfetch()función. Finalmente se almacena como un marco de datos en R.
# Query the "actor" tables to get all the rows.
result = dbSendQuery(mysqlconnection, "select * from actor")
# Store the result in a R data frame object. n = 5 is used to fetch first 5 rows.
data.frame = fetch(result, n = 5)
print(data.fame)Cuando ejecutamos el código anterior, produce el siguiente resultado:
actor_id first_name last_name last_update
1 1 PENELOPE GUINESS 2006-02-15 04:34:33
2 2 NICK WAHLBERG 2006-02-15 04:34:33
3 3 ED CHASE 2006-02-15 04:34:33
4 4 JENNIFER DAVIS 2006-02-15 04:34:33
5 5 JOHNNY LOLLOBRIGIDA 2006-02-15 04:34:33Consulta con cláusula de filtro
Podemos pasar cualquier consulta de selección válida para obtener el resultado.
result = dbSendQuery(mysqlconnection, "select * from actor where last_name = 'TORN'")
# Fetch all the records(with n = -1) and store it as a data frame.
data.frame = fetch(result, n = -1)
print(data)Cuando ejecutamos el código anterior, produce el siguiente resultado:
actor_id first_name last_name last_update
1 18 DAN TORN 2006-02-15 04:34:33
2 94 KENNETH TORN 2006-02-15 04:34:33
3 102 WALTER TORN 2006-02-15 04:34:33Actualizar filas en las tablas
Podemos actualizar las filas en una tabla Mysql pasando la consulta de actualización a la función dbSendQuery ().
dbSendQuery(mysqlconnection, "update mtcars set disp = 168.5 where hp = 110")Después de ejecutar el código anterior podemos ver la tabla actualizada en el entorno MySql.
Insertar datos en las tablas
dbSendQuery(mysqlconnection,
"insert into mtcars(row_names, mpg, cyl, disp, hp, drat, wt, qsec, vs, am, gear, carb)
values('New Mazda RX4 Wag', 21, 6, 168.5, 110, 3.9, 2.875, 17.02, 0, 1, 4, 4)"
)Después de ejecutar el código anterior, podemos ver la fila insertada en la tabla en el entorno MySql.
Creando tablas en MySql
Podemos crear tablas en MySql usando la función dbWriteTable(). Sobrescribe la tabla si ya existe y toma un marco de datos como entrada.
# Create the connection object to the database where we want to create the table.
mysqlconnection = dbConnect(MySQL(), user = 'root', password = '', dbname = 'sakila',
host = 'localhost')
# Use the R data frame "mtcars" to create the table in MySql.
# All the rows of mtcars are taken inot MySql.
dbWriteTable(mysqlconnection, "mtcars", mtcars[, ], overwrite = TRUE)Después de ejecutar el código anterior, podemos ver la tabla creada en el entorno MySql.
Soltar tablas en MySql
Podemos colocar las tablas en la base de datos MySql pasando la declaración de eliminación de la tabla a dbSendQuery () de la misma manera que la usamos para consultar datos de tablas.
dbSendQuery(mysqlconnection, 'drop table if exists mtcars')Después de ejecutar el código anterior, podemos ver que la tabla se coloca en el entorno MySql.
El lenguaje de programación R tiene numerosas bibliotecas para crear cuadros y gráficos. Un gráfico circular es una representación de valores como porciones de un círculo con diferentes colores. Los cortes están etiquetados y los números correspondientes a cada corte también se representan en el gráfico.
En R, el gráfico circular se crea utilizando el pie()función que toma números positivos como entrada vectorial. Los parámetros adicionales se utilizan para controlar etiquetas, color, título, etc.
Sintaxis
La sintaxis básica para crear un gráfico circular usando la R es:
pie(x, labels, radius, main, col, clockwise)A continuación se muestra la descripción de los parámetros utilizados:
x es un vector que contiene los valores numéricos utilizados en el gráfico circular.
labels se utiliza para dar una descripción a los cortes.
radius indica el radio del círculo del gráfico circular (valor entre -1 y +1).
main indica el título del gráfico.
col indica la paleta de colores.
clockwise es un valor lógico que indica si los cortes se dibujan en sentido horario o antihorario.
Ejemplo
Se crea un gráfico circular muy simple utilizando solo el vector de entrada y las etiquetas. El siguiente script creará y guardará el gráfico circular en el directorio de trabajo actual de R.
# Create data for the graph.
x <- c(21, 62, 10, 53)
labels <- c("London", "New York", "Singapore", "Mumbai")
# Give the chart file a name.
png(file = "city.png")
# Plot the chart.
pie(x,labels)
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
Título y colores del gráfico circular
Podemos expandir las características del gráfico agregando más parámetros a la función. Usaremos el parámetromain para agregar un título al gráfico y otro parámetro es colque hará uso de la paleta de colores del arco iris mientras dibuja el gráfico. La longitud de la paleta debe ser la misma que la cantidad de valores que tenemos para la tabla. Por lo tanto, usamos longitud (x).
Ejemplo
El siguiente script creará y guardará el gráfico circular en el directorio de trabajo actual de R.
# Create data for the graph.
x <- c(21, 62, 10, 53)
labels <- c("London", "New York", "Singapore", "Mumbai")
# Give the chart file a name.
png(file = "city_title_colours.jpg")
# Plot the chart with title and rainbow color pallet.
pie(x, labels, main = "City pie chart", col = rainbow(length(x)))
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
Porcentajes de sector y leyenda del gráfico
Podemos agregar un porcentaje de corte y una leyenda de gráfico creando variables de gráfico adicionales.
# Create data for the graph.
x <- c(21, 62, 10,53)
labels <- c("London","New York","Singapore","Mumbai")
piepercent<- round(100*x/sum(x), 1)
# Give the chart file a name.
png(file = "city_percentage_legends.jpg")
# Plot the chart.
pie(x, labels = piepercent, main = "City pie chart",col = rainbow(length(x)))
legend("topright", c("London","New York","Singapore","Mumbai"), cex = 0.8,
fill = rainbow(length(x)))
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
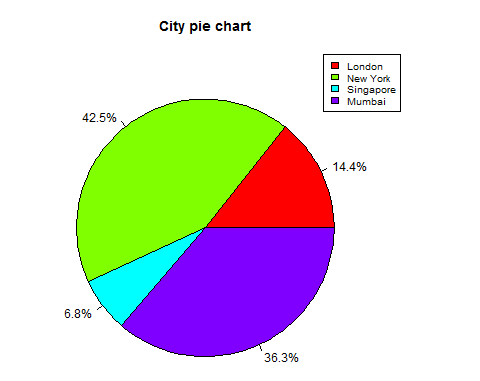
Gráfico circular 3D
Se puede dibujar un gráfico circular con 3 dimensiones utilizando paquetes adicionales. El paqueteplotrix tiene una función llamada pie3D() que se utiliza para esto.
# Get the library.
library(plotrix)
# Create data for the graph.
x <- c(21, 62, 10,53)
lbl <- c("London","New York","Singapore","Mumbai")
# Give the chart file a name.
png(file = "3d_pie_chart.jpg")
# Plot the chart.
pie3D(x,labels = lbl,explode = 0.1, main = "Pie Chart of Countries ")
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
Un gráfico de barras representa datos en barras rectangulares con una longitud de la barra proporcional al valor de la variable. R usa la funciónbarplot()para crear gráficos de barras. R puede dibujar barras verticales y horizontales en el gráfico de barras. En el gráfico de barras, cada una de las barras puede tener diferentes colores.
Sintaxis
La sintaxis básica para crear un gráfico de barras en R es:
barplot(H,xlab,ylab,main, names.arg,col)A continuación se muestra la descripción de los parámetros utilizados:
- H es un vector o matriz que contiene valores numéricos utilizados en un gráfico de barras.
- xlab es la etiqueta del eje x.
- ylab es la etiqueta del eje y.
- main es el título del gráfico de barras.
- names.arg es un vector de nombres que aparecen debajo de cada barra.
- col se utiliza para dar colores a las barras del gráfico.
Ejemplo
Se crea un gráfico de barras simple utilizando solo el vector de entrada y el nombre de cada barra.
El siguiente script creará y guardará el gráfico de barras en el directorio de trabajo actual de R.
# Create the data for the chart
H <- c(7,12,28,3,41)
# Give the chart file a name
png(file = "barchart.png")
# Plot the bar chart
barplot(H)
# Save the file
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
Etiquetas, título y colores del gráfico de barras
Las características del gráfico de barras se pueden expandir agregando más parámetros. losmain el parámetro se usa para agregar title. loscolEl parámetro se usa para agregar colores a las barras. losargs.name es un vector que tiene el mismo número de valores que el vector de entrada para describir el significado de cada barra.
Ejemplo
El siguiente script creará y guardará el gráfico de barras en el directorio de trabajo actual de R.
# Create the data for the chart
H <- c(7,12,28,3,41)
M <- c("Mar","Apr","May","Jun","Jul")
# Give the chart file a name
png(file = "barchart_months_revenue.png")
# Plot the bar chart
barplot(H,names.arg=M,xlab="Month",ylab="Revenue",col="blue",
main="Revenue chart",border="red")
# Save the file
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
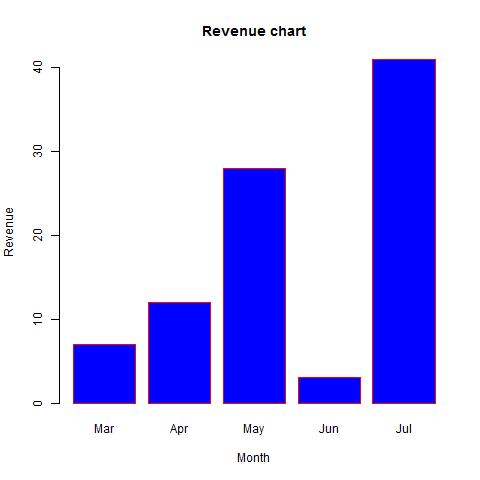
Gráfico de barras de grupo y gráfico de barras apiladas
Podemos crear un gráfico de barras con grupos de barras y pilas en cada barra usando una matriz como valores de entrada.
Más de dos variables se representan como una matriz que se utiliza para crear el gráfico de barras de grupo y el gráfico de barras apiladas.
# Create the input vectors.
colors = c("green","orange","brown")
months <- c("Mar","Apr","May","Jun","Jul")
regions <- c("East","West","North")
# Create the matrix of the values.
Values <- matrix(c(2,9,3,11,9,4,8,7,3,12,5,2,8,10,11), nrow = 3, ncol = 5, byrow = TRUE)
# Give the chart file a name
png(file = "barchart_stacked.png")
# Create the bar chart
barplot(Values, main = "total revenue", names.arg = months, xlab = "month", ylab = "revenue", col = colors)
# Add the legend to the chart
legend("topleft", regions, cex = 1.3, fill = colors)
# Save the file
dev.off()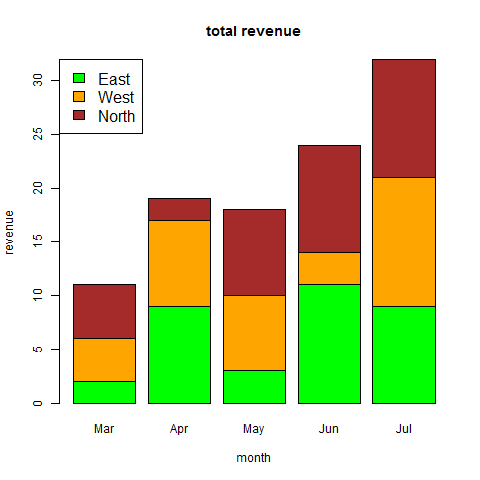
Los diagramas de caja son una medida de qué tan bien distribuidos están los datos en un conjunto de datos. Divide el conjunto de datos en tres cuartiles. Este gráfico representa el mínimo, el máximo, la mediana, el primer cuartil y el tercer cuartil del conjunto de datos. También es útil para comparar la distribución de datos entre conjuntos de datos dibujando diagramas de caja para cada uno de ellos.
Los diagramas de caja se crean en R usando el boxplot() función.
Sintaxis
La sintaxis básica para crear un diagrama de caja en R es:
boxplot(x, data, notch, varwidth, names, main)A continuación se muestra la descripción de los parámetros utilizados:
x es un vector o una fórmula.
data es el marco de datos.
notches un valor lógico. Establecer como VERDADERO para dibujar una muesca.
varwidthes un valor lógico. Establecer como verdadero para dibujar el ancho del cuadro proporcional al tamaño de la muestra.
names son las etiquetas de grupo que se imprimirán debajo de cada diagrama de caja.
main se utiliza para dar un título al gráfico.
Ejemplo
Usamos el conjunto de datos "mtcars" disponible en el entorno R para crear un diagrama de caja básico. Veamos las columnas "mpg" y "cyl" en mtcars.
input <- mtcars[,c('mpg','cyl')]
print(head(input))Cuando ejecutamos el código anterior, produce el siguiente resultado:
mpg cyl
Mazda RX4 21.0 6
Mazda RX4 Wag 21.0 6
Datsun 710 22.8 4
Hornet 4 Drive 21.4 6
Hornet Sportabout 18.7 8
Valiant 18.1 6Crear el diagrama de caja
El siguiente script creará un gráfico de diagrama de caja para la relación entre mpg (millas por galón) y cilindros (número de cilindros).
# Give the chart file a name.
png(file = "boxplot.png")
# Plot the chart.
boxplot(mpg ~ cyl, data = mtcars, xlab = "Number of Cylinders",
ylab = "Miles Per Gallon", main = "Mileage Data")
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
Diagrama de caja con Notch
Podemos dibujar un diagrama de caja con muesca para averiguar cómo las medianas de los diferentes grupos de datos coinciden entre sí.
El siguiente script creará un gráfico de diagrama de caja con muesca para cada uno de los grupos de datos.
# Give the chart file a name.
png(file = "boxplot_with_notch.png")
# Plot the chart.
boxplot(mpg ~ cyl, data = mtcars,
xlab = "Number of Cylinders",
ylab = "Miles Per Gallon",
main = "Mileage Data",
notch = TRUE,
varwidth = TRUE,
col = c("green","yellow","purple"),
names = c("High","Medium","Low")
)
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
Un histograma representa las frecuencias de los valores de una variable agrupados en rangos. El histograma es similar al chat de barra, pero la diferencia es que agrupa los valores en rangos continuos. Cada barra del histograma representa la altura del número de valores presentes en ese rango.
R crea histograma usando hist()función. Esta función toma un vector como entrada y usa algunos parámetros más para trazar histogramas.
Sintaxis
La sintaxis básica para crear un histograma usando R es:
hist(v,main,xlab,xlim,ylim,breaks,col,border)A continuación se muestra la descripción de los parámetros utilizados:
v es un vector que contiene valores numéricos utilizados en histograma.
main indica el título del gráfico.
col se utiliza para establecer el color de las barras.
border se utiliza para establecer el color del borde de cada barra.
xlab se utiliza para dar una descripción del eje x.
xlim se utiliza para especificar el rango de valores en el eje x.
ylim se utiliza para especificar el rango de valores en el eje y.
breaks se utiliza para mencionar el ancho de cada barra.
Ejemplo
Se crea un histograma simple utilizando los parámetros de vector de entrada, etiqueta, col y borde.
El script que se proporciona a continuación creará y guardará el histograma en el directorio de trabajo actual de R.
# Create data for the graph.
v <- c(9,13,21,8,36,22,12,41,31,33,19)
# Give the chart file a name.
png(file = "histogram.png")
# Create the histogram.
hist(v,xlab = "Weight",col = "yellow",border = "blue")
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
Rango de valores X e Y
Para especificar el rango de valores permitidos en el eje X y el eje Y, podemos usar los parámetros xlim e ylim.
El ancho de cada una de las barras se puede decidir utilizando descansos.
# Create data for the graph.
v <- c(9,13,21,8,36,22,12,41,31,33,19)
# Give the chart file a name.
png(file = "histogram_lim_breaks.png")
# Create the histogram.
hist(v,xlab = "Weight",col = "green",border = "red", xlim = c(0,40), ylim = c(0,5),
breaks = 5)
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
Un gráfico de líneas es un gráfico que conecta una serie de puntos dibujando segmentos de línea entre ellos. Estos puntos están ordenados en uno de sus valores de coordenadas (generalmente la coordenada x). Los gráficos de líneas se utilizan generalmente para identificar las tendencias en los datos.
los plot() La función en R se usa para crear el gráfico lineal.
Sintaxis
La sintaxis básica para crear un gráfico de líneas en R es:
plot(v,type,col,xlab,ylab)A continuación se muestra la descripción de los parámetros utilizados:
v es un vector que contiene los valores numéricos.
type toma el valor "p" para dibujar solo los puntos, "l" para dibujar solo las líneas y "o" para dibujar ambos puntos y líneas.
xlab es la etiqueta del eje x.
ylab es la etiqueta del eje y.
main es el título del gráfico.
col se utiliza para dar colores tanto a los puntos como a las líneas.
Ejemplo
Se crea un gráfico de líneas simple utilizando el vector de entrada y el parámetro de tipo como "O". El siguiente script creará y guardará un gráfico de líneas en el directorio de trabajo actual de R.
# Create the data for the chart.
v <- c(7,12,28,3,41)
# Give the chart file a name.
png(file = "line_chart.jpg")
# Plot the bar chart.
plot(v,type = "o")
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
Título, color y etiquetas del gráfico de líneas
Las características del gráfico de líneas se pueden ampliar mediante el uso de parámetros adicionales. Agregamos color a los puntos y líneas, le damos un título al gráfico y agregamos etiquetas a los ejes.
Ejemplo
# Create the data for the chart.
v <- c(7,12,28,3,41)
# Give the chart file a name.
png(file = "line_chart_label_colored.jpg")
# Plot the bar chart.
plot(v,type = "o", col = "red", xlab = "Month", ylab = "Rain fall",
main = "Rain fall chart")
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
Varias líneas en un gráfico de líneas
Se puede dibujar más de una línea en el mismo gráfico usando el lines()función.
Después de trazar la primera línea, la función lines () puede usar un vector adicional como entrada para dibujar la segunda línea en el gráfico,
# Create the data for the chart.
v <- c(7,12,28,3,41)
t <- c(14,7,6,19,3)
# Give the chart file a name.
png(file = "line_chart_2_lines.jpg")
# Plot the bar chart.
plot(v,type = "o",col = "red", xlab = "Month", ylab = "Rain fall",
main = "Rain fall chart")
lines(t, type = "o", col = "blue")
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
Los diagramas de dispersión muestran muchos puntos trazados en el plano cartesiano. Cada punto representa los valores de dos variables. Se elige una variable en el eje horizontal y otra en el eje vertical.
El diagrama de dispersión simple se crea usando el plot() función.
Sintaxis
La sintaxis básica para crear un diagrama de dispersión en R es:
plot(x, y, main, xlab, ylab, xlim, ylim, axes)A continuación se muestra la descripción de los parámetros utilizados:
x es el conjunto de datos cuyos valores son las coordenadas horizontales.
y es el conjunto de datos cuyos valores son las coordenadas verticales.
main es el mosaico del gráfico.
xlab es la etiqueta en el eje horizontal.
ylab es la etiqueta en el eje vertical.
xlim son los límites de los valores de x utilizados para graficar.
ylim son los límites de los valores de y utilizados para graficar.
axes indica si ambos ejes deben dibujarse en el gráfico.
Ejemplo
Usamos el conjunto de datos "mtcars"disponible en el entorno R para crear un diagrama de dispersión básico. Usemos las columnas "wt" y "mpg" en mtcars.
input <- mtcars[,c('wt','mpg')]
print(head(input))Cuando ejecutamos el código anterior, produce el siguiente resultado:
wt mpg
Mazda RX4 2.620 21.0
Mazda RX4 Wag 2.875 21.0
Datsun 710 2.320 22.8
Hornet 4 Drive 3.215 21.4
Hornet Sportabout 3.440 18.7
Valiant 3.460 18.1Crear el diagrama de dispersión
El siguiente script creará un gráfico de dispersión para la relación entre peso (peso) y mpg (millas por galón).
# Get the input values.
input <- mtcars[,c('wt','mpg')]
# Give the chart file a name.
png(file = "scatterplot.png")
# Plot the chart for cars with weight between 2.5 to 5 and mileage between 15 and 30.
plot(x = input$wt,y = input$mpg,
xlab = "Weight",
ylab = "Milage",
xlim = c(2.5,5),
ylim = c(15,30),
main = "Weight vs Milage"
)
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
Matrices de gráficos de dispersión
Cuando tenemos más de dos variables y queremos encontrar la correlación entre una variable y las restantes, usamos la matriz de diagrama de dispersión. Usamospairs() función para crear matrices de diagramas de dispersión.
Sintaxis
La sintaxis básica para crear matrices de diagramas de dispersión en R es:
pairs(formula, data)A continuación se muestra la descripción de los parámetros utilizados:
formula representa la serie de variables utilizadas en pares.
data representa el conjunto de datos del que se tomarán las variables.
Ejemplo
Cada variable se empareja con cada una de las variables restantes. Se traza una gráfica de dispersión para cada par.
# Give the chart file a name.
png(file = "scatterplot_matrices.png")
# Plot the matrices between 4 variables giving 12 plots.
# One variable with 3 others and total 4 variables.
pairs(~wt+mpg+disp+cyl,data = mtcars,
main = "Scatterplot Matrix")
# Save the file.
dev.off()Cuando se ejecuta el código anterior, obtenemos el siguiente resultado.
El análisis estadístico en R se realiza mediante el uso de muchas funciones integradas. La mayoría de estas funciones forman parte del paquete básico de R. Estas funciones toman el vector R como entrada junto con los argumentos y dan el resultado.
Las funciones que discutimos en este capítulo son media, mediana y moda.
Media
Se calcula tomando la suma de los valores y dividiendo por el número de valores en una serie de datos.
La función mean() se utiliza para calcular esto en R.
Sintaxis
La sintaxis básica para calcular la media en R es:
mean(x, trim = 0, na.rm = FALSE, ...)A continuación se muestra la descripción de los parámetros utilizados:
x es el vector de entrada.
trim se utiliza para eliminar algunas observaciones de ambos extremos del vector ordenado.
na.rm se utiliza para eliminar los valores perdidos del vector de entrada.
Ejemplo
# Create a vector.
x <- c(12,7,3,4.2,18,2,54,-21,8,-5)
# Find Mean.
result.mean <- mean(x)
print(result.mean)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 8.22Aplicación de la opción de recorte
Cuando se proporciona el parámetro de recorte, los valores en el vector se ordenan y luego se eliminan los números requeridos de observaciones del cálculo de la media.
Cuando trim = 0.3, 3 valores de cada extremo se eliminarán de los cálculos para encontrar la media.
En este caso, el vector ordenado es (−21, −5, 2, 3, 4.2, 7, 8, 12, 18, 54) y los valores eliminados del vector para calcular la media son (−21, −5,2) desde la izquierda y (12,18,54) desde la derecha.
# Create a vector.
x <- c(12,7,3,4.2,18,2,54,-21,8,-5)
# Find Mean.
result.mean <- mean(x,trim = 0.3)
print(result.mean)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 5.55Aplicación de la opción NA
Si faltan valores, la función media devuelve NA.
Para eliminar los valores faltantes del cálculo, utilice na.rm = TRUE. lo que significa eliminar los valores NA.
# Create a vector.
x <- c(12,7,3,4.2,18,2,54,-21,8,-5,NA)
# Find mean.
result.mean <- mean(x)
print(result.mean)
# Find mean dropping NA values.
result.mean <- mean(x,na.rm = TRUE)
print(result.mean)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] NA
[1] 8.22Mediana
El valor más medio de una serie de datos se llama mediana. losmedian() La función se utiliza en R para calcular este valor.
Sintaxis
La sintaxis básica para calcular la mediana en R es:
median(x, na.rm = FALSE)A continuación se muestra la descripción de los parámetros utilizados:
x es el vector de entrada.
na.rm se utiliza para eliminar los valores perdidos del vector de entrada.
Ejemplo
# Create the vector.
x <- c(12,7,3,4.2,18,2,54,-21,8,-5)
# Find the median.
median.result <- median(x)
print(median.result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 5.6Modo
La moda es el valor que tiene el mayor número de ocurrencias en un conjunto de datos. A diferencia de la media y la mediana, la moda puede tener datos numéricos y de caracteres.
R no tiene una función incorporada estándar para calcular el modo. Entonces creamos una función de usuario para calcular el modo de un conjunto de datos en R. Esta función toma el vector como entrada y da el valor del modo como salida.
Ejemplo
# Create the function.
getmode <- function(v) {
uniqv <- unique(v)
uniqv[which.max(tabulate(match(v, uniqv)))]
}
# Create the vector with numbers.
v <- c(2,1,2,3,1,2,3,4,1,5,5,3,2,3)
# Calculate the mode using the user function.
result <- getmode(v)
print(result)
# Create the vector with characters.
charv <- c("o","it","the","it","it")
# Calculate the mode using the user function.
result <- getmode(charv)
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 2
[1] "it"El análisis de regresión es una herramienta estadística muy utilizada para establecer un modelo de relación entre dos variables. Una de estas variables se llama variable predictora cuyo valor se recopila mediante experimentos. La otra variable se llama variable de respuesta cuyo valor se deriva de la variable predictora.
En la regresión lineal, estas dos variables están relacionadas a través de una ecuación, donde el exponente (potencia) de ambas variables es 1. Matemáticamente, una relación lineal representa una línea recta cuando se traza como un gráfico. Una relación no lineal donde el exponente de cualquier variable no es igual a 1 crea una curva.
La ecuación matemática general para una regresión lineal es:
y = ax + bA continuación se muestra la descripción de los parámetros utilizados:
y es la variable de respuesta.
x es la variable predictora.
a y b son constantes que se llaman coeficientes.
Pasos para establecer una regresión
Un ejemplo simple de regresión es predecir el peso de una persona cuando se conoce su altura. Para hacer esto, necesitamos tener la relación entre la altura y el peso de una persona.
Los pasos para crear la relación son:
Realice el experimento de recolectar una muestra de valores observados de altura y peso correspondiente.
Cree un modelo de relación utilizando el lm() funciones en R.
Encuentre los coeficientes del modelo creado y cree la ecuación matemática usando estos
Obtenga un resumen del modelo de relación para conocer el error promedio en la predicción. También llamadoresiduals.
Para predecir el peso de nuevas personas, utilice el predict() función en R.
Los datos de entrada
A continuación se muestran los datos de muestra que representan las observaciones:
# Values of height
151, 174, 138, 186, 128, 136, 179, 163, 152, 131
# Values of weight.
63, 81, 56, 91, 47, 57, 76, 72, 62, 48Función lm ()
Esta función crea el modelo de relación entre el predictor y la variable de respuesta.
Sintaxis
La sintaxis básica para lm() función en regresión lineal es -
lm(formula,data)A continuación se muestra la descripción de los parámetros utilizados:
formula es un símbolo que presenta la relación entre xey.
data es el vector sobre el que se aplicará la fórmula.
Cree un modelo de relación y obtenga los coeficientes
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
print(relation)Cuando ejecutamos el código anterior, produce el siguiente resultado:
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
-38.4551 0.6746Obtenga el resumen de la relación
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
print(summary(relation))Cuando ejecutamos el código anterior, produce el siguiente resultado:
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-6.3002 -1.6629 0.0412 1.8944 3.9775
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -38.45509 8.04901 -4.778 0.00139 **
x 0.67461 0.05191 12.997 1.16e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.253 on 8 degrees of freedom
Multiple R-squared: 0.9548, Adjusted R-squared: 0.9491
F-statistic: 168.9 on 1 and 8 DF, p-value: 1.164e-06Función predecir ()
Sintaxis
La sintaxis básica de predict () en regresión lineal es:
predict(object, newdata)A continuación se muestra la descripción de los parámetros utilizados:
object es la fórmula que ya se creó con la función lm ().
newdata es el vector que contiene el nuevo valor de la variable predictora.
Predecir el peso de nuevas personas
# The predictor vector.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
# The resposne vector.
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
# Find weight of a person with height 170.
a <- data.frame(x = 170)
result <- predict(relation,a)
print(result)Cuando ejecutamos el código anterior, produce el siguiente resultado:
1
76.22869Visualice la regresión gráficamente
# Create the predictor and response variable.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
relation <- lm(y~x)
# Give the chart file a name.
png(file = "linearregression.png")
# Plot the chart.
plot(y,x,col = "blue",main = "Height & Weight Regression",
abline(lm(x~y)),cex = 1.3,pch = 16,xlab = "Weight in Kg",ylab = "Height in cm")
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
La regresión múltiple es una extensión de la regresión lineal a la relación entre más de dos variables. En la relación lineal simple tenemos un predictor y una variable de respuesta, pero en la regresión múltiple tenemos más de una variable de predicción y una variable de respuesta.
La ecuación matemática general para la regresión múltiple es:
y = a + b1x1 + b2x2 +...bnxnA continuación se muestra la descripción de los parámetros utilizados:
y es la variable de respuesta.
a, b1, b2...bn son los coeficientes.
x1, x2, ...xn son las variables predictoras.
Creamos el modelo de regresión usando el lm()función en R. El modelo determina el valor de los coeficientes utilizando los datos de entrada. A continuación, podemos predecir el valor de la variable de respuesta para un conjunto dado de variables predictoras utilizando estos coeficientes.
Función lm ()
Esta función crea el modelo de relación entre el predictor y la variable de respuesta.
Sintaxis
La sintaxis básica para lm() la función en regresión múltiple es -
lm(y ~ x1+x2+x3...,data)A continuación se muestra la descripción de los parámetros utilizados:
formula es un símbolo que presenta la relación entre la variable de respuesta y las variables predictoras.
data es el vector sobre el que se aplicará la fórmula.
Ejemplo
Los datos de entrada
Considere el conjunto de datos "mtcars" disponible en el entorno R. Ofrece una comparación entre diferentes modelos de automóviles en términos de kilometraje por galón (mpg), cilindrada ("disp"), caballos de fuerza ("hp"), peso del automóvil ("wt") y algunos parámetros más.
El objetivo del modelo es establecer la relación entre "mpg" como variable de respuesta con "disp", "hp" y "wt" como variables predictoras. Creamos un subconjunto de estas variables a partir del conjunto de datos mtcars para este propósito.
input <- mtcars[,c("mpg","disp","hp","wt")]
print(head(input))Cuando ejecutamos el código anterior, produce el siguiente resultado:
mpg disp hp wt
Mazda RX4 21.0 160 110 2.620
Mazda RX4 Wag 21.0 160 110 2.875
Datsun 710 22.8 108 93 2.320
Hornet 4 Drive 21.4 258 110 3.215
Hornet Sportabout 18.7 360 175 3.440
Valiant 18.1 225 105 3.460Cree un modelo de relación y obtenga los coeficientes
input <- mtcars[,c("mpg","disp","hp","wt")]
# Create the relationship model.
model <- lm(mpg~disp+hp+wt, data = input)
# Show the model.
print(model)
# Get the Intercept and coefficients as vector elements.
cat("# # # # The Coefficient Values # # # ","\n")
a <- coef(model)[1]
print(a)
Xdisp <- coef(model)[2]
Xhp <- coef(model)[3]
Xwt <- coef(model)[4]
print(Xdisp)
print(Xhp)
print(Xwt)Cuando ejecutamos el código anterior, produce el siguiente resultado:
Call:
lm(formula = mpg ~ disp + hp + wt, data = input)
Coefficients:
(Intercept) disp hp wt
37.105505 -0.000937 -0.031157 -3.800891
# # # # The Coefficient Values # # #
(Intercept)
37.10551
disp
-0.0009370091
hp
-0.03115655
wt
-3.800891Crear ecuación para modelo de regresión
Basándonos en los valores de intersección y coeficiente anteriores, creamos la ecuación matemática.
Y = a+Xdisp.x1+Xhp.x2+Xwt.x3
or
Y = 37.15+(-0.000937)*x1+(-0.0311)*x2+(-3.8008)*x3Aplicar ecuación para predecir nuevos valores
Podemos utilizar la ecuación de regresión creada anteriormente para predecir el kilometraje cuando se proporciona un nuevo conjunto de valores de desplazamiento, potencia y peso.
Para un automóvil con disp = 221, hp = 102 y wt = 2.91, el kilometraje predicho es -
Y = 37.15+(-0.000937)*221+(-0.0311)*102+(-3.8008)*2.91 = 22.7104La regresión logística es un modelo de regresión en el que la variable de respuesta (variable dependiente) tiene valores categóricos como Verdadero / Falso o 0/1. En realidad, mide la probabilidad de una respuesta binaria como el valor de la variable de respuesta según la ecuación matemática que la relaciona con las variables predictoras.
La ecuación matemática general para la regresión logística es:
y = 1/(1+e^-(a+b1x1+b2x2+b3x3+...))A continuación se muestra la descripción de los parámetros utilizados:
y es la variable de respuesta.
x es la variable predictora.
a y b son los coeficientes que son constantes numéricas.
La función utilizada para crear el modelo de regresión es la glm() función.
Sintaxis
La sintaxis básica para glm() función en la regresión logística es -
glm(formula,data,family)A continuación se muestra la descripción de los parámetros utilizados:
formula es el símbolo que presenta la relación entre las variables.
data es el conjunto de datos que da los valores de estas variables.
familyes un objeto R para especificar los detalles del modelo. Su valor es binomial para la regresión logística.
Ejemplo
El conjunto de datos incorporado "mtcars" describe diferentes modelos de un automóvil con sus diversas especificaciones de motor. En el conjunto de datos "mtcars", el modo de transmisión (automático o manual) se describe mediante la columna am, que es un valor binario (0 o 1). Podemos crear un modelo de regresión logística entre las columnas "am" y otras 3 columnas: hp, wt y cyl.
# Select some columns form mtcars.
input <- mtcars[,c("am","cyl","hp","wt")]
print(head(input))Cuando ejecutamos el código anterior, produce el siguiente resultado:
am cyl hp wt
Mazda RX4 1 6 110 2.620
Mazda RX4 Wag 1 6 110 2.875
Datsun 710 1 4 93 2.320
Hornet 4 Drive 0 6 110 3.215
Hornet Sportabout 0 8 175 3.440
Valiant 0 6 105 3.460Crear modelo de regresión
Usamos el glm() función para crear el modelo de regresión y obtener su resumen para el análisis.
input <- mtcars[,c("am","cyl","hp","wt")]
am.data = glm(formula = am ~ cyl + hp + wt, data = input, family = binomial)
print(summary(am.data))Cuando ejecutamos el código anterior, produce el siguiente resultado:
Call:
glm(formula = am ~ cyl + hp + wt, family = binomial, data = input)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.17272 -0.14907 -0.01464 0.14116 1.27641
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 19.70288 8.11637 2.428 0.0152 *
cyl 0.48760 1.07162 0.455 0.6491
hp 0.03259 0.01886 1.728 0.0840 .
wt -9.14947 4.15332 -2.203 0.0276 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 43.2297 on 31 degrees of freedom
Residual deviance: 9.8415 on 28 degrees of freedom
AIC: 17.841
Number of Fisher Scoring iterations: 8Conclusión
En el resumen, como el valor p en la última columna es más de 0.05 para las variables "cyl" y "hp", las consideramos insignificantes para contribuir al valor de la variable "am". Solo el peso (wt) afecta el valor "am" en este modelo de regresión.
En una recopilación aleatoria de datos de fuentes independientes, generalmente se observa que la distribución de datos es normal. Lo que significa que, al trazar un gráfico con el valor de la variable en el eje horizontal y el recuento de los valores en el eje vertical, obtenemos una curva en forma de campana. El centro de la curva representa la media del conjunto de datos. En el gráfico, el cincuenta por ciento de los valores se encuentra a la izquierda de la media y el otro cincuenta por ciento se encuentra a la derecha del gráfico. Esto se conoce como distribución normal en estadísticas.
R tiene cuatro funciones integradas para generar una distribución normal. Se describen a continuación.
dnorm(x, mean, sd)
pnorm(x, mean, sd)
qnorm(p, mean, sd)
rnorm(n, mean, sd)A continuación se muestra la descripción de los parámetros utilizados en las funciones anteriores:
x es un vector de números.
p es un vector de probabilidades.
n es el número de observaciones (tamaño de la muestra).
meanes el valor medio de los datos de la muestra. Su valor predeterminado es cero.
sdes la desviación estándar. Su valor predeterminado es 1.
dnorm ()
Esta función da la altura de la distribución de probabilidad en cada punto para una media y una desviación estándar dadas.
# Create a sequence of numbers between -10 and 10 incrementing by 0.1.
x <- seq(-10, 10, by = .1)
# Choose the mean as 2.5 and standard deviation as 0.5.
y <- dnorm(x, mean = 2.5, sd = 0.5)
# Give the chart file a name.
png(file = "dnorm.png")
plot(x,y)
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
pnorm ()
Esta función da la probabilidad de que un número aleatorio distribuido normalmente sea menor que el valor de un número dado. También se denomina "Función de distribución acumulativa".
# Create a sequence of numbers between -10 and 10 incrementing by 0.2.
x <- seq(-10,10,by = .2)
# Choose the mean as 2.5 and standard deviation as 2.
y <- pnorm(x, mean = 2.5, sd = 2)
# Give the chart file a name.
png(file = "pnorm.png")
# Plot the graph.
plot(x,y)
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
qnorm ()
Esta función toma el valor de probabilidad y da un número cuyo valor acumulativo coincide con el valor de probabilidad.
# Create a sequence of probability values incrementing by 0.02.
x <- seq(0, 1, by = 0.02)
# Choose the mean as 2 and standard deviation as 3.
y <- qnorm(x, mean = 2, sd = 1)
# Give the chart file a name.
png(file = "qnorm.png")
# Plot the graph.
plot(x,y)
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
rnorm ()
Esta función se utiliza para generar números aleatorios cuya distribución es normal. Toma el tamaño de la muestra como entrada y genera esa cantidad de números aleatorios. Dibujamos un histograma para mostrar la distribución de los números generados.
# Create a sample of 50 numbers which are normally distributed.
y <- rnorm(50)
# Give the chart file a name.
png(file = "rnorm.png")
# Plot the histogram for this sample.
hist(y, main = "Normal DIstribution")
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
El modelo de distribución binomial trata de encontrar la probabilidad de éxito de un evento que tiene solo dos resultados posibles en una serie de experimentos. Por ejemplo, lanzar una moneda siempre da cara o cruz. La probabilidad de encontrar exactamente 3 caras al lanzar una moneda repetidamente durante 10 veces se estima durante la distribución binomial.
R tiene cuatro funciones integradas para generar una distribución binomial. Se describen a continuación.
dbinom(x, size, prob)
pbinom(x, size, prob)
qbinom(p, size, prob)
rbinom(n, size, prob)A continuación se muestra la descripción de los parámetros utilizados:
x es un vector de números.
p es un vector de probabilidades.
n es el número de observaciones.
size es el número de ensayos.
prob es la probabilidad de éxito de cada ensayo.
dbinom ()
Esta función da la distribución de densidad de probabilidad en cada punto.
# Create a sample of 50 numbers which are incremented by 1.
x <- seq(0,50,by = 1)
# Create the binomial distribution.
y <- dbinom(x,50,0.5)
# Give the chart file a name.
png(file = "dbinom.png")
# Plot the graph for this sample.
plot(x,y)
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
pbinom ()
Esta función da la probabilidad acumulada de un evento. Es un valor único que representa la probabilidad.
# Probability of getting 26 or less heads from a 51 tosses of a coin.
x <- pbinom(26,51,0.5)
print(x)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 0.610116qbinom ()
Esta función toma el valor de probabilidad y da un número cuyo valor acumulativo coincide con el valor de probabilidad.
# How many heads will have a probability of 0.25 will come out when a coin
# is tossed 51 times.
x <- qbinom(0.25,51,1/2)
print(x)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 23rbinom ()
Esta función genera el número requerido de valores aleatorios de probabilidad dada de una muestra dada.
# Find 8 random values from a sample of 150 with probability of 0.4.
x <- rbinom(8,150,.4)
print(x)Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 58 61 59 66 55 60 61 67La regresión de Poisson implica modelos de regresión en los que la variable de respuesta está en forma de recuentos y no de números fraccionarios. Por ejemplo, el recuento del número de nacimientos o el número de victorias en una serie de partidos de fútbol. Además, los valores de las variables de respuesta siguen una distribución de Poisson.
La ecuación matemática general para la regresión de Poisson es:
log(y) = a + b1x1 + b2x2 + bnxn.....A continuación se muestra la descripción de los parámetros utilizados:
y es la variable de respuesta.
a y b son los coeficientes numéricos.
x es la variable predictora.
La función utilizada para crear el modelo de regresión de Poisson es la glm() función.
Sintaxis
La sintaxis básica para glm() función en la regresión de Poisson es -
glm(formula,data,family)A continuación se muestra la descripción de los parámetros utilizados en las funciones anteriores:
formula es el símbolo que presenta la relación entre las variables.
data es el conjunto de datos que da los valores de estas variables.
familyes un objeto R para especificar los detalles del modelo. Su valor es 'Poisson' para Regresión logística.
Ejemplo
Tenemos el conjunto de datos incorporado "roturas de urdimbre" que describe el efecto del tipo de lana (A o B) y la tensión (baja, media o alta) en el número de roturas de urdimbre por telar. Consideremos "descansos" como la variable de respuesta que es un recuento del número de descansos. El "tipo" y la "tensión" de la lana se toman como variables predictoras.
Input Data
input <- warpbreaks
print(head(input))Cuando ejecutamos el código anterior, produce el siguiente resultado:
breaks wool tension
1 26 A L
2 30 A L
3 54 A L
4 25 A L
5 70 A L
6 52 A LCrear modelo de regresión
output <-glm(formula = breaks ~ wool+tension, data = warpbreaks,
family = poisson)
print(summary(output))Cuando ejecutamos el código anterior, produce el siguiente resultado:
Call:
glm(formula = breaks ~ wool + tension, family = poisson, data = warpbreaks)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.6871 -1.6503 -0.4269 1.1902 4.2616
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 3.69196 0.04541 81.302 < 2e-16 ***
woolB -0.20599 0.05157 -3.994 6.49e-05 ***
tensionM -0.32132 0.06027 -5.332 9.73e-08 ***
tensionH -0.51849 0.06396 -8.107 5.21e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 297.37 on 53 degrees of freedom
Residual deviance: 210.39 on 50 degrees of freedom
AIC: 493.06
Number of Fisher Scoring iterations: 4En el resumen, buscamos que el valor p en la última columna sea menor que 0.05 para considerar un impacto de la variable predictora en la variable de respuesta. Como se ve, el tipo de lana B que tiene un tipo de tensión M y H tiene un impacto en el recuento de roturas.
Usamos el análisis de regresión para crear modelos que describen el efecto de la variación en las variables predictoras sobre la variable de respuesta. A veces, si tenemos una variable categórica con valores como Sí / No o Masculino / Femenino, etc. El análisis de regresión simple da múltiples resultados para cada valor de la variable categórica. En tal escenario, podemos estudiar el efecto de la variable categórica usándola junto con la variable predictora y comparando las líneas de regresión para cada nivel de la variable categórica. Tal análisis se denomina comoAnalysis of Covariance también llamado como ANCOVA.
Ejemplo
Considere el conjunto de datos R integrado mtcars. En él observamos que el campo "am" representa el tipo de transmisión (automática o manual). Es una variable categórica con valores 0 y 1. El valor de millas por galón (mpg) de un automóvil también puede depender de él además del valor de los caballos de fuerza ("hp").
Estudiamos el efecto del valor de "am" sobre la regresión entre "mpg" y "hp". Se hace usando elaov() función seguida por la anova() función para comparar las regresiones múltiples.
Los datos de entrada
Cree un marco de datos que contenga los campos "mpg", "hp" y "am" del conjunto de datos mtcars. Aquí tomamos "mpg" como la variable de respuesta, "hp" como la variable predictiva y "am" como la variable categórica.
input <- mtcars[,c("am","mpg","hp")]
print(head(input))Cuando ejecutamos el código anterior, produce el siguiente resultado:
am mpg hp
Mazda RX4 1 21.0 110
Mazda RX4 Wag 1 21.0 110
Datsun 710 1 22.8 93
Hornet 4 Drive 0 21.4 110
Hornet Sportabout 0 18.7 175
Valiant 0 18.1 105Análisis ANCOVA
Creamos un modelo de regresión tomando "hp" como variable predictora y "mpg" como variable de respuesta teniendo en cuenta la interacción entre "am" y "hp".
Modelo con interacción entre variable categórica y variable predictora
# Get the dataset.
input <- mtcars
# Create the regression model.
result <- aov(mpg~hp*am,data = input)
print(summary(result))Cuando ejecutamos el código anterior, produce el siguiente resultado:
Df Sum Sq Mean Sq F value Pr(>F)
hp 1 678.4 678.4 77.391 1.50e-09 ***
am 1 202.2 202.2 23.072 4.75e-05 ***
hp:am 1 0.0 0.0 0.001 0.981
Residuals 28 245.4 8.8
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Este resultado muestra que tanto los caballos de fuerza como el tipo de transmisión tienen un efecto significativo en las millas por galón, ya que el valor p en ambos casos es menor a 0.05. Pero la interacción entre estas dos variables no es significativa ya que el valor p es más de 0.05.
Modelo sin interacción entre variable categórica y variable predictora
# Get the dataset.
input <- mtcars
# Create the regression model.
result <- aov(mpg~hp+am,data = input)
print(summary(result))Cuando ejecutamos el código anterior, produce el siguiente resultado:
Df Sum Sq Mean Sq F value Pr(>F)
hp 1 678.4 678.4 80.15 7.63e-10 ***
am 1 202.2 202.2 23.89 3.46e-05 ***
Residuals 29 245.4 8.5
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Este resultado muestra que tanto los caballos de fuerza como el tipo de transmisión tienen un efecto significativo en las millas por galón, ya que el valor p en ambos casos es menor a 0.05.
Comparación de dos modelos
Ahora podemos comparar los dos modelos para concluir si la interacción de las variables es realmente insignificante. Para esto usamos elanova() función.
# Get the dataset.
input <- mtcars
# Create the regression models.
result1 <- aov(mpg~hp*am,data = input)
result2 <- aov(mpg~hp+am,data = input)
# Compare the two models.
print(anova(result1,result2))Cuando ejecutamos el código anterior, produce el siguiente resultado:
Model 1: mpg ~ hp * am
Model 2: mpg ~ hp + am
Res.Df RSS Df Sum of Sq F Pr(>F)
1 28 245.43
2 29 245.44 -1 -0.0052515 6e-04 0.9806Como el valor p es mayor que 0.05, concluimos que la interacción entre caballos de fuerza y tipo de transmisión no es significativa. Por lo tanto, el millaje por galón dependerá de manera similar de la potencia del automóvil en el modo de transmisión automática y manual.
La serie temporal es una serie de puntos de datos en los que cada punto de datos está asociado con una marca de tiempo. Un ejemplo simple es el precio de una acción en el mercado de valores en diferentes momentos de un día determinado. Otro ejemplo es la cantidad de lluvia en una región en diferentes meses del año. El lenguaje R usa muchas funciones para crear, manipular y trazar los datos de series de tiempo. Los datos de la serie temporal se almacenan en un objeto R llamadotime-series object. También es un objeto de datos R como un vector o un marco de datos.
El objeto de serie temporal se crea mediante el ts() función.
Sintaxis
La sintaxis básica para ts() La función en el análisis de series de tiempo es:
timeseries.object.name <- ts(data, start, end, frequency)A continuación se muestra la descripción de los parámetros utilizados:
data es un vector o matriz que contiene los valores usados en la serie de tiempo.
start especifica la hora de inicio de la primera observación en una serie de tiempo.
end especifica la hora de finalización de la última observación de la serie temporal.
frequency especifica el número de observaciones por unidad de tiempo.
Excepto el parámetro "datos", todos los demás parámetros son opcionales.
Ejemplo
Considere los detalles de la precipitación anual en un lugar a partir de enero de 2012. Creamos un objeto de serie de tiempo R para un período de 12 meses y lo trazamos.
# Get the data points in form of a R vector.
rainfall <- c(799,1174.8,865.1,1334.6,635.4,918.5,685.5,998.6,784.2,985,882.8,1071)
# Convert it to a time series object.
rainfall.timeseries <- ts(rainfall,start = c(2012,1),frequency = 12)
# Print the timeseries data.
print(rainfall.timeseries)
# Give the chart file a name.
png(file = "rainfall.png")
# Plot a graph of the time series.
plot(rainfall.timeseries)
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado y gráfico:
Jan Feb Mar Apr May Jun Jul Aug Sep
2012 799.0 1174.8 865.1 1334.6 635.4 918.5 685.5 998.6 784.2
Oct Nov Dec
2012 985.0 882.8 1071.0El gráfico de series de tiempo -
Diferentes intervalos de tiempo
El valor de la frequencyEl parámetro de la función ts () decide los intervalos de tiempo en los que se miden los puntos de datos. Un valor de 12 indica que la serie temporal es de 12 meses. Otros valores y su significado es el siguiente:
frequency = 12 fija los puntos de datos para cada mes del año.
frequency = 4 fija los puntos de datos para cada trimestre de un año.
frequency = 6 fija los puntos de datos cada 10 minutos de una hora.
frequency = 24*6 fija los puntos de datos cada 10 minutos del día.
Varias series de tiempo
Podemos trazar múltiples series de tiempo en un gráfico combinando ambas series en una matriz.
# Get the data points in form of a R vector.
rainfall1 <- c(799,1174.8,865.1,1334.6,635.4,918.5,685.5,998.6,784.2,985,882.8,1071)
rainfall2 <-
c(655,1306.9,1323.4,1172.2,562.2,824,822.4,1265.5,799.6,1105.6,1106.7,1337.8)
# Convert them to a matrix.
combined.rainfall <- matrix(c(rainfall1,rainfall2),nrow = 12)
# Convert it to a time series object.
rainfall.timeseries <- ts(combined.rainfall,start = c(2012,1),frequency = 12)
# Print the timeseries data.
print(rainfall.timeseries)
# Give the chart file a name.
png(file = "rainfall_combined.png")
# Plot a graph of the time series.
plot(rainfall.timeseries, main = "Multiple Time Series")
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado y gráfico:
Series 1 Series 2
Jan 2012 799.0 655.0
Feb 2012 1174.8 1306.9
Mar 2012 865.1 1323.4
Apr 2012 1334.6 1172.2
May 2012 635.4 562.2
Jun 2012 918.5 824.0
Jul 2012 685.5 822.4
Aug 2012 998.6 1265.5
Sep 2012 784.2 799.6
Oct 2012 985.0 1105.6
Nov 2012 882.8 1106.7
Dec 2012 1071.0 1337.8El gráfico de series temporales múltiples -
Al modelar datos del mundo real para el análisis de regresión, observamos que rara vez es el caso de que la ecuación del modelo sea una ecuación lineal que dé un gráfico lineal. La mayoría de las veces, la ecuación del modelo de datos del mundo real involucra funciones matemáticas de mayor grado como un exponente de 3 o una función sin. En tal escenario, la gráfica del modelo da una curva en lugar de una línea. El objetivo de la regresión lineal y no lineal es ajustar los valores de los parámetros del modelo para encontrar la línea o curva que se acerque más a sus datos. Al encontrar estos valores, podremos estimar la variable de respuesta con buena precisión.
En la regresión de mínimos cuadrados, establecemos un modelo de regresión en el que se minimiza la suma de los cuadrados de las distancias verticales de diferentes puntos de la curva de regresión. Generalmente comenzamos con un modelo definido y asumimos algunos valores para los coeficientes. Luego aplicamos elnls() función de R para obtener los valores más precisos junto con los intervalos de confianza.
Sintaxis
La sintaxis básica para crear una prueba de mínimos cuadrados no lineal en R es:
nls(formula, data, start)A continuación se muestra la descripción de los parámetros utilizados:
formula es una fórmula de modelo no lineal que incluye variables y parámetros.
data es un marco de datos utilizado para evaluar las variables en la fórmula.
start es una lista con nombre o un vector numérico con nombre de estimaciones iniciales.
Ejemplo
Consideraremos un modelo no lineal con el supuesto de valores iniciales de sus coeficientes. A continuación, veremos cuáles son los intervalos de confianza de estos valores asumidos para poder juzgar qué tan bien estos valores se incorporan al modelo.
Así que consideremos la siguiente ecuación para este propósito:
a = b1*x^2+b2Supongamos que los coeficientes iniciales son 1 y 3 y ajustamos estos valores en la función nls ().
xvalues <- c(1.6,2.1,2,2.23,3.71,3.25,3.4,3.86,1.19,2.21)
yvalues <- c(5.19,7.43,6.94,8.11,18.75,14.88,16.06,19.12,3.21,7.58)
# Give the chart file a name.
png(file = "nls.png")
# Plot these values.
plot(xvalues,yvalues)
# Take the assumed values and fit into the model.
model <- nls(yvalues ~ b1*xvalues^2+b2,start = list(b1 = 1,b2 = 3))
# Plot the chart with new data by fitting it to a prediction from 100 data points.
new.data <- data.frame(xvalues = seq(min(xvalues),max(xvalues),len = 100))
lines(new.data$xvalues,predict(model,newdata = new.data))
# Save the file.
dev.off()
# Get the sum of the squared residuals.
print(sum(resid(model)^2))
# Get the confidence intervals on the chosen values of the coefficients.
print(confint(model))Cuando ejecutamos el código anterior, produce el siguiente resultado:
[1] 1.081935
Waiting for profiling to be done...
2.5% 97.5%
b1 1.137708 1.253135
b2 1.497364 2.496484
Podemos concluir que el valor de b1 está más cerca de 1 mientras que el valor de b2 está más cerca de 2 y no de 3.
El árbol de decisiones es un gráfico para representar las opciones y sus resultados en forma de árbol. Los nodos del gráfico representan un evento o una elección y los bordes del gráfico representan las reglas o condiciones de decisión. Se utiliza principalmente en aplicaciones de Machine Learning y Data Mining que utilizan R.
Algunos ejemplos del uso de las vías de decisión son: predecir un correo electrónico como spam o no, predecir que un tumor es canceroso o predecir un préstamo como un riesgo crediticio bueno o malo en función de los factores de cada uno de ellos. Generalmente, un modelo se crea con datos observados, también llamados datos de entrenamiento. Luego, se utiliza un conjunto de datos de validación para verificar y mejorar el modelo. R tiene paquetes que se utilizan para crear y visualizar árboles de decisiones. Para un nuevo conjunto de variables predictoras, usamos este modelo para llegar a una decisión sobre la categoría (sí / No, spam / no spam) de los datos.
El paquete R "party" se utiliza para crear árboles de decisión.
Instalar paquete R
Utilice el siguiente comando en la consola de R para instalar el paquete. También debe instalar los paquetes dependientes, si los hubiera.
install.packages("party")El paquete "fiesta" tiene la función ctree() que se utiliza para crear y analizar el árbol de decisiones.
Sintaxis
La sintaxis básica para crear un árbol de decisiones en R es:
ctree(formula, data)A continuación se muestra la descripción de los parámetros utilizados:
formula es una fórmula que describe las variables de predicción y respuesta.
data es el nombre del conjunto de datos utilizado.
Los datos de entrada
Usaremos el conjunto de datos incorporado de R llamado readingSkillspara crear un árbol de decisiones. Describe la puntuación de las habilidades de lectura de alguien si conocemos las variables "edad", "tamaño de los zapatos", "puntuación" y si la persona es un hablante nativo o no.
Aquí están los datos de muestra.
# Load the party package. It will automatically load other
# dependent packages.
library(party)
# Print some records from data set readingSkills.
print(head(readingSkills))Cuando ejecutamos el código anterior, produce el siguiente resultado y gráfico:
nativeSpeaker age shoeSize score
1 yes 5 24.83189 32.29385
2 yes 6 25.95238 36.63105
3 no 11 30.42170 49.60593
4 yes 7 28.66450 40.28456
5 yes 11 31.88207 55.46085
6 yes 10 30.07843 52.83124
Loading required package: methods
Loading required package: grid
...............................
...............................Ejemplo
Usaremos el ctree() función para crear el árbol de decisiones y ver su gráfico.
# Load the party package. It will automatically load other
# dependent packages.
library(party)
# Create the input data frame.
input.dat <- readingSkills[c(1:105),]
# Give the chart file a name.
png(file = "decision_tree.png")
# Create the tree.
output.tree <- ctree(
nativeSpeaker ~ age + shoeSize + score,
data = input.dat)
# Plot the tree.
plot(output.tree)
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado:
null device
1
Loading required package: methods
Loading required package: grid
Loading required package: mvtnorm
Loading required package: modeltools
Loading required package: stats4
Loading required package: strucchange
Loading required package: zoo
Attaching package: ‘zoo’
The following objects are masked from ‘package:base’:
as.Date, as.Date.numeric
Loading required package: sandwich
Conclusión
A partir del árbol de decisiones que se muestra arriba, podemos concluir que cualquier persona cuya puntuación en habilidades de lectura sea inferior a 38,3 y la edad sea superior a 6 no es un hablante nativo.
En el enfoque de bosque aleatorio, se crea una gran cantidad de árboles de decisión. Cada observación se incorpora a cada árbol de decisiones. El resultado más común de cada observación se utiliza como resultado final. Se alimenta una nueva observación en todos los árboles y se obtiene una mayoría de votos para cada modelo de clasificación.
Se realiza una estimación de error para los casos que no se utilizaron durante la construcción del árbol. Eso se llama unOOB (Out-of-bag) estimación del error que se menciona como porcentaje.
El paquete R "randomForest" se utiliza para crear bosques aleatorios.
Instalar paquete R
Utilice el siguiente comando en la consola de R para instalar el paquete. También debe instalar los paquetes dependientes, si los hubiera.
install.packages("randomForest)El paquete "randomForest" tiene la función randomForest() que se utiliza para crear y analizar bosques aleatorios.
Sintaxis
La sintaxis básica para crear un bosque aleatorio en R es:
randomForest(formula, data)A continuación se muestra la descripción de los parámetros utilizados:
formula es una fórmula que describe las variables de predicción y respuesta.
data es el nombre del conjunto de datos utilizado.
Los datos de entrada
Usaremos el conjunto de datos incorporado de R llamado readingSkills para crear un árbol de decisiones. Describe la puntuación de las habilidades de lectura de alguien si conocemos las variables "edad", "tamaño de los zapatos", "puntuación" y si la persona es un hablante nativo.
Aquí están los datos de muestra.
# Load the party package. It will automatically load other
# required packages.
library(party)
# Print some records from data set readingSkills.
print(head(readingSkills))Cuando ejecutamos el código anterior, produce el siguiente resultado y gráfico:
nativeSpeaker age shoeSize score
1 yes 5 24.83189 32.29385
2 yes 6 25.95238 36.63105
3 no 11 30.42170 49.60593
4 yes 7 28.66450 40.28456
5 yes 11 31.88207 55.46085
6 yes 10 30.07843 52.83124
Loading required package: methods
Loading required package: grid
...............................
...............................Ejemplo
Usaremos el randomForest() función para crear el árbol de decisiones y ver su gráfico.
# Load the party package. It will automatically load other
# required packages.
library(party)
library(randomForest)
# Create the forest.
output.forest <- randomForest(nativeSpeaker ~ age + shoeSize + score,
data = readingSkills)
# View the forest results.
print(output.forest)
# Importance of each predictor.
print(importance(fit,type = 2))Cuando ejecutamos el código anterior, produce el siguiente resultado:
Call:
randomForest(formula = nativeSpeaker ~ age + shoeSize + score,
data = readingSkills)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 1
OOB estimate of error rate: 1%
Confusion matrix:
no yes class.error
no 99 1 0.01
yes 1 99 0.01
MeanDecreaseGini
age 13.95406
shoeSize 18.91006
score 56.73051Conclusión
Del bosque aleatorio que se muestra arriba podemos concluir que el tamaño de los zapatos y la puntuación son los factores importantes para decidir si alguien es un hablante nativo o no. Además, el modelo tiene solo un 1% de error, lo que significa que podemos predecir con un 99% de precisión.
El análisis de supervivencia se ocupa de predecir el momento en que ocurrirá un evento específico. También se conoce como análisis del tiempo de falla o análisis del tiempo hasta la muerte. Por ejemplo, predecir la cantidad de días que sobrevivirá una persona con cáncer o predecir el momento en que fallará un sistema mecánico.
El paquete R llamado survivalse utiliza para realizar análisis de supervivencia. Este paquete contiene la funciónSurv()que toma los datos de entrada como una fórmula R y crea un objeto de supervivencia entre las variables elegidas para el análisis. Entonces usamos la funciónsurvfit() para crear un gráfico para el análisis.
Paquete de instalación
install.packages("survival")Sintaxis
La sintaxis básica para crear análisis de supervivencia en R es:
Surv(time,event)
survfit(formula)A continuación se muestra la descripción de los parámetros utilizados:
time es el tiempo de seguimiento hasta que ocurre el evento.
event indica el estado de ocurrencia del evento esperado.
formula es la relación entre las variables predictoras.
Ejemplo
Consideraremos el conjunto de datos denominado "pbc" presente en los paquetes de supervivencia instalados anteriormente. Describe los puntos de datos de supervivencia de las personas afectadas con cirrosis biliar primaria (CBP) del hígado. Entre las muchas columnas presentes en el conjunto de datos, nos ocupamos principalmente de los campos "tiempo" y "estado". El tiempo representa el número de días entre el registro del paciente y antes del evento entre que el paciente recibe un trasplante de hígado o la muerte del paciente.
# Load the library.
library("survival")
# Print first few rows.
print(head(pbc))Cuando ejecutamos el código anterior, produce el siguiente resultado y gráfico:
id time status trt age sex ascites hepato spiders edema bili chol
1 1 400 2 1 58.76523 f 1 1 1 1.0 14.5 261
2 2 4500 0 1 56.44627 f 0 1 1 0.0 1.1 302
3 3 1012 2 1 70.07255 m 0 0 0 0.5 1.4 176
4 4 1925 2 1 54.74059 f 0 1 1 0.5 1.8 244
5 5 1504 1 2 38.10541 f 0 1 1 0.0 3.4 279
6 6 2503 2 2 66.25873 f 0 1 0 0.0 0.8 248
albumin copper alk.phos ast trig platelet protime stage
1 2.60 156 1718.0 137.95 172 190 12.2 4
2 4.14 54 7394.8 113.52 88 221 10.6 3
3 3.48 210 516.0 96.10 55 151 12.0 4
4 2.54 64 6121.8 60.63 92 183 10.3 4
5 3.53 143 671.0 113.15 72 136 10.9 3
6 3.98 50 944.0 93.00 63 NA 11.0 3A partir de los datos anteriores, estamos considerando el tiempo y el estado para nuestro análisis.
Aplicación de la función Surv () y survfit ()
Ahora procedemos a aplicar el Surv() función al conjunto de datos anterior y crear un gráfico que muestre la tendencia.
# Load the library.
library("survival")
# Create the survival object.
survfit(Surv(pbc$time,pbc$status == 2)~1) # Give the chart file a name. png(file = "survival.png") # Plot the graph. plot(survfit(Surv(pbc$time,pbc$status == 2)~1))
# Save the file.
dev.off()Cuando ejecutamos el código anterior, produce el siguiente resultado y gráfico:
Call: survfit(formula = Surv(pbc$time, pbc$status == 2) ~ 1)
n events median 0.95LCL 0.95UCL
418 161 3395 3090 3853
La tendencia en el gráfico anterior nos ayuda a predecir la probabilidad de supervivencia al final de un cierto número de días.
Chi-Square testes un método estadístico para determinar si dos variables categóricas tienen una correlación significativa entre ellas. Ambas variables deben ser de la misma población y deben ser categóricas como: Sí / No, Hombre / Mujer, Rojo / Verde, etc.
Por ejemplo, podemos construir un conjunto de datos con observaciones sobre el patrón de compra de helados de las personas y tratar de correlacionar el género de una persona con el sabor del helado que prefieren. Si se encuentra una correlación, podemos planificar el stock adecuado de sabores conociendo el número de género de las personas que nos visitan.
Sintaxis
La función utilizada para realizar la prueba de chi-cuadrado es chisq.test().
La sintaxis básica para crear una prueba de chi-cuadrado en R es:
chisq.test(data)A continuación se muestra la descripción de los parámetros utilizados:
data son los datos en forma de tabla que contienen el valor de recuento de las variables en la observación.
Ejemplo
Tomaremos los datos de Cars93 en la biblioteca "MASS" que representa las ventas de diferentes modelos de automóvil en el año 1993.
library("MASS")
print(str(Cars93))Cuando ejecutamos el código anterior, produce el siguiente resultado:
'data.frame': 93 obs. of 27 variables:
$ Manufacturer : Factor w/ 32 levels "Acura","Audi",..: 1 1 2 2 3 4 4 4 4 5 ...
$ Model : Factor w/ 93 levels "100","190E","240",..: 49 56 9 1 6 24 54 74 73 35 ... $ Type : Factor w/ 6 levels "Compact","Large",..: 4 3 1 3 3 3 2 2 3 2 ...
$ Min.Price : num 12.9 29.2 25.9 30.8 23.7 14.2 19.9 22.6 26.3 33 ... $ Price : num 15.9 33.9 29.1 37.7 30 15.7 20.8 23.7 26.3 34.7 ...
$ Max.Price : num 18.8 38.7 32.3 44.6 36.2 17.3 21.7 24.9 26.3 36.3 ... $ MPG.city : int 25 18 20 19 22 22 19 16 19 16 ...
$ MPG.highway : int 31 25 26 26 30 31 28 25 27 25 ... $ AirBags : Factor w/ 3 levels "Driver & Passenger",..: 3 1 2 1 2 2 2 2 2 2 ...
$ DriveTrain : Factor w/ 3 levels "4WD","Front",..: 2 2 2 2 3 2 2 3 2 2 ... $ Cylinders : Factor w/ 6 levels "3","4","5","6",..: 2 4 4 4 2 2 4 4 4 5 ...
$ EngineSize : num 1.8 3.2 2.8 2.8 3.5 2.2 3.8 5.7 3.8 4.9 ... $ Horsepower : int 140 200 172 172 208 110 170 180 170 200 ...
$ RPM : int 6300 5500 5500 5500 5700 5200 4800 4000 4800 4100 ... $ Rev.per.mile : int 2890 2335 2280 2535 2545 2565 1570 1320 1690 1510 ...
$ Man.trans.avail : Factor w/ 2 levels "No","Yes": 2 2 2 2 2 1 1 1 1 1 ... $ Fuel.tank.capacity: num 13.2 18 16.9 21.1 21.1 16.4 18 23 18.8 18 ...
$ Passengers : int 5 5 5 6 4 6 6 6 5 6 ... $ Length : int 177 195 180 193 186 189 200 216 198 206 ...
$ Wheelbase : int 102 115 102 106 109 105 111 116 108 114 ... $ Width : int 68 71 67 70 69 69 74 78 73 73 ...
$ Turn.circle : int 37 38 37 37 39 41 42 45 41 43 ... $ Rear.seat.room : num 26.5 30 28 31 27 28 30.5 30.5 26.5 35 ...
$ Luggage.room : int 11 15 14 17 13 16 17 21 14 18 ... $ Weight : int 2705 3560 3375 3405 3640 2880 3470 4105 3495 3620 ...
$ Origin : Factor w/ 2 levels "USA","non-USA": 2 2 2 2 2 1 1 1 1 1 ... $ Make : Factor w/ 93 levels "Acura Integra",..: 1 2 4 3 5 6 7 9 8 10 ...El resultado anterior muestra que el conjunto de datos tiene muchas variables de factor que pueden considerarse variables categóricas. Para nuestro modelo consideraremos las variables "AirBags" y "Tipo". Aquí nuestro objetivo es descubrir cualquier correlación significativa entre los tipos de automóviles vendidos y el tipo de bolsas de aire que tiene. Si se observa correlación, podemos estimar qué tipos de automóviles se pueden vender mejor con qué tipos de bolsas de aire.
# Load the library.
library("MASS")
# Create a data frame from the main data set.
car.data <- data.frame(Cars93$AirBags, Cars93$Type)
# Create a table with the needed variables.
car.data = table(Cars93$AirBags, Cars93$Type)
print(car.data)
# Perform the Chi-Square test.
print(chisq.test(car.data))Cuando ejecutamos el código anterior, produce el siguiente resultado:
Compact Large Midsize Small Sporty Van
Driver & Passenger 2 4 7 0 3 0
Driver only 9 7 11 5 8 3
None 5 0 4 16 3 6
Pearson's Chi-squared test
data: car.data
X-squared = 33.001, df = 10, p-value = 0.0002723
Warning message:
In chisq.test(car.data) : Chi-squared approximation may be incorrectConclusión
El resultado muestra el valor p de menos de 0,05, lo que indica una correlación de cadenas.