Ciencia ficción - CSGraph
CSGraph significa Compressed Sparse Graph, que se centra en algoritmos de gráficos rápidos basados en representaciones matriciales dispersas.
Representaciones gráficas
Para empezar, entendamos qué es un gráfico disperso y cómo ayuda en las representaciones de gráficos.
¿Qué es exactamente un gráfico disperso?
Un gráfico es solo una colección de nodos, que tienen vínculos entre ellos. Los gráficos pueden representar casi cualquier cosa: conexiones de redes sociales, donde cada nodo es una persona y está conectado a conocidos; imágenes, donde cada nodo es un píxel y está conectado a píxeles vecinos; puntos en una distribución de alta dimensión, donde cada nodo está conectado a sus vecinos más cercanos; y prácticamente cualquier otra cosa que puedas imaginar.
Una forma muy eficiente de representar datos gráficos es en una matriz dispersa: llamémosla G. La matriz G es de tamaño N x N, y G [i, j] da el valor de la conexión entre el nodo 'i' y el nodo 'j'. Un gráfico disperso contiene principalmente ceros, es decir, la mayoría de los nodos tienen solo unas pocas conexiones. Esta propiedad resulta ser cierta en la mayoría de los casos de interés.
La creación del submódulo de gráfico disperso fue motivada por varios algoritmos utilizados en scikit-learn que incluían lo siguiente:
Isomap - Un algoritmo de aprendizaje múltiple, que requiere encontrar los caminos más cortos en un gráfico.
Hierarchical clustering - Un algoritmo de agrupamiento basado en un árbol de expansión mínimo.
Spectral Decomposition - Un algoritmo de proyección basado en laplacianos de grafos dispersos.
Como ejemplo concreto, imagine que nos gustaría representar el siguiente gráfico no dirigido:
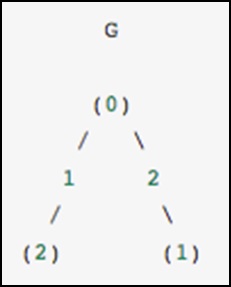
Este gráfico tiene tres nodos, donde el nodo 0 y 1 están conectados por un borde de peso 2, y los nodos 0 y 2 están conectados por un borde de peso 1. Podemos construir las representaciones densas, enmascaradas y dispersas como se muestra en el siguiente ejemplo , teniendo en cuenta que un gráfico no dirigido está representado por una matriz simétrica.
G_dense = np.array([ [0, 2, 1],
[2, 0, 0],
[1, 0, 0] ])
G_masked = np.ma.masked_values(G_dense, 0)
from scipy.sparse import csr_matrix
G_sparse = csr_matrix(G_dense)
print G_sparse.dataEl programa anterior generará la siguiente salida.
array([2, 1, 2, 1])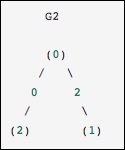
Esto es idéntico al gráfico anterior, excepto que los nodos 0 y 2 están conectados por un borde de peso cero. En este caso, la representación densa anterior conduce a ambigüedades: cómo se pueden representar los no bordes, si cero es un valor significativo. En este caso, se debe utilizar una representación enmascarada o dispersa para eliminar la ambigüedad.
Consideremos el siguiente ejemplo.
from scipy.sparse.csgraph import csgraph_from_dense
G2_data = np.array
([
[np.inf, 2, 0 ],
[2, np.inf, np.inf],
[0, np.inf, np.inf]
])
G2_sparse = csgraph_from_dense(G2_data, null_value=np.inf)
print G2_sparse.dataEl programa anterior generará la siguiente salida.
array([ 2., 0., 2., 0.])Escaleras de palabras usando gráficos dispersos
Escaleras de palabras es un juego inventado por Lewis Carroll, en el que las palabras se unen cambiando una sola letra en cada paso. Por ejemplo
APE → APT → AIT → BIT → BIG → BAG → MAG → MAN
Aquí, hemos pasado de "APE" a "MAN" en siete pasos, cambiando una letra cada vez. La pregunta es: ¿Podemos encontrar un camino más corto entre estas palabras usando la misma regla? Este problema se expresa naturalmente como un problema de gráfico disperso. Los nodos corresponderán a palabras individuales, y crearemos conexiones entre palabras que difieren como máximo en una letra.
Obtener una lista de palabras
Primero, por supuesto, debemos obtener una lista de palabras válidas. Estoy ejecutando Mac, y Mac tiene un diccionario de palabras en la ubicación indicada en el siguiente bloque de código. Si está en una arquitectura diferente, es posible que deba buscar un poco para encontrar el diccionario de su sistema.
wordlist = open('/usr/share/dict/words').read().split()
print len(wordlist)El programa anterior generará la siguiente salida.
235886Ahora queremos ver palabras de longitud 3, así que seleccionemos solo aquellas palabras de longitud correcta. También eliminaremos palabras que comiencen con mayúsculas (nombres propios) o que contengan caracteres no alfanuméricos como apóstrofes y guiones. Finalmente, nos aseguraremos de que todo esté en minúsculas para una comparación más adelante.
word_list = [word for word in word_list if len(word) == 3]
word_list = [word for word in word_list if word[0].islower()]
word_list = [word for word in word_list if word.isalpha()]
word_list = map(str.lower, word_list)
print len(word_list)El programa anterior generará la siguiente salida.
1135Ahora, tenemos una lista de 1135 palabras válidas de tres letras (el número exacto puede cambiar dependiendo de la lista particular utilizada). Cada una de estas palabras se convertirá en un nodo en nuestro gráfico, y crearemos bordes conectando los nodos asociados con cada par de palabras, que se diferencian por una sola letra.
import numpy as np
word_list = np.asarray(word_list)
word_list.dtype
word_list.sort()
word_bytes = np.ndarray((word_list.size, word_list.itemsize),
dtype = 'int8',
buffer = word_list.data)
print word_bytes.shapeEl programa anterior generará la siguiente salida.
(1135, 3)Usaremos la distancia de Hamming entre cada punto para determinar qué pares de palabras están conectadas. La distancia de Hamming mide la fracción de entradas entre dos vectores, que difieren: dos palabras cualesquiera con una distancia de Hamming igual a 1 / N1 / N, donde NN es el número de letras, que están conectadas en la escalera de palabras.
from scipy.spatial.distance import pdist, squareform
from scipy.sparse import csr_matrix
hamming_dist = pdist(word_bytes, metric = 'hamming')
graph = csr_matrix(squareform(hamming_dist < 1.5 / word_list.itemsize))Al comparar las distancias, no utilizamos la igualdad porque esto puede ser inestable para valores de coma flotante. La desigualdad produce el resultado deseado siempre que no haya dos entradas de la lista de palabras idénticas. Ahora que nuestro gráfico está configurado, usaremos la búsqueda de ruta más corta para encontrar la ruta entre dos palabras cualesquiera en el gráfico.
i1 = word_list.searchsorted('ape')
i2 = word_list.searchsorted('man')
print word_list[i1],word_list[i2]El programa anterior generará la siguiente salida.
ape, manTenemos que comprobar que coincidan, porque si las palabras no están en la lista habrá un error en la salida. Ahora, todo lo que necesitamos es encontrar el camino más corto entre estos dos índices en el gráfico. Usaremosdijkstra’s algoritmo, porque nos permite encontrar la ruta para un solo nodo.
from scipy.sparse.csgraph import dijkstra
distances, predecessors = dijkstra(graph, indices = i1, return_predecessors = True)
print distances[i2]El programa anterior generará la siguiente salida.
5.0Por lo tanto, vemos que el camino más corto entre 'mono' y 'hombre' contiene solo cinco pasos. Podemos usar los predecesores devueltos por el algoritmo para reconstruir esta ruta.
path = []
i = i2
while i != i1:
path.append(word_list[i])
i = predecessors[i]
path.append(word_list[i1])
print path[::-1]i2]El programa anterior generará la siguiente salida.
['ape', 'ope', 'opt', 'oat', 'mat', 'man']