Comptabilité analytique - Analyse CVP
L'analyse coût-volume-profit (CVP) est également appelée analyse du seuil de rentabilité. Chaque organisation commerciale travaille pour maximiser ses profits. À l'aide de l'analyse CVP, la direction étudie la co-relation entre le profit et le niveau de production.
L'analyse CVP concerne le niveau d'activité où les ventes totales sont égales au coût total et elle est appelée le seuil de rentabilité. En d'autres termes, nous étudions la valeur des ventes, le coût et le profit à différents niveaux de production. L'analyse CVP met en évidence la relation entre le coût, la valeur des ventes et le profit.
Hypothèses
Passons en revue les hypothèses pour l'analyse CVP:
Les coûts variables restent variables et les coûts fixes restent statiques à tous les niveaux de production.
Le volume des ventes n'affecte pas le prix de vente du produit. Nous pouvons supposer que le prix de vente est constant.
À tous les niveaux de vente, les coûts de volume, de matériel et de main-d'œuvre restent constants.
L'efficacité et la productivité restent inchangées à tous les niveaux de volume des ventes.
Le mix des ventes à tous les niveaux de ventes reste constant dans une situation multi-produits.
Le facteur pertinent qui affecte le coût et les revenus est uniquement le volume.
Le volume des ventes est égal au volume de production.
Équation du coût marginal
Les équations pour les éléments de coût sont les suivantes:
Sales = Variable costs + Fixed Expenses ± Profit /Loss
Or
Sales – Variable Cost = Fixed Expenses ± Profit /Loss
Or
Sales – Variable Cost = ContributionIl est nécessaire de comprendre les quatre concepts suivants, leurs calculs et leurs applications pour connaître la relation mathématique entre le coût, le volume et le profit:
- Contribution
- Ratio Volume Profit (Ratio P / V ou Contribution / Ventes (C / S))
- Point de rentabilité
- Marge de sécurité
Contribution
Contribution = Sales – Marginal CostNous avons déjà discuté de la contribution au sujet des coûts marginaux ci-dessus.
Rapport profit-volume
Le rapport Profit / Volume (P / V) est calculé en étudiant la rentabilité des opérations d'une entreprise et pour établir une relation entre les ventes et la contribution. C'est l'un des ratios les plus importants, calculé comme suit:
Le rapport P / V partage une relation directe avec les bénéfices. Plus le rapport P / V est élevé, plus le profit et vice-versa.
Point de rentabilité
Lorsque le coût total de l'exécution des affaires est égal au chiffre d'affaires total, on parle de seuil de rentabilité. La contribution est égale au coût fixe à ce stade. Voici une formule pour calculer le seuil de rentabilité:
Seuil de rentabilité basé sur les ventes totales:
Calcul de la production ou de la valeur des ventes à laquelle un profit souhaité est réalisé:
Point de rentabilité composite
Une entreprise peut avoir des unités de production différentes, où elles peuvent produire le même produit. Dans ce cas, le coût fixe combiné de chaque unité de production et les ventes totales combinées sont pris en compte pour connaître le BEP.
Constant Product - Approche Mix Dans cette approche, le ratio est constant pour les produits de toutes les unités de production.
Variable Product - Approche mixte Dans cette approche, la préférence des produits est basée sur un ratio plus élevé.
Marge de sécurité
L'excès de vente chez BEP est connu comme une marge de sécurité. Par conséquent,
Margin of safety = Actual Sales − Sales at BEPLa marge de sécurité peut être calculée à l'aide de la formule suivante:
Tableau de rentabilité
Le tableau de rentabilité est la représentation graphique la plus utile du coût marginal. Il convertit les données comptables en un rapport lisible utile. Les bénéfices, pertes et coûts estimés peuvent être déterminés à différents niveaux de production. Prenons un exemple.
Exemple
Calculez le seuil de rentabilité et dessinez le graphique du seuil de rentabilité à partir des données suivantes:
Fixed Cost = Rs 2,50,000
Variable Cost = Rs 15 per unit
Selling Price = Rs 25 per unit
Production level in units 12,000, 15,000, 20,000, 25,000, 30,000, and 40,000.Solution:
Au niveau de production de 25 000 unités, le coût total sera de 6,25 000 Rs.
(Calculé comme (25000 × 14) + 2,50000)
| Déclaration montrant le bénéfice et la marge de sécurité à différents niveaux de production Solde à l'équilibre = Rs 6,25,000 (25,000 x 25) | ||||
| Production (En unités) |
Vente totale (En Rs) |
Coût total (En Rs) |
Profit (Ventes - Coût) (En Rs) |
Marge de sécurité (Profit / Contribution par unité) (En unités) |
| 12 000 | 3,00 000 | 430 000 | -1,30 000 | |
| 15 000 | 3,75 000 | 4,75 000 | -1,00 000 | |
| 20000 | 5,00 000 | 5 50 000 | -50 000 | |
| 25 000 | 6,25 000 | 6,25 000 | (BEP) | (BEP) |
| 30000 | 7 50 000 | 7,00 000 | 50 000 | 5 000 |
| 40000 | 10,00 000 | 8 50 000 | 1,50,000 | 15 000 |
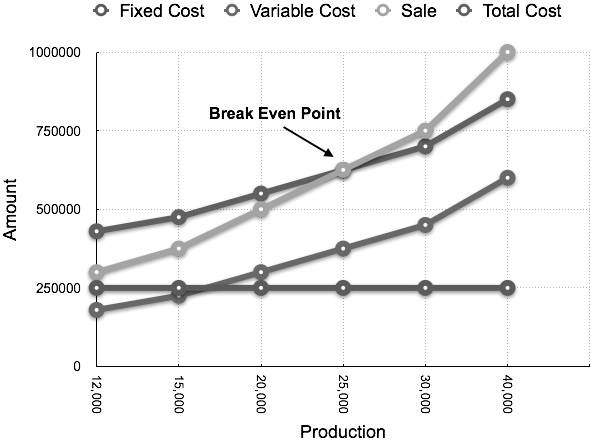
Le graphique correspondant représenté par rapport à la production par rapport au montant apparaît comme suit: