Apache MXNet - Paquets Python

Dans ce chapitre, nous allons découvrir les packages Python disponibles dans Apache MXNet.

Packages MXNet Python importants

MXNet a les packages Python importants suivants dont nous discuterons un par un -

Autograd (différenciation automatique)
NDArray
KVStore
Gluon
Visualization

Commençons par Autograd Package Python pour Apache MXNet.

Autograd

Autograd signifie automatic differentiationutilisé pour rétropropropager les gradients de la métrique de perte à chacun des paramètres. Parallèlement à la rétropropagation, il utilise une approche de programmation dynamique pour calculer efficacement les gradients. Elle est également appelée différenciation automatique en mode inverse. Cette technique est très efficace dans les situations de «fan-in» où de nombreux paramètres affectent une seule métrique de perte.

Que sont les dégradés?

Les dégradés sont les principes fondamentaux du processus de formation des réseaux neuronaux. Ils nous disent essentiellement comment modifier les paramètres du réseau pour améliorer ses performances.

Comme on le sait, les réseaux de neurones (NN) sont composés d'opérateurs tels que sommes, produit, convolutions, etc. Ces opérateurs, pour leurs calculs, utilisent des paramètres tels que les poids dans les noyaux de convolution. Nous devrions avoir à trouver les valeurs optimales pour ces paramètres et les gradients nous montrent le chemin et nous conduisent également à la solution.

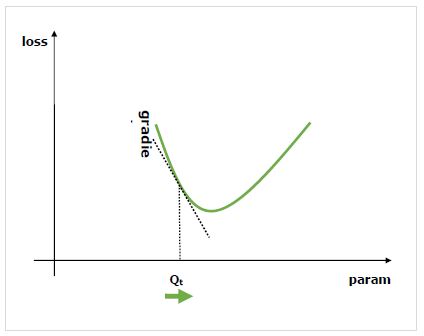
Nous nous intéressons à l'effet du changement d'un paramètre sur les performances du réseau et les gradients nous indiquent à quel point une variable donnée augmente ou diminue lorsque nous modifions une variable dont elle dépend. Les performances sont généralement définies en utilisant une métrique de perte que nous essayons de minimiser. Par exemple, pour la régression, nous pourrions essayer de minimiserL2 perte entre nos prédictions et la valeur exacte, alors que pour la classification, nous pourrions minimiser cross-entropy loss.

Une fois que nous calculons le gradient de chaque paramètre par rapport à la perte, nous pouvons alors utiliser un optimiseur, tel que la descente de gradient stochastique.

Comment calculer les dégradés?

Nous avons les options suivantes pour calculer les dégradés -

Symbolic Differentiation- La toute première option est la différenciation symbolique, qui calcule les formules pour chaque gradient. L'inconvénient de cette méthode est qu'elle conduira rapidement à des formules incroyablement longues à mesure que le réseau s'approfondit et que les opérateurs deviennent plus complexes.
Finite Differencing- Une autre option consiste à utiliser la différenciation finie qui essaie de légères différences sur chaque paramètre et voit comment la métrique de perte répond. L'inconvénient de cette méthode est qu'elle serait coûteuse en calcul et pourrait avoir une précision numérique médiocre.
Automatic differentiation- La solution aux inconvénients des méthodes ci-dessus consiste à utiliser la différenciation automatique pour rétropropropager les gradients de la métrique de perte à chacun des paramètres. La propagation nous permet une approche de programmation dynamique pour calculer efficacement les gradients. Cette méthode est également appelée différenciation automatique en mode inverse.

Différenciation automatique (autograd)

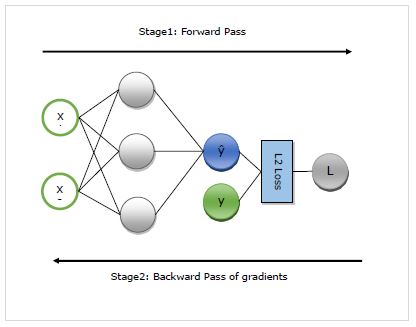
Ici, nous allons comprendre en détail le fonctionnement de l'autogradation. Cela fonctionne essentiellement en deux étapes -

Stage 1 - Cette étape s'appelle ‘Forward Pass’de la formation. Comme son nom l'indique, à cette étape, il crée l'enregistrement de l'opérateur utilisé par le réseau pour faire des prédictions et calculer la métrique de perte.

Stage 2 - Cette étape s'appelle ‘Backward Pass’de la formation. Comme son nom l'indique, à ce stade, il fonctionne à rebours à travers ce disque. À rebours, il évalue les dérivées partielles de chaque opérateur, jusqu'au paramètre réseau.

Avantages de l'autograd

Voici les avantages de l'utilisation de la différenciation automatique (autograd) -

Flexible- La flexibilité, qu'elle nous donne lors de la définition de notre réseau, est l'un des énormes avantages de l'utilisation d'autograd. Nous pouvons changer les opérations à chaque itération. Ceux-ci sont appelés les graphes dynamiques, qui sont beaucoup plus complexes à implémenter dans des frameworks nécessitant un graphe statique. Autograd, même dans de tels cas, pourra toujours propager correctement les dégradés.
Automatic- Autograd est automatique, c'est-à-dire que les complexités de la procédure de rétropropagation sont prises en charge par lui pour vous. Nous avons juste besoin de spécifier les gradients que nous souhaitons calculer.
Efficient - Autogard calcule les dégradés très efficacement.
Can use native Python control flow operators- Nous pouvons utiliser les opérateurs de flux de contrôle Python natifs tels que la condition if et la boucle while. L'autograde sera toujours capable de rétropropropager les dégradés de manière efficace et correcte.

Utilisation d'autograd dans MXNet Gluon

Ici, à l'aide d'un exemple, nous verrons comment nous pouvons utiliser autograd dans MXNet Gluon.

Exemple d'implémentation

Dans l'exemple suivant, nous allons implémenter le modèle de régression à deux couches. Après la mise en œuvre, nous utiliserons autograd pour calculer automatiquement le gradient de la perte en référence à chacun des paramètres de poids -

Importez d'abord l'autogrard et les autres packages requis comme suit -

from mxnet import autograd
import mxnet as mx
from mxnet.gluon.nn import HybridSequential, Dense
from mxnet.gluon.loss import L2Loss

Maintenant, nous devons définir le réseau comme suit -

N_net = HybridSequential()
N_net.add(Dense(units=3))
N_net.add(Dense(units=1))
N_net.initialize()

Nous devons maintenant définir la perte comme suit -

loss_function = L2Loss()

Ensuite, nous devons créer les données factices comme suit -

x = mx.nd.array([[0.5, 0.9]])
y = mx.nd.array([[1.5]])

Nous sommes maintenant prêts pour notre premier passage avant à travers le réseau. Nous voulons qu'autograd enregistre le graphe de calcul afin de pouvoir calculer les gradients. Pour cela, nous devons exécuter le code réseau dans le cadre deautograd.record contexte comme suit -

with autograd.record():
   y_hat = N_net(x)
   loss = loss_function(y_hat, y)

Maintenant, nous sommes prêts pour la passe en arrière, que nous commençons par appeler la méthode en arrière sur la quantité d'intérêt. La quantité d'intérêt dans notre exemple est la perte car nous essayons de calculer le gradient de perte en référence aux paramètres -

loss.backward()

Maintenant, nous avons des gradients pour chaque paramètre du réseau, qui seront utilisés par l'optimiseur pour mettre à jour la valeur du paramètre pour améliorer les performances. Vérifions les dégradés de la 1ère couche comme suit -

N_net[0].weight.grad()

Output

La sortie est la suivante -

[[-0.00470527 -0.00846948]
[-0.03640365 -0.06552657]
[ 0.00800354 0.01440637]]
<NDArray 3x2 @cpu(0)>

Exemple d'implémentation complet

Vous trouverez ci-dessous l'exemple complet de mise en œuvre.

from mxnet import autograd
import mxnet as mx
from mxnet.gluon.nn import HybridSequential, Dense
from mxnet.gluon.loss import L2Loss
N_net = HybridSequential()
N_net.add(Dense(units=3))
N_net.add(Dense(units=1))
N_net.initialize()
loss_function = L2Loss()
x = mx.nd.array([[0.5, 0.9]])
y = mx.nd.array([[1.5]])
with autograd.record():
y_hat = N_net(x)
loss = loss_function(y_hat, y)
loss.backward()
N_net[0].weight.grad()