AI avec Python - Analyse des données de séries chronologiques
Prédire le suivant dans une séquence d'entrée donnée est un autre concept important de l'apprentissage automatique. Ce chapitre vous donne une explication détaillée sur l'analyse des données de séries chronologiques.
introduction
Les données de série chronologique désignent les données qui se trouvent dans une série d'intervalles de temps particuliers. Si nous voulons créer une prédiction de séquence dans l'apprentissage automatique, nous devons gérer des données séquentielles et du temps. Les données de série sont un résumé des données séquentielles. L'ordre des données est une caractéristique importante des données séquentielles.
Concept de base de l'analyse de séquence ou de l'analyse des séries chronologiques
L'analyse de séquence ou l'analyse de séries chronologiques consiste à prédire la suivante dans une séquence d'entrée donnée en fonction de l'observation précédente. La prédiction peut être de tout ce qui peut venir: un symbole, un nombre, la météo du lendemain, le prochain terme de discours, etc. L'analyse de séquence peut être très pratique dans des applications telles que l'analyse boursière, les prévisions météorologiques et les recommandations de produits.
Example
Prenons l'exemple suivant pour comprendre la prédiction de séquence. IciA,B,C,D sont les valeurs données et vous devez prédire la valeur E en utilisant un modèle de prédiction de séquence.

Installer des packages utiles
Pour l'analyse des données de séries chronologiques à l'aide de Python, nous devons installer les packages suivants -
Pandas
Pandas est une bibliothèque open source sous licence BSD qui fournit des outils haute performance, faciles à utiliser et d'analyse de la structure de données pour Python. Vous pouvez installer Pandas à l'aide de la commande suivante -
pip install pandasSi vous utilisez Anaconda et que vous souhaitez installer en utilisant le conda gestionnaire de packages, vous pouvez utiliser la commande suivante -
conda install -c anaconda pandashmmlearn
Il s'agit d'une bibliothèque open source sous licence BSD qui se compose d'algorithmes et de modèles simples pour apprendre les modèles de Markov cachés (HMM) en Python. Vous pouvez l'installer à l'aide de la commande suivante -
pip install hmmlearnSi vous utilisez Anaconda et que vous souhaitez installer en utilisant le conda gestionnaire de packages, vous pouvez utiliser la commande suivante -
conda install -c omnia hmmlearnPyStruct
Il s'agit d'une bibliothèque d'apprentissage et de prédiction structurée. Les algorithmes d'apprentissage implémentés dans PyStruct ont des noms tels que les champs aléatoires conditionnels (CRF), les réseaux aléatoires de Markov à marge maximale (M3N) ou les machines vectorielles de support structurel. Vous pouvez l'installer à l'aide de la commande suivante -
pip install pystructCVXOPT
Il est utilisé pour l'optimisation convexe basée sur le langage de programmation Python. C'est aussi un progiciel gratuit. Vous pouvez l'installer à l'aide de la commande suivante -
pip install cvxoptSi vous utilisez Anaconda et que vous souhaitez installer en utilisant le conda gestionnaire de packages, vous pouvez utiliser la commande suivante -
conda install -c anaconda cvdoxtPandas: gestion, découpage et extraction de statistiques à partir de données de séries chronologiques
Pandas est un outil très utile si vous devez travailler avec des données de séries chronologiques. Avec l'aide de Pandas, vous pouvez effectuer les opérations suivantes -
Créez une plage de dates à l'aide du pd.date_range paquet
Indexez les pandas avec des dates en utilisant le pd.Series paquet
Rééchantillonner en utilisant le ts.resample paquet
Changer la fréquence
Exemple
L'exemple suivant montre comment gérer et découper les données de séries chronologiques à l'aide de Pandas. Notez qu'ici, nous utilisons les données mensuelles d'oscillation arctique, qui peuvent être téléchargées à partir de Monthly.ao.index.b50.current.ascii et peuvent être converties au format texte pour notre utilisation.
Gestion des données de séries chronologiques
Pour gérer les données de séries chronologiques, vous devrez effectuer les étapes suivantes -
La première étape consiste à importer les packages suivants -
import numpy as np
import matplotlib.pyplot as plt
import pandas as pdEnsuite, définissez une fonction qui lira les données du fichier d'entrée, comme indiqué dans le code ci-dessous -
def read_data(input_file):
input_data = np.loadtxt(input_file, delimiter = None)Maintenant, convertissez ces données en séries chronologiques. Pour cela, créez la plage de dates de notre série chronologique. Dans cet exemple, nous conservons un mois comme fréquence de données. Notre fichier contient les données qui commencent à partir de janvier 1950.
dates = pd.date_range('1950-01', periods = input_data.shape[0], freq = 'M')Dans cette étape, nous créons les données de séries chronologiques à l'aide de Pandas Series, comme indiqué ci-dessous -
output = pd.Series(input_data[:, index], index = dates)
return output
if __name__=='__main__':Entrez le chemin du fichier d'entrée comme indiqué ici -
input_file = "/Users/admin/AO.txt"Maintenant, convertissez la colonne au format de série temporelle, comme indiqué ici -
timeseries = read_data(input_file)Enfin, tracez et visualisez les données, en utilisant les commandes affichées -
plt.figure()
timeseries.plot()
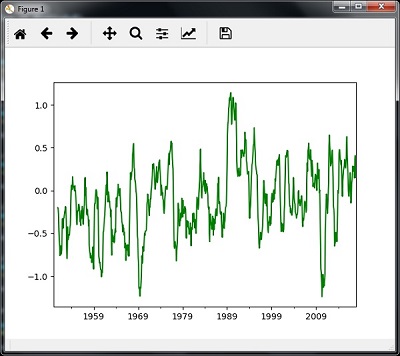
plt.show()Vous observerez les parcelles comme indiqué dans les images suivantes -


Découpage des données de séries chronologiques
Le découpage consiste à ne récupérer qu'une partie des données de la série chronologique. Dans le cadre de l'exemple, nous découpons les données uniquement de 1980 à 1990. Observez le code suivant qui effectue cette tâche -
timeseries['1980':'1990'].plot()
<matplotlib.axes._subplots.AxesSubplot at 0xa0e4b00>
plt.show()Lorsque vous exécutez le code pour découper les données de la série chronologique, vous pouvez observer le graphique suivant comme indiqué dans l'image ici -

Extraction de statistiques à partir de données de séries chronologiques
Vous devrez extraire des statistiques à partir d'une donnée donnée, dans les cas où vous devez tirer des conclusions importantes. La moyenne, la variance, la corrélation, la valeur maximale et la valeur minimale font partie de ces statistiques. Vous pouvez utiliser le code suivant si vous souhaitez extraire de telles statistiques à partir d'une série chronologique donnée -
Signifier
Vous pouvez utiliser le mean() fonction, pour trouver la moyenne, comme indiqué ici -
timeseries.mean()Ensuite, la sortie que vous observerez pour l'exemple discuté est -
-0.11143128165238671Maximum
Vous pouvez utiliser le max() fonction, pour trouver le maximum, comme indiqué ici -
timeseries.max()Ensuite, la sortie que vous observerez pour l'exemple discuté est -
3.4952999999999999Le minimum
Vous pouvez utiliser la fonction min (), pour trouver le minimum, comme indiqué ici -
timeseries.min()Ensuite, la sortie que vous observerez pour l'exemple discuté est -
-4.2656999999999998Tout obtenir en même temps
Si vous souhaitez calculer toutes les statistiques à la fois, vous pouvez utiliser le describe() fonction comme indiqué ici -
timeseries.describe()Ensuite, la sortie que vous observerez pour l'exemple discuté est -
count 817.000000
mean -0.111431
std 1.003151
min -4.265700
25% -0.649430
50% -0.042744
75% 0.475720
max 3.495300
dtype: float64Rééchantillonnage
Vous pouvez rééchantillonner les données sur une fréquence de temps différente. Les deux paramètres pour effectuer le rééchantillonnage sont -
- Période de temps
- Method
Rééchantillonnage avec moyenne ()
Vous pouvez utiliser le code suivant pour rééchantillonner les données avec la méthode mean (), qui est la méthode par défaut -
timeseries_mm = timeseries.resample("A").mean()
timeseries_mm.plot(style = 'g--')
plt.show()Ensuite, vous pouvez observer le graphique suivant comme la sortie du rééchantillonnage à l'aide de mean () -

Rééchantillonnage avec médiane ()
Vous pouvez utiliser le code suivant pour rééchantillonner les données à l'aide du median()méthode -
timeseries_mm = timeseries.resample("A").median()
timeseries_mm.plot()
plt.show()Ensuite, vous pouvez observer le graphique suivant comme la sortie du ré-échantillonnage avec median () -

Rolling Mean
Vous pouvez utiliser le code suivant pour calculer la moyenne de roulement (mobile) -
timeseries.rolling(window = 12, center = False).mean().plot(style = '-g')
plt.show()Ensuite, vous pouvez observer le graphique suivant comme la sortie de la moyenne de roulement (mobile) -
Analyse des données séquentielles par modèle de Markov caché (HMM)
HMM est un modèle statistique largement utilisé pour les données ayant une continuité et une extensibilité telles que l'analyse du marché boursier de séries chronologiques, le bilan de santé et la reconnaissance vocale. Cette section traite en détail de l'analyse des données séquentielles à l'aide du modèle de Markov caché (HMM).
Modèle de Markov caché (HMM)
HMM est un modèle stochastique basé sur le concept de chaîne de Markov basé sur l'hypothèse que la probabilité de futures statistiques dépend uniquement de l'état actuel du processus plutôt que de tout état qui l'a précédé. Par exemple, lorsque vous lancez une pièce, nous ne pouvons pas dire que le résultat du cinquième tirage sera une tête. En effet, une pièce n'a pas de mémoire et le résultat suivant ne dépend pas du résultat précédent.
Mathématiquement, HMM se compose des variables suivantes -
États (S)
C'est un ensemble d'états cachés ou latents présents dans un HMM. Il est noté S.
Symboles de sortie (O)
Il s'agit d'un ensemble de symboles de sortie possibles présents dans un HMM. Il est noté O.
Matrice de probabilité de transition d'état (A)
C'est la probabilité de faire la transition d'un état à chacun des autres états. Il est noté A.
Matrice de probabilité d'émission d'observation (B)
C'est la probabilité d'émettre / d'observer un symbole dans un état particulier. Il est noté B.
Matrice de probabilité antérieure (Π)
C'est la probabilité de démarrer à un état particulier à partir de divers états du système. Il est noté Π.
Par conséquent, un HMM peut être défini comme = (S,O,A,B,),
où,
- S = {s1,s2,…,sN} est un ensemble de N états possibles,
- O = {o1,o2,…,oM} est un ensemble de M symboles d'observation possibles,
- A est un NN Matrice de probabilité de transition d'état (TPM),
- B est un NM observation ou matrice de probabilité d'émission (EPM),
- π est un vecteur de distribution de probabilité d'état initial à N dimensions.
Exemple: analyse des données boursières
Dans cet exemple, nous allons analyser les données du marché boursier, étape par étape, pour avoir une idée du fonctionnement du HMM avec des données séquentielles ou chronologiques. Veuillez noter que nous implémentons cet exemple en Python.
Importez les packages nécessaires comme indiqué ci-dessous -
import datetime
import warningsMaintenant, utilisez les données boursières du matpotlib.finance paquet, comme indiqué ici -
import numpy as np
from matplotlib import cm, pyplot as plt
from matplotlib.dates import YearLocator, MonthLocator
try:
from matplotlib.finance import quotes_historical_yahoo_och1
except ImportError:
from matplotlib.finance import (
quotes_historical_yahoo as quotes_historical_yahoo_och1)
from hmmlearn.hmm import GaussianHMMChargez les données à partir d'une date de début et d'une date de fin, c'est-à-dire entre deux dates spécifiques comme indiqué ici -
start_date = datetime.date(1995, 10, 10)
end_date = datetime.date(2015, 4, 25)
quotes = quotes_historical_yahoo_och1('INTC', start_date, end_date)Dans cette étape, nous extrairons les guillemets de clôture chaque jour. Pour cela, utilisez la commande suivante -
closing_quotes = np.array([quote[2] for quote in quotes])Maintenant, nous allons extraire le volume d'actions échangées chaque jour. Pour cela, utilisez la commande suivante -
volumes = np.array([quote[5] for quote in quotes])[1:]Ici, prenez la différence en pourcentage des cours de clôture des actions, en utilisant le code ci-dessous -
diff_percentages = 100.0 * np.diff(closing_quotes) / closing_quotes[:-]
dates = np.array([quote[0] for quote in quotes], dtype = np.int)[1:]
training_data = np.column_stack([diff_percentages, volumes])Dans cette étape, créez et entraînez le HMM gaussien. Pour cela, utilisez le code suivant -
hmm = GaussianHMM(n_components = 7, covariance_type = 'diag', n_iter = 1000)
with warnings.catch_warnings():
warnings.simplefilter('ignore')
hmm.fit(training_data)Maintenant, générez des données en utilisant le modèle HMM, en utilisant les commandes affichées -
num_samples = 300
samples, _ = hmm.sample(num_samples)Enfin, dans cette étape, nous traçons et visualisons le pourcentage de différence et le volume des actions échangées en sortie sous forme de graphique.
Utilisez le code suivant pour tracer et visualiser les pourcentages de différence -
plt.figure()
plt.title('Difference percentages')
plt.plot(np.arange(num_samples), samples[:, 0], c = 'black')Utilisez le code suivant pour tracer et visualiser le volume d'actions échangées -
plt.figure()
plt.title('Volume of shares')
plt.plot(np.arange(num_samples), samples[:, 1], c = 'black')
plt.ylim(ymin = 0)
plt.show()