Diverses méthodes de classification

Ici, nous discuterons d'autres méthodes de classification telles que les algorithmes génétiques, l'approche par ensemble approximatif et l'approche par ensemble flou.

Algorithmes génétiques

L'idée d'algorithme génétique est dérivée de l'évolution naturelle. Dans l'algorithme génétique, tout d'abord, la population initiale est créée. Cette population initiale est constituée de règles générées aléatoirement. Nous pouvons représenter chaque règle par une chaîne de bits.

Par exemple, dans un ensemble d'apprentissage donné, les échantillons sont décrits par deux attributs booléens tels que A1 et A2. Et cet ensemble d'entraînement donné contient deux classes telles que C1 et C2.

On peut encoder la règle IF A1 AND NOT A2 THEN C2 en une petite chaîne 100. Dans cette représentation binaire, les deux bits les plus à gauche représentent l'attribut A1 et A2, respectivement.

De même, la règle IF NOT A1 AND NOT A2 THEN C1 peut être encodé comme 001.

Note- Si l'attribut a K valeurs où K> 2, alors nous pouvons utiliser les K bits pour coder les valeurs d'attribut. Les classes sont également codées de la même manière.

Points à retenir -

• Sur la base de la notion de survie du plus apte, une nouvelle population est formée qui comprend les règles les plus aptes de la population actuelle et les valeurs de progéniture de ces règles également.

• L'aptitude d'une règle est évaluée par sa précision de classification sur un ensemble d'échantillons d'entraînement.

• Les opérateurs génétiques tels que le croisement et la mutation sont appliqués pour créer une progéniture.

• En crossover, la sous-chaîne de la paire de règles est permutée pour former une nouvelle paire de règles.

• Dans la mutation, les bits sélectionnés au hasard dans la chaîne d'une règle sont inversés.

Approche d'ensemble approximative

Nous pouvons utiliser l'approche des ensembles approximatifs pour découvrir une relation structurelle dans des données imprécises et bruyantes.

Note- Cette approche ne peut être appliquée que sur des attributs à valeurs discrètes. Par conséquent, les attributs à valeur continue doivent être discrétisés avant leur utilisation.

La théorie des ensembles approximatifs est basée sur l'établissement de classes d'équivalence dans les données d'apprentissage données. Les tuples qui forment la classe d'équivalence sont indiscernables. Cela signifie que les échantillons sont identiques en ce qui concerne les attributs décrivant les données.

Il existe certaines classes dans les données du monde réel données, qui ne peuvent pas être distinguées en termes d'attributs disponibles. Nous pouvons utiliser les ensembles bruts pourroughly définir de telles classes.

Pour une classe C donnée, la définition d'ensemble approximative est approximée par deux ensembles comme suit -

• Lower Approximation of C - L'approximation inférieure de C est constituée de tous les tuples de données, qui, basés sur la connaissance de l'attribut, appartiennent certainement à la classe C.

• Upper Approximation of C - L'approximation supérieure de C est constituée de tous les tuples, celle basée sur la connaissance des attributs ne peut pas être décrite comme n'appartenant pas à C.

Le diagramme suivant montre l'approximation supérieure et inférieure de la classe C -

Approches d'ensemble flou

La théorie des ensembles flous est également appelée théorie des possibilités. Cette théorie a été proposée par Lotfi Zadeh en 1965 comme alternativetwo-value logic et probability theory. Cette théorie nous permet de travailler à un haut niveau d'abstraction. Cela nous donne également les moyens de faire face à une mesure imprécise des données.

La théorie des ensembles flous nous permet également de traiter des faits vagues ou inexacts. Par exemple, être membre d'un groupe de revenus élevés est exact (par exemple, si 50 000 $ est élevé, qu'en est-il de 49 000 $ et 48 000 $). Contrairement à l'ensemble CRISP traditionnel où l'élément appartient soit à S, soit à son complément, mais dans la théorie des ensembles flous, l'élément peut appartenir à plus d'un ensemble flou.

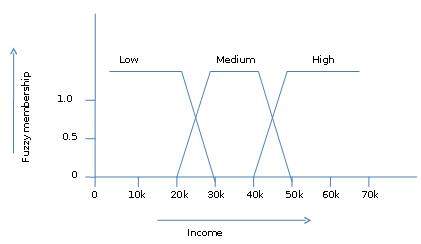
Par exemple, la valeur de revenu de 49 000 $ appartient à la fois aux ensembles flous moyens et élevés, mais à des degrés différents. La notation d'ensemble floue pour cette valeur de revenu est la suivante -

mmedium_income($49k)=0.15 and mhigh_income($49k)=0.96

où 'm' est la fonction d'appartenance qui opère respectivement sur les ensembles flous de medium_income et high_income. Cette notation peut être représentée schématiquement comme suit -