Circuits électroniques - Mise en forme d'onde linéaire
Un signal peut également être appelé Wave. Chaque vague a une certaine forme lorsqu'elle est représentée dans un graphique. Cette forme peut être de différents types tels que sinusoïdale, carrée, triangulaire, etc. qui varient en fonction de la période de temps ou ils peuvent avoir certaines formes aléatoires indépendamment de la période de temps.
Types de mise en forme des vagues
Il existe deux principaux types de mise en forme d'onde. Ils sont -
- Mise en forme d'onde linéaire
- Mise en forme d'onde non linéaire
Forme d'onde linéaire
Des éléments linéaires tels que des résistances, des condensateurs et des inducteurs sont utilisés pour mettre en forme un signal dans cette mise en forme d'onde linéaire. Une entrée d'onde sinusoïdale a une sortie d'onde sinusoïdale et, par conséquent, les entrées non sinusoïdales sont utilisées de manière plus visible pour comprendre la mise en forme d'onde linéaire.
Filtering est le processus d'atténuation du signal indésirable ou de reproduction des parties sélectionnées des composantes de fréquence d'un signal particulier.
Filtres
Dans le processus de mise en forme d'un signal, si certaines parties du signal sont ressenties comme indésirables, elles peuvent être coupées à l'aide d'un circuit de filtrage. A Filter is a circuit that can remove unwanted portions of a signal at its input. Le processus de réduction de la force du signal est également appeléAttenuation.
Nous avons peu de composants qui nous aident dans les techniques de filtrage.
UNE Capacitor a la propriété de allow AC et à block DC
Un Inductor a la propriété de allow DC mais blocks AC.
Grâce à ces propriétés, ces deux composants sont notamment utilisés pour bloquer ou autoriser AC ou DC. Les filtres peuvent être conçus en fonction de ces propriétés.
Nous avons quatre principaux types de filtres -
- Filtre passe bas
- Filtre passe-haut
- Filtre passe-bande
- Filtre d'arrêt de bande
Parlons maintenant de ces types de filtres en détail.
Filtre passe bas
Un circuit de filtre qui autorise un ensemble de fréquences inférieures à une valeur spécifiée peut être qualifié de Low pass filter. Ce filtre passe les basses fréquences. Le schéma de circuit d'un filtre passe-bas utilisant RC et RL est présenté ci-dessous.
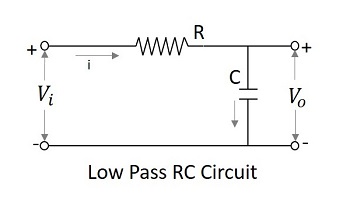
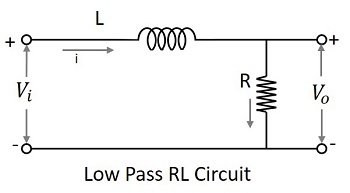
Le filtre condensateur ou RC filtre et le filtre inducteur ou filtre RL agissent tous deux comme des filtres passe-bas.
The RC filter- Le condensateur étant placé en shunt, le courant alternatif qu'il autorise est mis à la terre. Cela contourne tous les composants haute fréquence tout en autorisant le courant continu à la sortie.
The RL filter- Comme l'inductance est placée en série, le CC est autorisé à la sortie. L'inductance bloque le courant alternatif, ce qui n'est pas autorisé en sortie.
Le symbole d'un filtre passe-bas (LPF) est indiqué ci-dessous.
Fréquence de réponse
La réponse en fréquence d'un filtre pratique est comme indiqué ci-dessous et la réponse en fréquence d'un LPF idéal lorsque les considérations pratiques des composants électroniques ne sont pas prises en compte sera la suivante.
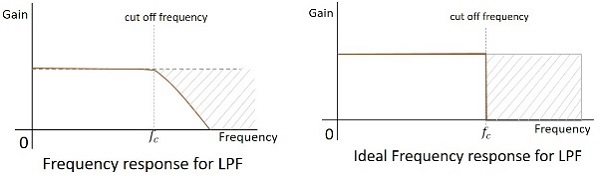
La fréquence de coupure de tout filtre est la fréquence critique $ f_ {c} $ pour laquelle le filtre est destiné à atténuer (couper) le signal. Un filtre idéal a une coupure parfaite alors qu'un filtre pratique a peu de limites.
Le filtre RLC
Après avoir connu les filtres RC et RL, on peut avoir une idée qu'il serait bon d'ajouter ces deux circuits afin d'avoir une meilleure réponse. La figure suivante montre à quoi ressemble le circuit RLC.
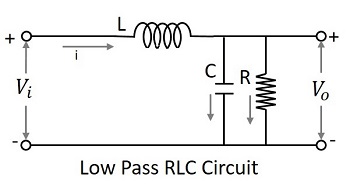
Le signal à l'entrée passe par l'inductance qui bloque le courant alternatif et autorise le courant continu. Maintenant, cette sortie est à nouveau passée à travers le condensateur en shunt, qui met à la terre le composant alternatif restant, le cas échéant, présent dans le signal, permettant le courant continu à la sortie. Ainsi, nous avons un DC pur en sortie. C'est un meilleur circuit passe-bas que les deux.
Filtre passe-haut
Un circuit de filtre qui permet un ensemble de fréquences above a specified value peut être qualifié de High pass filter. Ce filtre laisse passer les fréquences les plus élevées. Le schéma de circuit d'un filtre passe-haut utilisant RC et RL est présenté ci-dessous.
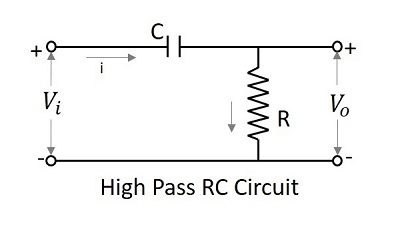
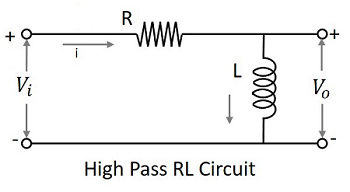
Le filtre condensateur ou RC filtre et le filtre inducteur ou RL les deux filtres agissent comme des filtres passe-haut.
Le filtre RC
Lorsque le condensateur est placé en série, il bloque les composants CC et autorise les composants CA à la sortie. Par conséquent, les composants haute fréquence apparaissent à la sortie aux bornes de la résistance.
Le filtre RL
Comme l'inducteur est placé en shunt, le DC peut être mis à la terre. Le composant AC restant apparaît à la sortie. Le symbole d'un filtre passe-haut (HPF) est indiqué ci-dessous.
Fréquence de réponse
La réponse en fréquence d'un filtre pratique est comme indiqué ci-dessous et la réponse en fréquence d'un HPF idéal lorsque les considérations pratiques des composants électroniques ne sont pas prises en compte sera la suivante.
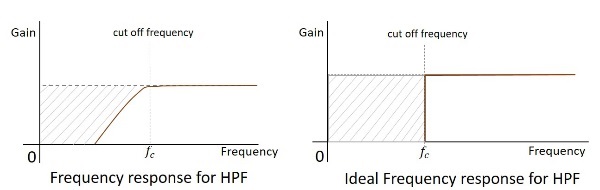
La fréquence de coupure de tout filtre est la fréquence critique $ f_ {c} $ pour laquelle le filtre est destiné à atténuer (couper) le signal. Un filtre idéal a une coupure parfaite alors qu'un filtre pratique a peu de limites.
Le filtre RLC
Après avoir connu les filtres RC et RL, on peut avoir une idée qu'il serait bon d'ajouter ces deux circuits afin d'avoir une meilleure réponse. La figure suivante montre à quoi ressemble le circuit RLC.

Le signal à l'entrée passe par le condensateur qui bloque le courant continu et autorise le courant alternatif. Maintenant, cette sortie est à nouveau passée à travers l'inductance en shunt, qui met à la terre la composante continue restante, le cas échéant, présente dans le signal, autorisant le courant alternatif en sortie. Ainsi, nous avons un AC pur en sortie. C'est un meilleur circuit passe-haut que les deux.
Filtre passe-bande
Un circuit de filtre qui permet un ensemble de fréquences between two specified values peut être qualifié de Band pass filter. Ce filtre laisse passer une bande de fréquences.
Comme nous devons éliminer quelques-unes des fréquences basses et élevées, pour sélectionner un ensemble de fréquences spécifiées, nous devons mettre en cascade un HPF et un LPF pour obtenir un BPF. Ceci peut être facilement compris même en observant les courbes de réponse en fréquence.
Le schéma de circuit d'un filtre passe-bande est illustré ci-dessous.
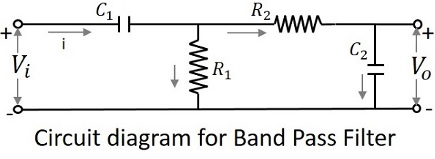
Le circuit ci-dessus peut également être construit en utilisant des circuits RL ou des circuits RLC. Celui ci-dessus est un circuit RC choisi pour une compréhension simple.
Le symbole d'un filtre passe-bande (BPF) est indiqué ci-dessous.
Fréquence de réponse
La réponse en fréquence d'un filtre pratique est comme indiqué ci-dessous et la réponse en fréquence d'un BPF idéal lorsque les considérations pratiques des composants électroniques ne sont pas prises en compte sera la suivante.
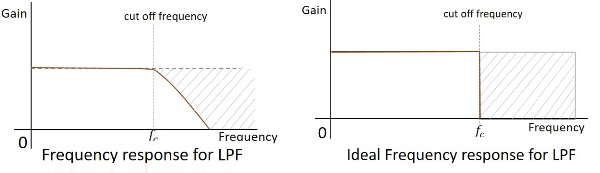
La fréquence de coupure de tout filtre est la fréquence critique $ f_ {c} $ pour laquelle le filtre est destiné à atténuer (couper) le signal. Un filtre idéal a une coupure parfaite alors qu'un filtre pratique a peu de limites.
Filtre d'arrêt de bande
Un circuit de filtre qui bloque ou atténue un ensemble de fréquences between two specified values peut être qualifié de Band Stop filter. Ce filtre rejette une bande de fréquences et peut donc également être appeléBand Reject Filter.
Comme nous devons éliminer peu de fréquences basses et hautes, pour sélectionner un ensemble de fréquences spécifiées, nous devons mettre en cascade un LPF et un HPF pour obtenir un BSF. Ceci peut être facilement compris même en observant les courbes de réponse en fréquence.
Le schéma de circuit d'un filtre coupe-bande est illustré ci-dessous.
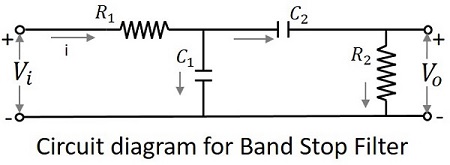
Le circuit ci-dessus peut également être construit en utilisant des circuits RL ou des circuits RLC. Celui ci-dessus est un circuit RC choisi pour une compréhension simple.
Le symbole d'un filtre coupe-bande (BSF) est indiqué ci-dessous.
Fréquence de réponse
La réponse en fréquence d'un filtre pratique est comme indiqué ci-dessous et la réponse en fréquence d'un BSF idéal lorsque les considérations pratiques des composants électroniques ne sont pas prises en compte sera la suivante.
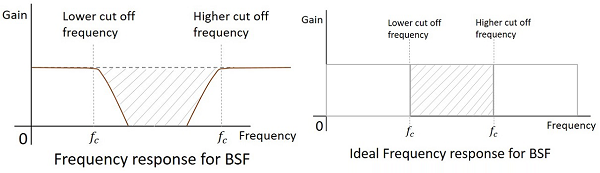
La fréquence de coupure de tout filtre est la fréquence critique $ f_ {c} $ pour laquelle le filtre est destiné à atténuer (couper) le signal. Un filtre idéal a une coupure parfaite alors qu'un filtre pratique a peu de limites.