Figures de Lissajous
Lissajous figureest le motif qui s'affiche à l'écran, lorsque des signaux sinusoïdaux sont appliqués à la fois aux plaques de déflexion horizontale et verticale du CRO. Ces modèles varieront en fonction des amplitudes, des fréquences et des différences de phase des signaux sinusoïdaux, qui sont appliqués à la fois aux plaques de déflexion horizontale et verticale du CRO.
La figure suivante montre un example de la figure de Lissajous.
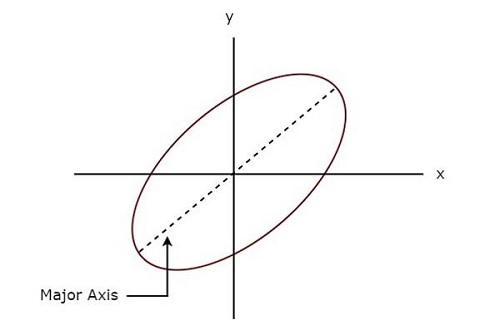
La figure de Lissajous ci-dessus est en elliptical shape et son axe principal a un certain angle d'inclinaison avec un axe x positif.
Mesures à l'aide de figures de Lissajous
Nous pouvons faire ce qui suit two measurements d'après une figure de Lissajous.
- Fréquence du signal sinusoïdal
- Différence de phase entre deux signaux sinusoïdaux
Maintenant, laissez-nous discuter de ces deux mesures une par une.
Mesure de fréquence
La figure de Lissajous sera affichée à l'écran, lorsque les signaux sinusoïdaux sont appliqués aux plaques de déflexion horizontale et verticale du CRO. Par conséquent, appliquez le signal sinusoïdal, qui a la normeknown frequencyaux plaques de déflexion horizontale du CRO. De même, appliquez le signal sinusoïdal, dontfrequency est unknown aux plaques de déflexion verticale du CRO
Soit $ f_ {H} $ et $ f_ {V} $ les fréquences des signaux sinusoïdaux, qui sont respectivement appliquées aux plaques de déflexion horizontale et verticale du CRO. La relation entre $ f_ {H} $ et $ f_ {V} $ peut êtremathematically représenté comme ci-dessous.
$$ \ frac {f_ {V}} {f_ {H}} = \ frac {n_ {H}} {n_ {V}} $$
À partir de la relation ci-dessus, nous obtiendrons la fréquence du signal sinusoïdal, qui est appliquée aux plaques de déflexion verticale du CRO comme
$ f_ {V} = \ gauche (\ frac {n_ {H}} {n_ {V}} \ droite) f_ {H} $ (équation 1)
Où,
$ n_ {H} $ est le nombre de tangences horizontales
$ n_ {V} $ est le nombre de tangences verticales
Nous pouvons trouver les valeurs de $ n_ {H} $ et $ n_ {V} $ à partir de la figure de Lissajous. Donc, en substituant les valeurs de $ n_ {H} $, $ n_ {V} $ et $ f_ {H} $ dans l'équation 1, nous obtiendrons la valeur de$f_{V}$, c'est-à-dire le frequency of sinusoidal signal qui est appliqué aux plaques de déflexion verticale du CRO.
Mesure de la différence de phase
Une figure de Lissajous est affichée à l'écran lorsque des signaux sinusoïdaux sont appliqués aux plaques de déflexion horizontale et verticale du CRO. Par conséquent, appliquez les signaux sinusoïdaux, qui ontsame amplitude and frequency aux plaques de déflexion horizontale et verticale du CRO.
Pour quelques figures de Lissajous en fonction de leur forme, nous pouvons dire directement la différence de phase entre les deux signaux sinusoïdaux.
Si la figure de Lissajous est un straight line avec une inclinaison de 45 $ ^ {\ circ} $ avec un axe x positif, alors le phase differenceentre les deux signaux sinusoïdaux sera $ 0 ^ {\ circ} $. Cela signifie qu'il n'y a pas de différence de phase entre ces deux signaux sinusoïdaux.
Si la figure de Lissajous est un straight line avec une inclinaison de 135 $ ^ {\ circ} $ avec un axe x positif, alors le phase differenceentre les deux signaux sinusoïdaux sera 180 $ ^ {\ circ} $. Cela signifie que ces deux signaux sinusoïdaux sont déphasés.
Si la figure de Lissajous est circular shape, alors la différence de phase entre les deux signaux sinusoïdaux sera de 90 $ ^ {\ circ} $ ou de 270 $ ^ {\ circ} $.
Nous pouvons calculer la différence de phase entre les deux signaux sinusoïdaux en utilisant des formules, lorsque les chiffres de Lissajous sont de elliptical shape.
Si le grand axe d'une figure de Lissajous de forme elliptique ayant un angle d'inclinaison est compris entre $ 0 ^ {\ circ} $ et $ 90 ^ {\ circ} $ avec un axe x positif, alors la différence de phase entre les deux signaux sinusoïdaux sera.
$$ \ phi = \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = \ sin ^ {- 1} \ left (\ frac {y_ {1} } {y_ {2}} \ right) $$
Si le grand axe d'une figure de Lissajous de forme elliptique ayant un angle d'inclinaison se situe entre $ 90 ^ {\ circ} $ et $ 180 ^ {\ circ} $ avec un axe x positif, alors la différence de phase entre les deux signaux sinusoïdaux sera.
$$ \ phi = 180 - \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = 180 - \ sin ^ {- 1} \ left (\ frac { y_ {1}} {y_ {2}} \ right) $$
Where,
$ x_ {1} $ est la distance de l'origine au point sur l'axe des x, où la figure de Lissajous de forme elliptique se coupe
$ x_ {2} $ est la distance de l'origine à la tangente verticale de la figure de Lissajous de forme elliptique
$ y_ {1} $ est la distance de l'origine au point sur l'axe des y, où la figure elliptique de Lissajous se croise
$ y_ {2} $ est la distance de l'origine à la tangente horizontale de la figure de Lissajous de forme elliptique
Dans ce chapitre, découvrez comment trouver la fréquence d'un signal sinusoïdal inconnu et la différence de phase entre deux signaux sinusoïdaux à partir de figures de Lissajous à l'aide de formules.