Théorie des graphes - Exemples
Dans ce chapitre, nous couvrirons quelques exemples standard pour démontrer les concepts que nous avons déjà abordés dans les chapitres précédents.
Exemple 1
Find the number of spanning trees in the following graph.
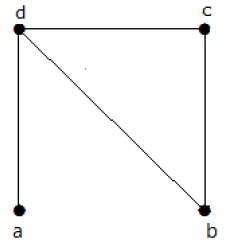
Solution
Le nombre d'arbres couvrant obtenu à partir du graphique ci-dessus est de 3. Ils sont les suivants -
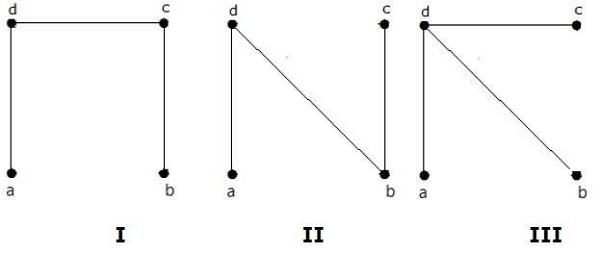
Ces trois sont les arbres couvrant les graphiques donnés. Ici, les graphes I et II sont isomorphes l'un par rapport à l'autre. De toute évidence, le nombre d'arbres couvrant non isomorphes est de deux.
Exemple 2
How many simple non-isomorphic graphs are possible with 3 vertices?
Solution
Il existe 4 graphes non isomorphes possibles avec 3 sommets. Ils sont présentés ci-dessous.
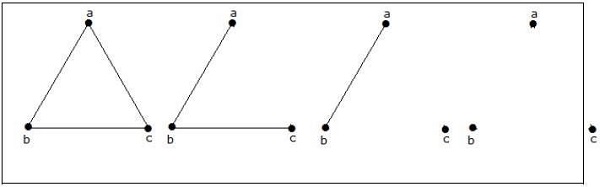
Exemple 3
Let ‘G’ be a connected planar graph with 20 vertices and the degree of each vertex is 3. Find the number of regions in the graph.
Solution
Par la somme du théorème des degrés,
20 Σ i = 1 degré (Vi) = 2 | E |
20 (3) = 2 | E |
| E | = 30
Par la formule d'Euler,
| V | + | R | = | E | + 2
20+ | R | = 30 + 2
| R | = 12
Par conséquent, le nombre de régions est de 12.
Exemple 4
What is the chromatic number of complete graph Kn?
Solution
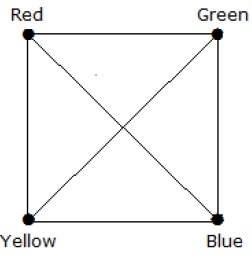
Dans un graphe complet, chaque sommet est adjacent à ses (n – 1) sommets restants. Par conséquent, chaque sommet nécessite une nouvelle couleur. D'où le nombre chromatique K n = n.
Exemple 5
What is the matching number for the following graph?
Solution
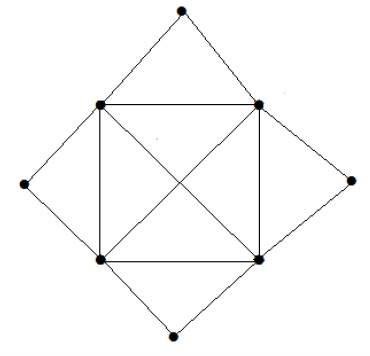
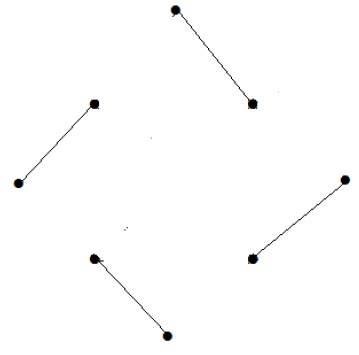
Nombre de sommets = 9
Nous ne pouvons faire correspondre que 8 sommets.
Le numéro correspondant est 4.
Exemple 6
What is the line covering number of for the following graph?
Solution
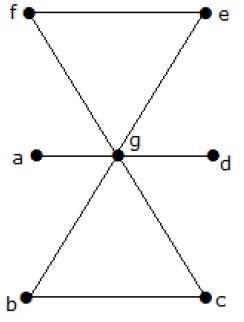
Nombre de sommets = | V | = n = 7
Numéro de couverture de ligne = (α 1 ) ≥ [n / 2] = 3
α 1 ≥ 3
En utilisant 3 arêtes, nous pouvons couvrir tous les sommets.
Par conséquent, le numéro de couverture de ligne est 3.