Keras - Réseau neuronal à convolution

Modifions le modèle de MPL en Convolution Neural Network (CNN) pour notre problème d'identification des chiffres antérieur.

CNN peut être représenté comme ci-dessous -

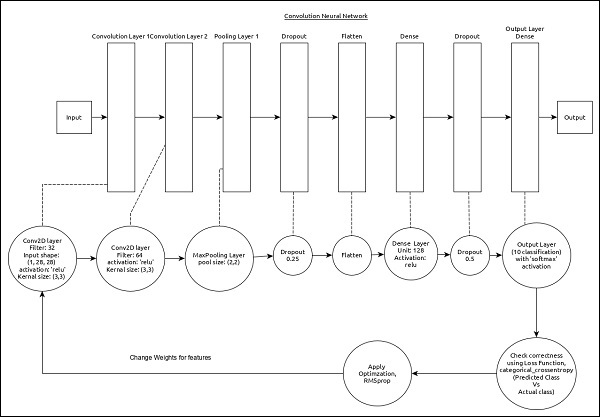
Les principales caractéristiques du modèle sont les suivantes -

La couche d'entrée se compose de (1, 8, 28) valeurs.
Première couche, Conv2D se compose de 32 filtres et d'une fonction d'activation 'relu' avec une taille de noyau, (3,3).
Deuxième couche, Conv2D se compose de 64 filtres et d'une fonction d'activation 'relu' avec une taille de noyau, (3,3).
Thrid couche, MaxPooling a une taille de piscine de (2, 2).
Cinquième couche, Flatten est utilisé pour aplatir toutes ses entrées en une seule dimension.
Sixième couche, Dense se compose de 128 neurones et d'une fonction d'activation «relu».
Septième couche, Dropout a 0,5 comme valeur.
La huitième et dernière couche se compose de 10 neurones et d'une fonction d'activation «softmax».
Utilisation categorical_crossentropy comme fonction de perte.
Utilisation Adadelta() comme Optimizer.
Utilisation accuracy comme métriques.
Utilisez 128 comme taille de lot.
Utilisez 20 comme époques.

Step 1 − Import the modules

Importons les modules nécessaires.

import keras 
from keras.datasets import mnist 
from keras.models import Sequential 
from keras.layers import Dense, Dropout, Flatten 
from keras.layers import Conv2D, MaxPooling2D 
from keras import backend as K 
import numpy as np

Step 2 − Load data

Importons le jeu de données mnist.

(x_train, y_train), (x_test, y_test) = mnist.load_data()

Step 3 − Process the data

Modifions le jeu de données en fonction de notre modèle, afin qu'il puisse être alimenté dans notre modèle.

img_rows, img_cols = 28, 28 

if K.image_data_format() == 'channels_first': 
   x_train = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols) 
   x_test = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols) 
   input_shape = (1, img_rows, img_cols) 
else: 
   x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1) 
   x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1) 
   input_shape = (img_rows, img_cols, 1) 
   
x_train = x_train.astype('float32') 
x_test = x_test.astype('float32') 
x_train /= 255 
x_test /= 255 

y_train = keras.utils.to_categorical(y_train, 10) 
y_test = keras.utils.to_categorical(y_test, 10)

Le traitement des données est similaire au modèle MPL à l'exception de la forme des données d'entrée et de la configuration du format d'image.

Step 4 − Create the model

Créons le modèle actuel.

model = Sequential() 
model.add(Conv2D(32, kernel_size = (3, 3),  
   activation = 'relu', input_shape = input_shape)) 
model.add(Conv2D(64, (3, 3), activation = 'relu')) 
model.add(MaxPooling2D(pool_size = (2, 2))) 
model.add(Dropout(0.25)) model.add(Flatten()) 
model.add(Dense(128, activation = 'relu')) 
model.add(Dropout(0.5)) 
model.add(Dense(10, activation = 'softmax'))

Step 5 − Compile the model

Compilons le modèle en utilisant la fonction de perte sélectionnée, l'optimiseur et les métriques.

model.compile(loss = keras.losses.categorical_crossentropy, 
   optimizer = keras.optimizers.Adadelta(), metrics = ['accuracy'])

Step 6 − Train the model

Entraînons le modèle en utilisant fit() méthode.

model.fit(
   x_train, y_train, 
   batch_size = 128, 
   epochs = 12, 
   verbose = 1, 
   validation_data = (x_test, y_test)
)

L'exécution de l'application produira les informations ci-dessous -

Train on 60000 samples, validate on 10000 samples Epoch 1/12 
60000/60000 [==============================] - 84s 1ms/step - loss: 0.2687 
- acc: 0.9173 - val_loss: 0.0549 - val_acc: 0.9827 Epoch 2/12 
60000/60000 [==============================] - 86s 1ms/step - loss: 0.0899 
- acc: 0.9737 - val_loss: 0.0452 - val_acc: 0.9845 Epoch 3/12 
60000/60000 [==============================] - 83s 1ms/step - loss: 0.0666 
- acc: 0.9804 - val_loss: 0.0362 - val_acc: 0.9879 Epoch 4/12 
60000/60000 [==============================] - 81s 1ms/step - loss: 0.0564 
- acc: 0.9830 - val_loss: 0.0336 - val_acc: 0.9890 Epoch 5/12 
60000/60000 [==============================] - 86s 1ms/step - loss: 0.0472 
- acc: 0.9861 - val_loss: 0.0312 - val_acc: 0.9901 Epoch 6/12 
60000/60000 [==============================] - 83s 1ms/step - loss: 0.0414 
- acc: 0.9877 - val_loss: 0.0306 - val_acc: 0.9902 Epoch 7/12 
60000/60000 [==============================] - 89s 1ms/step - loss: 0.0375 
-acc: 0.9883 - val_loss: 0.0281 - val_acc: 0.9906 Epoch 8/12 
60000/60000 [==============================] - 91s 2ms/step - loss: 0.0339 
- acc: 0.9893 - val_loss: 0.0280 - val_acc: 0.9912 Epoch 9/12 
60000/60000 [==============================] - 89s 1ms/step - loss: 0.0325 
- acc: 0.9901 - val_loss: 0.0260 - val_acc: 0.9909 Epoch 10/12 
60000/60000 [==============================] - 89s 1ms/step - loss: 0.0284 
- acc: 0.9910 - val_loss: 0.0250 - val_acc: 0.9919 Epoch 11/12 
60000/60000 [==============================] - 86s 1ms/step - loss: 0.0287 
- acc: 0.9907 - val_loss: 0.0264 - val_acc: 0.9916 Epoch 12/12 
60000/60000 [==============================] - 86s 1ms/step - loss: 0.0265 
- acc: 0.9920 - val_loss: 0.0249 - val_acc: 0.9922

Step 7 − Evaluate the model

Évaluons le modèle à l'aide de données de test.

score = model.evaluate(x_test, y_test, verbose = 0) 

print('Test loss:', score[0]) 
print('Test accuracy:', score[1])

L'exécution du code ci-dessus produira les informations ci-dessous -

Test loss: 0.024936060590433316 
Test accuracy: 0.9922

La précision du test est de 99,22%. Nous avons créé un meilleur modèle pour identifier les chiffres de l'écriture manuscrite.

Step 8 − Predict

Enfin, prédisez le chiffre à partir d'images comme ci-dessous -

pred = model.predict(x_test) 
pred = np.argmax(pred, axis = 1)[:5] 
label = np.argmax(y_test,axis = 1)[:5] 

print(pred) 
print(label)

La sortie de l'application ci-dessus est la suivante -

[7 2 1 0 4] 
[7 2 1 0 4]

La sortie des deux tableaux est identique et indique que notre modèle prédit correctement les cinq premières images.