LISP - Arbre
Vous pouvez construire des structures de données arborescentes à partir de cellules cons, sous forme de listes de listes.
Pour implémenter des structures arborescentes, vous devrez concevoir des fonctionnalités qui traverseraient les cellules cons, dans un ordre spécifique, par exemple, pré-ordre, ordre et post-ordre pour les arbres binaires.
Arborescence en tant que liste de listes
Considérons une arborescence composée de contre-cellules qui forment la liste de listes suivante -
((1 2) (3 4) (5 6)).
Schématiquement, il pourrait être exprimé comme -
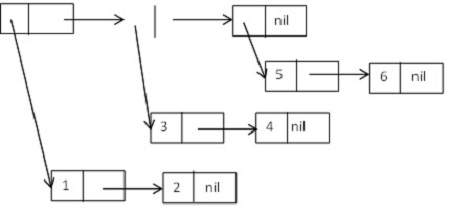
Fonctions d'arborescence dans LISP
Bien que vous ayez principalement besoin d'écrire vos propres fonctionnalités d'arborescence en fonction de vos besoins spécifiques, LISP fournit certaines fonctions d'arborescence que vous pouvez utiliser.
Outre toutes les fonctions de liste, les fonctions suivantes fonctionnent en particulier sur les structures arborescentes -
| N ° Sr. | Description de la fonction |
|---|---|
| 1 | copy-tree x & vecp facultatif Il renvoie une copie de l'arbre des contre-cellules x. Il copie récursivement à la fois la voiture et les directions cdr. Si x n'est pas une cellule contre, la fonction renvoie simplement x inchangé. Si l'argument optionnel vecp est vrai, cette fonction copie les vecteurs (récursivement) ainsi que les cellules cons. |
| 2 | tree-equal xy & key: test: test-not: key Il compare deux arbres de cellules contre. Si x et y sont tous les deux des cellules contre, leurs voitures et leurs cdr sont comparés récursivement. Si ni x ni y ne sont une cellule contre, ils sont comparés par eql, ou selon le test spécifié. La fonction: key, si elle est spécifiée, est appliquée aux éléments des deux arbres. |
| 3 | subst nouvel ancien arbre et clé: test: test-not: clé Il remplace les occurrences d'un ancien élément donné par un nouvel élément, dans l' arborescence , qui est un arbre de contre-cellules. |
| 4 | nsubst nouvel ancien arbre et clé: test: test-not: clé Cela fonctionne de la même manière que subst, mais il détruit l'arbre d'origine. |
| 5 | sublis arborescence & clé: test: test-not: clé Il fonctionne comme Subst, sauf qu'il faut une liste association alist de paires nouveaux-anciens. Chaque élément de l'arbre (après application de la fonction: key, le cas échéant), est comparé aux voitures d'alist; s'il correspond, il est remplacé par le cdr correspondant. |
| 6 | nsublis arborescence & clé: test: test-not: clé Cela fonctionne de la même manière que sublis, mais une version destructrice. |
Exemple 1
Créez un nouveau fichier de code source nommé main.lisp et tapez le code suivant dedans.
(setq lst (list '(1 2) '(3 4) '(5 6)))
(setq mylst (copy-list lst))
(setq tr (copy-tree lst))
(write lst)
(terpri)
(write mylst)
(terpri)
(write tr)Lorsque vous exécutez le code, il renvoie le résultat suivant -
((1 2) (3 4) (5 6))
((1 2) (3 4) (5 6))
((1 2) (3 4) (5 6))Exemple 2
Créez un nouveau fichier de code source nommé main.lisp et tapez le code suivant dedans.
(setq tr '((1 2 (3 4 5) ((7 8) (7 8 9)))))
(write tr)
(setq trs (subst 7 1 tr))
(terpri)
(write trs)Lorsque vous exécutez le code, il renvoie le résultat suivant -
((1 2 (3 4 5) ((7 8) (7 8 9))))
((7 2 (3 4 5) ((7 8) (7 8 9))))Construire votre propre arbre
Essayons de construire notre propre arbre, en utilisant les fonctions de liste disponibles dans LISP.
Commençons par créer un nouveau nœud contenant des données
(defun make-tree (item)
"it creates a new node with item."
(cons (cons item nil) nil)
)Ensuite, ajoutons un nœud enfant dans l'arborescence - il faudra deux nœuds d'arbre et ajouter le deuxième arbre en tant qu'enfant du premier.
(defun add-child (tree child)
(setf (car tree) (append (car tree) child))
tree)Cette fonction retournera le premier enfant d'un arbre donné - elle prendra un nœud d'arbre et retournera le premier enfant de ce nœud, ou nil, si ce nœud n'a pas de nœud enfant.
(defun first-child (tree)
(if (null tree)
nil
(cdr (car tree))
)
)Cette fonction retournera le prochain frère d'un nœud donné - elle prend un nœud d'arbre comme argument et renvoie une référence au nœud frère suivant, ou nil, si le nœud n'en a pas.
(defun next-sibling (tree)
(cdr tree)
)Enfin, nous avons besoin d'une fonction pour renvoyer les informations dans un nœud -
(defun data (tree)
(car (car tree))
)Exemple
Cet exemple utilise les fonctionnalités ci-dessus -
Créez un nouveau fichier de code source nommé main.lisp et tapez le code suivant dedans.
(defun make-tree (item)
"it creates a new node with item."
(cons (cons item nil) nil)
)
(defun first-child (tree)
(if (null tree)
nil
(cdr (car tree))
)
)
(defun next-sibling (tree)
(cdr tree)
)
(defun data (tree)
(car (car tree))
)
(defun add-child (tree child)
(setf (car tree) (append (car tree) child))
tree
)
(setq tr '((1 2 (3 4 5) ((7 8) (7 8 9)))))
(setq mytree (make-tree 10))
(write (data mytree))
(terpri)
(write (first-child tr))
(terpri)
(setq newtree (add-child tr mytree))
(terpri)
(write newtree)Lorsque vous exécutez le code, il renvoie le résultat suivant -
10
(2 (3 4 5) ((7 8) (7 8 9)))
((1 2 (3 4 5) ((7 8) (7 8 9)) (10)))