PNL - Analyse au niveau du mot
Dans ce chapitre, nous allons comprendre l'analyse de niveau mondial dans le traitement du langage naturel.
Expressions régulières
Une expression régulière (RE) est un langage permettant de spécifier des chaînes de recherche de texte. RE nous aide à faire correspondre ou à trouver d'autres chaînes ou ensembles de chaînes, en utilisant une syntaxe spécialisée contenue dans un modèle. Les expressions régulières sont utilisées pour rechercher des textes sous UNIX ainsi que dans MS WORD de la même manière. Nous avons différents moteurs de recherche utilisant un certain nombre de fonctionnalités RE.
Propriétés des expressions régulières
Voici quelques-unes des propriétés importantes de RE -
Le mathématicien américain Stephen Cole Kleene a officialisé le langage des expressions régulières.
RE est une formule dans un langage spécial, qui peut être utilisée pour spécifier des classes simples de chaînes, une séquence de symboles. En d'autres termes, on peut dire que RE est une notation algébrique pour caractériser un ensemble de chaînes.
L'expression régulière nécessite deux choses, l'une est le modèle que nous souhaitons rechercher et l'autre est un corpus de texte à partir duquel nous devons rechercher.
Mathématiquement, une expression régulière peut être définie comme suit -
ε est une expression régulière, qui indique que la langue a une chaîne vide.
φ est une expression régulière qui indique qu'il s'agit d'une langue vide.
Si X et Y sont des expressions régulières, alors
X, Y
X.Y(Concatenation of XY)
X+Y (Union of X and Y)
X*, Y* (Kleen Closure of X and Y)
sont également des expressions régulières.
Si une chaîne est dérivée des règles ci-dessus, ce serait également une expression régulière.
Exemples d'expressions régulières
Le tableau suivant montre quelques exemples d'expressions régulières -
| Expressions régulières | Ensemble régulier |
|---|---|
| (0 + 10 *) | {0, 1, 10, 100, 1 000, 10 000,…} |
| (0 * 10 *) | {1, 01, 10, 010, 0010,…} |
| (0 + ε) (1 + ε) | {ε, 0, 1, 01} |
| (a + b) * | Ce serait un ensemble de chaînes de a et b de n'importe quelle longueur qui inclut également la chaîne nulle, c'est-à-dire {ε, a, b, aa, ab, bb, ba, aaa …….} |
| (a + b) * abb | Ce serait un ensemble de chaînes de a et b se terminant par la chaîne abb ie {abb, aabb, babb, aaabb, ababb, ………… ..} |
| (11) * | Il serait composé d'un nombre pair de 1 qui comprend également une chaîne vide, c'est-à-dire {ε, 11, 1111, 111111, ……….} |
| (aa) * (bb) * b | Ce serait un ensemble de chaînes composé d'un nombre pair de a suivi d'un nombre impair de b, c'est-à-dire {b, aab, aabbb, aabbbbb, aaaab, aaaabbb, ………… ..} |
| (aa + ab + ba + bb) * | Ce serait une chaîne de a et b de longueur paire qui peut être obtenue en concaténant n'importe quelle combinaison des chaînes aa, ab, ba et bb y compris null ie {aa, ab, ba, bb, aaab, aaba, …………. .} |
Ensembles réguliers et leurs propriétés
Il peut être défini comme l'ensemble qui représente la valeur de l'expression régulière et comprend des propriétés spécifiques.
Propriétés des ensembles réguliers
Si nous faisons l'union de deux ensembles réguliers, alors l'ensemble résultant serait également regula.
Si nous faisons l'intersection de deux ensembles réguliers, alors l'ensemble résultant serait également régulier.
Si nous faisons le complément d'ensembles réguliers, alors l'ensemble résultant serait également régulier.
Si nous faisons la différence de deux ensembles réguliers, alors l'ensemble résultant serait également régulier.
Si nous inversons les ensembles réguliers, alors l'ensemble résultant serait également régulier.
Si nous prenons la fermeture des ensembles réguliers, alors l'ensemble résultant serait également régulier.
Si nous faisons la concaténation de deux ensembles réguliers, alors l'ensemble résultant serait également régulier.
Automates à états finis
Le terme automates, dérivé du mot grec «αὐτόματα» signifiant «auto-agissant», est le pluriel d'automate qui peut être défini comme un dispositif informatique autopropulsé abstrait qui suit automatiquement une séquence prédéterminée d'opérations.
Un automate ayant un nombre fini d'états est appelé un automate fini (FA) ou automate à états finis (FSA).
Mathématiquement, un automate peut être représenté par un 5-uplet (Q, Σ, δ, q0, F), où -
Q est un ensemble fini d'états.
Σ est un ensemble fini de symboles, appelé alphabet de l'automate.
δ est la fonction de transition
q0 est l'état initial à partir duquel toute entrée est traitée (q0 ∈ Q).
F est un ensemble d'états / états finaux de Q (F ⊆ Q).
Relation entre les automates finis, les grammaires régulières et les expressions régulières
Les points suivants nous donneront une vision claire de la relation entre les automates finis, les grammaires régulières et les expressions régulières -
Comme nous savons que les automates à états finis sont le fondement théorique du travail de calcul et que les expressions régulières sont une façon de les décrire.
Nous pouvons dire que toute expression régulière peut être implémentée en tant que FSA et que tout FSA peut être décrit avec une expression régulière.
D'autre part, l'expression régulière est un moyen de caractériser une sorte de langage appelé langage régulier. Par conséquent, nous pouvons dire que le langage régulier peut être décrit à l'aide de FSA et d'expression régulière.
La grammaire régulière, une grammaire formelle qui peut être régulière à droite ou régulière à gauche, est une autre façon de caractériser la langue régulière.
Le diagramme suivant montre que les automates finis, les expressions régulières et les grammaires régulières sont les moyens équivalents de décrire les langages réguliers.
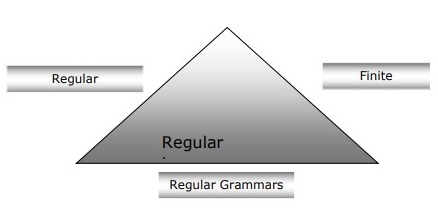
Types d'automatisation à états finis (FSA)
L'automatisation à l'état fini est de deux types. Voyons quels sont les types.
Automatisation déterministe finie (DFA)
Il peut être défini comme le type d'automatisation finie dans lequel, pour chaque symbole d'entrée, nous pouvons déterminer l'état vers lequel la machine se déplacera. Il a un nombre fini d'états, c'est pourquoi la machine est appelée Automate Déterministe Fini (DFA).
Mathématiquement, un DFA peut être représenté par un 5-tuple (Q, Σ, δ, q0, F), où -
Q est un ensemble fini d'états.
Σ est un ensemble fini de symboles, appelé alphabet de l'automate.
δ est la fonction de transition où δ: Q × Σ → Q.
q0 est l'état initial à partir duquel toute entrée est traitée (q0 ∈ Q).
F est un ensemble d'états / états finaux de Q (F ⊆ Q).
Alors que graphiquement, un DFA peut être représenté par des diagraphies appelés diagrammes d'état où -
Les états sont représentés par vertices.
Les transitions sont indiquées par étiquetées arcs.
L'état initial est représenté par un empty incoming arc.
L'état final est représenté par double circle.
Exemple de DFA
Supposons qu'un DFA soit
Q = {a, b, c},
Σ = {0, 1},
q 0 = {a},
F = {c},
La fonction de transition δ est représentée dans le tableau comme suit -
| État actuel | État suivant pour l'entrée 0 | État suivant pour l'entrée 1 |
|---|---|---|
| UNE | une | B |
| B | b | UNE |
| C | c | C |
La représentation graphique de ce DFA serait la suivante:

Automatisation finie non déterministe (NDFA)
Il peut être défini comme le type d'automatisation finie où, pour chaque symbole d'entrée, nous ne pouvons pas déterminer l'état vers lequel la machine se déplacera, c'est-à-dire que la machine peut passer à n'importe quelle combinaison d'états. Il a un nombre fini d'états, c'est pourquoi la machine est appelée Automatisation Finie Non déterministe (NDFA).
Mathématiquement, NDFA peut être représenté par un 5-tuple (Q, Σ, δ, q0, F), où -
Q est un ensemble fini d'états.
Σ est un ensemble fini de symboles, appelé alphabet de l'automate.
δ: -est la fonction de transition où δ: Q × Σ → 2 Q .
q0: -est l'état initial à partir duquel toute entrée est traitée (q0 ∈ Q).
F: -est un ensemble d'états finaux de Q (F ⊆ Q).
Alors que graphiquement (identique à DFA), un NDFA peut être représenté par des diagraphies appelées diagrammes d'état où -
Les états sont représentés par vertices.
Les transitions sont indiquées par étiquetées arcs.
L'état initial est représenté par un empty incoming arc.
L'état final est représenté par double circle.
Exemple de NDFA
Supposons qu'un NDFA soit
Q = {a, b, c},
Σ = {0, 1},
q 0 = {a},
F = {c},
La fonction de transition δ est représentée dans le tableau comme suit -
| État actuel | État suivant pour l'entrée 0 | État suivant pour l'entrée 1 |
|---|---|---|
| UNE | un B | B |
| B | C | a, c |
| C | avant JC | C |
La représentation graphique de cette NDFA serait la suivante -

Analyse morphologique
Le terme analyse morphologique est lié à l'analyse des morphèmes. Nous pouvons définir l'analyse morphologique comme le problème consistant à reconnaître qu'un mot se décompose en unités significatives plus petites appelées morphèmes, produisant une sorte de structure linguistique pour lui. Par exemple, nous pouvons diviser le mot renards en deux, renard et -es . Nous pouvons voir que le mot renards , est composé de deux morphèmes, l'un est renard et l'autre est -es .
En un autre sens, on peut dire que la morphologie est l'étude de -
La formation des mots.
L'origine des mots.
Formes grammaticales des mots.
Utilisation de préfixes et suffixes dans la formation des mots.
Comment les parties du discours (PoS) d'une langue sont formées.
Types de morphèmes
Les morphèmes, les plus petites unités porteuses de sens, peuvent être divisés en deux types -
Stems
Ordre des mots
Tiges
C'est l'unité centrale significative d'un mot. On peut aussi dire que c'est la racine du mot. Par exemple, dans le mot renards, la tige est le renard.
Affixes- Comme leur nom l'indique, ils ajoutent du sens et des fonctions grammaticales supplémentaires aux mots. Par exemple, dans le mot renards, l'affixe est - es.
En outre, les affixes peuvent également être divisés en quatre types suivants -
Prefixes- Comme son nom l'indique, les préfixes précèdent le radical. Par exemple, dans le mot unbuckle, un est le préfixe.
Suffixes- Comme son nom l'indique, les suffixes suivent la racine. Par exemple, dans le mot chats, -s est le suffixe.
Infixes- Comme son nom l'indique, des infixes sont insérés à l'intérieur de la tige. Par exemple, le mot cupful peut être mis au pluriel en cupsful en utilisant -s comme infixe.
Circumfixes- Ils précèdent et suivent la tige. Il y a très moins d'exemples de circonfixes en langue anglaise. Un exemple très courant est «A-ing» où nous pouvons utiliser -A précéder et -ing suit la tige.
Ordre des mots
L'ordre des mots serait décidé par analyse morphologique. Voyons maintenant les exigences pour construire un analyseur morphologique -
Lexique
La toute première exigence pour construire un analyseur morphologique est le lexique, qui comprend la liste des tiges et des affixes ainsi que les informations de base les concernant. Par exemple, les informations comme si la racine est la racine du nom ou la racine du verbe, etc.
Morphotactique
Il s'agit essentiellement du modèle de classement des morphèmes. En un autre sens, le modèle expliquant quelles classes de morphèmes peuvent suivre d'autres classes de morphèmes à l'intérieur d'un mot. Par exemple, le fait morphotactique est que le morphème pluriel anglais suit toujours le nom plutôt que de le précéder.
Règles orthographiques
Ces règles d'orthographe sont utilisées pour modéliser les changements intervenant dans un mot. Par exemple, la règle de conversion de y en ie en mot comme ville + s = villes et non villes.