NGN - Modulation de code d'impulsion
L'avènement des communications vocales et de données à haut débit a entraîné le besoin d'un moyen rapide pour le transport des informations. Les circuits ou liaisons numériques ont évolué à partir de la nécessité de transmettre la voix ou les données sous forme numérique.
La conversion de la forme analogique à la forme numérique suit un processus en quatre étapes ( voir la figure suivante ) et sera détaillée dans les sections suivantes.

Échantillonnage
Les fréquences vocales prennent la forme d'un signal analogique, c'est-à-dire une onde sinusoïdale ( voir la figure suivante ). Ce signal doit être converti en une forme binaire pour être transporté sur un support numérique. La première étape de cette conversion consiste à convertir le signal audio en unPulse Amplitude Modulation(PAM)signal. Ce processus est généralement appelésampling.
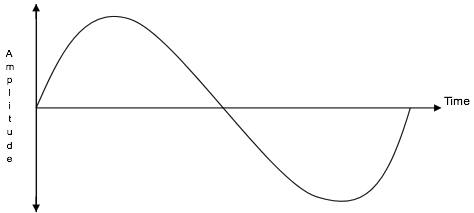
Le processus d'échantillonnage doit collecter suffisamment d'informations à partir des fréquences vocales entrantes pour permettre une copie du signal d'origine. Les fréquences vocales sont normalement de l'ordre de300Hz to 3400Hz, généralement connu sous le nom de commercial speech band.
Pour obtenir un échantillon, une fréquence d'échantillonnage est appliquée à la fréquence vocale d'origine. La fréquence d'échantillonnage est déterminée par leNyquist Sampling Theorem, qui dicte que “the frequency of sampling should be at least twice the highest frequency component.”
Cela garantit qu'un échantillon est prélevé au moins une fois dans chaque demi-cycle, éliminant ainsi la possibilité d'échantillonner à des points nuls du cycle, qui n'auraient aucune amplitude. Il en résulte que la fréquence d'échantillonnage est au minimum de 6,8 KHz.
La norme européenne échantillonne un signal entrant à 8 KHZ, assurant un échantillon, est prélevé chaque 125micro secondsou 1 / 8000e de seconde ( voir la figure suivante ).
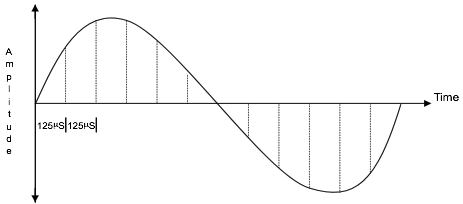
Quantification
L'amplitude de chaque échantillon se verrait idéalement attribuer un code binaire (1 ou 0), mais comme il peut y avoir un nombre infini d'amplitudes; par conséquent, il doit y avoir un nombre infini de codes binaires disponibles. Ce ne serait pas pratique, donc un autre processus doit être utilisé, qui est connu commequantizing.
La quantification compare le signal PAM à une échelle de quantification, qui a un nombre fini de niveaux discrets. L'échelle de quantification se divise en 256 niveaux de quantification, dont 128 sont des niveaux positifs et 128 sont des niveaux négatifs.
L'étape de quantification consiste à attribuer un code binaire unique à 8 bits approprié à l'intervalle de quantification dans lequel tombe l'amplitude du signal PAM ( voir la figure suivante ).
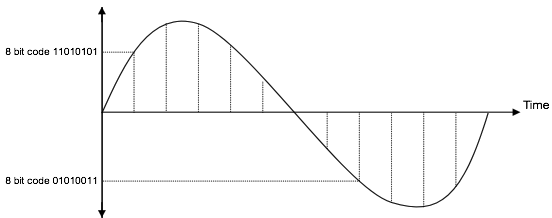
Celui-ci comprend 1 bit de polarité avec les 7 bits restants utilisés pour identifier le niveau de quantification ( comme indiqué sur la figure ci-dessus ).
Le premier bit comme vu précédemment est le bit de polarité, les trois bits suivants pour le code de segment, donnant huit codes de segment, et les quatre bits restants pour le niveau de quantification, donnant seize niveaux de quantification.
Companding
Le processus de quantification lui-même conduit à un phénomène connu sous le nom de quantization distortion. Cela se produit lorsque l'amplitude du signal échantillonné se situe entre les niveaux de quantification. Le signal est toujours arrondi au niveau entier le plus proche. Cette différence entre le niveau échantillonné et le niveau de quantification est une distorsion de quantification.
Le taux de changement de l'amplitude d'un signal varie à différentes parties du cycle. Cela se produit le plus aux hautes fréquences car l'amplitude du signal change plus rapidement qu'aux basses fréquences. Pour surmonter cela, le premier code de segment a les niveaux de quantification proches les uns des autres. Le code du segment suivant est alors le double de la hauteur du précédent et ainsi de suite. Ce processus est connu sous le nom decompanding, car il comprime des signaux plus grands et étend des signaux plus petits.

En Europe, ils utilisent le A-law de companding, par rapport à l'Amérique du Nord et au Japon qui utilisent le μ law.
Comme la distorsion de quantification est équivalente au bruit, la compression améliore le rapport signal sur bruit sur les signaux de faible amplitude et produit un rapport signal sur bruit acceptable sur toute la gamme d'amplitudes.
Codage
Pour que les informations binaires soient transmises sur un chemin numérique, les informations doivent être modifiées en un code de ligne approprié. La technique d'encodage utilisée en Europe est connue sous le nom deHigh Density Bipolar 3 (HDB3).
HDB3 est dérivé d'un code de ligne appelé AMI ou Alternate Mark Inversion. Dans le codage AMI, 3 valeurs sont utilisées: aucun signal pour représenter un 0 binaire et un signal positif ou négatif qui est utilisé alternativement pour représenter un 1 binaire.
Un problème associé au codage AMI se produit lorsqu'une longue chaîne de zéros est transmise. Cela peut entraîner des problèmes de boucle de verrouillage de phase au niveau du récepteur distant.
HDB3fonctionne de manière similaire à AMI, mais incorpore une étape d'encodage supplémentaire qui remplace toute chaîne de quatre zéros par trois zéros suivis d'un «bit de violation». Cette violation est de la même polarité que la transition précédente ( voir la figure suivante ).

Comme on peut le voir dans l'exemple, 000V remplace la première chaîne de quatre zéros. Cependant, l'utilisation de ce type de codage pourrait conduire à l'introduction d'un niveau DC moyen dans le signal, car une longue chaîne de zéros pourrait être présente, tous étant codés de la même manière. Pour éviter cela, le codage de chaque quatre zéros successifs est changé en B00V, en utilisant un bit «violation bipolaire» qui alterne en polarité.
À partir de là, on peut supposer qu'avec le codage HDB3, le nombre maximum de zéros sans transition est de trois. Cette technique de codage est souvent appeléemodulation format.