Modulation d'impulsions
Jusqu'à présent, nous avons discuté de la modulation en onde continue. Il est maintenant temps pour les signaux discrets. lePulse modulationtechniques, traite des signaux discrets. Voyons comment convertir un signal continu en un signal discret. Le processus appelé Sampling nous aide avec cela.
Échantillonnage
Le processus de conversion de signaux temporels continus en signaux temporels discrets équivalents peut être appelé Sampling. Un certain instant de données est continuellement échantillonné dans le processus d'échantillonnage.
La figure suivante indique un signal continu x(t) et un signal échantillonné xs(t). Quandx(t) est multiplié par un train d'impulsions périodique, le signal échantillonné xs(t) Est obtenu.
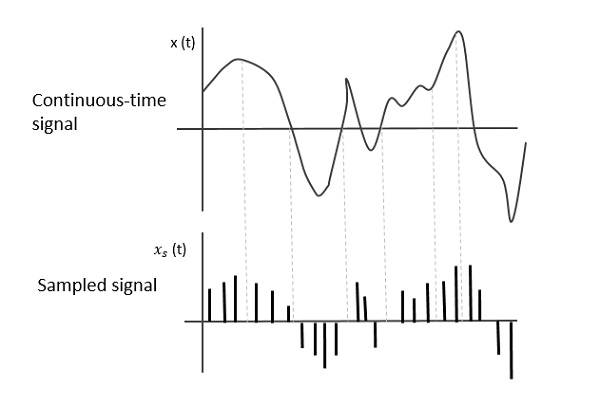
UNE sampling signal est un train périodique d'impulsions, ayant unit amplitude, échantillonné à intervalles de temps égaux Ts, qui est appelé comme le Sampling time. Ces données sont transmises aux instants de tempsTs et le signal de porteuse est transmis au temps restant.
Taux d'échantillonnage
Pour discrétiser les signaux, l'écart entre les échantillons doit être corrigé. Cet écart peut être qualifié desampling period Ts.
$$ Échantillonnage \: Frequency = \ frac {1} {T_s} = f_s $$
Où,
Ts = le temps d'échantillonnage
fs = la fréquence d'échantillonnage ou le taux d'échantillonnage
Théorème d'échantillonnage
Tout en considérant le taux d'échantillonnage, un point important concernant la valeur du taux doit être pris en compte. lerate of sampling doit être tel que les données du signal de message ne soient ni perdues ni surchargées.
le sampling theorem déclare qu '«un signal peut être reproduit exactement s'il est échantillonné au taux fs qui est supérieure ou égale à deux fois la fréquence maximale W. »
Pour le dire plus simplement, pour une reproduction efficace du signal original, la fréquence d'échantillonnage doit être deux fois la fréquence la plus élevée.
Ce qui signifie,
$$ f_s \ geq 2W $$
Où,
fs = la fréquence d'échantillonnage
W est la fréquence la plus élevée
Ce taux d'échantillonnage est appelé Nyquist rate.
Le théorème d'échantillonnage, également appelé Nyquist theorem, fournit la théorie d'une fréquence d'échantillonnage suffisante en termes de bande passante pour la classe de fonctions à bande limitée.
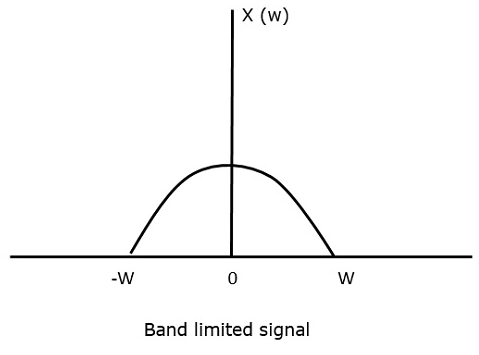
Pour le signal à temps continu x(t), le signal à bande limitée dans le domaine fréquentiel, peut être représenté comme illustré dans la figure suivante.
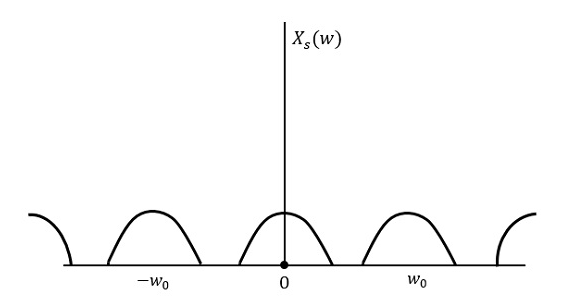
Si le signal est échantillonné au-dessus du taux de Nyquist, le signal d'origine peut être récupéré. La figure suivante explique un signal, s'il est échantillonné à un débit supérieur à 2w dans le domaine fréquentiel.
Si le même signal est échantillonné à une fréquence inférieure à 2 W, le signal échantillonné ressemblera à la figure suivante.
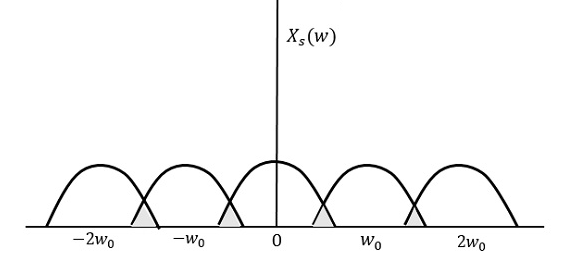
Nous pouvons observer à partir du schéma ci-dessus que le chevauchement d'informations est effectué, ce qui conduit à un mélange et à une perte d'informations. Ce phénomène indésirable de chevauchement est appeléAliasing.
Le crénelage peut être appelé "le phénomène d'une composante haute fréquence dans le spectre d'un signal, prenant l'identité d'une composante basse fréquence dans le spectre de sa version échantillonnée."
Par conséquent, l'échantillonnage du signal est choisi pour être à la fréquence de Nyquist, comme cela a été indiqué dans le théorème d'échantillonnage. Si la fréquence d'échantillonnage est égale à deux fois la fréquence la plus élevée (2W).
Cela signifie,
$$ f_s = 2W $$
Où,
fs = la fréquence d'échantillonnage
W est la fréquence la plus élevée

Le résultat sera comme indiqué dans la figure ci-dessus. Les informations sont remplacées sans aucune perte. C'est donc un bon taux d'échantillonnage.