Python - Divisez pour conquérir

Dans l'approche de division pour conquérir, le problème en cours est divisé en sous-problèmes plus petits, puis chaque problème est résolu indépendamment. Lorsque nous continuons à diviser les sous-problèmes en sous-problèmes encore plus petits, nous pouvons éventuellement atteindre un stade où plus aucune division n'est possible. Ces plus petits sous-problèmes "atomiques" (fractions) sont résolus. La solution de tous les sous-problèmes est finalement fusionnée afin d'obtenir la solution d'un problème original.

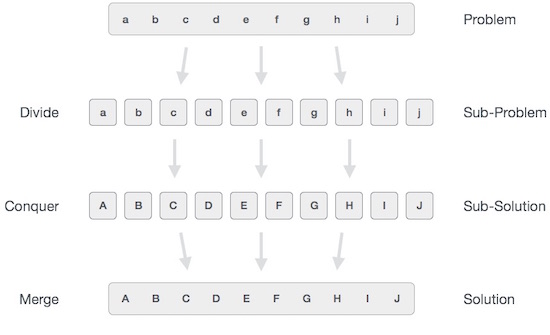
Globalement, nous pouvons comprendre divide-and-conquer approche dans un processus en trois étapes.

Diviser / Pause

Cette étape consiste à diviser le problème en sous-problèmes plus petits. Les sous-problèmes doivent représenter une partie du problème d'origine. Cette étape adopte généralement une approche récursive pour diviser le problème jusqu'à ce qu'aucun sous-problème ne soit davantage divisible. À ce stade, les sous-problèmes deviennent de nature atomique mais représentent encore une partie du problème réel.

Conquérir / Résoudre

Cette étape reçoit beaucoup de sous-problèmes plus petits à résoudre. Généralement, à ce niveau, les problèmes sont considérés comme «résolus» d'eux-mêmes.

Fusionner / Combiner

Lorsque les sous-problèmes plus petits sont résolus, cette étape les combine de manière récursive jusqu'à ce qu'ils formulent une solution du problème d'origine. Cette approche algorithmique fonctionne de manière récursive et les étapes de conquête et de fusion fonctionnent si étroitement qu'elles apparaissent comme une seule.

Exemples

Le programme suivant est un exemple de divide-and-conquer approche de programmation où la recherche binaire est implémentée en utilisant python.

Implémentation de la recherche binaire

Dans la recherche binaire, nous prenons une liste triée d'éléments et commençons à rechercher un élément au milieu de la liste. Si la valeur de recherche correspond à la valeur du milieu de la liste, nous terminons la recherche. Sinon, nous éliminons la moitié de la liste des éléments en choisissant de procéder avec la moitié droite ou gauche de la liste en fonction de la valeur de l'élément recherché. Ceci est possible car la liste est triée et c'est beaucoup plus rapide que la recherche linéaire. Ici, nous divisons la liste donnée et conquérons en choisissant la moitié appropriée de la liste. Nous répétons cette approche jusqu'à ce que nous trouvions l'élément ou que nous concluions à son absence dans la liste.

def bsearch(list, val):

    list_size = len(list) - 1

    idx0 = 0
    idxn = list_size
# Find the middle most value

    while idx0 <= idxn:
        midval = (idx0 + idxn)// 2

        if list[midval] == val:
            return midval
# Compare the value the middle most value
        if val > list[midval]:
            idx0 = midval + 1
        else:
            idxn = midval - 1

    if idx0 > idxn:
        return None
# Initialize the sorted list
list = [2,7,19,34,53,72]

# Print the search result
print(bsearch(list,72))
print(bsearch(list,11))

Lorsque le code ci-dessus est exécuté, il produit le résultat suivant:

5
None