Scikit Learn - Guide rapide
Dans ce chapitre, nous allons comprendre ce qu'est Scikit-Learn ou Sklearn, l'origine de Scikit-Learn et d'autres sujets connexes tels que les communautés et les contributeurs responsables du développement et de la maintenance de Scikit-Learn, ses prérequis, son installation et ses fonctionnalités.
Qu'est-ce que Scikit-Learn (Sklearn)
Scikit-learn (Sklearn) est la bibliothèque la plus utile et la plus robuste pour l'apprentissage automatique en Python. Il fournit une sélection d'outils efficaces pour l'apprentissage automatique et la modélisation statistique, notamment la classification, la régression, le clustering et la réduction de dimensionnalité via une interface de cohérence en Python. Cette bibliothèque, qui est en grande partie écrite en Python, est construite surNumPy, SciPy et Matplotlib.
Origine de Scikit-Learn
Il s'appelait à l'origine scikits.learn et a été initialement développé par David Cournapeau en tant que projet d'été de code Google en 2007. Plus tard, en 2010, Fabian Pedregosa, Gael Varoquaux, Alexandre Gramfort et Vincent Michel, du FIRCA (Institut français de recherche en informatique et en automatisation), ont ce projet à un autre niveau et a fait la première version publique (v0.1 beta) le 1er février 2010.
Jetons un coup d'œil à son historique des versions -
Mai 2019: scikit-learn 0.21.0
Mars 2019: scikit-learn 0.20.3
Décembre 2018: scikit-learn 0.20.2
Novembre 2018: scikit-learn 0.20.1
Septembre 2018: scikit-learn 0.20.0
Juillet 2018: scikit-learn 0.19.2
Juillet 2017: scikit-learn 0.19.0
Septembre 2016. scikit-learn 0.18.0
Novembre 2015. scikit-learn 0.17.0
Mars 2015. scikit-learn 0.16.0
Juillet 2014. scikit-learn 0.15.0
Août 2013. scikit-learn 0.14
Communauté et contributeurs
Scikit-learn est un effort communautaire et tout le monde peut y contribuer. Ce projet est hébergé surhttps://github.com/scikit-learn/scikit-learn. Les personnes suivantes sont actuellement les principaux contributeurs au développement et à la maintenance de Sklearn -
Joris Van den Bossche (Data Scientist)
Thomas J Fan (développeur de logiciels)
Alexandre Gramfort (chercheur en apprentissage automatique)
Olivier Grisel (Expert en apprentissage automatique)
Nicolas Hug (chercheur associé)
Andreas Mueller (scientifique en apprentissage automatique)
Hanmin Qin (ingénieur logiciel)
Adrin Jalali (Développeur Open Source)
Nelle Varoquaux (chercheuse en science des données)
Roman Yurchak (Data Scientist)
Diverses organisations comme Booking.com, JP Morgan, Evernote, Inria, AWeber, Spotify et bien d'autres utilisent Sklearn.
Conditions préalables
Avant de commencer à utiliser la dernière version de scikit-learn, nous avons besoin des éléments suivants:
Python (> = 3,5)
NumPy (> = 1.11.0)
Scipy (> = 0,17,0) li
Joblib (> = 0,11)
Matplotlib (> = 1.5.1) est requis pour les capacités de traçage de Sklearn.
Pandas (> = 0.18.0) est requis pour certains des exemples scikit-learn utilisant la structure et l'analyse des données.
Installation
Si vous avez déjà installé NumPy et Scipy, voici les deux façons les plus simples d'installer scikit-learn -
Utilisation de pip
La commande suivante peut être utilisée pour installer scikit-learn via pip -
pip install -U scikit-learnUtilisation de conda
La commande suivante peut être utilisée pour installer scikit-learn via conda -
conda install scikit-learnD'autre part, si NumPy et Scipy ne sont pas encore installés sur votre poste de travail Python, vous pouvez les installer en utilisant soit pip ou conda.
Une autre option pour utiliser scikit-learn est d'utiliser des distributions Python comme Canopy et Anaconda car ils livrent tous les deux la dernière version de scikit-learn.
traits
Plutôt que de se concentrer sur le chargement, la manipulation et la synthèse des données, la bibliothèque Scikit-learn se concentre sur la modélisation des données. Certains des groupes de modèles les plus populaires fournis par Sklearn sont les suivants:
Supervised Learning algorithms - Presque tous les algorithmes d'apprentissage supervisé populaires, tels que la régression linéaire, la machine vectorielle de support (SVM), l'arbre de décision, etc., font partie de scikit-learn.
Unsupervised Learning algorithms - D'autre part, il dispose également de tous les algorithmes d'apprentissage non supervisé populaires, du clustering, de l'analyse factorielle, de l'ACP (analyse en composantes principales) aux réseaux de neurones non supervisés.
Clustering - Ce modèle est utilisé pour regrouper des données non étiquetées.
Cross Validation - Il est utilisé pour vérifier l'exactitude des modèles supervisés sur des données invisibles.
Dimensionality Reduction - Il est utilisé pour réduire le nombre d'attributs dans les données qui peuvent ensuite être utilisés pour la synthèse, la visualisation et la sélection des caractéristiques.
Ensemble methods - Comme son nom l'indique, il est utilisé pour combiner les prédictions de plusieurs modèles supervisés.
Feature extraction - Il est utilisé pour extraire les caractéristiques des données pour définir les attributs dans les données image et texte.
Feature selection - Il est utilisé pour identifier les attributs utiles pour créer des modèles supervisés.
Open Source - C'est une bibliothèque open source et également utilisable commercialement sous licence BSD.
Ce chapitre traite du processus de modélisation impliqué dans Sklearn. Comprenons la même chose en détail et commençons par le chargement de l'ensemble de données.
Chargement de l'ensemble de données
Une collection de données est appelée ensemble de données. Il a les deux composants suivants -
Features- Les variables de données sont appelées ses caractéristiques. Ils sont également appelés prédicteurs, entrées ou attributs.
Feature matrix - C'est la collection de fonctionnalités, au cas où il y en aurait plus d'une.
Feature Names - C'est la liste de tous les noms des fonctionnalités.
Response- C'est la variable de sortie qui dépend essentiellement des variables de fonctionnalité. Ils sont également appelés cible, étiquette ou sortie.
Response Vector- Il est utilisé pour représenter la colonne de réponse. En général, nous n'avons qu'une seule colonne de réponse.
Target Names - Il représente les valeurs possibles prises par un vecteur de réponse.
Scikit-learn a quelques exemples d'ensembles de données comme iris et digits pour la classification et le Boston house prices pour la régression.
Exemple
Voici un exemple de chargement iris ensemble de données -
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
feature_names = iris.feature_names
target_names = iris.target_names
print("Feature names:", feature_names)
print("Target names:", target_names)
print("\nFirst 10 rows of X:\n", X[:10])Production
Feature names: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
Target names: ['setosa' 'versicolor' 'virginica']
First 10 rows of X:
[
[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]
[5.4 3.9 1.7 0.4]
[4.6 3.4 1.4 0.3]
[5. 3.4 1.5 0.2]
[4.4 2.9 1.4 0.2]
[4.9 3.1 1.5 0.1]
]Fractionner l'ensemble de données
Pour vérifier l'exactitude de notre modèle, nous pouvons diviser l'ensemble de données en deux parties -a training set et a testing set. Utilisez l'ensemble d'entraînement pour entraîner le modèle et l'ensemble de test pour tester le modèle. Après cela, nous pouvons évaluer les performances de notre modèle.
Exemple
L'exemple suivant divisera les données en un rapport de 70:30, c'est-à-dire que 70% des données seront utilisées comme données d'entraînement et 30% seront utilisées comme données de test. L'ensemble de données est l'ensemble de données iris comme dans l'exemple ci-dessus.
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size = 0.3, random_state = 1
)
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)Production
(105, 4)
(45, 4)
(105,)
(45,)Comme le montre l'exemple ci-dessus, il utilise train_test_split()fonction de scikit-learn pour diviser l'ensemble de données. Cette fonction a les arguments suivants -
X, y - Ici, X est le feature matrix et y est le response vector, qui doivent être divisés.
test_size- Ceci représente le rapport entre les données de test et le total des données données. Comme dans l'exemple ci-dessus, nous définissonstest_data = 0.3 pour 150 lignes de X. Cela produira des données de test de 150 * 0,3 = 45 lignes.
random_size- Il est utilisé pour garantir que la répartition sera toujours la même. Ceci est utile dans les situations où vous souhaitez des résultats reproductibles.
Former le modèle
Ensuite, nous pouvons utiliser notre ensemble de données pour entraîner un modèle de prédiction. Comme discuté, scikit-learn propose un large éventail deMachine Learning (ML) algorithms qui ont une interface cohérente pour l'ajustement, la prédiction de la précision, le rappel, etc.
Exemple
Dans l'exemple ci-dessous, nous allons utiliser le classificateur KNN (K plus proches voisins). N'allez pas dans les détails des algorithmes KNN, car il y aura un chapitre séparé pour cela. Cet exemple est utilisé pour vous faire comprendre uniquement la partie implémentation.
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size = 0.4, random_state=1
)
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
classifier_knn = KNeighborsClassifier(n_neighbors = 3)
classifier_knn.fit(X_train, y_train)
y_pred = classifier_knn.predict(X_test)
# Finding accuracy by comparing actual response values(y_test)with predicted response value(y_pred)
print("Accuracy:", metrics.accuracy_score(y_test, y_pred))
# Providing sample data and the model will make prediction out of that data
sample = [[5, 5, 3, 2], [2, 4, 3, 5]]
preds = classifier_knn.predict(sample)
pred_species = [iris.target_names[p] for p in preds] print("Predictions:", pred_species)Production
Accuracy: 0.9833333333333333
Predictions: ['versicolor', 'virginica']Persistance du modèle
Une fois que vous avez entraîné le modèle, il est souhaitable que le modèle soit conservé pour une utilisation future afin que nous n'ayons pas besoin de le recycler encore et encore. Cela peut être fait avec l'aide dedump et load les caractéristiques de joblib paquet.
Prenons l'exemple ci-dessous dans lequel nous enregistrerons le modèle entraîné ci-dessus (classifier_knn) pour une utilisation future -
from sklearn.externals import joblib
joblib.dump(classifier_knn, 'iris_classifier_knn.joblib')Le code ci-dessus enregistrera le modèle dans un fichier nommé iris_classifier_knn.joblib. Maintenant, l'objet peut être rechargé à partir du fichier à l'aide du code suivant -
joblib.load('iris_classifier_knn.joblib')Prétraitement des données
Comme nous traitons beaucoup de données et que ces données sont sous forme brute, avant de les saisir dans des algorithmes d'apprentissage automatique, nous devons les convertir en données significatives. Ce processus s'appelle le prétraitement des données. Scikit-learn a un package nommépreprocessingdans ce but. lepreprocessing package a les techniques suivantes -
Binarisation
Cette technique de prétraitement est utilisée lorsque nous devons convertir nos valeurs numériques en valeurs booléennes.
Exemple
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]]
)
data_binarized = preprocessing.Binarizer(threshold=0.5).transform(input_data)
print("\nBinarized data:\n", data_binarized)Dans l'exemple ci-dessus, nous avons utilisé threshold value = 0,5 et c'est pourquoi, toutes les valeurs supérieures à 0,5 seraient converties en 1, et toutes les valeurs inférieures à 0,5 seraient converties en 0.
Production
Binarized data:
[
[ 1. 0. 1.]
[ 0. 1. 1.]
[ 0. 0. 1.]
[ 1. 1. 0.]
]Élimination moyenne
Cette technique est utilisée pour éliminer la moyenne du vecteur d'entités de sorte que chaque entité soit centrée sur zéro.
Exemple
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]]
)
#displaying the mean and the standard deviation of the input data
print("Mean =", input_data.mean(axis=0))
print("Stddeviation = ", input_data.std(axis=0))
#Removing the mean and the standard deviation of the input data
data_scaled = preprocessing.scale(input_data)
print("Mean_removed =", data_scaled.mean(axis=0))
print("Stddeviation_removed =", data_scaled.std(axis=0))Production
Mean = [ 1.75 -1.275 2.2 ]
Stddeviation = [ 2.71431391 4.20022321 4.69414529]
Mean_removed = [ 1.11022302e-16 0.00000000e+00 0.00000000e+00]
Stddeviation_removed = [ 1. 1. 1.]Mise à l'échelle
Nous utilisons cette technique de prétraitement pour mettre à l'échelle les vecteurs de caractéristiques. La mise à l'échelle des vecteurs de caractéristiques est importante, car les caractéristiques ne doivent pas être synthétiquement grandes ou petites.
Exemple
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]
]
)
data_scaler_minmax = preprocessing.MinMaxScaler(feature_range=(0,1))
data_scaled_minmax = data_scaler_minmax.fit_transform(input_data)
print ("\nMin max scaled data:\n", data_scaled_minmax)Production
Min max scaled data:
[
[ 0.48648649 0.58252427 0.99122807]
[ 0. 1. 0.81578947]
[ 0.27027027 0. 1. ]
[ 1. 0.99029126 0. ]
]Normalisation
Nous utilisons cette technique de prétraitement pour modifier les vecteurs de caractéristiques. La normalisation des vecteurs de caractéristiques est nécessaire pour que les vecteurs de caractéristiques puissent être mesurés à une échelle commune. Il existe deux types de normalisation comme suit -
Normalisation L1
Il est également appelé écarts les moins absolus. Il modifie la valeur de telle manière que la somme des valeurs absolues reste toujours jusqu'à 1 dans chaque ligne. L'exemple suivant montre l'implémentation de la normalisation L1 sur les données d'entrée.
Exemple
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]
]
)
data_normalized_l1 = preprocessing.normalize(input_data, norm='l1')
print("\nL1 normalized data:\n", data_normalized_l1)Production
L1 normalized data:
[
[ 0.22105263 -0.2 0.57894737]
[-0.2027027 0.32432432 0.47297297]
[ 0.03571429 -0.56428571 0.4 ]
[ 0.42142857 0.16428571 -0.41428571]
]Normalisation L2
Aussi appelé moindres carrés. Il modifie la valeur de telle manière que la somme des carrés reste toujours jusqu'à 1 dans chaque ligne. L'exemple suivant montre l'implémentation de la normalisation L2 sur les données d'entrée.
Exemple
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]
]
)
data_normalized_l2 = preprocessing.normalize(input_data, norm='l2')
print("\nL1 normalized data:\n", data_normalized_l2)Production
L2 normalized data:
[
[ 0.33946114 -0.30713151 0.88906489]
[-0.33325106 0.53320169 0.7775858 ]
[ 0.05156558 -0.81473612 0.57753446]
[ 0.68706914 0.26784051 -0.6754239 ]
]Comme nous le savons, l'apprentissage automatique est sur le point de créer un modèle à partir de données. À cette fin, l'ordinateur doit d'abord comprendre les données. Ensuite, nous allons discuter de différentes manières de représenter les données afin d'être comprises par ordinateur -
Données sous forme de tableau
La meilleure façon de représenter les données dans Scikit-learn est sous forme de tableaux. Un tableau représente une grille de données 2D où les lignes représentent les éléments individuels de l'ensemble de données et les colonnes représentent les quantités liées à ces éléments individuels.
Exemple
Avec l'exemple donné ci-dessous, nous pouvons télécharger iris dataset sous la forme d'un Pandas DataFrame avec l'aide de python seaborn bibliothèque.
import seaborn as sns
iris = sns.load_dataset('iris')
iris.head()Production
sepal_length sepal_width petal_length petal_width species
0 5.1 3.5 1.4 0.2 setosa
1 4.9 3.0 1.4 0.2 setosa
2 4.7 3.2 1.3 0.2 setosa
3 4.6 3.1 1.5 0.2 setosa
4 5.0 3.6 1.4 0.2 setosaÀ partir de la sortie ci-dessus, nous pouvons voir que chaque ligne de données représente une seule fleur observée et le nombre de lignes représente le nombre total de fleurs dans l'ensemble de données. En général, nous référons les lignes de la matrice à des échantillons.
En revanche, chaque colonne des données représente une information quantitative décrivant chaque échantillon. En général, nous désignons les colonnes de la matrice comme des caractéristiques.
Données comme matrice de caractéristiques
La matrice de caractéristiques peut être définie comme la mise en page du tableau dans laquelle les informations peuvent être considérées comme une matrice 2D. Il est stocké dans une variable nomméeXet supposé être bidimensionnel de forme [n_samples, n_features]. La plupart du temps, il est contenu dans un tableau NumPy ou un Pandas DataFrame. Comme indiqué précédemment, les échantillons représentent toujours les objets individuels décrits par l'ensemble de données et les caractéristiques représentent les observations distinctes qui décrivent chaque échantillon de manière quantitative.
Données en tant que tableau cible
En plus de la matrice de fonctionnalités, notée X, nous avons également un tableau cible. Il est également appelé étiquette. Il est noté y. L'étiquette ou le tableau cible est généralement unidimensionnel et a une longueur de n_ échantillons. Il est généralement contenu dans NumPyarray ou Pandas Series. Le tableau cible peut avoir à la fois les valeurs, les valeurs numériques continues et les valeurs discrètes.
En quoi le tableau cible diffère-t-il des colonnes d'entités?
Nous pouvons distinguer les deux par un point que le tableau cible est généralement la quantité que nous voulons prédire à partir des données, c'est-à-dire en termes statistiques, c'est la variable dépendante.
Exemple
Dans l'exemple ci-dessous, à partir du jeu de données sur l'iris, nous prédisons les espèces de fleurs en fonction des autres mesures. Dans ce cas, la colonne Espèce serait considérée comme la fonction.
import seaborn as sns
iris = sns.load_dataset('iris')
%matplotlib inline
import seaborn as sns; sns.set()
sns.pairplot(iris, hue='species', height=3);Production
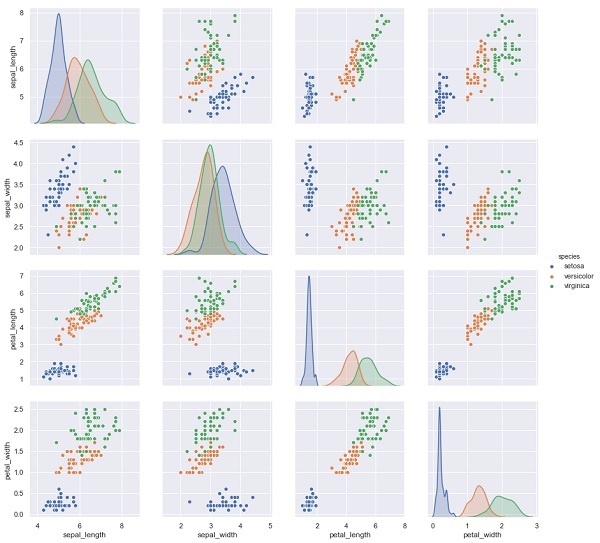
X_iris = iris.drop('species', axis=1)
X_iris.shape
y_iris = iris['species']
y_iris.shapeProduction
(150,4)
(150,)Dans ce chapitre, nous allons découvrir Estimator API(Interface de programmation d'applications). Commençons par comprendre ce qu'est une API Estimator.
Qu'est-ce que l'API Estimator
C'est l'une des principales API implémentées par Scikit-learn. Il fournit une interface cohérente pour une large gamme d'applications ML, c'est pourquoi tous les algorithmes d'apprentissage automatique de Scikit-Learn sont implémentés via l'API Estimator. L'objet qui apprend des données (ajustement des données) est un estimateur. Il peut être utilisé avec l'un des algorithmes tels que la classification, la régression, le clustering ou même avec un transformateur, qui extrait des fonctionnalités utiles à partir de données brutes.
Pour ajuster les données, tous les objets estimateur exposent une méthode d'ajustement qui prend un ensemble de données présenté comme suit -
estimator.fit(data)Ensuite, tous les paramètres d'un estimateur peuvent être fixés, comme suit, lorsqu'il est instancié par l'attribut correspondant.
estimator = Estimator (param1=1, param2=2)
estimator.param1La sortie de ce qui précède serait 1.
Une fois que les données sont équipées d'un estimateur, les paramètres sont estimés à partir des données disponibles. Maintenant, tous les paramètres estimés seront les attributs de l'objet estimateur se terminant par un trait de soulignement comme suit -
estimator.estimated_param_Utilisation de l'API Estimator
Les principales utilisations des estimateurs sont les suivantes -
Estimation et décodage d'un modèle
L'objet Estimator est utilisé pour l'estimation et le décodage d'un modèle. De plus, le modèle est estimé comme une fonction déterministe de ce qui suit -
Les paramètres fournis dans la construction d'objet.
L'état aléatoire global (numpy.random) si le paramètre random_state de l'estimateur est défini sur aucun.
Toutes les données transmises à l'appel le plus récent à fit, fit_transform, or fit_predict.
Toutes les données transmises dans une séquence d'appels à partial_fit.
Mappage de la représentation de données non rectangulaire en données rectangulaires
Il mappe une représentation de données non rectangulaire en données rectangulaires. En termes simples, il prend une entrée où chaque échantillon n'est pas représenté comme un objet de type tableau de longueur fixe, et produit un objet de type tableau de fonctionnalités pour chaque échantillon.
Distinction entre les échantillons carottés et périphériques
Il modélise la distinction entre les échantillons de base et les échantillons périphériques en utilisant les méthodes suivantes -
fit
fit_predict si transductif
prédire si inductif
Des principes directeurs
Lors de la conception de l'API Scikit-Learn, en gardant à l'esprit les principes directeurs suivants:
Cohérence
Ce principe stipule que tous les objets doivent partager une interface commune tirée d'un ensemble limité de méthodes. La documentation doit également être cohérente.
Hiérarchie d'objets limitée
Ce principe directeur dit -
Les algorithmes doivent être représentés par des classes Python
Les ensembles de données doivent être représentés dans un format standard comme les tableaux NumPy, Pandas DataFrames, SciPy sparse matrix.
Les noms de paramètres doivent utiliser des chaînes Python standard.
Composition
Comme nous le savons, les algorithmes de ML peuvent être exprimés comme la séquence de nombreux algorithmes fondamentaux. Scikit-learn utilise ces algorithmes fondamentaux chaque fois que nécessaire.
Valeurs par défaut sensibles
Selon ce principe, la bibliothèque Scikit-learn définit une valeur par défaut appropriée chaque fois que les modèles ML nécessitent des paramètres spécifiés par l'utilisateur.
Inspection
Conformément à ce principe directeur, chaque valeur de paramètre spécifiée est exposée en tant qu'attributs publics.
Étapes d'utilisation de l'API Estimator
Voici les étapes d'utilisation de l'API d'estimation Scikit-Learn -
Étape 1: Choisissez une classe de modèle
Dans cette première étape, nous devons choisir une classe de modèle. Cela peut être fait en important la classe Estimator appropriée depuis Scikit-learn.
Étape 2: Choisissez les hyperparamètres du modèle
Dans cette étape, nous devons choisir des hyperparamètres de modèle de classe. Cela peut être fait en instanciant la classe avec les valeurs souhaitées.
Étape 3: Organisation des données
Ensuite, nous devons organiser les données en matrice de caractéristiques (X) et vecteur cible (y).
Étape 4: montage du modèle
Maintenant, nous devons adapter le modèle à vos données. Cela peut être fait en appelant la méthode fit () de l'instance de modèle.
Étape 5: application du modèle
Une fois le modèle ajusté, nous pouvons l'appliquer à de nouvelles données. Pour un apprentissage supervisé, utilisezpredict()méthode pour prédire les étiquettes des données inconnues. Alors que pour l'apprentissage non supervisé, utilisezpredict() ou transform() pour déduire les propriétés des données.
Exemple d'apprentissage supervisé
Ici, comme exemple de ce processus, nous prenons le cas courant de l'ajustement d'une ligne à des données (x, y) ie simple linear regression.
Tout d'abord, nous devons charger l'ensemble de données, nous utilisons l'ensemble de données iris -
Exemple
import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shapeProduction
(150, 4)Exemple
y_iris = iris['species']
y_iris.shapeProduction
(150,)Exemple
Maintenant, pour cet exemple de régression, nous allons utiliser les exemples de données suivants -
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);Production
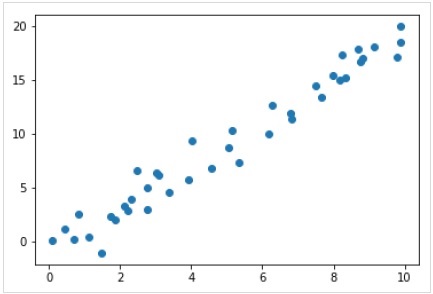
Nous avons donc les données ci-dessus pour notre exemple de régression linéaire.
Maintenant, avec ces données, nous pouvons appliquer les étapes mentionnées ci-dessus.
Choisissez une classe de modèle
Ici, pour calculer un modèle de régression linéaire simple, nous devons importer la classe de régression linéaire comme suit -
from sklearn.linear_model import LinearRegressionChoisissez les hyperparamètres du modèle
Une fois que nous avons choisi une classe de modèle, nous devons faire des choix importants qui sont souvent représentés sous forme d'hyperparamètres, ou les paramètres qui doivent être définis avant que le modèle ne soit adapté aux données. Ici, pour cet exemple de régression linéaire, nous aimerions ajuster l'intersection en utilisant lafit_intercept hyperparamètre comme suit -
Example
model = LinearRegression(fit_intercept = True)
modelOutput
LinearRegression(copy_X = True, fit_intercept = True, n_jobs = None, normalize = False)Organisation des données
Maintenant, comme nous savons que notre variable cible y est en forme correcte c'est-à-dire une longueur n_samplestableau de 1-D. Mais nous devons remodeler la matrice de caractéristiquesX en faire une matrice de taille [n_samples, n_features]. Cela peut être fait comme suit -
Example
X = x[:, np.newaxis]
X.shapeOutput
(40, 1)Montage du modèle
Une fois que nous avons arrangé les données, il est temps d'ajuster le modèle, c'est-à-dire d'appliquer notre modèle aux données. Cela peut être fait avec l'aide defit() méthode comme suit -
Example
model.fit(X, y)Output
LinearRegression(copy_X = True, fit_intercept = True, n_jobs = None,normalize = False)Dans Scikit-learn, le fit() processus ont des traits de soulignement à la fin.
Pour cet exemple, le paramètre ci-dessous montre la pente de l'ajustement linéaire simple des données -
Example
model.coef_Output
array([1.99839352])Le paramètre ci-dessous représente l'intersection de l'ajustement linéaire simple aux données -
Example
model.intercept_Output
-0.9895459457775022Application du modèle à de nouvelles données
Après avoir entraîné le modèle, nous pouvons l'appliquer à de nouvelles données. La tâche principale de l'apprentissage automatique supervisé étant d'évaluer le modèle sur la base de nouvelles données qui ne font pas partie de l'ensemble d'apprentissage. Cela peut être fait avec l'aide depredict() méthode comme suit -
Example
xfit = np.linspace(-1, 11)
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)
plt.scatter(x, y)
plt.plot(xfit, yfit);Output
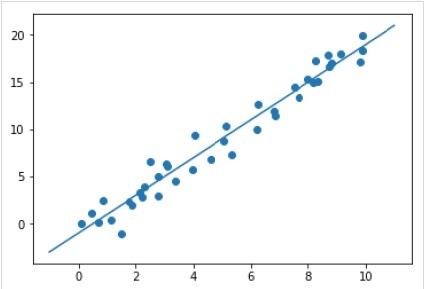
Exemple de travail / exécutable complet
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
y_iris = iris['species']
y_iris.shape
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)
model
X = x[:, np.newaxis]
X.shape
model.fit(X, y)
model.coef_
model.intercept_
xfit = np.linspace(-1, 11)
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)
plt.scatter(x, y)
plt.plot(xfit, yfit);Exemple d'apprentissage non supervisé
Ici, comme exemple de ce processus, nous prenons un cas courant de réduction de la dimensionnalité de l'ensemble de données Iris afin que nous puissions le visualiser plus facilement. Pour cet exemple, nous allons utiliser l'analyse en composantes principales (ACP), une technique de réduction de dimensionnalité linéaire rapide.
Comme l'exemple ci-dessus, nous pouvons charger et tracer les données aléatoires à partir du jeu de données iris. Après cela, nous pouvons suivre les étapes ci-dessous -
Choisissez une classe de modèle
from sklearn.decomposition import PCAChoisissez les hyperparamètres du modèle
Example
model = PCA(n_components=2)
modelOutput
PCA(copy = True, iterated_power = 'auto', n_components = 2, random_state = None,
svd_solver = 'auto', tol = 0.0, whiten = False)Montage du modèle
Example
model.fit(X_iris)Output
PCA(copy = True, iterated_power = 'auto', n_components = 2, random_state = None,
svd_solver = 'auto', tol = 0.0, whiten = False)Transformez les données en deux dimensions
Example
X_2D = model.transform(X_iris)Maintenant, nous pouvons tracer le résultat comme suit -
Output
iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue = 'species', data = iris, fit_reg = False);Output
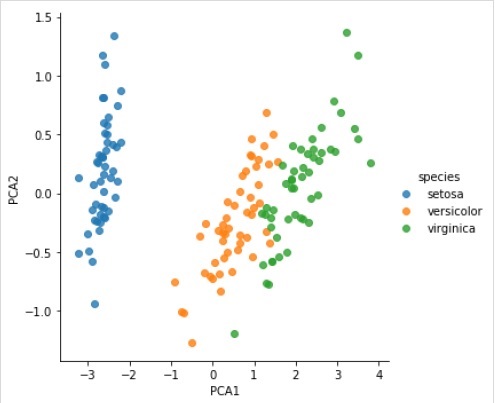
Exemple de travail / exécutable complet
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
y_iris = iris['species']
y_iris.shape
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
from sklearn.decomposition import PCA
model = PCA(n_components=2)
model
model.fit(X_iris)
X_2D = model.transform(X_iris)
iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue='species', data=iris, fit_reg=False);Les objets de Scikit-learn partagent une API de base uniforme qui se compose des trois interfaces complémentaires suivantes -
Estimator interface - C'est pour la construction et le montage des modèles.
Predictor interface - C'est pour faire des prédictions.
Transformer interface - C'est pour convertir des données.
Les API adoptent des conventions simples et les choix de conception ont été guidés de manière à éviter la prolifération du code-cadre.
Objet des conventions
Le but des conventions est de s'assurer que l'API respecte les grands principes suivants -
Consistency - Tous les objets, qu'ils soient basiques ou composites, doivent partager une interface cohérente qui se compose en outre d'un ensemble limité de méthodes.
Inspection - Les paramètres du constructeur et les valeurs des paramètres déterminés par l'algorithme d'apprentissage doivent être stockés et exposés en tant qu'attributs publics.
Non-proliferation of classes - Les ensembles de données doivent être représentés sous forme de tableaux NumPy ou de matrice scipy sparse, tandis que les noms et valeurs des hyper-paramètres doivent être représentés sous forme de chaînes Python standard pour éviter la prolifération du code cadre.
Composition - Les algorithmes, qu'ils soient exprimables sous forme de séquences ou de combinaisons de transformations des données ou bien considérés comme des méta-algorithmes paramétrés sur d'autres algorithmes, doivent être mis en œuvre et composés à partir de blocs de construction existants.
Sensible defaults- Dans scikit-learn chaque fois qu'une opération nécessite un paramètre défini par l'utilisateur, une valeur par défaut appropriée est définie. Cette valeur par défaut devrait entraîner l'exécution de l'opération d'une manière raisonnable, par exemple, en donnant une solution de base pour la tâche à accomplir.
Diverses conventions
Les conventions disponibles dans Sklearn sont expliquées ci-dessous -
Type de moulage
Il indique que l'entrée doit être convertie en float64. Dans l'exemple suivant, dans lequelsklearn.random_projection module utilisé pour réduire la dimensionnalité des données, l'expliquera -
Example
import numpy as np
from sklearn import random_projection
rannge = np.random.RandomState(0)
X = range.rand(10,2000)
X = np.array(X, dtype = 'float32')
X.dtype
Transformer_data = random_projection.GaussianRandomProjection()
X_new = transformer.fit_transform(X)
X_new.dtypeOutput
dtype('float32')
dtype('float64')Dans l'exemple ci-dessus, nous pouvons voir que X est float32 qui est jeté à float64 par fit_transform(X).
Réaménagement et mise à jour des paramètres
Les hyper-paramètres d'un estimateur peuvent être mis à jour et réajustés après sa construction via le set_params()méthode. Voyons l'exemple suivant pour le comprendre -
Example
import numpy as np
from sklearn.datasets import load_iris
from sklearn.svm import SVC
X, y = load_iris(return_X_y = True)
clf = SVC()
clf.set_params(kernel = 'linear').fit(X, y)
clf.predict(X[:5])Output
array([0, 0, 0, 0, 0])Une fois l'estimateur construit, le code ci-dessus changera le noyau par défaut rbf à linéaire via SVC.set_params().
Maintenant, le code suivant rétablira le noyau en rbf pour refaire l'estimateur et faire une seconde prédiction.
Example
clf.set_params(kernel = 'rbf', gamma = 'scale').fit(X, y)
clf.predict(X[:5])Output
array([0, 0, 0, 0, 0])Code complet
Ce qui suit est le programme exécutable complet -
import numpy as np
from sklearn.datasets import load_iris
from sklearn.svm import SVC
X, y = load_iris(return_X_y = True)
clf = SVC()
clf.set_params(kernel = 'linear').fit(X, y)
clf.predict(X[:5])
clf.set_params(kernel = 'rbf', gamma = 'scale').fit(X, y)
clf.predict(X[:5])Raccord multiclasse et multi-étiquettes
En cas d'ajustement multiclasse, les tâches d'apprentissage et de prédiction dépendent du format de l'ajustement des données cibles. Le module utilisé estsklearn.multiclass. Consultez l'exemple ci-dessous, où le classificateur multiclasse est adapté à un tableau 1d.
Example
from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier
from sklearn.preprocessing import LabelBinarizer
X = [[1, 2], [3, 4], [4, 5], [5, 2], [1, 1]]
y = [0, 0, 1, 1, 2]
classif = OneVsRestClassifier(estimator = SVC(gamma = 'scale',random_state = 0))
classif.fit(X, y).predict(X)Output
array([0, 0, 1, 1, 2])Dans l'exemple ci-dessus, le classificateur est adapté à un tableau dimensionnel d'étiquettes multiclasses et le predict()La méthode fournit donc une prédiction multiclasse correspondante. Mais d'un autre côté, il est également possible de s'adapter sur un tableau bidimensionnel d'indicateurs d'étiquettes binaires comme suit -
Example
from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier
from sklearn.preprocessing import LabelBinarizer
X = [[1, 2], [3, 4], [4, 5], [5, 2], [1, 1]]
y = LabelBinarizer().fit_transform(y)
classif.fit(X, y).predict(X)Output
array(
[
[0, 0, 0],
[0, 0, 0],
[0, 1, 0],
[0, 1, 0],
[0, 0, 0]
]
)De même, dans le cas d'un ajustement à plusieurs étiquettes, une instance peut se voir attribuer plusieurs étiquettes comme suit -
Example
from sklearn.preprocessing import MultiLabelBinarizer
y = [[0, 1], [0, 2], [1, 3], [0, 2, 3], [2, 4]]
y = MultiLabelBinarizer().fit_transform(y)
classif.fit(X, y).predict(X)Output
array(
[
[1, 0, 1, 0, 0],
[1, 0, 1, 0, 0],
[1, 0, 1, 1, 0],
[1, 0, 1, 1, 0],
[1, 0, 1, 0, 0]
]
)Dans l'exemple ci-dessus, sklearn.MultiLabelBinarizerest utilisé pour binariser le tableau bidimensionnel de multilabels à ajuster. C'est pourquoi la fonction predict () donne un tableau 2d en sortie avec plusieurs étiquettes pour chaque instance.
Ce chapitre vous aidera à découvrir la modélisation linéaire dans Scikit-Learn. Commençons par comprendre ce qu'est la régression linéaire dans Sklearn.
Le tableau suivant répertorie les différents modèles linéaires fournis par Scikit-Learn -
| Sr.Non | Description du modèle |
|---|---|
| 1 | Régression linéaire C'est l'un des meilleurs modèles statistiques qui étudie la relation entre une variable dépendante (Y) et un ensemble donné de variables indépendantes (X). |
| 2 | Régression logistique La régression logistique, malgré son nom, est un algorithme de classification plutôt qu'un algorithme de régression. Sur la base d'un ensemble donné de variables indépendantes, il est utilisé pour estimer une valeur discrète (0 ou 1, oui / non, vrai / faux). |
| 3 | Régression Ridge La régression de crête ou régularisation de Tikhonov est la technique de régularisation qui effectue la régularisation L2. Il modifie la fonction de perte en ajoutant la pénalité (quantité de retrait) équivalente au carré de la grandeur des coefficients. |
| 4 | Régression de la crête bayésienne La régression bayésienne permet à un mécanisme naturel de survivre à des données insuffisantes ou à des données mal distribuées en formulant une régression linéaire en utilisant des distributeurs de probabilité plutôt que des estimations ponctuelles. |
| 5 | LASSO LASSO est la technique de régularisation qui effectue la régularisation L1. Il modifie la fonction de perte en ajoutant la pénalité (quantité de retrait) équivalente à la sommation de la valeur absolue des coefficients. |
| 6 | LASSO multi-tâches Il permet d'ajuster plusieurs problèmes de régression en imposant conjointement les caractéristiques sélectionnées pour être identiques pour tous les problèmes de régression, également appelés tâches. Sklearn fournit un modèle linéaire nommé MultiTaskLasso, formé avec une norme mixte L1, L2 pour la régularisation, qui estime conjointement les coefficients clairsemés pour les problèmes de régression multiples. |
| sept | Elastic-Net Elastic-Net est une méthode de régression régularisée qui combine linéairement les deux pénalités, c'est-à-dire L1 et L2 des méthodes de régression Lasso et Ridge. Il est utile lorsqu'il existe plusieurs fonctionnalités corrélées. |
| 8 | Elastic-Net multi-tâches C'est un modèle Elastic-Net qui permet d'ajuster plusieurs problèmes de régression en imposant conjointement les fonctionnalités sélectionnées pour être les mêmes pour tous les problèmes de régression, également appelés tâches |
Ce chapitre se concentre sur les fonctions polynomiales et les outils de pipelining de Sklearn.
Introduction aux caractéristiques polynomiales
Les modèles linéaires formés sur les fonctions non linéaires des données maintiennent généralement les performances rapides des méthodes linéaires. Cela leur permet également d'adapter une gamme beaucoup plus large de données. C'est la raison pour laquelle, dans l'apprentissage automatique, de tels modèles linéaires, entraînés sur des fonctions non linéaires, sont utilisés.
Un tel exemple est qu'une régression linéaire simple peut être étendue en construisant des caractéristiques polynomiales à partir des coefficients.
Mathématiquement, supposons que nous ayons un modèle de régression linéaire standard, alors pour les données 2D, cela ressemblerait à ceci -
$$Y=W_{0}+W_{1}X_{1}+W_{2}X_{2}$$Maintenant, nous pouvons combiner les caractéristiques dans des polynômes du second ordre et notre modèle ressemblera à ceci:
$$Y=W_{0}+W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{1}X_{2}+W_{4}X_1^2+W_{5}X_2^2$$Ce qui précède est toujours un modèle linéaire. Ici, nous avons vu que la régression polynomiale résultante est dans la même classe de modèles linéaires et peut être résolue de manière similaire.
Pour ce faire, scikit-learn fournit un module nommé PolynomialFeatures. Ce module transforme une matrice de données d'entrée en une nouvelle matrice de données d'un degré donné.
Paramètres
Le tableau suivant comprend les paramètres utilisés par PolynomialFeatures module
| Sr.Non | Paramètre et description |
|---|---|
| 1 | degree - entier, par défaut = 2 Il représente le degré des caractéristiques polynomiales. |
| 2 | interaction_only - Booléen, par défaut = false Par défaut, il est faux, mais s'il est défini sur true, les fonctionnalités qui sont les produits des fonctionnalités d'entrée les plus distinctes sont produites. Ces fonctionnalités sont appelées fonctionnalités d'interaction. |
| 3 | include_bias - Booléen, par défaut = true Il comprend une colonne de biais, c'est-à-dire la caractéristique dans laquelle toutes les puissances polynomiales sont nulles. |
| 4 | order - str in {'C', 'F'}, par défaut = 'C' Ce paramètre représente l'ordre du tableau de sortie dans le cas dense. L'ordre «F» signifie plus rapide à calculer, mais d'un autre côté, il peut ralentir les estimateurs ultérieurs. |
Les attributs
Le tableau suivant comprend les attributs utilisés par PolynomialFeatures module
| Sr.Non | Attributs et description |
|---|---|
| 1 | powers_ - tableau, forme (n_output_features, n_input_features) Il montre que powers_ [i, j] est l'exposant de la j ième entrée dans la ième sortie. |
| 2 | n_input_features _ - int Comme son nom l'indique, il donne le nombre total d'entités d'entrée. |
| 3 | n_output_features _ - int Comme son nom l'indique, il donne le nombre total de caractéristiques de sortie polynomiales. |
Exemple d'implémentation
Suivre les utilisations de script Python PolynomialFeatures transformateur pour transformer un tableau de 8 en forme (4,2) -
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
Y = np.arange(8).reshape(4, 2)
poly = PolynomialFeatures(degree=2)
poly.fit_transform(Y)Production
array(
[
[ 1., 0., 1., 0., 0., 1.],
[ 1., 2., 3., 4., 6., 9.],
[ 1., 4., 5., 16., 20., 25.],
[ 1., 6., 7., 36., 42., 49.]
]
)Rationalisation à l'aide des outils Pipeline
Le type de prétraitement ci-dessus, c'est-à-dire la transformation d'une matrice de données d'entrée en une nouvelle matrice de données d'un degré donné, peut être rationalisé avec le Pipeline outils, qui sont essentiellement utilisés pour enchaîner plusieurs estimateurs en un seul.
Exemple
Les scripts python ci-dessous utilisant les outils Pipeline de Scikit-learn pour rationaliser le prétraitement (s'adapteront à des données polynomiales d'ordre 3).
#First, import the necessary packages.
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
import numpy as np
#Next, create an object of Pipeline tool
Stream_model = Pipeline([('poly', PolynomialFeatures(degree=3)), ('linear', LinearRegression(fit_intercept=False))])
#Provide the size of array and order of polynomial data to fit the model.
x = np.arange(5)
y = 3 - 2 * x + x ** 2 - x ** 3
Stream_model = model.fit(x[:, np.newaxis], y)
#Calculate the input polynomial coefficients.
Stream_model.named_steps['linear'].coef_Production
array([ 3., -2., 1., -1.])La sortie ci-dessus montre que le modèle linéaire formé sur les entités polynomiales est capable de récupérer les coefficients polynomiaux d'entrée exacts.
Ici, nous allons découvrir un algorithme d'optimisation dans Sklearn, appelé Stochastic Gradient Descent (SGD).
La descente de gradient stochastique (SGD) est un algorithme d'optimisation simple mais efficace utilisé pour trouver les valeurs de paramètres / coefficients de fonctions qui minimisent une fonction de coût. En d'autres termes, il est utilisé pour l'apprentissage discriminatif des classificateurs linéaires sous des fonctions de perte convexe telles que SVM et régression logistique. Il a été appliqué avec succès aux ensembles de données à grande échelle car la mise à jour des coefficients est effectuée pour chaque instance d'entraînement, plutôt qu'à la fin des instances.
Classificateur SGD
Le classificateur SGD (Stochastic Gradient Descent) implémente essentiellement une routine d'apprentissage SGD simple prenant en charge diverses fonctions de perte et pénalités pour la classification. Scikit-learn fournitSGDClassifier module pour implémenter la classification SGD.
Paramètres
Le tableau suivant comprend les paramètres utilisés par SGDClassifier module -
| Sr.Non | Paramètre et description |
|---|---|
| 1 | loss - str, default = 'charnière' Il représente la fonction de perte à utiliser lors de la mise en œuvre. La valeur par défaut est 'hinge' qui nous donnera un SVM linéaire. Les autres options qui peuvent être utilisées sont -
|
| 2 | penalty - str, 'aucun', 'l2', 'l1', 'élastiquenet' C'est le terme de régularisation utilisé dans le modèle. Par défaut, c'est L2. Nous pouvons utiliser L1 ou 'Elasticnet; aussi mais les deux peuvent apporter une parcimonie au modèle, donc impossible à réaliser avec L2. |
| 3 | alpha - flottant, par défaut = 0,0001 Alpha, la constante qui multiplie le terme de régularisation, est le paramètre de réglage qui décide à quel point nous voulons pénaliser le modèle. La valeur par défaut est 0,0001. |
| 4 | l1_ratio - flottant, par défaut = 0,15 C'est ce qu'on appelle le paramètre de mixage ElasticNet. Son intervalle est 0 <= l1_ratio <= 1. Si l1_ratio = 1, la pénalité serait une pénalité L1. Si l1_ratio = 0, la pénalité serait une pénalité L2. |
| 5 | fit_intercept - Booléen, par défaut = True Ce paramètre spécifie qu'une constante (biais ou interception) doit être ajoutée à la fonction de décision. Aucune interception ne sera utilisée dans le calcul et les données seront supposées déjà centrées, si elles sont définies sur false. |
| 6 | tol - float ou aucun, facultatif, par défaut = 1.e-3 Ce paramètre représente le critère d'arrêt des itérations. Sa valeur par défaut est False mais si elle est définie sur None, les itérations s'arrêteront lorsqueloss > best_loss - tol for n_iter_no_changeépoques successives. |
| sept | shuffle - Booléen, facultatif, par défaut = True Ce paramètre représente cela si nous voulons que nos données d'entraînement soient mélangées après chaque époque ou non. |
| 8 | verbose - entier, par défaut = 0 Il représente le niveau de verbosité. Sa valeur par défaut est 0. |
| 9 | epsilon - flottant, par défaut = 0,1 Ce paramètre spécifie la largeur de la région insensible. Si loss = 'epsilon-insensitive', toute différence, entre la prédiction actuelle et l'étiquette correcte, inférieure au seuil serait ignorée. |
| dix | max_iter - int, facultatif, par défaut = 1000 Comme son nom l'indique, il représente le nombre maximum de passages sur les époques, c'est-à-dire les données d'apprentissage. |
| 11 | warm_start - booléen, facultatif, par défaut = faux Avec ce paramètre défini sur True, nous pouvons réutiliser la solution de l'appel précédent pour l'ajuster comme initialisation. Si nous choisissons default, c'est-à-dire false, cela effacera la solution précédente. |
| 12 | random_state - int, instance RandomState ou None, facultatif, par défaut = aucun Ce paramètre représente la graine du nombre pseudo aléatoire généré qui est utilisé lors du brassage des données. Voici les options.
|
| 13 | n_jobs - int ou aucun, facultatif, par défaut = aucun Il représente le nombre de processeurs à utiliser dans le calcul OVA (One Versus All), pour les problèmes multi-classes. La valeur par défaut est aucune, ce qui signifie 1. |
| 14 | learning_rate - chaîne, facultatif, par défaut = 'optimal'
|
| 15 | eta0 - double, par défaut = 0,0 Il représente le taux d'apprentissage initial pour les options de taux d'apprentissage mentionnées ci-dessus, c'est-à-dire «constant», «invscall» ou «adaptatif». |
| 16 | power_t - idouble, par défaut = 0,5 C'est l'exposant du taux d'apprentissage «incscalling». |
| 17 | early_stopping - booléen, par défaut = False Ce paramètre représente l'utilisation de l'arrêt précoce pour mettre fin à l'entraînement lorsque le score de validation ne s'améliore pas. Sa valeur par défaut est false, mais lorsqu'elle est définie sur true, elle met automatiquement de côté une fraction stratifiée des données d'entraînement comme validation et arrête la formation lorsque le score de validation ne s'améliore pas. |
| 18 | validation_fraction - flottant, par défaut = 0,1 Il n'est utilisé que lorsque early_stopping est vrai. Il représente la proportion de données d'entraînement à mettre de côté comme ensemble de validation pour l'arrêt prématuré des données d'entraînement. |
| 19 | n_iter_no_change - int, par défaut = 5 Il représente le nombre d'itérations sans amélioration si l'algorithme doit s'exécuter avant l'arrêt prématuré. |
| 20 | classs_weight - dict, {class_label: weight} ou "balancé", ou Aucun, facultatif Ce paramètre représente les poids associés aux classes. Si elles ne sont pas fournies, les classes sont censées avoir un poids de 1. |
| 20 | warm_start - booléen, facultatif, par défaut = faux Avec ce paramètre défini sur True, nous pouvons réutiliser la solution de l'appel précédent pour l'ajuster comme initialisation. Si nous choisissons default, c'est-à-dire false, cela effacera la solution précédente. |
| 21 | average - iBoolean ou int, facultatif, par défaut = false Il représente le nombre de processeurs à utiliser dans le calcul OVA (One Versus All), pour les problèmes multi-classes. La valeur par défaut est aucune, ce qui signifie 1. |
Les attributs
Le tableau suivant comprend les attributs utilisés par SGDClassifier module -
| Sr.Non | Attributs et description |
|---|---|
| 1 | coef_ - tableau, forme (1, n_features) si n_classes == 2, sinon (n_classes, n_features) Cet attribut fournit le poids attribué aux entités. |
| 2 | intercept_ - tableau, forme (1,) si n_classes == 2, sinon (n_classes,) Il représente le terme indépendant dans la fonction de décision. |
| 3 | n_iter_ - int Il donne le nombre d'itérations pour atteindre le critère d'arrêt. |
Implementation Example
Comme les autres classificateurs, la descente de gradient stochastique (SGD) doit être équipée des deux tableaux suivants -
Un tableau X contenant les échantillons d'apprentissage. Il est de taille [n_samples, n_features].
Un tableau Y contenant les valeurs cibles, c'est-à-dire des étiquettes de classe pour les échantillons d'apprentissage. Il est de taille [n_samples].
Example
Le script Python suivant utilise le modèle linéaire SGDClassifier -
import numpy as np
from sklearn import linear_model
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
Y = np.array([1, 1, 2, 2])
SGDClf = linear_model.SGDClassifier(max_iter = 1000, tol=1e-3,penalty = "elasticnet")
SGDClf.fit(X, Y)Output
SGDClassifier(
alpha = 0.0001, average = False, class_weight = None,
early_stopping = False, epsilon = 0.1, eta0 = 0.0, fit_intercept = True,
l1_ratio = 0.15, learning_rate = 'optimal', loss = 'hinge', max_iter = 1000,
n_iter = None, n_iter_no_change = 5, n_jobs = None, penalty = 'elasticnet',
power_t = 0.5, random_state = None, shuffle = True, tol = 0.001,
validation_fraction = 0.1, verbose = 0, warm_start = False
)Example
Maintenant, une fois ajusté, le modèle peut prédire de nouvelles valeurs comme suit -
SGDClf.predict([[2.,2.]])Output
array([2])Example
Pour l'exemple ci-dessus, nous pouvons obtenir le vecteur de poids à l'aide du script python suivant -
SGDClf.coef_Output
array([[19.54811198, 9.77200712]])Example
De même, nous pouvons obtenir la valeur d'interception à l'aide du script python suivant -
SGDClf.intercept_Output
array([10.])Example
Nous pouvons obtenir la distance signée par rapport à l'hyperplan en utilisant SGDClassifier.decision_function tel qu'utilisé dans le script python suivant -
SGDClf.decision_function([[2., 2.]])Output
array([68.6402382])Régresseur SGD
Le régresseur SGD (Stochastic Gradient Descent) implémente essentiellement une routine d'apprentissage SGD simple prenant en charge diverses fonctions de perte et pénalités pour s'adapter aux modèles de régression linéaire. Scikit-learn fournitSGDRegressor module pour implémenter la régression SGD.
Paramètres
Paramètres utilisés par SGDRegressorsont presque les mêmes que ceux utilisés dans le module SGDClassifier. La différence réside dans le paramètre «perte». PourSGDRegressor paramètre de perte des modules les valeurs positives sont les suivantes -
squared_loss - Il se réfère à l'ajustement ordinaire des moindres carrés.
huber: SGDRegressor- corriger les valeurs aberrantes en passant de la perte quadratique à la perte linéaire au-delà d'une distance de epsilon. Le travail de «huber» est de modifier «squared_loss» pour que l'algorithme se concentre moins sur la correction des valeurs aberrantes.
epsilon_insensitive - En fait, il ignore les erreurs moins que epsilon.
squared_epsilon_insensitive- C'est la même chose que epsilon_insensitive. La seule différence est que cela devient une perte au carré au-delà d'une tolérance de epsilon.
Une autre différence est que le paramètre nommé 'power_t' a la valeur par défaut de 0,25 au lieu de 0,5 comme dans SGDClassifier. De plus, il n'a pas de paramètres 'class_weight' et 'n_jobs'.
Les attributs
Les attributs de SGDRegressor sont également les mêmes que ceux du module SGDClassifier. Il a plutôt trois attributs supplémentaires comme suit -
average_coef_ - tableau, forme (n_features,)
Comme son nom l'indique, il fournit les poids moyens attribués aux fonctionnalités.
average_intercept_ - tableau, forme (1,)
Comme son nom l'indique, il fournit le terme d'interception moyen.
t_ - int
Il fournit le nombre de mises à jour de poids effectuées pendant la phase d'entraînement.
Note - les attributs average_coef_ et average_intercept_ fonctionneront après avoir activé le paramètre 'average' sur True.
Implementation Example
Suivre les utilisations de script Python SGDRegressor modèle linéaire -
import numpy as np
from sklearn import linear_model
n_samples, n_features = 10, 5
rng = np.random.RandomState(0)
y = rng.randn(n_samples)
X = rng.randn(n_samples, n_features)
SGDReg =linear_model.SGDRegressor(
max_iter = 1000,penalty = "elasticnet",loss = 'huber',tol = 1e-3, average = True
)
SGDReg.fit(X, y)Output
SGDRegressor(
alpha = 0.0001, average = True, early_stopping = False, epsilon = 0.1,
eta0 = 0.01, fit_intercept = True, l1_ratio = 0.15,
learning_rate = 'invscaling', loss = 'huber', max_iter = 1000,
n_iter = None, n_iter_no_change = 5, penalty = 'elasticnet', power_t = 0.25,
random_state = None, shuffle = True, tol = 0.001, validation_fraction = 0.1,
verbose = 0, warm_start = False
)Example
Maintenant, une fois ajusté, nous pouvons obtenir le vecteur de poids à l'aide du script python suivant -
SGDReg.coef_Output
array([-0.00423314, 0.00362922, -0.00380136, 0.00585455, 0.00396787])Example
De même, nous pouvons obtenir la valeur d'interception à l'aide du script python suivant -
SGReg.intercept_Output
SGReg.intercept_Example
Nous pouvons obtenir le nombre de mises à jour de poids pendant la phase d'entraînement à l'aide du script python suivant -
SGDReg.t_Output
61.0Avantages et inconvénients de SGD
Suivre les pros de SGD -
La descente de gradient stochastique (SGD) est très efficace.
Il est très facile à mettre en œuvre car il existe de nombreuses possibilités de réglage du code.
Suite aux inconvénients de SGD -
La descente de gradient stochastique (SGD) nécessite plusieurs hyperparamètres comme les paramètres de régularisation.
Il est sensible à la mise à l'échelle des fonctionnalités.
Ce chapitre traite d'une méthode d'apprentissage automatique appelée Support Vector Machines (SVM).
introduction
Les machines vectorielles de support (SVM) sont des méthodes d'apprentissage automatique supervisé puissantes mais flexibles utilisées pour la classification, la régression et la détection des valeurs aberrantes. Les SVM sont très efficaces dans les espaces de grandes dimensions et sont généralement utilisés dans les problèmes de classification. Les SVM sont populaires et économes en mémoire car ils utilisent un sous-ensemble de points d'apprentissage dans la fonction de décision.
L'objectif principal des SVM est de diviser les ensembles de données en nombre de classes afin de trouver un maximum marginal hyperplane (MMH) ce qui peut être fait dans les deux étapes suivantes -
Les machines vectorielles de support généreront d'abord des hyperplans de manière itérative qui séparent les classes de la meilleure façon.
Après cela, il choisira l'hyperplan qui sépare correctement les classes.
Voici quelques concepts importants de SVM:
Support Vectors- Ils peuvent être définis comme les points de données les plus proches de l'hyperplan. Les vecteurs de support aident à décider de la ligne de séparation.
Hyperplane - Le plan de décision ou l'espace qui divise un ensemble d'objets ayant différentes classes.
Margin - L'écart entre deux lignes sur les points de données de placard de différentes classes est appelé marge.
Les diagrammes suivants vous donneront un aperçu de ces concepts SVM -
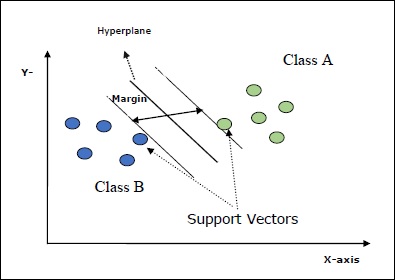
SVM dans Scikit-learn prend en charge les vecteurs d'échantillons clairsemés et denses en entrée.
Classification des SVM
Scikit-learn propose trois classes à savoir SVC, NuSVC et LinearSVC qui peut effectuer une classification de classes multiclasses.
SVC
Il s'agit d'une classification vectorielle de support C dont l'implémentation est basée sur libsvm. Le module utilisé par scikit-learn estsklearn.svm.SVC. Cette classe gère la prise en charge multiclasse selon un schéma un contre un.
Paramètres
Le tableau suivant comprend les paramètres utilisés par sklearn.svm.SVC classe -
| Sr.Non | Paramètre et description |
|---|---|
| 1 | C - float, facultatif, par défaut = 1.0 C'est le paramètre de pénalité du terme d'erreur. |
| 2 | kernel - chaîne, facultatif, par défaut = 'rbf' Ce paramètre spécifie le type de noyau à utiliser dans l'algorithme. nous pouvons choisir n'importe lequel parmi,‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’. La valeur par défaut du noyau serait‘rbf’. |
| 3 | degree - int, facultatif, par défaut = 3 Il représente le degré de la fonction noyau 'poly' et sera ignoré par tous les autres noyaux. |
| 4 | gamma - {'scale', 'auto'} ou float, C'est le coefficient de noyau pour les noyaux «rbf», «poly» et «sigmoïde». |
| 5 | optinal default - = 'échelle' Si vous choisissez default ie gamma = 'scale' alors la valeur de gamma à utiliser par SVC est 1 / (_ ∗. ()). Par contre, si gamma = 'auto', il utilise 1 / _. |
| 6 | coef0 - float, facultatif, par défaut = 0,0 Un terme indépendant dans la fonction du noyau qui n'est significatif que dans «poly» et «sigmoïde». |
| sept | tol - float, optionnel, par défaut = 1.e-3 Ce paramètre représente le critère d'arrêt des itérations. |
| 8 | shrinking - Booléen, facultatif, par défaut = True Ce paramètre représente cela, que nous souhaitons utiliser une heuristique de réduction ou non. |
| 9 | verbose - Booléen, par défaut: false Il active ou désactive la sortie verbeuse. Sa valeur par défaut est false. |
| dix | probability - booléen, facultatif, par défaut = true Ce paramètre active ou désactive les estimations de probabilité. La valeur par défaut est false, mais elle doit être activée avant d'appeler fit. |
| 11 | max_iter - int, facultatif, par défaut = -1 Comme son nom l'indique, il représente le nombre maximum d'itérations dans le solveur. La valeur -1 signifie qu'il n'y a pas de limite sur le nombre d'itérations. |
| 12 | cache_size - flotteur, en option Ce paramètre spécifiera la taille du cache du noyau. La valeur sera en Mo (mégaoctets). |
| 13 | random_state - int, instance RandomState ou None, facultatif, par défaut = aucun Ce paramètre représente la graine du nombre pseudo aléatoire généré qui est utilisé lors du brassage des données. Voici les options -
|
| 14 | class_weight - {dict, 'balancé'}, facultatif Ce paramètre définira le paramètre C de la classe j sur _ℎ [] ∗ pour SVC. Si nous utilisons l'option par défaut, cela signifie que toutes les classes sont censées avoir un poids un. D'autre part, si vous choisissezclass_weight:balanced, il utilisera les valeurs de y pour ajuster automatiquement les poids. |
| 15 | decision_function_shape - ovo ',' ovr ', default =' ovr ' Ce paramètre décidera si l'algorithme retournera ‘ovr’ (one-vs-rest) fonction de décision de la forme comme tous les autres classificateurs, ou l'original ovo(un contre un) fonction de décision de libsvm. |
| 16 | break_ties - booléen, facultatif, par défaut = faux True - Le prédicteur rompra les égalités selon les valeurs de confiance de la fonction decision_function False - Le prédicteur renverra la première classe parmi les classes à égalité. |
Les attributs
Le tableau suivant comprend les attributs utilisés par sklearn.svm.SVC classe -
| Sr.Non | Attributs et description |
|---|---|
| 1 | support_ - en forme de tableau, forme = [n_SV] Il renvoie les indices des vecteurs de support. |
| 2 | support_vectors_ - en forme de tableau, forme = [n_SV, n_features] Il renvoie les vecteurs de support. |
| 3 | n_support_ - de type tableau, dtype = int32, shape = [n_class] Il représente le nombre de vecteurs de support pour chaque classe. |
| 4 | dual_coef_ - tableau, forme = [n_class-1, n_SV] Ce sont les coefficients des vecteurs de support dans la fonction de décision. |
| 5 | coef_ - tableau, forme = [n_class * (n_class-1) / 2, n_features] Cet attribut, disponible uniquement en cas de noyau linéaire, fournit le poids attribué aux entités. |
| 6 | intercept_ - tableau, forme = [n_class * (n_class-1) / 2] Il représente le terme indépendant (constante) dans la fonction de décision. |
| sept | fit_status_ - int La sortie serait 0 si elle est correctement installée. La sortie serait 1 si elle est mal installée. |
| 8 | classes_ - tableau de forme = [n_classes] Il donne les étiquettes des classes. |
Implementation Example
Comme les autres classificateurs, SVC doit également être équipé des deux tableaux suivants -
Un tableau Xtenant les échantillons de formation. Il est de taille [n_samples, n_features].
Un tableau Ycontenant les valeurs cibles, c'est-à-dire les étiquettes de classe pour les échantillons d'apprentissage. Il est de taille [n_samples].
Suivre les utilisations de script Python sklearn.svm.SVC classe -
import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import SVC
SVCClf = SVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
SVCClf.fit(X, y)Output
SVC(C = 1.0, cache_size = 200, class_weight = None, coef0 = 0.0,
decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
max_iter = -1, probability = False, random_state = None, shrinking = False,
tol = 0.001, verbose = False)Example
Maintenant, une fois ajusté, nous pouvons obtenir le vecteur de poids à l'aide du script python suivant -
SVCClf.coef_Output
array([[0.5, 0.5]])Example
De même, nous pouvons obtenir la valeur d'autres attributs comme suit -
SVCClf.predict([[-0.5,-0.8]])Output
array([1])Example
SVCClf.n_support_Output
array([1, 1])Example
SVCClf.support_vectors_Output
array(
[
[-1., -1.],
[ 1., 1.]
]
)Example
SVCClf.support_Output
array([0, 2])Example
SVCClf.intercept_Output
array([-0.])Example
SVCClf.fit_status_Output
0NuSVC
NuSVC est la classification vectorielle de support Nu. C'est une autre classe fournie par scikit-learn qui peut effectuer une classification multi-classes. C'est comme SVC mais NuSVC accepte des ensembles de paramètres légèrement différents. Le paramètre qui est différent de SVC est le suivant -
nu - float, facultatif, par défaut = 0,5
Il représente une limite supérieure de la fraction des erreurs d'apprentissage et une limite inférieure de la fraction des vecteurs de support. Sa valeur doit être dans l'intervalle de (o, 1].
Les autres paramètres et attributs sont identiques à ceux de SVC.
Exemple d'implémentation
Nous pouvons implémenter le même exemple en utilisant sklearn.svm.NuSVC classe aussi.
import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import NuSVC
NuSVCClf = NuSVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
NuSVCClf.fit(X, y)Production
NuSVC(cache_size = 200, class_weight = None, coef0 = 0.0,
decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
max_iter = -1, nu = 0.5, probability = False, random_state = None,
shrinking = False, tol = 0.001, verbose = False)Nous pouvons obtenir les sorties du reste des attributs comme dans le cas de SVC.
LinéaireSVC
C'est la classification de vecteur de support linéaire. C'est similaire à SVC ayant kernel = 'linear'. La différence entre eux est queLinearSVC implémenté en termes de liblinear tandis que SVC est implémenté en libsvm. C'est la raisonLinearSVCa plus de flexibilité dans le choix des pénalités et des fonctions de perte. Il s'adapte également mieux à un grand nombre d'échantillons.
Si nous parlons de ses paramètres et attributs, il ne prend pas en charge ‘kernel’ car il est supposé linéaire et il lui manque également certains attributs tels que support_, support_vectors_, n_support_, fit_status_ et, dual_coef_.
Cependant, il prend en charge penalty et loss paramètres comme suit -
penalty − string, L1 or L2(default = ‘L2’)
Ce paramètre permet de spécifier la norme (L1 ou L2) utilisée en pénalisation (régularisation).
loss − string, hinge, squared_hinge (default = squared_hinge)
Il représente la fonction de perte où «charnière» est la perte SVM standard et «squared_hinge» est le carré de la perte de charnière.
Exemple d'implémentation
Suivre les utilisations de script Python sklearn.svm.LinearSVC classe -
from sklearn.svm import LinearSVC
from sklearn.datasets import make_classification
X, y = make_classification(n_features = 4, random_state = 0)
LSVCClf = LinearSVC(dual = False, random_state = 0, penalty = 'l1',tol = 1e-5)
LSVCClf.fit(X, y)Production
LinearSVC(C = 1.0, class_weight = None, dual = False, fit_intercept = True,
intercept_scaling = 1, loss = 'squared_hinge', max_iter = 1000,
multi_class = 'ovr', penalty = 'l1', random_state = 0, tol = 1e-05, verbose = 0)Exemple
Maintenant, une fois ajusté, le modèle peut prédire de nouvelles valeurs comme suit -
LSVCClf.predict([[0,0,0,0]])Production
[1]Exemple
Pour l'exemple ci-dessus, nous pouvons obtenir le vecteur de poids à l'aide du script python suivant -
LSVCClf.coef_Production
[[0. 0. 0.91214955 0.22630686]]Exemple
De même, nous pouvons obtenir la valeur d'interception à l'aide du script python suivant -
LSVCClf.intercept_Production
[0.26860518]Régression avec SVM
Comme indiqué précédemment, SVM est utilisé pour les problèmes de classification et de régression. La méthode de classification des vecteurs de support (SVC) de Scikit-learn peut également être étendue pour résoudre les problèmes de régression. Cette méthode étendue est appelée régression vectorielle de support (SVR).
Similitude de base entre SVM et SVR
Le modèle créé par SVC dépend uniquement d'un sous-ensemble de données d'entraînement. Pourquoi? Parce que la fonction de coût de création du modèle ne se soucie pas des points de données d'entraînement qui se trouvent en dehors de la marge.
Alors que le modèle produit par SVR (Support Vector Regression) ne dépend également que d'un sous-ensemble des données d'apprentissage. Pourquoi? Parce que la fonction de coût de création du modèle ignore tous les points de données d'entraînement proches de la prédiction du modèle.
Scikit-learn propose trois classes à savoir SVR, NuSVR and LinearSVR comme trois implémentations différentes de SVR.
SVR
C'est la régression vectorielle support Epsilon dont la mise en œuvre est basée sur libsvm. À l'opposé deSVC Il y a deux paramètres libres dans le modèle à savoir ‘C’ et ‘epsilon’.
epsilon - float, facultatif, par défaut = 0,1
Il représente l'epsilon dans le modèle epsilon-SVR, et spécifie le tube epsilon dans lequel aucune pénalité n'est associée dans la fonction de perte d'apprentissage avec des points prédits à une distance epsilon de la valeur réelle.
Les autres paramètres et attributs sont similaires à ceux utilisés dans SVC.
Exemple d'implémentation
Suivre les utilisations de script Python sklearn.svm.SVR classe -
from sklearn import svm
X = [[1, 1], [2, 2]]
y = [1, 2]
SVRReg = svm.SVR(kernel = ’linear’, gamma = ’auto’)
SVRReg.fit(X, y)Production
SVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, epsilon = 0.1, gamma = 'auto',
kernel = 'linear', max_iter = -1, shrinking = True, tol = 0.001, verbose = False)Exemple
Maintenant, une fois ajusté, nous pouvons obtenir le vecteur de poids à l'aide du script python suivant -
SVRReg.coef_Production
array([[0.4, 0.4]])Exemple
De même, nous pouvons obtenir la valeur d'autres attributs comme suit -
SVRReg.predict([[1,1]])Production
array([1.1])De même, nous pouvons également obtenir les valeurs d'autres attributs.
NuSVR
NuSVR est la régression vectorielle de Nu Support. C'est comme NuSVC, mais NuSVR utilise un paramètrenupour contrôler le nombre de vecteurs de support. Et de plus, contrairement à NuSVC oùnu a remplacé le paramètre C, ici il remplace epsilon.
Exemple d'implémentation
Suivre les utilisations de script Python sklearn.svm.SVR classe -
from sklearn.svm import NuSVR
import numpy as np
n_samples, n_features = 20, 15
np.random.seed(0)
y = np.random.randn(n_samples)
X = np.random.randn(n_samples, n_features)
NuSVRReg = NuSVR(kernel = 'linear', gamma = 'auto',C = 1.0, nu = 0.1)^M
NuSVRReg.fit(X, y)Production
NuSVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, gamma = 'auto',
kernel = 'linear', max_iter = -1, nu = 0.1, shrinking = True, tol = 0.001,
verbose = False)Exemple
Maintenant, une fois ajusté, nous pouvons obtenir le vecteur de poids à l'aide du script python suivant -
NuSVRReg.coef_Production
array(
[
[-0.14904483, 0.04596145, 0.22605216, -0.08125403, 0.06564533,
0.01104285, 0.04068767, 0.2918337 , -0.13473211, 0.36006765,
-0.2185713 , -0.31836476, -0.03048429, 0.16102126, -0.29317051]
]
)De même, nous pouvons également obtenir la valeur d'autres attributs.
LinéaireSVR
C'est la régression vectorielle de support linéaire. C'est similaire à SVR ayant kernel = 'linear'. La différence entre eux est queLinearSVR mis en œuvre en termes de liblinear, tandis que SVC implémenté dans libsvm. C'est la raisonLinearSVRa plus de flexibilité dans le choix des pénalités et des fonctions de perte. Il s'adapte également mieux à un grand nombre d'échantillons.
Si nous parlons de ses paramètres et attributs, il ne prend pas en charge ‘kernel’ car il est supposé linéaire et il lui manque également certains attributs tels que support_, support_vectors_, n_support_, fit_status_ et, dual_coef_.
Cependant, il prend en charge les paramètres de `` perte '' comme suit -
loss - chaîne, facultative, par défaut = 'epsilon_insensitive'
Elle représente la fonction de perte où la perte epsilon_insensitive est la perte L1 et la perte au carré insensible epsilon est la perte L2.
Exemple d'implémentation
Suivre les utilisations de script Python sklearn.svm.LinearSVR classe -
from sklearn.svm import LinearSVR
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 4, random_state = 0)
LSVRReg = LinearSVR(dual = False, random_state = 0,
loss = 'squared_epsilon_insensitive',tol = 1e-5)
LSVRReg.fit(X, y)Production
LinearSVR(
C=1.0, dual=False, epsilon=0.0, fit_intercept=True,
intercept_scaling=1.0, loss='squared_epsilon_insensitive',
max_iter=1000, random_state=0, tol=1e-05, verbose=0
)Exemple
Maintenant, une fois ajusté, le modèle peut prédire de nouvelles valeurs comme suit -
LSRReg.predict([[0,0,0,0]])Production
array([-0.01041416])Exemple
Pour l'exemple ci-dessus, nous pouvons obtenir le vecteur de poids à l'aide du script python suivant -
LSRReg.coef_Production
array([20.47354746, 34.08619401, 67.23189022, 87.47017787])Exemple
De même, nous pouvons obtenir la valeur d'interception à l'aide du script python suivant -
LSRReg.intercept_Production
array([-0.01041416])Ici, nous allons découvrir ce qu'est la détection d'anomalies dans Sklearn et comment elle est utilisée dans l'identification des points de données.
La détection d'anomalies est une technique utilisée pour identifier les points de données dans l'ensemble de données qui ne correspondent pas bien au reste des données. Il a de nombreuses applications dans les entreprises telles que la détection de fraude, la détection d'intrusion, la surveillance de l'état du système, la surveillance et la maintenance prédictive. Les anomalies, également appelées aberrantes, peuvent être divisées en trois catégories:
Point anomalies - Cela se produit lorsqu'une instance de données individuelle est considérée comme anormale par rapport au reste des données.
Contextual anomalies- Ce type d'anomalie est spécifique au contexte. Cela se produit si une instance de données est anormale dans un contexte spécifique.
Collective anomalies - Cela se produit lorsqu'une collection d'instances de données associées est anormale par rapport à l'ensemble de données plutôt qu'à des valeurs individuelles.
Méthodes
Deux méthodes à savoir outlier detection et novelty detectionpeut être utilisé pour la détection d'anomalies. Il faut voir la distinction entre eux.
Détection des valeurs aberrantes
Les données d'entraînement contiennent des valeurs aberrantes qui sont loin du reste des données. Ces valeurs aberrantes sont définies comme des observations. C'est la raison pour laquelle les estimateurs de détection des valeurs aberrantes essaient toujours d'ajuster la région ayant les données d'entraînement les plus concentrées tout en ignorant les observations déviantes. Elle est également connue sous le nom de détection d'anomalies non supervisée.
Détection de nouveauté
Il s'agit de détecter un modèle non observé dans de nouvelles observations qui n'est pas inclus dans les données d'apprentissage. Ici, les données d'apprentissage ne sont pas polluées par les valeurs aberrantes. Elle est également connue sous le nom de détection d'anomalies semi-supervisée.
Il existe un ensemble d'outils ML, fournis par scikit-learn, qui peuvent être utilisés à la fois pour la détection des valeurs aberrantes et pour la détection de nouveauté. Ces outils implémentent d'abord l'apprentissage d'objets à partir des données dans une méthode non supervisée en utilisant la méthode fit () comme suit -
estimator.fit(X_train)Maintenant, les nouvelles observations seraient triées comme inliers (labeled 1) ou outliers (labeled -1) en utilisant la méthode predict () comme suit -
estimator.fit(X_test)L'estimateur calculera d'abord la fonction de notation brute, puis la méthode de prédiction utilisera le seuil sur cette fonction de notation brute. Nous pouvons accéder à cette fonction de notation brute à l'aide descore_sample méthode et peut contrôler le seuil en contamination paramètre.
On peut aussi définir decision_function méthode qui définit les valeurs aberrantes comme une valeur négative et les inliers comme une valeur non négative.
estimator.decision_function(X_test)Algorithmes Sklearn pour la détection des valeurs aberrantes
Commençons par comprendre ce qu'est une enveloppe elliptique.
Mise en place d'une enveloppe elliptique
Cet algorithme suppose que les données régulières proviennent d'une distribution connue telle que la distribution gaussienne. Pour la détection des valeurs aberrantes, Scikit-learn fournit un objet nommécovariance.EllipticEnvelop.
Cet objet ajuste une estimation de covariance robuste aux données, et donc, ajuste une ellipse aux points de données centraux. Il ignore les points en dehors du mode central.
Paramètres
Le tableau suivant contient les paramètres utilisés par sklearn. covariance.EllipticEnvelop méthode -
| Sr.Non | Paramètre et description |
|---|---|
| 1 | store_precision - Booléen, facultatif, par défaut = True Nous pouvons le spécifier si la précision estimée est stockée. |
| 2 | assume_centered - Booléen, facultatif, par défaut = False Si nous le définissons sur False, il calculera l'emplacement robuste et la covariance directement à l'aide de l'algorithme FastMCD. D'autre part, s'il est défini sur True, il calculera la prise en charge de l'emplacement robuste et du covarian. |
| 3 | support_fraction - float in (0., 1.), optionnel, par défaut = Aucun Ce paramètre indique à la méthode la proportion de points à inclure dans le support des estimations brutes MCD. |
| 4 | contamination - float in (0., 1.), optionnel, par défaut = 0,1 Il fournit la proportion des valeurs aberrantes dans l'ensemble de données. |
| 5 | random_state - int, instance RandomState ou None, facultatif, par défaut = aucun Ce paramètre représente la graine du nombre pseudo aléatoire généré qui est utilisé lors du brassage des données. Voici les options -
|
Les attributs
Le tableau suivant comprend les attributs utilisés par sklearn. covariance.EllipticEnvelop méthode -
| Sr.Non | Attributs et description |
|---|---|
| 1 | support_ - en forme de tableau, forme (n_samples,) Il représente le masque des observations utilisé pour calculer des estimations robustes de l'emplacement et de la forme. |
| 2 | location_ - forme de type tableau (n_features) Il renvoie l'emplacement robuste estimé. |
| 3 | covariance_ - en forme de tableau, forme (n_features, n_features) Elle renvoie la matrice de covariance robuste estimée. |
| 4 | precision_ - en forme de tableau, forme (n_features, n_features) Il renvoie la pseudo matrice inverse estimée. |
| 5 | offset_ - flotter Il permet de définir la fonction de décision à partir des scores bruts. decision_function = score_samples -offset_ |
Implementation Example
import numpy as np^M
from sklearn.covariance import EllipticEnvelope^M
true_cov = np.array([[.5, .6],[.6, .4]])
X = np.random.RandomState(0).multivariate_normal(mean = [0, 0], cov=true_cov,size=500)
cov = EllipticEnvelope(random_state = 0).fit(X)^M
# Now we can use predict method. It will return 1 for an inlier and -1 for an outlier.
cov.predict([[0, 0],[2, 2]])Output
array([ 1, -1])Forêt d'isolement
Dans le cas d'un jeu de données de grande dimension, un moyen efficace de détection des valeurs aberrantes consiste à utiliser des forêts aléatoires. Le scikit-learn fournitensemble.IsolationForestméthode qui isole les observations en sélectionnant au hasard une entité. Ensuite, il sélectionne au hasard une valeur entre les valeurs maximale et minimale des caractéristiques sélectionnées.
Ici, le nombre de fractionnements nécessaires pour isoler un échantillon équivaut à la longueur du chemin du nœud racine au nœud de terminaison.
Paramètres
Le tableau suivant comprend les paramètres utilisés par sklearn. ensemble.IsolationForest méthode -
| Sr.Non | Paramètre et description |
|---|---|
| 1 | n_estimators - int, facultatif, par défaut = 100 Il représente le nombre d'estimateurs de base dans l'ensemble. |
| 2 | max_samples - int ou float, facultatif, par défaut = "auto" Il représente le nombre d'échantillons à tirer de X pour entraîner chaque estimateur de base. Si nous choisissons int comme valeur, il tirera des échantillons max_samples. Si nous choisissons float comme valeur, il tirera max_samples ∗ .shape [0] échantillons. Et, si nous choisissons auto comme valeur, il dessinera max_samples = min (256, n_samples). |
| 3 | support_fraction - float in (0., 1.), optionnel, par défaut = Aucun Ce paramètre indique à la méthode la proportion de points à inclure dans le support des estimations brutes MCD. |
| 4 | contamination - auto ou float, facultatif, par défaut = auto Il fournit la proportion des valeurs aberrantes dans l'ensemble de données. Si nous le définissons par défaut, c'est-à-dire auto, il déterminera le seuil comme dans le papier d'origine. S'il est réglé sur float, la plage de contamination sera dans la plage de [0,0,5]. |
| 5 | random_state - int, instance RandomState ou None, facultatif, par défaut = aucun Ce paramètre représente la graine du nombre pseudo aléatoire généré qui est utilisé lors du brassage des données. Voici les options -
|
| 6 | max_features - int ou float, facultatif (par défaut = 1.0) Il représente le nombre d'entités à tirer de X pour entraîner chaque estimateur de base. Si nous choisissons int comme valeur, il dessinera des fonctionnalités max_features. Si nous choisissons float comme valeur, il tirera des échantillons max_features * X.shape []. |
| sept | bootstrap - Booléen, facultatif (par défaut = False) Son option par défaut est False, ce qui signifie que l'échantillonnage serait effectué sans remplacement. Et d'autre part, s'il est défini sur True, signifie que les arbres individuels sont ajustés sur un sous-ensemble aléatoire des données d'apprentissage échantillonnées avec remplacement. |
| 8 | n_jobs - int ou None, facultatif (par défaut = None) Il représente le nombre de travaux à exécuter en parallèle pendant fit() et predict() méthodes à la fois. |
| 9 | verbose - int, facultatif (par défaut = 0) Ce paramètre contrôle la verbosité du processus de création de l'arborescence. |
| dix | warm_start - Bool, facultatif (par défaut = False) Si warm_start = true, nous pouvons réutiliser la solution des appels précédents pour ajuster et ajouter plus d'estimateurs à l'ensemble. Mais si est défini sur false, nous devons adapter une toute nouvelle forêt. |
Les attributs
Le tableau suivant comprend les attributs utilisés par sklearn. ensemble.IsolationForest méthode -
| Sr.Non | Attributs et description |
|---|---|
| 1 | estimators_ - liste de DecisionTreeClassifier Fournir la collection de tous les sous-estimateurs ajustés. |
| 2 | max_samples_ - entier Il fournit le nombre réel d'échantillons utilisés. |
| 3 | offset_ - flotter Il permet de définir la fonction de décision à partir des scores bruts. decision_function = score_samples -offset_ |
Implementation Example
Le script Python ci-dessous utilisera sklearn. ensemble.IsolationForest méthode pour ajuster 10 arbres sur des données données
from sklearn.ensemble import IsolationForest
import numpy as np
X = np.array([[-1, -2], [-3, -3], [-3, -4], [0, 0], [-50, 60]])
OUTDClf = IsolationForest(n_estimators = 10)
OUTDclf.fit(X)Output
IsolationForest(
behaviour = 'old', bootstrap = False, contamination='legacy',
max_features = 1.0, max_samples = 'auto', n_estimators = 10, n_jobs=None,
random_state = None, verbose = 0
)Facteur de valeur aberrante locale
L'algorithme LOF (Local Outlier Factor) est un autre algorithme efficace pour effectuer la détection des valeurs aberrantes sur des données de grande dimension. Le scikit-learn fournitneighbors.LocalOutlierFactorméthode qui calcule un score, appelé facteur aberrant local, reflétant le degré d'anomalie des observations. La logique principale de cet algorithme est de détecter les échantillons qui ont une densité nettement inférieure à celle de ses voisins. C'est pourquoi il mesure l'écart de densité locale de points de données donnés par rapport à leurs voisins.
Paramètres
Le tableau suivant comprend les paramètres utilisés par sklearn. neighbors.LocalOutlierFactor méthode
| Sr.Non | Paramètre et description |
|---|---|
| 1 | n_neighbors − int, optional, default = 20 It represents the number of neighbors use by default for kneighbors query. All samples would be used if . |
| 2 | algorithm − optional Which algorithm to be used for computing nearest neighbors.
|
| 3 | leaf_size − int, optional, default = 30 The value of this parameter can affect the speed of the construction and query. It also affects the memory required to store the tree. This parameter is passed to BallTree or KdTree algorithms. |
| 4 | contamination − auto or float, optional, default = auto It provides the proportion of the outliers in the data set. If we set it default i.e. auto, it will determine the threshold as in the original paper. If set to float, the range of contamination will be in the range of [0,0.5]. |
| 5 | metric − string or callable, default It represents the metric used for distance computation. |
| 6 | P − int, optional (default = 2) It is the parameter for the Minkowski metric. P=1 is equivalent to using manhattan_distance i.e. L1, whereas P=2 is equivalent to using euclidean_distance i.e. L2. |
| 7 | novelty − Boolean, (default = False) By default, LOF algorithm is used for outlier detection but it can be used for novelty detection if we set novelty = true. |
| 8 | n_jobs − int or None, optional (default = None) It represents the number of jobs to be run in parallel for fit() and predict() methods both. |
Attributes
Following table consist the attributes used by sklearn.neighbors.LocalOutlierFactor method −
| Sr.No | Attributes & Description |
|---|---|
| 1 | negative_outlier_factor_ − numpy array, shape(n_samples,) Providing opposite LOF of the training samples. |
| 2 | n_neighbors_ − integer It provides the actual number of neighbors used for neighbors queries. |
| 3 | offset_ − float It is used to define the binary labels from the raw scores. |
Implementation Example
The Python script given below will use sklearn.neighbors.LocalOutlierFactor method to construct NeighborsClassifier class from any array corresponding our data set
from sklearn.neighbors import NearestNeighbors
samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]]
LOFneigh = NearestNeighbors(n_neighbors = 1, algorithm = "ball_tree",p=1)
LOFneigh.fit(samples)Output
NearestNeighbors(
algorithm = 'ball_tree', leaf_size = 30, metric='minkowski',
metric_params = None, n_jobs = None, n_neighbors = 1, p = 1, radius = 1.0
)Example
Now, we can ask from this constructed classifier is the closet point to [0.5, 1., 1.5] by using the following python script −
print(neigh.kneighbors([[.5, 1., 1.5]])Output
(array([[1.7]]), array([[1]], dtype = int64))One-Class SVM
The One-Class SVM, introduced by Schölkopf et al., is the unsupervised Outlier Detection. It is also very efficient in high-dimensional data and estimates the support of a high-dimensional distribution. It is implemented in the Support Vector Machines module in the Sklearn.svm.OneClassSVM object. For defining a frontier, it requires a kernel (mostly used is RBF) and a scalar parameter.
For better understanding let's fit our data with svm.OneClassSVM object −
Example
from sklearn.svm import OneClassSVM
X = [[0], [0.89], [0.90], [0.91], [1]]
OSVMclf = OneClassSVM(gamma = 'scale').fit(X)Now, we can get the score_samples for input data as follows −
OSVMclf.score_samples(X)Output
array([1.12218594, 1.58645126, 1.58673086, 1.58645127, 1.55713767])This chapter will help you in understanding the nearest neighbor methods in Sklearn.
Neighbor based learning method are of both types namely supervised and unsupervised. Supervised neighbors-based learning can be used for both classification as well as regression predictive problems but, it is mainly used for classification predictive problems in industry.
Neighbors based learning methods do not have a specialised training phase and uses all the data for training while classification. It also does not assume anything about the underlying data. That’s the reason they are lazy and non-parametric in nature.
The main principle behind nearest neighbor methods is −
To find a predefined number of training samples closet in distance to the new data point
Predict the label from these number of training samples.
Here, the number of samples can be a user-defined constant like in K-nearest neighbor learning or vary based on the local density of point like in radius-based neighbor learning.
sklearn.neighbors Module
Scikit-learn have sklearn.neighbors module that provides functionality for both unsupervised and supervised neighbors-based learning methods. As input, the classes in this module can handle either NumPy arrays or scipy.sparse matrices.
Types of algorithms
Different types of algorithms which can be used in neighbor-based methods’ implementation are as follows −
Brute Force
The brute-force computation of distances between all pairs of points in the dataset provides the most naïve neighbor search implementation. Mathematically, for N samples in D dimensions, brute-force approach scales as 0[DN2]
For small data samples, this algorithm can be very useful, but it becomes infeasible as and when number of samples grows. Brute force neighbor search can be enabled by writing the keyword algorithm=’brute’.
K-D Tree
One of the tree-based data structures that have been invented to address the computational inefficiencies of the brute-force approach, is KD tree data structure. Basically, the KD tree is a binary tree structure which is called K-dimensional tree. It recursively partitions the parameters space along the data axes by dividing it into nested orthographic regions into which the data points are filled.
Advantages
Following are some advantages of K-D tree algorithm −
Construction is fast − As the partitioning is performed only along the data axes, K-D tree’s construction is very fast.
Less distance computations − This algorithm takes very less distance computations to determine the nearest neighbor of a query point. It only takes [ ()] distance computations.
Disadvantages
Fast for only low-dimensional neighbor searches − It is very fast for low-dimensional (D < 20) neighbor searches but as and when D grow it becomes inefficient. As the partitioning is performed only along the data axes,
K-D tree neighbor searches can be enabled by writing the keyword algorithm=’kd_tree’.
Ball Tree
As we know that KD Tree is inefficient in higher dimensions, hence, to address this inefficiency of KD Tree, Ball tree data structure was developed. Mathematically, it recursively divides the data, into nodes defined by a centroid C and radius r, in such a way that each point in the node lies within the hyper-sphere defined by centroid C and radius r. It uses triangle inequality, given below, which reduces the number of candidate points for a neighbor search
$$\arrowvert X+Y\arrowvert\leq \arrowvert X\arrowvert+\arrowvert Y\arrowvert$$Advantages
Following are some advantages of Ball Tree algorithm −
Efficient on highly structured data − As ball tree partition the data in a series of nesting hyper-spheres, it is efficient on highly structured data.
Out-performs KD-tree − Ball tree out-performs KD tree in high dimensions because it has spherical geometry of the ball tree nodes.
Disadvantages
Costly − Partition the data in a series of nesting hyper-spheres makes its construction very costly.
Ball tree neighbor searches can be enabled by writing the keyword algorithm=’ball_tree’.
Choosing Nearest Neighbors Algorithm
The choice of an optimal algorithm for a given dataset depends upon the following factors −
Number of samples (N) and Dimensionality (D)
These are the most important factors to be considered while choosing Nearest Neighbor algorithm. It is because of the reasons given below −
The query time of Brute Force algorithm grows as O[DN].
The query time of Ball tree algorithm grows as O[D log(N)].
The query time of KD tree algorithm changes with D in a strange manner that is very difficult to characterize. When D < 20, the cost is O[D log(N)] and this algorithm is very efficient. On the other hand, it is inefficient in case when D > 20 because the cost increases to nearly O[DN].
Structure de données
Un autre facteur qui affecte les performances de ces algorithmes est la dimensionnalité intrinsèque des données ou la rareté des données. C'est parce que les temps de requête des algorithmes d'arbre à billes et d'arbre KD peuvent en être grandement influencés. Alors que le temps de requête de l'algorithme Brute Force est inchangé par la structure de données. Généralement, les algorithmes d'arbre à billes et d'arbre KD produisent un temps de requête plus rapide lorsqu'ils sont implantés sur des données plus éparses avec une dimensionnalité intrinsèque plus petite.
Nombre de voisins (k)
Le nombre de voisins (k) demandé pour un point de requête affecte le temps de requête des algorithmes d'arbre à billes et d'arbre KD. Leur temps de requête devient plus lent à mesure que le nombre de voisins (k) augmente. Alors que le temps de requête de Brute Force ne sera pas affecté par la valeur de k.
Nombre de points de requête
Parce qu'ils ont besoin d'une phase de construction, les algorithmes d'arbre KD et d'arbre à billes seront efficaces s'il y a un grand nombre de points de requête. D'un autre côté, s'il y a un plus petit nombre de points de requête, l'algorithme Brute Force fonctionne mieux que les algorithmes d'arbre KD et d'arbre à billes.
k-NN (k-Nearest Neighbor), l'un des algorithmes d'apprentissage automatique les plus simples, est non paramétrique et paresseux par nature. Non paramétrique signifie qu'il n'y a pas d'hypothèse pour la distribution de données sous-jacente, c'est-à-dire que la structure du modèle est déterminée à partir de l'ensemble de données. L'apprentissage paresseux ou basé sur une instance signifie qu'aux fins de la génération de modèle, il ne nécessite aucun point de données d'entraînement et des données d'entraînement entières sont utilisées dans la phase de test.
L'algorithme k-NN comprend les deux étapes suivantes -
Étape 1
Dans cette étape, il calcule et stocke les k voisins les plus proches pour chaque échantillon de l'ensemble d'apprentissage.
Étape 2
Dans cette étape, pour un échantillon non étiqueté, il récupère les k voisins les plus proches de l'ensemble de données. Ensuite, parmi ces k voisins les plus proches, il prédit la classe par le vote (la classe à voix majoritaire l'emporte).
Le module, sklearn.neighbors qui implémente l'algorithme des k voisins les plus proches, fournit la fonctionnalité pour unsupervised aussi bien que supervised méthodes d'apprentissage basées sur les voisins.
Les plus proches voisins non supervisés implémentent différents algorithmes (BallTree, KDTree ou Brute Force) pour trouver le ou les voisins les plus proches pour chaque échantillon. Cette version non supervisée n'est fondamentalement que l'étape 1, qui est discutée ci-dessus, et le fondement de nombreux algorithmes (KNN et K-means étant le célèbre) qui nécessitent la recherche de voisins. En termes simples, il s'agit d'un apprenant non supervisé pour la mise en œuvre de recherches de voisins.
D'autre part, l'apprentissage supervisé basé sur les voisins est utilisé pour la classification ainsi que la régression.
Apprentissage KNN non supervisé
Comme discuté, il existe de nombreux algorithmes tels que KNN et K-Means qui nécessitent des recherches de voisins les plus proches. C'est pourquoi Scikit-learn a décidé de mettre en œuvre la partie de recherche de voisins comme son propre «apprenant». La raison pour laquelle la recherche de voisin est un apprenant distinct est que le calcul de toutes les distances par paires pour trouver un voisin le plus proche n'est évidemment pas très efficace. Voyons le module utilisé par Sklearn pour implémenter l'apprentissage du voisin le plus proche non supervisé avec un exemple.
Module Scikit-learn
sklearn.neighbors.NearestNeighborsest le module utilisé pour implémenter l'apprentissage du plus proche voisin non supervisé. Il utilise des algorithmes spécifiques de voisinage le plus proche nommés BallTree, KDTree ou Brute Force. En d'autres termes, il agit comme une interface uniforme avec ces trois algorithmes.
Paramètres
Le tableau suivant comprend les paramètres utilisés par NearestNeighbors module -
| Sr.Non | Paramètre et description |
|---|---|
| 1 | n_neighbors - int, facultatif Le nombre de voisins à obtenir. La valeur par défaut est 5. |
| 2 | radius - flotteur, en option Il limite la distance des voisins aux retours. La valeur par défaut est 1.0. |
| 3 | algorithm - {'auto', 'ball_tree', 'kd_tree', 'brute'}, facultatif Ce paramètre prendra l'algorithme (BallTree, KDTree ou Brute-force) que vous souhaitez utiliser pour calculer les voisins les plus proches. Si vous fournissez 'auto', il tentera de décider de l'algorithme le plus approprié en fonction des valeurs transmises à la méthode fit. |
| 4 | leaf_size - int, facultatif Cela peut affecter la vitesse de construction et de requête ainsi que la mémoire requise pour stocker l'arborescence. Il est transmis à BallTree ou KDTree. Bien que la valeur optimale dépende de la nature du problème, sa valeur par défaut est 30. |
| 5 | metric - chaîne ou appelable C'est la métrique à utiliser pour le calcul de la distance entre les points. Nous pouvons le passer sous forme de chaîne ou de fonction appelable. En cas de fonction appelable, la métrique est appelée sur chaque paire de lignes et la valeur résultante est enregistrée. C'est moins efficace que de transmettre le nom de la métrique sous forme de chaîne. Nous pouvons choisir entre la métrique scikit-learn ou scipy.spatial.distance. les valeurs valides sont les suivantes - Scikit-learn - ['cosinus', 'manhattan', 'euclidien', 'l1', 'l2', 'cityblock'] Scipy.spatial.distance - ['braycurtis', 'canberra', 'chebyshev', 'dice', 'hamming', 'jaccard', 'correlation', 'kulsinski', 'mahalanobis', 'minkowski', 'rogerstanimoto', 'russellrao', ' sokalmicheme ',' sokalsneath ',' seuclidean ',' sqeuclidean ',' yule ']. La métrique par défaut est «Minkowski». |
| 6 | P - entier, facultatif C'est le paramètre de la métrique de Minkowski. La valeur par défaut est 2, ce qui équivaut à utiliser Euclidean_distance (l2). |
| sept | metric_params - dict, facultatif Il s'agit des arguments de mot clé supplémentaires pour la fonction métrique. La valeur par défaut est Aucun. |
| 8 | N_jobs - int ou None, facultatif Il redéfinit le nombre de travaux parallèles à exécuter pour la recherche de voisins. La valeur par défaut est Aucun. |
Implementation Example
L'exemple ci-dessous trouvera les voisins les plus proches entre deux ensembles de données en utilisant le sklearn.neighbors.NearestNeighbors module.
Tout d'abord, nous devons importer le module et les packages requis -
from sklearn.neighbors import NearestNeighbors
import numpy as npMaintenant, après avoir importé les packages, définissez les ensembles de données entre nous voulons trouver les voisins les plus proches -
Input_data = np.array([[-1, 1], [-2, 2], [-3, 3], [1, 2], [2, 3], [3, 4],[4, 5]])Ensuite, appliquez l'algorithme d'apprentissage non supervisé, comme suit -
nrst_neigh = NearestNeighbors(n_neighbors = 3, algorithm = 'ball_tree')Ensuite, ajustez le modèle avec l'ensemble de données d'entrée.
nrst_neigh.fit(Input_data)Maintenant, trouvez les K-voisins de l'ensemble de données. Il renverra les indices et les distances des voisins de chaque point.
distances, indices = nbrs.kneighbors(Input_data)
indicesOutput
array(
[
[0, 1, 3],
[1, 2, 0],
[2, 1, 0],
[3, 4, 0],
[4, 5, 3],
[5, 6, 4],
[6, 5, 4]
], dtype = int64
)
distancesOutput
array(
[
[0. , 1.41421356, 2.23606798],
[0. , 1.41421356, 1.41421356],
[0. , 1.41421356, 2.82842712],
[0. , 1.41421356, 2.23606798],
[0. , 1.41421356, 1.41421356],
[0. , 1.41421356, 1.41421356],
[0. , 1.41421356, 2.82842712]
]
)La sortie ci-dessus montre que le plus proche voisin de chaque point est le point lui-même, c'est-à-dire à zéro. C'est parce que l'ensemble de requêtes correspond à l'ensemble d'apprentissage.
Example
Nous pouvons également montrer une connexion entre des points voisins en produisant un graphe clairsemé comme suit -
nrst_neigh.kneighbors_graph(Input_data).toarray()Output
array(
[
[1., 1., 0., 1., 0., 0., 0.],
[1., 1., 1., 0., 0., 0., 0.],
[1., 1., 1., 0., 0., 0., 0.],
[1., 0., 0., 1., 1., 0., 0.],
[0., 0., 0., 1., 1., 1., 0.],
[0., 0., 0., 0., 1., 1., 1.],
[0., 0., 0., 0., 1., 1., 1.]
]
)Une fois que nous ajustons le non supervisé NearestNeighbors model, les données seront stockées dans une structure de données basée sur la valeur définie pour l'argument ‘algorithm’. Après cela, nous pouvons utiliser cet apprenant non supervisékneighbors dans un modèle qui nécessite des recherches de voisins.
Complete working/executable program
from sklearn.neighbors import NearestNeighbors
import numpy as np
Input_data = np.array([[-1, 1], [-2, 2], [-3, 3], [1, 2], [2, 3], [3, 4],[4, 5]])
nrst_neigh = NearestNeighbors(n_neighbors = 3, algorithm='ball_tree')
nrst_neigh.fit(Input_data)
distances, indices = nbrs.kneighbors(Input_data)
indices
distances
nrst_neigh.kneighbors_graph(Input_data).toarray()Apprentissage KNN supervisé
L'apprentissage supervisé basé sur les voisins est utilisé pour suivre -
- Classification, pour les données avec des étiquettes discrètes
- Régression, pour les données avec des étiquettes continues.
Classificateur de voisin le plus proche
Nous pouvons comprendre la classification basée sur les voisins à l'aide de deux caractéristiques suivantes -
- Il est calculé à partir d'un vote à la majorité simple des voisins les plus proches de chaque point.
- Il stocke simplement des instances des données d'entraînement, c'est pourquoi il s'agit d'un type d'apprentissage non généralisant.
Modules Scikit-learn
Les éléments suivants sont les deux types différents de classificateurs de voisins les plus proches utilisés par scikit-learn -
| S.No. | Classificateurs et description |
|---|---|
| 1. | KNeighborsClassifier Le K dans le nom de ce classificateur représente les k voisins les plus proches, où k est une valeur entière spécifiée par l'utilisateur. Par conséquent, comme son nom l'indique, ce classificateur implémente l'apprentissage basé sur les k voisins les plus proches. Le choix de la valeur de k dépend des données. |
| 2. | RadiusNeighborsClassifier Le rayon dans le nom de ce classificateur représente les voisins les plus proches dans un rayon spécifié r, où r est une valeur à virgule flottante spécifiée par l'utilisateur. Par conséquent, comme son nom l'indique, ce classificateur implémente l'apprentissage basé sur le nombre de voisins dans un rayon fixe r de chaque point d'apprentissage. |
Régresseur de voisin le plus proche
Il est utilisé dans les cas où les étiquettes de données sont de nature continue. Les étiquettes de données attribuées sont calculées sur la base de la moyenne des étiquettes de ses voisins les plus proches.
Les éléments suivants sont les deux types différents de régresseurs voisins les plus proches utilisés par scikit-learn -
KNeighboursRegressor
Le K au nom de ce régresseur représente les k voisins les plus proches, où k est un integer valuespécifié par l'utilisateur. Par conséquent, comme son nom l'indique, ce régresseur implémente l'apprentissage basé sur les k voisins les plus proches. Le choix de la valeur de k dépend des données. Comprenons-le davantage à l'aide d'un exemple d'implémentation.
Les éléments suivants sont les deux types différents de régresseurs voisins les plus proches utilisés par scikit-learn -
Exemple d'implémentation
Dans cet exemple, nous allons implémenter KNN sur un ensemble de données nommé Iris Flower à l'aide de scikit-learn KNeighborsRegressor.
Tout d'abord, importez le jeu de données iris comme suit -
from sklearn.datasets import load_iris
iris = load_iris()Maintenant, nous devons diviser les données en données d'entraînement et de test. Nous utiliserons Sklearntrain_test_split fonction pour diviser les données dans le rapport de 70 (données d'entraînement) et 20 (données de test) -
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20)Ensuite, nous ferons la mise à l'échelle des données à l'aide du module de prétraitement Sklearn comme suit -
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)Ensuite, importez le KNeighborsRegressor classe de Sklearn et fournissez la valeur des voisins comme suit.
Exemple
import numpy as np
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors = 8)
knnr.fit(X_train, y_train)Production
KNeighborsRegressor(
algorithm = 'auto', leaf_size = 30, metric = 'minkowski',
metric_params = None, n_jobs = None, n_neighbors = 8, p = 2,
weights = 'uniform'
)Exemple
Maintenant, nous pouvons trouver la MSE (erreur quadratique moyenne) comme suit -
print ("The MSE is:",format(np.power(y-knnr.predict(X),4).mean()))Production
The MSE is: 4.4333349609375Exemple
Maintenant, utilisez-le pour prédire la valeur comme suit -
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors = 3)
knnr.fit(X, y)
print(knnr.predict([[2.5]]))Production
[0.66666667]Programme de travail / exécutable complet
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
import numpy as np
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=8)
knnr.fit(X_train, y_train)
print ("The MSE is:",format(np.power(y-knnr.predict(X),4).mean()))
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=3)
knnr.fit(X, y)
print(knnr.predict([[2.5]]))RadiusVoisinsRégresseur
Le rayon dans le nom de ce régresseur représente les voisins les plus proches dans un rayon spécifié r, où r est une valeur à virgule flottante spécifiée par l'utilisateur. Par conséquent, comme son nom l'indique, ce régresseur implémente l'apprentissage basé sur le nombre de voisins dans un rayon fixe r de chaque point d'apprentissage. Comprenons-le davantage avec l'aide si un exemple d'implémentation -
Exemple d'implémentation
Dans cet exemple, nous allons implémenter KNN sur un ensemble de données nommé Iris Flower à l'aide de scikit-learn RadiusNeighborsRegressor -
Tout d'abord, importez le jeu de données iris comme suit -
from sklearn.datasets import load_iris
iris = load_iris()Maintenant, nous devons diviser les données en données d'entraînement et de test. Nous utiliserons la fonction Sklearn train_test_split pour diviser les données en un rapport de 70 (données d'entraînement) et 20 (données de test) -
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)Ensuite, nous ferons la mise à l'échelle des données à l'aide du module de prétraitement Sklearn comme suit -
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)Ensuite, importez le RadiusneighborsRegressor classe de Sklearn et fournissez la valeur de rayon comme suit -
import numpy as np
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius=1)
knnr_r.fit(X_train, y_train)Exemple
Maintenant, nous pouvons trouver la MSE (erreur quadratique moyenne) comme suit -
print ("The MSE is:",format(np.power(y-knnr_r.predict(X),4).mean()))Production
The MSE is: The MSE is: 5.666666666666667Exemple
Maintenant, utilisez-le pour prédire la valeur comme suit -
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius=1)
knnr_r.fit(X, y)
print(knnr_r.predict([[2.5]]))Production
[1.]Programme de travail / exécutable complet
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
import numpy as np
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius = 1)
knnr_r.fit(X_train, y_train)
print ("The MSE is:",format(np.power(y-knnr_r.predict(X),4).mean()))
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius = 1)
knnr_r.fit(X, y)
print(knnr_r.predict([[2.5]]))Les méthodes naïves de Bayes sont un ensemble d'algorithmes d'apprentissage supervisé basés sur l'application du théorème de Bayes avec une forte hypothèse que tous les prédicteurs sont indépendants les uns des autres, c'est-à-dire que la présence d'une entité dans une classe est indépendante de la présence de toute autre caractéristique dans la même classe. Il s'agit d'une hypothèse naïve, c'est pourquoi ces méthodes sont appelées méthodes Naïve Bayes.
Le théorème de Bayes énonce la relation suivante afin de trouver la probabilité postérieure de classe c'est-à-dire la probabilité d'une étiquette et de certaines caractéristiques observées, $P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)$.
$$P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)=\left(\frac{P\lgroup Y\rgroup P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)}{P\left(\begin{array}{c} features\end{array}\right)}\right)$$Ici, $P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)$ est la probabilité postérieure de classe.
$P\left(\begin{array}{c} Y\end{array}\right)$ est la probabilité de classe a priori.
$P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)$ est la vraisemblance qui est la probabilité du prédicteur de la classe donnée.
$P\left(\begin{array}{c} features\end{array}\right)$ est la probabilité a priori du prédicteur.
Le Scikit-learn fournit différents modèles de classificateurs Bayes naïfs, à savoir Gaussian, Multinomial, Complement et Bernoulli. Tous diffèrent principalement par l'hypothèse qu'ils émettent concernant la distribution des$P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)$ c'est-à-dire la probabilité du prédicteur de la classe donnée.
| Sr.Non | Description du modèle |
|---|---|
| 1 | Bayes naïves gaussiennes Le classificateur Gaussian Naïve Bayes suppose que les données de chaque étiquette sont tirées d'une simple distribution gaussienne. |
| 2 | Bayes naïves multinomiales Il suppose que les entités sont tirées d'une simple distribution multinomiale. |
| 3 | Bernoulli Naïve Bayes L'hypothèse dans ce modèle est que les caractéristiques binaires (0 et 1) sont de nature. Une application de la classification Bernoulli Naïve Bayes est la classification de texte avec le modèle `` sac de mots '' |
| 4 | Complément Naïve Bayes Il a été conçu pour corriger les hypothèses sévères faites par le classificateur multinomial de Bayes. Ce type de classificateur NB convient aux ensembles de données déséquilibrés |
Construire un classificateur Bayes naïf
Nous pouvons également appliquer le classificateur Naïve Bayes sur l'ensemble de données Scikit-learn. Dans l'exemple ci-dessous, nous appliquons GaussianNB et ajustons le jeu de données breast_cancer de Scikit-leran.
Exemple
Import Sklearn
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
data = load_breast_cancer()
label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']
print(label_names)
print(labels[0])
print(feature_names[0])
print(features[0])
train, test, train_labels, test_labels = train_test_split(
features,labels,test_size = 0.40, random_state = 42
)
from sklearn.naive_bayes import GaussianNB
GNBclf = GaussianNB()
model = GNBclf.fit(train, train_labels)
preds = GNBclf.predict(test)
print(preds)Production
[
1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1
1 1 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1
1 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0
1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0
1 1 0 1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1
0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1
1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0
1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1
1 1 1 1 0 1 0 0 1 1 0 1
]La sortie ci-dessus consiste en une série de 0 et de 1 qui sont essentiellement les valeurs prédites des classes de tumeurs à savoir malignes et bénignes.
Dans ce chapitre, nous en apprendrons davantage sur la méthode d'apprentissage de Sklearn, appelée arbres de décision.
Les décisions tress (DT) sont la méthode d'apprentissage supervisé non paramétrique la plus puissante. Ils peuvent être utilisés pour les tâches de classification et de régression. L'objectif principal des DT est de créer un modèle prédisant la valeur de la variable cible en apprenant des règles de décision simples déduites des caractéristiques des données. Les arbres de décision ont deux entités principales; l'un est le nœud racine, où les données se divisent, et l'autre est les nœuds de décision ou les feuilles, où nous avons obtenu la sortie finale.
Algorithmes d'arbre de décision
Différents algorithmes d'arbre de décision sont expliqués ci-dessous -
ID3
Il a été développé par Ross Quinlan en 1986. Il est également appelé Iterative Dichotomiser 3. Le but principal de cet algorithme est de trouver les caractéristiques catégorielles, pour chaque nœud, qui donneront le plus grand gain d'information pour les cibles catégorielles.
Il permet à l'arbre de croître à sa taille maximale, puis pour améliorer la capacité de l'arbre sur des données invisibles, applique une étape d'élagage. La sortie de cet algorithme serait un arbre multi-voies.
C4.5
Il est le successeur de ID3 et définit dynamiquement un attribut discret qui partitionne la valeur d'attribut continu en un ensemble discret d'intervalles. C'est la raison pour laquelle il a supprimé la restriction des fonctionnalités catégorielles. Il convertit l'arbre formé ID3 en ensembles de règles «IF-THEN».
Afin de déterminer l'ordre dans lequel ces règles doivent s'appliquer, l'exactitude de chaque règle sera évaluée en premier.
C5.0
Il fonctionne de la même manière que C4.5 mais il utilise moins de mémoire et crée des ensembles de règles plus petits. Il est plus précis que C4.5.
CHARIOT
C'est ce qu'on appelle l'algorithme des arbres de classification et de régression. Il génère essentiellement des fractionnements binaires en utilisant les fonctionnalités et le seuil générant le plus grand gain d'informations à chaque nœud (appelé index Gini).
L'homogénéité dépend de l'indice de Gini, plus la valeur de l'indice de Gini est élevée, plus l'homogénéité est élevée. C'est comme l'algorithme C4.5, mais la différence est qu'il ne calcule pas les ensembles de règles et ne prend pas en charge les variables cibles numériques (régression).
Classification avec arbres de décision
Dans ce cas, les variables de décision sont catégoriques.
Sklearn Module - La bibliothèque Scikit-learn fournit le nom du module DecisionTreeClassifier pour effectuer une classification multiclasse sur un ensemble de données.
Paramètres
Le tableau suivant contient les paramètres utilisés par sklearn.tree.DecisionTreeClassifier module -
| Sr.Non | Paramètre et description |
|---|---|
| 1 | criterion - chaîne, option par défaut = "gini" Il représente la fonction permettant de mesurer la qualité d'un fractionnement. Les critères pris en charge sont «gini» et «entropie». La valeur par défaut est gini qui est pour l'impureté Gini tandis que l'entropie est pour le gain d'information. |
| 2 | splitter - chaîne, option par défaut = "meilleur" Il indique au modèle, quelle stratégie parmi «meilleure» ou «aléatoire» pour choisir la division à chaque nœud. |
| 3 | max_depth - int ou None, facultatif par défaut = None Ce paramètre décide de la profondeur maximale de l'arbre. La valeur par défaut est None, ce qui signifie que les nœuds s'étendent jusqu'à ce que toutes les feuilles soient pures ou jusqu'à ce que toutes les feuilles contiennent moins de min_smaples_split échantillons. |
| 4 | min_samples_split - int, float, option par défaut = 2 Ce paramètre fournit le nombre minimum d'échantillons requis pour fractionner un nœud interne. |
| 5 | min_samples_leaf - int, float, optionnel par défaut = 1 Ce paramètre fournit le nombre minimum d'échantillons requis pour être au niveau d'un nœud feuille. |
| 6 | min_weight_fraction_leaf - float, option par défaut = 0. Avec ce paramètre, le modèle obtiendra la fraction pondérée minimale de la somme des poids requis pour être au niveau d'un nœud feuille. |
| sept | max_features - int, float, string ou None, option par défaut = None Il donne au modèle le nombre de fonctionnalités à prendre en compte lors de la recherche de la meilleure répartition. |
| 8 | random_state - int, instance RandomState ou None, facultatif, par défaut = aucun Ce paramètre représente la graine du nombre pseudo aléatoire généré qui est utilisé lors du brassage des données. Voici les options -
|
| 9 | max_leaf_nodes - int ou None, facultatif par défaut = None Ce paramètre permettra de développer un arbre avec max_leaf_nodes de la meilleure façon. La valeur par défaut est aucun, ce qui signifie qu'il y aurait un nombre illimité de nœuds feuilles. |
| dix | min_impurity_decrease - float, option par défaut = 0. Cette valeur fonctionne comme un critère de division d'un nœud car le modèle divisera un nœud si cette division induit une diminution de l'impureté supérieure ou égale à min_impurity_decrease value. |
| 11 | min_impurity_split - float, par défaut = 1e-7 Il représente le seuil d'arrêt précoce de la croissance des arbres. |
| 12 | class_weight - dict, liste des dictionnaires, «équilibré» ou Aucun, par défaut = Aucun Il représente les poids associés aux classes. La forme est {class_label: weight}. Si nous utilisons l'option par défaut, cela signifie que toutes les classes sont censées avoir un poids un. D'autre part, si vous choisissezclass_weight: balanced, il utilisera les valeurs de y pour ajuster automatiquement les poids. |
| 13 | presort - booléen, option par défaut = False Il indique au modèle s'il faut pré-trier les données pour accélérer la recherche des meilleures divisions dans l'ajustement. La valeur par défaut est false mais définie sur true, cela peut ralentir le processus d'entraînement. |
Les attributs
Le tableau suivant comprend les attributs utilisés par sklearn.tree.DecisionTreeClassifier module -
| Sr.Non | Paramètre et description |
|---|---|
| 1 | feature_importances_ - tableau de forme = [n_features] Cet attribut renverra l'importance de la fonctionnalité. |
| 2 | classes_: - tableau de forme = [n_classes] ou une liste de tels tableaux Il représente les étiquettes de classes, c'est-à-dire le problème de sortie unique, ou une liste de tableaux d'étiquettes de classe, c'est-à-dire le problème à sorties multiples. |
| 3 | max_features_ - int Il représente la valeur déduite du paramètre max_features. |
| 4 | n_classes_ - int ou liste Il représente le nombre de classes, c'est-à-dire le problème de sortie unique, ou une liste de nombre de classes pour chaque sortie, c'est-à-dire le problème à sorties multiples. |
| 5 | n_features_ - int Il donne le nombre de features lorsque la méthode fit () est exécutée. |
| 6 | n_outputs_ - int Il donne le nombre de outputs lorsque la méthode fit () est exécutée. |
Méthodes
Le tableau suivant contient les méthodes utilisées par sklearn.tree.DecisionTreeClassifier module -
| Sr.Non | Paramètre et description |
|---|---|
| 1 | apply(self, X [, check_input]) Cette méthode retournera l'index de la feuille. |
| 2 | decision_path(self, X [, check_input]) Comme son nom l'indique, cette méthode retournera le chemin de décision dans l'arborescence |
| 3 | fit(soi, X, y [, poids_échantillon,…]) fit () construira un classificateur d'arbre de décision à partir d'un ensemble d'apprentissage donné (X, y). |
| 4 | get_depth(soi) Comme son nom l'indique, cette méthode retournera la profondeur de l'arbre de décision |
| 5 | get_n_leaves(soi) Comme son nom l'indique, cette méthode retournera le nombre de feuilles de l'arbre de décision. |
| 6 | get_params(soi [, profond]) Nous pouvons utiliser cette méthode pour obtenir les paramètres de l'estimateur. |
| sept | predict(self, X [, check_input]) Il prédira la valeur de classe pour X. |
| 8 | predict_log_proba(soi, X) Il prédira les probabilités logarithmiques de classe des échantillons d'entrée fournis par nous, X. |
| 9 | predict_proba(self, X [, check_input]) Il prédira les probabilités de classe des échantillons d'entrée fournis par nous, X. |
| dix | score(soi, X, y [, poids_échantillon]) Comme son nom l'indique, la méthode score () retournera la précision moyenne sur les données de test et les étiquettes données. |
| 11 | set_params(self, \ * \ * paramètres) Nous pouvons définir les paramètres de l'estimateur avec cette méthode. |
Exemple d'implémentation
Le script Python ci-dessous utilisera sklearn.tree.DecisionTreeClassifier module pour construire un classificateur pour prédire l'homme ou la femme à partir de notre ensemble de données contenant 25 échantillons et deux caractéristiques à savoir la `` hauteur '' et la `` longueur des cheveux '' -
from sklearn import tree
from sklearn.model_selection import train_test_split
X=[[165,19],[175,32],[136,35],[174,65],[141,28],[176,15]
,[131,32],[166,6],[128,32],[179,10],[136,34],[186,2],[12
6,25],[176,28],[112,38],[169,9],[171,36],[116,25],[196,2
5], [196,38], [126,40], [197,20], [150,25], [140,32],[136,35]]
Y=['Man','Woman','Woman','Man','Woman','Man','Woman','Ma
n','Woman','Man','Woman','Man','Woman','Woman','Woman','
Man','Woman','Woman','Man', 'Woman', 'Woman', 'Man', 'Man', 'Woman', 'Woman']
data_feature_names = ['height','length of hair']
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.3, random_state = 1)
DTclf = tree.DecisionTreeClassifier()
DTclf = clf.fit(X,Y)
prediction = DTclf.predict([[135,29]])
print(prediction)Production
['Woman']Nous pouvons également prédire la probabilité de chaque classe en utilisant la méthode python predict_proba () suivante:
Exemple
prediction = DTclf.predict_proba([[135,29]])
print(prediction)Production
[[0. 1.]]Régression avec arbres de décision
Dans ce cas, les variables de décision sont continues.
Sklearn Module - La bibliothèque Scikit-learn fournit le nom du module DecisionTreeRegressor pour appliquer des arbres de décision sur des problèmes de régression.
Paramètres
Paramètres utilisés par DecisionTreeRegressor sont presque les mêmes que ceux utilisés dans DecisionTreeClassifiermodule. La différence réside dans le paramètre «critère». PourDecisionTreeRegressor modules ‘criterion: string, optionnel default = "mse" 'paramètre a les valeurs suivantes -
mse- Il représente l'erreur quadratique moyenne. Il est égal à la réduction de la variance comme critère de sélection des caractéristiques. Il minimise la perte L2 en utilisant la moyenne de chaque nœud terminal.
freidman_mse - Il utilise également l'erreur quadratique moyenne mais avec le score d'amélioration de Friedman.
mae- Il représente l'erreur absolue moyenne. Il minimise la perte L1 en utilisant la médiane de chaque nœud terminal.
Une autre différence est qu'il n'a pas ‘class_weight’ paramètre.
Les attributs
Attributs de DecisionTreeRegressor sont également les mêmes que ceux de DecisionTreeClassifiermodule. La différence est qu'il n'a pas‘classes_’ et ‘n_classes_' les attributs.
Méthodes
Méthodes de DecisionTreeRegressor sont également les mêmes que ceux de DecisionTreeClassifiermodule. La différence est qu'il n'a pas‘predict_log_proba()’ et ‘predict_proba()’' les attributs.
Exemple d'implémentation
La méthode fit () dans le modèle de régression d'arbre de décision prendra des valeurs en virgule flottante de y. voyons un exemple d'implémentation simple en utilisantSklearn.tree.DecisionTreeRegressor -
from sklearn import tree
X = [[1, 1], [5, 5]]
y = [0.1, 1.5]
DTreg = tree.DecisionTreeRegressor()
DTreg = clf.fit(X, y)Une fois ajusté, nous pouvons utiliser ce modèle de régression pour faire des prédictions comme suit -
DTreg.predict([[4, 5]])Production
array([1.5])Ce chapitre vous aidera à comprendre les arbres de décision aléatoires dans Sklearn.
Algorithmes d'arbre de décision aléatoire
Comme nous savons qu'un DT est généralement formé en fractionnant les données de manière récursive, mais étant enclin au surajustement, ils ont été transformés en forêts aléatoires en entraînant de nombreux arbres sur divers sous-échantillons de données. lesklearn.ensemble module a les deux algorithmes suivants basés sur des arbres de décision aléatoires -
L'algorithme Random Forest
Pour chaque fonctionnalité considérée, il calcule la combinaison fonctionnalité / fractionnement localement optimale. Dans Random forest, chaque arbre de décision de l'ensemble est construit à partir d'un échantillon tiré avec remplacement de l'ensemble d'apprentissage, puis obtient la prédiction de chacun d'eux et sélectionne finalement la meilleure solution par vote. Il peut être utilisé à la fois pour les tâches de classification et de régression.
Classification avec Random Forest
Pour créer un classificateur de forêt aléatoire, le module Scikit-learn fournit sklearn.ensemble.RandomForestClassifier. Lors de la construction d'un classificateur de forêt aléatoire, les principaux paramètres utilisés par ce module sont‘max_features’ et ‘n_estimators’.
Ici, ‘max_features’est la taille des sous-ensembles aléatoires d'entités à prendre en compte lors de la division d'un nœud. Si nous choisissons la valeur de ce paramètre sur aucune, il considérera toutes les fonctionnalités plutôt qu'un sous-ensemble aléatoire. D'autre part,n_estimatorssont le nombre d'arbres dans la forêt. Plus le nombre d'arbres est élevé, meilleur sera le résultat. Mais le calcul prendra également plus de temps.
Exemple d'implémentation
Dans l'exemple suivant, nous construisons un classificateur de forêt aléatoire en utilisant sklearn.ensemble.RandomForestClassifier et aussi vérifier sa précision en utilisant cross_val_score module.
from sklearn.model_selection import cross_val_score
from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier
X, y = make_blobs(n_samples = 10000, n_features = 10, centers = 100,random_state = 0) RFclf = RandomForestClassifier(n_estimators = 10,max_depth = None,min_samples_split = 2, random_state = 0)
scores = cross_val_score(RFclf, X, y, cv = 5)
scores.mean()Production
0.9997Exemple
Nous pouvons également utiliser le jeu de données sklearn pour créer un classificateur Random Forest. Comme dans l'exemple suivant, nous utilisons le jeu de données iris. Nous retrouverons également son score de précision et sa matrice de confusion.
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
path = "https://archive.ics.uci.edu/ml/machine-learning-database
s/iris/iris.data"
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
dataset = pd.read_csv(path, names = headernames)
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30)
RFclf = RandomForestClassifier(n_estimators = 50)
RFclf.fit(X_train, y_train)
y_pred = RFclf.predict(X_test)
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)Production
Confusion Matrix:
[[14 0 0]
[ 0 18 1]
[ 0 0 12]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 14
Iris-versicolor 1.00 0.95 0.97 19
Iris-virginica 0.92 1.00 0.96 12
micro avg 0.98 0.98 0.98 45
macro avg 0.97 0.98 0.98 45
weighted avg 0.98 0.98 0.98 45
Accuracy: 0.9777777777777777Régression avec Random Forest
Pour créer une régression de forêt aléatoire, le module Scikit-learn fournit sklearn.ensemble.RandomForestRegressor. Lors de la construction du régresseur de forêt aléatoire, il utilisera les mêmes paramètres que ceux utilisés parsklearn.ensemble.RandomForestClassifier.
Exemple d'implémentation
Dans l'exemple suivant, nous construisons un régresseur de forêt aléatoire en utilisant sklearn.ensemble.RandomForestregressor et également la prédiction de nouvelles valeurs à l'aide de la méthode prédire ().
from sklearn.ensemble import RandomForestRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
RFregr = RandomForestRegressor(max_depth = 10,random_state = 0,n_estimators = 100)
RFregr.fit(X, y)Production
RandomForestRegressor(
bootstrap = True, criterion = 'mse', max_depth = 10,
max_features = 'auto', max_leaf_nodes = None,
min_impurity_decrease = 0.0, min_impurity_split = None,
min_samples_leaf = 1, min_samples_split = 2,
min_weight_fraction_leaf = 0.0, n_estimators = 100, n_jobs = None,
oob_score = False, random_state = 0, verbose = 0, warm_start = False
)Une fois ajustés, nous pouvons prédire à partir du modèle de régression comme suit -
print(RFregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))Production
[98.47729198]Méthodes extra-arborescentes
Pour chaque fonctionnalité considérée, il sélectionne une valeur aléatoire pour le fractionnement. L'avantage d'utiliser des méthodes d'arborescence supplémentaires est que cela permet de réduire un peu plus la variance du modèle. L'inconvénient de l'utilisation de ces méthodes est que cela augmente légèrement le biais.
Classification avec la méthode extra-arbre
Pour créer un classificateur à l'aide de la méthode Extra-tree, le module Scikit-learn fournit sklearn.ensemble.ExtraTreesClassifier. Il utilise les mêmes paramètres que ceux utilisés parsklearn.ensemble.RandomForestClassifier. La seule différence réside dans la façon dont, discutée ci-dessus, ils construisent des arbres.
Exemple d'implémentation
Dans l'exemple suivant, nous construisons un classificateur de forêt aléatoire en utilisant sklearn.ensemble.ExtraTreeClassifier et aussi vérifier sa précision en utilisant cross_val_score module.
from sklearn.model_selection import cross_val_score
from sklearn.datasets import make_blobs
from sklearn.ensemble import ExtraTreesClassifier
X, y = make_blobs(n_samples = 10000, n_features = 10, centers=100,random_state = 0)
ETclf = ExtraTreesClassifier(n_estimators = 10,max_depth = None,min_samples_split = 10, random_state = 0)
scores = cross_val_score(ETclf, X, y, cv = 5)
scores.mean()Production
1.0Exemple
Nous pouvons également utiliser l'ensemble de données sklearn pour créer un classificateur à l'aide de la méthode Extra-Tree. Comme dans l'exemple suivant, nous utilisons un ensemble de données Pima-Indian.
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import ExtraTreesClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 7
kfold = KFold(n_splits=10, random_state=seed)
num_trees = 150
max_features = 5
ETclf = ExtraTreesClassifier(n_estimators=num_trees, max_features=max_features)
results = cross_val_score(ETclf, X, Y, cv=kfold)
print(results.mean())Production
0.7551435406698566Régression avec méthode extra-arborescente
Pour créer un Extra-Tree régression, le module Scikit-learn fournit sklearn.ensemble.ExtraTreesRegressor. Lors de la construction du régresseur de forêt aléatoire, il utilisera les mêmes paramètres que ceux utilisés parsklearn.ensemble.ExtraTreesClassifier.
Exemple d'implémentation
Dans l'exemple suivant, nous appliquons sklearn.ensemble.ExtraTreesregressoret sur les mêmes données que celles utilisées lors de la création d'un régresseur de forêt aléatoire. Voyons la différence dans la sortie
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
ETregr = ExtraTreesRegressor(max_depth = 10,random_state = 0,n_estimators = 100)
ETregr.fit(X, y)Production
ExtraTreesRegressor(bootstrap = False, criterion = 'mse', max_depth = 10,
max_features = 'auto', max_leaf_nodes = None,
min_impurity_decrease = 0.0, min_impurity_split = None,
min_samples_leaf = 1, min_samples_split = 2,
min_weight_fraction_leaf = 0.0, n_estimators = 100, n_jobs = None,
oob_score = False, random_state = 0, verbose = 0, warm_start = False)Exemple
Une fois ajustés, nous pouvons prédire à partir du modèle de régression comme suit -
print(ETregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))Production
[85.50955817]Dans ce chapitre, nous découvrirons les méthodes d'amplification de Sklearn, qui permettent de créer un modèle d'ensemble.
Les méthodes de stimulation construisent le modèle d'ensemble de manière incrémentielle. Le principe principal est de construire le modèle de manière incrémentielle en entraînant chaque estimateur de modèle de base de manière séquentielle. Afin de créer un ensemble puissant, ces méthodes combinent essentiellement plusieurs apprenants d'une semaine qui sont entraînés séquentiellement sur plusieurs itérations de données d'entraînement. Le module sklearn.ensemble dispose de deux méthodes de boosting suivantes.
AdaBoost
C'est l'une des méthodes d'ensemble d'amplification les plus réussies dont la clé principale réside dans la façon dont elles donnent des pondérations aux instances dans l'ensemble de données. C'est pourquoi l'algorithme doit accorder moins d'attention aux instances lors de la construction des modèles suivants.
Classification avec AdaBoost
Pour créer un classificateur AdaBoost, le module Scikit-learn fournit sklearn.ensemble.AdaBoostClassifier. Lors de la construction de ce classificateur, le paramètre principal utilisé par ce module estbase_estimator. Ici, base_estimator est la valeur dubase estimatorà partir duquel l'ensemble boosté est construit. Si nous choisissons la valeur de ce paramètre sur aucune, l'estimateur de base seraitDecisionTreeClassifier(max_depth=1).
Exemple d'implémentation
Dans l'exemple suivant, nous construisons un classificateur AdaBoost en utilisant sklearn.ensemble.AdaBoostClassifier et aussi prédire et vérifier son score.
from sklearn.ensemble import AdaBoostClassifier
from sklearn.datasets import make_classification
X, y = make_classification(n_samples = 1000, n_features = 10,n_informative = 2, n_redundant = 0,random_state = 0, shuffle = False)
ADBclf = AdaBoostClassifier(n_estimators = 100, random_state = 0)
ADBclf.fit(X, y)Production
AdaBoostClassifier(algorithm = 'SAMME.R', base_estimator = None,
learning_rate = 1.0, n_estimators = 100, random_state = 0)Exemple
Une fois ajustés, nous pouvons prédire les nouvelles valeurs comme suit -
print(ADBclf.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))Production
[1]Exemple
Nous pouvons maintenant vérifier le score comme suit -
ADBclf.score(X, y)Production
0.995Exemple
Nous pouvons également utiliser l'ensemble de données sklearn pour créer un classificateur à l'aide de la méthode Extra-Tree. Par exemple, dans un exemple donné ci-dessous, nous utilisons un ensemble de données Pima-Indian.
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import AdaBoostClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names = headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 5
kfold = KFold(n_splits = 10, random_state = seed)
num_trees = 100
max_features = 5
ADBclf = AdaBoostClassifier(n_estimators = num_trees, max_features = max_features)
results = cross_val_score(ADBclf, X, Y, cv = kfold)
print(results.mean())Production
0.7851435406698566Régression avec AdaBoost
Pour créer un régresseur avec la méthode Ada Boost, la bibliothèque Scikit-learn fournit sklearn.ensemble.AdaBoostRegressor. Lors de la construction du régresseur, il utilisera les mêmes paramètres que ceux utilisés parsklearn.ensemble.AdaBoostClassifier.
Exemple d'implémentation
Dans l'exemple suivant, nous construisons un régresseur AdaBoost en utilisant sklearn.ensemble.AdaBoostregressor et également la prédiction de nouvelles valeurs à l'aide de la méthode prédire ().
from sklearn.ensemble import AdaBoostRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
ADBregr = RandomForestRegressor(random_state = 0,n_estimators = 100)
ADBregr.fit(X, y)Production
AdaBoostRegressor(base_estimator = None, learning_rate = 1.0, loss = 'linear',
n_estimators = 100, random_state = 0)Exemple
Une fois ajustés, nous pouvons prédire à partir du modèle de régression comme suit -
print(ADBregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))Production
[85.50955817]Boosting d'arbre de dégradé
Il est également appelé Gradient Boosted Regression Trees(GRBT). Il s'agit essentiellement d'une généralisation de l'augmentation des fonctions de perte différentiables arbitraires. Il produit un modèle de prédiction sous la forme d'un ensemble de modèles de prédiction hebdomadaire. Il peut être utilisé pour les problèmes de régression et de classification. Leur principal avantage réside dans le fait qu'ils gèrent naturellement les données de type mixte.
Classification avec Gradient Tree Boost
Pour créer un classificateur Gradient Tree Boost, le module Scikit-learn fournit sklearn.ensemble.GradientBoostingClassifier. Lors de la construction de ce classificateur, le paramètre principal utilisé par ce module est la «perte». Ici, «perte» est la valeur de la fonction de perte à optimiser. Si nous choisissons perte = déviance, cela fait référence à la déviance pour la classification avec des sorties probabilistes.
En revanche, si nous choisissons la valeur de ce paramètre à exponentielle, alors il récupère l'algorithme AdaBoost. Le paramètren_estimatorscontrôlera le nombre d'apprenants par semaine. Un hyper-paramètre nommélearning_rate (dans la plage de (0,0, 1,0]) contrôlera le surajustement via le retrait.
Exemple d'implémentation
Dans l'exemple suivant, nous construisons un classificateur Gradient Boosting en utilisant sklearn.ensemble.GradientBoostingClassifier. Nous équipons ce classificateur avec des apprenants de 50 semaines.
from sklearn.datasets import make_hastie_10_2
from sklearn.ensemble import GradientBoostingClassifier
X, y = make_hastie_10_2(random_state = 0)
X_train, X_test = X[:5000], X[5000:]
y_train, y_test = y[:5000], y[5000:]
GDBclf = GradientBoostingClassifier(n_estimators = 50, learning_rate = 1.0,max_depth = 1, random_state = 0).fit(X_train, y_train)
GDBclf.score(X_test, y_test)Production
0.8724285714285714Exemple
Nous pouvons également utiliser l'ensemble de données sklearn pour créer un classificateur à l'aide du Gradient Boosting Classifier. Comme dans l'exemple suivant, nous utilisons un ensemble de données Pima-Indian.
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import GradientBoostingClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names = headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 5
kfold = KFold(n_splits = 10, random_state = seed)
num_trees = 100
max_features = 5
ADBclf = GradientBoostingClassifier(n_estimators = num_trees, max_features = max_features)
results = cross_val_score(ADBclf, X, Y, cv = kfold)
print(results.mean())Production
0.7946582356674234Régression avec Boost d'arbre de dégradé
Pour créer un régresseur avec la méthode Gradient Tree Boost, la bibliothèque Scikit-learn fournit sklearn.ensemble.GradientBoostingRegressor. Il peut spécifier la fonction de perte pour la régression via la perte de nom de paramètre. La valeur par défaut de la perte est «ls».
Exemple d'implémentation
Dans l'exemple suivant, nous construisons un régresseur d'amplification de dégradé en utilisant sklearn.ensemble.GradientBoostingregressor et aussi trouver l'erreur quadratique moyenne en utilisant la méthode mean_squared_error ().
import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.datasets import make_friedman1
from sklearn.ensemble import GradientBoostingRegressor
X, y = make_friedman1(n_samples = 2000, random_state = 0, noise = 1.0)
X_train, X_test = X[:1000], X[1000:]
y_train, y_test = y[:1000], y[1000:]
GDBreg = GradientBoostingRegressor(n_estimators = 80, learning_rate=0.1,
max_depth = 1, random_state = 0, loss = 'ls').fit(X_train, y_train)Une fois ajusté, nous pouvons trouver l'erreur quadratique moyenne comme suit -
mean_squared_error(y_test, GDBreg.predict(X_test))Production
5.391246106657164Ici, nous étudierons les méthodes de clustering dans Sklearn qui aideront à identifier toute similitude dans les échantillons de données.
Méthodes de clustering, l'une des méthodes de ML non supervisées les plus utiles, utilisées pour trouver des modèles de similarité et de relation parmi des échantillons de données. Après cela, ils regroupent ces échantillons en groupes ayant une similitude basée sur des fonctionnalités. Le clustering détermine le regroupement intrinsèque parmi les données non étiquetées actuelles, c'est pourquoi il est important.
La bibliothèque Scikit-learn a sklearn.clusterpour effectuer le regroupement de données non étiquetées. Sous ce module scikit-leran ont les méthodes de clustering suivantes -
KMeans
Cet algorithme calcule les centroïdes et les itère jusqu'à ce qu'il trouve le centroïde optimal. Il nécessite que le nombre de clusters soit spécifié, c'est pourquoi il suppose qu'ils sont déjà connus. La logique principale de cet algorithme est de regrouper les données séparant les échantillons en n nombre de groupes de variances égales en minimisant les critères connus sous le nom d'inertie. Le nombre de clusters identifiés par l'algorithme est représenté par 'K.
Scikit-learn ont sklearn.cluster.KMeansmodule pour effectuer le clustering K-Means. Lors du calcul des centres de cluster et de la valeur de l'inertie, le paramètre nommésample_weight permet sklearn.cluster.KMeans module pour attribuer plus de poids à certains échantillons.
Propagation d'affinité
Cet algorithme est basé sur le concept de «passage de message» entre différentes paires d'échantillons jusqu'à convergence. Il ne nécessite pas que le nombre de clusters soit spécifié avant d'exécuter l'algorithme. L'algorithme a une complexité temporelle de l'ordre (2), ce qui en est le plus gros inconvénient.
Scikit-learn ont sklearn.cluster.AffinityPropagation module pour effectuer le clustering de propagation d'affinité.
Changement moyen
Cet algorithme découvre principalement blobsdans une densité lisse d'échantillons. Il attribue itérativement les points de données aux clusters en décalant les points vers la densité de points de données la plus élevée. Au lieu de s'appuyer sur un paramètre nommébandwidth dictant la taille de la région à parcourir, il définit automatiquement le nombre de clusters.
Scikit-learn ont sklearn.cluster.MeanShift module pour effectuer le clustering Mean Shift.
Clustering spectral
Avant le regroupement, cet algorithme utilise essentiellement les valeurs propres, c'est-à-dire le spectre de la matrice de similarité des données pour effectuer une réduction de dimensionnalité dans moins de dimensions. L'utilisation de cet algorithme n'est pas recommandée lorsqu'il y a un grand nombre de clusters.
Scikit-learn ont sklearn.cluster.SpectralClustering module pour effectuer un clustering spectral.
Classification hiérarchique
Cet algorithme crée des clusters imbriqués en fusionnant ou en fractionnant les clusters successivement. Cette hiérarchie de cluster est représentée par un dendrogramme, c'est-à-dire un arbre. Il entre dans les deux catégories suivantes -
Agglomerative hierarchical algorithms- Dans ce type d'algorithme hiérarchique, chaque point de données est traité comme un seul cluster. Il agglomère ensuite successivement les paires de grappes. Cela utilise l'approche ascendante.
Divisive hierarchical algorithms- Dans cet algorithme hiérarchique, tous les points de données sont traités comme un grand cluster. Dans ce processus, le processus de regroupement implique de diviser, en utilisant une approche descendante, le seul grand cluster en plusieurs petits clusters.
Scikit-learn ont sklearn.cluster.AgglomerativeClustering module pour effectuer le clustering hiérarchique agglomératif.
DBSCAN
Ça signifie “Density-based spatial clustering of applications with noise”. Cet algorithme est basé sur la notion intuitive de «clusters» et de «bruit» selon laquelle les clusters sont des régions denses de densité inférieure dans l'espace de données, séparées par des régions de moindre densité de points de données.
Scikit-learn ont sklearn.cluster.DBSCANmodule pour effectuer le clustering DBSCAN. Il existe deux paramètres importants à savoir min_samples et eps utilisés par cet algorithme pour définir dense.
Valeur plus élevée du paramètre min_samples ou une valeur inférieure du paramètre eps donnera une indication sur la densité plus élevée de points de données qui est nécessaire pour former un cluster.
OPTIQUE
Ça signifie “Ordering points to identify the clustering structure”. Cet algorithme trouve également des clusters basés sur la densité dans les données spatiales. Sa logique de travail de base est comme DBSCAN.
Il résout une faiblesse majeure de l'algorithme DBSCAN - le problème de la détection de clusters significatifs dans des données de densité variable - en ordonnant les points de la base de données de telle manière que les points spatialement les plus proches deviennent voisins dans l'ordre.
Scikit-learn ont sklearn.cluster.OPTICS module pour effectuer le clustering OPTICS.
BOULEAU
Il est synonyme de réduction itérative équilibrée et de regroupement à l'aide de hiérarchies. Il est utilisé pour effectuer un clustering hiérarchique sur de grands ensembles de données. Il construit un arbre nomméCFT c'est à dire Characteristics Feature Tree, pour les données données.
L'avantage de CFT est que les nœuds de données appelés nœuds CF (Characteristics Feature) contiennent les informations nécessaires pour la mise en cluster, ce qui évite en outre de devoir conserver toutes les données d'entrée en mémoire.
Scikit-learn ont sklearn.cluster.Birch module pour effectuer le clustering BIRCH.
Comparaison des algorithmes de clustering
Le tableau suivant donnera une comparaison (basée sur les paramètres, l'évolutivité et la métrique) des algorithmes de clustering dans scikit-learn.
| Sr.Non | Nom de l'algorithme | Paramètres | Évolutivité | Métrique utilisée |
|---|---|---|---|---|
| 1 | K-Means | Nbre de grappes | Très gros n_samples | La distance entre les points. |
| 2 | Propagation d'affinité | Amortissement | Ce n'est pas évolutif avec n_samples | Distance du graphique |
| 3 | Déplacement moyen | Bande passante | Ce n'est pas évolutif avec n_samples. | La distance entre les points. |
| 4 | Clustering spectral | Nombre de clusters | Niveau d'évolutivité moyen avec n_samples. Petit niveau d'évolutivité avec n_clusters. | Distance du graphique |
| 5 | Classification hiérarchique | Seuil de distance ou nombre de clusters | Grand n_samples Grand n_clusters | La distance entre les points. |
| 6 | DBSCAN | Taille du quartier | Très grands n_samples et n_clusters moyens. | Distance du point le plus proche |
| sept | OPTIQUE | Appartenance minimale au cluster | Très grands n_samples et grands n_clusters. | La distance entre les points. |
| 8 | BOULEAU | Seuil, facteur de branchement | Grand n_samples Grand n_clusters | La distance euclidienne entre les points. |
Clustering K-Means sur un ensemble de données Scikit-learn Digit
Dans cet exemple, nous appliquerons le clustering K-means sur un ensemble de données de chiffres. Cet algorithme identifiera des chiffres similaires sans utiliser les informations d'étiquette d'origine. L'implémentation se fait sur le notebook Jupyter.
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shapeProduction
1797, 64)Cette sortie montre que l'ensemble de données numériques contient 1797 échantillons avec 64 caractéristiques.
Exemple
Maintenant, effectuez le clustering K-Means comme suit -
kmeans = KMeans(n_clusters = 10, random_state = 0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shapeProduction
(10, 64)Cette sortie montre que le clustering K-means a créé 10 clusters avec 64 fonctionnalités.
Exemple
fig, ax = plt.subplots(2, 5, figsize = (8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks = [], yticks = [])
axi.imshow(center, interpolation = 'nearest', cmap = plt.cm.binary)Production
La sortie ci-dessous contient des images montrant les centres de clusters appris par le clustering K-Means.

Ensuite, le script Python ci-dessous fera correspondre les étiquettes de cluster apprises (par K-Means) avec les vraies étiquettes qu'elles contiennent -
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]Nous pouvons également vérifier la précision à l'aide de la commande mentionnée ci-dessous.
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)Production
0.7935447968836951Exemple d'implémentation complet
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape
kmeans = KMeans(n_clusters = 10, random_state = 0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shape
fig, ax = plt.subplots(2, 5, figsize = (8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks=[], yticks = [])
axi.imshow(center, interpolation = 'nearest', cmap = plt.cm.binary)
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)Il existe différentes fonctions à l'aide desquelles nous pouvons évaluer les performances des algorithmes de clustering.
Voici quelques fonctions importantes et principalement utilisées fournies par Scikit-learn pour évaluer les performances de clustering -
Index Rand ajusté
Rand Index est une fonction qui calcule une mesure de similarité entre deux regroupements. Pour ce calcul, l'index rand considère toutes les paires d'échantillons et les paires de comptage qui sont attribuées dans les clusters similaires ou différents dans le clustering prédit et vrai. Ensuite, le score brut de l'indice Rand est `` ajusté pour le hasard '' dans le score de l'indice Rand ajusté en utilisant la formule suivante -
$$Adjusted\:RI=\left(RI-Expected_{-}RI\right)/\left(max\left(RI\right)-Expected_{-}RI\right)$$Il a deux paramètres à savoir labels_true, qui sont les étiquettes de classe de vérité terrain, et labels_pred, qui sont des étiquettes de clusters à évaluer.
Exemple
from sklearn.metrics.cluster import adjusted_rand_score
labels_true = [0, 0, 1, 1, 1, 1]
labels_pred = [0, 0, 2, 2, 3, 3]
adjusted_rand_score(labels_true, labels_pred)Production
0.4444444444444445Un étiquetage parfait serait noté 1 et un mauvais étiquetage ou un étiquetage indépendant serait noté 0 ou négatif.
Score basé sur les informations mutuelles
L'information mutuelle est une fonction qui calcule l'accord des deux affectations. Il ignore les permutations. Les versions suivantes sont disponibles -
Information mutuelle normalisée (NMI)
Scikit learn avoir sklearn.metrics.normalized_mutual_info_score module.
Exemple
from sklearn.metrics.cluster import normalized_mutual_info_score
labels_true = [0, 0, 1, 1, 1, 1]
labels_pred = [0, 0, 2, 2, 3, 3]
normalized_mutual_info_score (labels_true, labels_pred)Production
0.7611702597222881Informations mutuelles ajustées (AMI)
Scikit learn avoir sklearn.metrics.adjusted_mutual_info_score module.
Exemple
from sklearn.metrics.cluster import adjusted_mutual_info_score
labels_true = [0, 0, 1, 1, 1, 1]
labels_pred = [0, 0, 2, 2, 3, 3]
adjusted_mutual_info_score (labels_true, labels_pred)Production
0.4444444444444448Score Fowlkes-Mallows
La fonction Fowlkes-Mallows mesure la similitude de deux regroupements d'un ensemble de points. Elle peut être définie comme la moyenne géométrique de la précision et du rappel par paires.
Mathématiquement,
$$FMS=\frac{TP}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)}}$$Ici, TP = True Positive - nombre de paires de points appartenant aux mêmes clusters dans les étiquettes vrai et prédit à la fois.
FP = False Positive - nombre de paires de points appartenant aux mêmes clusters dans les étiquettes vraies mais pas dans les étiquettes prédites.
FN = False Negative - nombre de paires de points appartenant aux mêmes clusters dans les étiquettes prédites mais pas dans les étiquettes vraies.
L'apprentissage Scikit a le module sklearn.metrics.fowlkes_mallows_score -
Exemple
from sklearn.metrics.cluster import fowlkes_mallows_score
labels_true = [0, 0, 1, 1, 1, 1]
labels_pred = [0, 0, 2, 2, 3, 3]
fowlkes_mallows__score (labels_true, labels_pred)Production
0.6546536707079771Coefficient de silhouette
La fonction Silhouette calculera le coefficient de silhouette moyen de tous les échantillons en utilisant la distance moyenne intra-cluster et la distance moyenne du cluster le plus proche pour chaque échantillon.
Mathématiquement,
$$S=\left(b-a\right)/max\left(a,b\right)$$Ici, a est la distance intra-cluster.
et b est la distance moyenne du groupe le plus proche.
Les Scikit apprennent ont sklearn.metrics.silhouette_score module -
Exemple
from sklearn import metrics.silhouette_score
from sklearn.metrics import pairwise_distances
from sklearn import datasets
import numpy as np
from sklearn.cluster import KMeans
dataset = datasets.load_iris()
X = dataset.data
y = dataset.target
kmeans_model = KMeans(n_clusters = 3, random_state = 1).fit(X)
labels = kmeans_model.labels_
silhouette_score(X, labels, metric = 'euclidean')Production
0.5528190123564091Matrice de contingence
Cette matrice indiquera la cardinalité d'intersection pour chaque paire de confiance de (vrai, prédit). La matrice de confusion pour les problèmes de classification est une matrice de contingence carrée.
Les Scikit apprennent ont sklearn.metrics.contingency_matrix module.
Exemple
from sklearn.metrics.cluster import contingency_matrix
x = ["a", "a", "a", "b", "b", "b"]
y = [1, 1, 2, 0, 1, 2]
contingency_matrix(x, y)Production
array([
[0, 2, 1],
[1, 1, 1]
])La première ligne de la sortie ci-dessus montre que parmi trois échantillons dont le vrai cluster est «a», aucun d'entre eux n'est à 0, deux d'entre eux sont dans 1 et 1 est dans 2. D'autre part, la deuxième ligne montre que parmi trois échantillons dont le vrai cluster est «b», 1 est en 0, 1 est en 1 et 1 est en 2.
La réduction de dimensionnalité, une méthode d'apprentissage automatique non supervisée, est utilisée pour réduire le nombre de variables de fonctionnalité pour chaque échantillon de données en sélectionnant un ensemble de fonctionnalités principales. L'analyse en composantes principales (ACP) est l'un des algorithmes populaires pour la réduction de la dimensionnalité.
PCA exact
Principal Component Analysis (PCA) est utilisé pour la réduction de dimensionnalité linéaire en utilisant Singular Value Decomposition(SVD) des données pour les projeter dans un espace dimensionnel inférieur. Lors de la décomposition à l'aide de PCA, les données d'entrée sont centrées mais pas mises à l'échelle pour chaque fonction avant d'appliquer le SVD.
La bibliothèque ML Scikit-learn fournit sklearn.decomposition.PCAmodule qui est implémenté comme un objet transformateur qui apprend n composants dans sa méthode fit (). Il peut également être utilisé sur de nouvelles données pour les projeter sur ces composants.
Exemple
L'exemple ci-dessous utilisera le module sklearn.decomposition.PCA pour trouver les 5 meilleurs composants principaux de l'ensemble de données Pima Indians Diabetes.
from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\Users\Leekha\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', ‘class']
dataframe = read_csv(path, names = names)
array = dataframe.values
X = array[:,0:8]
Y = array[:,8]
pca = PCA(n_components = 5)
fit = pca.fit(X)
print(("Explained Variance: %s") % (fit.explained_variance_ratio_))
print(fit.components_)Production
Explained Variance: [0.88854663 0.06159078 0.02579012 0.01308614 0.00744094]
[
[-2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-029.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03]
[-2.26488861e-02 -9.72210040e-01 -1.41909330e-01 5.78614699e-029.46266913e-02 -4.69729766e-02 -8.16804621e-04 -1.40168181e-01]
[-2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-012.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]
[-4.90459604e-02 1.19830016e-01 -2.62742788e-01 8.84369380e-01-6.55503615e-02 1.92801728e-01 2.69908637e-03 -3.01024330e-01]
[ 1.51612874e-01 -8.79407680e-02 -2.32165009e-01 2.59973487e-01-1.72312241e-04 2.14744823e-02 1.64080684e-03 9.20504903e-01]
]ACP incrémentale
Incremental Principal Component Analysis (IPCA) est utilisé pour traiter la plus grande limitation de l'analyse en composants principaux (PCA) et c'est-à-dire que PCA ne prend en charge que le traitement par lots, ce qui signifie que toutes les données d'entrée à traiter doivent tenir dans la mémoire.
La bibliothèque ML Scikit-learn fournit sklearn.decomposition.IPCA module qui permet d'implémenter Out-of-Core PCA soit en utilisant son partial_fit méthode sur des blocs de données extraits séquentiellement ou en permettant l'utilisation de np.memmap, un fichier mappé en mémoire, sans charger le fichier entier en mémoire.
Identique à PCA, lors de la décomposition utilisant IPCA, les données d'entrée sont centrées mais pas mises à l'échelle pour chaque fonction avant d'appliquer le SVD.
Exemple
L'exemple ci-dessous utilisera sklearn.decomposition.IPCA module sur l'ensemble de données numériques Sklearn.
from sklearn.datasets import load_digits
from sklearn.decomposition import IncrementalPCA
X, _ = load_digits(return_X_y = True)
transformer = IncrementalPCA(n_components = 10, batch_size = 100)
transformer.partial_fit(X[:100, :])
X_transformed = transformer.fit_transform(X)
X_transformed.shapeProduction
(1797, 10)Ici, nous pouvons partiellement adapter sur de plus petits lots de données (comme nous l'avons fait sur 100 par lot) ou vous pouvez laisser le fit() fonction pour diviser les données en lots.
PCA du noyau
L'analyse en composantes principales du noyau, une extension de l'ACP, permet une réduction de dimensionnalité non linéaire à l'aide de noyaux. Il prend en charge à la foistransform and inverse_transform.
La bibliothèque ML Scikit-learn fournit sklearn.decomposition.KernelPCA module.
Exemple
L'exemple ci-dessous utilisera sklearn.decomposition.KernelPCAmodule sur l'ensemble de données numériques Sklearn. Nous utilisons un noyau sigmoïde.
from sklearn.datasets import load_digits
from sklearn.decomposition import KernelPCA
X, _ = load_digits(return_X_y = True)
transformer = KernelPCA(n_components = 10, kernel = 'sigmoid')
X_transformed = transformer.fit_transform(X)
X_transformed.shapeProduction
(1797, 10)PCA utilisant SVD randomisé
L'analyse en composantes principales (ACP) utilisant la SVD randomisée est utilisée pour projeter des données dans un espace de dimension inférieure préservant la majeure partie de la variance en supprimant le vecteur singulier des composants associés aux valeurs singulières inférieures. Ici lesklearn.decomposition.PCA module avec le paramètre optionnel svd_solver=’randomized’ va être très utile.
Exemple
L'exemple ci-dessous utilisera sklearn.decomposition.PCA module avec le paramètre facultatif svd_solver = 'randomized' pour trouver les 7 meilleurs composants principaux de l'ensemble de données Pima Indians Diabetes.
from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\Users\Leekha\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names = names)
array = dataframe.values
X = array[:,0:8]
Y = array[:,8]
pca = PCA(n_components = 7,svd_solver = 'randomized')
fit = pca.fit(X)
print(("Explained Variance: %s") % (fit.explained_variance_ratio_))
print(fit.components_)Production
Explained Variance: [8.88546635e-01 6.15907837e-02 2.57901189e-02 1.30861374e-027.44093864e-03 3.02614919e-03 5.12444875e-04]
[
[-2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-029.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03]
[-2.26488861e-02 -9.72210040e-01 -1.41909330e-01 5.78614699e-029.46266913e-02 -4.69729766e-02 -8.16804621e-04 -1.40168181e-01]
[-2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-012.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]
[-4.90459604e-02 1.19830016e-01 -2.62742788e-01 8.84369380e-01-6.55503615e-02 1.92801728e-01 2.69908637e-03 -3.01024330e-01]
[ 1.51612874e-01 -8.79407680e-02 -2.32165009e-01 2.59973487e-01-1.72312241e-04 2.14744823e-02 1.64080684e-03 9.20504903e-01]
[-5.04730888e-03 5.07391813e-02 7.56365525e-02 2.21363068e-01-6.13326472e-03 -9.70776708e-01 -2.02903702e-03 -1.51133239e-02]
[ 9.86672995e-01 8.83426114e-04 -1.22975947e-03 -3.76444746e-041.42307394e-03 -2.73046214e-03 -6.34402965e-03 -1.62555343e-01]
]