Conception VLSI - Transistor MOS
La technologie MOSFET complémentaire (CMOS) est aujourd'hui largement utilisée pour former des circuits dans des applications nombreuses et variées. Les ordinateurs, processeurs et téléphones portables actuels utilisent le CMOS en raison de plusieurs avantages clés. Le CMOS offre une faible dissipation de puissance, une vitesse relativement élevée, des marges de bruit élevées dans les deux états et fonctionnera sur une large gamme de tensions de source et d'entrée (à condition que la tension de la source soit fixe)
Pour les processus que nous allons discuter, le type de transistor disponible est le transistor à effet de champ métal-oxyde-semi-conducteur (MOSFET). Ces transistors sont formésas a ‘sandwich’consistant en une couche semi-conductrice, généralement une tranche, ou plaquette, à partir d'un monocristal de silicium; une couche de dioxyde de silicium (l'oxyde) et une couche de métal.
Structure d'un MOSFET
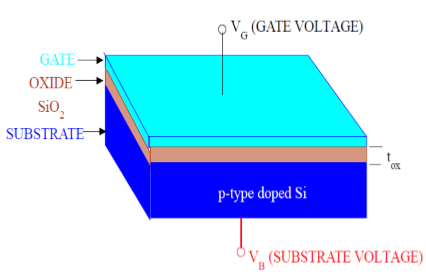
Comme le montre la figure, la structure MOS contient trois couches -
The Metal Gate Electrode
The Insulating Oxide Layer (SiO2)
P – type Semiconductor (Substrate)
La structure MOS forme un condensateur, la grille et le substrat étant en tant que deux plaques et une couche d'oxyde en tant que matériau diélectrique. L'épaisseur du matériau diélectrique (SiO 2 ) est généralement comprise entre 10 nm et 50 nm. La concentration et la distribution des porteurs dans le substrat peuvent être manipulées par une tension externe appliquée à la grille et à la borne du substrat. Maintenant, pour comprendre la structure du MOS, considérons d'abord les propriétés électriques de base du substrat semi-conducteur de type P.
La concentration du support dans le matériau semi-conducteur suit toujours la Mass Action Law. La loi de l'action de masse est donnée par -
$$ np = n_ {i} ^ {2} $$
Où,
n est la concentration de porteurs d'électrons
p est la concentration de porteurs de trous
ni est la concentration intrinsèque des porteurs de silicium
Supposons maintenant que le substrat est également dopée avec l' accepteur (bore) concentration N A . Ainsi, la concentration d'électrons et de trous dans un substrat de type p est
$$ n_ {po} = \ frac {n_ {i} ^ {2}} {N_ {A}} $$
$$ p_ {po} = N_ {A} $$
Ici, concentration de dopage NAest (10 15 à 10 16 cm -3 ) supérieure à la concentration intrinsèque ni. Maintenant, pour comprendre la structure MOS, considérons le diagramme de niveau d'énergie du substrat de silicium de type p.
Comme le montre la figure, la bande interdite entre la bande de conduction et la bande de cantonnière est de 1,1 eV. Ici, le potentiel de Fermi Φ F est la différence entre le niveau de Fermi intrinsèque (E i ) et le niveau de Fermi (E FP ).
Où le niveau de Fermi E F dépend de la concentration de dopage. Le potentiel de Fermi Φ F est la différence entre le niveau de Fermi intrinsèque (E i ) et le niveau de Fermi (E FP ).
Mathématiquement,
$$ \ Phi_ {Fp} = \ frac {E_ {F} -E_ {i}} {q} $$
La différence de potentiel entre la bande de conduction et l'espace libre est appelée affinité électronique et est notée qx.
Ainsi, l'énergie requise pour qu'un électron passe du niveau de Fermi à l'espace libre est appelée fonction de travail (qΦ S ) et est donnée par
$$ q \ Phi _ {s} = (E_ {c} -E_ {F}) + qx $$
La figure suivante montre le diagramme de bande d'énergie des composants qui composent le MOS.
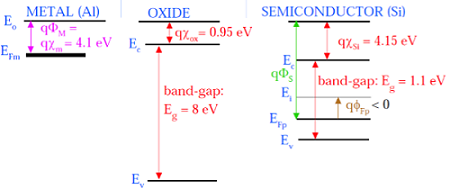
Comme le montre la figure ci-dessus, la couche isolante de SiO 2 a une large bande interdite d'énergie de 8 eV et la fonction de travail est de 0,95 eV. Le portail métallique a une fonction de travail de 4,1 eV. Ici, les fonctions de travail sont différentes, donc cela créera une chute de tension dans le système MOS. La figure ci-dessous montre le diagramme de bande d'énergie combinée du système MOS.
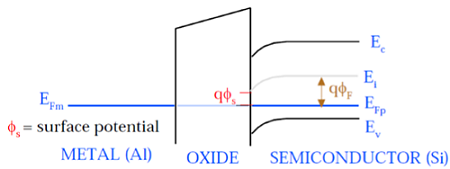
Comme le montre cette figure, le niveau de potentiel fermi de la grille métallique et du semi-conducteur (Si) sont au même potentiel. Le potentiel de Fermi en surface est appelé potentiel de surface Φ S et il est plus petit que le potentiel de Fermi Φ F en magnitude.
Fonctionnement d'un MOSFET
Le MOSFET se compose d'un condensateur MOS avec deux jonctions pn placées à proximité de la région de canal et cette région est contrôlée par la tension de grille. Pour rendre la jonction pn polarisée en inverse, le potentiel du substrat est maintenu inférieur au potentiel des trois autres bornes.
Si la tension de grille est augmentée au-delà de la tension de seuil (V GS > V TO ), une couche d'inversion sera établie en surface et un canal de type n se formera entre la source et le drain. Ce canal de type n transportera le courant de drain en fonction de la valeur V DS .
Pour différentes valeurs de V DS , le MOSFET peut fonctionner dans différentes régions comme expliqué ci-dessous.
Région linéaire
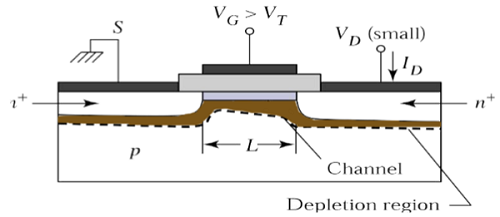
À V DS = 0, l'équilibre thermique existe dans la région du canal inversé et le courant de drain I D = 0. Maintenant, si une petite tension de drain, V DS > 0 est appliquée, un courant de drain proportionnel à la V DS commencera à circuler de la source à égoutter par le canal.
Le canal donne un chemin continu pour le flux de courant de la source au drain. Ce mode de fonctionnement est appelélinear region. La vue en coupe transversale d'un MOSFET à canal n, fonctionnant dans une région linéaire, est représentée sur la figure ci-dessous.
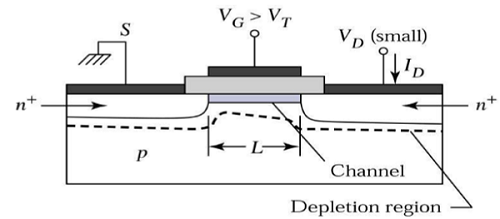
Au bord de la région de saturation
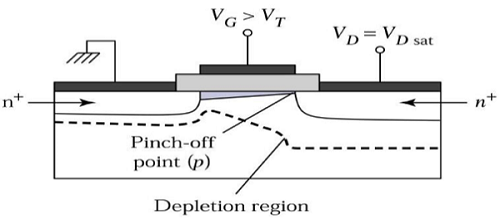
Maintenant, si le V DS est augmenté, les charges dans le canal et la profondeur du canal diminuent à la fin du drain. Pour V DS = V DSAT , les charges dans le canal sont réduites à zéro, ce qui est appelépinch – off point. La vue en coupe transversale du MOSFET à canal n fonctionnant au bord de la région de saturation est représentée sur la figure ci-dessous.
Région de saturation
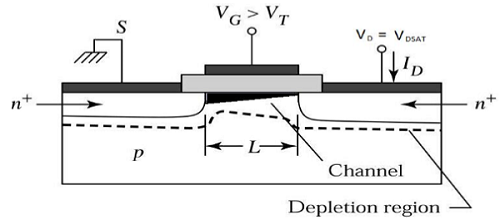
Pour V DS > V DSAT , une surface appauvrie se forme près du drain, et en augmentant la tension de drain, cette région appauvrie s'étend jusqu'à la source.
Ce mode de fonctionnement est appelé Saturation region. Les électrons venant de la source à l'extrémité du canal, entrent dans la région d'appauvrissement du drain et sont accélérés vers le drain dans un champ électrique élevé.
Courant MOSFET - Caractéristiques de tension
Pour comprendre la caractéristique courant-tension du MOSFET, une approximation du canal est effectuée. Sans cette approximation, l'analyse en trois dimensions du système MOS devient complexe. leGradual Channel Approximation (GCA) pour la caractéristique courant-tension réduira le problème d'analyse.
Approximation graduelle des canaux (GCA)
Considérons la vue en coupe transversale du MOSFET à canal n fonctionnant en mode linéaire. Ici, la source et le substrat sont connectés à la terre. V S = V B = 0. La porte - à - source (V GS ) et de drain - à - tension de source (V DS ) de tension sont les paramètres externes qui contrôlent le courant de drain I D .
La tension, V GS est fixée à une tension supérieure à la tension de seuil V TO , pour créer un canal entre la source et le drain. Comme le montre la figure, la direction x est perpendiculaire à la surface et la direction y est parallèle à la surface.
Ici, y = 0 à l'extrémité source comme indiqué sur la figure. La tension du canal, par rapport à la source, est représentée parVC(Y). Supposons que la tension de seuil VTO soit constante le long de la région de canal, entre y = 0 et y = L. Les conditions aux limites pour la tension de canal V C sont -
$$ V_ {c} \ left (y = 0 \ right) = V_ {s} = 0 \, et \, V_ {c} \ left (y = L \ right) = V_ {DS} $$
On peut aussi supposer que
$$ V_ {GS} \ geq V_ {TO} $$ et
$$ V_ {GD} = V_ {GS} -V_ {DS} \ geq V_ {TO} $$
Soit Q1 (y) la charge totale d'électrons mobiles dans la couche d'inversion de surface. Cette charge électronique peut être exprimée par -
$$ Q1 (y) = - C_ {ox}. [V_ {GS} -V_ {C (Y)} - V_ {TO}] $$
La figure ci-dessous montre la géométrie spatiale de la couche d'inversion de surface et indique ses dimensions. La couche d'inversion se rétrécit au fur et à mesure que nous passons du drain à la source. Maintenant, si nous considérons la petite région dy de la longueur de canal L, alors la résistance incrémentale dR offerte par cette région peut être exprimée comme -
$$ dR = - \ frac {dy} {w. \ mu _ {n} .Q1 (y)} $$
Ici, le signe moins est dû à la polarité négative de la charge de couche d'inversion Q1 et μ n est la mobilité de surface, qui est constante. Maintenant, remplacez la valeur de Q1 (y) dans l'équation dR -
$$ dR = - \ frac {dy} {w. \ mu _ {n}. \ left \ {-C_ {ox} \ left [V_ {GS} -V_ {C \ left (Y \ right)} \ right ] -V_ {TO} \ right \}} $$
$$ dR = \ frac {dy} {w. \ mu _ {n} .C_ {ox} \ left [V_ {GS} -V_ {C \ left (Y \ right)} \ right] -V_ {TO} } $$
Maintenant, la chute de tension dans la petite région de dy peut être donnée par
$$ dV_ {c} = I_ {D} .dR $$
Mettez la valeur de dR dans l'équation ci-dessus
$$ dV_ {C} = I_ {D}. \ frac {dy} {w. \ mu_ {n} .C_ {ox} \ left [V_ {GS} -V_ {C (Y)} \ right] -V_ {TO}} $$
$$ w. \ mu _ {n} .C_ {ox} \ gauche [V_ {GS} -V_ {C (Y)} - V_ {TO} \ right] .dV_ {C} = I_ {D} .dy $$
Pour obtenir le courant de drain ID sur toute la région du canal, l'équation ci-dessus peut être intégrée le long du canal de y = 0 à y = L et des tensions V C (y) = 0 à V C (y) = V DS ,
$$ C_ {ox} .w. \ Mu _ {n}. \ Int_ {V_ {c} = 0} ^ {V_ {DS}} \ left [V_ {GS} -V_ {C \ left (Y \ right )} - V_ {TO} \ right] .dV_ {C} = \ int_ {Y = 0} ^ {L} I_ {D} .dy $$
$$ \ frac {C_ {ox} .w. \ mu _ {n}} {2} \ left (2 \ left [V_ {GS} -V_ {TO} \ right] V_ {DS} -V_ {DS} ^ {2} \ right) = I_ {D} \ left [L-0 \ right] $$
$$ I_ {D} = \ frac {C_ {ox}. \ Mu _ {n}} {2}. \ Frac {w} {L} \ left (2 \ left [V_ {GS} -V_ {TO} \ right] V_ {DS} -V_ {DS} ^ {2} \ right) $$
Pour la région linéaire V DS <V GS - V TO . Pour la région de saturation, la valeur de V DS est supérieure à (V GS - V TO ). Par conséquent, pour la région de saturation V DS = (V GS - V TO ).
$$ I_ {D} = C_ {ox}. \ Mu _ {n}. \ Frac {w} {2} \ left (\ frac {\ left [2V_ {DS} \ right] V_ {DS} -V_ { DS} ^ {2}} {L} \ right) $$
$$ I_ {D} = C_ {ox}. \ Mu _ {n}. \ Frac {w} {2} \ left (\ frac {2V_ {DS} ^ {2} -V_ {DS} ^ {2} } {L} \ droite) $$
$$ I_ {D} = C_ {ox}. \ Mu _ {n}. \ Frac {w} {2} \ left (\ frac {V_ {DS} ^ {2}} {L} \ right) $$
$$ I_ {D} = C_ {ox}. \ Mu _ {n}. \ Frac {w} {2} \ left (\ frac {\ left [V_ {GS} -V_ {TO} \ right] ^ { 2}} {L} \ droite) $$