पायथन के साथ एअर इंडिया - अनसुपर्वीकृत लर्निंग: क्लस्टरिंग
Unsupervised मशीन लर्निंग एल्गोरिदम में किसी भी प्रकार का मार्गदर्शन प्रदान करने के लिए कोई पर्यवेक्षक नहीं होता है। यही कारण है कि वे कुछ सही कृत्रिम बुद्धिमत्ता के साथ निकटता से जुड़े हुए हैं।
अनिश्चित सीखने में, मार्गदर्शन के लिए कोई सही उत्तर नहीं होगा और कोई शिक्षक नहीं होगा। एल्गोरिदम को सीखने के लिए डेटा में दिलचस्प पैटर्न की खोज करने की आवश्यकता है।
क्लस्टरिंग क्या है?
मूल रूप से, यह एक प्रकार की अप्रशिक्षित शिक्षण पद्धति है और कई क्षेत्रों में उपयोग किए जाने वाले सांख्यिकीय डेटा विश्लेषण के लिए एक आम तकनीक है। क्लस्टरिंग मुख्य रूप से अवलोकनों के सेट को उप-समूहों में विभाजित करने का एक कार्य है, जिसे क्लस्टर कहा जाता है, इस तरह से कि एक ही क्लस्टर में अवलोकन एक अर्थ में समान होते हैं और वे अन्य समूहों में टिप्पणियों के लिए भिन्न होते हैं। सरल शब्दों में, हम कह सकते हैं कि क्लस्टरिंग का मुख्य लक्ष्य समानता और असमानता के आधार पर डेटा को समूहित करना है।
उदाहरण के लिए, निम्न आरेख अलग-अलग समूहों में समान डेटा दिखाता है -
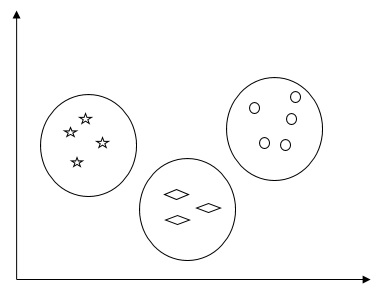
डेटा क्लस्टरिंग के लिए एल्गोरिदम
डेटा क्लस्टर करने के लिए कुछ सामान्य एल्गोरिदम निम्नलिखित हैं -
K- मीन्स एल्गोरिथ्म
K- साधन क्लस्टरिंग एल्गोरिथ्म डेटा क्लस्टरिंग के लिए प्रसिद्ध एल्गोरिदम में से एक है। हमें यह मानने की आवश्यकता है कि समूहों की संख्या पहले से ही ज्ञात है। इसे फ्लैट क्लस्टरिंग भी कहा जाता है। यह एक पुनरावृत्त क्लस्टरिंग एल्गोरिथ्म है। इस एल्गोरिथम के लिए नीचे दिए गए चरणों का पालन करने की आवश्यकता है -
Step 1 - हमें K उपसमूहों की वांछित संख्या निर्दिष्ट करने की आवश्यकता है।
Step 2- समूहों की संख्या को ठीक करें और प्रत्येक डेटा बिंदु को एक क्लस्टर में बेतरतीब ढंग से असाइन करें। या दूसरे शब्दों में, हमें समूहों की संख्या के आधार पर अपने डेटा को वर्गीकृत करने की आवश्यकता है।
इस चरण में, क्लस्टर सेंट्रोइड्स की गणना की जानी चाहिए।
जैसा कि यह एक पुनरावृत्त एल्गोरिथ्म है, हमें K प्रत्याक्षेपों के स्थानों को हर पुनरावृत्ति के साथ अद्यतन करने की आवश्यकता है जब तक कि हम वैश्विक ऑप्टिमा नहीं पाते हैं या दूसरे शब्दों में केन्द्रक उनके इष्टतम स्थानों पर पहुंच जाते हैं।
निम्नलिखित कोड पायथन में K- साधन क्लस्टरिंग एल्गोरिदम को लागू करने में मदद करेगा। हम स्किटिट-लर्न मॉड्यूल का उपयोग करने जा रहे हैं।
हमें आवश्यक पैकेज आयात करें -
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeansकोड की निम्नलिखित पंक्ति दो आयामी डेटासेट बनाने में मदद करेगी, जिसमें चार बूँदें होती हैं, उपयोग करके make_blob वहाँ से sklearn.dataset पैकेज।
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples = 500, centers = 4,
cluster_std = 0.40, random_state = 0)हम निम्नलिखित कोड का उपयोग करके डेटासेट की कल्पना कर सकते हैं -
plt.scatter(X[:, 0], X[:, 1], s = 50);
plt.show()
यहाँ, हम कितने किलोमीटर (n_clusters) के आवश्यक पैरामीटर के साथ किमी को एल्गोरिदम होने के लिए आरम्भ कर रहे हैं।
kmeans = KMeans(n_clusters = 4)हमें इनपुट डेटा के साथ K- साधन मॉडल को प्रशिक्षित करने की आवश्यकता है।
kmeans.fit(X)
y_kmeans = kmeans.predict(X)
plt.scatter(X[:, 0], X[:, 1], c = y_kmeans, s = 50, cmap = 'viridis')
centers = kmeans.cluster_centers_नीचे दिए गए कोड से हमें अपने डेटा के आधार पर मशीन के निष्कर्षों की साजिश करने और कल्पना करने में मदद मिलेगी, और जिन समूहों को मिलना है, उनके अनुसार फिटमेंट।
plt.scatter(centers[:, 0], centers[:, 1], c = 'black', s = 200, alpha = 0.5);
plt.show()
मीन शिफ्ट एल्गोरिथम
यह एक और लोकप्रिय और शक्तिशाली क्लस्टरिंग एल्गोरिथ्म है जिसका उपयोग अप्रशिक्षित शिक्षा में किया जाता है। यह कोई धारणा नहीं बनाता है इसलिए यह एक गैर पैरामीट्रिक एल्गोरिथ्म है। इसे पदानुक्रमित क्लस्टरिंग या मीन शिफ्ट क्लस्टर विश्लेषण भी कहा जाता है। अनुसरण इस एल्गोरिथ्म के मूल चरण होंगे -
सबसे पहले, हमें अपने स्वयं के क्लस्टर में निर्दिष्ट डेटा बिंदुओं से शुरू करने की आवश्यकता है।
अब, यह केन्द्रक की गणना करता है और नए केन्द्रक के स्थान को अद्यतन करता है।
इस प्रक्रिया को दोहराते हुए, हम क्लस्टर के शिखर यानी उच्च घनत्व वाले क्षेत्र की ओर बढ़ते हैं।
यह एल्गोरिथ्म उस चरण में बंद हो जाता है जहां केन्द्रक अब और नहीं चलते हैं।
निम्नलिखित कोड की मदद से हम पायथन में मीन शिफ्ट क्लस्टरिंग एल्गोरिदम को लागू कर रहे हैं। हम स्किकिट-लर्न मॉड्यूल का उपयोग करने जा रहे हैं।
हमें आवश्यक पैकेज आयात करें -
import numpy as np
from sklearn.cluster import MeanShift
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")निम्न कोड दो आयामी डेटासेट बनाने में मदद करेगा, जिसमें चार बूँदें होंगी, का उपयोग करके make_blob वहाँ से sklearn.dataset पैकेज।
from sklearn.datasets.samples_generator import make_blobsहम निम्नलिखित कोड के साथ डेटासेट की कल्पना कर सकते हैं
centers = [[2,2],[4,5],[3,10]]
X, _ = make_blobs(n_samples = 500, centers = centers, cluster_std = 1)
plt.scatter(X[:,0],X[:,1])
plt.show()
अब, हमें इनपुट डेटा के साथ मीन शिफ्ट क्लस्टर मॉडल को प्रशिक्षित करने की आवश्यकता है।
ms = MeanShift()
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_निम्न कोड इनपुट डेटा के अनुसार क्लस्टर केंद्रों और क्लस्टर की अपेक्षित संख्या को प्रिंट करेगा -
print(cluster_centers)
n_clusters_ = len(np.unique(labels))
print("Estimated clusters:", n_clusters_)
[[ 3.23005036 3.84771893]
[ 3.02057451 9.88928991]]
Estimated clusters: 2नीचे दिया गया कोड हमारे डेटा के आधार पर मशीन के निष्कर्षों की साजिश और कल्पना करने में मदद करेगा, और जो क्लस्टर पाए जाने हैं उनकी संख्या के अनुसार फिटमेंट।
colors = 10*['r.','g.','b.','c.','k.','y.','m.']
for i in range(len(X)):
plt.plot(X[i][0], X[i][1], colors[labels[i]], markersize = 10)
plt.scatter(cluster_centers[:,0],cluster_centers[:,1],
marker = "x",color = 'k', s = 150, linewidths = 5, zorder = 10)
plt.show()
क्लस्टरिंग प्रदर्शन को मापने
वास्तविक विश्व डेटा स्वाभाविक रूप से विशिष्ट समूहों की संख्या में व्यवस्थित नहीं है। इस कारण के कारण, अनुमानों को कल्पना करना और आकर्षित करना आसान नहीं है। इसलिए हमें क्लस्टरिंग प्रदर्शन के साथ-साथ उसकी गुणवत्ता को भी मापना होगा। यह सिल्हूट विश्लेषण की मदद से किया जा सकता है।
सिल्हूट विश्लेषण
इस विधि का उपयोग क्लस्टर के बीच की दूरी को मापकर क्लस्टरिंग की गुणवत्ता की जांच करने के लिए किया जा सकता है। मूल रूप से, यह सिल्हूट स्कोर देकर समूहों की संख्या जैसे मापदंडों का आकलन करने का एक तरीका प्रदान करता है। यह स्कोर एक मीट्रिक है जो मापता है कि एक क्लस्टर में प्रत्येक बिंदु पड़ोसी समूहों के बिंदुओं के कितने करीब है।
सिल्हूट स्कोर का विश्लेषण
स्कोर में [-1, 1] की सीमा होती है। इस स्कोर का विश्लेषण निम्नलिखित है -
Score of +1 - +1 के पास स्कोर इंगित करता है कि नमूना पड़ोसी क्लस्टर से बहुत दूर है।
Score of 0 - स्कोर 0 इंगित करता है कि नमूना दो पड़ोसी समूहों के बीच निर्णय सीमा पर या बहुत करीब है।
Score of -1 - नकारात्मक अंक इंगित करता है कि नमूने गलत समूहों को सौंपा गया है।
सिल्हूट स्कोर की गणना
इस खंड में, हम सीखेंगे कि सिल्हूट स्कोर की गणना कैसे करें।
सिल्हूट स्कोर की गणना निम्न सूत्र का उपयोग करके की जा सकती है -
$$ सिल्हूट स्कोर = \ frac {\ बाएँ (pq \ दाएँ)} {अधिकतम \ बाएँ (p, q \ दाएँ)} $
यहां, निकटतम क्लस्टर में बिंदुओं के लिए औसत दूरी है जो डेटा बिंदु का हिस्सा नहीं है। और, अपने स्वयं के क्लस्टर में सभी बिंदुओं के लिए औसत अंतर-क्लस्टर दूरी है।
समूहों की इष्टतम संख्या को खोजने के लिए, हमें आयात करके पुन: क्लस्टरिंग एल्गोरिथ्म को चलाने की आवश्यकता है metrics मॉड्यूल से sklearnपैकेज। निम्नलिखित उदाहरण में, हम क्लस्टर की इष्टतम संख्या ज्ञात करने के लिए K- साधन क्लस्टरिंग एल्गोरिथ्म चलाएंगे -
दिखाए गए अनुसार आवश्यक पैकेज आयात करें -
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeansनिम्न कोड की मदद से, हम दो आयामी डेटा जनरेट करेंगे, जिसमें चार बूँदें होंगी, का उपयोग करके make_blob वहाँ से sklearn.dataset पैकेज।
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples = 500, centers = 4, cluster_std = 0.40, random_state = 0)दिखाए गए अनुसार चरों को प्रारंभ करें -
scores = []
values = np.arange(2, 10)हमें सभी मूल्यों के माध्यम से K- साधन मॉडल को पुनरावृत्त करने की आवश्यकता है और इसे इनपुट डेटा के साथ प्रशिक्षित करने की भी आवश्यकता है।
for num_clusters in values:
kmeans = KMeans(init = 'k-means++', n_clusters = num_clusters, n_init = 10)
kmeans.fit(X)अब, यूक्लिडियन दूरी मीट्रिक का उपयोग करके वर्तमान क्लस्टरिंग मॉडल के लिए सिल्हूट स्कोर का अनुमान लगाएं -
score = metrics.silhouette_score(X, kmeans.labels_,
metric = 'euclidean', sample_size = len(X))कोड की निम्न पंक्ति समूहों की संख्या और साथ ही सिल्हूट स्कोर को प्रदर्शित करने में मदद करेगी।
print("\nNumber of clusters =", num_clusters)
print("Silhouette score =", score)
scores.append(score)आपको निम्न आउटपुट प्राप्त होंगे -
Number of clusters = 9
Silhouette score = 0.340391138371
num_clusters = np.argmax(scores) + values[0]
print('\nOptimal number of clusters =', num_clusters)अब, क्लस्टरों की इष्टतम संख्या के लिए आउटपुट निम्नानुसार होगा -
Optimal number of clusters = 2निकटतम पड़ोसियों का पता लगाना
यदि हम एक फिल्म सिफारिश प्रणाली जैसी सिफारिशकर्ता प्रणाली का निर्माण करना चाहते हैं तो हमें निकटतम पड़ोसियों को खोजने की अवधारणा को समझने की आवश्यकता है। इसका कारण यह है कि सिफारिशकर्ता प्रणाली निकटतम पड़ोसियों की अवधारणा का उपयोग करती है।
concept of finding nearest neighborsदिए गए डेटासेट से इनपुट बिंदु के निकटतम बिंदु को खोजने की प्रक्रिया के रूप में परिभाषित किया जा सकता है। इस KNN) K- निकटतम पड़ोसियों का मुख्य उपयोग) एल्गोरिथ्म वर्गीकरण प्रणालियों का निर्माण करना है जो विभिन्न वर्गों के लिए इनपुट डेटा बिंदु की निकटता पर एक डेटा बिंदु को वर्गीकृत करता है।
नीचे दिया गया पायथन कोड किसी दिए गए डेटा सेट के K- निकटतम पड़ोसियों को खोजने में मदद करता है -
आवश्यक पैकेज आयात करें जैसा कि नीचे दिखाया गया है। यहाँ, हम उपयोग कर रहे हैंNearestNeighbors मॉड्यूल से sklearn पैकेज
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import NearestNeighborsआइये अब इनपुट डेटा को परिभाषित करते हैं -
A = np.array([[3.1, 2.3], [2.3, 4.2], [3.9, 3.5], [3.7, 6.4], [4.8, 1.9],
[8.3, 3.1], [5.2, 7.5], [4.8, 4.7], [3.5, 5.1], [4.4, 2.9],])अब, हमें निकटतम पड़ोसियों को परिभाषित करने की आवश्यकता है -
k = 3हमें परीक्षण डेटा भी देने की आवश्यकता है जिससे निकटतम पड़ोसियों को ढूंढना है -
test_data = [3.3, 2.9]निम्नलिखित कोड हमारे द्वारा परिभाषित इनपुट डेटा की कल्पना और साजिश कर सकते हैं -
plt.figure()
plt.title('Input data')
plt.scatter(A[:,0], A[:,1], marker = 'o', s = 100, color = 'black')
अब, हमें K निकटतम पड़ोसी का निर्माण करने की आवश्यकता है। ऑब्जेक्ट को भी प्रशिक्षित करने की आवश्यकता है
knn_model = NearestNeighbors(n_neighbors = k, algorithm = 'auto').fit(X)
distances, indices = knn_model.kneighbors([test_data])अब, हम K निकटतम पड़ोसियों को निम्नानुसार प्रिंट कर सकते हैं
print("\nK Nearest Neighbors:")
for rank, index in enumerate(indices[0][:k], start = 1):
print(str(rank) + " is", A[index])हम परीक्षण डेटा बिंदु के साथ निकटतम पड़ोसियों की कल्पना कर सकते हैं
plt.figure()
plt.title('Nearest neighbors')
plt.scatter(A[:, 0], X[:, 1], marker = 'o', s = 100, color = 'k')
plt.scatter(A[indices][0][:][:, 0], A[indices][0][:][:, 1],
marker = 'o', s = 250, color = 'k', facecolors = 'none')
plt.scatter(test_data[0], test_data[1],
marker = 'x', s = 100, color = 'k')
plt.show()
उत्पादन
K Nearest Neighbors
1 is [ 3.1 2.3]
2 is [ 3.9 3.5]
3 is [ 4.4 2.9]K- निकटतम पड़ोसी क्लासिफायर
K-निकटतम पड़ोसी (KNN) क्लासिफायर एक वर्गीकरण मॉडल है जो किसी दिए गए डेटा बिंदु को वर्गीकृत करने के लिए निकटतम पड़ोसियों के एल्गोरिथ्म का उपयोग करता है। हमने पिछले भाग में KNN एल्गोरिथ्म को लागू किया है, अब हम उस एल्गोरिथ्म का उपयोग करते हुए KNN क्लासिफायर बनाने जा रहे हैं।
KNN क्लासिफायर की अवधारणा
K- निकटतम पड़ोसी वर्गीकरण की मूल अवधारणा एक पूर्वनिर्धारित संख्या, अर्थात, 'k' को खोजने के लिए है - एक नए नमूने के लिए दूरी में निकटतम प्रशिक्षण नमूनों की, जिन्हें वर्गीकृत किया जाना है। नए नमूने अपने लेबल पड़ोसियों से ही प्राप्त करेंगे। केएनएन क्लासिफायर में एक निश्चित उपयोगकर्ता होता है, जो निर्धारित किए जाने वाले पड़ोसियों की संख्या के लिए स्थिर होता है। दूरी के लिए, मानक यूक्लिडियन दूरी सबसे आम पसंद है। केएनएन क्लासिफायर सीधे सीखने के नियमों को बनाने के बजाय सीखा नमूनों पर काम करता है। KNN एल्गोरिथम सभी मशीन लर्निंग एल्गोरिदम में से सबसे सरल है। यह बड़ी संख्या में वर्गीकरण और प्रतिगमन समस्याओं में सफल रहा है, उदाहरण के लिए, चरित्र मान्यता या छवि विश्लेषण।
Example
हम अंकों को पहचानने के लिए एक KNN क्लासिफायरियर का निर्माण कर रहे हैं। इसके लिए, हम MNIST डेटासेट का उपयोग करेंगे। हम इस कोड को Jupyter नोटबुक में लिखेंगे।
आवश्यक पैकेज आयात करें जैसा कि नीचे दिखाया गया है।
यहाँ हम उपयोग कर रहे हैं KNeighborsClassifier मॉड्यूल से sklearn.neighbors पैकेज -
from sklearn.datasets import *
import pandas as pd
%matplotlib inline
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
import numpy as npनिम्न कोड यह दर्शाने के लिए अंकों की छवि प्रदर्शित करेगा कि हमें किस छवि का परीक्षण करना है -
def Image_display(i):
plt.imshow(digit['images'][i],cmap = 'Greys_r')
plt.show()अब, हमें MNIST डेटासेट लोड करने की आवश्यकता है। वास्तव में कुल 1797 छवियां हैं लेकिन हम पहले 1600 चित्रों को प्रशिक्षण नमूने के रूप में उपयोग कर रहे हैं और शेष 197 को परीक्षण के उद्देश्य से रखा जाएगा।
digit = load_digits()
digit_d = pd.DataFrame(digit['data'][0:1600])अब, छवियों को प्रदर्शित करने पर हम आउटपुट को निम्नानुसार देख सकते हैं -
Image_display(0)Image_display (0)
0 की छवि निम्नानुसार प्रदर्शित की गई है -

Image_display (9)
9 की छवि निम्नानुसार प्रदर्शित की गई है -

digit.keys ()
अब, हमें प्रशिक्षण और परीक्षण डेटा सेट बनाने और केएनएन क्लासिफायर के लिए परीक्षण डेटा सेट की आपूर्ति करने की आवश्यकता है।
train_x = digit['data'][:1600]
train_y = digit['target'][:1600]
KNN = KNeighborsClassifier(20)
KNN.fit(train_x,train_y)निम्न आउटपुट K निकटतम पड़ोसी क्लासिफायर निर्माता बनाएंगे -
KNeighborsClassifier(algorithm = 'auto', leaf_size = 30, metric = 'minkowski',
metric_params = None, n_jobs = 1, n_neighbors = 20, p = 2,
weights = 'uniform')हमें 1600 से अधिक किसी भी मनमानी संख्या प्रदान करके परीक्षण नमूना बनाने की आवश्यकता है, जो प्रशिक्षण नमूने थे।
test = np.array(digit['data'][1725])
test1 = test.reshape(1,-1)
Image_display(1725)Image_display (6)
6 की छवि निम्नानुसार प्रदर्शित की गई है -

अब हम परीक्षण डेटा की भविष्यवाणी इस प्रकार करेंगे -
KNN.predict(test1)उपरोक्त कोड निम्नलिखित आउटपुट उत्पन्न करेगा -
array([6])अब, निम्नलिखित पर विचार करें -
digit['target_names']उपरोक्त कोड निम्नलिखित आउटपुट उत्पन्न करेगा -
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])