त्वरित गाइड
इलेक्ट्रॉनिक्स की आधुनिक दुनिया में, शब्द Digital आम तौर पर एक कंप्यूटर के साथ जुड़ा हुआ है क्योंकि शब्द Digitalअंकों की गणना के द्वारा कंप्यूटर ऑपरेशन करने के तरीके से प्राप्त होता है। कई सालों तक, डिजिटल इलेक्ट्रॉनिक्स का अनुप्रयोग केवल कंप्यूटर सिस्टम में था। लेकिन अब एक दिन में, डिजिटल इलेक्ट्रॉनिक्स का उपयोग कई अन्य अनुप्रयोगों में किया जाता है। निम्नलिखित कुछ उदाहरण हैं जिनमेंDigital electronics भारी उपयोग किया जाता है।
- औद्योगिक प्रक्रिया नियंत्रण
- सैन्य प्रणाली
- Television
- संचार तंत्र
- चिकित्सा उपकरण
- Radar
- Navigation
संकेत
Signalभौतिक मात्रा के रूप में परिभाषित किया जा सकता है, जिसमें कुछ जानकारी होती है। यह एक या एक से अधिक स्वतंत्र चर का कार्य है। सिग्नल दो प्रकार के होते हैं।
- एनालॉग संकेत
- डिजिटल सिग्नल
एनालॉग संकेत
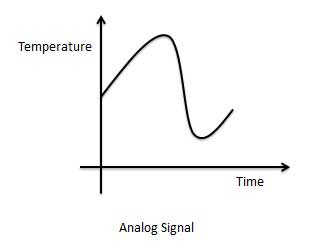
एक analog signalनिरंतर मूल्यों वाले संकेत के रूप में परिभाषित किया गया है। एनालॉग सिग्नल में विभिन्न मूल्यों की अनंत संख्या हो सकती है। वास्तविक दुनिया के परिदृश्य में, प्रकृति में देखी गई अधिकांश चीजें एनालॉग हैं। एनालॉग सिग्नल के उदाहरण निम्नलिखित हैं।
- Temperature
- Pressure
- Distance
- Sound
- Voltage
- Current
- Power
एनालॉग सिग्नल का ग्राफिकल प्रतिनिधित्व (तापमान)
सर्किट जो एनालॉग सिग्नल को प्रोसेस करते हैं, उन्हें एनालॉग सर्किट या सिस्टम कहा जाता है। एनालॉग सिस्टम के उदाहरण निम्नलिखित हैं।
- Filter
- Amplifiers
- टेलीविजन रिसीवर
- मोटर गति नियंत्रक
एनालॉग सिस्टम का नुकसान
- कम सटीकता
- कम चंचलता
- अधिक शोर प्रभाव
- अधिक विकृति
- मौसम का अधिक प्रभाव
डिजिटल सिग्नल
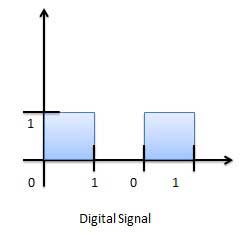
ए digital signalको उस संकेत के रूप में परिभाषित किया जाता है जिसमें केवल विशिष्ट मानों की सीमित संख्या होती है। डिजिटल सिग्नल निरंतर सिग्नल नहीं हैं। डिजिटल इलेक्ट्रॉनिक कैलकुलेटर में, स्विच की मदद से इनपुट दिया जाता है। यह इनपुट इलेक्ट्रिकल सिग्नल में परिवर्तित हो जाता है जिसमें दो असतत मान या स्तर होते हैं। इनमें से एक को निम्न स्तर कहा जा सकता है और दूसरे को उच्च स्तर कहा जाता है। सिग्नल हमेशा दो स्तरों में से एक होगा। इस प्रकार के सिग्नल को डिजिटल सिग्नल कहा जाता है। डिजिटल सिग्नल के उदाहरण निम्नलिखित हैं।
- बाइनरी सिग्नल
- ऑक्टल सिग्नल
- हेक्साडेसिमल सिग्नल
डिजिटल सिग्नल का ग्राफिकल प्रतिनिधित्व (बाइनरी)
डिजिटल सिग्नल को प्रोसेस करने वाले सर्किट को डिजिटल सिस्टम या डिजिटल सर्किट कहा जाता है। डिजिटल सिस्टम के उदाहरण निम्नलिखित हैं।
- Registers
- Flip-flop
- Counters
- Microprocessors
डिजिटल सिस्टम का लाभ
- अधिक सटीकता
- अधिक बहुमुखी प्रतिभा
- कम विकृति
- आसान संवाद
- सूचना का संभावित भंडारण
एनालॉग और डिजिटल सिग्नल की तुलना
| एस.एन. | एनालॉग संकेत | डिजिटल सिग्नल |
|---|---|---|
| 1 | एनालॉग सिग्नल में अनंत मूल्य हैं। | डिजिटल सिग्नल में मूल्यों की एक सीमित संख्या होती है। |
| 2 | एनालॉग सिग्नल में एक निरंतर प्रकृति है। | डिजिटल सिग्नल की एक असतत प्रकृति है। |
| 3 | एनालॉग सिग्नल ट्रांसड्यूसर्स और सिग्नल जनरेटर द्वारा उत्पन्न होता है। | डिजिटल सिग्नल ए से डी कनवर्टर द्वारा उत्पन्न होता है। |
| 4 | एनालॉग सिग्नल का उदाहरण - साइन लहर, त्रिकोणीय तरंगें। | डिजिटल सिग्नल का उदाहरण - बाइनरी सिग्नल। |
एक डिजिटल सिस्टम केवल स्थिति संख्या प्रणाली को समझ सकता है जहां कुछ प्रतीक होते हैं जिन्हें अंक कहा जाता है और ये प्रतीक संख्या में मौजूद स्थिति के आधार पर विभिन्न मूल्यों का प्रतिनिधित्व करते हैं।
एक संख्या में प्रत्येक अंक के मूल्य का उपयोग करके निर्धारित किया जा सकता है
अंक
संख्या में अंकों की स्थिति
संख्या प्रणाली का आधार (जहां आधार को संख्या प्रणाली में उपलब्ध अंकों की कुल संख्या के रूप में परिभाषित किया गया है)।
दशमलव संख्या प्रणाली
हमारे दिन-प्रतिदिन के जीवन में हम जिस संख्या प्रणाली का उपयोग करते हैं वह दशमलव संख्या प्रणाली है। दशमलव संख्या प्रणाली में आधार 10 है क्योंकि यह 0 से 9. तक 10 अंकों का उपयोग करता है। दशमलव संख्या प्रणाली में, दशमलव बिंदु के बाईं ओर स्थित क्रमिक इकाइयाँ, दसियों, सैकड़ों, हजारों और इसी तरह का प्रतिनिधित्व करती हैं।
प्रत्येक स्थिति आधार (10) की एक विशिष्ट शक्ति का प्रतिनिधित्व करती है। उदाहरण के लिए, दशमलव संख्या 1234 में इकाइयों की स्थिति में अंक 4, दसियों की स्थिति में 3, सैकड़ों की स्थिति में 2, और हजारों की संख्या में 1 होते हैं, और इसके मूल्य के रूप में लिखा जा सकता है।
(1×1000) + (2×100) + (3×10) + (4×l)
(1×103) + (2×102) + (3×101) + (4×l00)
1000 + 200 + 30 + 1
1234एक कंप्यूटर प्रोग्रामर या एक आईटी पेशेवर के रूप में, आपको निम्नलिखित संख्या प्रणालियों को समझना चाहिए जो अक्सर कंप्यूटर में उपयोग किए जाते हैं।
| एस.एन. | संख्या प्रणाली और विवरण |
|---|---|
| 1 | Binary Number System आधार 2. अंकों का उपयोग: 0, 1 |
| 2 | Octal Number System आधार 8. अंकों का उपयोग: 0 से 7 |
| 3 | Hexa Decimal Number System बेस 16. उपयोग किए गए अंक: 0 से 9, पत्र का उपयोग: ए- एफ |
बाइनरी नंबर सिस्टम
विशेषताएँ
दो अंकों, 0 और 1 का उपयोग करता है।
जिसे बेस 2 नंबर सिस्टम भी कहा जाता है
एक बाइनरी संख्या में प्रत्येक स्थिति आधार की 0 शक्ति (2) का प्रतिनिधित्व करती है। उदाहरण: २ ०
एक बाइनरी संख्या में अंतिम स्थिति आधार की एक x शक्ति (2) का प्रतिनिधित्व करती है। उदाहरण: 2 x जहां x अंतिम स्थिति का प्रतिनिधित्व करता है - 1।
उदाहरण
बाइनरी संख्या: 10101 2
दशमलव समतुल्य की गणना -
| कदम | बाइनरी संख्या | दशमलव संख्या |
|---|---|---|
| चरण 1 | 10101 2 | ((1 × 2 4 ) + (0 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 )) 10 |
| चरण 2 | 10101 2 | (१६ + ० + ४ + ० + १) १० |
| चरण 3 | 10101 2 | २१ १० |
Note:10101 2 को आमतौर पर 10101 के रूप में लिखा जाता है।
ऑक्टल नंबर सिस्टम
विशेषताएँ
आठ अंकों का उपयोग करता है, 0,1,2,3,4,5,6,7।
जिसे बेस 8 नंबर सिस्टम भी कहा जाता है
एक अष्टक संख्या में प्रत्येक स्थिति आधार की एक 0 शक्ति (8) का प्रतिनिधित्व करती है। उदाहरण: 8 ०
एक अष्टक संख्या में अंतिम स्थिति आधार की एक x शक्ति (8) का प्रतिनिधित्व करती है। उदाहरण: 8 x जहां x अंतिम स्थिति का प्रतिनिधित्व करता है - 1।
उदाहरण
अष्टक संख्या - 12570 8
दशमलव समतुल्य की गणना -
| कदम | अष्टक संख्या | दशमलव संख्या |
|---|---|---|
| चरण 1 | 12570 8 | ((1 × 8 4 ) + (2 × 8 3 ) + (5 × 8 2 ) + (7 × 8 1 ) + (0 × 8 0 )) 10 |
| चरण 2 | 12570 8 | (4096 + 1024 + 320 + 56 + 0) 10 |
| चरण 3 | 12570 8 | 5496 10 |
Note:12570 8 को सामान्यतः 12570 लिखा जाता है।
हेक्साडेसिमल नंबर सिस्टम
विशेषताएँ
10 अंकों और 6 अक्षरों, 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F का उपयोग करता है।
पत्र 10. ए = 10, बी = 11, सी = 12, डी = 13, ई = 14, एफ = 15 से शुरू होने वाली संख्याओं का प्रतिनिधित्व करते हैं।
जिसे बेस 16 नंबर सिस्टम भी कहा जाता है।
हेक्साडेसिमल संख्या में प्रत्येक स्थिति आधार की 0 शक्ति (16) का प्रतिनिधित्व करती है। उदाहरण १६ ० ।
हेक्साडेसिमल संख्या में अंतिम स्थिति आधार की एक x शक्ति (16) का प्रतिनिधित्व करती है। उदाहरण 16 x जहां x अंतिम स्थिति का प्रतिनिधित्व करता है - 1।
उदाहरण -
हेक्साडेसिमल संख्या: 19FDE 16
दशमलव समतुल्य की गणना -
| कदम | हेक्साडेसिमल संख्या | दशमलव संख्या |
|---|---|---|
| चरण 1 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (F × 16 2 ) + (D × 16 1 ) + (E × 16 0 )) 10 |
| चरण 2 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (15 × 16 2 ) + (13 × 16 1 ) + (14 × 16 0 )) 10 |
| चरण 3 | 19FDE 16 | (65536 + 36864 + 3840 + 208 + 14) 10 |
| चरण 4 | 19FDE 16 | 106462 10 |
Note −19FDE 16 को आम तौर पर 19FDE के रूप में लिखा जाता है।
कई विधियाँ या तकनीकें हैं जिनका उपयोग संख्याओं को एक आधार से दूसरे में बदलने के लिए किया जा सकता है। हम यहाँ निम्न प्रदर्शित करेंगे -
- अन्य बेस सिस्टम के लिए दशमलव
- अन्य आधार प्रणाली दशमलव के लिए
- गैर-दशमलव के लिए अन्य आधार प्रणाली
- शॉर्टकट विधि - अष्टाधारी को बाइनरी
- शॉर्टकट विधि - ऑक्टल टू बाइनरी
- शॉर्टकट विधि - हेक्साडेसिमल के लिए बाइनरी
- शॉर्टकट विधि - हेक्साडेसिमल से बाइनरी
अन्य बेस सिस्टम के लिए दशमलव
कदम
Step 1 - नए आधार के मान द्वारा परिवर्तित की जाने वाली दशमलव संख्या को विभाजित करें।
Step 2 - चरण 1 से शेष को नए आधार नंबर के सबसे सही अंक (कम से कम महत्वपूर्ण अंक) के रूप में प्राप्त करें।
Step 3 - पिछले आधार के भाग को नए आधार से विभाजित करें।
Step 4 - नए आधार नंबर के अगले अंक (बाईं ओर) के रूप में चरण 3 से शेष को रिकॉर्ड करें।
चरण 3 और 4 को दोहराएं, जब तक कि चरण 3 में भागफल शून्य नहीं हो जाता, तब तक दाएं से बाएं ओर अवशेष प्राप्त होते रहेंगे।
इस प्रकार प्राप्त अंतिम शेष नया आधार संख्या का सबसे महत्वपूर्ण अंक (MSD) होगा।
उदाहरण -
दशमलव संख्या: 29 10
बाइनरी समतुल्य की गणना -
| कदम | ऑपरेशन | परिणाम | शेष |
|---|---|---|---|
| चरण 1 | २ ९ / २ | 14 | 1 |
| चरण 2 | १४ / २ | 7 | 0 |
| चरण 3 | / २ | 3 | 1 |
| चरण 4 | 3/2 | 1 | 1 |
| चरण 5 | 1/2 | 0 | 1 |
जैसा कि चरण 2 और 4 में उल्लेख किया गया है, अवशेषों को उल्टे क्रम में व्यवस्थित किया जाना है ताकि पहला शेष कम से कम महत्वपूर्ण अंक (LSD) बन जाए और अंतिम शेष सबसे महत्वपूर्ण अंक (MSD) बन जाए।
दशमलव संख्या - 29 10 = बाइनरी संख्या - 11101 2 ।
अन्य बेस सिस्टम दशमलव प्रणाली के लिए
कदम
Step 1 - प्रत्येक अंक के स्तंभ (स्थिति) का निर्धारण करें (यह अंक की स्थिति और संख्या प्रणाली के आधार पर निर्भर करता है)।
Step 2 - प्राप्त कॉलम मूल्यों (चरण 1 में) को संबंधित कॉलम में अंकों से गुणा करें।
Step 3 - चरण 2 में गणना किए गए उत्पादों को योग। कुल दशमलव में बराबर मूल्य है।
उदाहरण
बाइनरी नंबर - 11101 2
दशमलव समतुल्य की गणना -
| कदम | बाइनरी संख्या | दशमलव संख्या |
|---|---|---|
| चरण 1 | 11101 2 | ((1 × 2 4 ) + (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 )) 10 |
| चरण 2 | 11101 2 | (१६ + 4 + ४ + ० + १) १० |
| चरण 3 | 11101 2 | २ ९ १० |
बाइनरी नंबर - 11101 2 = दशमलव संख्या - 29 10
गैर-दशमलव प्रणाली के लिए अन्य आधार प्रणाली
कदम
Step 1 - मूल संख्या को दशमलव संख्या (आधार 10) में बदलें।
Step 2 - नई आधार संख्या के लिए प्राप्त दशमलव संख्या को परिवर्तित करें।
उदाहरण
अष्टक संख्या - २५ 8
बाइनरी समतुल्य की गणना -
चरण 1 - दशमलव में परिवर्तित करें
| कदम | अष्टक संख्या | दशमलव संख्या |
|---|---|---|
| चरण 1 | २५ 8 | ((2 × 8 1 ) + (5 × 8 0 )) 10 |
| चरण 2 | २५ 8 | (१६ + ५) १० |
| चरण 3 | २५ 8 | २१ १० |
ऑक्टल संख्या - 25 8 = दशमलव संख्या - 21 10
चरण 2 - दशमलव को बाइनरी में बदलें
| कदम | ऑपरेशन | परिणाम | शेष |
|---|---|---|---|
| चरण 1 | २१ / २ | 10 | 1 |
| चरण 2 | १० / २ | 5 | 0 |
| चरण 3 | ५ / २ | 2 | 1 |
| चरण 4 | २ / २ | 1 | 0 |
| चरण 5 | 1/2 | 0 | 1 |
दशमलव संख्या - 21 10 = बाइनरी संख्या - 10101 2
ऑक्टल संख्या - 25 8 = बाइनरी संख्या - 10101 2
शॉर्टकट विधि - अष्टाधारी को बाइनरी
कदम
Step 1 - बाइनरी अंकों को तीन (सही से शुरू) के समूहों में विभाजित करें।
Step 2 - तीन बाइनरी अंकों के प्रत्येक समूह को एक अष्टक अंक में परिवर्तित करें।
उदाहरण
बाइनरी नंबर - 10101 2
अष्टक समतुल्य की गणना -
| कदम | बाइनरी संख्या | अष्टक संख्या |
|---|---|---|
| चरण 1 | 10101 2 | 010 101 |
| चरण 2 | 10101 2 | २ 2 ५ 5 |
| चरण 3 | 10101 2 | २५ 8 |
बाइनरी नंबर - 10101 2 = ऑक्टल नंबर - 25 8
शॉर्टकट विधि - ऑक्टल टू बाइनरी
कदम
Step 1 - प्रत्येक ऑक्टल अंक को 3 अंकों के बाइनरी नंबर में परिवर्तित करें (इस रूपांतरण के लिए ऑक्टल अंकों को दशमलव के रूप में माना जा सकता है)।
Step 2 - सभी परिणामी बाइनरी समूहों (प्रत्येक में 3 अंकों का) को एक बाइनरी संख्या में मिलाएं।
उदाहरण
अष्टक संख्या - २५ 8
बाइनरी समतुल्य की गणना -
| कदम | अष्टक संख्या | बाइनरी संख्या |
|---|---|---|
| चरण 1 | २५ 8 | २ १० ५ १० |
| चरण 2 | २५ 8 | 010 2 101 2 |
| चरण 3 | २५ 8 | 010101 2 |
ऑक्टल संख्या - 25 8 = बाइनरी संख्या - 10101 2
शॉर्टकट विधि - हेक्साडेसिमल के लिए बाइनरी
कदम
Step 1 - बाइनरी अंकों को चार (दाएं से शुरू) के समूहों में विभाजित करें।
Step 2 - चार बाइनरी अंकों के प्रत्येक समूह को एक हेक्साडेसिमल प्रतीक में परिवर्तित करें।
उदाहरण
बाइनरी नंबर - 10101 2
हेक्साडेसिमल समतुल्य की गणना -
| कदम | बाइनरी संख्या | हेक्साडेसिमल संख्या |
|---|---|---|
| चरण 1 | 10101 2 | 0001 0101 |
| चरण 2 | 10101 2 | 1 10 5 10 |
| चरण 3 | 10101 2 | १५ १६ |
बाइनरी संख्या - 10101 2 = हेक्साडेसिमल संख्या - 15 16
शॉर्टकट विधि - हेक्साडेसिमल से बाइनरी
कदम
Step 1 - प्रत्येक हेक्साडेसिमल अंक को 4 अंकों के बाइनरी नंबर में परिवर्तित करें (हेक्साडेसिमल अंकों को इस रूपांतरण के लिए दशमलव के रूप में माना जा सकता है)।
Step 2 - सभी परिणामी बाइनरी समूहों (प्रत्येक के 4 अंक) को एक बाइनरी संख्या में मिलाएं।
उदाहरण
हेक्साडेसिमल संख्या - १५ १६
बाइनरी समतुल्य की गणना -
| कदम | हेक्साडेसिमल संख्या | बाइनरी संख्या |
|---|---|---|
| चरण 1 | १५ १६ | 1 10 5 10 |
| चरण 2 | १५ १६ | 0001 2 0101 2 |
| चरण 3 | १५ १६ | 00010101 2 |
हेक्साडेसिमल संख्या - 15 16 = बाइनरी संख्या - 10101 2
कोडिंग में, जब संख्याओं, अक्षरों या शब्दों को प्रतीकों के एक विशिष्ट समूह द्वारा दर्शाया जाता है, तो यह कहा जाता है कि संख्या, अक्षर या शब्द को एन्कोड किया जा रहा है। प्रतीकों के समूह को एक कोड के रूप में कहा जाता है। डिजिटल डेटा को बाइनरी बिट्स के समूह के रूप में दर्शाया, संग्रहीत और प्रेषित किया जाता है। इस समूह को भी कहा जाता हैbinary code। बाइनरी कोड को संख्या के साथ-साथ अल्फ़ान्यूमेरिक पत्र द्वारा दर्शाया जाता है।
बाइनरी कोड के लाभ
निम्नलिखित उन लाभों की सूची है जो बाइनरी कोड प्रदान करता है।
बाइनरी कोड कंप्यूटर अनुप्रयोगों के लिए उपयुक्त हैं।
बाइनरी कोड डिजिटल संचार के लिए उपयुक्त हैं।
यदि हम बाइनरी कोड का उपयोग करते हैं तो बाइनरी कोड डिजिटल सर्किट का विश्लेषण और डिजाइन बनाते हैं।
चूंकि केवल 0 और 1 का उपयोग किया जा रहा है, कार्यान्वयन आसान हो जाता है।
बाइनरी कोड का वर्गीकरण
कोड को मोटे तौर पर चार श्रेणियों में वर्गीकृत किया गया है।
- भारित कोड
- गैर-भारित कोड
- बाइनरी कोडेड दशमलव कोड
- अल्फ़ान्यूमेरिक कोड
- कोड का पता लगाने में त्रुटि
- कोड्स को सुधारने में त्रुटि
भारित कोड
भारित बाइनरी कोड उन बाइनरी कोड हैं जो स्थितिगत वजन सिद्धांत का पालन करते हैं। संख्या की प्रत्येक स्थिति एक विशिष्ट भार का प्रतिनिधित्व करती है। कोड की कई प्रणालियों का उपयोग दशमलव अंकों को 0 के माध्यम से व्यक्त करने के लिए किया जाता है। इन कोडों में प्रत्येक दशमलव अंक को चार बिट्स के समूह द्वारा दर्शाया जाता है।
गैर-भारित कोड
इस प्रकार के बाइनरी कोड में, स्थितिगत भार नहीं सौंपा गया है। गैर-भारित कोड के उदाहरण अतिरिक्त -3 कोड और ग्रे कोड हैं।
अतिरिक्त -3 कोड
अतिरिक्त -3 कोड को XS-3 कोड भी कहा जाता है। यह गैर-भारित कोड है जिसका उपयोग दशमलव संख्याओं को व्यक्त करने के लिए किया जाता है। अतिरिक्त -3 कोड शब्द 8421 बीसीडी कोड शब्द से जोड़े गए हैं (0011) 2 या (3) 10 प्रत्येक कोड वर्ड में 8421 में। अतिरिक्त -3 कोड निम्नानुसार प्राप्त होते हैं -

उदाहरण
ग्रे कोड
यह गैर-भारित कोड है और यह अंकगणित कोड नहीं है। इसका मतलब है कि बिट स्थिति को निर्दिष्ट कोई विशिष्ट वजन नहीं हैं। इसकी एक बहुत ही खास विशेषता है कि, अंजीर में दिखाए अनुसार दशमलव संख्या बढ़ने पर प्रत्येक बार केवल एक बिट बदल जाएगा। जैसे ही एक समय में केवल एक बिट बदलता है, ग्रे कोड को यूनिट दूरी कोड कहा जाता है। ग्रे कोड एक चक्रीय कोड है। अंकगणितीय ऑपरेशन के लिए ग्रे कोड का उपयोग नहीं किया जा सकता है।
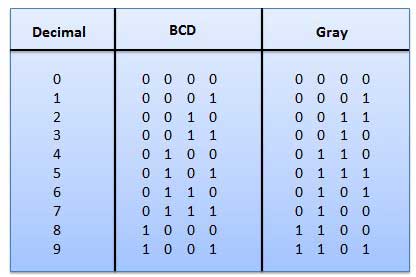
ग्रे कोड का आवेदन
ग्रे कोड शाफ्ट की स्थिति एनकोडर में लोकप्रिय रूप से उपयोग किया जाता है।
एक शाफ्ट स्थिति एनकोडर एक कोड शब्द का उत्पादन करता है जो शाफ्ट की कोणीय स्थिति का प्रतिनिधित्व करता है।
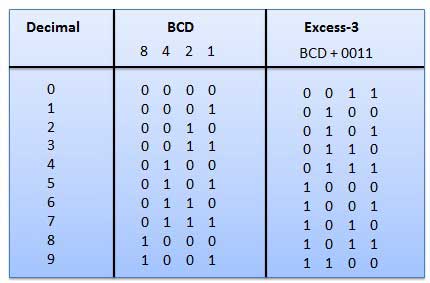
बाइनरी कोडेड डेसीमल (BCD) कोड
इस कोड में प्रत्येक दशमलव अंक को 4-बिट बाइनरी नंबर द्वारा दर्शाया गया है। बीसीडी प्रत्येक दशमलव अंकों को एक बाइनरी कोड के साथ व्यक्त करने का एक तरीका है। बीसीडी में, चार बिट्स के साथ हम सोलह संख्याओं (0000 से 1111) का प्रतिनिधित्व कर सकते हैं। लेकिन बीसीडी कोड में इनमें से केवल दस का उपयोग किया जाता है (0000 से 1001)। शेष छह कोड संयोजन यानी 1010 से 1111 बीसीडी में अमान्य हैं।
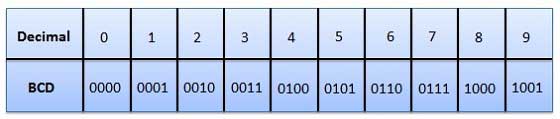
बीसीडी कोड के लाभ
- यह दशमलव प्रणाली के समान है।
- हमें केवल 0 से 9 तक बाइनरी को दशमलव संख्या के बराबर याद रखना होगा।
बीसीडी कोड का नुकसान
बीसीडी के जोड़ और घटाव के अलग-अलग नियम हैं।
बीसीडी अंकगणित थोड़ा अधिक जटिल है।
BCD को दशमलव संख्या का प्रतिनिधित्व करने के लिए बाइनरी की तुलना में अधिक संख्या में बिट्स की आवश्यकता होती है। तो बीसीडी बाइनरी की तुलना में कम कुशल है।
अल्फ़ान्यूमेरिक कोड
एक द्विआधारी अंक या बिट केवल दो प्रतीकों का प्रतिनिधित्व कर सकता है क्योंकि इसमें केवल दो राज्य '0' या '1' हैं। लेकिन यह दो कंप्यूटरों के बीच संचार के लिए पर्याप्त नहीं है क्योंकि संचार के लिए हमें कई और प्रतीकों की आवश्यकता है। इन प्रतीकों को पूंजी और छोटे अक्षरों, 0 से 9 तक की संख्या, विराम चिह्न और अन्य प्रतीकों के साथ 26 अक्षर का प्रतिनिधित्व करना आवश्यक है।
अल्फ़ान्यूमेरिक कोड वे कोड होते हैं जो संख्याओं और अल्फ़ाबेटिक वर्णों का प्रतिनिधित्व करते हैं। अधिकतर ऐसे कोड अन्य वर्णों का भी प्रतिनिधित्व करते हैं जैसे कि प्रतीक और जानकारी को संप्रेषित करने के लिए आवश्यक विभिन्न निर्देश। एक अल्फ़ान्यूमेरिक कोड में कम से कम 10 अंक और वर्णमाला के 26 अक्षर यानी कुल 36 आइटम का प्रतिनिधित्व करना चाहिए। निम्नलिखित तीन अल्फ़ान्यूमेरिक कोड आमतौर पर डेटा प्रतिनिधित्व के लिए उपयोग किए जाते हैं।
- सूचना मानक के लिए अमेरिकी मानक कोड (ASCII)।
- विस्तारित बाइनरी कोडेड डेसीमल इंटरचेंज कोड (EBCDIC)।
- पांच बिट Baudot कोड।
ASCII कोड 7-बिट कोड है जबकि EBCDIC 8-बिट कोड है। ASCII कोड आमतौर पर दुनिया भर में उपयोग किया जाता है जबकि EBCDIC का उपयोग मुख्य रूप से बड़े आईबीएम कंप्यूटरों में किया जाता है।
त्रुटि कोड
डेटा ट्रांसमिशन के दौरान डेटा का पता लगाने और सही करने के लिए बाइनरी कोड तकनीक उपलब्ध हैं।
| एरर कोड | विवरण |
|---|---|
त्रुटि का पता लगाने और सुधार |
त्रुटि का पता लगाने और सुधार कोड तकनीक |
कई विधियाँ या तकनीकें हैं जिनका उपयोग कोड को एक प्रारूप से दूसरे में बदलने के लिए किया जा सकता है। हम यहाँ निम्न प्रदर्शित करेंगे
- बीसीडी रूपांतरण के लिए बाइनरी
- बीसीडी बाइनरी रूपांतरण के लिए
- बीसीडी से एक्सट्रा -3 तक
- अतिरिक्त -3 से बीसीडी
बीसीडी रूपांतरण के लिए बाइनरी
कदम
Step 1 - बाइनरी नंबर को दशमलव में बदलें।
Step 2 - दशमलव संख्या को बीसीडी में बदलें।
उदाहरण - कन्वर्ट (11101) 2 से बीसीडी।
चरण 1 - दशमलव में परिवर्तित करें
बाइनरी नंबर - 11101 2
दशमलव समतुल्य की गणना -
| कदम | बाइनरी संख्या | दशमलव संख्या |
|---|---|---|
| चरण 1 | 11101 2 | ((1 × 2 4 ) + (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 )) 10 |
| चरण 2 | 11101 2 | (१६ + 4 + ४ + ० + १) १० |
| चरण 3 | 11101 2 | २ ९ १० |
बाइनरी नंबर - 11101 2 = दशमलव संख्या - 29 10
चरण 2 - बीसीडी में कनवर्ट करें
दशमलव संख्या - २ ९ १०
बीसीडी समतुल्य गणना। प्रत्येक अंक को चार बाइनरी अंकों के समूहों में बराबर में बदलें।
| कदम | दशमलव संख्या | परिवर्तन |
|---|---|---|
| चरण 1 | २ ९ १० | 0010 2 1001 2 |
| चरण 2 | २ ९ १० | 00101001 बीसीडी |
परिणाम
(11101)2 = (00101001)BCDबीसीडी बाइनरी रूपांतरण के लिए
कदम
Step 1 - BCD नंबर को दशमलव में बदलें।
Step 2 - दशमलव को बाइनरी में बदलें।
उदाहरण - कन्वर्ट (00101001) बीसीडी बाइनरी में।
चरण 1 - बीसीडी में कनवर्ट करें
बीसीडी नंबर - (00101001) बीसीडी
दशमलव समतुल्य की गणना। प्रत्येक चार अंकों को एक समूह में परिवर्तित करें और प्रत्येक समूह के लिए दशमलव बराबर प्राप्त करें।
| कदम | बीसीडी नंबर | परिवर्तन |
|---|---|---|
| चरण 1 | (00101001) बीसीडी | 0010 2 1001 2 |
| चरण 2 | (00101001) बीसीडी | २ १० ९ १० |
| चरण 3 | (00101001) बीसीडी | २ ९ १० |
बीसीडी नंबर - (00101001) बीसीडी = दशमलव संख्या - २ ९ १०
चरण 2 - बाइनरी में कनवर्ट करें
द्विआधारी रूपांतरण के लिए दशमलव के लिए लंबी विभाजन विधि का उपयोग किया।
दशमलव संख्या - २ ९ १०
बाइनरी समतुल्य की गणना -
| कदम | ऑपरेशन | परिणाम | शेष |
|---|---|---|---|
| चरण 1 | २ ९ / २ | 14 | 1 |
| चरण 2 | १४ / २ | 7 | 0 |
| चरण 3 | / २ | 3 | 1 |
| चरण 4 | 3/2 | 1 | 1 |
| चरण 5 | 1/2 | 0 | 1 |
जैसा कि चरण 2 और 4 में उल्लेख किया गया है, अवशेषों को उल्टे क्रम में व्यवस्थित किया जाना है ताकि पहला शेष कम से कम महत्वपूर्ण अंक (एलएसडी) बन जाए और अंतिम शेष सबसे महत्वपूर्ण अंक (एमएसडी) बन जाए।
दशमलव संख्या - 29 10 = बाइनरी संख्या - 11101 2
परिणाम
(00101001)BCD = (11101)2बीसीडी से एक्सट्रा -3 तक
कदम
Step 1 - BCD को दशमलव में बदलें।
Step 2- इस दशमलव संख्या में (3) 10 जोड़ें ।
Step 3 - अतिरिक्त -3 कोड प्राप्त करने के लिए बाइनरी में कनवर्ट करें।
उदाहरण - कन्वर्ट (0110) बीसीडी से एक्सिस -3।
चरण 1 - दशमलव में कनवर्ट करें
(0110) बीसीडी = 6 10
चरण 2 - दशमलव में 3 जोड़ें
(६) १० + (३) १० = (९) १०
चरण 3 - अतिरिक्त -3 में कनवर्ट करें
(९) १० = (१००१) २
परिणाम
(0110)BCD = (1001)XS-3अतिरिक्त -3 से बीसीडी रूपांतरण
कदम
Step 1- संबंधित बीसीडी कोड प्राप्त करने के लिए प्रत्येक 4-बिट के अतिरिक्त 3 अंक से घटाना (0011) 2 ।
उदाहरण - कन्वर्ट (10011010) XS-3 से BCD।
Given XS-3 number = 1 0 0 1 1 0 1 0
Subtract (0011)2 = 1 0 0 1 0 1 1 1
--------------------
BCD = 0 1 1 0 0 1 1 1परिणाम
(10011010)XS-3 = (01100111)BCDघटाव ऑपरेशन को सरल बनाने और तार्किक जोड़तोड़ के लिए डिजिटल कंप्यूटर में पूर्णता का उपयोग किया जाता है। प्रत्येक मूलांक-आर प्रणाली के लिए (मूलांक r संख्या प्रणाली के आधार का प्रतिनिधित्व करता है) दो प्रकार के पूरक होते हैं।
| एस.एन. | पूरक हैं | विवरण |
|---|---|---|
| 1 | मूलांक पूरक | मूलांक पूरक को आर के पूरक के रूप में जाना जाता है |
| 2 | घटा हुआ मूलांक पूरक | मंद मूलांक पूरक को (r-1) के पूरक के रूप में जाना जाता है |
बाइनरी सिस्टम के पूरक
जैसा कि बाइनरी सिस्टम में बेस आर = 2 है। इसलिए बाइनरी सिस्टम के लिए दो प्रकार के कंपल्स 2 के पूरक और 1 के पूरक हैं।
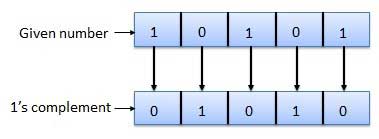
1 का पूरक
1 की संख्या के पूरक को 1 के सभी को 0 में और सभी को 0 के 1 को बदलकर पाया जाता है। इसे पूरक या 1 का पूरक लेना कहा जाता है। 1 के पूरक का उदाहरण इस प्रकार है।
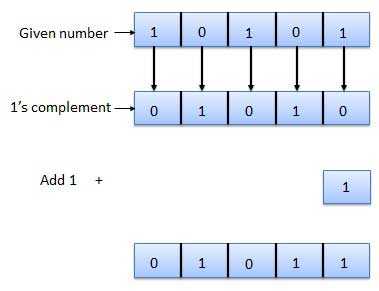
2 का पूरक
बाइनरी नंबर के 2 के पूरक को संख्या के पूरक के 1 के कम से कम महत्वपूर्ण बिट (एलएसबी) में 1 जोड़कर प्राप्त किया जाता है।
2 का पूरक = 1 का पूरक + 1
2 के पूरक का उदाहरण इस प्रकार है।
बाइनरी अंकगणित सभी डिजिटल कंप्यूटर और कई अन्य डिजिटल प्रणाली का आवश्यक हिस्सा है।
बाइनरी एडिशन
यह बाइनरी घटाव, गुणन, विभाजन के लिए एक कुंजी है। बाइनरी जोड़ के चार नियम हैं।
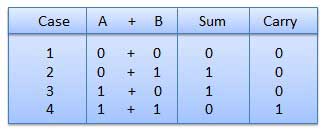
चौथे मामले में, एक द्विआधारी जोड़ एक (1 + 1 = 10) का योग बना रहा है अर्थात 0 दिए गए कॉलम में लिखा है और अगले कॉलम पर 1 ओवर का कैरी है।
उदाहरण - जोड़
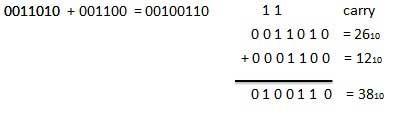
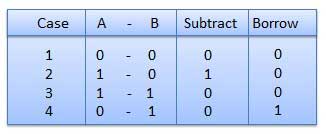
बाइनरी घटाव
Subtraction and Borrow, इन दो शब्दों का उपयोग बाइनरी घटाव के लिए बहुत बार किया जाएगा। बाइनरी घटाव के चार नियम हैं।
उदाहरण - घटाव
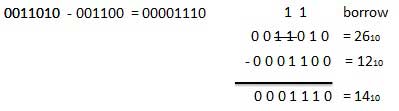
बाइनरी गुणा
बाइनरी गुणा दशमलव गुणन के समान है। यह दशमलव गुणन की तुलना में सरल है क्योंकि इसमें केवल 0s और 1s शामिल होते हैं। बाइनरी गुणा के चार नियम हैं।
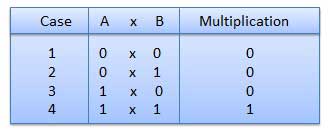
उदाहरण - गुणन

बाइनरी डिवीजन
बाइनरी डिवीजन दशमलव विभाजन के समान है। इसे लंबी विभाजन प्रक्रिया कहा जाता है।
उदाहरण - मंडल

ऑक्टल नंबर सिस्टम
निम्नलिखित एक ऑक्टल संख्या प्रणाली की विशेषताएं हैं।
आठ अंकों का उपयोग करता है, 0,1,2,3,4,5,6,7।
जिसे बेस 8 नंबर सिस्टम भी कहा जाता है।
एक अष्टक संख्या में प्रत्येक स्थिति आधार की एक 0 शक्ति (8) का प्रतिनिधित्व करती है। उदाहरण: 8 ०
एक अष्टक संख्या में अंतिम स्थिति आधार की एक x शक्ति (8) का प्रतिनिधित्व करती है। उदाहरण: 8 x जहां x अंतिम स्थिति का प्रतिनिधित्व करता है - 1।
उदाहरण
अष्टक संख्या - 12570 8
दशमलव समतुल्य की गणना -
| कदम | अष्टक संख्या | दशमलव संख्या |
|---|---|---|
| चरण 1 | 12570 8 | ((1 × 8 4 ) + (2 × 8 3 ) + (5 × 8 2 ) + (7 × 8 1 ) + (0 × 8 0 )) 10 |
| चरण 2 | 12570 8 | (4096 + 1024 + 320 + 56 + 0) 10 |
| चरण 3 | 12570 8 | 5496 10 |
Note −12570 8 को सामान्यतः 12570 लिखा जाता है।
अष्टक जोड़
ऑक्टल जोड़ तालिका के बाद आपको ऑक्टल जोड़ को संभालने में मदद मिलेगी।

इस तालिका का उपयोग करने के लिए, बस इस उदाहरण में उपयोग किए गए निर्देशों का पालन करें: 6 8 और 5 8 जोड़ें । A कॉलम में 6 का पता लगाएं, फिर B कॉलम में 5 खोजें। 'सम' क्षेत्र का वह बिंदु जहाँ ये दो स्तंभ प्रतिच्छेद करते हैं, दो संख्याओं का 'योग' है।
68 + 58 = 138.उदाहरण - जोड़
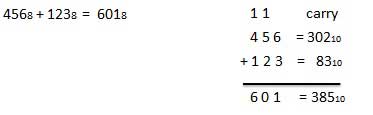
अष्ट घटाव
अष्टक संख्याओं का घटाव किसी अन्य संख्या प्रणाली में संख्याओं के घटाव के समान नियमों का पालन करता है। केवल भिन्नता उधार संख्या में है। दशमलव प्रणाली में, आप 10 10 के समूह को उधार लेते हैं । बाइनरी सिस्टम में, आप 2 10 का एक समूह उधार लेते हैं । अष्टक प्रणाली में आप 8 10 का समूह उधार लेते हैं ।
उदाहरण - घटाव
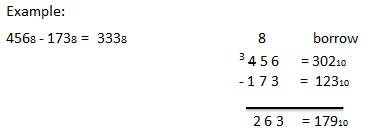
हेक्साडेसिमल नंबर सिस्टम
एक हेक्साडेसिमल संख्या प्रणाली की विशेषताएं निम्नलिखित हैं।
10 अंकों और 6 अक्षरों, 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F का उपयोग करता है।
पत्र 10. ए = 10, बी = 11, सी = 12, डी = 13, ई = 14, एफ = 15 से शुरू होने वाली संख्याओं का प्रतिनिधित्व करते हैं।
जिसे बेस 16 नंबर सिस्टम भी कहा जाता है।
हेक्साडेसिमल संख्या में प्रत्येक स्थिति आधार की 0 शक्ति (16) का प्रतिनिधित्व करती है। उदाहरण - १६ ०
हेक्साडेसिमल संख्या में अंतिम स्थिति आधार की एक x शक्ति (16) का प्रतिनिधित्व करती है। उदाहरण - 16 x जहां x अंतिम स्थिति का प्रतिनिधित्व करता है - 1।
उदाहरण
हेक्साडेसिमल संख्या - 19FDE 16
दशमलव समतुल्य की गणना -
| कदम | हेक्साडेसिमल संख्या | दशमलव संख्या |
|---|---|---|
| चरण 1 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (F × 16 2 ) + (D × 16 1 ) + (E × 16 0 )) 10 |
| चरण 2 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (15 × 16 2 ) + (13 × 16 1 ) + (14 × 16 0 )) 10 |
| चरण 3 | 19FDE 16 | (65536 + 36864 + 3840 + 208 + 14) 10 |
| चरण 4 | 19FDE 16 | 106462 10 |
Note −19FDE 16 को आम तौर पर 19FDE के रूप में लिखा जाता है।
हेक्साडेसिमल जोड़
हेक्साडेसिमल जोड़ तालिका का अनुसरण करने से आपको हेक्साडेसिमल जोड़ को संभालने में बहुत मदद मिलेगी।
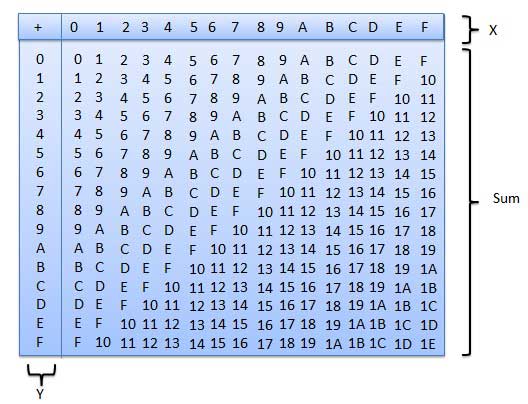
इस तालिका का उपयोग करने के लिए, बस इस उदाहरण में उपयोग किए गए निर्देशों का पालन करें - A 16 और 5 16 जोड़ें । X कॉलम में A की स्थिति जानें फिर Y कॉलम में 5 का पता लगाएं। 'सम' क्षेत्र का वह बिंदु जहाँ ये दो स्तंभ प्रतिच्छेद करते हैं, दो संख्याओं का योग है।
A16 + 516 = F16.उदाहरण - जोड़
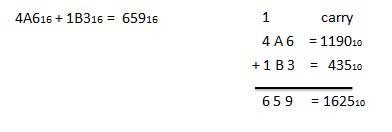
हेक्साडेसिमल घटाव
हेक्साडेसिमल संख्याओं का घटाव किसी अन्य संख्या प्रणाली में संख्याओं के घटाव के समान नियमों का पालन करता है। केवल भिन्नता उधार संख्या में है। दशमलव प्रणाली में, आप 10 10 के समूह को उधार लेते हैं । बाइनरी सिस्टम में, आप 2 10 का एक समूह उधार लेते हैं । हेक्साडेसिमल प्रणाली में आप 16 10 का समूह उधार लेते हैं ।
उदाहरण - घटाव

बूलियन बीजगणित का उपयोग डिजिटल (तर्क) सर्किट का विश्लेषण और सरल बनाने के लिए किया जाता है। यह केवल द्विआधारी संख्याओं का उपयोग करता है अर्थात 0 और 1. इसे भी कहा जाता हैBinary Algebra या logical Algebra। बूलियन बीजगणित द्वारा आविष्कार किया गया थाGeorge Boole 1854 में।
बूलियन बीजगणित में नियम
बुलियन बीजगणित में उपयोग किए जाने वाले महत्वपूर्ण नियम निम्नलिखित हैं।
प्रयुक्त चर के केवल दो मूल्य हो सकते हैं। उच्च के लिए बाइनरी 1 और एलओडब्ल्यू के लिए बाइनरी 0।
एक चर के पूरक को एक ओवरबार (-) द्वारा दर्शाया गया है। इस प्रकार, चर बी के पूरक के रूप में दर्शाया गया है
। इस प्रकार यदि B = 0 तो = 1 और B = 1 तो
= 1 और B = 1 तो = 0।
= 0।
चरों की ओरिंग उनके बीच एक प्लस (+) चिन्ह द्वारा दर्शायी जाती है। उदाहरण के लिए A, B, C की ओरिंग को A + B + C के रूप में दर्शाया गया है।
दो या दो से अधिक वेरिएबल की लॉजिकल एंडिंग का प्रतिनिधित्व उनके बीच एक बिंदी लिखकर किया जाता है जैसे एबीसी कुछ समय के लिए डॉट एबीसी की तरह छोड़ा जा सकता है।
बूलियन कानून
छह प्रकार के बूलियन कानून हैं।
विनिमेय कानून
कोई भी बाइनरी ऑपरेशन जो निम्नलिखित अभिव्यक्ति को संतुष्ट करता है, को कम्यूटेटिव ऑपरेशन कहा जाता है।

कम्यूटेटिव कानून कहता है कि चर के अनुक्रम को बदलने से लॉजिक सर्किट के आउटपुट पर कोई प्रभाव नहीं पड़ता है।
सहयोगी कानून
इस कानून में कहा गया है कि जिस क्रम में तर्क संचालन किया जाता है वह अप्रासंगिक है क्योंकि उनका प्रभाव समान है।
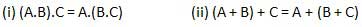
वितरण संबंधी कानून
वितरण कानून निम्नलिखित स्थिति बताता है।
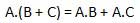
और कानून
ये कानून AND ऑपरेशन का उपयोग करते हैं। इसलिए उन्हें कहा जाता हैAND कानून।
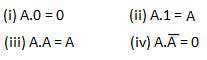
या कानून
ये कानून OR ऑपरेशन का उपयोग करते हैं। इसलिए उन्हें कहा जाता हैOR कानून।
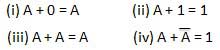
चालान कानून
यह कानून NOT ऑपरेशन का उपयोग करता है। उलटा कानून बताता है कि एक चर का दोहराव मूल चर में ही परिणाम है।
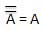
महत्वपूर्ण बूलियन सिद्धांत
निम्नलिखित कुछ महत्वपूर्ण बूलियन प्रमेय हैं।
| बूलियन फ़ंक्शन / प्रमेय | विवरण |
|---|---|
बूलियन फ़ंक्शंस |
बूलियन फ़ंक्शंस और एक्सप्रेशंस, के-मैप और नंद गेट्स अहसास |
डी मॉर्गन के सिद्धांत |
डी मॉर्गन के प्रमेय 1 और प्रमेय 2 |
लॉजिक गेट किसी भी डिजिटल सिस्टम के मूल बिल्डिंग ब्लॉक हैं। यह एक इलेक्ट्रॉनिक सर्किट होता है जिसमें एक या एक से अधिक इनपुट होते हैं और केवल एक आउटपुट होता है। इनपुट और आउटपुट के बीच संबंध ए पर आधारित हैcertain logic। इसके आधार पर, लॉजिक गेट्स को AND गेट, OR गेट, NOT गेट आदि नाम दिए गए हैं।
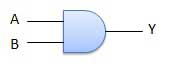
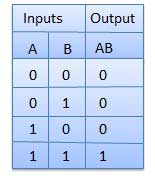
और गेट
एक सर्किट जो AND और ऑपरेशन करता है, उसे चित्र में दिखाया गया है। इसमें n इनपुट (n> = 2) और एक आउटपुट है।

तर्क आरेख
सच्ची तालिका
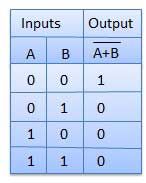
या गेट
एक सर्किट जो OR ऑपरेशन करता है, उसे चित्र में दिखाया गया है। इसमें n इनपुट (n> = 2) और एक आउटपुट है।
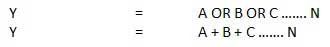
तर्क आरेख
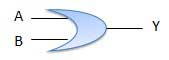
सच्ची तालिका
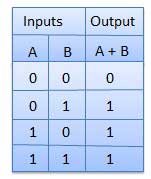
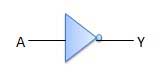
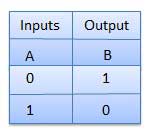
गेट नहीं
गेट के रूप में भी नहीं जाना जाता है Inverter। इसमें एक इनपुट A और एक आउटपुट Y है।
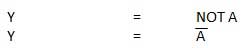
तर्क आरेख
सच्ची तालिका
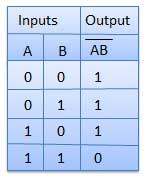
नंद द्वार
एक NOT-AND ऑपरेशन को NAND ऑपरेशन के रूप में जाना जाता है। इसमें n इनपुट (n> = 2) और एक आउटपुट है।
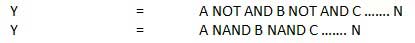
तर्क आरेख
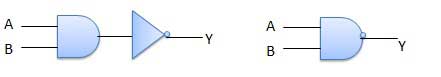
सच्ची तालिका
NOR गेट
NOT-OR ऑपरेशन को NOR ऑपरेशन के रूप में जाना जाता है। इसमें n इनपुट (n> = 2) और एक आउटपुट है।
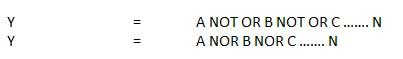
तर्क आरेख
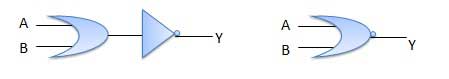
सच्ची तालिका
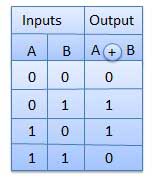
XOR गेट
XOR या Ex-OR गेट एक विशेष प्रकार का गेट है। इसका उपयोग आधे योजक, पूर्ण योजक और घटाव में किया जा सकता है। अनन्य-OR गेट को EX-OR गेट या कुछ समय X-OR गेट के रूप में संक्षिप्त किया जाता है। इसमें n इनपुट (n> = 2) और एक आउटपुट है।
तर्क आरेख
सच्ची तालिका
XNOR गेट
XNOR गेट एक विशेष प्रकार का गेट है। इसका उपयोग आधे योजक, पूर्ण योजक और घटाव में किया जा सकता है। अनन्य-NOR गेट को EX-NOR गेट या कभी-कभी X-NOR गेट के रूप में संक्षिप्त किया जाता है। इसमें n इनपुट (n> = 2) और एक आउटपुट है।
तर्क आरेख
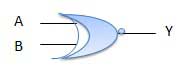
सच्ची तालिका
कॉम्बिनेशन सर्किट एक ऐसा सर्किट होता है, जिसमें हम सर्किट में अलग-अलग गेट्स को जोड़ते हैं, उदाहरण के लिए एनकोडर, डिकोडर, मल्टीप्लेक्स और डेमूलिप्लेक्सर। कॉम्बीनेशन सर्किट की कुछ विशेषताएं निम्नलिखित हैं -
किसी भी समय कॉम्बिनेशन सर्किट का आउटपुट केवल इनपुट टर्मिनलों पर मौजूद स्तरों पर निर्भर करता है।
कॉम्बिनेशन सर्किट किसी भी मेमोरी का उपयोग नहीं करता है। सर्किट की वर्तमान स्थिति पर इनपुट की पिछली स्थिति का कोई प्रभाव नहीं पड़ता है।
एक कॉम्बीनेशन सर्किट में n संख्या में इनपुट और मीटर संख्या में आउटपुट हो सकते हैं।
खंड आरेख
हम कुछ महत्वपूर्ण कॉम्बिनेशन सर्किटों का विवरण निम्नानुसार करने जा रहे हैं।
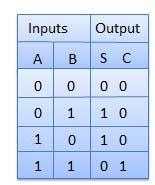
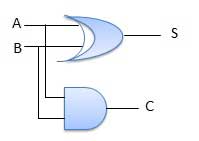
आधा योजक
आधा योजक दो इनपुट और दो आउटपुट के साथ एक संयोजन तर्क सर्किट है। आधा योजक सर्किट दो सिंगल बिट बाइनरी नंबर ए और बी को जोड़ने के लिए डिज़ाइन किया गया है। यह दो के अलावा के लिए बुनियादी बिल्डिंग ब्लॉक हैsingleबिट संख्या। इस सर्किट में दो आउटपुट हैंcarry तथा sum।
खंड आरेख

सच्ची तालिका
सर्किट आरेख
पूर्ण योजक
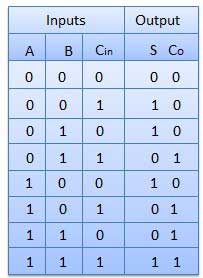
आधा योजक सर्किट की खामी को दूर करने के लिए पूर्ण योजक विकसित किया गया है। यह दो एक-बिट संख्या A और B जोड़ सकता है और c ले जा सकता है। पूर्ण योजक एक तीन इनपुट और दो आउटपुट कॉम्बिनेशन सर्किट है।
खंड आरेख

सच्ची तालिका
सर्किट आरेख
एन-बिट समानांतर योजक
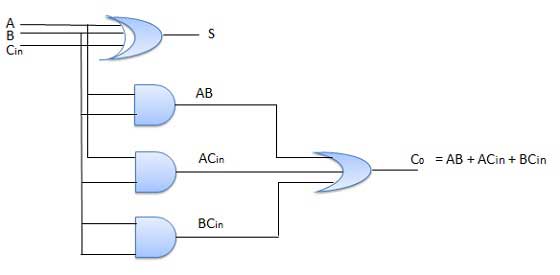
फुल अडर कैरी इनपुट के साथ केवल दो सिंगल डिजिट बाइनरी नंबर जोड़ने में सक्षम है। लेकिन व्यावहारिक रूप से हमें द्विआधारी संख्याओं को जोड़ने की जरूरत है जो कि केवल एक बिट की तुलना में बहुत अधिक हैं। दो एन-बिट बाइनरी संख्याओं को जोड़ने के लिए हमें एन-बिट समानांतर योजक का उपयोग करने की आवश्यकता है। यह कैस्केड में कई पूर्ण योजक का उपयोग करता है। पिछले पूर्ण योजक का कैरी आउटपुट अगले पूर्ण योजक के इनपुट को ले जाने के लिए जुड़ा हुआ है।
4 बिट समानांतर योजक
ब्लॉक आरेख में, ए 0 और बी 0 चार बिट शब्दों के एलएसबी का प्रतिनिधित्व करते हैं ए और बी। इसलिए पूर्ण योजक -0 सबसे कम चरण है। इसलिए अपनी सी में स्थायी रूप से 0. कनेक्शन के आराम के लिए बनाया गया है एन-बिट समानांतर योजक के उन लोगों के चित्र में दिखाया गया है के रूप में बिल्कुल वैसा ही कर रहे हैं। चार बिट समानांतर योजक एक बहुत ही सामान्य तर्क सर्किट है।
खंड आरेख

एन-बिट समानांतर घटाव
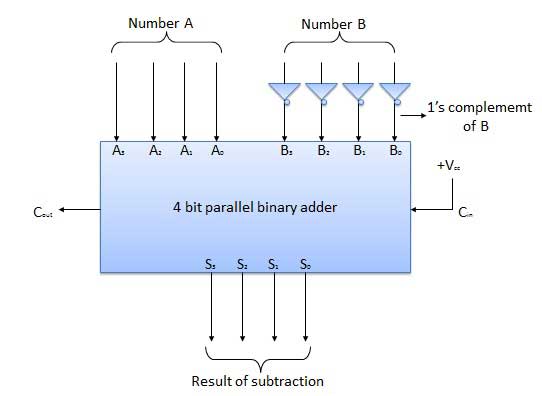
घटाव को संख्या के 1 या 2 के पूरक को घटाकर ले जाया जा सकता है। उदाहरण के लिए हम 1 से या 2 से B के A. के पूरक को जोड़कर घटाव (AB) कर सकते हैं। इसका मतलब है कि हम बाइनरी घटाव को करने के लिए एक बाइनरी योजक का उपयोग कर सकते हैं।
4 बिट पैरेलल सबट्रैक्टर
घटाया जाने वाला नंबर (B) सबसे पहले इनवर्टर से होकर गुजरता है। 4-बिट योजक फिर A और 2 को B का पूरक जोड़कर घटाव उत्पन्न करता है। एस 3 एस 2 एस 1 एस 0 बाइनरी घटाव (एबी) के परिणाम का प्रतिनिधित्व करता है और आउटपुट सी बाहर ले जाने के परिणाम की ध्रुवीयता का प्रतिनिधित्व करता है। यदि एक> तो बी अदालत = 0 और बाइनरी रूप (एबी) का परिणाम तो सी बाहर = 1 और परिणाम 2 के पूरक रूप में है।
Block diagram
Half Subtractors
Half subtractor is a combination circuit with two inputs and two outputs (difference and borrow). It produces the difference between the two binary bits at the input and also produces an output (Borrow) to indicate if a 1 has been borrowed. In the subtraction (A-B), A is called as Minuend bit and B is called as Subtrahend bit.
Truth Table
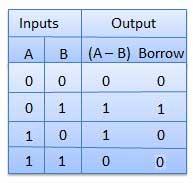
Circuit Diagram
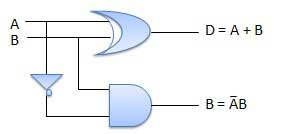
Full Subtractors
The disadvantage of a half subtractor is overcome by full subtractor. The full subtractor is a combinational circuit with three inputs A,B,C and two output D and C'. A is the 'minuend', B is 'subtrahend', C is the 'borrow' produced by the previous stage, D is the difference output and C' is the borrow output.
Truth Table
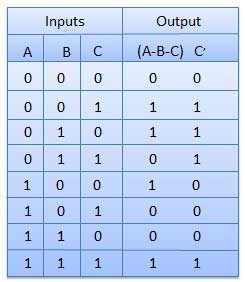
Circuit Diagram
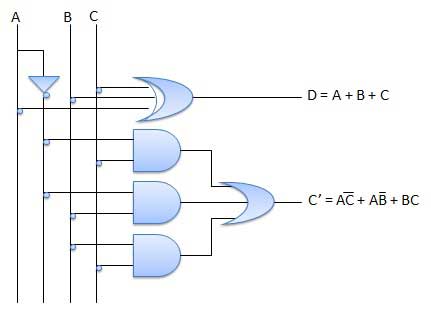
Multiplexers
Multiplexer is a special type of combinational circuit. There are n-data inputs, one output and m select inputs with 2m = n. It is a digital circuit which selects one of the n data inputs and routes it to the output. The selection of one of the n inputs is done by the selected inputs. Depending on the digital code applied at the selected inputs, one out of n data sources is selected and transmitted to the single output Y. E is called the strobe or enable input which is useful for the cascading. It is generally an active low terminal that means it will perform the required operation when it is low.
Block diagram
Multiplexers come in multiple variations
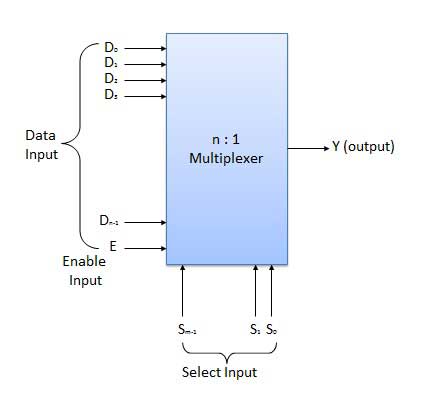
- 2 : 1 multiplexer
- 4 : 1 multiplexer
- 16 : 1 multiplexer
- 32 : 1 multiplexer
Block Diagram
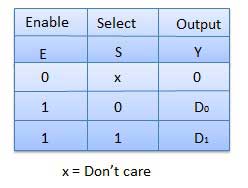
Truth Table
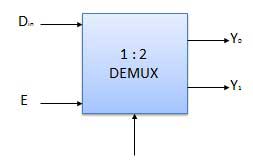
Demultiplexers
A demultiplexer performs the reverse operation of a multiplexer i.e. it receives one input and distributes it over several outputs. It has only one input, n outputs, m select input. At a time only one output line is selected by the select lines and the input is transmitted to the selected output line. A de-multiplexer is equivalent to a single pole multiple way switch as shown in fig.
Demultiplexers comes in multiple variations.
- 1 : 2 demultiplexer
- 1 : 4 demultiplexer
- 1 : 16 demultiplexer
- 1 : 32 demultiplexer
Block diagram
Truth Table
Decoder
A decoder is a combinational circuit. It has n input and to a maximum m = 2n outputs. Decoder is identical to a demultiplexer without any data input. It performs operations which are exactly opposite to those of an encoder.
Block diagram

Examples of Decoders are following.
- Code converters
- BCD to seven segment decoders
- Nixie tube decoders
- Relay actuator
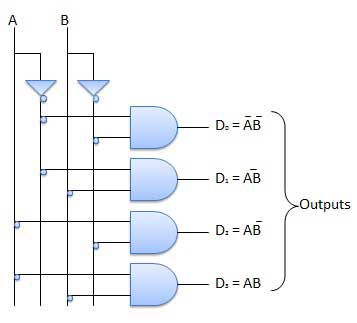
2 to 4 Line Decoder
The block diagram of 2 to 4 line decoder is shown in the fig. A and B are the two inputs where D through D are the four outputs. Truth table explains the operations of a decoder. It shows that each output is 1 for only a specific combination of inputs.
Block diagram

Truth Table

Logic Circuit
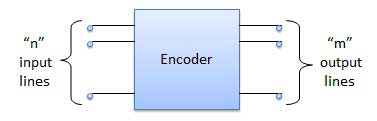
Encoder
Encoder is a combinational circuit which is designed to perform the inverse operation of the decoder. An encoder has n number of input lines and m number of output lines. An encoder produces an m bit binary code corresponding to the digital input number. The encoder accepts an n input digital word and converts it into an m bit another digital word.
Block diagram
Examples of Encoders are following.
- Priority encoders
- Decimal to BCD encoder
- Octal to binary encoder
- Hexadecimal to binary encoder
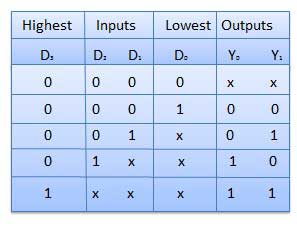
Priority Encoder
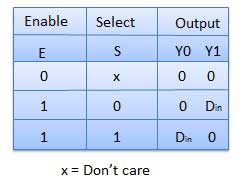
This is a special type of encoder. Priority is given to the input lines. If two or more input line are 1 at the same time, then the input line with highest priority will be considered. There are four input D0, D1, D2, D3 and two output Y0, Y1. Out of the four input D3 has the highest priority and D0 has the lowest priority. That means if D3 = 1 then Y1 Y1 = 11 irrespective of the other inputs. Similarly if D3 = 0 and D2 = 1 then Y1 Y0 = 10 irrespective of the other inputs.
Block diagram

Truth Table
Logic Circuit
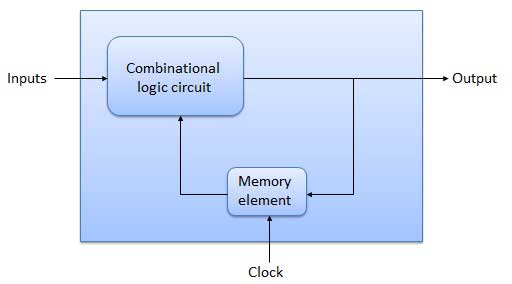
The combinational circuit does not use any memory. Hence the previous state of input does not have any effect on the present state of the circuit. But sequential circuit has memory so output can vary based on input. This type of circuits uses previous input, output, clock and a memory element.
Block diagram
Flip Flop
Flip flop is a sequential circuit which generally samples its inputs and changes its outputs only at particular instants of time and not continuously. Flip flop is said to be edge sensitive or edge triggered rather than being level triggered like latches.
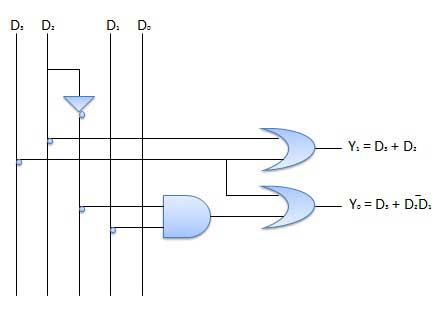
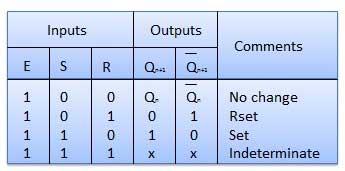
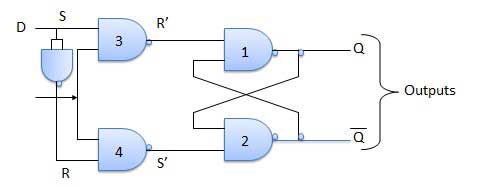
S-R Flip Flop
It is basically S-R latch using NAND gates with an additional enable input. It is also called as level triggered SR-FF. For this, circuit in output will take place if and only if the enable input (E) is made active. In short this circuit will operate as an S-R latch if E = 1 but there is no change in the output if E = 0.
Block Diagram
Circuit Diagram
Truth Table
Operation
| S.N. | Condition | Operation |
|---|---|---|
| 1 | S = R = 0 : No change | If S = R = 0 then output of NAND gates 3 and 4 are forced to become 1. Hence R' and S' both will be equal to 1. Since S' and R' are the input of the basic S-R latch using NAND gates, there will be no change in the state of outputs. |
| 2 | S = 0, R = 1, E = 1 | Since S = 0, output of NAND-3 i.e. R' = 1 and E = 1 the output of NAND-4 i.e. S' = 0. Hence Qn+1 = 0 and Qn+1 bar = 1. This is reset condition. |
| 3 | S = 1, R = 0, E = 1 | Output of NAND-3 i.e. R' = 0 and output of NAND-4 i.e. S' = 1. Hence output of S-R NAND latch is Qn+1 = 1 and Qn+1 bar = 0. This is the reset condition. |
| 4 | S = 1, R = 1, E = 1 | As S = 1, R = 1 and E = 1, the output of NAND gates 3 and 4 both are 0 i.e. S' = R' = 0. Hence the Race condition will occur in the basic NAND latch. |
Master Slave JK Flip Flop
Master slave JK FF is a cascade of two S-R FF with feedback from the output of second to input of first. Master is a positive level triggered. But due to the presence of the inverter in the clock line, the slave will respond to the negative level. Hence when the clock = 1 (positive level) the master is active and the slave is inactive. Whereas when clock = 0 (low level) the slave is active and master is inactive.
Circuit Diagram
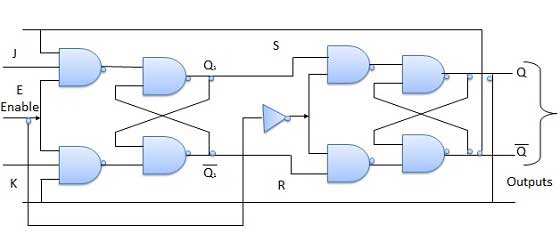
Truth Table
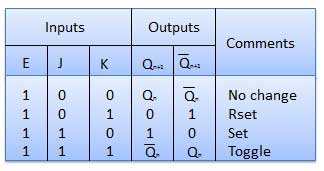
Operation
| S.N. | Condition | Operation |
|---|---|---|
| 1 | J = K = 0 (No change) | When clock = 0, the slave becomes active and master is inactive. But since the S and R inputs have not changed, the slave outputs will also remain unchanged. Therefore outputs will not change if J = K =0. |
| 2 | J = 0 and K = 1 (Reset) | Clock = 1 − Master active, slave inactive. Therefore outputs of the master become Q1 = 0 and Q1 bar = 1. That means S = 0 and R =1. Clock = 0 − Slave active, master inactive. Therefore outputs of the slave become Q = 0 and Q bar = 1. Again clock = 1 − Master active, slave inactive. Therefore even with the changed outputs Q = 0 and Q bar = 1 fed back to master, its output will be Q1 = 0 and Q1 bar = 1. That means S = 0 and R = 1. Hence with clock = 0 and slave becoming active the outputs of slave will remain Q = 0 and Q bar = 1. Thus we get a stable output from the Master slave. |
| 3 | J = 1 and K = 0 (Set) | Clock = 1 − Master active, slave inactive. Therefore outputs of the master become Q1 = 1 and Q1 bar = 0. That means S = 1 and R =0. Clock = 0 − Slave active, master inactive. Therefore outputs of the slave become Q = 1 and Q bar = 0. Again clock = 1 − then it can be shown that the outputs of the slave are stabilized to Q = 1 and Q bar = 0. |
| 4 | J = K = 1 (Toggle) | Clock = 1 − Master active, slave inactive. Outputs of master will toggle. So S and R also will be inverted. Clock = 0 − Slave active, master inactive. Outputs of slave will toggle. These changed output are returned back to the master inputs. But since clock = 0, the master is still inactive. So it does not respond to these changed outputs. This avoids the multiple toggling which leads to the race around condition. The master slave flip flop will avoid the race around condition. |
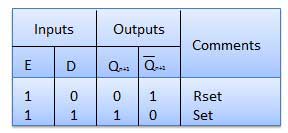
Delay Flip Flop / D Flip Flop
Delay Flip Flop or D Flip Flop is the simple gated S-R latch with a NAND inverter connected between S and R inputs. It has only one input. The input data is appearing at the output after some time. Due to this data delay between i/p and o/p, it is called delay flip flop. S and R will be the complements of each other due to NAND inverter. Hence S = R = 0 or S = R = 1, these input condition will never appear. This problem is avoid by SR = 00 and SR = 1 conditions.
Block Diagram
Circuit Diagram
Truth Table
Operation
| S.N. | Condition | Operation |
|---|---|---|
| 1 | E = 0 | Latch is disabled. Hence no change in output. |
| 2 | E = 1 and D = 0 | If E = 1 and D = 0 then S = 0 and R = 1. Hence irrespective of the present state, the next state is Qn+1 = 0 and Qn+1 bar = 1. This is the reset condition. |
| 3 | E = 1 and D = 1 | If E = 1 and D = 1, then S = 1 and R = 0. This will set the latch and Qn+1 = 1 and Qn+1 bar = 0 irrespective of the present state. |
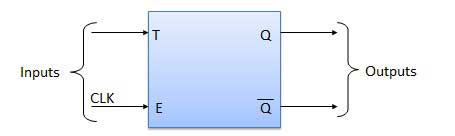
Toggle Flip Flop / T Flip Flop
Toggle flip flop is basically a JK flip flop with J and K terminals permanently connected together. It has only input denoted by T as shown in the Symbol Diagram. The symbol for positive edge triggered T flip flop is shown in the Block Diagram.
Symbol Diagram
Block Diagram
Truth Table
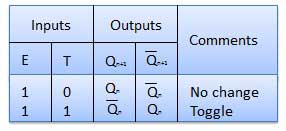
Operation
| S.N. | Condition | Operation |
|---|---|---|
| 1 | T = 0, J = K = 0 | The output Q and Q bar won't change |
| 2 | T = 1, J = K = 1 | Output will toggle corresponding to every leading edge of clock signal. |
Flip-flop is a 1 bit memory cell which can be used for storing the digital data. To increase the storage capacity in terms of number of bits, we have to use a group of flip-flop. Such a group of flip-flop is known as a Register. The n-bit register will consist of n number of flip-flop and it is capable of storing an n-bit word.
The binary data in a register can be moved within the register from one flip-flop to another. The registers that allow such data transfers are called as shift registers. There are four mode of operations of a shift register.
- सीरियल इनपुट सीरियल आउटपुट
- सीरियल इनपुट समानांतर आउटपुट
- समानांतर इनपुट सीरियल आउटपुट
- समानांतर इनपुट समानांतर आउटपुट
सीरियल इनपुट सीरियल आउटपुट
सभी फ्लिप-फ्लॉप शुरू में रीसेट स्थिति में होना चाहिए अर्थात क्यू 3 = क्यू 2 = क्यू 1 = क्यू 0 = 0. यदि चार बिट बाइनरी नंबर 1 1 1 की प्रविष्टि रजिस्टर में की गई है, तो यह संख्या होनी चाहिए पर लागू किया गयाDinएलएसबी बिट के साथ पहले आवेदन किया। FF-3 यानी D 3 का D इनपुट सीरियल डेटा इनपुट से जुड़ा हैDin। एफएफ -3 यानी क्यू 3 का आउटपुट अगले फ्लिप-फ्लॉप यानी डी 2 और इसी तरह के इनपुट से जुड़ा है ।
खंड आरेख
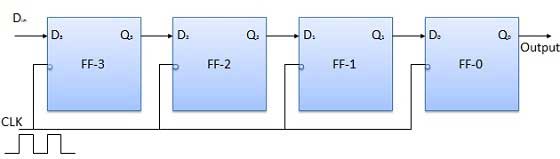
ऑपरेशन
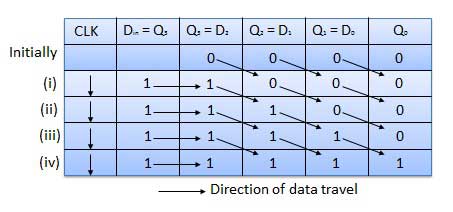
क्लॉक सिग्नल के आवेदन से पहले, क्यू 3 क्यू 2 क्यू 1 क्यू 0 = 0000 और डी में प्रवेश करने के लिए एलएसबी बिट को लागू करें । तो D में = D 3 = 1. घड़ी लगाओ। घड़ी के पहले गिरने वाले किनारे पर, एफएफ -3 सेट किया गया है, और रजिस्टर में संग्रहीत शब्द क्यू 3 क्यू 2 क्यू 1 क्यू 1 = 1000 है।
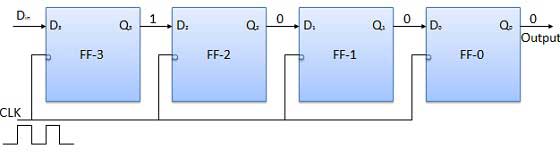
अगले बिट को D में लागू करें । तो डी = 1 में । जैसे ही घड़ी के अगले नकारात्मक किनारे हिट होते हैं, एफएफ -2 सेट हो जाएगा और संग्रहीत शब्द क्यू 3 क्यू 2 क्यू 1 क्यू 0 = 1100 में बदल जाएगा।
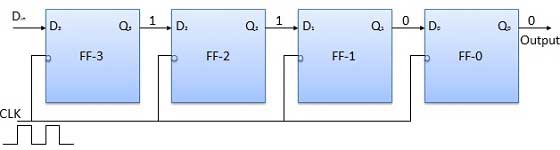
स्टोर किए जाने वाले अगले बिट को 1 से डी में लागू करें । घड़ी की नाड़ी लगाओ। जैसे ही तीसरी नकारात्मक घड़ी की बढ़त हिट होती है, एफएफ -1 सेट हो जाएगा और आउटपुट क्यू 3 क्यू 2 क्यू 1 क्यू 0 = 1110 में संशोधित किया जाएगा ।
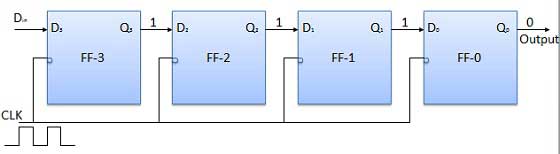
डी के साथ इसी तरह के = 1 और चौथे नकारात्मक घड़ी किनारे पहुंचने के साथ, रजिस्टर में संग्रहीत शब्द क्यू है 3 क्यू 2 क्यू 1 क्यू 0 = 1111।
सच्ची तालिका
waveforms

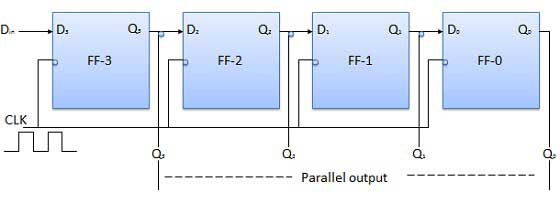
सीरियल इनपुट समानांतर आउटपुट
इस तरह के ऑपरेशन में, डेटा को क्रमिक रूप से दर्ज किया जाता है और समानांतर फैशन में निकाला जाता है।
डेटा को थोड़ा-थोड़ा करके लोड किया जाता है। जब तक डेटा लोड हो रहा है आउटपुट आउटपुट अक्षम हैं।
जैसे ही डेटा लोडिंग पूरी हो जाती है, सभी फ्लिप-फ्लॉप में उनके आवश्यक डेटा होते हैं, आउटपुट सक्षम होते हैं ताकि सभी लोड किए गए डेटा को एक ही समय में सभी आउटपुट लाइनों पर उपलब्ध कराया जा सके।
एक चार बिट शब्द को लोड करने के लिए 4 घड़ी चक्र की आवश्यकता होती है। इसलिए SIPO मोड के संचालन की गति SISO मोड के समान है।
खंड आरेख
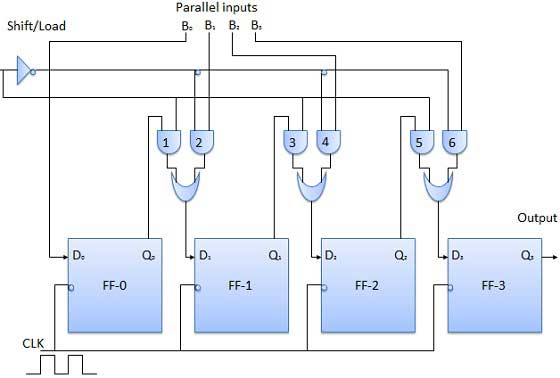
समानांतर इनपुट सीरियल आउटपुट (PISO)
डेटा बिट्स समानांतर फैशन में दर्ज किए गए हैं।
नीचे दिखाया गया सर्किट चार समानांतर इनपुट सीरियल आउटपुट रजिस्टर है।
पिछले फ्लिप फ्लॉप का आउटपुट कॉम्बिनेशन सर्किट के माध्यम से अगले एक के इनपुट से जुड़ा हुआ है।
बाइनरी इनपुट शब्द बी 0 , बी 1 , बी 2 , बी 3 को एक ही कॉम्बिनेशन सर्किट के बावजूद लागू किया जाता है।
दो तरीके हैं जिनमें यह सर्किट काम कर सकता है - शिफ्ट मोड या लोड मोड।
लोड मोड
जब शिफ्ट / लोड बार लाइन कम (0) होती है, और AND 2, 4 और 6 सक्रिय हो जाते हैं, तो वे बी 1 , बी 2 , बी 3 बिट्स को संबंधित फ्लिप-फ्लॉप से गुजरेंगे । घड़ी के निचले किनारे पर, बाइनरी इनपुट बी 0 , बी 1 , बी 2 , बी 3 संबंधित फ्लिप-फ्लॉप में लोड हो जाएंगे। इस प्रकार समानांतर लोडिंग होती है।
शिफ्ट मोड
जब शिफ्ट / लोड बार लाइन कम (1) होती है, तो AND गेट 2, 4 और 6 निष्क्रिय हो जाते हैं। इसलिए डेटा का समानांतर लोडिंग असंभव हो जाता है। लेकिन AND गेट 1,3 और 5 सक्रिय हो जाते हैं। इसलिए घड़ी की दालों के अनुप्रयोग पर डेटा को बाएं से दाएं बिट में स्थानांतरित करना। इस प्रकार सीरियल आउट ऑपरेशन में समानांतर जगह लेता है।
खंड आरेख
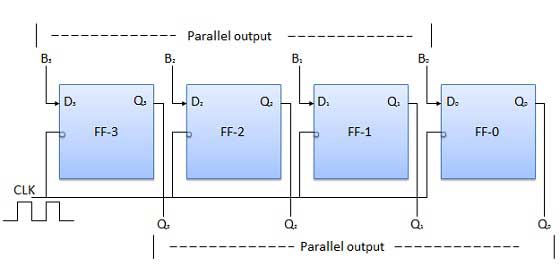
समानांतर इनपुट समानांतर आउटपुट (PIPO)
इस मोड में, 4 बिट बाइनरी इनपुट बी 0 , बी 1 , बी 2 , बी 3 चार फ्लिप-फ्लॉप के क्रमशः डेटा इनपुट डी 0 , डी 1 , डी 2 , डी 3 पर लागू होते हैं। जैसे ही एक नकारात्मक घड़ी का किनारा लगाया जाता है, इनपुट बाइनरी बिट्स को एक साथ फ्लिप-फ्लॉप में लोड किया जाएगा। लोड किए गए बिट्स आउटपुट साइड में एक साथ दिखाई देंगे। सभी बिट्स को लोड करने के लिए केवल क्लॉक पल्स आवश्यक है।
खंड आरेख
द्विदिश शिफ्ट रजिस्टर
यदि एक बाइनरी नंबर को एक स्थिति से छोड़ दिया जाता है, तो यह मूल संख्या को 2 से गुणा करने के बराबर है। इसी तरह यदि एक बाइनरी नंबर को एक स्थिति से दाएं स्थानांतरित किया जाता है, तो यह मूल संख्या को 2 से विभाजित करने के बराबर है।
इसलिए यदि हम दिए गए बाइनरी नंबर को गुणा और विभाजित करने के लिए शिफ्ट रजिस्टर का उपयोग करना चाहते हैं, तो हमें डेटा को बाईं या दाईं दिशा में स्थानांतरित करने में सक्षम होना चाहिए।
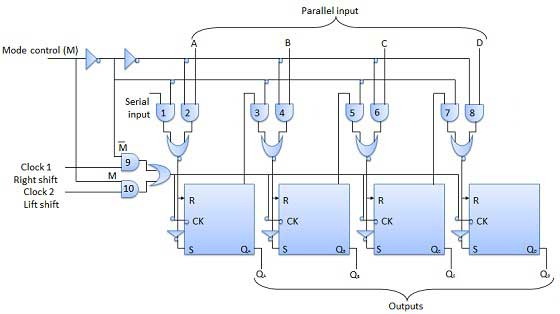
इस तरह के रजिस्टर को द्वि-दिशात्मक रजिस्टर कहा जाता है। एक चार बिट द्वि-दिशात्मक पारी रजिस्टर अंजीर में दिखाया गया है।
सीरियल राइट शिफ्ट डेटा इनपुट डीआर, और सीरियल लेफ्ट डेटा इनपुट डीएल के साथ-साथ एक मोड सेलेक्ट इनपुट (एम) नाम से दो सीरियल इनपुट हैं।
खंड आरेख
ऑपरेशन
| एस.एन. | स्थिति | ऑपरेशन |
|---|---|---|
| 1 | With M = 1 − Shift right operation | यदि M = 1 है, तो AND गेट 1, 3, 5 और 7 सक्षम हैं जबकि शेष और गेट 2, 4, 6 और 8 अक्षम हो जाएंगे। डी आर पर डेटा घड़ी दालों के आवेदन पर FF-3 से FF-0 से थोड़ा सा दाएं बिट में स्थानांतरित कर दिया गया है। इस प्रकार एम = 1 के साथ हमें सीरियल राइट शिफ्ट ऑपरेशन मिलता है। |
| 2 | With M = 0 − Shift left operation | जब मोड नियंत्रण M 0 से जुड़ा होता है तो AND 2, 4, 6 और 8 सक्षम होते हैं जबकि 1, 3, 5 और 7 अक्षम होते हैं। D L का डेटा घड़ी की दालों के अनुप्रयोग पर FF-0 से FF-3 तक थोड़ा-थोड़ा छोड़ दिया जाता है। इस प्रकार M = 0 से हमें सीरियल राइट शिफ्ट ऑपरेशन मिलता है। |
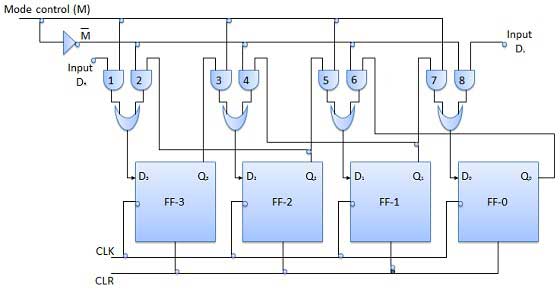
यूनिवर्सल शिफ्ट रजिस्टर
एक शिफ्ट रजिस्टर जो डेटा को केवल एक दिशा में शिफ्ट कर सकता है, एक यूनी-डायरेक्शनल शिफ्ट रजिस्टर कहलाता है। एक शिफ्ट रजिस्टर जो दोनों दिशाओं में डेटा को शिफ्ट कर सकता है, द्वि-दिशात्मक शिफ्ट रजिस्टर कहलाता है। एक ही तर्क को लागू करते हुए, एक शिफ्ट रजिस्टर जो डेटा को दोनों दिशाओं में स्थानांतरित कर सकता है और साथ ही इसे समान रूप से लोड कर सकता है, एक सार्वभौमिक शिफ्ट रजिस्टर के रूप में जाना जाता है। शिफ्ट रजिस्टर निम्नलिखित ऑपरेशन करने में सक्षम है -
- समानांतर लोडिंग
- वाम शिफ्टिंग
- राइट शिफ्टिंग
मोड कंट्रोल इनपुट समानांतर लोडिंग ऑपरेशन के लिए लॉजिक 1 से जुड़ा है जबकि यह सीरियल शिफ्टिंग के लिए 0 से जुड़ा है। जमीन से जुड़े मोड कंट्रोल पिन के साथ, यूनिवर्सल शिफ्ट रजिस्टर एक द्वि-दिशात्मक रजिस्टर के रूप में कार्य करता है। सीरियल लेफ्ट ऑपरेशन के लिए, इनपुट को सीरियल इनपुट पर लागू किया जाता है जो चित्र में दिखाए गए AND-गेट -1 पर जाता है। जबकि शिफ्ट राइट ऑपरेशन के लिए, सीरियल इनपुट को डी इनपुट पर लागू किया जाता है।
खंड आरेख
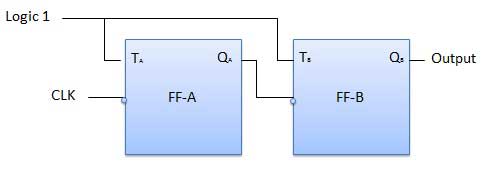
काउंटर एक अनुक्रमिक सर्किट है। एक डिजिटल सर्किट जो एक गिनती दालों के लिए उपयोग किया जाता है, काउंटर के रूप में जाना जाता है। काउंटर फ्लिप-फ्लॉप का सबसे व्यापक अनुप्रयोग है। यह फ्लिप-फ्लॉप का एक समूह है जिसमें एक घड़ी सिग्नल लगाया जाता है। काउंटर दो प्रकार के होते हैं।
- अतुल्यकालिक या तरंग काउंटर।
- तुल्यकालिक काउंटर।
अतुल्यकालिक या तरंग काउंटर
2-बिट रिपल अप काउंटर का लॉजिक आरेख चित्र में दिखाया गया है। टॉगल (T) फ्लिप-फ्लॉप का उपयोग किया जा रहा है। लेकिन हम JK और फ्लिप के साथ JK फ्लिप-फ्लॉप को भी स्थायी रूप से तर्क से जोड़कर उपयोग कर सकते हैं। बाहरी फ्लिप फ्लिप-फ्लॉप A और Q के क्लॉक इनपुट पर लागू होता है और अगले फ्लिप-फ्लॉप के क्लॉक इनपुट पर एक आउटपुट लागू होता है। एफएफ बी।
तार्किक आरेख
ऑपरेशन
| एस.एन. | स्थिति | ऑपरेशन |
|---|---|---|
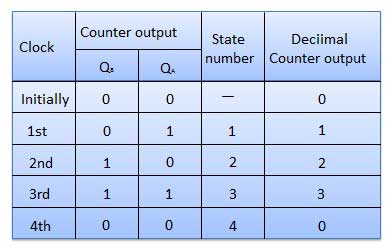
| 1 | Initially let both the FFs be in the reset state | प्रारंभ में Q B Q A = 00 |
| 2 | After 1st negative clock edge | जैसे ही पहली नकारात्मक घड़ी का किनारा लगाया जाता है, एफएफ-ए विल टॉगल और क्यू ए 1 के बराबर होगा। Q A FF-B के क्लॉक इनपुट से जुड़ा है। चूंकि क्यू ए 0 से 1 में बदल गया है, इसलिए इसे एफएफ-बी द्वारा सकारात्मक घड़ी बढ़त के रूप में माना जाता है। क्यू बी में कोई बदलाव नहीं है क्योंकि एफएफ-बी एक नकारात्मक बढ़त है जो एफएफ को ट्रिगर करता है। Q B Q A = 01 पहली घड़ी नाड़ी के बाद। |
| 3 | After 2nd negative clock edge | दूसरी नकारात्मक घड़ी के किनारे पर, एफएफ-ए टॉगल फिर से और क्यू ए = 0। क्यू ए में परिवर्तन एफएफ-बी के लिए नकारात्मक घड़ी के रूप में कार्य करता है। तो यह भी टॉगल करेगा, और क्यू बी 1 होगा। दूसरी घड़ी की नाड़ी के बाद Q B Q A = 10। |
| 4 | After 3rd negative clock edge | 3rd नेगेटिव क्लॉक एज के आने पर, FF-A फिर से टॉगल करता है और Q A 0 से 1 हो जाता है। चूंकि यह एक सकारात्मक बदलाव है, एफएफ-बी इसका जवाब नहीं देता है और निष्क्रिय रहता है। तो क्यू बी नहीं बदलता है और 1 के बराबर जारी रहता है। तीसरी घड़ी नाड़ी के बाद Q B Q A = 11। |
| 5 | After 4th negative clock edge | 4th नेगेटिव क्लॉक एज के आने पर, FF-A फिर से टॉगल करता है और Q A 0 से 1 हो जाता है। क्यू ए में यह नकारात्मक परिवर्तन एफएफ-बी के लिए घड़ी नाड़ी के रूप में कार्य करता है। इसलिए यह Q B को 1 से 0 तक बदल देता है । चौथी घड़ी पल्स के बाद Q B Q A = 00। |
सच्ची तालिका
तुल्यकालिक काउंटर
यदि "घड़ी" दालों को एक साथ एक काउंटर में सभी फ्लिप-फ्लॉप पर लागू किया जाता है, तो ऐसे काउंटर को सिंक्रोनस काउंटर कहा जाता है।
2-बिट सिंक्रोनस काउंटर
एफएफ-ए के जे ए और के ए इनपुट तर्क 1 से बंधे हैं। इसलिए एफएफ-ए टॉगल फ्लिप-फ्लॉप के रूप में काम करेगा। J B और K B इनपुट Q A से जुड़े हैं ।
तार्किक आरेख

ऑपरेशन
| एस.एन. | स्थिति | ऑपरेशन |
|---|---|---|
| 1 | Initially let both the FFs be in the reset state | प्रारंभ में Q B Q A = 00। |
| 2 | After 1st negative clock edge | जैसे ही पहला नकारात्मक घड़ी का किनारा लगाया जाता है, एफएफ-ए विल टॉगल और क्यू ए 0 से 1 में बदल जाएगा। लेकिन नकारात्मक घड़ी के किनारे के अनुप्रयोग के तत्काल पर, क्यू ए , जे बी = के बी = 0. इसलिए एफएफ-बी अपनी स्थिति को नहीं बदलेगा। तो Q B 0 रहेगा। Q B Q A = 01 पहली घड़ी नाड़ी के बाद। |
| 3 | After 2nd negative clock edge | दूसरी नकारात्मक घड़ी के बढ़त के आगमन पर, एफएफ-ए टॉगल फिर से और क्यू ए 1 से 0 में बदल जाता है। लेकिन इस इंस्टेंट Q A पर 1. तो J B = K B = 1 और FF-B टॉगल होगा। इसलिए Q B 0 से 1 तक बदलता है। दूसरी घड़ी की नाड़ी के बाद Q B Q A = 10। |
| 4 | After 3rd negative clock edge | तीसरे गिरने वाली घड़ी के किनारे के आवेदन पर, एफएफ-ए 0 से 1 तक टॉगल करेगा लेकिन एफएफ-बी के लिए राज्य का कोई परिवर्तन नहीं है। तीसरी घड़ी नाड़ी के बाद Q B Q A = 11। |
| 5 | After 4th negative clock edge | अगली घड़ी की नाड़ी के आवेदन पर, क्यू ए 1 से 0 तक बदल जाएगा क्योंकि क्यू बी भी 1 से 0 तक बदल जाएगा। चौथी घड़ी पल्स के बाद Q B Q A = 00। |
काउंटरों का वर्गीकरण
गणना की प्रगति के तरीके के आधार पर, तुल्यकालिक या अतुल्यकालिक काउंटरों को निम्नानुसार वर्गीकृत किया जाता है -
- ऊपर काउंटर
- नीचे काउंटर
- ऊपर / नीचे काउंटर
यूपी / नीचे काउंटर
UP / DOWN काउंटर प्राप्त करने के लिए अप काउंटर और डाउन काउंटर को एक साथ जोड़ा जाता है। एक मोड नियंत्रण (एम) इनपुट भी ऊपर या नीचे मोड का चयन करने के लिए प्रदान किया जाता है। अप / डाउन ऑपरेशन को प्राप्त करने के लिए फ्लिप-फ्लॉप के प्रत्येक जोड़े के बीच एक कॉम्बिनेशन सर्किट को डिजाइन और उपयोग करने की आवश्यकता होती है।
- ऊपर / नीचे काउंटरों का प्रकार
- UP / DOWN ripple काउंटर
- यूपी / नीचे तुल्यकालिक काउंटर
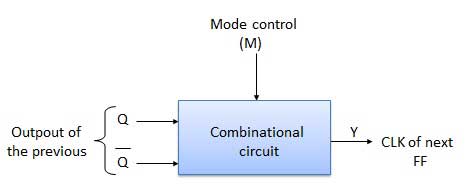
उत्तर प्रदेश / रिप्पल काउंटर
UP / DOWN ripple काउंटर में सभी FFs टॉगल मोड में काम करते हैं। तो या तो T फ्लिप-फ्लॉप या JK फ्लिप-फ्लॉप का उपयोग किया जाना है। एलएसबी फ्लिप-फ्लॉप सीधे घड़ी प्राप्त करता है। लेकिन हर दूसरे एफएफ को घड़ी पिछले एफएफ के आउटपुट (क्यू = क्यू बार) से प्राप्त होती है।
UP counting mode (M=0)- पूर्ववर्ती एफएफ का क्यू आउटपुट अगले चरण की घड़ी से जुड़ा हुआ है यदि ऊपर की गिनती प्राप्त की जानी है। इस मोड के लिए, मोड सेलेक्ट इनपुट M लॉजिक 0 (M = 0) पर है।
DOWN counting mode (M=1)- यदि एम = 1 है, तो पूर्ववर्ती एफएफ का क्यू बार आउटपुट अगले एफएफ से जुड़ा हुआ है। यह काउंटिंग मोड में काउंटर को संचालित करेगा।
उदाहरण
3-बिट बाइनरी अप / डाउन रिपल काउंटर।
3-बिट - इसलिए तीन एफएफ की आवश्यकता होती है।
UP / DOWN - इसलिए एक मोड कंट्रोल इनपुट आवश्यक है।
रिपल अप काउंटर के लिए, पूर्ववर्ती एफएफ का क्यू आउटपुट अगले एक के क्लॉक इनपुट से जुड़ा हुआ है।
रिपल अप काउंटर के लिए, पूर्ववर्ती एफएफ का क्यू आउटपुट अगले एक के क्लॉक इनपुट से जुड़ा हुआ है।
रिपल डाउन काउंटर के लिए, पूर्ववर्ती एफएफ का क्यू बार आउटपुट अगले एक के क्लॉक इनपुट से जुड़ा हुआ है।
बता दें कि पूर्ववर्ती एफएफ के क्यू और क्यू बार आउटपुट को मोड कंट्रोल इनपुट एम द्वारा नियंत्रित किया जाता है जैसे कि, यदि एम = 0, यूपी की गिनती। इसलिए Q को CLK से कनेक्ट करें। यदि M = 1 है, तो गिनती गिनें। तो क्यू बार को सीएलके से कनेक्ट करें।
खंड आरेख
सच्ची तालिका
ऑपरेशन
| एस.एन. | स्थिति | ऑपरेशन |
|---|---|---|
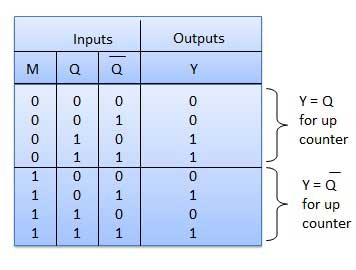
| 1 | Case 1 − With M = 0 (Up counting mode) | यदि M = 0 और M बार = 1 है, तो AND 1 और 3 का अनुमान लगाता है। सक्षम हो जाएगा, जबकि 2 और 4 गेट अक्षम हो जाएंगे। इसलिए क्यू ए एफएफ-बी के क्लॉक इनपुट से जुड़ जाता है और क्यू बी एफएफ-सी के क्लॉक इनपुट से जुड़ जाता है। ये कनेक्शन सामान्य अप काउंटर के लिए समान हैं। इस प्रकार एम = 0 के साथ सर्किट एक अप काउंटर के रूप में काम करता है। |
| 2 | Case 2: With M = 1 (Down counting mode) | यदि M = 1 है, तो अंजीर में 2 और 4 गेट करें। सक्षम हैं, जबकि गेट 1 और 3 अक्षम हैं। इसलिए Q A बार FF-B के क्लॉक इनपुट से जुड़ जाता है और Q B बार FF-C के क्लॉक इनपुट से जुड़ जाता है। ये कनेक्शन एक डाउन काउंटर का उत्पादन करेंगे। इस प्रकार एम = 1 के साथ सर्किट डाउन काउंटर के रूप में काम करता है। |
मापांक काउंटर (MOD-N काउंटर)
2-बिट रिपल काउंटर को MOD-4 काउंटर और 3-बिट रिपल काउंटर को MOD-8 काउंटर के रूप में कहा जाता है। तो सामान्य तौर पर, एन-बिट रिपल काउंटर को मोडुलो-एन काउंटर कहा जाता है। जहां, एमओडी नंबर = 2 एन ।
मापांक का प्रकार
- 2-बिट अप या डाउन (MOD-4)
- 3-बिट अप या डाउन (MOD-8)
- 4-बिट अप या डाउन (MOD-16)
काउंटरों का आवेदन
- फ्रीक्वेंसी काउंटर
- डिजिटल घड़ी
- समय का मापन
- A से D कन्वर्टर
- फ्रीक्वेंसी डिवाइडर सर्किट
- डिजिटल त्रिकोणीय तरंग जनरेटर।
एक स्मृति मानव मस्तिष्क के समान है। इसका इस्तेमाल डाटा और इंस्ट्रक्शन को स्टोर करने के लिए किया जाता है। कंप्यूटर की मेमोरी कंप्यूटर में स्टोरेज स्पेस होती है जहाँ डेटा को प्रोसेस करना होता है और प्रोसेसिंग के लिए आवश्यक निर्देश संग्रहीत होते हैं।
मेमोरी को बड़ी संख्या में छोटे भागों में विभाजित किया गया है। प्रत्येक भाग को एक सेल कहा जाता है। प्रत्येक स्थान या सेल का एक अनूठा पता होता है जो शून्य से मेमोरी साइज माइनस एक में भिन्न होता है।
उदाहरण के लिए यदि कंप्यूटर में 64k शब्द हैं, तो इस मेमोरी यूनिट में 64 * 1024 = 65536 मेमोरी स्थान है। इन स्थानों का पता 0 से 65535 तक भिन्न है।
मेमोरी मुख्य रूप से दो प्रकार की होती है
Internal Memory - कैश मेमोरी और प्राथमिक / मुख्य मेमोरी
External Memory - मैग्नेटिक डिस्क / ऑप्टिकल डिस्क आदि।
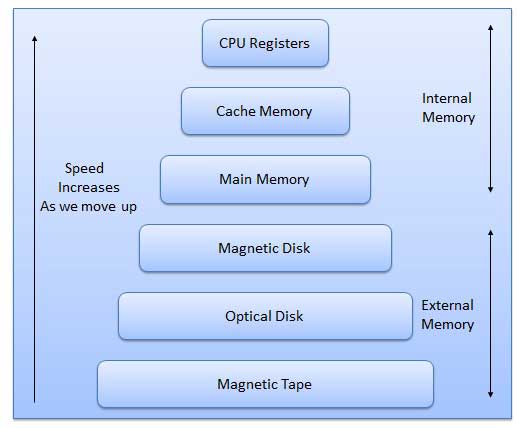
स्मृति पदानुक्रम की विशेषताएँ निम्नलिखित हैं जब हम ऊपर से नीचे जाते हैं।
- भंडारण के संदर्भ में क्षमता बढ़ जाती है।
- प्रति बिट भंडारण की लागत घट जाती है।
- सीपीयू द्वारा मेमोरी की पहुंच की आवृत्ति घट जाती है।
- सीपीयू द्वारा एक्सेस टाइम बढ़ता है।
राम
डेटा, प्रोग्राम और प्रोग्राम रिजल्ट को स्टोर करने के लिए एक RAM सीपीयू की आंतरिक मेमोरी का गठन करती है। यह पढ़ने / लिखने की मेमोरी है। इसे रैंडम एक्सेस मेमोरी (RAM) कहा जाता है।
चूंकि RAM में पहुंच का समय उस शब्द के पते से स्वतंत्र होता है, जो कि मेमोरी के अंदर प्रत्येक स्टोरेज लोकेशन को अन्य स्थान तक पहुंचने में उतना ही आसान है और उतनी ही मात्रा में समय लेता है। हम रैंडम और बेहद तेज मेमोरी में पहुंच सकते हैं लेकिन यह काफी महंगा भी हो सकता है।
RAM अस्थिर है, अर्थात जब हम कंप्यूटर बंद करते हैं या यदि कोई बिजली की विफलता होती है, तो उसमें संग्रहीत डेटा खो जाता है। इसलिए, अक्सर कंप्यूटर के साथ एक बैकअप निर्बाध बिजली प्रणाली (यूपीएस) का उपयोग किया जाता है। रैम छोटा है, दोनों के भौतिक आकार के संदर्भ में और डेटा की मात्रा में।
RAM दो प्रकार की होती है
- स्टेटिक रैम (SRAM)
- गतिशील रैम (DRAM)
स्टेटिक रैम (SRAM)
शब्द staticइंगित करता है कि मेमोरी अपनी सामग्री को तब तक बरकरार रखती है जब तक बिजली लागू रहती है। हालांकि, अस्थिर प्रकृति के कारण बिजली के नीचे जाने पर डेटा खो जाता है। SRAM चिप्स 6-ट्रांजिस्टर के मैट्रिक्स का उपयोग करते हैं और कोई कैपेसिटर नहीं। ट्रांजिस्टर को रिसाव को रोकने के लिए बिजली की आवश्यकता नहीं होती है, इसलिए SRAM को नियमित रूप से ताज़ा करने की आवश्यकता नहीं होती है।
मैट्रिक्स में अतिरिक्त स्थान के कारण, SRAM DRAM की तुलना में अधिक मात्रा में भंडारण स्थान का उपयोग करता है, इस प्रकार विनिर्माण लागत अधिक हो जाती है।
स्टैटिक रैम का उपयोग कैश मेमोरी के रूप में किया जाता है जो बहुत तेज और छोटी होनी चाहिए।
गतिशील रैम (DRAM)
DRAM, SRAM के विपरीत, लगातार होना चाहिए refreshedइसके लिए डेटा को बनाए रखने के लिए। यह मेमोरी को रिफ्रेश सर्किट पर रखकर किया जाता है जो डेटा को प्रति सेकंड कई सौ बार फिर से लिखता है। DRAM का इस्तेमाल ज्यादातर सिस्टम मेमोरी के लिए किया जाता है क्योंकि यह सस्ती और छोटी होती है। सभी DRAM मेमोरी सेल से बने होते हैं। ये कोशिकाएँ एक संधारित्र और एक ट्रांजिस्टर से बनी होती हैं।
रोम
ROM का मतलब Read Only Memory है। वह मेमोरी जिससे हम केवल पढ़ सकते हैं लेकिन उस पर नहीं लिख सकते। इस प्रकार की मेमोरी गैर-वाष्पशील होती है। जानकारी निर्माण के दौरान ऐसी यादों में स्थायी रूप से संग्रहीत होती है।
एक ROM, कंप्यूटर को चालू करने के लिए ऐसे निर्देश को संग्रहीत करता है जब बिजली को चालू किया जाता है, इस ऑपरेशन को बूटस्ट्रैप कहा जाता है। ROM चिप का उपयोग केवल कंप्यूटर में ही नहीं बल्कि वाशिंग मशीन और माइक्रोवेव ओवन जैसी अन्य इलेक्ट्रॉनिक वस्तुओं में भी किया जाता है।
निम्नलिखित रॉम के विभिन्न प्रकार हैं -
MROM (मुखौटा रस्क)
बहुत पहले रोम हार्ड-वायर्ड डिवाइस थे जिसमें डेटा या निर्देशों का पूर्व-प्रोग्राम सेट होता था। इस तरह के ROM को नकाबपोश ROM के नाम से जाना जाता है। यह सस्ती रॉम है।
PROM (प्रोग्रामेबल रीड ओनली मेमोरी)
PROM केवल पढ़ने योग्य मेमोरी है जिसे केवल एक बार उपयोगकर्ता द्वारा संशोधित किया जा सकता है। उपयोगकर्ता एक रिक्त PROM खरीदता है और एक PROM प्रोग्रामर का उपयोग करके वांछित सामग्री में प्रवेश करता है। PROM चिप के अंदर छोटे फ़्यूज़ होते हैं जिन्हें प्रोग्रामिंग के दौरान जलाया जाता है। इसे केवल एक बार ही प्रोग्राम किया जा सकता है और यह इरेज़ेबल नहीं है।
EPROM (इरेज़ेबल और प्रोग्रामेबल रीड ओनली मेमोरी)
EPROM को 40 मिनट तक की अवधि के लिए अल्ट्रा-वायलेट प्रकाश में उजागर करके मिटाया जा सकता है। आमतौर पर, EPROM इरेज़र इस फ़ंक्शन को प्राप्त करता है। प्रोग्रामिंग के दौरान एक विद्युत चार्ज एक अछूता गेट क्षेत्र में फंस जाता है। चार्ज को दस साल से अधिक समय तक बरकरार रखा जाता है क्योंकि चार्ज में कोई लीकेज पथ नहीं होता है। इस चार्ज को मिटाने के लिए, अल्ट्रा-वॉयलेट लाइट को क्वार्ट्ज क्रिस्टल विंडो (ढक्कन) से गुजारा जाता है। अल्ट्रा-वायलेट लाइट के संपर्क में आने से यह चार्ज समाप्त हो जाता है। सामान्य उपयोग के दौरान क्वार्ट्ज ढक्कन को स्टिकर के साथ सील कर दिया जाता है।
EEPROM (विद्युत रूप से इरेज़ेबल और प्रोग्रामेबल रीड ओनली मेमोरी)
EEPROM को प्रोग्राम किया जाता है और विद्युत रूप से मिटा दिया जाता है। इसे लगभग दस हज़ार बार मिटाया और दोबारा बनाया जा सकता है। इरेज़िंग और प्रोग्रामिंग दोनों लगभग 4 से 10 एमएस (मिलीसेकंड) लेते हैं। EEPROM में, किसी भी स्थान को चुनिंदा रूप से मिटाया और प्रोग्राम किया जा सकता है। पूरे चिप को मिटाने के बजाय EEPROM को एक बार में एक बाइट मिटाया जा सकता है। इसलिए, री-प्रोग्रामिंग की प्रक्रिया लचीली लेकिन धीमी है।
सीरियल एक्सेस मेमोरी
अनुक्रमिक पहुंच का मतलब है कि सिस्टम को मेमोरी एड्रेस की शुरुआत से स्टोरेज डिवाइस को खोजना होगा, जब तक कि उसे डेटा का आवश्यक टुकड़ा नहीं मिल जाता। मेमोरी डिवाइस जो इस तरह के एक्सेस को सपोर्ट करता है, उसे सेक्शनल एक्सेस मेमोरी या सीरियल एक्सेस मेमोरी कहा जाता है। मैग्नेटिक टेप सीरियल एक्सेस मेमोरी का एक उदाहरण है।
डायरेक्ट एक्सेस मेमोरी
डायरेक्ट एक्सेस मेमोरी या रैंडम एक्सेस मेमोरी, उन स्थितियों को संदर्भित करता है जिसमें एक सिस्टम सीधे उस जानकारी पर जा सकता है जो उपयोगकर्ता चाहता है। मेमोरी डिवाइस जो इस तरह के एक्सेस को सपोर्ट करता है उसे डायरेक्ट एक्सेस मेमोरी कहा जाता है। चुंबकीय डिस्क, ऑप्टिकल डिस्क प्रत्यक्ष पहुंच स्मृति के उदाहरण हैं।
कैश मेमरी
कैश मेमोरी बहुत ही हाई स्पीड सेमीकंडक्टर मेमोरी है जो CPU को गति प्रदान कर सकती है। यह सीपीयू और मुख्य मेमोरी के बीच बफर के रूप में कार्य करता है। इसका उपयोग डेटा और प्रोग्राम के उन हिस्सों को रखने के लिए किया जाता है जो सीपीयू द्वारा सबसे अधिक बार उपयोग किए जाते हैं। डेटा और प्रोग्राम के हिस्से, डिस्क से कैश मेमोरी में ऑपरेटिंग सिस्टम द्वारा स्थानांतरित किए जाते हैं, जहां से सीपीयू उन्हें एक्सेस कर सकता है।
लाभ
- कैश मेमोरी मुख्य मेमोरी से तेज है।
- यह मुख्य मेमोरी की तुलना में कम एक्सेस समय का उपभोग करता है।
- यह उस कार्यक्रम को संग्रहीत करता है जिसे थोड़े समय के भीतर निष्पादित किया जा सकता है।
- यह अस्थायी उपयोग के लिए डेटा संग्रहीत करता है।
नुकसान
- कैशे मेमोरी की क्षमता सीमित है।
- यह बहुत महंगा है।
वर्चुअल मेमोरी एक तकनीक है जो उन प्रक्रियाओं के निष्पादन की अनुमति देती है जो स्मृति में पूरी तरह से उपलब्ध नहीं हैं। इस योजना का मुख्य दृश्य लाभ यह है कि कार्यक्रम भौतिक मेमोरी से बड़े हो सकते हैं। वर्चुअल मेमोरी भौतिक मेमोरी से उपयोगकर्ता की तार्किक मेमोरी का पृथक्करण है।
यह पृथक्करण प्रोग्रामर के लिए एक बहुत बड़ी आभासी स्मृति प्रदान करने की अनुमति देता है जब केवल एक छोटी भौतिक स्मृति उपलब्ध होती है। निम्नलिखित परिस्थितियां हैं, जब पूरे कार्यक्रम को मुख्य मेमोरी में पूरी तरह से लोड करने की आवश्यकता नहीं होती है।
उपयोगकर्ता लिखित त्रुटि हैंडलिंग दिनचर्या का उपयोग केवल तभी किया जाता है जब डेटा या गणना में कोई त्रुटि हुई हो।
एक कार्यक्रम के कुछ विकल्प और सुविधाओं का उपयोग शायद ही कभी किया जा सकता है।
कई तालिकाओं को पता स्थान की एक निश्चित मात्रा में असाइन किया गया है, भले ही तालिका की केवल थोड़ी मात्रा का उपयोग किया जाता है।
एक प्रोग्राम को निष्पादित करने की क्षमता जो केवल आंशिक रूप से मेमोरी में है, कई लाभों का मुकाबला करेगा।
प्रत्येक उपयोगकर्ता प्रोग्राम को मेमोरी में लोड या स्वैप करने के लिए I / O की कम संख्या की आवश्यकता होगी।
एक प्रोग्राम अब उपलब्ध भौतिक स्मृति की मात्रा से विवश नहीं होगा।
प्रत्येक उपयोगकर्ता प्रोग्राम कम भौतिक मेमोरी ले सकता है, सीपीयू उपयोग और थ्रूपुट में इसी वृद्धि के साथ, अधिक कार्यक्रम उसी समय चलाए जा सकते हैं।
सहायक स्मृति
सहायक मेमोरी मुख्य मेमोरी की तुलना में आकार में बहुत बड़ी है लेकिन धीमी है। यह आम तौर पर सिस्टम प्रोग्राम, इंस्ट्रक्शन और डेटा फाइलों को स्टोर करता है। इसे द्वितीयक स्मृति के रूप में भी जाना जाता है। मुख्य मेमोरी क्षमता से अधिक होने की स्थिति में इसे एक अतिप्रवाह / आभासी मेमोरी के रूप में भी इस्तेमाल किया जा सकता है। माध्यमिक यादों को एक प्रोसेसर द्वारा सीधे एक्सेस नहीं किया जा सकता है। पहले सहायक मेमोरी का डेटा / सूचना मुख्य मेमोरी में स्थानांतरित की जाती है और फिर उस जानकारी को सीपीयू द्वारा एक्सेस किया जा सकता है। सहायक मेमोरी के लक्षण निम्नलिखित हैं -
Non-volatile memory - बिजली कट जाने पर डेटा नहीं खोता है।
Reusable - डेटा स्थायी आधार पर द्वितीयक भंडारण में रहता है जब तक कि इसे उपयोगकर्ता द्वारा अधिलेखित या हटा नहीं दिया जाता है।
Reliable - सेकेंडरी स्टोरेज डिवाइस में डाटा ज्यादा होने के कारण सेकेंडरी स्टोरेज में डाटा सुरक्षित रहता है।
Convenience - कंप्यूटर सॉफ्टवेयर की सहायता से, अधिकृत लोग डेटा का शीघ्र पता लगा सकते हैं और उसका उपयोग कर सकते हैं।
Capacity - सेकेंडरी स्टोरेज कई डिस्क के सेट में बड़ी मात्रा में डेटा स्टोर कर सकता है।
Cost - प्राथमिक मेमोरी की तुलना में टेप या डिस्क पर डेटा स्टोर करना बहुत कम महंगा है।
माइक्रोप्रोसेसिंग यूनिट केंद्रीय प्रसंस्करण इकाई, पारंपरिक कंप्यूटर में उपयोग किए जाने वाले सीपीयू का पर्याय है। माइक्रोप्रोसेसर (MPU) एक उपकरण या उपकरणों के समूह के रूप में कार्य करता है जो निम्नलिखित कार्य करते हैं।
- बाह्य उपकरणों के साथ संवाद
- समय संकेत प्रदान करें
- प्रत्यक्ष डेटा प्रवाह
- स्मृति में दिए गए निर्देशों के अनुसार कंप्यूटर कार्य करें
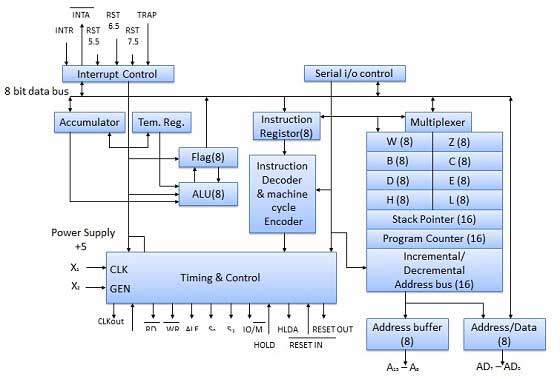
8085 माइक्रोप्रोसेसर
8085 माइक्रोप्रोसेसर एक 8-बिट सामान्य प्रयोजन माइक्रोप्रोसेसर है जो 64k मेमोरी को संबोधित करने में सक्षम है। इस प्रोसेसर में चालीस पिन होते हैं, इसके लिए +5 वी एकल बिजली की आपूर्ति और 3-मेगाहर्ट्ज सिंगल-फेज घड़ी की आवश्यकता होती है।
खंड आरेख
आलू
ALU माइक्रोप्रोसेसर का कंप्यूटिंग कार्य करता है। इसमें संचायक, अस्थायी रजिस्टर, अंकगणित और तर्क सर्किट और पांच झंडे शामिल हैं। परिणाम संचायक और झंडे में संग्रहीत किया जाता है।
खंड आरेख

बिजली संचयक यंत्र
यह 8-बिट रजिस्टर है जो ALU का हिस्सा है। इस रजिस्टर का उपयोग 8-बिट डेटा को संग्रहीत करने और अंकगणितीय और तर्क संचालन करने में किया जाता है। ऑपरेशन का परिणाम संचायक में संग्रहीत किया जाता है।
आरेख
झंडे
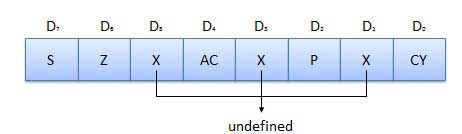
झंडे प्रोग्राम करने योग्य हैं। उन्हें निर्देश का उपयोग करके रजिस्टरों से डेटा को स्टोर करने और स्थानांतरित करने के लिए उपयोग किया जा सकता है। ALU में पाँच फ़्लिप-फ़्लॉप शामिल होते हैं जो संचायक और अन्य रजिस्टरों में डेटा स्थिति के अनुसार सेट और रीसेट होते हैं।
S (Sign) flag- एक अंकगणितीय ऑपरेशन के निष्पादन के बाद, यदि परिणाम का बिट डी 7 1 है, तो संकेत ध्वज सेट है। इसका उपयोग हस्ताक्षरित संख्या के लिए किया जाता है। किसी दिए गए बाइट में, यदि D 7 1 का अर्थ ऋणात्मक संख्या है। यदि यह शून्य है, तो यह एक सकारात्मक संख्या है।
Z (Zero) flag - यदि ALU ऑपरेशन का परिणाम 0 है तो शून्य ध्वज सेट किया गया है।
AC (Auxiliary Carry) flag- अंकगणितीय ऑपरेशन में, जब कैरी को डिजिट डी 3 द्वारा जनरेट किया जाता है और डिजिट डी 4 पर पास किया जाता है , तो एसी फ्लैग सेट किया जाता है। इस ध्वज का उपयोग केवल आंतरिक रूप से BCD ऑपरेशन में किया जाता है।
P (Parity) flag- अंकगणित या तर्क संचालन के बाद, यदि परिणाम में 1s की संख्या भी है, तो ध्वज सेट है। यदि इसमें विषम संख्या 1s है, तो ध्वज रीसेट है।
C (Carry) flag - यदि अंकगणित संचालन परिणाम एक कैरी में है, तो कैरी फ्लैग सेट किया जाता है, अन्यथा इसे रीसेट किया जाता है।
रजिस्टर अनुभाग
यह मूल रूप से एक भंडारण उपकरण है और निर्देशों का उपयोग करके रजिस्टरों से डेटा स्थानांतरित करता है।
Stack Pointer (SP)- स्टैक पॉइंटर भी एक 16-बिट रजिस्टर है जो मेमोरी पॉइंटर के रूप में उपयोग किया जाता है। यह स्टैक के रूप में जानी जाने वाली रीड / राइट मेमोरी में मेमोरी लोकेशन की ओर इशारा करता है। कार्यक्रम के निष्पादन के बीच, कभी-कभी स्टैक में संग्रहीत किए जाने वाले डेटा। स्टैक की शुरुआत स्टैक पॉइंटर में 16-बिट पते को लोड करके परिभाषित की जाती है।
Program Counter (PC)- यह 16-बिट रजिस्टर अनुदेश के निष्पादन के लिए चौथे ऑपरेशन से संबंधित है। यह रजिस्टर एक मेमोरी पॉइंटर भी है। मेमोरी लोकेशन में 16-बिट एड्रेस होता है। इसका उपयोग निष्पादन पते को संग्रहीत करने के लिए किया जाता है। प्रोग्राम काउंटर का कार्य मेमोरी एड्रेस को इंगित करना है जहां से अगले बाइट को लाना है।
Storage registers- ये रजिस्टर एक कार्यक्रम के निष्पादन के दौरान 8-बिट डेटा संग्रहीत करते हैं। इन रजिस्टरों को बी, सी, डी, ई, एच, एल के रूप में पहचाना जाता है। इन्हें कुछ 16 बिट ऑपरेशंस को करने के लिए रजिस्टर बीसी, डीई और एचएल के रूप में जोड़ा जा सकता है।
समय और नियंत्रण अनुभाग
यह इकाई घड़ी के पल्स के अनुसार माइक्रोप्रोसेसर ऑपरेशन को सिंक्रनाइज़ करने और नियंत्रण संकेतों को उत्पन्न करने के लिए जिम्मेदार है जो माइक्रोप्रोसेसर और बाह्य उपकरणों के बीच सहज संचार के लिए आवश्यक हैं। आरडी बार और डब्ल्यूआर बार सिग्नल सिंक्रोनस दालों हैं जो इंगित करते हैं कि डेटा बस में डेटा उपलब्ध है या नहीं। नियंत्रण इकाई माइक्रोप्रोसेसर, मेमोरी और परिधीय उपकरणों के बीच डेटा के प्रवाह को नियंत्रित करने के लिए जिम्मेदार है।
पिन आरेख

सभी सिग्नल को छह समूहों में वर्गीकृत किया जा सकता है
| एस.एन. | समूह | विवरण |
|---|---|---|
| 1 | Address bus | 8085 माइक्रोप्रोसेसर में 8 सिग्नल लाइन, ए 15 - ए 8 हैं जो यूनी दिशात्मक हैं और एक उच्च आदेश पता बस के रूप में उपयोग किया जाता है। |
| 2 | Data bus | सिग्नल लाइन AD7 - AD0 दोहरे उद्देश्य के लिए द्वि-दिशात्मक है। उनका उपयोग कम ऑर्डर एड्रेस बस के साथ-साथ डेटा बस के रूप में किया जाता है। |
| 3 | Control signal and Status signal | नियंत्रण संकेत RD bar- यह एक रीड कंट्रोल सिग्नल (सक्रिय कम) है। यदि यह सक्रिय है तो मेमोरी डेटा को पढ़ती है। WR bar- इसे कंट्रोल सिग्नल (एक्टिव लो) लिखा जाता है। यह चयनित मेमोरी में लिखे जाने पर सक्रिय होता है। स्थिति संकेत ALU (Address Latch Enable)- जब ALU अधिक होता है। 8085 माइक्रोप्रोसेसर पता बस का उपयोग करें। जब ALU कम है। 8085 माइक्रोप्रोसेसर डेटा बस का उपयोग है। IO/M bar- यह एक स्थिति संकेत है जिसका उपयोग i / o और मेमोरी ऑपरेशन के बीच अंतर करने के लिए किया जाता है। जब यह उच्च होता है, तो यह i / o ऑपरेशन को इंगित करता है और जब यह कम होता है, तो यह मेमोरी ऑपरेशन को इंगित करता है। S1 and S0 - आई / ओ और मेमोरी बार के समान ये स्थिति संकेत, विभिन्न ऑपरेशनों की पहचान कर सकते हैं, लेकिन वे शायद ही कभी छोटे सिस्टम में उपयोग किए जाते हैं। |
| 4 | Power supply and frequency signal | Vcc - + 5v बिजली की आपूर्ति। Vss - जमीनी संदर्भ X, X- इन दो पिनों पर एक क्रिस्टल जुड़ा होता है। आवृत्ति को आंतरिक रूप से 3-मेगाहर्ट्ज में दो ऑपरेटिंग सिस्टम द्वारा विभाजित किया गया है, क्रिस्टल में 6-मेगाहर्ट्ज की आवृत्ति होनी चाहिए। CLK out - इस सिग्नल को अन्य उपकरणों के लिए सिस्टम घड़ी के रूप में इस्तेमाल किया जा सकता है। |
| 5 | Externally initiated signal | INTR (i/p) - बाधित अनुरोध। INTA bar (o/p) - इसका उपयोग स्वीकारोक्ति में बाधा के रूप में किया जाता है। TRAP (i/p) - यह गैर-नकाबपोश व्यवधान है और इसकी सर्वोच्च प्राथमिकता है। HOLD (i/p) - इसका इस्तेमाल एक्जीक्यूटिंग प्रोग्राम को होल्ड करने के लिए किया जाता है। HLDA (o/p) - होल्ड स्वीकार करें। READY (i/p) - इस सिग्नल का उपयोग माइक्रोप्रोसेसर को पढ़ने या लिखने में देरी करने के लिए किया जाता है जब तक कि धीमी गति से प्रतिक्रिया करने वाला परिधीय डेटा स्वीकार करने या भेजने के लिए तैयार न हो। RESET IN bar - जब इस पिन पर सिग्नल कम हो जाता है, तो प्रोग्राम काउंटर शून्य पर सेट हो जाता है, बस त्रि-बताई जाती है, और MPU रीसेट हो जाता है। RESET OUT- यह संकेत बताता है कि MPU को रीसेट किया जा रहा है। सिग्नल का उपयोग अन्य उपकरणों को रीसेट करने के लिए किया जा सकता है। RST 7.5, RST 6.5, RST 5.5 (Request interrupt)- इसका उपयोग प्रोग्राम कंट्रोल को विशिष्ट मेमोरी लोकेशन में ट्रांसफर करने के लिए किया जाता है। उनके पास INTR की तुलना में अधिक प्राथमिकता है। |
| 6 | Serial I/O ports | 8085 माइक्रोप्रोसेसर में सीरियल ट्रांसमिशन सीरियल इनपुट डेटा और सीरियल आउटपुट डेटा को लागू करने के लिए दो सिग्नल हैं। |
निर्देश प्रारूप
प्रत्येक निर्देश को कंप्यूटर के भीतर बिट्स के अनुक्रम द्वारा दर्शाया जाता है। निर्देश को बिट्स के समूह में विभाजित किया जाता है जिसे फ़ील्ड कहा जाता है। जिस तरह से निर्देश व्यक्त किया जाता है उसे अनुदेश प्रारूप के रूप में जाना जाता है। इसे आमतौर पर आयताकार बॉक्स के रूप में दर्शाया जाता है। अनुदेश प्रारूप निम्न प्रकार का हो सकता है।
परिवर्तनीय निर्देश प्रारूप
ये निर्देश प्रारूप हैं जिसमें निर्देश की लंबाई opcode और पते के विवरण के आधार पर भिन्न होती है। उदाहरण के लिए, VAX निर्देश 1 और 53 बाइट्स के बीच भिन्न होता है जबकि X86 निर्देश 1 और 17 बाइट्स के बीच भिन्न होता है।
प्रारूप

फायदा
इन प्रारूपों में अच्छा कोड घनत्व है।
कमी
इन अनुदेश प्रारूपों को डिकोड और पाइपलाइन करना बहुत मुश्किल है।
निश्चित निर्देश प्रारूप
इस प्रकार के निर्देश प्रारूप में, सभी निर्देश समान आकार के होते हैं। उदाहरण के लिए, एमआइपी, पावर पीसी, अल्फा, एआरएम।
प्रारूप

फायदा
वे डीकोड और पाइपलाइन करना आसान है।
कमी
उनके पास अच्छा कोड घनत्व नहीं है।
हाइब्रिड निर्देश प्रारूप
इस प्रकार के इंस्ट्रक्शन फॉर्मेट में, हमारे पास opcode द्वारा निर्दिष्ट कई फॉर्मेट की लंबाई होती है। उदाहरण के लिए, IBM 360/70, MIPS 16, अंगूठा।
प्रारूप

फायदा
कोड घनत्व और इन प्रकार के निर्देश के बीच ये समझौता करना बहुत आसान है।
मोड्स को संबोधित करते हुए
एड्रेसिंग मोड एक प्रोसेसर को दिए गए डेटा तक किसी पते तक पहुंचने के लिए अलग-अलग तरीके प्रदान करता है। संचालित डेटा को मेमोरी लोकेशन में संग्रहीत किया जाता है, प्रत्येक निर्देश के लिए कुछ निश्चित डेटा की आवश्यकता होती है, जिस पर इसे संचालित करना होता है। डेटा का पता निर्दिष्ट करने के लिए विभिन्न तकनीकें हैं। इन तकनीकों को एड्रेसिंग मोड कहा जाता है।
Direct addressing mode- डायरेक्ट एड्रेसिंग मोड में, ऑपरेंड का एड्रेस इंस्ट्रक्शन में दिया गया है और डेटा मैमोरी लोकेशन में उपलब्ध है जो इंस्ट्रक्शन में दिया गया है। हम इस डेटा को वांछित स्थान पर ले जाएंगे।
Indirect addressing mode- अप्रत्यक्ष पता मोड में, निर्देश एक रजिस्टर को निर्दिष्ट करता है जिसमें ऑपरेंड का पता होता है। दोनों आंतरिक रैम और बाहरी रैम को अप्रत्यक्ष पते के माध्यम से पहुँचा जा सकता है।
Immediate addressing mode- तत्काल एड्रेसिंग मोड में, ऑपरेंड में डायरेक्ट डेटा दिया जाता है जो डेटा को संचायक में स्थानांतरित करता है। यह बहुत तेज़ है।
Relative addressing mode- सापेक्षिक पता मोड में, प्रभावी पता इंडेक्स मोड द्वारा प्रोग्राम काउंटर का उपयोग करके सामान्य प्रयोजन प्रोसेसर रजिस्टर के अनुसार निर्धारित किया जाता है। इस मोड को सापेक्ष पता मोड कहा जाता है।
Index addressing mode- इंडेक्स एड्रेस मोड में, रजिस्टर के कंटेंट में एक कंटेंट वैल्यू जोड़कर ऑपरेंड का प्रभावी एड्रेस जेनरेट किया जाता है। इस मोड को इंडेक्स एड्रेस मोड कहा जाता है।