सार्वजनिक कुंजी एन्क्रिप्शन
सार्वजनिक कुंजी क्रिप्टोग्राफी
सममित कुंजी क्रिप्टोग्राफ़ी के विपरीत, हमें सार्वजनिक-कुंजी क्रिप्टोग्राफ़ी का ऐतिहासिक उपयोग नहीं मिलता है। यह अपेक्षाकृत नई अवधारणा है।
सममितीय क्रिप्टोग्राफी सरकार, सैन्य जैसे संगठनों के लिए अच्छी तरह से अनुकूल थी, और वर्गीकृत संचार में बड़े वित्तीय निगम शामिल थे।
पिछले कुछ दशकों में अधिक असुरक्षित कंप्यूटर नेटवर्क के प्रसार के साथ, बड़े पैमाने पर क्रिप्टोग्राफी का उपयोग करने के लिए एक वास्तविक आवश्यकता महसूस की गई थी। मुख्य प्रबंधन के लिए चुनौतियों का सामना करने के कारण सममित कुंजी गैर-व्यावहारिक पाई गई थी। इसने सार्वजनिक कुंजी क्रिप्टोकरंसीज को जन्म दिया।
एन्क्रिप्शन और डिक्रिप्शन की प्रक्रिया को निम्न चित्रण में दर्शाया गया है -
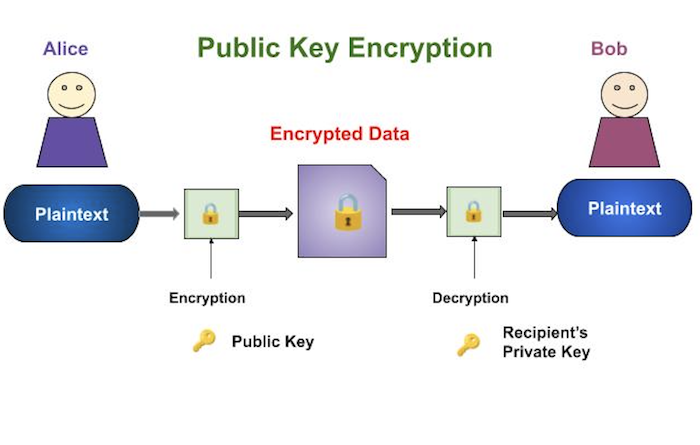
सार्वजनिक कुंजी एन्क्रिप्शन योजना के सबसे महत्वपूर्ण गुण हैं -
एन्क्रिप्शन और डिक्रिप्शन के लिए विभिन्न कुंजियों का उपयोग किया जाता है। यह एक संपत्ति है जिसने इस योजना को सममित एन्क्रिप्शन योजना से अलग सेट किया है।
प्रत्येक रिसीवर के पास एक अद्वितीय डिक्रिप्शन कुंजी होती है, जिसे आमतौर पर उसकी निजी कुंजी कहा जाता है।
रिसीवर को एक एन्क्रिप्शन कुंजी प्रकाशित करने की आवश्यकता होती है, जिसे उसकी सार्वजनिक कुंजी कहा जाता है।
एक सार्वजनिक कुंजी की प्रामाणिकता का कुछ आश्वासन इस योजना में आवश्यक है कि रिसीवर के रूप में विरोधी द्वारा स्पूफिंग से बचने के लिए। आम तौर पर, इस प्रकार के क्रिप्टोकरेंसी में विश्वसनीय तृतीय पक्ष शामिल होता है जो प्रमाणित करता है कि एक विशेष सार्वजनिक कुंजी केवल किसी विशिष्ट व्यक्ति या संस्था से संबंधित है।
एन्क्रिप्शन एल्गोरिथ्म जटिल है, जो हमलावर को प्लेनेटेक्स को सिफरटेक्स्ट और एन्क्रिप्शन (सार्वजनिक) कुंजी से हटाने से रोक सकता है।
यद्यपि निजी और सार्वजनिक कुंजी गणितीय रूप से संबंधित हैं, लेकिन सार्वजनिक कुंजी से निजी कुंजी की गणना करना संभव नहीं है। वास्तव में, किसी भी सार्वजनिक-कुंजी क्रिप्टोसिस्टम का बुद्धिमान हिस्सा दो चाबियों के बीच संबंध बनाने में है।
तीन प्रकार की सार्वजनिक कुंजी एन्क्रिप्शन योजनाएँ हैं। हम निम्नलिखित वर्गों में उनकी चर्चा करते हैं -
आरएसए क्रिप्टोसिस्टम
यह क्रिप्टोकरेंसी एक प्रारंभिक प्रणाली है। यह आज भी सबसे अधिक कार्यरत क्रिप्टोकरेंसी है। प्रणाली का आविष्कार तीन विद्वानों ने किया थाRon Rivest, Adi Shamir, तथा Len Adleman और इसलिए, इसे आरएसए क्रिप्टो सिस्टम कहा जाता है।
हम आरएसए क्रिप्टोसिस्टम के दो पहलुओं को देखेंगे, पहली कुंजी जोड़ी की पीढ़ी और दूसरी एन्क्रिप्शन-डिक्रिप्शन एल्गोरिदम।
आरएसए कुंजी जोड़ी की पीढ़ी
प्रत्येक व्यक्ति या एक पार्टी जो एन्क्रिप्शन का उपयोग करके संचार में भाग लेने की इच्छा रखता है, उसे सार्वजनिक कुंजी और निजी कुंजी की कुंजी की एक जोड़ी उत्पन्न करने की आवश्यकता होती है। कुंजी के निर्माण में निम्नलिखित प्रक्रिया का वर्णन नीचे किया गया है -
Generate the RSA modulus (n)
दो बड़े primes, p और q का चयन करें।
N = p * q की गणना करें। मजबूत अटूट एन्क्रिप्शन के लिए, चलो n एक बड़ी संख्या है, आमतौर पर न्यूनतम 512 बिट्स।
Find Derived Number (e)
संख्या e 1 से अधिक और उससे कम होना चाहिए (p - 1) (q - 1)।
E और (p - 1) (q - 1) के लिए कोई सामान्य कारक नहीं होना चाहिए। 1 को छोड़कर। दूसरे शब्दों में दो नंबर e और (p - 1) (q - 1) coprime हैं।
Form the public key
संख्याओं की संख्या (n, e) RSA सार्वजनिक कुंजी बनाती है और इसे सार्वजनिक किया जाता है।
दिलचस्प बात यह है कि यद्यपि n सार्वजनिक कुंजी का हिस्सा है, एक बड़ी अभाज्य संख्या को फैक्ट करने में कठिनाई यह सुनिश्चित करती है कि हमलावर n को प्राप्त करने के लिए उपयोग किए जाने वाले दो प्राइम (p & q) को परिमित समय में नहीं पा सकता है। यह आरएसए की ताकत है।
Generate the private key
प्राइवेट की d की गणना p, q और e से की जाती है। दिए गए n और e के लिए, अद्वितीय संख्या d है।
संख्या d, e modulo (p - 1) (q - 1) का विलोम है। इसका अर्थ है कि d, संख्या से कम है (p - 1) (q - 1) ऐसा है कि जब e से गुणा किया जाता है, तो यह 1 modulo (p - 1) (q - 1) के बराबर होता है।
यह संबंध गणितीय रूप से निम्नानुसार लिखा गया है -
ed = 1 mod (p − 1)(q − 1)विस्तारित यूक्लिडियन एल्गोरिथ्म पी, क्यू और ई को इनपुट के रूप में लेता है और आउटपुट के रूप में डी देता है।
उदाहरण
RSA की जोड़ी बनाने का एक उदाहरण नीचे दिया गया है। (आसानी से समझने के लिए, यहां लिए गए primes p & q छोटे मान हैं। व्यावहारिक रूप से, ये मूल्य बहुत अधिक हैं)।
बता दें कि दो प्राइम्स p = 7 और q = 13. इस प्रकार हैं, मापांक n = pq = 7 x 13 = 91।
E = 5 का चयन करें, जो कि एक वैध विकल्प है क्योंकि कोई संख्या नहीं है जो कि 5 का आम कारक है और (p - 1) (q - 1) = 6 × 12 = 72, को छोड़कर 1 है।
संख्याओं की जोड़ी (n, e) = (91, 5) सार्वजनिक कुंजी बनाती है और जिसे भी हम एन्क्रिप्टेड संदेश भेजने में सक्षम होना चाहते हैं, उसे उपलब्ध कराया जा सकता है।
इनपुट p = 7, q = 13, और e = 5 विस्तारित यूक्लिडियन एल्गोरिथ्म के लिए। आउटपुट d = 29 होगा।
जाँच करें कि गणना द्वारा d सही है -
de = 29 × 5 = 145 = 1 mod 72इसलिए, सार्वजनिक कुंजी (91, 5) है और निजी कुंजी (91, 29) है।
एन्क्रिप्शन और डिक्रिप्शन
एक बार कुंजी जोड़ी उत्पन्न हो जाने के बाद, एन्क्रिप्शन और डिक्रिप्शन की प्रक्रिया अपेक्षाकृत सरल और कम्प्यूटेशनल रूप से आसान है।
दिलचस्प बात यह है कि आरएसए सीधे बिट्स के तारों पर काम नहीं करता है जैसा कि सममित कुंजी एन्क्रिप्शन के मामले में होता है। यह संख्याओं पर काम करता है modulo n। इसलिए, एन से कम संख्या की एक श्रृंखला के रूप में प्लेटेक्स्ट का प्रतिनिधित्व करना आवश्यक है।
RSA एन्क्रिप्शन
मान लीजिए कि प्रेषक किसी ऐसे व्यक्ति को कुछ पाठ संदेश भेजना चाहता है जिसकी सार्वजनिक कुंजी है (n, e)।
इसके बाद प्रेषक n की तुलना में संख्याओं की एक श्रृंखला के रूप में सादा पाठ का प्रतिनिधित्व करता है।
पहला प्लेनटेक्स्ट पी एन्क्रिप्ट करने के लिए, जो एक नंबर मोडुलो एन है। एन्क्रिप्शन प्रक्रिया सरल गणितीय कदम है -
C = Pe mod nदूसरे शब्दों में, सिफरटेक्स्ट सी, प्लेटेक्स्ट पी के बराबर होता है, जो कि कई बार ई से गुणा होता है और फिर मॉडुलो एन कम हो जाता है। इसका मतलब है कि C भी n से कम की संख्या है।
प्लेनेटेक्स P = 10 के साथ हमारी मुख्य पीढ़ी के उदाहरण पर लौटते हुए, हमें सिफरटेक्स्ट C मिलता है -
C = 105 mod 91आरएसए डिक्रिप्शन
RSA के लिए डिक्रिप्शन प्रक्रिया भी बहुत सीधी है। मान लीजिए कि सार्वजनिक-कुंजी जोड़ी (एन, ई) के रिसीवर को एक सिफरटेक्स्ट सी प्राप्त हुआ है।
रिसीवर अपने निजी कुंजी की शक्ति के लिए सी उठाता है d। परिणाम modulo n प्लेटेक्स्ट P होगा।
Plaintext = Cd mod nफिर से हमारे संख्यात्मक उदाहरण पर लौटते हुए, सिफरटेक्स्ट C = 82 को निजी कुंजी 29 का उपयोग करके नंबर 10 में डिक्रिप्ट किया जाएगा -
Plaintext = 8229 mod 91 = 10RSA विश्लेषण
आरएसए की सुरक्षा दो अलग-अलग कार्यों की ताकत पर निर्भर करती है। आरएसए क्रिप्टोसिस्टम सबसे लोकप्रिय सार्वजनिक-कुंजी क्रिप्टोसिस्टम ताकत है, जो बहुत बड़ी संख्या को फैक्टर करने की व्यावहारिक कठिनाई पर आधारित है।
Encryption Function - इसे प्लेनटेक्स्ट को सिफरटेक्स्ट में परिवर्तित करने का एक तरफ़ा कार्य माना जाता है और इसे केवल निजी कुंजी d के ज्ञान के साथ उलटा किया जा सकता है।
Key Generation- एक आरएसए सार्वजनिक कुंजी से एक निजी कुंजी का निर्धारण करने की कठिनाई मापांक एन फैक्टरिंग के बराबर है। इस प्रकार एक हमलावर एक RSA सार्वजनिक कुंजी के ज्ञान का उपयोग तब तक नहीं कर सकता जब तक कि वह n n कारक नहीं कर सकता। यह एक तरह से फ़ंक्शन भी है, p & q मानों से मापांक n तक जाना आसान है, लेकिन रिवर्स संभव नहीं है।
यदि इन दोनों कार्यों में से कोई भी एकतरफा साबित नहीं होता है, तो आरएसए को तोड़ दिया जाएगा। वास्तव में, यदि कुशलता से फैक्टरिंग की तकनीक विकसित की जाती है तो आरएसए सुरक्षित नहीं रहेगा।
आरएसए एन्क्रिप्शन की ताकत काफी हद तक हमलों के खिलाफ जाती है अगर नंबर पी और क्यू बड़े प्राइम नहीं हैं और / या चुने गए सार्वजनिक कुंजी ई एक छोटी संख्या है।
एलगमाल क्रिप्टोसिस्टम
आरएसए के साथ, अन्य सार्वजनिक-कुंजी क्रिप्टोकरंसी प्रस्तावित हैं। उनमें से कई असतत लघुगणक समस्या के विभिन्न संस्करणों पर आधारित हैं।
ElGamal cryptosystem, जिसे Elliptic Curve Variant कहा जाता है, असतत लघुगणक समस्या पर आधारित है। यह इस धारणा से ताकत प्राप्त करता है कि असतत लॉगरिदम किसी दिए गए नंबर के लिए व्यावहारिक समय सीमा में नहीं मिल सकता है, जबकि शक्ति के व्युत्क्रम संचालन को कुशलता से गणना की जा सकती है।
आइए हम ElGamal के एक सरल संस्करण से गुजरते हैं जो संख्याओं के साथ काम करता है modulo p। अण्डाकार वक्र संस्करण के मामले में, यह काफी भिन्न संख्या प्रणालियों पर आधारित है।
एलगमाल कुंजी जोड़ी की पीढ़ी
ElGamal cryptosystem का प्रत्येक उपयोगकर्ता निम्न के माध्यम से प्रमुख जोड़ी बनाता है -
Choosing a large prime p. आम तौर पर 1024 से 2048 बिट्स लंबाई की एक प्रमुख संख्या को चुना जाता है।
Choosing a generator element g.
यह संख्या 1 और p - 1 के बीच होनी चाहिए, लेकिन कोई भी संख्या नहीं हो सकती है।
यह पूर्णांक modulo p के गुणक समूह का एक जनरेटर है। इसका मतलब है कि प्रत्येक पूर्णांक m सह-प्रधान से p तक, पूर्णांक k है जो कि g k = a mod n है।
उदाहरण के लिए, 3 समूह 5 (जेड 5 = {1, 2, 3, 4}) का जनरेटर है ।
| एन | 3 एन | 3 एन मॉड 5 |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 9 | 4 |
| 3 | 27 | 2 |
| 4 | 81 | 1 |
Choosing the private key. निजी कुंजी x किसी भी संख्या में 1 से बड़ा और p। 1 से छोटा है।
Computing part of the public key. मान y की गणना पैरामीटर p, g और निजी कुंजी x से निम्नानुसार की जाती है -
y = gx mod pObtaining Public key. ElGamal सार्वजनिक कुंजी में तीन पैरामीटर (p, g, y) होते हैं।
उदाहरण के लिए, मान लीजिए कि पी = 17 और वह जी = 6 (यह पुष्टि की जा सकती है कि 6 समूह Z 17 का एक जनरेटर है )। निजी कुंजी x किसी भी संख्या में 1 से बड़ी और 71 से छोटी हो सकती है, इसलिए हम x = 5. का चयन करते हैं। मान y को तब निम्न प्रकार से गणना की जाती है:
y = 65 mod 17 = 7इस प्रकार निजी कुंजी 62 है और सार्वजनिक कुंजी (17, 6, 7) है।
एन्क्रिप्शन और डिक्रिप्शन
आरएसए के लिए समकक्ष प्रक्रिया की तुलना में एक एलगमाल कुंजी जोड़ी की पीढ़ी तुलनात्मक रूप से सरल है। लेकिन एन्क्रिप्शन और डिक्रिप्शन RSA की तुलना में थोड़ा अधिक जटिल हैं।
ElGamal एन्क्रिप्शन
मान लीजिए कि प्रेषक किसी ऐसे व्यक्ति को एक सादा भेजना चाहता है, जिसकी ElGamal सार्वजनिक कुंजी है (p, g, y), तो -
प्रेषक संख्याओं की एक श्रृंखला के रूप में प्लेटेक्स्ट का प्रतिनिधित्व करता है modulo p।
पहले प्लेनटेक्स्ट पी को एन्क्रिप्ट करने के लिए, जिसे एक नंबर मोडुलो पी के रूप में दर्शाया गया है। सिफरटेक् सी प्राप्त करने के लिए एन्क्रिप्शन प्रक्रिया निम्नानुसार है -
- बेतरतीब ढंग से एक नंबर k;
- दो मूल्यों C1 और C2 की गणना करें, जहां -
C1 = gk mod p
C2 = (P*yk) mod pदो अलग-अलग मूल्यों (C1, C2) से मिलकर सिफरटेक् सी भेजें, एक साथ भेजे।
ऊपर दिए गए हमारे ElGamal प्रमुख पीढ़ी के उदाहरण का उल्लेख करते हुए, सादा P = 13 को निम्नानुसार एन्क्रिप्ट किया गया है -
- बेतरतीब ढंग से एक संख्या उत्पन्न, k = 10 कहते हैं
- दो मूल्यों C1 और C2 की गणना करें, जहां -
C1 = 610 mod 17
C2 = (13*710) mod 17 = 9सिफरटेक्स्ट C = (C1, C2) = (15, 9) भेजें।
ElGamal डिक्रिप्शन
निजी कुंजी x का उपयोग करके सिफरटेक्स्ट (C1, C2) को डिक्रिप्ट करने के लिए, निम्नलिखित दो कदम उठाए गए हैं -
(C1) x मोडुलो पी के मॉड्यूलर व्युत्क्रम की गणना करें , जो (C1) -x है , जिसे आम तौर पर डिक्रिप्शन फैक्टर के रूप में जाना जाता है।
निम्नलिखित फार्मूले का उपयोग करके सादा को प्राप्त करें -
C2 × (C1)-x mod p = Plaintextहमारे उदाहरण में, निजी कुंजी x = 5 का उपयोग करके सिफरटेक्स्ट C = (C1, C2) = (15, 9) को डिक्रिप्ट करने का कारक
15-5 mod 17 = 9प्लेनटेक्स्ट P = (9 × 9) मॉड 17 = 13 निकालें।
ElGamal विश्लेषण
ElGamal प्रणाली में, प्रत्येक उपयोगकर्ता के पास एक निजी कुंजी x है। और हैthree components सार्वजनिक कुंजी की - prime modulus p, generator g, and public Y = gx mod p। ElGamal की ताकत असतत लघुगणक समस्या की कठिनाई पर आधारित है।
सुरक्षित कुंजी का आकार आम तौर पर> 1024 बिट्स होता है। आज भी 2048 बिट्स लंबी कुंजी का उपयोग किया जाता है। प्रसंस्करण गति के मोर्चे पर, एल्गामल काफी धीमा है, इसका उपयोग मुख्य रूप से मुख्य प्रमाणीकरण प्रोटोकॉल के लिए किया जाता है। उच्च प्रसंस्करण दक्षता के कारण, एलगमाल के एलिप्टिक वक्र संस्करण तेजी से लोकप्रिय हो रहे हैं।
अण्डाकार वक्र क्रिप्टोग्राफी (ECC)
एलिप्टिक कर्व क्रिप्टोग्राफी (ईसीसी) एक शब्द है जिसका उपयोग क्रिप्टोग्राफिक टूल और प्रोटोकॉल के एक सूट का वर्णन करने के लिए किया जाता है, जिसकी सुरक्षा असतत लघुगणक समस्या के विशेष संस्करणों पर आधारित है। यह संख्या modulo पी का उपयोग नहीं करता है।
ईसीसी उन संख्याओं के सेट पर आधारित है जो गणितीय वस्तुओं से संबंधित हैं जिन्हें दीर्घवृत्तीय वक्र कहा जाता है। इन संख्याओं के गुणकों को जोड़ने और उनकी गणना करने के नियम हैं, ठीक उसी तरह जैसे संख्याओं के लिए मोडुलो पी।
ईसीसी में कई क्रिप्टोग्राफ़िक योजनाओं का एक संस्करण शामिल है, जिन्हें शुरू में एलगामल एन्क्रिप्शन और डिजिटल सिग्नेचर एल्गोरिथम जैसे मॉड्यूलर नंबर के लिए डिज़ाइन किया गया था।
यह माना जाता है कि अण्डाकार वक्र पर बिंदुओं पर लागू होने पर असतत लघुगणक समस्या बहुत कठिन है। यह एक अण्डाकार वक्र पर अंक मोडुलो पी से बिंदुओं पर स्विच करने का संकेत देता है। यदि हम अण्डाकार वक्र-आधारित वेरिएंट का उपयोग करते हैं, तो भी एक समान सुरक्षा स्तर छोटी कुंजी के साथ प्राप्त किया जा सकता है।
छोटी कुंजी के परिणामस्वरूप दो लाभ होते हैं -
- प्रमुख प्रबंधन में आसानी
- कुशल संगणना
ये लाभ एन्क्रिप्शन योजना के अण्डाकार-वक्र-आधारित वेरिएंट को आवेदन के लिए अत्यधिक आकर्षक बनाते हैं जहाँ कंप्यूटिंग संसाधन विवश हैं।
आरएसए और एलगमाल योजनाएँ - एक तुलना
आइए हम विभिन्न पहलुओं पर आरएसए और एलगमाल योजनाओं की संक्षेप में तुलना करें।
| आरएसए | ElGamal |
|---|---|
| यह एन्क्रिप्शन के लिए अधिक कुशल है। | यह डिक्रिप्शन के लिए अधिक कुशल है। |
| यह डिक्रिप्शन के लिए कम कुशल है। | यह डिक्रिप्शन के लिए अधिक कुशल है। |
| एक विशेष सुरक्षा स्तर के लिए, आरएसए में लंबी कुंजी की आवश्यकता होती है। | समान स्तर की सुरक्षा के लिए, बहुत कम कुंजी की आवश्यकता होती है। |
| इसे व्यापक रूप से स्वीकार और उपयोग किया जाता है। | यह नया है और बाजार में बहुत लोकप्रिय नहीं है। |