एलपीएफ और एचपीएफ के विशेष कार्य
कई अनुप्रयोगों में विशेष सर्किट के रूप में कम-पास और उच्च-पास फिल्टर सर्किट का उपयोग किया जाता है। लो-पास फिल्टर (एलपीएफ) एक के रूप में काम कर सकता हैIntegrator, जबकि हाई-पास फिल्टर (एचपीएफ) एक के रूप में काम कर सकता है Differentiator। ये दो गणितीय कार्य केवल इन सर्किटों से संभव हैं जो कई अनुप्रयोगों में एक इलेक्ट्रॉनिक्स इंजीनियर के प्रयासों को कम करते हैं।
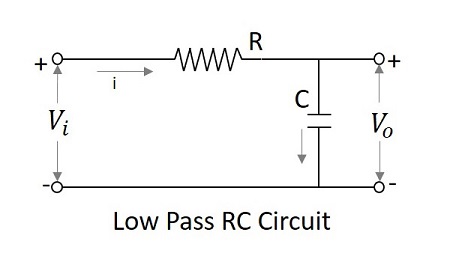
इंटीग्रेटर के रूप में लो पास फिल्टर
कम आवृत्तियों पर, कैपेसिटिव रिएक्शन अनंत हो जाता है और उच्च आवृत्तियों पर प्रतिक्रिया शून्य हो जाती है। इसलिए कम आवृत्तियों पर, एलपीएफ में परिमित आउटपुट होता है और उच्च आवृत्तियों पर आउटपुट शून्य होता है, जो एक इंटीग्रेटर सर्किट के लिए समान होता है। इसलिए कम पास फिल्टर को ए के रूप में काम करने के लिए कहा जा सकता हैintegrator।
एलपीएफ के लिए एक इंटीग्रेटर के रूप में व्यवहार करना
$$ \ tau \ gg T $ $
जहां $ \ tau = RC $ सर्किट का समय स्थिर है
फिर C में वोल्टेज भिन्नता बहुत कम है।
$ $ V_ {i} = iR + \ frac {1} {C} \ int i \: dt $ $
$ $ V_ {i} \ cong iR $ $
$ $ \ _: \: \ Frac {1} {C} \ int i \: dt \ ll iR $ $
$$ मैं \ frac = {{V_ मैं}} {R} $$
$$ \ _: \: V_ {0} = \ frac {1} {C} \ int i dt = \ frac {1} {RC} \ int V_ {i} dt = \ frac {1} {\ _ t} \ int V_ {i} dt $ $
$ $ आउटपुट \ propto \ int इनपुट $ $
इसलिए बड़े समय के साथ एक एलपीएफ एक आउटपुट का उत्पादन करता है जो एक इनपुट के अभिन्न अंग के समानुपाती होता है।
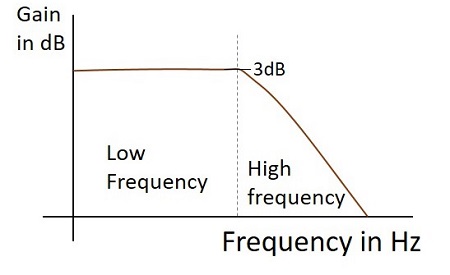
आवृत्ति प्रतिक्रिया
एक व्यावहारिक कम पास फिल्टर की आवृत्ति प्रतिक्रिया, जब यह एक इंटीग्रेटर के रूप में काम करता है जैसा कि नीचे दिखाया गया है।
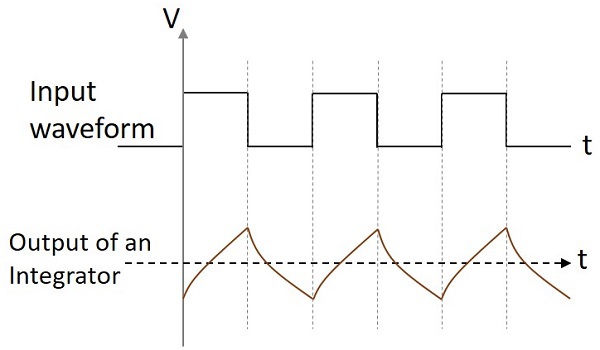
आउटपुट तरंग
यदि इंटीग्रेटर सर्किट को एक साइनवेव इनपुट दिया जाता है, तो आउटपुट एक कोसिन तरंग होगा। यदि इनपुट एक स्क्वायर वेव है, तो आउटपुट वेव फॉर्म अपना आकार बदलता है और नीचे दिए गए चित्र में दिखाई देता है।
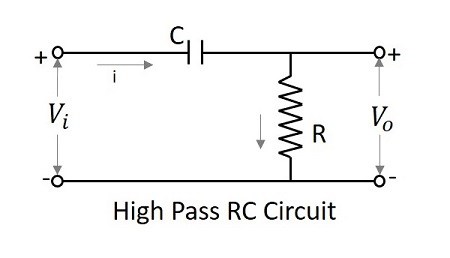
विभेदक के रूप में हाई पास फिल्टर
कम आवृत्तियों पर, एक विभाजक का उत्पादन शून्य होता है जबकि उच्च आवृत्तियों पर इसका उत्पादन कुछ परिमित मूल्य का होता है। यह एक विभेदक के लिए समान है। इसलिए उच्च पास फिल्टर को एक विभेदक के रूप में व्यवहार किया जाता है।
यदि आरसी एचपीएफ का निरंतर समय इनपुट सिग्नल की समय अवधि से बहुत छोटा है, तो सर्किट एक विभेदक के रूप में व्यवहार करता है। फिर आर के पार की तुलना में आर के पार वोल्टेज गिरना बहुत कम है।
$ $ V_ {i} = \ frac {1} {C} \ int i \: dt + iR $$
लेकिन $ iR = V_ {0} $ छोटा है
$ $ V_ {i} = \ frac {1} {C} \ int i \: dt $$
$$ मैं \ frac {V_ {0}} {R} = $$
$ $ \ _: \ _ V_ {i} = \ frac {1} {\ tau} \ int V_ {0} \: dt $ $
जहां $ \ tau = RC $ सर्किट का समय स्थिर है।
दोनों पक्षों में अंतर,
$$ \ frac {dV_ {i}} {dt} = \ frac {V_0} {\ tt}
$ $ V_ {0} = \ tau \ frac {dV_ {i}} {dt} $ $
$ $ \ _ के बाद से: V_ {0} \ propto \ frac {dV_ {i}} {dt} $ $
आउटपुट इनपुट सिग्नल के अंतर के लिए आनुपातिक है।
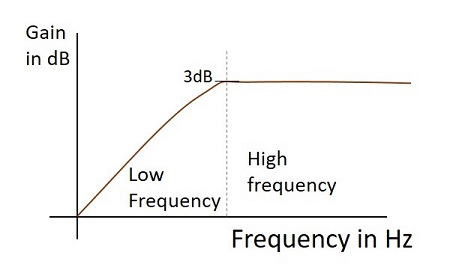
आवृत्ति प्रतिक्रिया
एक व्यावहारिक उच्च पास फिल्टर की आवृत्ति प्रतिक्रिया, जब यह विभेदक के रूप में काम करता है जैसा कि नीचे दिखाया गया है।
आउटपुट वेव फॉर्म
यदि विभेदक सर्किट को एक साइनव इनपुट दिया जाता है, तो आउटपुट कोसाइन तरंग होगा। यदि इनपुट एक स्क्वायर वेव है, तो आउटपुट वेव फॉर्म अपना आकार बदलता है और नीचे दिए गए चित्र में दिखाई देता है।
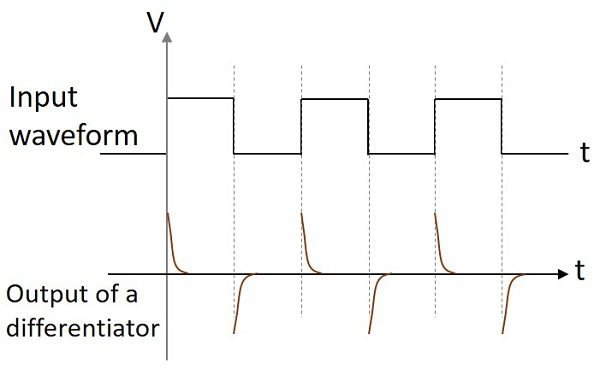
ये दो सर्किट ज्यादातर विभिन्न इलेक्ट्रॉनिक अनुप्रयोगों में उपयोग किए जाते हैं। एक विभेदक सर्किट एक निरंतर आउटपुट वोल्टेज पैदा करता है जब इनपुट लागू होता है तेजी से बदलता है। एक इंटीग्रेटर सर्किट इनपुट वोल्टेज स्थिर होने पर लगातार बदलते आउटपुट वोल्टेज का उत्पादन करता है।