जेनेटिक एल्गोरिदम - त्वरित गाइड
जेनेटिक एलगोरिदम (जीए) एक खोज-आधारित अनुकूलन तकनीक है, जिसके सिद्धांतों पर आधारित है Genetics and Natural Selection। यह अक्सर कठिन समस्याओं के लिए इष्टतम या निकट-इष्टतम समाधान खोजने के लिए उपयोग किया जाता है जो अन्यथा हल करने के लिए जीवन भर ले जाएगा। यह अक्सर अनुकूलन समस्याओं को हल करने के लिए, अनुसंधान में, और मशीन सीखने में उपयोग किया जाता है।
अनुकूलन का परिचय
अनुकूलन की प्रक्रिया है making something better। किसी भी प्रक्रिया में, हमारे पास इनपुट का एक सेट और आउटपुट का एक सेट होता है जैसा कि निम्नलिखित आकृति में दिखाया गया है।

ऑप्टिमाइज़ेशन का तात्पर्य इनपुट के मूल्यों को इस तरह से खोजना है जिससे हमें "सर्वश्रेष्ठ" आउटपुट वैल्यू मिले। "सर्वश्रेष्ठ" की परिभाषा समस्या से समस्या में भिन्न होती है, लेकिन गणितीय शब्दों में, यह इनपुट मापदंडों को अलग-अलग करके एक या एक से अधिक उद्देश्य कार्यों को अधिकतम या कम करने के लिए संदर्भित करता है।
सभी संभावित समाधानों या मूल्यों का सेट जो इनपुट खोज स्थान को बना सकते हैं। इस खोज स्थान में, एक बिंदु या एक बिंदु होता है जो इष्टतम समाधान देता है। अनुकूलन का उद्देश्य खोज स्थान में उस बिंदु या बिंदुओं का पता लगाना है।
जेनेटिक एल्गोरिदम क्या हैं?
प्रकृति हमेशा सभी मानव जाति के लिए प्रेरणा का एक बड़ा स्रोत रही है। जेनेटिक एल्गोरिदम (जीए) प्राकृतिक चयन और आनुवंशिकी की अवधारणाओं के आधार पर खोज आधारित एल्गोरिदम हैं। GAs संगणना की एक बहुत बड़ी शाखा का सबसेट हैंEvolutionary Computation।
GA को जॉन हॉलैंड और उनके छात्रों और सहयोगियों द्वारा मिशिगन विश्वविद्यालय में विकसित किया गया था, विशेष रूप से डेविड ई। गोल्डबर्ग के बाद से और उच्च सफलता के साथ विभिन्न अनुकूलन समस्याओं पर कोशिश की गई है।
जीए में, हमारे पास ए pool or a population of possible solutionsदी गई समस्या के लिए। इसके बाद ये समाधान पुनर्संयोजन और उत्परिवर्तन (जैसे प्राकृतिक आनुवांशिकी) से गुजरते हैं, नए बच्चे पैदा करते हैं, और इस प्रक्रिया को विभिन्न पीढ़ियों से दोहराया जाता है। प्रत्येक व्यक्ति (या उम्मीदवार समाधान) को एक फिटनेस मूल्य (इसके उद्देश्य फ़ंक्शन मूल्य के आधार पर) सौंपा गया है और फिटर व्यक्तियों को अधिक "फिटर" व्यक्तियों को संभोग करने और उपज देने का एक उच्च मौका दिया जाता है। यह "सर्वाइवल ऑफ द फिटेस्ट" की डार्विनियन थ्योरी के अनुरूप है।
इस तरह हम पीढ़ियों तक "विकसित" बेहतर व्यक्तियों या समाधानों को बनाए रखते हैं, जब तक कि हम एक रोक की कसौटी पर नहीं पहुंचते।
आनुवंशिक एल्गोरिदम प्रकृति में पर्याप्त रूप से यादृच्छिक रूप से यादृच्छिक हैं, लेकिन वे यादृच्छिक स्थानीय खोज की तुलना में बहुत बेहतर प्रदर्शन करते हैं (जिसमें हम अभी तक विभिन्न यादृच्छिक समाधानों का प्रयास करते हैं, अब तक का सबसे अच्छा ट्रैक रखते हुए), क्योंकि वे ऐतिहासिक जानकारी का भी शोषण करते हैं।
जीए के लाभ
जीएएस के विभिन्न फायदे हैं जिन्होंने उन्हें बेहद लोकप्रिय बना दिया है। इनमें शामिल हैं -
किसी भी व्युत्पन्न जानकारी की आवश्यकता नहीं है (जो कई वास्तविक दुनिया की समस्याओं के लिए उपलब्ध नहीं हो सकती है)।
पारंपरिक तरीकों की तुलना में तेज और अधिक कुशल है।
बहुत अच्छी समानांतर क्षमताएं हैं।
निरंतर और असतत दोनों कार्यों का अनुकूलन करता है और बहुउद्देश्यीय समस्याओं का भी।
"अच्छे" समाधानों की सूची प्रदान करता है, न कि केवल एक समाधान।
हमेशा समस्या का जवाब मिलता है, जो समय के साथ बेहतर हो जाता है।
उपयोगी जब खोज स्थान बहुत बड़ा है और इसमें बड़ी संख्या में पैरामीटर शामिल हैं।
जीए की सीमाएं
किसी भी तकनीक की तरह, जीए भी कुछ सीमाओं से ग्रस्त हैं। इनमें शामिल हैं -
जीए सभी समस्याओं के लिए अनुकूल नहीं हैं, विशेष रूप से ऐसी समस्याएं जो सरल हैं और जिनके लिए व्युत्पन्न जानकारी उपलब्ध है।
फिटनेस मूल्य की बार-बार गणना की जाती है जो कुछ समस्याओं के लिए कम्प्यूटेशनल रूप से महंगा हो सकता है।
स्टोकेस्टिक होने के नाते, इष्टतमता या समाधान की गुणवत्ता पर कोई गारंटी नहीं है।
यदि ठीक से लागू नहीं किया गया है, तो जीए इष्टतम समाधान में परिवर्तित नहीं हो सकता है।
जीए - प्रेरणा
जेनेटिक एल्गोरिदम में "अच्छा-पर्याप्त" समाधान "फास्ट-पर्याप्त" देने की क्षमता है। यह अनुकूलन समस्याओं को हल करने में उपयोग के लिए आनुवंशिक एल्गोरिदम को आकर्षक बनाता है। जीए की आवश्यकता के कारण निम्नानुसार हैं -
कठिन समस्याओं का समाधान
कंप्यूटर विज्ञान में, समस्याओं का एक बड़ा समूह है, जो हैं NP-Hard। इसका अनिवार्य रूप से मतलब यह है कि, उस समस्या को हल करने के लिए, यहां तक कि सबसे शक्तिशाली कंप्यूटिंग सिस्टम बहुत लंबा समय (यहां तक कि!) लेते हैं। ऐसे परिदृश्य में, GA प्रदान करने के लिए एक कुशल उपकरण साबित होता हैusable near-optimal solutions कम समय में।
ग्रेडिएंट आधारित विधियों की विफलता
पारंपरिक कलन आधारित विधियाँ एक यादृच्छिक बिंदु पर शुरू करके और ढाल की दिशा में चलते हुए तब तक काम करती हैं, जब तक हम पहाड़ी की चोटी पर नहीं पहुँच जाते। यह तकनीक कुशल है और रैखिक प्रतिगमन में लागत समारोह जैसे एकल-शिखर उद्देश्य कार्यों के लिए बहुत अच्छी तरह से काम करती है। लेकिन, अधिकांश वास्तविक दुनिया की स्थितियों में, हमें एक बहुत ही जटिल समस्या होती है जिसे परिदृश्य कहा जाता है, जो कई चोटियों और कई घाटियों से बनी होती हैं, जो इस तरह के तरीकों को विफल कर देती हैं, क्योंकि वे स्थानीय ऑप्टिमा पर फंसने की अंतर्निहित प्रवृत्ति से पीड़ित हैं जैसा कि निम्नलिखित आकृति में दिखाया गया है।

एक अच्छा समाधान तेजी से हो रही है
ट्रैवलिंग सेलर प्रॉब्लम (TSP) जैसी कुछ कठिन समस्याएं, वास्तविक दुनिया में पथ खोजने और वीएलएसआई डिज़ाइन जैसे एप्लिकेशन हैं। अब कल्पना करें कि आप अपने जीपीएस नेविगेशन सिस्टम का उपयोग कर रहे हैं, और स्रोत से गंतव्य तक "इष्टतम" पथ की गणना करने में कुछ मिनट (या कुछ घंटे) लगते हैं। ऐसे वास्तविक विश्व अनुप्रयोगों में देरी स्वीकार्य नहीं है और इसलिए एक "अच्छा-पर्याप्त" समाधान है, जिसे "तेज" वितरित किया जाता है जो आवश्यक है।
यह खंड GA को समझने के लिए आवश्यक मूल शब्दावली का परिचय देता है। इसके अलावा, दोनों में GAs की एक सामान्य संरचना प्रस्तुत की गई हैpseudo-code and graphical forms। पाठक को सलाह दी जाती है कि इस खंड में प्रस्तुत सभी अवधारणाओं को ठीक से समझें और इस ट्यूटोरियल के अन्य खंडों को भी पढ़ते समय उन्हें ध्यान में रखें।
मूल शब्दावली
जेनेटिक एल्गोरिदम पर चर्चा शुरू करने से पहले, कुछ बुनियादी शब्दावली से परिचित होना आवश्यक है जो इस पूरे ट्यूटोरियल में उपयोग की जाएगी।
Population- यह दी गई समस्या के सभी संभावित (एन्कोडेड) समाधानों का सबसेट है। जीए के लिए जनसंख्या मानव के लिए जनसंख्या के अनुरूप है, सिवाय इसके कि मनुष्य के बजाय, हमारे पास कैंडीडेट सॉल्यूशंस हैं जो मानव का प्रतिनिधित्व करते हैं।
Chromosomes - गुणसूत्र दी गई समस्या का एक ऐसा समाधान है।
Gene - एक जीन एक गुणसूत्र का एक तत्व स्थिति है।
Allele - यह वह मान है जो एक जीन एक विशेष गुणसूत्र के लिए लेता है।
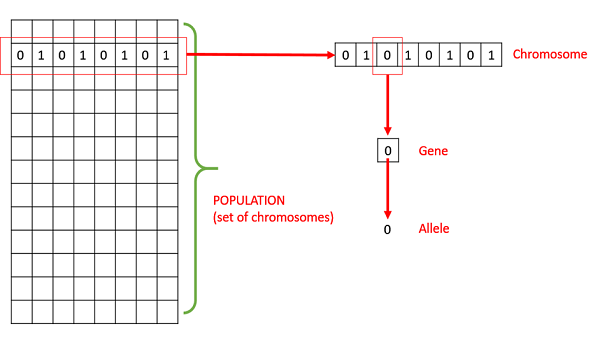
Genotype- जीनोटाइप गणना स्थान में जनसंख्या है। कम्प्यूटेशन स्पेस में, समाधानों को एक ऐसे तरीके से दर्शाया जाता है जिसे कंप्यूटिंग सिस्टम का उपयोग करके आसानी से समझा और हेरफेर किया जा सकता है।
Phenotype - फेनोटाइप वास्तविक वास्तविक विश्व समाधान स्थान में जनसंख्या है जिसमें समाधानों का प्रतिनिधित्व एक तरह से किया जाता है ताकि वे वास्तविक विश्व स्थितियों में प्रतिनिधित्व कर सकें।
Decoding and Encoding - सरल समस्याओं के लिए, phenotype and genotypeरिक्त स्थान समान हैं। हालांकि, ज्यादातर मामलों में, फेनोटाइप और जीनोटाइप रिक्त स्थान भिन्न होते हैं। डिकोडिंग जीनोटाइप से फेनोटाइप स्पेस में एक समाधान को बदलने की एक प्रक्रिया है, जबकि एन्कोडिंग फेनोटाइप से जीनोटाइप स्पेस में बदलने की एक प्रक्रिया है। डिकोडिंग तेजी से होनी चाहिए क्योंकि यह फिटनेस मान गणना के दौरान जीए में बार-बार किया जाता है।
उदाहरण के लिए, 0/1 नैकपैक समस्या पर विचार करें। फेनोटाइप स्पेस में ऐसे समाधान होते हैं जिनमें केवल आइटम के आइटम नंबर होते हैं जिन्हें उठाया जाना है।
हालांकि, जीनोटाइप स्पेस में इसे लंबाई n (जहां n वस्तुओं की संख्या है) के बाइनरी स्ट्रिंग के रूप में दर्शाया जा सकता है। ए0 at position x उस का प्रतिनिधित्व करता है xthआइटम उठाया जाता है, जबकि 1 रिवर्स का प्रतिनिधित्व करता है। यह एक ऐसा मामला है जहां जीनोटाइप और फेनोटाइप स्पेस अलग हैं।

Fitness Function- केवल परिभाषित एक फिटनेस फ़ंक्शन एक फ़ंक्शन है जो समाधान को इनपुट के रूप में लेता है और आउटपुट के रूप में समाधान की उपयुक्तता पैदा करता है। कुछ मामलों में, फिटनेस फ़ंक्शन और उद्देश्य फ़ंक्शन समान हो सकते हैं, जबकि अन्य में यह समस्या के आधार पर भिन्न हो सकता है।
Genetic Operators- ये संतानों की आनुवंशिक संरचना में परिवर्तन करते हैं। इनमें क्रॉसओवर, म्यूटेशन, चयन आदि शामिल हैं।
बुनियादी संरचना
जीए की मूल संरचना इस प्रकार है -
हम एक प्रारंभिक जनसंख्या से शुरू करते हैं (जो यादृच्छिक या अन्य उत्तराधिकारियों द्वारा विकसित की जा सकती है), संभोग के लिए इस आबादी से माता-पिता का चयन करें। नई ऑफ-स्प्रिंग्स उत्पन्न करने के लिए माता-पिता पर क्रॉसओवर और म्यूटेशन ऑपरेटरों को लागू करें। और अंत में ये ऑफ-स्प्रिंग्स आबादी में मौजूदा व्यक्तियों की जगह लेते हैं और प्रक्रिया दोहराते हैं। इस तरह से आनुवंशिक एल्गोरिदम वास्तव में कुछ हद तक मानव विकास की नकल करने की कोशिश करते हैं।
इस ट्यूटोरियल में निम्नलिखित प्रत्येक चरण को एक अलग अध्याय के रूप में कवर किया गया है।

GA के लिए एक सामान्यीकृत छद्म कोड निम्नलिखित कार्यक्रम में समझाया गया है -
GA()
initialize population
find fitness of population
while (termination criteria is reached) do
parent selection
crossover with probability pc
mutation with probability pm
decode and fitness calculation
survivor selection
find best
return bestआनुवांशिक एल्गोरिथ्म को लागू करते समय किए जाने वाले सबसे महत्वपूर्ण निर्णयों में से एक यह निर्णय लेना है कि हम अपने समाधानों का प्रतिनिधित्व करने के लिए क्या उपयोग करेंगे। यह देखा गया है कि अनुचित प्रतिनिधित्व जीए के खराब प्रदर्शन का कारण बन सकता है।
इसलिए, एक उचित प्रतिनिधित्व का चयन, फेनोटाइप और जीनोटाइप रिक्त स्थान के बीच मैपिंग की एक उचित परिभाषा होना एक जीए की सफलता के लिए आवश्यक है।
इस खंड में, हम आनुवंशिक एल्गोरिदम के लिए सबसे अधिक इस्तेमाल किए जाने वाले कुछ अभ्यावेदन प्रस्तुत करते हैं। हालाँकि, प्रतिनिधित्व अत्यधिक समस्या विशिष्ट है और पाठक को यह पता चल सकता है कि एक और प्रतिनिधित्व या यहाँ वर्णित अभ्यावेदन का मिश्रण उसकी समस्या को बेहतर ढंग से प्रस्तुत कर सकता है।
बाइनरी प्रतिनिधित्व
यह GA में सबसे सरल और सबसे व्यापक रूप से उपयोग किया जाने वाला प्रतिनिधित्व है। इस प्रकार के प्रतिनिधित्व में जीनोटाइप में बिट स्ट्रिंग्स होते हैं।
कुछ समस्याओं के लिए जब समाधान स्थान में बूलियन निर्णय चर होते हैं - हां या नहीं, द्विआधारी प्रतिनिधित्व स्वाभाविक है। उदाहरण के लिए 0/1 Knapsack समस्या लें। देखते हैं n आइटम है, तो हम n तत्वों के बाइनरी स्ट्रिंग, जहां x द्वारा एक समाधान का प्रतिनिधित्व कर सकते वें तत्व बताता आइटम एक्स उठाया गया है या नहीं (1) या (0) नहीं।

अन्य समस्याओं के लिए, विशेष रूप से संख्याओं से निपटने वाले, हम संख्याओं का प्रतिनिधित्व उनके द्विआधारी प्रतिनिधित्व के साथ कर सकते हैं। इस तरह की एन्कोडिंग के साथ समस्या यह है कि अलग-अलग बिट्स का अलग-अलग महत्व है और इसलिए म्यूटेशन और क्रॉसओवर ऑपरेटरों के अवांछित परिणाम हो सकते हैं। इसका उपयोग करके कुछ हद तक हल किया जा सकता हैGray Coding, एक बिट में परिवर्तन के रूप में समाधान पर बड़े पैमाने पर प्रभाव नहीं पड़ता है।
वास्तविक मान्यताप्राप्त प्रतिनिधि
उन समस्याओं के लिए जहां हम असतत चर के बजाय निरंतर का उपयोग करके जीन को परिभाषित करना चाहते हैं, वास्तविक मूल्यवान प्रतिनिधित्व सबसे स्वाभाविक है। इन वास्तविक मूल्यवान या फ़्लोटिंग पॉइंट नंबरों की सटीकता हालांकि कंप्यूटर तक सीमित है।

पूर्णांक प्रतिनिधित्व
असतत मूल्यवान जीन के लिए, हम हमेशा समाधान स्थान को 'हां' या 'नहीं' बाइनरी तक सीमित नहीं कर सकते हैं। उदाहरण के लिए, यदि हम चार दूरियों - उत्तर, दक्षिण, पूर्व और पश्चिम को एनकोड करना चाहते हैं, तो हम उन्हें एनकोड कर सकते हैं{0,1,2,3}। ऐसे मामलों में, पूर्णांक प्रतिनिधित्व वांछनीय है।

क्रमपरिवर्तन प्रतिनिधित्व
कई समस्याओं में, समाधान को तत्वों के एक आदेश द्वारा दर्शाया जाता है। ऐसे मामलों में क्रमपरिवर्तन प्रतिनिधित्व सबसे अनुकूल है।
इस प्रतिनिधित्व का एक उत्कृष्ट उदाहरण यात्रा सेल्समैन समस्या (टीएसपी) है। इसमें सेल्समैन को सभी शहरों का दौरा करना होता है, प्रत्येक शहर में एक बार जाना होता है और शुरुआती शहर में वापस आना होता है। दौरे की कुल दूरी को कम से कम करना होगा। इस टीएसपी का समाधान स्वाभाविक रूप से सभी शहरों का एक आदेश या क्रमबद्धता है और इसलिए क्रमपरिवर्तन प्रतिनिधित्व का उपयोग इस समस्या के लिए समझ में आता है।

वर्तमान पीढ़ी में जनसंख्या समाधानों का एक सबसेट है। इसे क्रोमोसोम के एक सेट के रूप में भी परिभाषित किया जा सकता है। जीए जनसंख्या से निपटने के दौरान कई बातों को ध्यान में रखा जाना चाहिए -
जनसंख्या की विविधता को बनाए रखा जाना चाहिए अन्यथा यह समय से पहले अभिसरण हो सकता है।
जनसंख्या का आकार बहुत बड़ा नहीं रखा जाना चाहिए क्योंकि यह जीए को धीमा कर सकता है, जबकि एक छोटी आबादी एक अच्छे पूल के लिए पर्याप्त नहीं हो सकती है। इसलिए, परीक्षण और त्रुटि से एक इष्टतम आबादी के आकार का फैसला किया जाना चाहिए।
जनसंख्या को आमतौर पर दो आयामी सरणी के रूप में परिभाषित किया जाता है - size population, size x, chromosome size।
जनसंख्या प्रारंभ
जीए में जनसंख्या को शुरू करने के लिए दो प्राथमिक विधियां हैं। वे हैं -
Random Initialization - प्रारंभिक आबादी को पूरी तरह से यादृच्छिक समाधान के साथ आबाद करें।
Heuristic initialization - समस्या के लिए ज्ञात हेयुरिस्टिक का उपयोग करके प्रारंभिक जनसंख्या को आबाद करें।
यह देखा गया है कि पूरी आबादी को एक हेयुरिस्टिक का उपयोग करके आरंभीकृत नहीं किया जाना चाहिए, क्योंकि इसके परिणामस्वरूप जनसंख्या समान समाधान और बहुत कम विविधता हो सकती है। यह प्रायोगिक तौर पर देखा गया है कि यादृच्छिक समाधान जनसंख्या को इष्टतमता तक ले जाने वाले होते हैं। इसलिए, हेयुरिस्टिक आरंभीकरण के साथ, हम सिर्फ जनसंख्या को कुछ अच्छे समाधानों के साथ बीज देते हैं, बाकी को पूरी आबादी को हेयुरिस्टिक आधारित समाधानों के साथ भरने के बजाय यादृच्छिक समाधानों के साथ भरते हैं।
यह भी देखा गया है कि कुछ मामलों में युरिस्टिक इनिशियलाइज़ेशन, केवल आबादी की शुरुआती फिटनेस को प्रभावित करता है, लेकिन अंत में, यह उन समाधानों की विविधता है जो इष्टतमता की ओर ले जाते हैं।
जनसंख्या मॉडल
दो जनसंख्या मॉडल व्यापक रूप से उपयोग में हैं -
स्थिर अवस्था
स्थिर अवस्था जीए में, हम प्रत्येक पुनरावृत्ति में एक या दो ऑफ-स्प्रिंग्स उत्पन्न करते हैं और वे आबादी से एक या दो व्यक्तियों को प्रतिस्थापित करते हैं। एक स्थिर अवस्था GA के रूप में भी जाना जाता हैIncremental GA।
पीढ़ीगत
एक पीढ़ीगत मॉडल में, हम 'एन' ऑफ-स्प्रिंग्स उत्पन्न करते हैं, जहां n जनसंख्या का आकार है, और संपूर्ण आबादी को पुनरावृत्ति के अंत में नए से बदल दिया जाता है।
फिटनेस फंक्शन को केवल एक फंक्शन परिभाषित किया गया है, जो एक लेता है candidate solution to the problem as input and produces as output कैसे "फिट" हमारे कैसे "अच्छा" समाधान विचार में समस्या के संबंध में है।
फिटनेस मान की गणना जीए में बार-बार की जाती है और इसलिए इसे पर्याप्त रूप से तेज होना चाहिए। फिटनेस मूल्य की धीमी गणना जीए पर प्रतिकूल प्रभाव डाल सकती है और इसे असाधारण रूप से धीमा कर सकती है।
ज्यादातर मामलों में फिटनेस फ़ंक्शन और उद्देश्य फ़ंक्शन समान होते हैं क्योंकि उद्देश्य दिए गए उद्देश्य फ़ंक्शन को अधिकतम या कम करना है। हालांकि, कई उद्देश्यों और बाधाओं के साथ अधिक जटिल समस्याओं के लिए, एAlgorithm Designer एक अलग फिटनेस फ़ंक्शन का चयन कर सकते हैं।
एक फिटनेस फ़ंक्शन में निम्नलिखित विशेषताएं होनी चाहिए -
फिटनेस फ़ंक्शन को गणना करने के लिए पर्याप्त रूप से तेज़ होना चाहिए।
यह मात्रात्मक रूप से मापना चाहिए कि किसी दिए गए समाधान में कितना फिट है या दिए गए समाधान से कैसे फिट व्यक्तियों का उत्पादन किया जा सकता है।
कुछ मामलों में, हाथ में समस्या की अंतर्निहित जटिलताओं के कारण सीधे फिटनेस फ़ंक्शन की गणना संभव नहीं हो सकती है। ऐसे मामलों में, हम अपनी आवश्यकताओं के अनुरूप फिटनेस सन्निकटन करते हैं।
निम्न छवि 0/1 नैकपैक के समाधान के लिए फिटनेस गणना दिखाती है। यह एक साधारण फिटनेस फंक्शन है, जो सिर्फ उठाए जा रहे आइटम (जो कि 1 है) के लाभ मूल्यों को बताता है, तत्वों को बाएं से दाएं तक पूरी तरह से स्कैन करता है जब तक कि नॉकपैक भर नहीं जाता।

माता-पिता का चयन माता-पिता को चुनने की प्रक्रिया है जो अगली पीढ़ी के लिए ऑफ-स्प्रिंग्स बनाने के लिए मेट और पुनर्संयोजन करता है। माता-पिता का चयन जीए के अभिसरण दर के लिए बहुत महत्वपूर्ण है क्योंकि अच्छे माता-पिता व्यक्तियों को बेहतर और फिटर समाधान के लिए प्रेरित करते हैं।
हालाँकि, कुछ पीढ़ियों में पूरी आबादी को संभालने के लिए एक अत्यंत फिट समाधान को रोकने के लिए देखभाल की जानी चाहिए, क्योंकि इससे समाधान एक दूसरे के करीब हो जाता है जिससे समाधान में विविधता का नुकसान होता है। Maintaining good diversityजीए की सफलता के लिए जनसंख्या अत्यंत महत्वपूर्ण है। यह पूरी आबादी को एक बेहद फिट समाधान द्वारा लेने के रूप में जाना जाता हैpremature convergence और जीए में एक अवांछनीय स्थिति है।
फिटनेस अनुपात चयन
फिटनेस आनुपातिक चयन माता-पिता के चयन के सबसे लोकप्रिय तरीकों में से एक है। इसमें प्रत्येक व्यक्ति एक अभिभावक बन सकता है जिसमें एक संभावना है जो इसकी फिटनेस के लिए आनुपातिक है। इसलिए, फिटर व्यक्तियों के पास अगली पीढ़ी के लिए अपनी विशेषताओं को संभोग और प्रचार करने का एक उच्च मौका है। इसलिए, इस तरह की चयन रणनीति आबादी में अधिक फिट व्यक्तियों के लिए एक चयन दबाव लागू करती है, समय के साथ बेहतर व्यक्तियों को विकसित करती है।
एक गोलाकार पहिया पर विचार करें। पहिया में विभाजित हैn pies, जहां n जनसंख्या में व्यक्तियों की संख्या है। प्रत्येक व्यक्ति को सर्कल का एक हिस्सा मिलता है जो उसके फिटनेस मूल्य के आनुपातिक है।
फिटनेस आनुपातिक चयन के दो कार्यान्वयन संभव हैं -
रूले व्हील चयन
रूलेट व्हील चयन में, परिपत्र पहिया को पहले से वर्णित के अनुसार विभाजित किया गया है। दिखाए गए अनुसार पहिया की परिधि पर एक निश्चित बिंदु चुना जाता है और पहिया घुमाया जाता है। पहिया का क्षेत्र जो निश्चित बिंदु के सामने आता है, उसे माता-पिता के रूप में चुना जाता है। दूसरे माता-पिता के लिए, वही प्रक्रिया दोहराई जाती है।
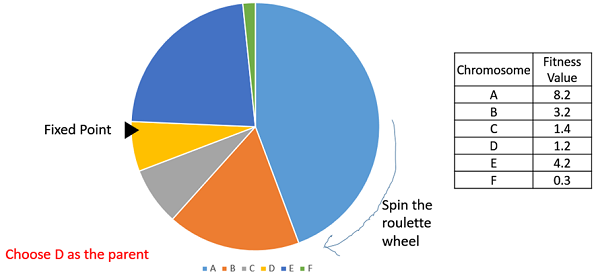
यह स्पष्ट है कि एक फिटर व्यक्ति के पहिये पर अधिक पाई होती है और इसलिए पहिया घूमने पर निश्चित बिंदु के सामने उतरने की अधिक संभावना होती है। इसलिए, किसी व्यक्ति को चुनने की संभावना सीधे उसकी फिटनेस पर निर्भर करती है।
कार्यान्वयन बुद्धिमान, हम निम्नलिखित चरणों का उपयोग करते हैं -
S = एक चालाकी का योग।
0 और S के बीच एक यादृच्छिक संख्या उत्पन्न करें।
जनसंख्या के शीर्ष से शुरू करके, आंशिक राशि P तक चालाकी को जोड़ते रहें, P <S तक।
जिस व्यक्ति के लिए P, S से अधिक है, वह चयनित व्यक्ति है।
स्टोचैस्टिक यूनिवर्सल सैंपलिंग (SUS)
स्टोचैस्टिक यूनिवर्सल सैंपलिंग रूले व्हील के चयन के काफी समान है, हालांकि, केवल एक निश्चित बिंदु होने के बजाय, हमारे पास कई निश्चित बिंदु हैं जैसा कि निम्नलिखित छवि में दिखाया गया है। इसलिए, सभी माता-पिता को पहिया के सिर्फ एक स्पिन में चुना जाता है। इसके अलावा, इस तरह के एक सेटअप से अत्यधिक फिट व्यक्तियों को कम से कम एक बार चुने जाने के लिए प्रोत्साहित किया जाता है।

यह ध्यान दिया जाना चाहिए कि फिटनेस आनुपातिक चयन विधियां उन मामलों के लिए काम नहीं करती हैं जहां फिटनेस एक नकारात्मक मूल्य ले सकता है।
टूर्नामेंट का चयन
K-Way टूर्नामेंट के चयन में, हम K व्यक्तियों को यादृच्छिक पर जनसंख्या से चुनते हैं और माता-पिता बनने के लिए इनमें से सर्वश्रेष्ठ का चयन करते हैं। अगले माता-पिता के चयन के लिए भी यही प्रक्रिया दोहराई जाती है। टूर्नामेंट चयन साहित्य में भी बेहद लोकप्रिय है क्योंकि यह नकारात्मक फिटनेस मूल्यों के साथ भी काम कर सकता है।

रैंक चयन
रैंक चयन नकारात्मक फिटनेस मूल्यों के साथ भी काम करता है और इसका उपयोग ज्यादातर तब किया जाता है जब आबादी में व्यक्तियों के पास बहुत करीब फिटनेस मूल्य होते हैं (यह आमतौर पर रन के अंत में होता है)। प्रत्येक व्यक्ति को पाई का लगभग बराबर हिस्सा मिलता है (जैसे फिटनेस आनुपातिक चयन के मामले में) जैसा कि निम्नलिखित छवि में दिखाया गया है और इसलिए प्रत्येक व्यक्ति को एक दूसरे के सापेक्ष कोई भी बात नहीं है कि एक के रूप में चयनित होने की लगभग समान संभावना है माता-पिता। यह बदले में फिटर व्यक्तियों की ओर चयन दबाव में कमी की ओर जाता है, जिससे जीए को ऐसी स्थितियों में गरीब माता-पिता का चयन करना पड़ता है।
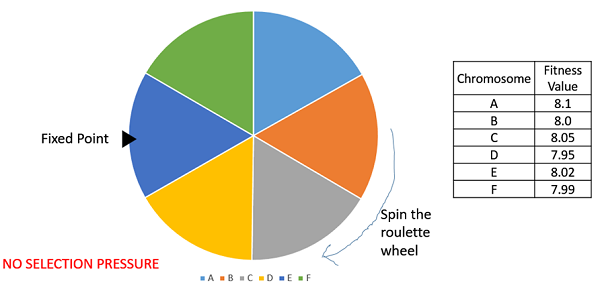
इसमें, हम माता-पिता का चयन करते समय फिटनेस मूल्य की अवधारणा को हटा देते हैं। हालाँकि, आबादी में प्रत्येक व्यक्ति को उनकी फिटनेस के अनुसार रैंक दिया गया है। माता-पिता का चयन प्रत्येक व्यक्ति की रैंक पर निर्भर करता है और फिटनेस पर नहीं। उच्च रैंक वाले व्यक्तियों को कम रैंक वाले लोगों की तुलना में अधिक पसंद किया जाता है।
| क्रोमोसाम | स्वास्थ्य मूल्य | पद |
|---|---|---|
| ए | 8.1 | 1 |
| ख | 8.0 | 4 |
| सी | 8.05 | 2 |
| घ | 7.95 | 6 |
| इ | 8.02 | 3 |
| एफ | 7.99 | 5 |
यादृच्छिक चयन
इस रणनीति में हम बेतरतीब ढंग से मौजूदा आबादी के माता-पिता का चयन करते हैं। फिटर व्यक्तियों के प्रति कोई चयन दबाव नहीं है और इसलिए इस रणनीति को आमतौर पर टाला जाता है।
इस अध्याय में, हम इस बारे में चर्चा करेंगे कि एक क्रॉसओवर ऑपरेटर अपने अन्य मॉड्यूल, उनके उपयोग और लाभों के साथ क्या है।
क्रॉसओवर का परिचय
क्रॉसओवर ऑपरेटर प्रजनन और जैविक क्रॉसओवर के अनुरूप है। इसमें एक से अधिक अभिभावकों का चयन किया जाता है और माता-पिता की आनुवंशिक सामग्री का उपयोग करके एक या अधिक ऑफ-स्प्रिंग्स का उत्पादन किया जाता है। क्रॉसओवर आमतौर पर GA में एक उच्च संभावना के साथ लागू किया जाता है -pc ।
क्रॉसओवर ऑपरेटर्स
इस खंड में हम कुछ सबसे लोकप्रिय इस्तेमाल किए गए क्रॉसओवर ऑपरेटरों के बारे में चर्चा करेंगे। यह ध्यान दिया जाना चाहिए कि ये क्रॉसओवर ऑपरेटर बहुत सामान्य हैं और जीए डिज़ाइनर एक समस्या-विशिष्ट क्रॉसओवर ऑपरेटर को भी लागू करने का विकल्प चुन सकते हैं।
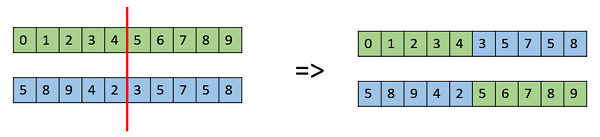
वन प्वाइंट क्रॉसओवर
इस एक-बिंदु क्रॉसओवर में, एक यादृच्छिक क्रॉसओवर बिंदु का चयन किया जाता है और इसके दो माता-पिता की पूंछ को नई ऑफ-स्प्रिंग्स प्राप्त करने के लिए स्वैप किया जाता है।
मल्टी प्वाइंट क्रॉसओवर
मल्टी पॉइंट क्रॉसओवर एक-पॉइंट क्रॉसओवर का एक सामान्यीकरण है, जिसमें नए ऑफ-स्प्रिंग्स प्राप्त करने के लिए वैकल्पिक सेगमेंट की अदला-बदली की जाती है।

यूनिफॉर्म क्रॉसओवर
एक समान क्रॉसओवर में, हम गुणसूत्र को खंडों में विभाजित नहीं करते हैं, बल्कि हम प्रत्येक जीन को अलग-अलग मानते हैं। इसमें, हम अनिवार्य रूप से प्रत्येक गुणसूत्र के लिए एक सिक्का फ्लिप करते हैं ताकि यह तय हो सके कि इसे ऑफ-स्प्रिंग में शामिल किया जाएगा या नहीं। हम उस माता-पिता से बच्चे में अधिक आनुवंशिक सामग्री होने के लिए एक माता-पिता के लिए भी पूर्वाग्रह कर सकते हैं।

पूरे अंकगणित पुनरुत्थान
यह आमतौर पर पूर्णांक अभिगम के लिए उपयोग किया जाता है और निम्न सूत्रों का उपयोग करके दोनों माता-पिता के भारित औसत को ले कर काम करता है -
- चाइल्ड 1 = α.x + (1-α) .y
- बाल 2 = α.x + (1-α) .y
जाहिर है, अगर α = 0.5 है, तो दोनों बच्चे समान होंगे जैसा कि निम्नलिखित छवि में दिखाया गया है।

डेविस ऑर्डर क्रॉसओवर (OX1)
ओएक्स 1 का उपयोग ऑफ-स्प्रिंग्स के सापेक्ष क्रमांकन के बारे में सूचना प्रसारित करने के इरादे से क्रमबद्धता आधारित क्रॉसओवर के लिए किया जाता है। यह निम्नानुसार काम करता है -
माता-पिता में दो यादृच्छिक क्रॉसओवर बिंदु बनाएं और उनके बीच के खंड को पहले माता-पिता से पहली संतानों में कॉपी करें।
अब, दूसरे माता-पिता में दूसरे क्रॉसओवर बिंदु से शुरू करते हुए, सूची के चारों ओर लपेटते हुए, दूसरे अप्रभावित संख्या को दूसरे माता-पिता से पहले बच्चे में कॉपी करें।
माता-पिता की भूमिका के साथ दूसरे बच्चे के लिए दोहराएं।

इसमें आंशिक रूप से मैप्ड क्रॉसओवर (PMX), ऑर्डर आधारित क्रॉसओवर (OX2), शफल क्रॉसओवर, रिंग क्रॉसओवर, आदि जैसे कई अन्य क्रॉसओवर मौजूद हैं।
म्यूटेशन का परिचय
सरल शब्दों में, उत्परिवर्तन को एक नया समाधान प्राप्त करने के लिए गुणसूत्र में एक छोटे से यादृच्छिक घुमाव के रूप में परिभाषित किया जा सकता है। इसका उपयोग आनुवंशिक आबादी में विविधता को बनाए रखने और शुरू करने के लिए किया जाता है और आमतौर पर कम संभावना के साथ लागू किया जाता है -pm। यदि संभावना बहुत अधिक है, तो जीए एक यादृच्छिक खोज में कम हो जाता है।
उत्परिवर्तन GA का हिस्सा है जो खोज स्थान के "अन्वेषण" से संबंधित है। यह देखा गया है कि उत्परिवर्तन GA के अभिसरण के लिए आवश्यक है जबकि क्रॉसओवर नहीं है।
म्यूटेशन ऑपरेटर्स
इस खंड में, हम कुछ सबसे अधिक इस्तेमाल किए जाने वाले म्यूटेशन ऑपरेटरों का वर्णन करते हैं। क्रॉसओवर ऑपरेटरों की तरह, यह एक विस्तृत सूची नहीं है और जीए डिज़ाइनर इन दृष्टिकोणों का संयोजन या समस्या-विशिष्ट म्यूटेशन ऑपरेटर को अधिक उपयोगी मान सकते हैं।
बिट फ्लिप म्यूटेशन
इस बिट फ्लिप म्यूटेशन में, हम एक या अधिक यादृच्छिक बिट्स का चयन करते हैं और उन्हें फ्लिप करते हैं। इसका उपयोग बाइनरी एनकोडेड GA के लिए किया जाता है।

रैंडम रीसेटिंग
रैंडम रिसेटिंग पूर्णांक प्रतिनिधित्व के लिए बिट फ्लिप का विस्तार है। इसमें, अनुमेय मूल्यों के सेट से एक यादृच्छिक मूल्य एक यादृच्छिक रूप से चुने गए जीन को सौंपा गया है।
स्वैप उत्परिवर्तन
स्वैप म्यूटेशन में, हम यादृच्छिक पर गुणसूत्र पर दो पदों का चयन करते हैं, और मूल्यों को इंटरचेंज करते हैं। यह क्रमपरिवर्तन आधारित एन्कोडिंग में आम है।

हाथापाई म्यूटेशन
क्रमपरिवर्तन अभ्यावेदन के साथ हाथापाई उत्परिवर्तन भी लोकप्रिय है। इसमें, पूरे गुणसूत्र से, जीन का एक सबसेट चुना जाता है और उनके मूल्यों को बेतरतीब ढंग से धोया जाता है या फेरबदल किया जाता है।

उलटा उत्परिवर्तन
उलटा म्यूटेशन में, हम स्क्रैम्बल म्यूटेशन की तरह जीन के एक उपसमूह का चयन करते हैं, लेकिन सबसेट को फेरबदल करने के बजाय, हम उपसमुच्चय में पूरे स्ट्रिंग को उल्टा करते हैं।

उत्तरजीवी चयन नीति यह निर्धारित करती है कि किन व्यक्तियों को बाहर रखा जाना है और जिन्हें अगली पीढ़ी में रखा जाना है। यह महत्वपूर्ण है क्योंकि यह सुनिश्चित करना चाहिए कि फिटर व्यक्तियों को आबादी से बाहर नहीं निकाला जाए, जबकि एक ही समय में आबादी में विविधता को बनाए रखा जाना चाहिए।
कुछ GAs कार्यरत हैं Elitism। सरल शब्दों में, इसका मतलब है कि आबादी का मौजूदा योग्य सदस्य हमेशा अगली पीढ़ी के लिए प्रचारित किया जाता है। इसलिए, किसी भी परिस्थिति में वर्तमान जनसंख्या के योग्यतम सदस्य को प्रतिस्थापित नहीं किया जा सकता है।
सबसे आसान नीति यादृच्छिक सदस्यों को आबादी से बाहर निकालना है, लेकिन इस तरह के दृष्टिकोण में अक्सर अभिसरण मुद्दे होते हैं, इसलिए निम्नलिखित रणनीतियों का व्यापक रूप से उपयोग किया जाता है।
आयु आधारित चयन
आयु-आधारित चयन में, हमारे पास एक फिटनेस की धारणा नहीं है। यह इस आधार पर है कि प्रत्येक व्यक्ति को परिमित पीढ़ी के लिए आबादी में अनुमति दी जाती है जहां उसे पुन: पेश करने की अनुमति दी जाती है, उसके बाद उसे आबादी से बाहर निकाल दिया जाता है, भले ही उसकी फिटनेस कितनी अच्छी हो।
उदाहरण के लिए, निम्नलिखित उदाहरण में, आयु उन पीढ़ियों की संख्या है जिनके लिए व्यक्ति आबादी में रहा है। जनसंख्या के सबसे पुराने सदस्य यानी P4 और P7 को आबादी से बाहर कर दिया जाता है और बाकी सदस्यों की उम्र एक से बढ़ाई जाती है।

फिटनेस आधारित चयन
इस फिटनेस आधारित चयन में, बच्चे आबादी में कम से कम फिट व्यक्तियों की जगह लेते हैं। कम से कम फिट व्यक्तियों का चयन पहले बताई गई चयन नीतियों में से किसी एक बदलाव का उपयोग करके किया जा सकता है - टूर्नामेंट चयन, फिटनेस आनुपातिक चयन, आदि।
उदाहरण के लिए, निम्नलिखित छवि में, बच्चे आबादी के कम से कम फिट व्यक्तियों पी 1 और पी 10 की जगह लेते हैं। यह ध्यान दिया जाना चाहिए कि चूंकि P1 और P9 का फिटनेस मूल्य समान है, इसलिए जनसंख्या से व्यक्ति को हटाने का निर्णय मनमाना है।

जीए रन समाप्त हो जाएगा, यह निर्धारित करने में एक आनुवंशिक एल्गोरिथम की समाप्ति की स्थिति महत्वपूर्ण है। यह देखा गया है कि शुरू में, जीए हर कुछ पुनरावृत्तियों में आने वाले बेहतर समाधानों के साथ बहुत तेजी से आगे बढ़ता है, लेकिन यह बाद के चरणों में संतृप्त हो जाता है जहां सुधार बहुत छोटे होते हैं। हम आम तौर पर एक समाप्ति की स्थिति चाहते हैं जैसे कि हमारा समाधान रन के अंत में इष्टतम के करीब है।
आमतौर पर, हम निम्नलिखित समाप्ति शर्तों में से एक रखते हैं -
- जब X पुनरावृत्तियों के लिए जनसंख्या में कोई सुधार नहीं हुआ है।
- जब हम कई पीढ़ियों तक पहुंचते हैं।
- जब उद्देश्य फ़ंक्शन मान एक निश्चित पूर्व-निर्धारित मूल्य पर पहुंच गया है।
उदाहरण के लिए, एक आनुवंशिक एल्गोरिथ्म में हम एक काउंटर रखते हैं जो उन पीढ़ियों पर नज़र रखता है जिनके लिए जनसंख्या में कोई सुधार नहीं हुआ है। प्रारंभ में, हम इस काउंटर को शून्य पर सेट करते हैं। हर बार हम ऑफ-स्प्रिंग्स उत्पन्न नहीं करते हैं जो आबादी में व्यक्तियों की तुलना में बेहतर होते हैं, हम काउंटर को बढ़ाते हैं।
हालांकि, अगर किसी भी ऑफ-स्प्रिंग्स फिटनेस बेहतर है, तो हम काउंटर को शून्य पर रीसेट करते हैं। एल्गोरिथ्म समाप्त हो जाता है जब काउंटर एक पूर्व निर्धारित मूल्य तक पहुंच जाता है।
जीए के अन्य मापदंडों की तरह, समाप्ति की स्थिति भी अत्यधिक विशिष्ट समस्या है और जीए डिजाइनर को यह देखने के लिए विभिन्न विकल्पों की कोशिश करनी चाहिए कि उनकी विशेष समस्या सबसे अच्छी है।
अब तक इस ट्यूटोरियल में हमने जो भी चर्चा की है वह विकास के डार्विनियन मॉडल से मेल खाती है - पुनर्संयोजन और उत्परिवर्तन के माध्यम से प्राकृतिक चयन और आनुवंशिक भिन्नता। प्रकृति में, केवल व्यक्ति के जीनोटाइप में निहित जानकारी को अगली पीढ़ी को प्रेषित किया जा सकता है। यह वह दृष्टिकोण है जिसे हम अब तक ट्यूटोरियल में अपना रहे हैं।
हालाँकि, जीवन भर अनुकूलन के अन्य मॉडल - Lamarckian Model तथा Baldwinian Modelभी मौजूद हैं। यह ध्यान दिया जाना चाहिए कि जो भी मॉडल सबसे अच्छा है, बहस के लिए खुला है और शोधकर्ताओं द्वारा प्राप्त परिणाम बताते हैं कि जीवन भर अनुकूलन का विकल्प अत्यधिक समस्या विशिष्ट है।
अक्सर, हम जीए को स्थानीय खोज के साथ संरेखित करते हैं - जैसे मेमोरियल एल्गोरिदम में। ऐसे मामलों में, कोई यह चुन सकता है कि स्थानीय खोज के बाद उत्पन्न व्यक्तियों के साथ क्या किया जाए, यह तय करने के लिए लैमार्कियन या बाल्डविनियन मॉडल के साथ जाएं।
लैमार्कियन मॉडल
लैमार्कियन मॉडल अनिवार्य रूप से कहता है कि वह लक्षण जो एक व्यक्ति अपने जीवनकाल में प्राप्त करता है, उसे अपने वंश को पारित किया जा सकता है। इसका नाम फ्रांसीसी जीवविज्ञानी जीन-बैप्टिस्ट लैमार्क के नाम पर रखा गया है।
हालांकि, प्राकृतिक जीव विज्ञान ने लैमार्किज्म की पूरी तरह से अवहेलना की है क्योंकि हम सभी जानते हैं कि जीनोटाइप में केवल सूचना प्रसारित की जा सकती है। हालांकि, एक गणना दृष्टिकोण से, यह दिखाया गया है कि लैमार्कियन मॉडल को अपनाने से कुछ समस्याओं के लिए अच्छे परिणाम मिलते हैं।
लैमार्कियन मॉडल में, एक स्थानीय खोज ऑपरेटर पड़ोस की जांच करता है (नए लक्षण प्राप्त करता है), और यदि एक बेहतर गुणसूत्र पाया जाता है, तो यह संतान बन जाता है।
बाल्डविनियन मॉडल
बाल्डविनियन मॉडल जेम्स मार्क बाल्डविन (1896) के नाम पर एक मध्यवर्ती विचार है। बाल्डविन मॉडल में, गुणसूत्र लाभकारी व्यवहार सीखने की प्रवृत्ति को कूटबद्ध कर सकते हैं। इसका मतलब यह है कि, लैमार्कियन मॉडल के विपरीत, हम अधिग्रहीत लक्षणों को अगली पीढ़ी तक नहीं पहुंचाते हैं, और न ही हम डार्विनियन मॉडल की तरह अर्जित लक्षणों को पूरी तरह से अनदेखा करते हैं।
बाल्डविन मॉडल इन दो चरम सीमाओं के बीच में है, जिसमें किसी व्यक्ति को कुछ लक्षण प्राप्त करने की प्रवृत्ति होती है, न कि स्वयं लक्षण के बजाय।
इस बाल्डविनियन मॉडल में, एक स्थानीय खोज ऑपरेटर पड़ोस (नए लक्षणों को प्राप्त करता है) की जांच करता है, और यदि एक बेहतर गुणसूत्र पाया जाता है, तो यह केवल गुणसूत्र को बेहतर फिटनेस प्रदान करता है और गुणसूत्र को ही संशोधित नहीं करता है। फिटनेस में बदलाव गुणसूत्रों की क्षमता को "विशेषता प्राप्त करने" का संकेत देता है, भले ही यह सीधे भावी पीढ़ियों के लिए पारित न हो।
GA प्रकृति में बहुत सामान्य हैं, और उन्हें किसी भी अनुकूलन समस्या में लागू करने से अच्छे परिणाम नहीं मिलेंगे। इस खंड में, हम कुछ बिंदुओं का वर्णन करते हैं जो उनके काम में जीए डिजाइनर या जीए कार्यान्वयनकर्ता की सहायता और सहायता करेंगे।
समस्या-विशिष्ट डोमेन ज्ञान का परिचय दें
यह देखा गया है कि अधिक समस्या-विशिष्ट डोमेन ज्ञान जिसे हम GA में शामिल करते हैं; बेहतर उद्देश्य मूल्य हम प्राप्त करते हैं। समस्या विशिष्ट जानकारी जोड़ना या तो समस्या विशिष्ट क्रॉसओवर या म्यूटेशन ऑपरेटरों, कस्टम अभ्यावेदन आदि का उपयोग करके किया जा सकता है।
निम्नलिखित छवि ईए के माइकलेविच के (1990) दृश्य को दिखाती है -

भीड़ कम करना
भीड़ तब होती है जब एक अत्यधिक फिट गुणसूत्र बहुत अधिक प्रजनन करने के लिए हो जाता है, और कुछ पीढ़ियों में पूरी आबादी समान फिटनेस वाले समान समाधानों से भर जाती है। यह विविधता को कम करता है जो जीए की सफलता सुनिश्चित करने के लिए एक बहुत ही महत्वपूर्ण तत्व है। भीड़ को सीमित करने के कई तरीके हैं। उनमें से कुछ हैं -
Mutation विविधता लाने के लिए।
इसमें स्विच हो रहा है rank selection तथा tournament selection जिनके पास समान फिटनेस वाले व्यक्तियों के लिए फिटनेस आनुपातिक चयन से अधिक चयन दबाव है।
Fitness Sharing - इसमें एक व्यक्ति की फिटनेस कम हो जाती है अगर जनसंख्या में पहले से ही समान व्यक्ति शामिल हैं।
रेंडमाइजेशन मदद करता है!
यह प्रयोगात्मक रूप से देखा गया है कि सबसे अच्छे समाधान यादृच्छिक गुणसूत्रों द्वारा संचालित होते हैं क्योंकि वे जनसंख्या को विविधता प्रदान करते हैं। जीए कार्यान्वयनकर्ता को सबसे अच्छे परिणामों के लिए आबादी में यादृच्छिककरण और विविधता की पर्याप्त मात्रा रखने के लिए सावधान रहना चाहिए।
स्थानीय खोज के साथ GA को हाइब्रिड करें
स्थानीय खोज का उद्देश्य किसी दिए गए समाधान के पड़ोस में समाधानों की जाँच करना है ताकि बेहतर उद्देश्य मूल्यों की तलाश हो सके।
जीए को स्थानीय खोज के साथ संकरण करने के लिए यह कभी-कभी उपयोगी हो सकता है। निम्न छवि विभिन्न स्थानों को दिखाती है जिसमें जीए में स्थानीय खोज पेश की जा सकती है।

मापदंडों और तकनीकों का परिवर्तन
आनुवंशिक एल्गोरिदम में, "सभी आकार एक फिट बैठता है" या एक जादू सूत्र है जो सभी समस्याओं के लिए काम करता है। प्रारंभिक जीए तैयार होने के बाद भी, विशेष समस्या के अनुरूप लोगों को खोजने के लिए जनसंख्या आकार, म्यूटेशन और क्रॉसओवर प्रायिकता आदि जैसे मापदंडों के साथ खेलने में बहुत समय और प्रयास लगता है।
इस खंड में, हम आनुवंशिक एल्गोरिथम में कुछ उन्नत विषयों का परिचय देते हैं। जीए के लिए सिर्फ एक परिचय की तलाश में एक पाठक इस अनुभाग को छोड़ना चुन सकता है।
विवश अनुकूलन समस्याएँ
विवश ऑप्टिमाइज़ेशन समस्याएँ उन ऑप्टिमाइज़ेशन समस्याएँ हैं जिनमें हमें किसी दिए गए ऑब्जेक्टिव फंक्शन वैल्यू को अधिकतम या कम करना पड़ता है जो कुछ बाधाओं के अधीन होता है। इसलिए, समाधान स्थान में सभी परिणाम संभव नहीं हैं, और समाधान स्थान में संभव क्षेत्र होते हैं जैसा कि निम्नलिखित छवि में दिखाया गया है।

ऐसे परिदृश्य में, क्रॉसओवर और म्यूटेशन ऑपरेटर हमें समाधान दे सकते हैं जो कि संभव हैं। इसलिए, विवश अनुकूलन समस्याओं से निपटने के लिए अतिरिक्त तंत्र को GA में नियोजित किया जाना चाहिए।
सबसे आम तरीकों में से कुछ हैं -
का उपयोग करते हुए penalty functions जो व्यावहारिक समाधानों की फिटनेस को कम कर देता है, अधिमानतः ताकि फिटनेस का उल्लंघन करने वाले बाधाओं की संख्या या संभव क्षेत्र से दूरी के अनुपात में कम हो।
का उपयोग करते हुए repair functions जो एक संक्रामक समाधान लेते हैं और इसे संशोधित करते हैं ताकि उल्लंघन की गई बाधाओं को संतुष्ट किया जा सके।
Not allowing infeasible solutions आबादी में प्रवेश करने के लिए।
का उपयोग special representation or decoder functions यह समाधान की व्यवहार्यता सुनिश्चित करता है।
मूल सैद्धांतिक पृष्ठभूमि
इस खंड में, हम बिल्डिंग ब्लॉक परिकल्पना के साथ स्कीमा और एनएफएल प्रमेय के बारे में चर्चा करेंगे।
स्कीमा प्रमेय
शोधकर्ता आनुवंशिक एल्गोरिदम के काम करने के पीछे गणित का पता लगाने की कोशिश कर रहे हैं, और हॉलैंड के स्कीमा प्रमेय उस दिशा में एक कदम है। स्कीम थ्योरम को और अधिक सामान्य बनाने के लिए वर्ष के विभिन्न सुधारों और सुझावों पर काम किया गया है।
इस खंड में, हम स्कीमा प्रमेय के गणित में नहीं आते हैं, बल्कि हम स्कीमा प्रमेय क्या है की एक बुनियादी समझ विकसित करने की कोशिश करते हैं। जानने के लिए मूल शब्दावली इस प्रकार है -
ए Schemaएक "टेम्पलेट" है। औपचारिक रूप से, यह वर्णमाला = {0,1, *} पर एक स्ट्रिंग है,
जहां * परवाह नहीं है और कोई भी मूल्य ले सकता है।
इसलिए, * 10 * 1 का मतलब 01001, 01011, 11001 या 11011 हो सकता है
ज्यामितीय रूप से, एक स्कीमा समाधान खोज स्थान में एक हाइपर-प्लेन है।
Order एक स्कीमा एक जीन में निर्दिष्ट निश्चित पदों की संख्या है।

Defining length जीन में दो सबसे प्यारे तय प्रतीकों के बीच की दूरी है।

स्कीमा प्रमेय में कहा गया है कि औसत फिटनेस, कम परिभाषित लंबाई और निचले क्रम के ऊपर यह स्कीमा क्रॉसओवर और म्यूटेशन से बचने की अधिक संभावना है।
बिल्डिंग ब्लॉक परिकल्पना
बिल्डिंग ब्लॉक निम्न क्रम हैं, ऊपर दी गई औसत फिटनेस के साथ कम परिभाषित लंबाई स्कीमाटा। बिल्डिंग ब्लॉक की परिकल्पना का कहना है कि इस तरह के बिल्डिंग ब्लॉक GAs में GA की सफलता और अनुकूलन की नींव के रूप में काम करते हैं क्योंकि यह क्रमिक रूप से "बिल्डिंग ब्लॉक" की पहचान और पुनर्संयोजन द्वारा प्रगति करता है।
नो फ्री लंच (एनएफएल) प्रमेय
1997 में वोल्परट और मैक्रिड ने "ऑप्टिमाइज़ेशन के लिए नो फ्री लंच थ्योरीज़" शीर्षक से एक पेपर प्रकाशित किया। यह अनिवार्य रूप से बताता है कि यदि हम सभी संभावित समस्याओं के स्थान पर औसत रखते हैं, तो सभी गैर-परिकल्पित ब्लैक बॉक्स एल्गोरिदम एक ही प्रदर्शन का प्रदर्शन करेंगे।
इसका मतलब यह है कि जितना अधिक हम किसी समस्या को समझते हैं, हमारा GA अधिक समस्या विशिष्ट हो जाता है और बेहतर प्रदर्शन देता है, लेकिन यह अन्य समस्याओं के लिए खराब प्रदर्शन करके इसके लिए बनाता है।
जीए आधारित मशीन लर्निंग
जेनेटिक एल्गोरिदम भी मशीन लर्निंग में आवेदन पाते हैं। Classifier systems का एक रूप हैं genetics-based machine learning(GBML) प्रणाली जो अक्सर मशीन सीखने के क्षेत्र में उपयोग की जाती है। GBML विधियाँ मशीन लर्निंग का एक आला तरीका है।
GBML सिस्टम की दो श्रेणियां हैं -
The Pittsburg Approach - इस दृष्टिकोण में, एक गुणसूत्र एक समाधान को इनकोड करता है, और इसलिए फिटनेस को समाधानों को सौंपा जाता है।
The Michigan Approach - एक समाधान को आमतौर पर कई गुणसूत्रों द्वारा दर्शाया जाता है और इसलिए फिटनेस को आंशिक समाधानों के लिए सौंपा जाता है।
यह ध्यान में रखा जाना चाहिए कि मानक मुद्दा जैसे क्रॉसओवर, म्यूटेशन, लैमार्कियन या डार्विनियन, आदि जीबीएमएल सिस्टम में भी मौजूद हैं।
जेनेटिक एल्गोरिदम का उपयोग मुख्य रूप से विभिन्न प्रकार की अनुकूलन समस्याओं में किया जाता है, लेकिन उनका उपयोग अक्सर अन्य एप्लिकेशन क्षेत्रों में भी किया जाता है।
इस खंड में, हम कुछ ऐसे क्षेत्रों को सूचीबद्ध करते हैं जिनमें जेनेटिक एल्गोरिदम का अक्सर उपयोग किया जाता है। ये हैं -
Optimization- जेनेटिक एल्गोरिदम का उपयोग आमतौर पर अनुकूलन समस्याओं में किया जाता है जिसमें हमें किसी दिए गए उद्देश्य फ़ंक्शन मान को किसी दिए गए अवरोध के तहत अधिकतम या कम करना पड़ता है। ऑप्टिमाइज़ेशन समस्याओं को हल करने के दृष्टिकोण को पूरे ट्यूटोरियल में हाइलाइट किया गया है।
Economics - जीएबी का उपयोग विभिन्न आर्थिक मॉडल जैसे कोबवे मॉडल, गेम सिद्धांत संतुलन संकल्प, परिसंपत्ति मूल्य निर्धारण, आदि की विशेषता के लिए भी किया जाता है।
Neural Networks - GA का उपयोग तंत्रिका नेटवर्क, विशेष रूप से आवर्तक तंत्रिका नेटवर्क को प्रशिक्षित करने के लिए भी किया जाता है।
Parallelization - जीएएस में भी बहुत अच्छी समानांतर क्षमताएं हैं, और कुछ समस्याओं को हल करने में बहुत प्रभावी साधन साबित होते हैं, और अनुसंधान के लिए एक अच्छा क्षेत्र भी प्रदान करते हैं।
Image Processing - जीएएस का उपयोग विभिन्न डिजिटल इमेज प्रोसेसिंग (डीआईपी) कार्यों के साथ-साथ घने पिक्सेल मिलान के लिए किया जाता है।
Vehicle routing problems - कई सॉफ्ट टाइम विंडो, मल्टीपल डिपो और विषम बेड़े के साथ।
Scheduling applications - GA का उपयोग विभिन्न समय-निर्धारण समस्याओं के समाधान के लिए किया जाता है, विशेष रूप से समय सारणी समस्या।
Machine Learning - जैसा कि पहले ही चर्चा है, जेनेटिक्स आधारित मशीन लर्निंग (GBML) मशीन लर्निंग का एक आला क्षेत्र है।
Robot Trajectory Generation - जीएएस का इस्तेमाल उस रास्ते की योजना बनाने के लिए किया गया है, जो एक हाथ से दूसरे बिंदु पर जाकर एक रोबोट बांह लेता है।
Parametric Design of Aircraft - GAs का उपयोग मापदंडों को अलग करके और बेहतर समाधान विकसित करके हवाई जहाजों को डिजाइन करने के लिए किया गया है।
DNA Analysis - नमूने के बारे में स्पेक्ट्रोमेट्रिक डेटा का उपयोग करके डीएनए की संरचना का निर्धारण करने के लिए GA का उपयोग किया गया है।
Multimodal Optimization - जीएएस मल्टीमॉडल अनुकूलन के लिए स्पष्ट रूप से बहुत अच्छे दृष्टिकोण हैं जिसमें हमें कई इष्टतम समाधान खोजने होंगे।
Traveling salesman problem and its applications - टीएएसपी को हल करने के लिए जीए का उपयोग किया गया है, जो उपन्यास क्रॉसओवर और पैकिंग रणनीतियों का उपयोग करते हुए एक प्रसिद्ध दहनशील समस्या है।
निम्नलिखित पुस्तकों को जेनेटिक एल्गोरिदम के पाठक के ज्ञान को बढ़ाने के लिए संदर्भित किया जा सकता है, और सामान्य रूप में विकासवादी संगणना -
खोज, अनुकूलन और मशीन लर्निंग में आनुवंशिक एल्गोरिथम David E. Goldberg।
आनुवंशिक एल्गोरिथम + डेटा संरचनाएं = विकासवादी कार्यक्रम Zbigniew Michalewicz।
द्वारा व्यावहारिक आनुवंशिक एल्गोरिदम Randy L. Haupt तथा Sue Ellen Haupt।
मल्टी ऑब्जेक्टिव ऑप्टिमाइज़ेशन बाय इवोल्यूशनरी अल्गोरिद्म का उपयोग करके Kalyanmoy Deb।