अंकगणित सर्किट
पिछले अध्याय में, हमने op-amp के मूल अनुप्रयोगों के बारे में चर्चा की। ध्यान दें कि वे एक op-amp के रैखिक संचालन के तहत आते हैं। इस अध्याय में, हम अंकगणित सर्किट के बारे में चर्चा करते हैं, जो कि ऑप-एम्प के रैखिक अनुप्रयोग भी हैं।
इलेक्ट्रॉनिक सर्किट, जो अंकगणितीय संचालन करते हैं, को कहा जाता है arithmetic circuits। Op-amps का उपयोग करके, आप बुनियादी अंकगणितीय सर्किट जैसे कि एक का निर्माण कर सकते हैंadder और एक subtractor। इस अध्याय में, आप उनमें से प्रत्येक के बारे में विस्तार से जानेंगे।
एडर
एक योजक एक इलेक्ट्रॉनिक सर्किट है जो एक आउटपुट का उत्पादन करता है, जो लागू इनपुट के योग के बराबर है। यह खंड op-amp आधारित योजक सर्किट के बारे में चर्चा करता है।
एक ऑप-एम्पी आधारित योजक इसके इनवर्टिंग टर्मिनल पर लगाए गए इनपुट वोल्टेज के योग के बराबर एक आउटपुट का उत्पादन करता है। इसे ए भी कहा जाता हैsumming amplifier, क्योंकि उत्पादन एक प्रवर्धित है।
circuit diagram एक सेशन-एम्पी आधारित योजक निम्नलिखित आकृति में दिखाया गया है -
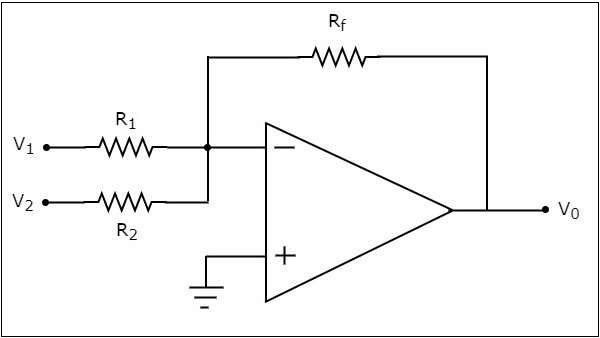
उपरोक्त सर्किट में, ऑप-एम्प का नॉन-इनवर्टिंग इनपुट टर्मिनल जमीन से जुड़ा हुआ है। इसका मतलब है कि शून्य वोल्ट इसके गैर-इनवर्टिंग इनपुट टर्मिनल पर लागू होता है।
के मुताबिक virtual short concept, सेशन-एम्पी के इनवर्टिंग इनपुट टर्मिनल पर वोल्टेज अपने नॉन-इनवर्टिंग इनपुट टर्मिनल पर वोल्टेज के समान होता है। तो, ऑप-एम्प के इनवर्टिंग इनपुट टर्मिनल पर वोल्टेज शून्य वोल्ट होगा।
nodal equation inverting इनपुट टर्मिनल का नोड है
$$ \ frac {0-V_1} {R_1} + \ frac {0-V_2} {R_2} + \ frac {0-V_0} {} R_f = 0 $$
$$ => \ frac {V_1} {R_1} - \ frac {V_2} {} R_2 = \ frac {V_0} {} R_f $$
$$ => V_ {0} = r_ {च} \ छोड़ दिया (\ frac {V_1} {R_1} + \ frac {V_2} {R_2} \ right) $$
यदि $ R_ {f} = R_ {1} = R_ {2} = R $ है, तो आउटपुट वोल्टेज $ V_ {0} $ होगा -
$$ V_ {0} = - आर {} \ छोड़ दिया (\ frac {V_1} {R} + \ frac {V_2} {आर} \ right) $$
$$ => V_ {0} = - (V_ {1} + V_ {2}) $$
इसलिए, ऊपर चर्चा की गई op-amp आधारित योजक सर्किट ऊपर दो इनपुट वोल्टेज का योग उत्पन्न करेगा v_ {1} $ और $ v_ {1} $, आउटपुट के रूप में, जब सर्किट में मौजूद सभी प्रतिरोध समान मूल्य के होते हैं । ध्यान दें कि आउटपुट वोल्टेज $ V_ {0} $ एक योजक सर्किट का हैnegative sign, जो इंगित करता है कि इनपुट और आउटपुट के बीच 180 0 चरण का अंतर मौजूद है ।
subtractor
एक सबट्रैक्टर एक इलेक्ट्रॉनिक सर्किट है जो आउटपुट का उत्पादन करता है, जो कि लागू इनपुट के अंतर के बराबर है। यह खंड op-amp- आधारित सबट्रैक्टर सर्किट के बारे में चर्चा करता है।
एक सेशन-एम्पी आधारित सबट्रैक्टर अपने inverting और नॉन-इनवर्टिंग टर्मिनलों पर लगाए गए इनपुट वोल्टेज के अंतर के बराबर आउटपुट उत्पन्न करता है। इसे ए भी कहा जाता हैdifference amplifier, क्योंकि उत्पादन एक प्रवर्धित है।
circuit diagram एक op-amp- आधारित सबट्रैक्टर को निम्न आकृति में दिखाया गया है -
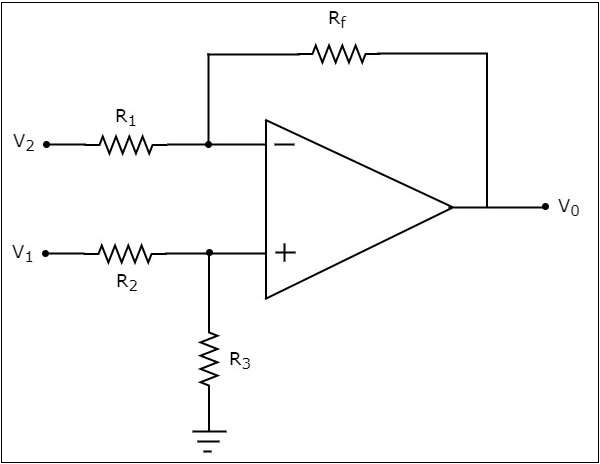
अब, ऊपर दिए गए सर्किट का उपयोग करके आउटपुट वोल्टेज $ V_ {0} $ के लिए अभिव्यक्ति पाते हैं superposition theorem निम्नलिखित चरणों का उपयोग कर -
चरण 1
सबसे पहले, हम केवल $ V_ {1} $ पर विचार करके आउटपुट वोल्टेज $ V_ {01} $ की गणना करते हैं।
इसके लिए, शॉर्ट सर्किट करके $ V_ {2} $ को खत्म करें। तब हम प्राप्त करते हैंmodified circuit diagram जैसा कि निम्नलिखित आकृति में दिखाया गया है -

अब, का उपयोग कर voltage division principle, ऑप-एम्प के गैर-इनवर्टिंग इनपुट टर्मिनल पर वोल्टेज की गणना करें।
$$ => V_ {पी} = V_ {1} \ छोड़ दिया (\ frac {R_3} {R_2 + R_3} \ right) $$
अब, उपरोक्त सर्किट इनपुट वोल्टेज $ V_ {p} $ वाले गैर-इनवर्टिंग एम्पलीफायर की तरह दिखता है। इसलिए, उपरोक्त सर्किट में आउटपुट वोल्टेज $ V_ {01} $ होगा
$$ V_ {01} = V_ {पी} \ छोड़ दिया (1 + \ frac {R_f} {R_1} \ right) $$
स्थानापन्न, $ V_ {p} $ के मूल्य से ऊपर के समीकरण में, हम आउटपुट वोल्टेज $ V_ {01} $ केवल $ V_ {1} $, पर विचार करके प्राप्त करते हैं, जैसे -
$$ V_ {01} = V_ {1} \ छोड़ दिया (\ frac {R_3} {R_2 + R_3} \ right) \ छोड़ दिया (1 + \ frac {R_f} {R_1} \ right) $$
चरण 2
इस चरण में, हम केवल $ V_ {2} $ पर विचार करके आउटपुट वोल्टेज, $ V_ {02} $ पाते हैं। उपरोक्त चरण के समान, इसे शॉर्ट सर्किट बनाकर $ V_ {1} $ को समाप्त करें। modified circuit diagram निम्नलिखित आकृति में दिखाया गया है।

आप देख सकते हैं कि ऑप-एम्प के नॉन-इनवर्टिंग इनपुट टर्मिनल पर वोल्टेज शून्य वोल्ट होगा। इसका मतलब है, उपरोक्त सर्किट बस एक हैinverting op-amp। इसलिए, उपरोक्त सर्किट का आउटपुट वोल्टेज $ V_ {02} $ होगा -
$$ V_ {02} = \ छोड़ दिया (- \ frac {R_f} {R_1} \ right) V_ {2} $$
चरण 3
इस चरण में, हम सबट्रैक्टर सर्किट के आउटपुट वोल्टेज $ V_ {0} $ प्राप्त करेंगे adding the output voltagesStep1 और Step2 में प्राप्त किया। गणितीय रूप से, इसे लिखा जा सकता है
$$ V_ {0} = V_ {01} + V_ {02} $$
उपरोक्त समीकरण में $ V_ {01} $ और $ V_ {02} $ के मूल्यों को प्रतिस्थापित करते हुए, हम प्राप्त करते हैं -
$$ V_ {0} = V_ {1} \ छोड़ दिया (\ frac {R_3} {R_2 + R_3} \ right) \ छोड़ दिया (1 + \ frac {R_f} {R_1} \ right) + \ छोड़ दिया (- \ frac {} {R_f R_1} \ right) V_ {2} $$
$$ => V_ {0} = V_ {1} \ छोड़ दिया (\ frac {R_3} {R_2 + R_3} \ right) \ छोड़ दिया (1 + \ frac {R_f} {R_1} \ right) - \ छोड़ दिया (\ frac {R_f} {R_1} \ right) V_ {2} $$
यदि $ R_ {f} = R_ {1} = R_ {2} = R_ {3} = R $ है, तो आउटपुट वोल्टेज $ V_ {0} $ होगा
$$ V_ {0} = V_ {1} \ छोड़ दिया (\ frac {आर} {आर + आर} \ right) \ छोड़ दिया (1 + \ frac {R} {R} \ right) - \ छोड़ दिया (\ frac { आर} {आर} \ right) V_ {2} $$
$$ => V_ {0} = V_ {1} \ छोड़ दिया (\ frac {आर} {2R} \ right) (2) - (1) V_ {2} $$
$$ V_ {0} = V_ {1} -V_ {2} $$
इस प्रकार, ऊपर चर्चा की गई ऑप-एम्पी आधारित सबट्रैक्टर सर्किट एक आउटपुट का उत्पादन करेगा, जो दो इनपुट वोल्टेज $ V_ {1} $ और $ V_ {2} $ का अंतर है, जब सर्किट में मौजूद सभी प्रतिरोध समान मूल्य के होते हैं ।